Как найти вершину равнобедренного треугольника формула - Исправление недочетов и поиск решений вместе с Examum.ru

Как находить высоту в равнобедренном треугольнике? Формула нахождения, свойства высоты в равнобедренном треугольнике

Геометрия – это не только предмет в школе, по которому нужно получить отличную оценку. Это еще и знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей необходимо рассчитать толщину бревен и их количество. Это несложно, если знать, как находить высоту в равнобедренном треугольнике. Архитектурные сооружения базируются на знании свойств геометрических фигур. Формы зданий зачастую визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северные росписи и даже пирожки – это все треугольники, окружающие человека. Как говорил Платон, весь мир базируется на треугольниках.

Равнобедренный треугольник

Чтобы было понятнее, о чем далее пойдет речь, стоит немного вспомнить азы геометрии.

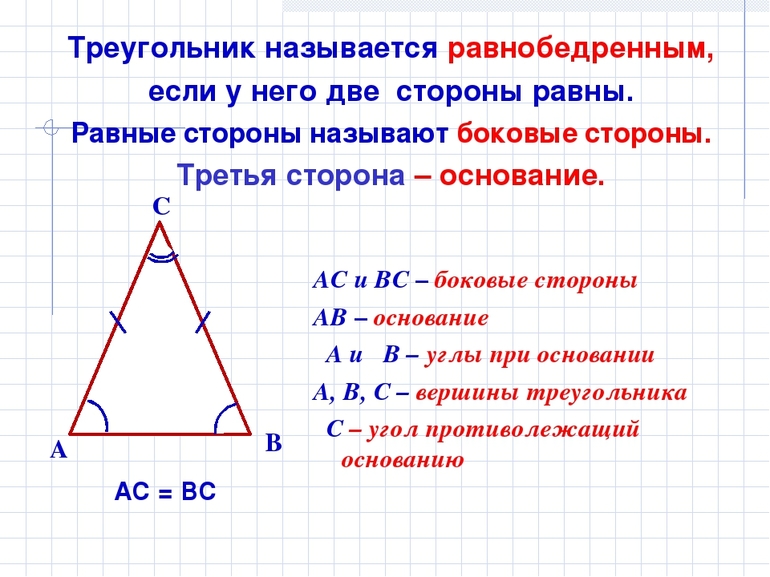
Треугольник является равнобедренным, если он имеет две равных стороны. Их всегда называют боковыми. Сторона, размеры которой отличаются, получила название основания.

Основные понятия

Как и любая наука, геометрия имеет свои основные правила и понятия. Их достаточно много. Рассмотрим лишь те, без которых наша тема будет несколько непонятна.

Высота – это прямая линия, проведенная перпендикулярно к противоположной стороне.

Медиана – это отрезок, направленный из любой вершины треугольника исключительно к середине противоположной стороны.

Биссектриса угла – это луч, разделяющий угол пополам.

Биссектриса треугольника – это прямая, вернее, отрезок биссектрисы угла, соединяющий вершину с противоположной стороной.

Очень важно запомнить, что биссектриса угла – это обязательно луч, а биссектриса треугольника – это часть такого луча.

Углы при основании

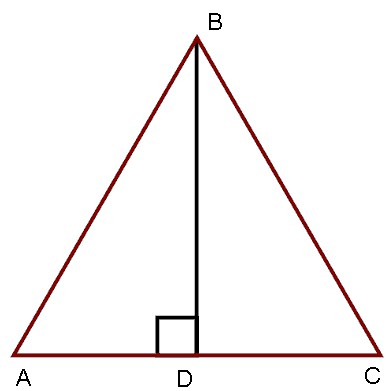
Теорема гласит, что углы, расположенные при основании любого равнобедренного треугольника, всегда равны. Доказать эту теорему очень просто. Рассмотрим изображенный равнобедренный треугольник АВС, у которого АВ=ВС. Из угла АВС необходимо провести биссектрису ВД. Теперь следует рассмотреть два полученных треугольника. По условию АВ=ВС, сторона ВД у треугольников общая, а углы АВД и СВД равны, ведь ВД – биссектриса. Вспомнив первый признак равенства, можно смело заключить, что рассматриваемые треугольники равны. А следовательно, равны все соответствующие углы. И, конечно, стороны, но к этому моменту вернемся позже.

Высота равнобедренного треугольника

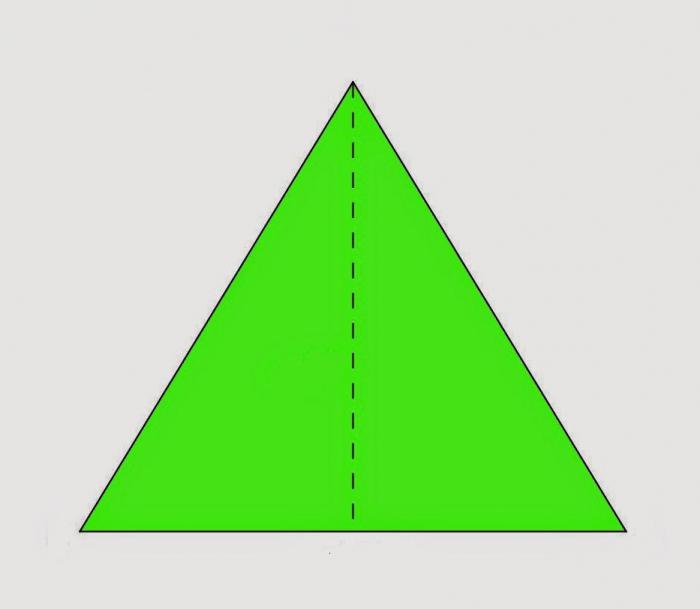
Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой. Чтобы понять её практический смысл (или суть), следует сделать вспомогательное пособие. Для этого необходимо вырезать из бумаги равнобедренный треугольник. Легче всего это сделать из обычного тетрадного листка в клеточку.

Согните полученный треугольник пополам, совместив боковые стороны. Что получилось? Два равных треугольника. Теперь следует проверить догадки. Разверните полученное оригами. Прочертите линию сгиба. При помощи транспортира проверьте угол между прочерченной линией и основанием треугольника. О чем говорит угол в 90 градусов? О том, что прочерченная линия – перпендикуляр. По определению – высота. Как находить высоту в равнобедренном треугольнике, мы разобрались. Теперь займемся углами при вершине. При помощи того же транспортира проверьте углы, образованные теперь уже высотой. Они равны. Значит, высота одновременно является и биссектрисой. Вооружившись линейкой, измерьте отрезки, на которые разбивает высота основание. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.

Доказательство теоремы

Наглядное пособие ярко демонстрирует истинность теоремы. Но геометрия – наука достаточно точная, поэтому требует доказательств.

Во время рассмотрения равенства углов при основании было доказано равенство треугольников. Напомним, ВД – биссектриса, а треугольники АВД и СВД равны. Вывод был таков: соответствующие стороны треугольника и, естественно, углы равны. Значит, АД = СД. Следовательно, ВД – медиана. Осталось доказать, что ВД является высотой. Исходя из равенства рассматриваемых треугольников, получается, что угол АДВ равен углу СДВ. Но эти два угла являются смежными, и, как известно, дают в сумме 180 градусов. Следовательно, чему они равны? Конечно, 90 градусам. Таким образом, ВД – это высота в равнобедренном треугольнике, проведенная к основанию. Что и требовалось доказать.

Основные признаки

Чтобы успешно решать задачи, следует запомнить основные признаки равнобедренных треугольников. Они как бы обратны теоремам.
Если в ходе решения задачи обнаруживается равенство двух углов, значит, вы имеете дело с равнобедренным треугольником.
Если удалось доказать, что медиана является одновременно и высотой треугольника, смело заключайте – треугольник равнобедренный.
Если биссектриса является и высотой, то, опираясь на основные признаки, треугольник относят к равнобедренным.
И, конечно, если медиана выступает и в роли высоты, то такой треугольник — равнобедренный.

Формула высоты 1

Однако для большинства задач требуется найти арифметическую величину высоты. Именно поэтому рассмотрим, как находить высоту в равнобедренном треугольнике.

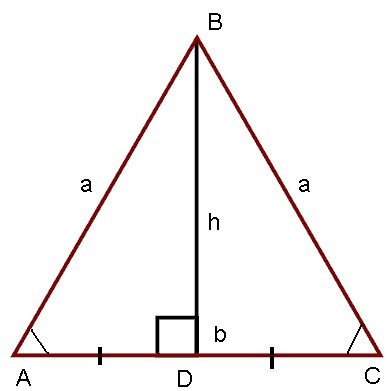
Вернемся к представленной выше фигуре АВС, у которой а – боковые стороны, в — основание. ВД – высота этого треугольника, она имеет обозначение h.

Что представляет собой треугольник АВД? Так как ВД – высота, то треугольник АВД – прямоугольный, катет которого необходимо найти. Воспользовавшись формулой Пифагора, получаем:

Определив из выражения ВД и подставив принятые ранее обозначения, получим:

Необходимо извлечь корень:

Если вынести из под знака корня ¼ , то формула будет иметь вид:

Так находится высота в равнобедренном треугольнике. Формула вытекает из теоремы Пифагора. Даже если забыть эту символическую запись, то, зная метод нахождения, всегда можно её вывести.

Формула высоты 2

Формула, описанная выше, является основной и чаще всего используется при решении большинства геометрических задач. Но она не единственная. Иногда в условии, вместо основания, дано значение угла. При таких данных как находить высоту в равнобедренном треугольнике? Для решения подобных задач целесообразно использовать другую формулу:

где Н – высота, направленная к основанию,

а – боковая сторона,

α – угол при основании.

Если в задаче дано значение угла при вершине, то высота в равнобедренном треугольнике находится следующим образом:

где Н – высота, опущенная на основание,,

β – угол при вершине,

а – боковая сторона.

Прямоугольный равнобедренный треугольник

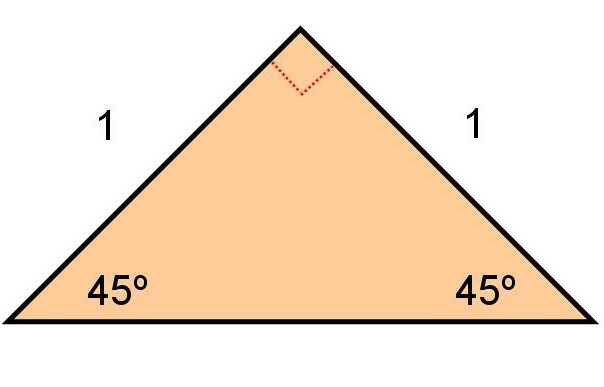
Очень интересным свойством обладает треугольник, вершина которого равна 90 градусам. Рассмотрим прямоугольный треугольник АВС. Как и в предыдущих случаях, ВД – высота, направленная к основанию.

Углы при основании равны. Вычислить их большого труда не составит:

Таким образом, углы, находящиеся при основании, всегда по 45 градусов. Теперь рассмотрим треугольник АДВ. Он также является прямоугольным. Найдем угол АВД. Путем несложных вычислений получаем 45 градусов. А, следовательно, этот треугольник не только прямоугольный, но и равнобедренный. Стороны АД и ВД являются боковыми сторонами и равны между собой.

Но сторона АД в то же время является половиной стороны АС. Получается, что высота в равнобедренном треугольнике равна половине основания, а если записать в виде формулы, то получим следующее выражение:

Следует не забывать, что данная формула является исключительно частным случаем, и может быть использована только для прямоугольных равнобедренных треугольников.

Золотые треугольники

Очень интересным является золотой треугольник. В этой фигуре отношение боковой стороны к основанию равняется величине, названной числом Фидия. Угол, расположенный при вершине — 36 градусов, при основании – 72 градуса. Этим треугольником восхищались пифагорейцы. Принципы золотого треугольника положены в основу множества бессмертных шедевров. Известная всем пятиконечная звезда построена на пересечении равнобедренных треугольников. Для многих творений Леонардо да Винчи использовал принцип «золотого треугольника». Композиция «Джоконды» основана как раз на фигурах, которые создают собой правильный звездчатый пятиугольник.

Картина «Кубизм», одно из творений Пабло Пикассо, завораживает взгляд положенными в основу равнобедренными треугольниками.

Угол при вершине равнобедренного треугольника

Как найти угол при вершине равнобедренного треугольника?

Каким может быть угол при вершине равнобедренного треугольника?

Найти угол при вершине равнобедренного треугольника, если угол при его основании равен α.

Дано: ∆ ABC,

∠A=∠C (как углы при основании равнобедренного треугольника).

Значит, α+∠B+α=180º, откуда ∠B=180º-2α.

1) Угол при вершине равнобедренного треугольника равен 180º минус удвоенный угол при его основании.

2) Чем больше угол при основании равнобедренного треугольника, тем меньше угол при его вершине.

3) Если угол при основании α=45º, угол при вершине равнобедренного треугольника — прямой, так как

Если угол при основании больше 45º, угол при вершине — острый, так как

при α>45º произведение 2α>90º, откуда 180º-2α 90º.

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

Если у треугольника два угла равны, то этот треугольник — равнобедренный.
Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

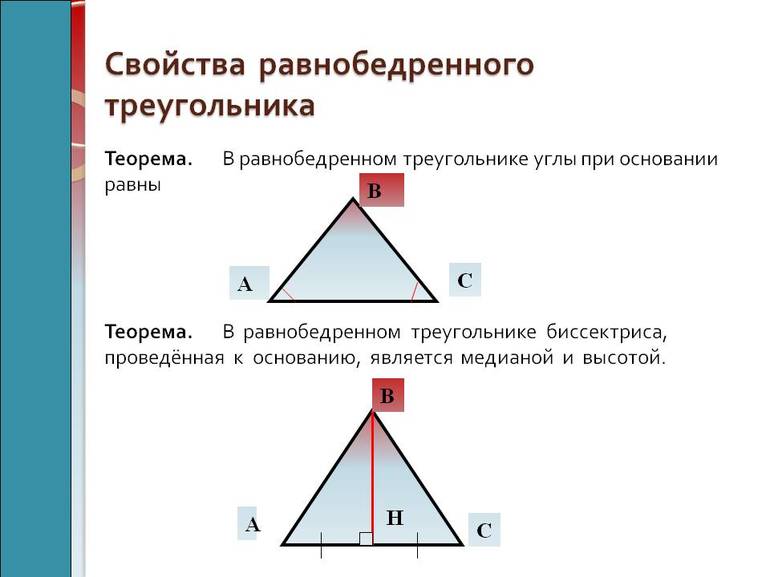
Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

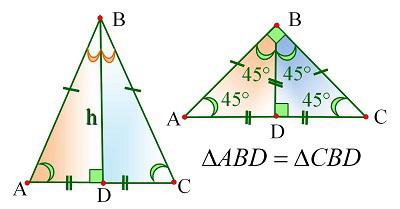
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

источники:

Угол при вершине равнобедренного треугольника

http://skysmart.ru/articles/mathematic/chto-takoe-ravnobedrennyj-treugolnik

Источник

Равнобедренный треугольник, свойства, признаки и формулы

Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.

Равнобедренный треугольник (понятие)

Свойства равнобедренного треугольника

Признаки равнобедренного треугольника

Формулы равнобедренного треугольника

Равнобедренный треугольник в природе, технике и культуре

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Равнобедренный треугольник (понятие):

Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.

Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.

Рис. 1. Равнобедренный треугольник

АВ = ВС – боковые стороны, АС – основание,

∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.

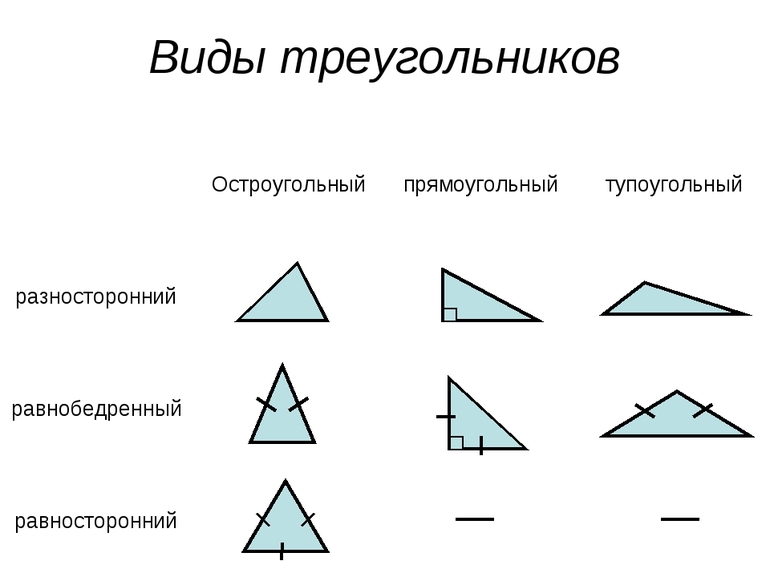
Различают следующие виды равнобедренных треугольников:

– остроугольный – все углы острые;

– прямоугольный – угол при вершине прямой, а при основании углы острые;

– тупоугольный – угол при вершине тупой, а при основании углы острые;

– равносторонний (или правильный) – все стороны равны и все углы равны.

Свойства равнобедренного треугольника:

1. В равнобедренном треугольнике углы при основании равны.

Рис. 2. Равнобедренный треугольник

∠ BАC = ∠ BСA

2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.

Рис. 3. Равнобедренный треугольник

АН₁ = СН₂ – высота, АМ₁ = СМ₂ – медиана, АL₁ = СL₂ – биссектриса, проведённые из углов при основании

3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Рис. 4. Равнобедренный треугольник

ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок

4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.

Рис. 5. Равнобедренный треугольник

R – радиус описанной окружности, r – радиус вписанной окружности

Признаки равнобедренного треугольника:

– если в треугольнике два угла равны, то он равнобедренный;

– если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;

– если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;

– если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.

Формулы равнобедренного треугольника:

Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).

Рис. 6. Равнобедренный треугольник

Формулы длины основания (b):

Формулы длины равных сторон (а):

Формулы углов:

Рис. 7. Равнобедренный треугольник

Формулы периметра (Р) равнобедренного треугольника:

Рис. 8. Равнобедренный треугольник

Формулы площади (S) равнобедренного треугольника:

Равнобедренный треугольник в природе, технике и культуре:

Например, молекула сероводорода имеет структуру равнобедренного треугольника с атомом серы S в центре.

Рис. 1. Структура молекулы сероводорода

Длина боковой стороны – связи HS = 133,6 пм, а вершинный угол ∠HSH = 92,1°.

Остроугольный треугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Тупоугольный треугольник

Примечание: © Фото https://www.pexels.com, https://pixabay.com

Коэффициент востребованности
9 708

Источник

Равнобедренный треугольник

Чтобы было понятнее, о чем далее пойдет речь, стоит немного вспомнить азы геометрии.

Основные понятия

Высота – это прямая линия, проведенная перпендикулярно к противоположной стороне.

Биссектриса угла – это луч, разделяющий угол пополам.

Углы при основании

Высота равнобедренного треугольника

Доказательство теоремы

Основные признаки

Чтобы успешно решать задачи, следует запомнить основные признаки равнобедренных треугольников. Они как бы обратны теоремам.
Если в ходе решения задачи обнаруживается равенство двух углов, значит, вы имеете дело с равнобедренным треугольником.
Если удалось доказать, что медиана является одновременно и высотой треугольника, смело заключайте – треугольник равнобедренный.
Если биссектриса является и высотой, то, опираясь на основные признаки, треугольник относят к равнобедренным.
И, конечно, если медиана выступает и в роли высоты, то такой треугольник — равнобедренный.

Формула высоты 1

АВ² = АД² + ВД²

Определив из выражения ВД и подставив принятые ранее обозначения, получим:

Н² = а² – (в/2)².

Необходимо извлечь корень:

Н = √а² – в²/4.

Если вынести из под знака корня ¼ , то формула будет иметь вид:

Н = ½ √4а² – в².

Формула высоты 2

Н = а/sin α,

где Н – высота, направленная к основанию,

а – боковая сторона,

α – угол при основании.

Н = а/cos (β/2),

где Н – высота, опущенная на основание,,

β – угол при вершине,

а – боковая сторона.

Прямоугольный равнобедренный треугольник

Углы при основании равны. Вычислить их большого труда не составит:

α = (180 – 90)/2.

Н = в/2.

Золотые треугольники

Источник

Общие сведения

Замкнутую фигуру, состоящую из трёх пересекающихся прямых и такого же количества внутренних углов, называют треугольником. Отрезки, которые соединяют точки, образующие фигуру, называют сторонами. Для обозначения используют малые латинские буквы. Точка, в которой соединяется 2 стороны, называется вершиной. Её принято подписывать заглавными буквами, например, A, B, C.

Существует несколько видов фигур по типу углов и по длинам сторон:

разносторонние — все отрезки, образующие многоугольник, имеют различную длину;
равнобедренные — 2 стороны одинаковы;
равносторонние — все 3 стороны равны;
остроугольными — 3 угла многоугольника являются острыми;
прямоугольными — 2 стороны образуют угол в 90 градусов;
тупоугольными — размер одного угла превышает 90 градусов.

Отличительная черта фигуры — сумма углов равняется 180 градусов. Это один из самых важных признаков, позволяющих отнести многоугольник к треугольникам. Причём каждая такая фигура имеет замечательные линии и точки.

Прежде всего это медиана — отрезок, построенный из вершины к центру противолежащей стороны, разделяющий фигуру на 2 равных треугольника. Биссектрисой называют линию, построенную к противоположной стороне и разделяющую угол на 2 равные части. Также можно опустить перпендикуляр на любую сторону из вершины. Называют такую линию высотой.

В треугольнике можно провести по 3 любых таких линии. Причём точка пересечения отрезков имеет своё название: 3 высоты встречаются в ортоцентре, а биссектрисы — инцентре. Если в треугольник вписать окружность, её центр совпадёт с местом пересечения медиан. Эта точка является центроидом, центром массы фигуры. Кроме этого, можно описать круг, в центре которого будут пересекаться серединные перпендикуляры.

Признаки равнобедренной фигуры

Существует 4 явления, с помощью которых можно определить принадлежность тела к треугольникам. Все они сгруппированы в 3 теоремы:

Если в треугольнике построить медиану, при этом она будет совпадать с высотой, он является равнобедренным. Аналогично можно утверждать о принадлежности фигуры к равнобедренному типу, когда биссектриса совпадает с высотой.
Если 2 угла равны, треугольник равнобедренный.
Если медиана и биссектриса совпадают, причём построены из одного угла, фигура называется равнобедренной.

Для доказательства первой теоремы нужно использовать признаки равенства треугольников. Если изобразить на чертеже фигуру ABC и из вершины B построить высоту, согласно заданным данным, она будет медианой или биссектрисой. В первом случае противоположная сторона будет разделена на 2 равные части AD и DC. Значит, треугольники ABD и DBC одинаковые. Отсюда следует, что у фигур есть равные стороны: AB = BC., то есть боковые грани имеют одинаковую длину, что и требуется по определению.

В случае с биссектрисой ход рассуждений будет такой же. Отличие заключается лишь в том, что используется второй признак равенства: если грань и 2 прилежащих к ней угла одного треугольника совпадают со стороной и двумя прилежащими к ней углам другого, они равны.

Доказательство второй теоремы следует построить на нахождении равных сторон. Для этого нужно отложить серединный перпендикуляр a и доказать, что линия будет проходить через вершину B. Если она не будет пересекать угол B, она касается AB или BC. Пусть точкой пересечения перпендикуляра будет M. Тогда по первому признаку AKM = CKM, значит, углы MCK и MAK также равны. По условию теоремы MCK = MAB → MAK = MAB, что противоречит аксиоме измерения углов. Отсюда можно утверждать, что серединный перпендикуляр не пересекает BC или AC. Значит, прямая проходит через вершину B.

Третью теорему легко можно доказать, отложив на луче BM равный ему по длине отрезок. Затем, соединив A и D, построить треугольник ADM. Углы ABM и ADM одинаковые. Отсюда AB = AD → AB = BC, что и требовалось доказать.

Свойства треугольника

Равнобедренный треугольник относится к особому виду многоугольника. Равные его стороны называют боковыми, а отличную от них — основанием. Любую фигуру можно охарактеризовать с помощью свойств.

Признаки позволяют определить, является ли фигура равнобедренной. Из сформулированной второй теоремы следует: каждая точка, лежащая на серединном перпендикуляре, будет равноудалённой от концов боковых отрезков. Из основных свойств равнобедренного треугольника можно выделить:

В равнобедренной фигуре лежащие при основании углы равны. Пусть имеется треугольник AB, в котором сторона AB=BC. Нужно доказать, что угол A=C. Можно построить биссектрису BD. Из первого признака равенства: ABD = CBD. Из этого следует, что соответствующие элементы в треугольниках одинаковые, то есть, угол A равен вершине C. Теорема доказана.
Биссектриса в равнобедренном треугольнике одновременно является медианой и высотой. Пусть есть фигура ABC, в которой AB = BC, а BD — биссектриса. Нужно доказать, что BD будет также высотой и медианой. Так как по условию дано, что 2 стороны равны, при этом BD — общая грань, угол ABD = CBD. Значит: ABD = CBD. Отсюда следует, что AD = DC, а точка D — середина отрезка AC. Следовательно BD — медиана.

А также из равенства треугольников следует, что ADB = CDB, а вершина ADC — развёрнутая. Её величина равна 180⁰. Значения углов, на которые она разбивается лучом DB, будет составлять 90⁰. Таким образом, ADB = CDB = 90⁰. Отрезок D перпендикулярен AC.

Из последнего свойства следует, что медиана является биссектрисой и высотой. Находящиеся при основании углы в равнобедренном треугольнике можно вычислить по формуле: ACB = BCA = 90⁰ — CAB/2, где CAB — вершина, расположенная напротив основания.

Из указанных свойств следует, что точка пересечения любых замечательных линий одновременно является ортоцентром, инцентром и центром тяжести фигуры. Это важное замечание, позволяющее вычислять параметры с помощью окружности, описываемой вокруг треугольника.

Формулы и пример задания

Правильный треугольник, где все 3 стороны равны, является частным случаем равнобедренного, поэтому все формулы для поиска параметров будут одинаковыми. Самым часто используемым выражением, применяемым на уроках, является формула для поиска площади: S = (b * h)/2, где: b – основание, h – высота. Существует и более сложное равенство, позволяющее определить S, зная размеры двух прилежащих сторон: S = (b * √(a2 – (b2 / 4)) / 2.

Кроме поиска площади фигуры, в треугольнике можно вычислить:

Периметр. Сумма всех сторон: P = a + b + c = 2ab + c.
Высоту (медиану, биссектрису), проведённую к основанию: h ²= b ²− a ²/ 4.
Соотношения между боковыми сторонами и основанием: b = 2 a*cos ( α ) , b = 2 a*sin ( β / 2).
Стороны. Они могут быть найдены с помощью формул, выражающих их размер через другие грани и углы, значения которых известны: a = b/(2 * cos ( a )); b = a * √ (2 * (1 – cos ( b )).
Радиус вписанной окружности. Его можно определить, зная основание и высоту: r = ( b * h )/b+* √ (4h + b ²); размеры боковых сторон: r = (b/2)*tg (a/2); боковые стороны и угол между ними: r = a*cos (a)*tg (a/2).
Радиус описанного круга. Его можно найти, зная длину боковой стороны и основания по формуле: R = b/2√((2a-b)/(2a+b)).

Формулы, признаки и свойства равнобедренного треугольника важны для геометрии. Используя их, можно решать сложные задачи, связанные с многогранниками различных видов.

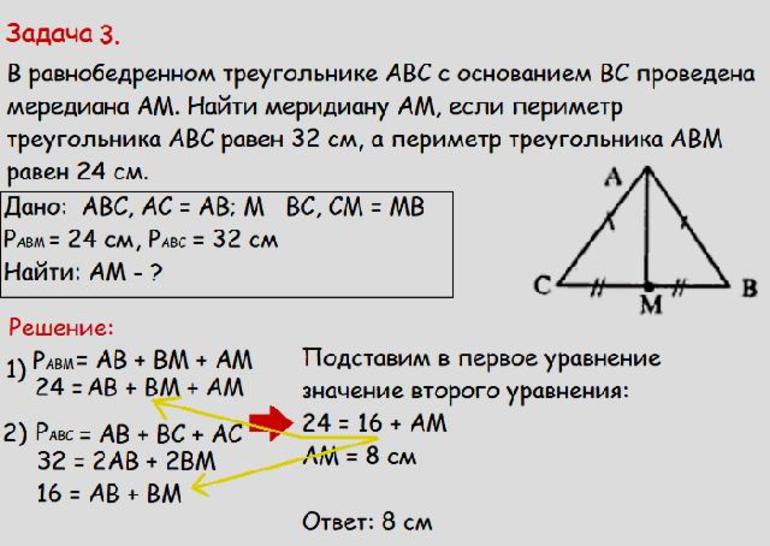
Пусть имеется равнобедренный треугольник ABC, в котором построена медиана BM. Известно, что периметр всего многоугольника 32, а фигуры ABM — 24. Нужно вычислить длину высоты. Следует понимать, что в равнобедренной фигуре медиана является высотой и биссектрисой. Сторону AB можно принять за X. Соответственно, противоположная сторона BC будет тоже равняться X. Из свойств треугольника AC разделяется в точке M на 2 одинаковых отрезка. Пусть каждый из них будет равняться Y.

По условию периметр ABC = 32, значит: 2x + 2 y = 32. Обе части равенства можно разделить на 2. В результате получится, что сумма AB и AM составляет 16. Так как периметр треугольника ABM=24, то BM = P – 16 = 24 – 16 = 8. Задача решена: длина высоты, построенная в ABC, будет равняться 8.

Источник

Доказательство равенства треугольников

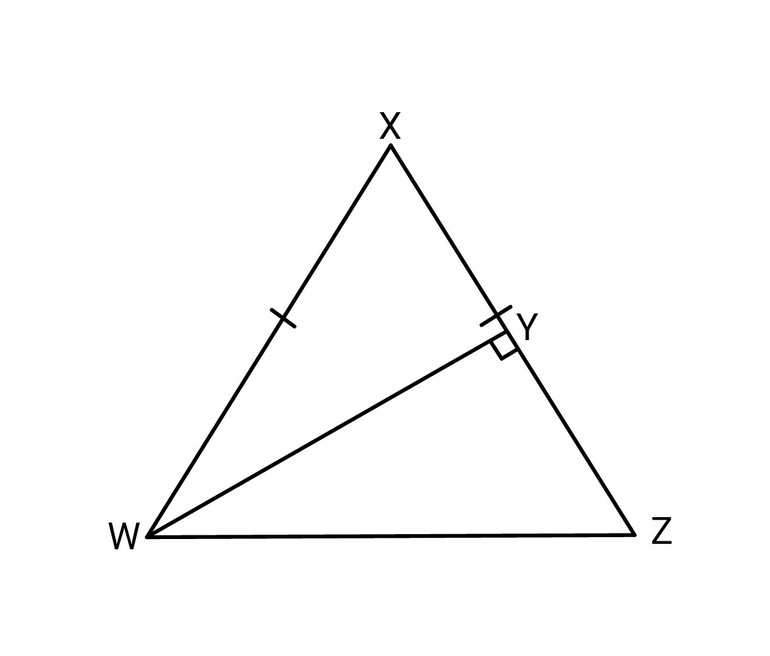
Посмотри внимательно, у нас есть:

( displaystyle underbrace{AB}_{гипотенуза в Delta ABH}=underbrace{BC}_{гипотенуза в Delta СBH})
( displaystyle BHtext{ }=text{ }BH) (ещё говорят, ( displaystyle BH)— общая)

И, значит, ( displaystyle AHtext{ }=text{ }CH)!

Почему?

Да мы просто найдём и ( displaystyle AH), и ( displaystyle CH) из теоремы Пифагора (помня ещё при этом, что ( displaystyle AB=BC))

( displaystyle AH=sqrt{A{{B}^{2}}-B{{H}^{2}}})

( displaystyle CH=sqrt{B{{C}^{2}}-B{{H}^{2}}})

Удостоверились? Ну вот, теперь у нас

( displaystyle begin{array}{l}AB=BC\BH=BH\AH=CHend{array})

А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.

Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.

Отметим на картинке все одинаковые элементы (углы и стороны).

vysota v ravnobedrennom treugolnike i ravnye treugolniki

Видишь, как интересно? Получилось, что:

В равнобедренном треугольнике углы при основании равны: ( displaystyle angle A=angle C);
Высота, проведенная к основанию ( displaystyle (ВH)), совпадает с медианой и биссектрисой
( displaystyle AH=CH)
( displaystyle angle 1=angle 2).

Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – делит угол.)

Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник.

Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.

И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?

То есть, как говорят математики, каковы признаки равнобедренного треугольника?

Источник