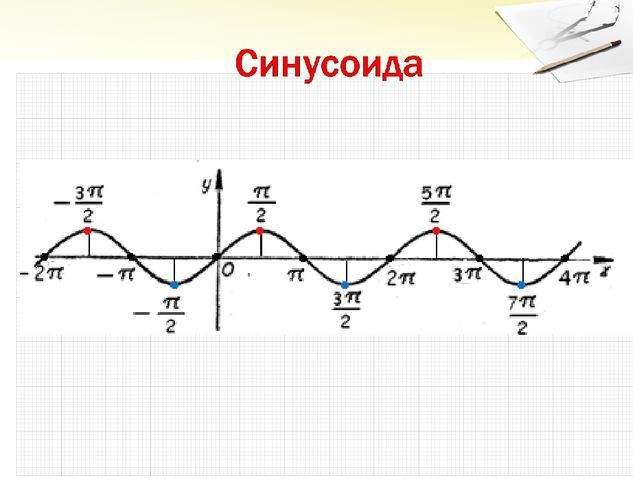
Основные понятия
Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:
- a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
- b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
- c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
- d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).
Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.
Особенности построения
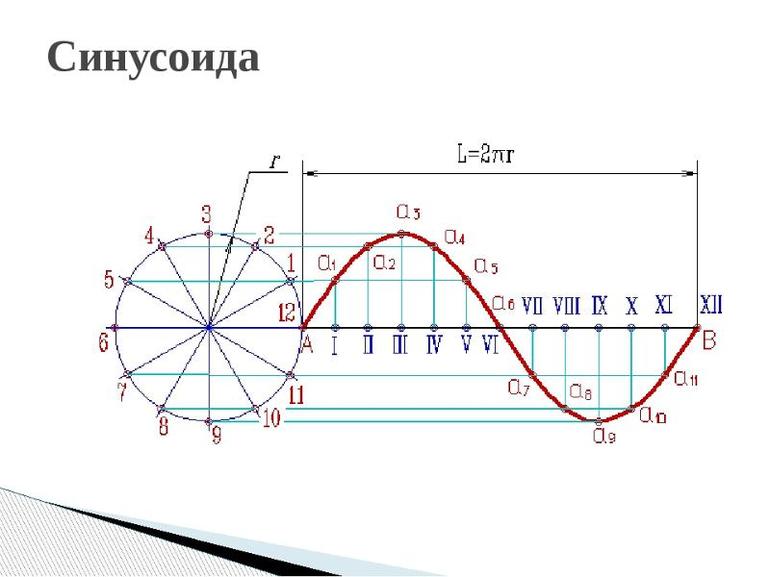
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:
- проводится горизонтальная ось, на которой откладывается заданная длина волны;
- отрезок делится на равные части;
- слева чертится окружность с радиусом, равным величине амплитуды;
- окружность делится на 12 одинаковых частей;
- через полученные точки проводятся прямые;
- из точек проводятся перпендикуляры к оси.
График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.
Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:
- размах;
- растяжение/сжатие;
- фазовые колебания;
- круговая частота.
При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:
- А (а) — модуль неизвестной (расстояние от начала координат до точки А);
- w — угловая частота;
- t — время.
Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.
Свойства и доказательства
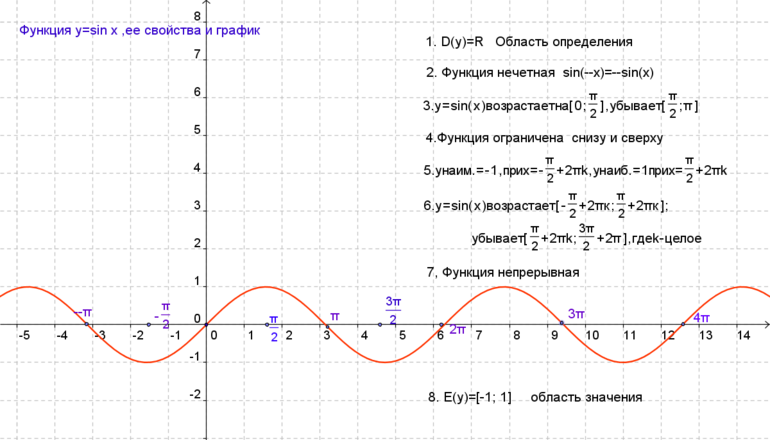
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.
Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.
Значения ординаты единичной окружности (ЕД) расположены на отрезке [—1; 1]. Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.
Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.
Нечётность и постоянство
Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.
Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.
Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.
Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.
Больше и меньше
С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.
Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.
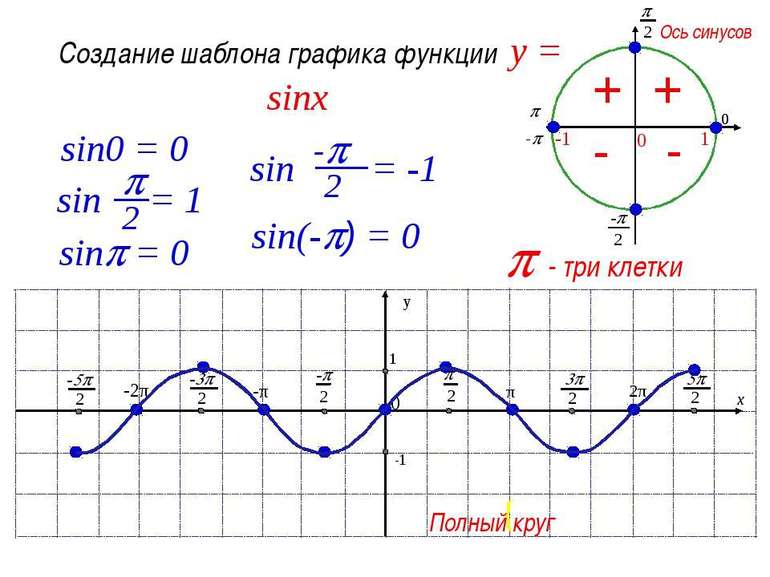
Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.
Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.
Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.
22
Окт 2013
Категория: Справочные материалыФункции и графики
Графики тригонометрических функций. Синусоида
2013-10-22
2019-09-21
Смешное видео по теме
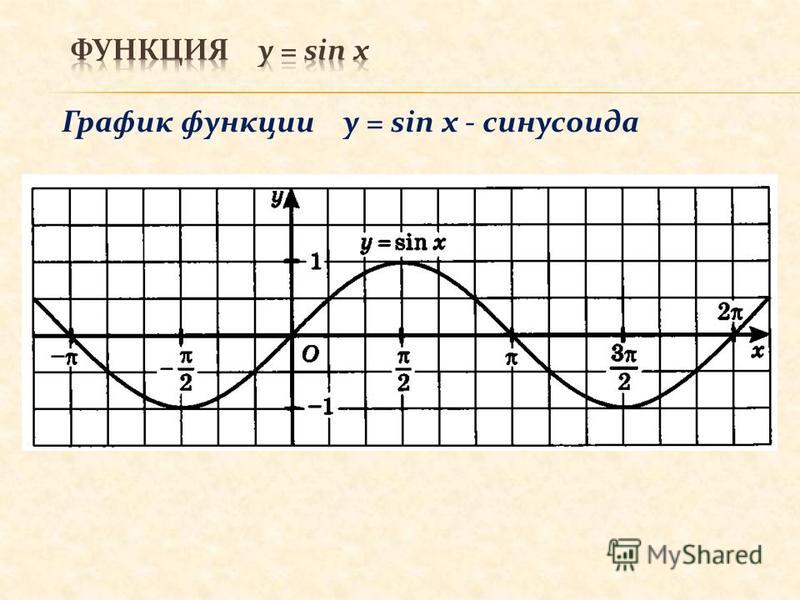
График функции y=sinx
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на
Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.
Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
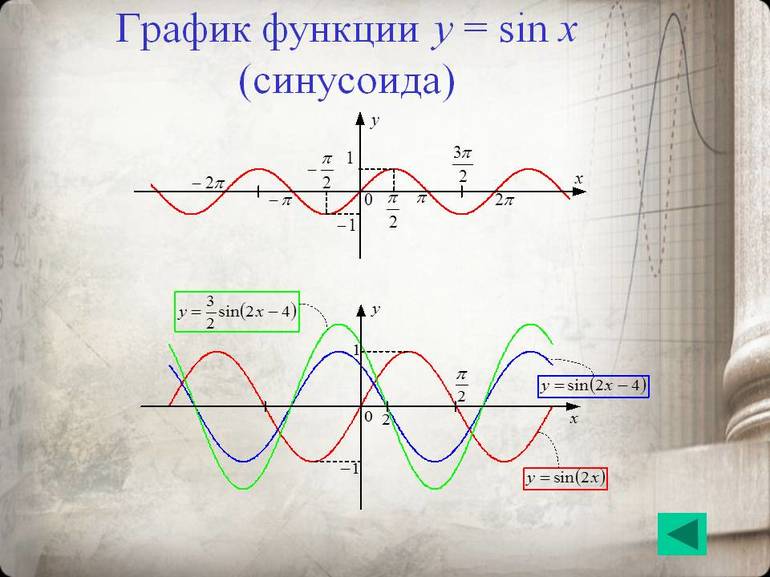
График функции называется синусоидой. График симметричен относительно начала координат.
График функции y=cosx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и
.
Поступим несколько иначе.
Согласно формулам приведения .
Из чего мы делаем вывод, что график функции будет получен смещением графика функции
на
единиц влево.
То есть график функции – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.
Преобразования синусоиды
Приглашаю посмотреть небольшой видеоролик о том, как меняется поведение синусоиды в зависимости от умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.
Автор: egeMax |
Нет комментариев
Печать страницы
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Свойства функции y=sin(x) и ее график.
График функции 
Свойства функции
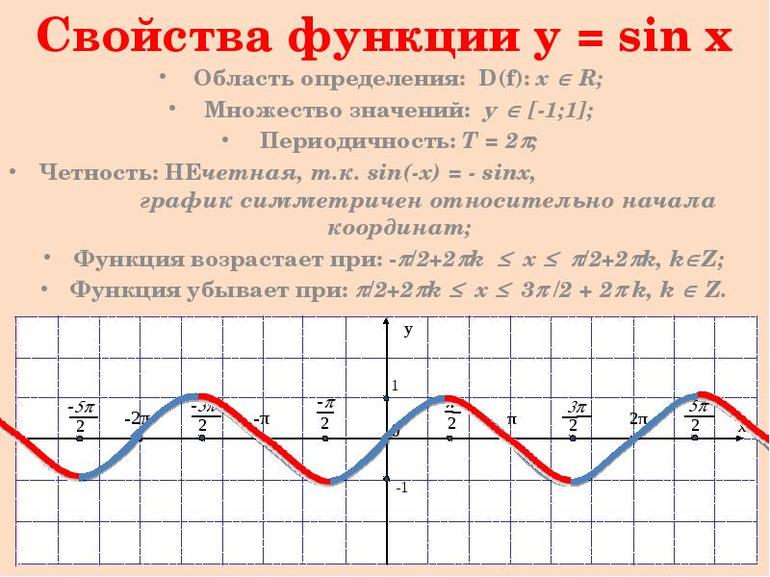
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции 
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции 
. Это можно записать так:
.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции


Синус — нечетная функция: 
Синус — периодическая функция с наименьшим положительным периодом :

вид графика функции

, а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение
. Тогда соответствующее значение
, то есть график функции
проходит через начало координат.
На оси значение

, при которых


Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 


Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 

Промежутки возрастания и убывания. Учитывая периодичность функции 



Если 




Рис.2 Рис.3
Если 




Проведенное исследование позволяет обоснованно построить график функции 







Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной 


на

Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
График функции 

. Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой

колебания, 


СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число)
.
- Область значений:
-
Функция четная:
(график симметричен относительно оси
).
- Функция периодическая с периодом
:
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции 

Рис.7
Для точек единичной окружности абсциссы находятся в промежутке 

точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции 

Как видим, наибольшее значение функции 

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при 
Косинус — четная функция: 

Косинус — периодическая функция с наименьшим положительным периодом 



Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 







Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 


Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому 
Промежутки возрастания и убывания. Учитывая периодичность функции 


Если 





Если 





Рис.8 Рис.9
Проведенное исследование позволяет построить график функции 
. Но график функции


Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки 
абсциссы и ординаты этих точек. Так как 
прямоугольника 



Укажем также формулы, которые нам понадобятся далее:
Тогда,
Таким образом, 
Учитывая, что 

его параллельным переносом вдоль оси


Рис.11
Рис.12
СВОЙСТВА ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции 
Свойства функции 
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
СВОЙСТВО ФУНКЦИИ  И ЕЕ ГРАФИК
И ЕЕ ГРАФИК
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида. Вариант для печати.
- Графики тригонометрических функций.
- Углы произвольной величины
- Построение синусоиды и косинусоиды
- Синусоидальные и косинусоидальные графики
- Периодические функции и период
- Углы запаздывания и опережения
- Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Графики тригонометрических функций.
Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах.
Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
- Графики синуса и косинуса колеблются в пределах между -1 и 1
- Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90o
- Кривые синуса и косинуса непрерывны и повторяются с периодом 360o , кривая тангенса имеет разрывы и повторяется с периодом 180o .
Углы произвольной величины
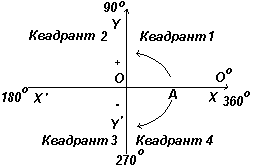
График. Положительное или отрицательное направление при движении по окружности.
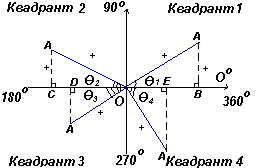
Пусть ОА вращается дальше таким образом, что Θ2 — любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
График. Поcтроение углов в различных квадрантах.
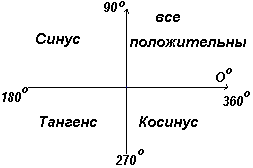
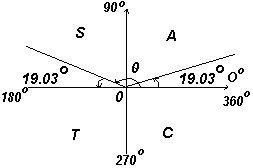
В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева.
График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0o и 360o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin-1, получим ответ 19,03o . Однако существует второй угол между 0o и 360o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180o — 19,03o = 160,97o . Таким образом, 19,03o и 160,97o — это углы в диапазоне от 0o до 360o , синус которых равен 0,3261.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 1
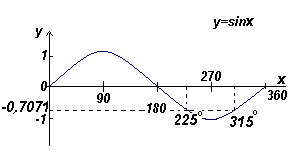
Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071
Решение:
Углы, синус которых равен -0,7071o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).
График. Нахождение всех углов по заданному значению синуса (пример)
Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o — 45 o = 315o .
Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по заданному значению синуса (пример)
Пример 2
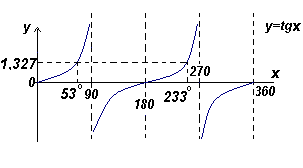
Найти все углы между 0o и 360o , тангенс которых равен 1, 327.
Решение:
Тангенс положителен в первом и третьем квадрантах — рис. слева.
График. Нахождение всех углов по заданному значению тангенса (пример)
Из рис ниже Θ = arctg1,327= 53o .
Два угла в диапазоне от 0o до 360o , тангенс которых равен 1,327, это 53o и 180o + 53 o, т.е. 233o .
График. Нахождение всех углов по заданному значению тангенса (пример)
Построение синусоиды и косинусоиды
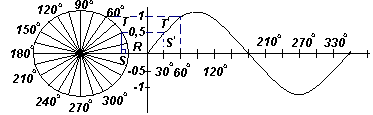
График. Построение синусоиды.
Из определения тригонометрических функций
sin30o=TS/TO=TS/1, т.е. TS= sin30o и cos30o=OS/TO=OS/1, т.e. OS=cos30o
Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90o.
График. Построение косинусоиды.
Синусоидальные и косинусоидальные графики
Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями.
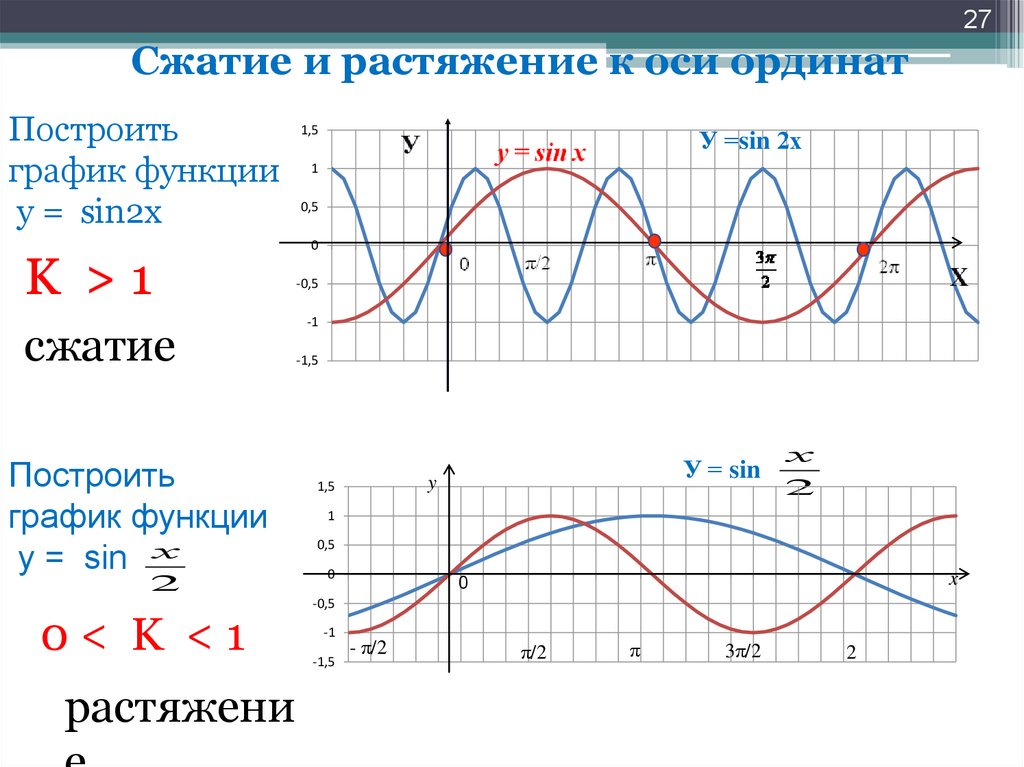
Функции y=sinA и y=cosA повторяются через каждые 360o (или 2π радиан), поэтому 360o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180o (или π радиан),поэтому 180o — это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р — константа), то период функции равен 360o/p (или 2π/p радиан ). Следовательно, если y=sin3A, то период этой функции равен 360o/3= 120o, если y=cos4A, то период этой функции равен 360o/4= 90o.
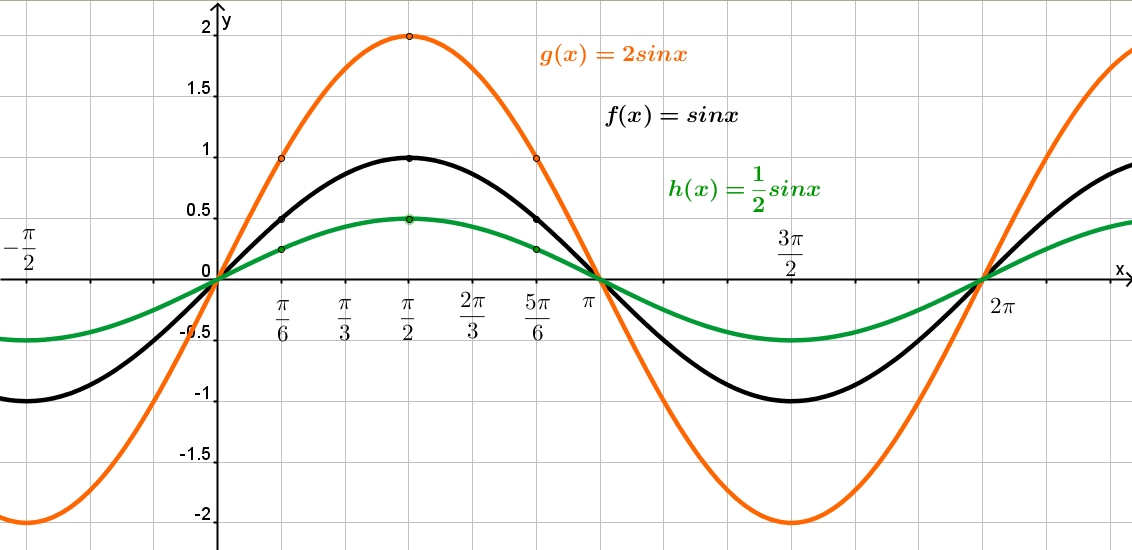
Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для y=5cos2A амплитуда равна 5, а период — 360o/2= 180o.
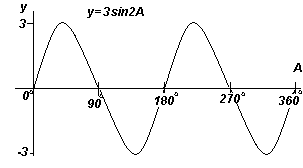
Пример 3.
Построить y=3sin2A в диапазоне от А= 0o до А=360o.
Решение:
Амплитуда =3, период = 360o/2 =180o.
График. Построение y=3sin2A (синусоида).
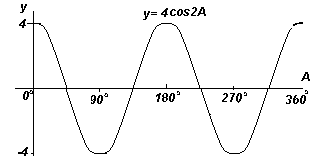
Пример 4.
Построить график y=4cos2x в диапазоне от х=0o до х=360o
Решение:
Амплитуда = 4. период = 360o/2 =180o.
График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α — сдвиг фазы относительно y=sinA и y=cosA.
.gif)
График. y=sin(A-60o) (синусоида).
.gif)
Если кривая y=cosA начинается в 0o, то кривая y=cos(A+45o) начинается на 45o левее (т.е. ее нулевая величина находится на 45o раньше ).
Таким образом, говорят, что график y=cos(A+45o) опережает график y=cosA на 45o.
График. y=cos(A+45o) (косинусоида).
В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90o левее, т.е. опережает ее на 90o. Следовательно, cosA=sin(A+90o).
Пример 5.
Построить график y=5sin(A+30o) в диапазоне от А=0o до А=360o
Решение:
Амплитуда = 5, период = 360o/1 = 360o.
5sin(A+30o) опережает 5sinA на 30o т.е. начинается на 30o раньше.
График y=5sin(A+30o) (синусоида).
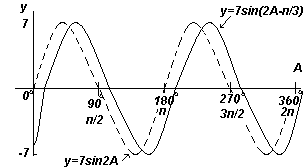
Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0o до А=360o.
Решение:
Амплитуда = 7, период =2π/2= π радиан
В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).
Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т — это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.
Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А — амплитуда
ω — угловая скорость
2π/ ω — период Т, с
ω/2π — частота f, Гц
α — угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.
Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)
Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π)o = 14,9o.
Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).
Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19o
Итак, смещение равно 3sin(110 πt + 0,33).
Пример 9.
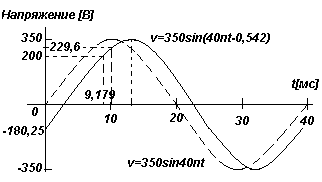
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение:
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31oс запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/103-0,542)=350sin(0,714)=350sin41o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)
График. Колебательный механизм (пример, синусоида).
v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс
python — Как построить на графике sin на максимуме и на минимуме
Вопрос задан
2 года 1 месяц назад
Изменён
2 года 1 месяц назад
Просмотрен
1k раза
Как в python можно нарисовать синусоиду заходящую на вершину и на низ графика?
Кусочек кода.
x1=[7,-1,-6,1,10] y1=[2,-2,7,12,22] plt.plot(x1,y1,color='blue',linewidth=3) x = np.arange(0,250,0.1) y = np.sin( (x - 0.01)) plt.plot(x,y,color='red',linewidth=2)
И картинка для наглядности.
Есть идея, как измудриться: нарисовать поверх основного графика ещё один растянутый график, но с осями от -1 до 1.
Но может есть нормальный вариант на одном графике?
PS Речь не о том, чтобы посчитать синусойду правильно, так как меняется масштаб и синусойда опять не у краев. Речь о том, как спомощью стандартных инструментов растянуть синусойду до краев графика.
- python
- matplotlib
6
- «синусойду растянуть до границ холста» — это значит, что вам известны максимальное и минимальное значение вашей синусоиды. Ну например, 10. Тогда
import matplotlib.pyplot as plt import numpy as np х=np.linspace(0, 10, 2000) lim=10 plt.ylim(-lim,lim) plt.plot(х,lim*np.sin(х))
Имеем:
Аналогично, если график надо обрезать до граничных значений синусоиды, то
х=np.linspace(0, 10, 2000) y=15*np.sin(х) plt.ylim(y.min(),y.max()) plt.plot(х,y)
получаем:
1
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Рисуем графики синуса и косинуса
В этой статье мы рассмотрим ещё один пример графопостроителя в более короткой форме записи:
- SCREEN 12
- VIEW (20, 150)-(620, 250)
- WINDOW (-6.
28, 1)-(6.28, -1)
- LINE (-6.28, 0)-(6.28, 0), 14
- LINE (0, -1)-(0, 1), 14
- LOCATE 14, 60
- PRINT «PI»
- LOCATE 14, 40
- PRINT «0»
- LOCATE 14, 20
- PRINT «-PI»
- LOCATE 14, 30
- PRINT «-PI / 2»
- LOCATE 14, 50
- PRINT «PI / 2»
- LOCATE 15, 4
- COLOR 3
- PRINT «Y = COS(X)»
- LOCATE 17, 26
- COLOR 10
- PRINT «Y = SIN(X)»
- FOR X = -6.28 TO 6.28 STEP .005
- PSET (X, SIN(X)), 10
- PSET (X, COS(X)), 3
- NEXT
Рисунок 1 – Исходный текст графопостроителя
Рисунок 2 – Построение графиков синуса и косинуса
Думаю, здесь вам будет все понятно (если вы знакомы управлением графикой), кроме двух новых операторов: VIEW и WINDOW.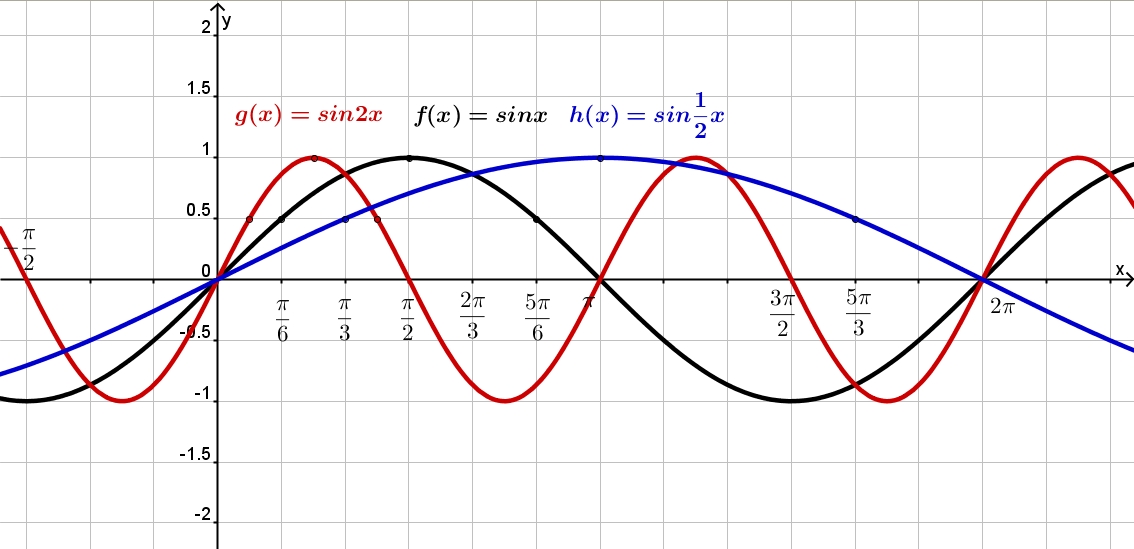
Оператор VIEW
Синтаксис:
VIEW [ [SCREEN](<X1, Y1>)-(<X2, Y2>)[, [<цвет>][, <цвет_границы>] ] ]
или
VIEW PRINT [<номер_верхней_строки> TO <номер_нижней_строки>]
Первая форма оператора позволяет получить графическое прямоугольное окно с физическими размерами, определяемыми координатами верхнего левого угла (Х1, У1) и нижнего левого (Х2, У2).
Если задана опция SCREEN, то в созданном окне будут сохранены результаты предыдущих графических операторов (естественно в пределах графического окна), хотя все координаты точек были определены для абсолютных размеров экрана. Задание параметров <цвет> и <цвет_границы> обеспечит закраску окна и обрисовку границ соответственно. Результаты работы всех последующих графических операторов будут выводится в графическом окне.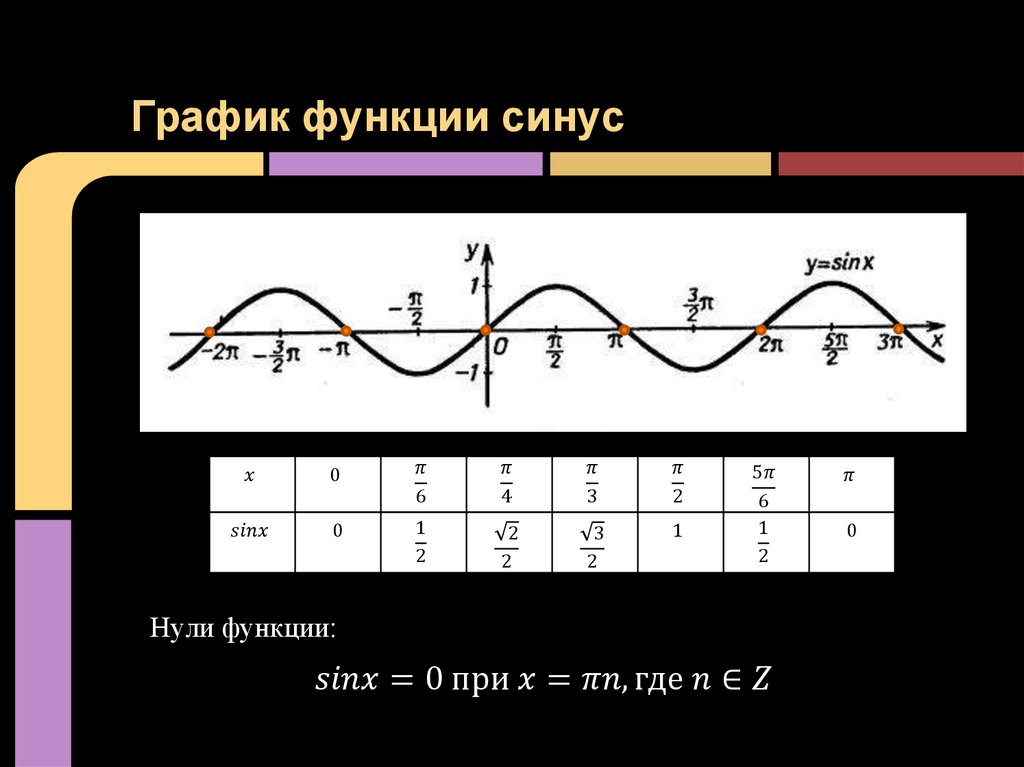
Вторая форма оператора используется для определения текстового прямоугольного окна, представляющего собой область физического экрана заключенную между строками с указанными номерами. Вывод текста операторами PRINT будет производится в это окно.
Например, если мы уберём этом оператор вообще, то полученные графики SIN и COS будут рисоваться во всю графическую область.
Оператор WINDOW
Оператор WINDOW определяет логические окна (координаты прямоугольной области) внутри текущего графического окна.
Синтаксис:
WINDOW [ [ SCREEN ] (<X1, Y1>)-(<X2, Y2>) ]
Значения (Х1, У1) и (Х2 ,У2) определяют координаты левого нижнего и правого верхнего углов окна соответственно. Опция SCREEN означает, что значения координаты Y возрастают от верхней границы графического окна к нижней.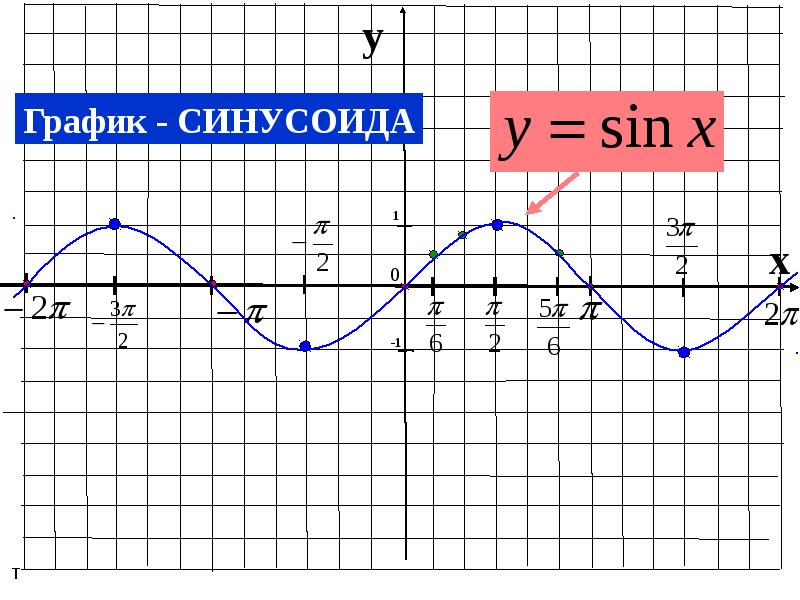
Подводя итоги
Как видите, можно по-разному запрограммировать одно и то же действие. В этой программе мы сначала создали графическое прямоугольное окно с физическими размерами. Затем задали координаты прямоугольной области внутри графического окна. Нарисовали линии (горизонтальную и вертикальную). При помощи операторов
PRINT и LOCATE подписали некоторые точки на графике. Ну и наконец, в цикле FOR, при помощи точек PSET и выбранного цвета для них построили графики SIN и COS.
Спасибо за прочтение этой статьи.
Прикрепленные файлы:
- draw-sin-and-cos-graph.bas
< Предыдущая статья
Графопостроитель с возможностью масштабирования
Следующая статья >
Еще один способ строить графики функций
Как построить график синусоидальной функции
Авторы: Ян Куанг и Эллейн Касе и
Обновлено: 26 марта 2016 г.
Функции позволяют измерять движение объектов, которые перемещаются вперед и назад или вверх и вниз через равные промежутки времени, например, маятников. Синусоидальные функции — идеальный способ выразить этот тип движения, потому что их графики повторяются, и они колеблются (как волна).
Волны поднимаются и падают снова и снова, потому что вы можете продолжать подставлять значения для
.
на всю оставшуюся жизнь. Следующие шаги показывают, как построить родительский график для синусоидальной функции
.
Имейте в виду, что, поскольку все значения синусоидальной функции исходят из единичного круга, перед тем, как продолжить, вам следует освоиться с единичным кругом. Вы можете построить график любой триггерной функции за четыре или пять шагов. Вот шаги для построения графика родительской функции
Поскольку график синусоидальной функции строится на плоскости x — y , вы перепишете это как радианы.
-
Найдите значения домена и диапазона.
Независимо от того, что вы подставите в функцию синуса, вы получите ответ на выходе, потому что
может вращаться вокруг единичного круга в любом направлении бесконечное количество раз. Следовательно, областью определения синуса являются все действительные числа, или 9.0005
На единичном круге значения и — это ваши значения синуса — то, что вы получите после подстановки значения
.
в функцию синуса. Поскольку радиус единичного круга равен 1, значения y не могут быть больше 1 или меньше отрицательной 1 — вашего диапазона для функции синуса. Таким образом, в направлении x- волна (или синусоида , на математическом языке) продолжается вечно, а в направлении y- синусоида колеблется только между -1 и 1, включая эти значения. В интервальной нотации вы записываете это как [–1, 1].
-
Вычислить
x- точек пересечения графика.Когда вы рисуете линии в алгебре, пересечения x- происходят, когда y = 0.
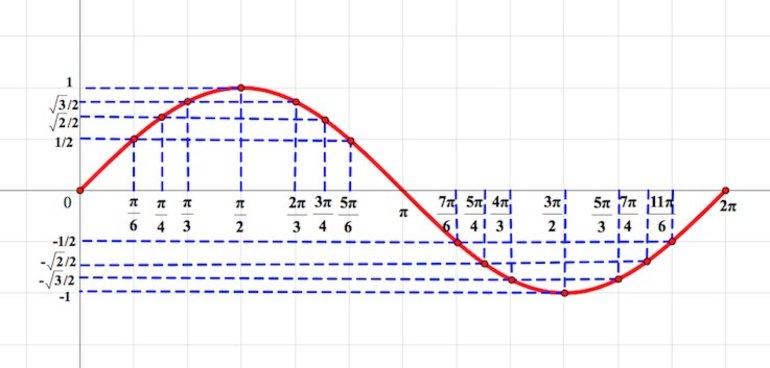
Узнайте, где график f ( x ) = sin x пересекает ось x-, найдя единичные углы окружности, где синус равен 0. Мы видим, что график f ( x ) = sin x пересекает ось x — три раза:
Теперь вы знаете, что три точки координат равны 9.0005
-
Вычислить максимальную и минимальную точки графика.
Чтобы выполнить этот шаг, используйте свои знания диапазона из шага 1. Вы знаете, что наибольшее значение, которое sin x может равняться , равно 1. При каких углах это происходит?
Теперь у вас есть еще одна координатная точка
.
Вы также можете видеть, что наименьшее значение sin x может быть равно –1, когда угол
x равен .Следовательно, у вас есть другая точка координат:
-
Нарисуйте график функции.
Используя пять ключевых точек в качестве ориентира, соедините точки плавной круглой кривой. На рисунке примерно показан родительский график синуса,
Помните, что исходный график синусоидальной функции имеет несколько важных характеристик, на которые стоит обратить внимание:
-
Повторяется каждые 2 — пи радиан.
Это повторение происходит потому, что 2-пи радиан — это один оборот по единичной окружности, называемый период синусоиды — и после этого снова начинаешь ходить. Обычно вас просят нарисовать график, чтобы показать один период функции, потому что в этот период вы фиксируете все возможные значения синуса, прежде чем он начнет повторяться снова и снова. График синуса называется
периодическим из-за этого повторяющегося шаблона. -
Симметрично относительно начала координат (таким образом, говоря языком математики, это нечетная функция ) . Функция синуса имеет 180-градусную симметрию относительно начала координат. Если посмотреть на него вверх ногами, то график выглядит точно так же. Официальное математическое определение нечетной функции , хотя и , таково: f (– x ) = – f ( x ) для каждого значения x в области . Другими словами, если вы введете противоположный вход, вы получите противоположный выход.
Например,
Этот артикул находится в категории:
- Pre-Calculus ,
Как нарисовать синусоидальную кривую в PowerPoint 2010
Если вам нужно нарисовать синусоидальную кривую в PowerPoint для ваших презентаций, то здесь мы покажем различные подходы, которые вы можете использовать в зависимости от ваших потребностей .
Синусоидальная волна или синусоидальная волна – это математическая кривая, описывающая плавные повторяющиеся колебания. Он назван в честь функции синуса, графиком которой он является. Согласно Википедии, синусоидальная волна часто встречается в чистой и прикладной математике, а также в физике, машиностроении, обработке сигналов и многих других областях, включая звуковую инженерию, структурную инженерию, музыкальные приложения, аэрокосмическую промышленность, электротехнику и многое другое. Например, колебания незатухающей системы пружины и массы вокруг точки равновесия представляют собой синусоидальную волну, которую можно смоделировать с помощью синусоидального метода, или вы также можете смоделировать колебания маятника.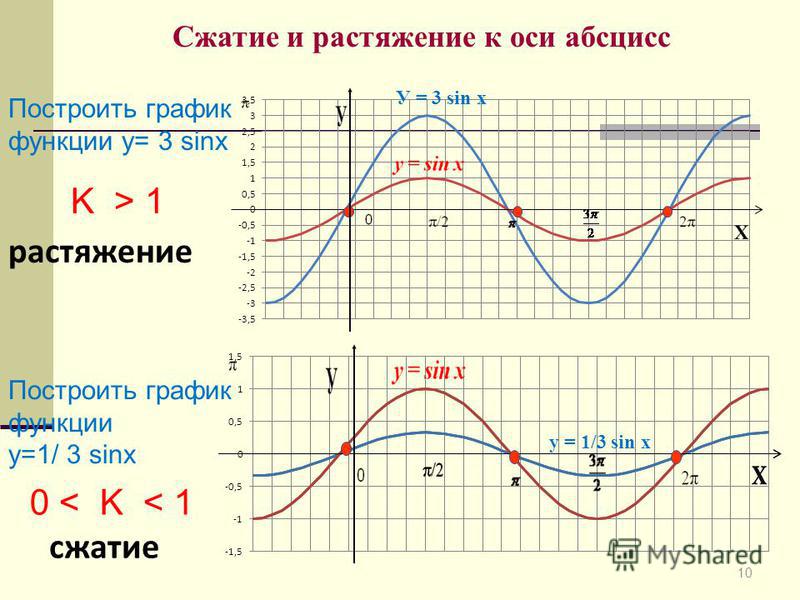
1. Используйте Fooplot , чтобы нарисовать идеальную синусоидальную кривую для PowerPoint
Как мы видели, Fooplot — это удобный онлайн-инструмент, который позволяет нам создавать графики и отображать любую функцию в режиме онлайн. Мы можем указать sin и cos и нарисовать красивую синусоидальную кривую для наших презентаций PowerPoint, а также другие математические графики для презентаций. Вы также можете использовать это, чтобы сделать шаблоны PowerPoint математических функций для загрузки.
Затем вы можете создать выходное изображение в формате PNG или любом другом и вставить его в PowerPoint 2010. Ниже вы можете увидеть пример слайда PowerPoint, показывающий функцию sin(x).
2. Построение синусоиды с использованием кривых Безье
Другой подход к рисованию кривых такого типа — использование кривых Безье. Однако результат, который вы можете получить, используя эти кривые, может быть не идеальным. В зависимости от ваших потребностей в презентации вы можете выбрать между созданием синусоидальной кривой с использованием этого подхода или более точным подходом, таким как построение синусоидальной кривой в Fooplot или Matlab.



![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)

![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)




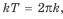







.gif)
.gif)
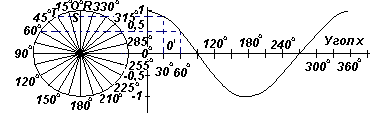
.gif)
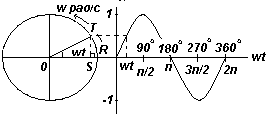
 28, 1)-(6.28, -1)
28, 1)-(6.28, -1)
 Узнайте, где график f ( x ) = sin x пересекает ось x-, найдя единичные углы окружности, где синус равен 0. Мы видим, что график f ( x ) = sin x пересекает ось x — три раза:
Узнайте, где график f ( x ) = sin x пересекает ось x-, найдя единичные углы окружности, где синус равен 0. Мы видим, что график f ( x ) = sin x пересекает ось x — три раза: 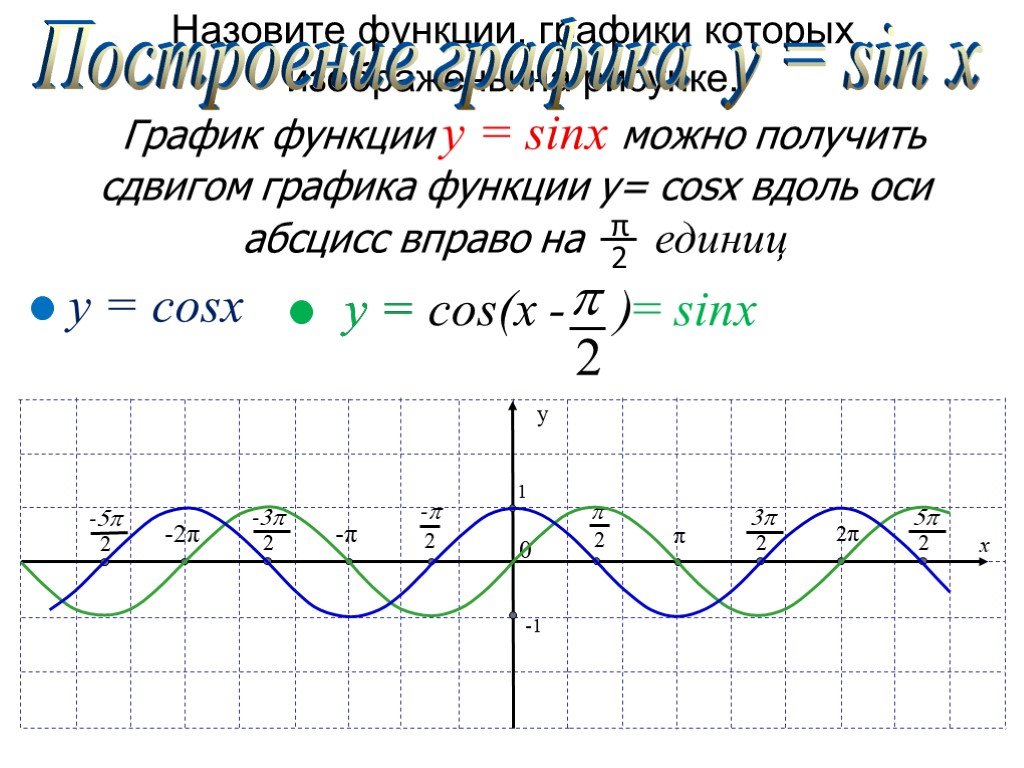 Это повторение происходит потому, что 2-пи радиан — это один оборот по единичной окружности, называемый период синусоиды — и после этого снова начинаешь ходить. Обычно вас просят нарисовать график, чтобы показать один период функции, потому что в этот период вы фиксируете все возможные значения синуса, прежде чем он начнет повторяться снова и снова. График синуса называется
Это повторение происходит потому, что 2-пи радиан — это один оборот по единичной окружности, называемый период синусоиды — и после этого снова начинаешь ходить. Обычно вас просят нарисовать график, чтобы показать один период функции, потому что в этот период вы фиксируете все возможные значения синуса, прежде чем он начнет повторяться снова и снова. График синуса называется  Например,
Например,