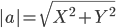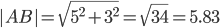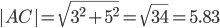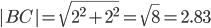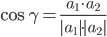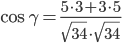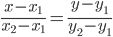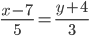Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Как найти координаты вершин треугольника через вектор
Даны координаты середин сторон треугольника: E(7, 8); F(-4, 5); K(1, -4). Определить координаты вершин треугольника.
пусть точки A, B и C — вершины треугольника, точка E — середина стороны AB, точка F — середина стороны AC, а K — середина стороны BC. Требуется найти координаты точек A, B и C.
(1)
(2)
(3)
Подставляя в эти формулы координаты точек E, F и K, мы для определения неизвестных получим следующие уравнения:
а) Уравнения, отмеченные (1), после подстановки в них координат точки E запишутся так:
Вычислительная геометрия, или как я стал заниматься олимпиадным программированием.Часть 1
Здравствуйте, уважаемые хабравчане! Это моя вторая статья, и мне хотелось бы поговорить о вычислительной геометрии.
Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b) 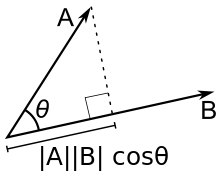
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число
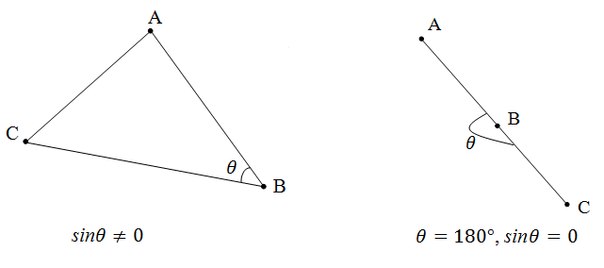
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2) 2 +(y1-y2) 2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
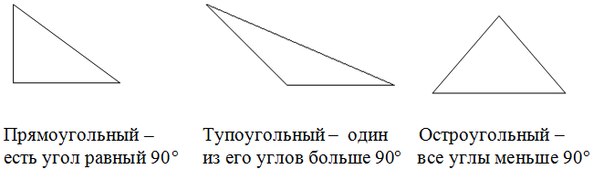
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Воспользуемся теоремой косинусов:
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a 2 2 + c 2 – треугольник остроугольный
- Если cosα = 0, то a 2 = b 2 + c 2 – треугольник прямоугольный
- Если cosα 2 > b 2 + c 2 – треугольник тупоугольный
где a – большая сторона.
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона. 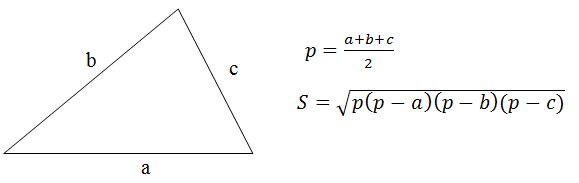
Кстати, никого не интересовало доказательство этой формулы?
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2) 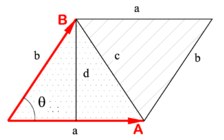
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
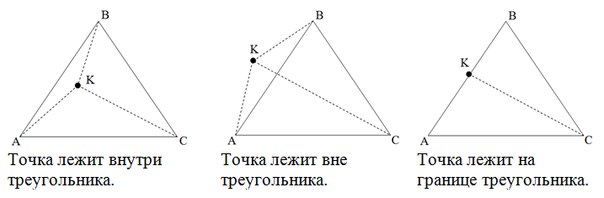
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника. 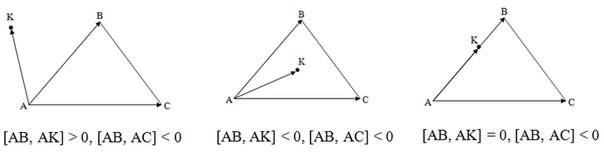
В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
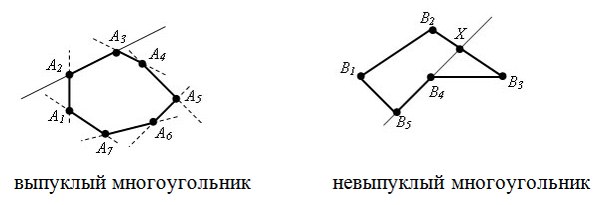
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
Метод трапеций
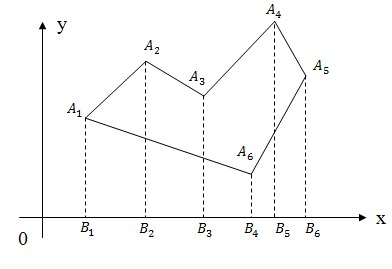
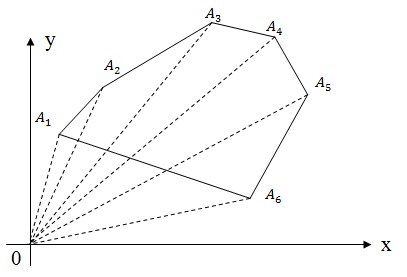
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1 A2 B2 B1 + SA2 A3 B3 B2 + SA3 A4 B5 B3 + SA4 A5 B6 B5 + SA5 A6 B4 B6 + SA6 A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1 A2 B2 B1 = 0.5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть.
Задача №9
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
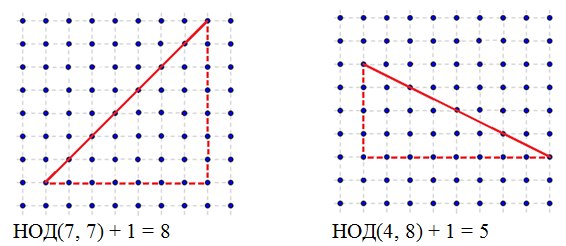
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример: 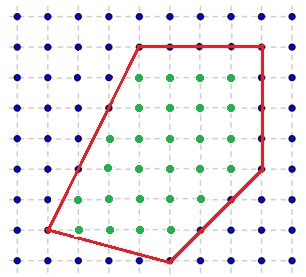
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.
http://www.pm298.ru/reshenie/fha0112.php
http://habr.com/ru/post/147691/
Как найти вершину треугольника?
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)
- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле:
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.88) = 28.07 0

Уравнение прямой AB . Каноническое уравнение прямой: 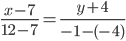
y= 3 /5x- 41 /5 или 5y-3x+41=0
Раз уж вы нашли косинус и синус угла в треугольнике — дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.
Но есть и решение в векторах, вообще без тригонометрии.
Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны — AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:
Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:
(rC-rA)² = a²
(rC-rB)² = b²
Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:
(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)
У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ — значит, это уравнение прямой CC’. Кстати, разности rB — rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).
В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием «сингулярность»: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная — деление на ноль будет при попытке выразить x через y.
Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:
r = r0 + t u
Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем — задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.
Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:
r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)
Подставим первое уравнение во второе и решим его относительно переменной t:
2(rA + tAB)·AB = a² - b² - (rA² - rB²)
2rA·AB + 2t AB² = a² - b² - (rA² - rB²)
t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²
t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²
t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²
t = (a² - b² + (rA - rB)²) / 2AB²
t = (a² - b² + AB²) / 2AB²
Осталось подставить эту переменную обратно в параметрическое уравнение:
t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB
Формула выглядит страшно, но не имеет сингулярностей пока A и B — разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.
Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.
И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB — xA, yB — yA) — то повёрнутый будет с координатами (-yB + yA, xB — xA). Почему так — объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.
Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.
rC = r0 + k AB^
(rC-rA)² = a²
И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):
(r0-rA + k AB^)² = a²
k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0
Тут есть и дальнейшие упрощения: вектор r0—rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.
Суммируя всё что написано выше, получаем следующую систему уравнений:
t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^
Осталось решить примитивное квадратное уравнение:
t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^
Дальше осталось перейти от векторов к координатам и решение готово.
Вариантов много. Например:
1. Найти середину отрезка AB, назовём точкой S.
2. Найти высоту треугольника. Учитывая, что треугольник равнобедренный, высота является срединным перпендикуляром.
3. Построить вектор, параллельный AB с длиной, равной высоте треугольника.
4. Повернуть его на 90 градусов влево или вправо.
5. Перенести начало вектора в точку S.
1) Строим из точки A окружность с радиусом AC
(x-xA)^2 + (y-yA)^2 = R^2 = AC^2
2) Строим из точки B окружность с радиусом BC
(x-xB)^2 + (y-yB)^2 = R^2 = BC^2
3) Решаем систему уравнений, получаем 0(пересечений нет), 1(пересечение в одной точке, касание) или 2 действительных корня(пересечение в 2х точках). Это и есть возможные варианты точки C.
Можно найти x, а потом подставить в любое из уравнений и получить y, или же наоборот.
Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.



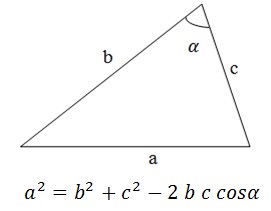


![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)