Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
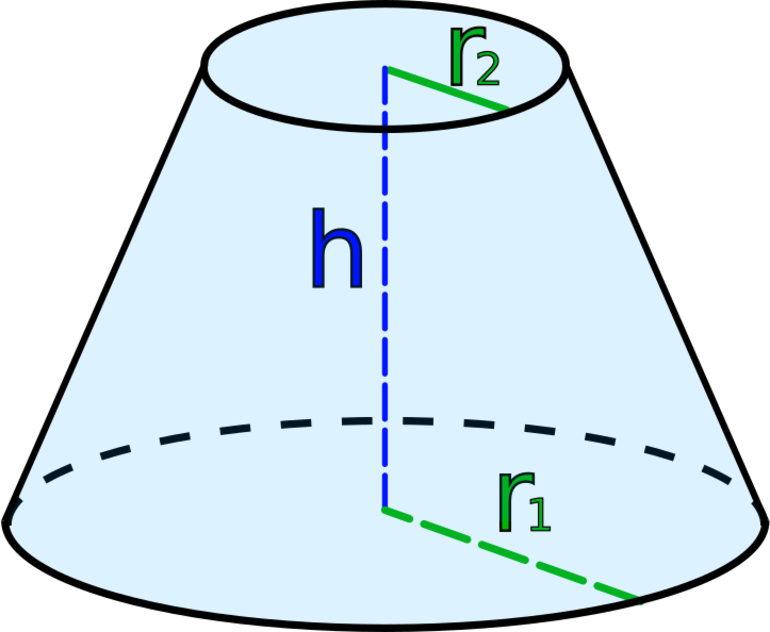
Формулы усеченного конуса
Для расчёта всех основных параметров усеченного конуса воспользуйтесь калькулятором.
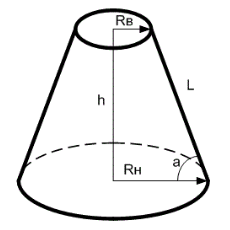
Объём усеченного конуса
$$
V = {1 over 3} * pi * h * (R_Н^2 + R_Н * R_В + R_В^2)
$$
Площадь боковой поверхности усечённого конуса
$$
S_Б = pi * (R_Н + R_В) * L
$$
Высота усеченного конуса через образующую и радиусы оснований
$$
h = sqrt{L^2 — (R_Н — R_В)^2}
$$
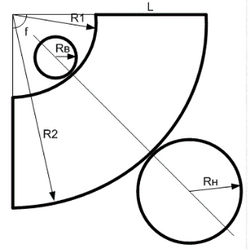
Развертка (выкройка) усеченного конуса
Длина образующей, L
$$
L = sqrt{(R_Н — R_В)^2 + h^2}
$$
$$
R_1 = {L * R_В over R_Н — R_В}
$$
$$
R_2 = L + R_1
$$
Угол ∠ f
$$
∠ f = 360° * {R_Н — R_В over L}
$$
Окружающий нас мир динамичен и разнообразен, и далеко не всякий объект можно просто обмерить линейкой. Для подобного переноса используются специальные техники, как то триангуляция.
Потребность в составлении сложных развёрток, как правило, возникает при моделировании, работе с бумагой и металлом, в слесарном деле. Написанная ниже статья, объясняет принципы построения развёрток тел вращения (цилиндр, конус) и их частных случаев (сечение конуса, конус с переходом с круга на квадрат).
Основы и инструмент[править]
- Все нижеописанные действия выполняются на бумаге, при помощи линейки, карандаша и циркуля. Рекомендуется комплект лекал, для повышения точности и качества развёрток.
- При изготовлении развёрток на металле используется метровая линейка, чертилка, циркуль по металлу, комплект лекал, молоток и керно, для отметки узловых точек.
- Длина окружности считается по формуле:

или

Где:




Как правило, для вычисления используется значение 
- Усечённый конус с доступной вершиной: Конус, при построении которого можно определить положение вершины.
- Усечённый конус с недоступной вершиной: Конус, при построении которого положение вершины определить затруднительно, в виду её удалённости.
- Триангуляция: способ построения разверток поверхностей неразвертывающихся, конических, общего вида и с ребром возврата.
- Восстановление размера: Многие размеры трёхмерного объекта, при проецировании в двумерную плоскость, оказываются мнимыми, поэтому их приходится восстанавливать по правилу треугольника: «Если известны две стороны — то можно получить третью». В этих случаях применяется прямая, с вертикалью, верхняя точка вертикали соответствует высоте объекта. Если из точки пересечения (на нижеследующих чертежах — точка O) отложить на прямой размер снятый с вида сверху — то размер из полученной из точки до вершины вертикали (на нижеследующих чертежах — точка O1) — является истинным.
- Следует помнить: Независимо от того, является рассматриваемая поверхность развертываемой или неразвертываемой, графически может быть построена только приближенная развертка. Это объясняется тем, что в процессе снятия и откладывания размеров и выполнения других графических операций неизбежны погрешности, обусловливаемые конструктивными особенностями чертежных инструментов, физическими возможностями глаза и погрешностями от замены дуг хордами и углов на поверхности плоскими углами. Приближенные развертки кривых не-развертывающихся поверхностей, кроме графических погрешностей, содержат погрешности, полученные за счет несовпадения элементов таких поверхностей с плоскими аппроксимирующими элементами. Поэтому для получения поверхности из такой развертки, кроме изгибания, необходимо произвести частичное растяжение и сжатие отдельных ее участков. Приближенные развертки при тщательном выполнении обладают точностью, достаточной для практических целей.
Представленный в статье материал, подразумевает, что вы имеете представление об основах черчения, умеете делить окружность, находить центр отрезка при помощи циркуля, снимать/переносить размеры циркулем, пользоваться лекалами, и соответствующим справочным материалом. Потому, объяснение многих моментов в статье опущено.
Построение развёртки цилиндра[править]
Построение развёртки конуса[править]
Конус с квадратным (многогранным) основанием.[править]
- В случае, если конус имеет ровное, радиальное, основание: (При построении окружности на виде с верху, путём установки циркуля в центр, и очерчивания окружности по произвольной вершине — все вершины основания укладываются на дугу окружности.) Построить конус, по аналогии с развёрткой обычного конуса (основание строить по окружности, от вида сверху). Отложить дугу из точки O. В произвольной части дуги поставить точку A1, и поочерёдно отложить все грани основания на дугу. Конечная точка последней грани будет B1.
- Во всех иных случаях конус строится по принципу триангуляции, с поочерёдным восстановлением высот от вида сверху.
Усечённый конус с доступной вершиной[править]
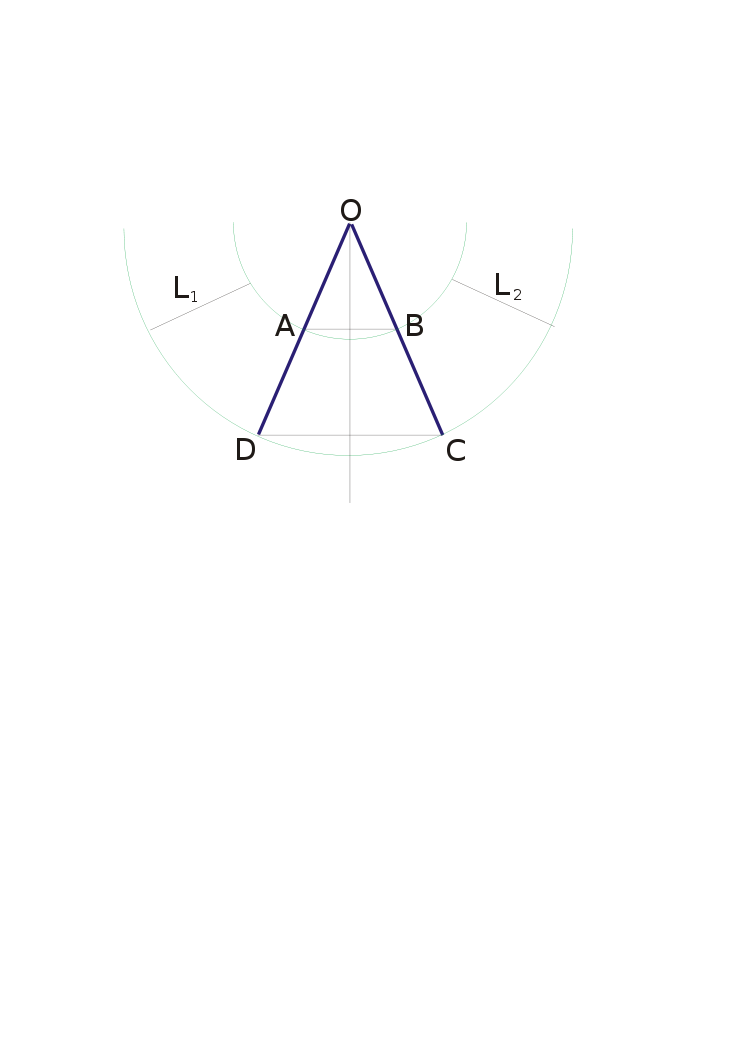
Построить усечённый конус ABCD в натуральную величину (См. чертёж).
Стороны AD и BC продолжить до появления точки пересечения O. Из точки пересечения O, провести дуги, с радиусом OB и OC.
На дуге OC, отложить длину окружности DC. На дуге OB, отложить длину окружности AB. Полученные точки соединить отрезками L1 и L2.
Для удобства, от можно откладывать половину длины окружности, в обе стороны от осевой линии конуса.
Как отложить длину окружности на дуге:
- При помощи нитки, длина которой равна длине окружности.
- При помощи металической линейки, которую следует изогнуть «по дуге», и поставить соответствующие риски.
- Построить окружность основания конуса в виде сверху, в натуральную величину. Разделить окружность на 12 или более равных частей, и отложить их на дуге поочерёдно.
Примечание: Совсем не обязательно, что отрезки L1 и L2, если их продолжить, будут сходится в точке O. Если быть до конца честным, то сойтись они должны, но с учётом поправок на погрешности инструмента, материала и глазомера — точка пересечения может оказаться чуть ниже или выше вершины, что не является ошибкой.
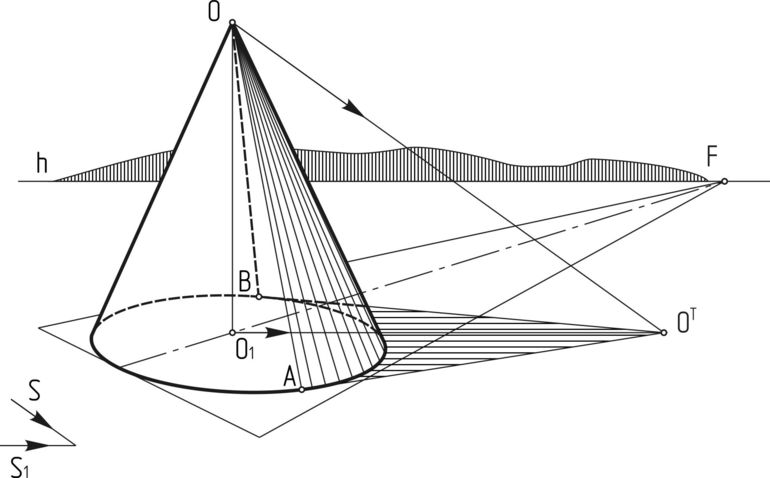
Чертёж: «Усечённый конус»
Усечённый конус с недоступной вершиной[править]
Строится так же, как усечённый конус со смещёнными основаниями.
Усечённый конус с переходом с круга на квадрат[править]
Подготовка:
Построить усечённый конус ABCD в натуральную величину (см. чертёж), построить вид сверху ABB1A1. Окружность поделить на равные части (в приведённом примере показано деление одной четверти). Точки AA1-AA4 соединить отрезками с точкой A. Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.
Ниже, первичные размеры снимаются с вида сверху.
Построение:
- Снять размер AD и построить произвольную вертикаль AA0-AA1. Снять размер AA0-A, и поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA1, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA1, до предполагаемой точки A. Соединить отрезками точки AA0-A-AA1.
- Снять размер AA1-AA2, из точки AA1 поставить «примерную точку», сделав отмашку циркулем. Снять размер A-AA2, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки A, до предполагаемой точки AA2. Провести отрезок A-AA2. Повторить, пока не будет отложен отрезок A-AA4.
- Снять размер A-AA5, из точки A поставить «примерную точку» AA5. Снять размер AA4-AA5, и на оси O, из точки O, отложить отрезок, снять размер из полученной точки до точки O1. Сделать отмашку циркулем из точки AA4, до предполагаемой точки AA5. Провести отрезок AA4-AA5.
Подобным образом построить остальные сегменты.
Примечание: Если конус имеет доступную вершину, и КВАДРАТНОЕ основание — то построение можно провести по принципу усечённого конуса с доступной вершиной, а основание — конуса с прямоугольным (многогранным) основанием. Точность будет ниже, но построение существенно проще.
Чертёж: «Конус с переходом с круга на квадрат»

Усечённый конус с непараллельными основаниями[править]
Чертёж: «Развёртка конуса с непараллельными основаниями»
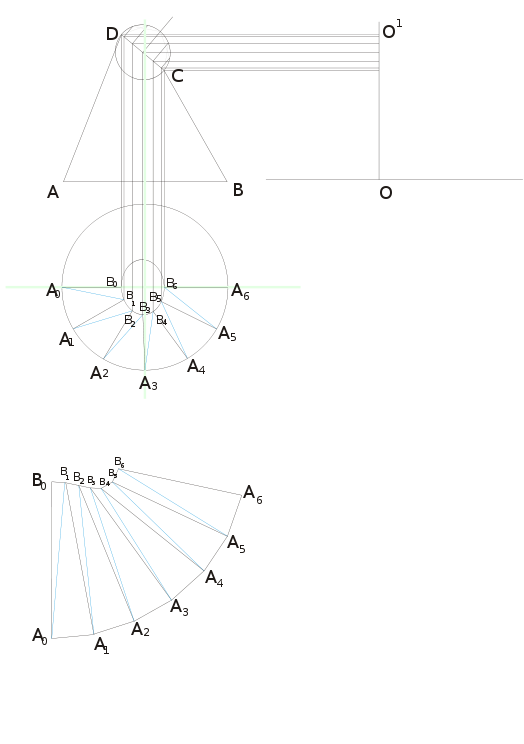
Усечённый конус со смещёнными основаниями[править]
Подготовка:
Построить усечённый конус ABCD в виде сбоку, в натуральную величину. Построить вид сверху (см.чертёж). Поделить верхнее и нижнее основание на равные части A0-6 и B0-6, соединив соответствующие точки отрезками. Построить вспомогательные диагонали (на чертеже выделены синим цветом). Провести ось O, из центра которой провести перпендикуляр O-O1, высотой равной высоте конуса.
Ниже, первичные размеры снимаются с вида сверху.
Построение:
- Построить вертикаль A0-B0. (В рассматриваемом случае, верхняя плоскость смещена влево так, что точки A и D находятся на одной вертикали. Поэтому размер AD, соответствующий размеру A0-B0 снимается с вида с боку. В иных случаях он получается восстановлением размера на оси O.)
- Снять размер A0-A1. Из точки A0, вертикали A0-B0, сделать примерную отмашку циркулем. Снять размер B0-B1. Из точки B0, вертикали A0-B0, сделать примерную отмашку циркулем. Снять размер вспомогательной диагонали A0-B1, из точки O, сделать отмашку циркулем на ось, из полученной точки снять размер до точки O1, полученным размером сделать отмашку из точки A0, для получения точки B1.
- Снять размер A1-B1, из точки O, сделать отмашку циркулем на ось, из полученной точки снять размер до точки O1, полученным размером сделать отмашку из точки B1, для получения точки A1.
- Соединить отрезками точки A0-B0-B1-A1.
Аналогичным образом продолжить построение до получения половины, либо цельной развёртки.
Чертёж: «Развёртка конуса со смещёнными основаниями»

Обобщения и замечания[править]
- Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
- При этом следует иметь в виду, что при работе с металлом следует брать внутренние размеры детали, т.к. при гибке и/или закатке, внешняя поверхность металла тянется, а внутренняя остаётся неизменной. (Верно при использовании современного гибочного оборудования. На устаревшем оборудовании, следует вводить поправки на износ поверхностей, и точность работы станка.)
- При работе с металлом, толщиной свыше 3 мм, в зависимости от типа, марки металла и используемого гибочного оборудования — размеры следует брать не по внутренней стороне, а по «средней линии», которая проходит на половине толщины металла. Либо считать места сгибов не как прямые углы, а как дуги.
- При изготовлении из металла, линии разметки (прямые, а не вспомогательные диагонали) могут использоваться как линии гиба, с последующей доводкой контура молотком/киянкой на вспомогательной поверхности.
См. также[править]
- ГОСТ 2.301-68* Форматы. (размеры форматов и их обозначение)
- Начертательная геометрия и черчение.Книга начертательная геометрия и машиностроительное черчение. Под редакцией Чекмарева А.А.
- Справочное руководство по черчению. Под редакцией Е.И. Годик и А.М. Хаскин. Москва «МАШИНОСТРОЕНИЕ» 1974г.
- ЧЕРЧЕНИЕ. Под редакцией Боголюбова С.К. Учебник для средних специальных учебных заведений (2-е изд.)
Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
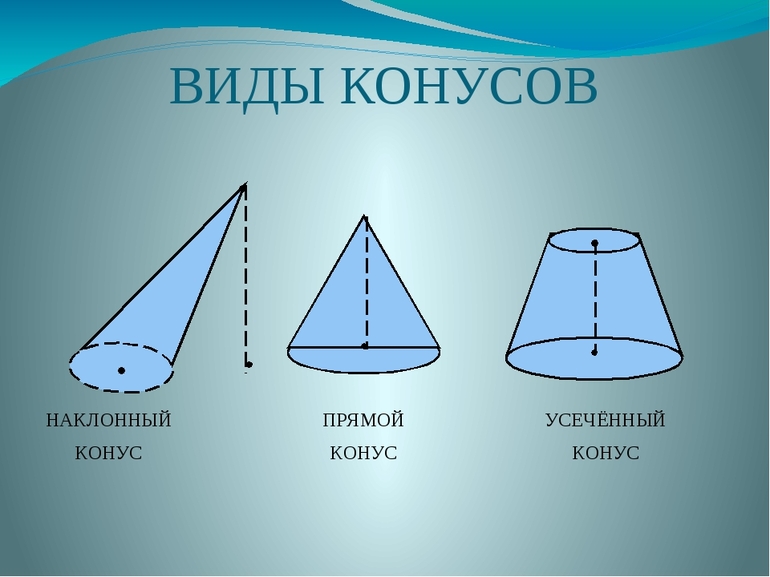
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
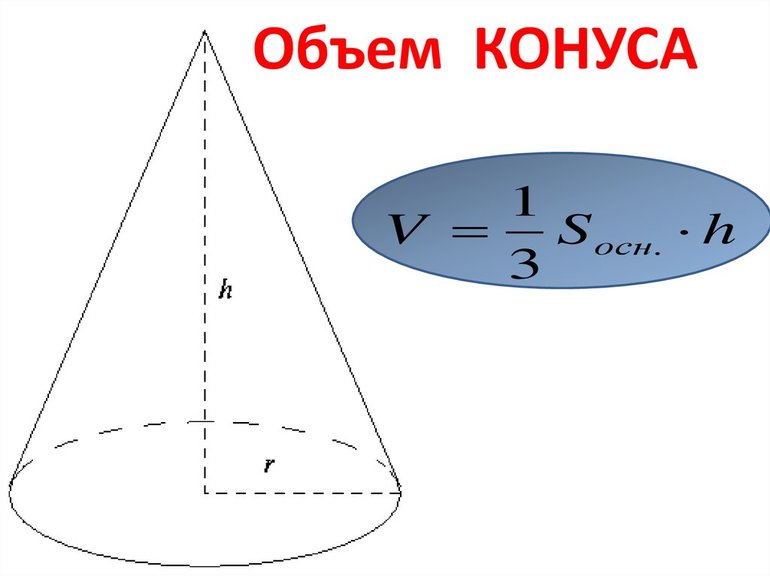
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
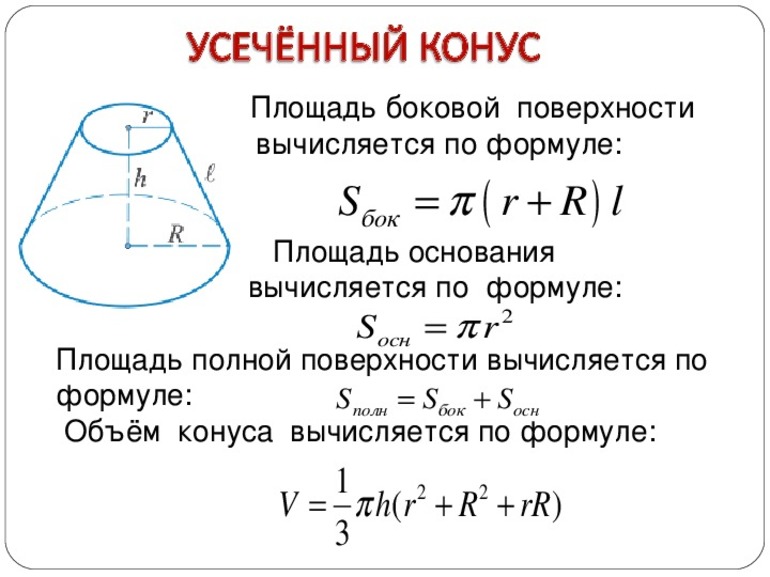
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
Выкройка для конуса

Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Обозначения:
Параметры выкройки рассчитываются по формулам:


где 
2. Усеченный конус
Обозначения:
Формулы для вычисления параметров выкройки:



где 
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них 
3. Угол при вершине конуса
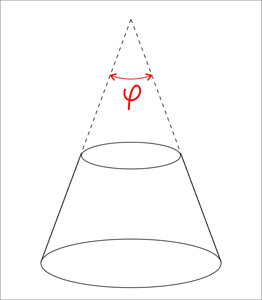

В этом случае мы можем его использовать вместо одного из трех входных значений: 


Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
4. Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Excel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.
На этом уроке мы познакомимся с понятием
усеченного конуса. Дадим определение усеченного конуса. Назовем и рассмотрим
его основные элементы. А затем выведем формулы для вычисления площади боковой поверхности
и площади полной поверхности усеченного конуса.
Итак, рассмотрим понятие усечённого конуса.
Вообще вокруг
нас существует множество предметов, имеющих форму усечённого конуса. Вафельные
стаканчики для мороженного имеют форму усечённого конуса, некоторые стаканы, светильники,
ведра обладают формой очень близкой к форме усечённого конуса.
Некоторые
архитектурные сооружения также имеют форму усечённого конуса. И многое другое.
Возьмём произвольный конус и проведём секущую
плоскость, параллельную его основанию. Эта плоскость пересекается с конусом по кругу
и разбивает конус на две части. Одна из частей (верхняя) представляет собой
конус, а вторая (нижняя) называется усечённым конусом.
Определение:
Усечённым конусом называется
часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной
оси конуса.
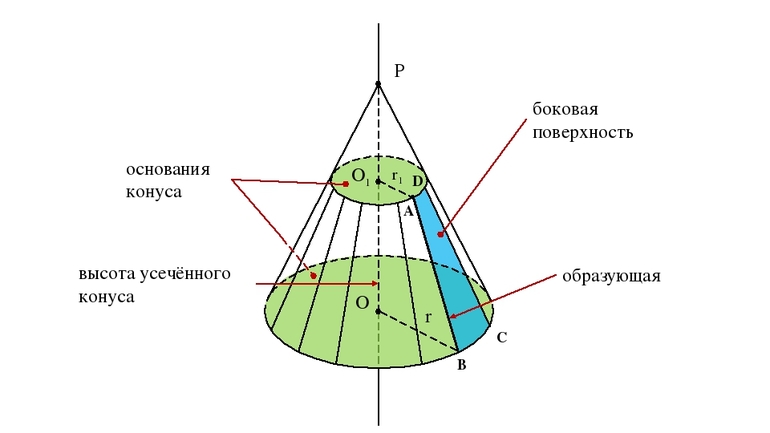
Назовём элементы усечённого конуса.
Основание исходного конуса и круг, полученный
в сечении этого конуса плоскостью, называются основаниями усечённого
конуса.
Высотой усечённого конуса
называется отрезок (или его длина), соединяющий центры его оснований.
Прямая называется его осью.
Часть конической поверхности, ограничивающая
усеченный конус, называется его боковой поверхностью, а отрезки
образующих конической поверхности, расположенные между основаниями, называются образующими
усечённого конуса.
Все образующие усечённого конуса равны друг
другу.
Усечённый конус может быть получен вращением на
прямоугольной трапеции
вокруг её боковой стороны, перпендикулярной к основаниям.
На экране вы видите усечённый конус,
полученный вращением прямоугольной трапеции вокруг стороны
, перпендикулярной к
основаниям и
. При этом основания усечённого
конуса образуются вращением оснований и
трапеции, а боковая
поверхность – вращением боковой стороны .
Выведем формулу для вычисления площади
боковой поверхности усечённого конуса.
Для этого нам нужно доказать, что площадь
боковой поверхности усечённого конуса равна , где
и
– радиусы оснований,
– образующая усечённого
конуса.
Доказательство. Пусть – вершина конуса, из
которого получен усечённый конус, – одна из образующих
усечённого конуса, а точки и
– центры его оснований.
Причём, . Тогда площадь боковой
поверхности усечённого конуса равна разности боковых поверхностей двух конусов,
т.е. . Преобразуем это
выражение.
Заметим, что длина образующей исходного конуса состоит
из суммы отрезков . Используя формулу для
вычисления площади боковой поверхности конуса, получаем: .
Отсюда, учитывая, что , получим следующее
выражение .
Теперь выразим через
,
и
. Прямоугольные
треугольники подобны
по двум углам. Отсюда следует, что , или
.
Значит, получаем, что .
Подставим это выражение в формулу.
Упростим.
В итоге приходим к следующей формуле: .
Этим мы с вами вывели формулу для
вычисления площади боковой поверхности усеченного конуса.
Таким образом, мы доказали, что площадь
боковой поверхности усечённого конуса равна произведению полусуммы длин
окружностей оснований на длину образующей, где и
– радиусы оснований,
– образующая усечённого
конуса.
Площадью полной поверхности усечённого
конуса называется сумма площадей его боковой поверхности и площади двух
его оснований. Формулу для вычисления площади боковой поверхности усечённого
конуса мы
с вами вывели выше. Площадь нижнего основания усеченного конуса равна , а площадь меньшего
основания – . Подставим все данные в
формулу.
Отсюда, получаем, что площадь полной
поверхности усеченного конуса можно вычислить по следующей формуле: .
Теперь давайте решим несколько задач.
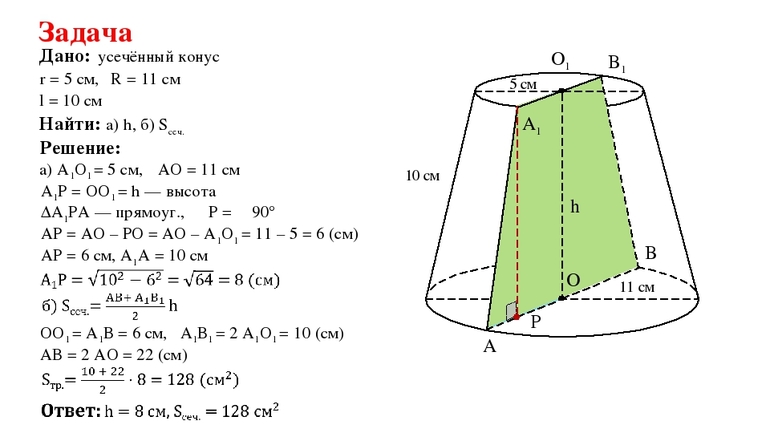
Задача: длины радиусов оснований
и образующей усечённого конуса равны соответственно см,
см и
см. Вычислите его высоту.
Решение: рассмотрим
четырехугольник .
Это есть прямоугольная трапеция с основаниями и
. Высота этой трапеции и
будет высотой нашего усечённого конуса . Для того чтобы её
найти, проведём из точки меньшего основания
перпендикуляр на большее основание трапеции . Фигура
является
прямоугольником, значит противоположные стороны равны, т.е. (см),
.
Рассмотрим . Он прямоугольный (по
построению). Катет (см). Применим теорему
Пифагора и найдём длину катета . Получаем, что
(см). Запишем ответ.
Задача: длины радиусов оснований
усечённого конуса равны см и
см. Вычислите площадь
боковой поверхности этого конуса, если угол между образующей и плоскостью его
основания равен .
Решение: запишем формулу для
вычисления площади боковой поверхности усечённого конуса.
Рассмотрим четырёхугольник .
Это есть прямоугольная трапеция с основаниями и
. Высота этой трапеции и
будет высотой нашего усечённого конуса .
Проведём из точки меньшего основания
перпендикуляр на большее основание трапеции . Фигура
является
прямоугольником, значит, противоположные стороны равны, т.е. (см),
.
Рассмотрим . Он прямоугольный (по
построению). По условию задачи образующая усечённого конуса наклонена к его
основанию под углом . Следовательно, катет
. В свою очередь,
. Применим теорему Пифагора
и найдём длину гипотенузы треугольника
. Получаем, что
(см). Значит, образующая
нашего усечённого конуса равна (см).
Подставим длины радиусов и образующей усечённого
конуса в формулу для вычисления площади боковой поверхности. Посчитаем.
Получим, что площадь боковой поверхности усеченного конуса равна (см2).
Не забудем записать ответ.
Итоги:
На этом уроке мы познакомились с понятием усечённого
конуса. Узнали, что усечённым конусом называется часть конуса, расположенная
между его основанием и секущей плоскостью, перпендикулярной оси конуса. Назвали
основные элементы усечённого конуса. А также вывели формулы для вычисления
площади боковой поверхности и площади полной поверхности усечённого конуса.