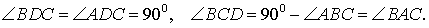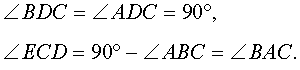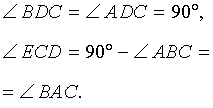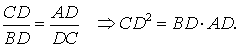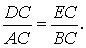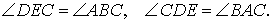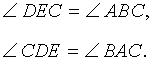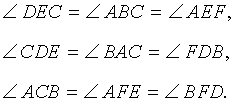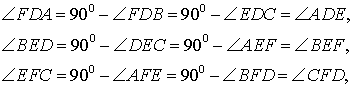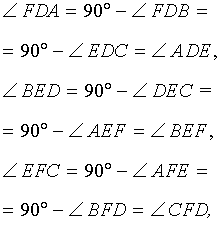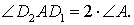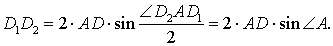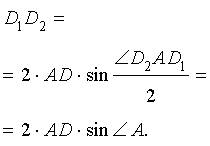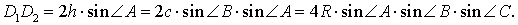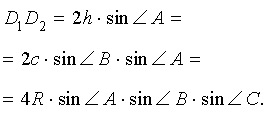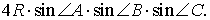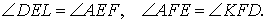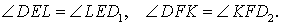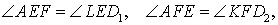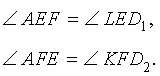Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Как найти вершины треугольника зная одну его вершину и уравнения высот
Даны уравнения высот треугольника 2x — 3y + 1 = 0 и x + y = 0 и координаты одной из его вершин A(1, 2). Найти уравнения сторон треугольника.
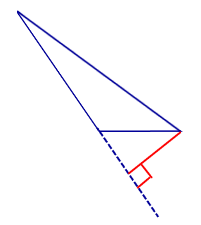
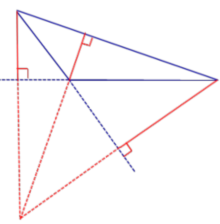
Точка A(1, 2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям: и . Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника B и C (см. рисунок)
Назовем их CD и BE, CD AB, BE AC. Пусть высота CD имеет уравнение x + y = 0, а уравнение высоты BE 2x — 3y + 1 = 0. Так как AC BE, то уравнение AC мы найдем из уравнения семейства прямых, перпендикулярных BE, приняв во внимание, что искомая прямая проходит через данную точку A(1, 2).
Сторона AC имеет уравнение 3x + 2y — 7 = 0. Уравнение прямой AB найдем, как уравнение прямой, проходящей через точку A(1, 2) перпендикулярно CD. Оно имеет вид
Теперь следует найти координаты точек B и C:
Уравнение стороны BC 2x + 3y + 7 = 0.
Таким образом, уравнения всех трех сторон треугольника найдены.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Как найти вершину треугольника?
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)
- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле:
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.88) = 28.07 0

Уравнение прямой AB . Каноническое уравнение прямой: 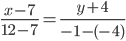
y= 3 /5x- 41 /5 или 5y-3x+41=0
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
1 |
|
Как найти координаты третьей вершины треугольника, зная все стороны и две вершины?07.07.2013, 16:27. Показов 98100. Ответов 19
Добрый день, подскажите как найти координаты третьей вершины треугольника?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:10 |
2 |
|
Зная то, что расстояние между двумя точками равно: Откуда и найдем координаты 3-ей точки
2 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:18 [ТС] |
3 |
|
А как вывести из формулы нужную?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:44 |
4 |
|
Например, можно произвести смещение точки А в начало координат.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:46 [ТС] |
5 |
|
Извени, но я не понимаю…
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,786 Записей в блоге: 12 |
|
|
07.07.2013, 19:38 |
6 |
|
А так понимаете?
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 20:07 [ТС] |
7 |
|
Рисунок не доступен пишет.
0 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
07.07.2013, 21:35 |
8 |
|
Известны координаты точек А(x1,y1), С(x2,y2). Условие некорректно — переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 23:27 [ТС] |
9 |
|
Условие некорректно — переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны. Длина и координаты две разные вещи.
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
07.07.2013, 23:52 |
10 |
|
Длина и координаты две разные вещи. А Том Ардер другого и не утверждал. Читайте внимательнее.
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,786 Записей в блоге: 12 |
|
|
08.07.2013, 11:23 |
11 |
|
Решение
Добрый день, подскажите как найти координаты третьей вершины треугольника? Вот картинка. Миниатюры
3 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
08.07.2013, 14:48 [ТС] |
12 |
|
А как вы выделили x и y из формулы?
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,786 Записей в блоге: 12 |
|
|
09.07.2013, 09:13 |
13 |
|
Справа на картинке записана система двух уравнениий — уравнений окружностей.Решив систему, получаем координаты двух точек. т.е. точек В может быть две.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
09.07.2013, 14:03 [ТС] |
14 |
|
проблема в том, что я не знаю как решить уравнение окружностей(
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
09.07.2013, 14:11 |
15 |
|
Раскройте скобки, вычтите из 1 уравнения другое. Уйдут квадраты, выразите одну переменную через другую. Подставите в 1 исходное.
0 |
|
1765 / 969 / 180 Регистрация: 24.02.2013 Сообщений: 2,786 Записей в блоге: 12 |
|
|
09.07.2013, 15:16 |
16 |
|
Только проще сначала вычесть из первого уравнение второе, затем воспользоваться формулой разности квадратов.
1 |
|
0 / 0 / 0 Регистрация: 10.04.2016 Сообщений: 7 |
|
|
28.04.2016, 22:07 |
17 |
|
А можно решить как-нибудь без системы уравнений?
0 |
|
0 / 0 / 0 Регистрация: 08.04.2019 Сообщений: 6 |
|
|
10.04.2019, 13:19 |
18 |
|
Я тоже был бы не против без системы уравнений
0 |
|
1471 / 826 / 140 Регистрация: 12.10.2013 Сообщений: 5,456 |
|||||
|
10.04.2019, 21:50 |
19 |
||||
|
del Для чего тут система уравнений?
Нормализуем вектор AC и множим на длину AB стороны и крутим матрицей поворота в 2д на нужный угол. Угол треугольника найти по трем сторонам. Эх раньше бы и рис и формулы кинул…но теперь лень =). Может кто из гуру не полениться…
0 |
|
pro4vayder 1 / 1 / 0 Регистрация: 25.05.2016 Сообщений: 2 |
||||
|
04.11.2020, 09:49 |
20 |
|||
|
Прошу глянуть решение здесь. Ответ выше был близок к ответу, но человеку далекому от математики (мне) — это не особо было понятно. P.S решение выводит 2 ответа точек пересечения Кликните здесь для просмотра всего текста http://algolist.ru/maths/geom/… rcle2d.php
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
04.11.2020, 09:49 |
|
20 |
Высота треугольника. Свойство высоты прямоугольного треугольника
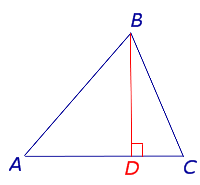
Определение 1 . Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника. Основанием высоты называют основание этого перпендикуляра (рис.1).
На рисунке 1 изображена высота BD , проведённая из вершины B треугольника ABC . Точка D – основание высоты.
Для высоты прямоугольного треугольника, проведённой из вершины прямого угла, справедливо следующее утверждение.
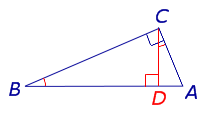
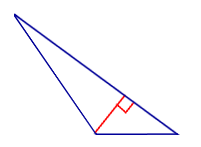
Утверждение . Длина высоты прямоугольного треугольника, опущенной на гипотенузу, является средним геометрическим между длинами отрезков, на которые основание высоты делит гипотенузу (рис.2).
Доказательство . Углы треугольников BCD и ACD (рис.2) удовлетворяют соотношениям
Таким образом, длина отрезка CD является средним геометрическим между длинами отрезков BD и AD , что и требовалось доказать.
Высоты можно провести из каждой вершины треугольника, однако у треугольников различных типов высоты располагаются по-разному, как показано в следующей таблице.
Расположение высот у треугольников различных типов
| Фигура | Рисунок | Описание |
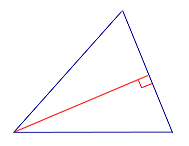
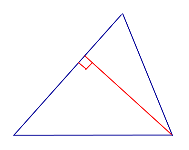
| Остроугольный треугольник | 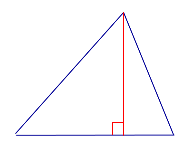 |
Все высоты остроугольного треугольника лежат внутри треугольника. |
 |
||
 |
||
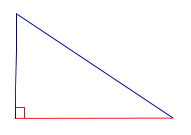
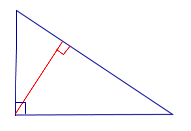
| Прямоугольный треугольник | 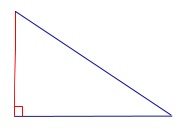 |
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника |
 |
||
 |
||
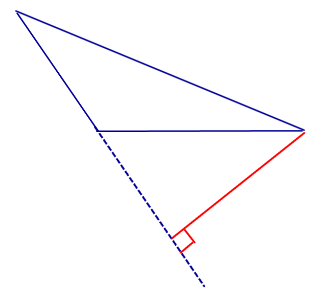
| Тупоугольный треугольник | 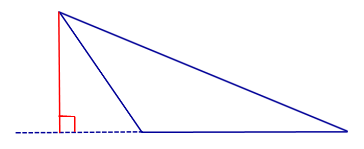 |
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
 |
||
 |
| Остроугольный треугольник | ||
 |
 |
 |
| Все высоты остроугольного треугольника лежат внутри треугольника. | ||
| Прямоугольный треугольник | ||
 |
 |
 |
| Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника | ||
| Тупоугольный треугольник | ||
 |
 |
 |
| Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника |
Все высоты остроугольного треугольника лежат внутри треугольника.
Высоты прямоугольного треугольника, проведённые из вершин острых углов, совпадают с катетами треугольника. Высота, проведённая из вершины прямого угла, лежит внутри треугольника
Высоты тупоугольного треугольника, проведённые из вершин острых углов, лежат вне треугольника. Высота, проведённая из вершины тупого угла, лежит внутри треугольника
Ортоцентр треугольника
Теорема 1 . Высоты треугольника (или их продолжения) пересекаются в одной точке.
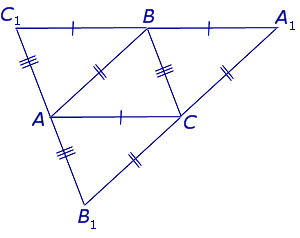
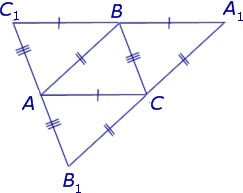
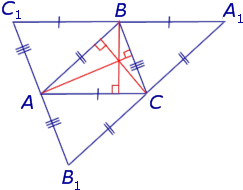
Доказательство . Рассмотрим произвольный треугольник ABC и проведём через каждую из его вершин прямую, параллельную противолежащей стороне (рис.3).
Обозначим точки пересечения этих прямых символами A1 , B1 и C1 , как показано на рисунке 3.
Следовательно, точка B является серединой стороны C1A1 .
Следовательно, точка A является серединой стороны C1B1 .
Следовательно, точка C является серединой стороны B1A1 .
и в силу теоремы о серединных перпендикулярах пересекаются в одной точке.
Теорема 1 доказана.
Определение 2 . Точку пересечения высот треугольника (или их продолжений) называют ортоцентром треугольника.
У треугольников различных типов ортоцентры располагаются по-разному, как показано в следующей таблице.
Расположение ортоцентров у треугольников различных типов
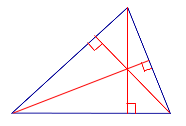
Ортоцентр остроугольного треугольника лежит внутри треугольника.
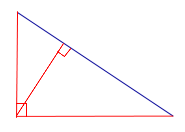
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
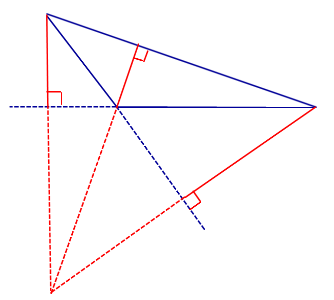
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла
Ортоцентр тупоугольного треугольника лежит вне треугольника.
В ортоцентре тупоугольного треугольника пересекаются не высоты, а продолжения высот треугольника.
Ортоцентрический треугольник
Решим следующую задачу.
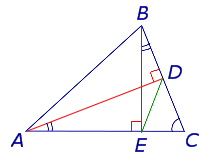
Задача . В остроугольном треугольнике ABC проведены высоты AD и BE (рис.5). Доказать, что треугольник DCE подобен треугольнику ABC .
Решение . Рассмотрим треугольники ADC и BEC . Эти треугольники подобны в силу признака подобия прямоугольных треугольников с равными острыми углами (угол C общий). Следовательно, справедливо равенство
Это равенство, а также наличие общего угла C позволяют на основании признака подобия треугольников заключить, что и треугольники DCE и ABC подобны. Решение задачи завершено.
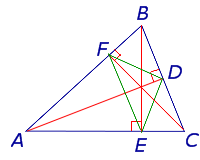
Определение 3 . Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника (рис 6).
Из определения 3 и следствия 1 вытекает следствие 2.
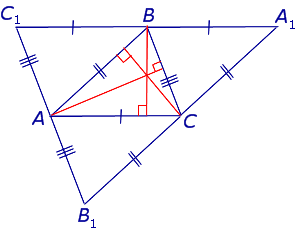
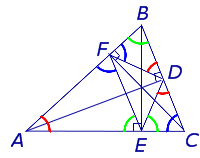
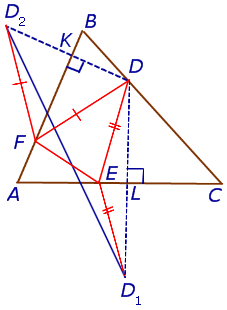
Следствие 2 . Пусть FDE – ортоцентрический треугольник с вершинами в основаниях высот остроугольного треугольника ABC (рис 7).
Тогда справедливы равенства
Из следствия 2 вытекает теорема 2.
Теорема 2 . Высоты остроугольного треугольника являются биссектрисами углов его ортоцентрического треугольника (рис.7).
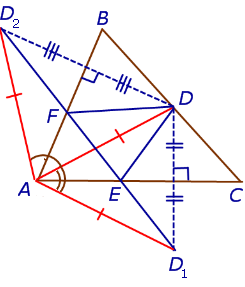
Доказательство . Воспользовавшись следствием 2, получаем:
что и требовалось доказать.
Задача Фаньяно
Задача Фаньяно . Рассматриваются всевозможные треугольники DEF , вершины D, E и F которых лежат на сторонах BC, AC и AB остроугольного треугольника ABC соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника ABC .
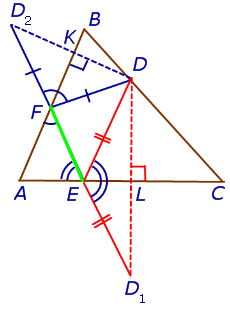
Решение . Пусть DEF – один из рассматриваемых треугольников. Обозначим символом D1 точку, симметричную точке D относительно прямой AC , и обозначим символом D2 точку, симметричную точке D относительно прямой AB (рис.8).
Поскольку отрезок прямой – кратчайшее расстояние между двумя точками, то периметр треугольника DEF оказывается не меньшим, чем длина отрезка D1D2 . Отсюда вытекает, что при фиксированной точке D наименьшим периметром обладает такой треугольник DEF , вершины F и E которого являются точками пересечения прямой D1D2 с прямыми AB и AC соответственно. Периметр этого треугольника равен длине отрезка D1D2 (рис.9).
Заметим также, что выполнено равенство
Кроме того, выполнено равенство
Отсюда вытекает, что длина отрезка D1D2 будет наименьшей тогда, когда длина отрезка AD будет наименьшей, т.е. в том случае, когда отрезок AD является высотой треугольника ABC . Другими словами, наименьшим периметром обладает такой треугольник DEF , у которого вершина D является основанием высоты треугольника ABC , проведённой из вершины A , а вершины E и F построены по описанной выше схеме. Таким образом, среди всевозможных треугольников DEF треугольник с наименьшим периметром является единственным.
Если обозначить длину высоты, проведённой из вершины A , длину стороны AB и радиус описанной около треугольника ABC окружности буквами h, c и R соответственно, то, воспользовавшись теоремой синусов, получим:
Следовательно, наименьший периметр рассматриваемых треугольников DEF равен
Теперь докажем, что ортоцентрический треугольник и является треугольником с наименьшим периметром. Для этого воспользуемся следующей леммой.
Лемма . Пусть DEF – ортоцентрический треугольник треугольника ABC (рис.10).
В этом случае отрезок D1D2 проходит через точки F и E .
Доказательство . Заметим, что в силу следствия 2 выполняются равенства:
Кроме того, в силу равенства треугольников DFK и KFD2 , а также в силу равенства треугольников DEL и LED1 выполняются равенства:
откуда вытекает, что углы AEF и D1EL , а также AFE и D2FK являются вертикальными углами. Это означает, что точки D1 , F, E , D2 лежат на одной прямой. Лемма доказана.
Доказательство леммы и завершает решение задачи Фаньяно.
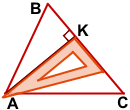
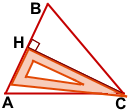
Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.
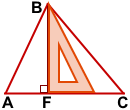
BF — высота треугольника ABC, опущенная из вершины B на сторону AC.
CH — высота треугольника ABC, проведённая из вершины C к стороне AB.
Все высоты треугольника пересекаются в одной точке.
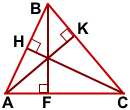
Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.
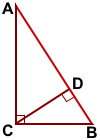
В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.
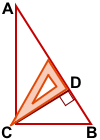
CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.
Точка пересечения высот прямоугольного треугольника — вершина прямого угла.
Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.
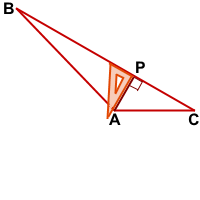
В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.
Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.
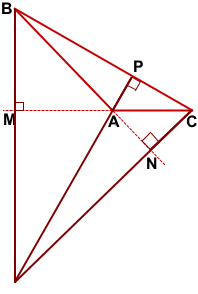
AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.
Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.
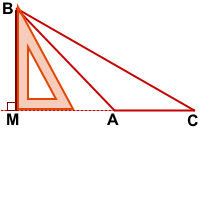
Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.
Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.
BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.
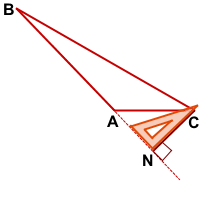
CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.
Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.
Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.
Мы рассмотрели, как строить высоты треугольника с помощью угольника.
Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».
Определения
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном это обычный треугольник и подход к решению таких фигур ничем не отличается.
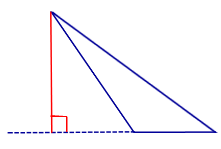
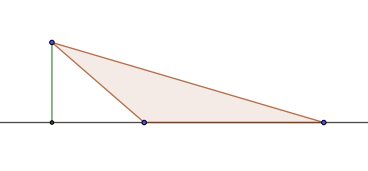
Рис. 1. Тупоугольный треугольник.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
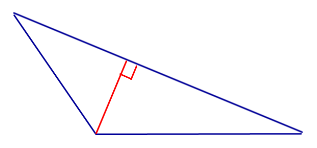
Рис. 2. Высота в тупоугольном треугольнике.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Пример решения задачи
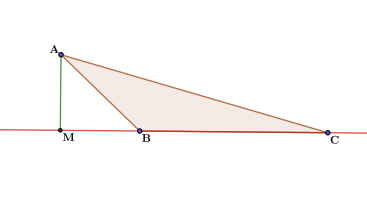
Рис. 3. Рисунок к задаче.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
- Через площадь треугольников. Площадь можно найти как половину произведения основания на высоту, проведенную к этому основанию. А можно как половину произведения двух сторон на синус угла между ними. Нам известен косинус угла, а через косинус всегда можно найти синус.
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
- Второй способ это достроить тупоугольный треугольник до прямоугольного. Если присмотреться, то можно заметить на чертеже два прямоугольных треугольника – это треугольники АМС и АМВ. В треугольнике АМВ можно найти косинус угла АВМ с помощью формул-приведений. Затем через значение косинуса найти значение синуса того же угла. А синус это отношение противолежащего катета к гипотенузе. Противолежащей катет – это искомая нами высота, а гипотенуза это сторона АВ прямоугольного треугольника.
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
- Третий метод это теорема синусов и косинусов. Для того, чтобы воспользоваться этим способом, через теорему косинусов найдем значение АС, потом через теорему синусов найдем синус угла АСВ и определим АМ из синуса угла АСВ большого прямоугольного треугольника АМС.
$$sqrt<13+4+4>=sqrt<21>=sqrt<9*3>=3sqrt<3>$$ – по теореме косинусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
Выразим искомый синус угла АСВ.
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
Ответы всех трех способов совпали, а значит задача решена верно.
Что мы узнали?
Мы поговорили об определении тупоугольного треугольника. Узнали и посмотрели на практике, какие методы решения тупоугольных треугольников существуют, а так же выяснили ,какие формулы и теоремы необходимо знать для успешного решения тупоугольного треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.6 . Всего получено оценок: 134.
Не понравилось? — Напиши в комментариях, чего не хватает.
Содержание
- Определения
- Пример решения задачи
- Что мы узнали?
Бонус
- Тест по теме
- Площадь прямоугольного треугольника
- Высота треугольника
- Площадь правильного треугольника
- Площадь прямого треугольника
- Площадь равностороннего треугольника
- Площадь равнобедренного треугольника
- Медиана треугольника
- Правильный треугольник Тупоугольный треугольник
- Остроугольный треугольник
- Свойства прямоугольного треугольника
- Стороны прямоугольного треугольника
- Средняя линия прямоугольного треугольника
- Признаки подобия прямоугольных треугольников
- Высота равностороннего треугольника
- Медиана равностороннего треугольника
- Неравенство треугольника
- Длина медианы правильного треугольника
- Равнобедренный тупоугольный треугольник
- Средняя линия прямоугольного треугольника
- Длина средней линии треугольника
показать все
По многочисленным просьбам теперь можно: сохранять все свои результаты, получать баллы и участвовать в общем рейтинге.
- 1.
Михаил Тяпин 214
- 2.
Наталия Дробот 198
- 3.
Мария Кауфман 192
- 4.
Игорь Проскуренко 157
- 5.
Соня Зверева 153
- 6.
Василиса Варавкина 119
- 7.
Иоанн Стефановский 107
- 8.
Софья Холена 94
- 9.
Оля Проскурина 85
- 10.
Татьяна Бежина 83
- 1.
Мария Николаевна 13,500
- 2.
Лариса Самодурова 12,695
- 3.
Liza 12,310
- 4.
Кристина Волосочева 11,445
- 5.
TorkMen 11,441
- 6.
Ekaterina 11,176
- 7.
Влад Лубенков 11,100
- 8.
Лиса 11,070
- 9.
Юлия Бронникова 11,060
- 10.
Вячеслав 10,840
Самые активные участники недели:
- 1. Виктория Нойманн — подарочная карта книжного магазина на 500 рублей.
- 2. Bulat Sadykov — подарочная карта книжного магазина на 500 рублей.
- 3. Дарья Волкова — подарочная карта книжного магазина на 500 рублей.
Три счастливчика, которые прошли хотя бы 1 тест:
- 1. Наталья Старостина — подарочная карта книжного магазина на 500 рублей.
- 2. Николай З — подарочная карта книжного магазина на 500 рублей.
- 3. Давид Мельников — подарочная карта книжного магазина на 500 рублей.
Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.
Раз уж вы нашли косинус и синус угла в треугольнике — дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.
Но есть и решение в векторах, вообще без тригонометрии.
Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны — AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:
Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:
(rC-rA)² = a²
(rC-rB)² = b²
Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:
(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)
У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ — значит, это уравнение прямой CC’. Кстати, разности rB — rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).
В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием «сингулярность»: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная — деление на ноль будет при попытке выразить x через y.
Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:
r = r0 + t u
Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем — задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.
Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:
r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)
Подставим первое уравнение во второе и решим его относительно переменной t:
2(rA + tAB)·AB = a² - b² - (rA² - rB²)
2rA·AB + 2t AB² = a² - b² - (rA² - rB²)
t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²
t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²
t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²
t = (a² - b² + (rA - rB)²) / 2AB²
t = (a² - b² + AB²) / 2AB²
Осталось подставить эту переменную обратно в параметрическое уравнение:
t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB
Формула выглядит страшно, но не имеет сингулярностей пока A и B — разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.
Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.
И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB — xA, yB — yA) — то повёрнутый будет с координатами (-yB + yA, xB — xA). Почему так — объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.
Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.
rC = r0 + k AB^
(rC-rA)² = a²
И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):
(r0-rA + k AB^)² = a²
k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0
Тут есть и дальнейшие упрощения: вектор r0—rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.
Суммируя всё что написано выше, получаем следующую систему уравнений:
t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^
Осталось решить примитивное квадратное уравнение:
t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^
Дальше осталось перейти от векторов к координатам и решение готово.



![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)

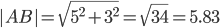
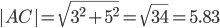
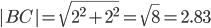
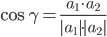
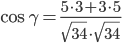
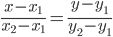
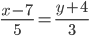


 Сообщение было отмечено как решение
Сообщение было отмечено как решение