Как найти вершины в черчении

Цели урока: (Слайд 2).

• Научиться находить и определять вершины, ребра
  и грани предмета, считать и назвать их,
• проецировать их на плоскости.
• Научиться применить полученные знания на
  практике.
• Познакомиться с понятиями вершин, ребер, граней
  предмета.
• Научиться находить и считать их количество.
• Ознакомимся со способом проецирования вершин,
  ребер и граней предмета на плоскости проекции.

ХОД УРОКА

1. Организационный момент (2 мин.)

Учитель: Здравствуйте ребята,
садитесь.

2. Объяснение нового материала (30 мин.)

Вступительное слово учителя:
Изображения любых самых простых объектов
окружающего нас мира состоят из простейших
геометрических элементов: вершин, ребер, граней и
кривых поверхностей. Изображение любого
предмета сводится к изображению вершин, ребер,
граней, кривых поверхностей.

Учитель сообщает тему урока, цели и план
изучения нового материала.  (Слайд 3)

– Выполним задание по заданной теме. Запишем
домашнее задание.
– Начинаем изучение нового материала с первого
пункта плана (по гиперссылке на Слайд 4).

Появляется наглядное изображение предмета
(можно спросить геометрическую форму заготовки,
из которой изготовлено изделие).

Учитель: С понятием вершина вы
знакомились на уроках геометрии – вершина
треугольника, четырехугольника и т.д. Мы сейчас
посмотрим, что же называется вершиной данной
фигуры. Вершину – будем обозначать заглавными
буквами латинского алфавита.

После того как проявились 11 вершин, учитель
задает вопрос: все ли вершины показаны па
изображении?

Учащиеся: Нет. Не показана вершина на
заднем плане  (появляется недостающая
вершина).

Учитель: Принято не показывать
вершины точками, а только обозначать (точки
исчезают, а обозначения остается). Назовите все
вершины.

Ученик: А, В, С, D, F, E, О, Р, Т, N, У, G.

Учитель: Понятие ребра вам тоже
знакомо. Как вы на геометрии называете отрезок,
соединяющий соседние вершины, например,
треугольника?

Ученик: Сторона треугольника.

Учитель: А мы будем называть отрезки,
соединяющие соседние вершины детали – ребрами.
Например, РА (на него указывает стрелка и
выделяется другим цветом), FD (на него указывает
стрелка и выделяется другим цветом). После
исчезновения указательных стрелок вопрос:
назовите еще ребра данной фигуры?

Ученик: АВ, ОР, и т.д.

Учитель: Понятие грани предмета для
вас ребята новое, но с этим понятием вы
познакомитесь подробнее в курсе геометрии. Это
многоугольники, из которых состоит поверхность
предмета. Рассмотрим грань, выделенную малиновым
цветом.

Учитель сам называет её, а стрелка указывает
(PABVNT). Другую грань, указанную стрелкой (розовую)
учитель просит назвать учеников.

Ученик: EТNP

Учитель: Назовите другие грани.

Ученик: DCBV и т.д.

После этого все указывающие стрелки исчезают.

Учитель: Мы с вами рассмотрели
вершины, ребра и грани предмета. Как вы это
усвоили мы сейчас проверим.

Вопросы:

– Сколько вершин? (12)
– Сколько ребер? (18)
– Сколько граней данного предмета? (8)

Ученики считают и сверяются с изображением
на слайде.

– Переходим к рассмотрению второго вопроса
нового материала (гиперссылка на СЛАЙД 5). Дано
наглядное изображение детали. Выполните три вида
данной детали (ученикам заранее раздается
заготовки габаритных рамок для эскизного
вычерчивания видов).

Учащиеся работают на заготовках, затем
сверяются с изображением на слайде.

Учитель: Рассмотрим на наглядном
изображении любые две вершины (А, В) и построим их
изображения на видах. Их мы будем обозначать
прописными буквами латинского алфавита, причём,
на главном один штрих, вид сверху – без штрихов,
вид слева – два штриха добавляют у буквы.

После построения проекций вершин на главном
виде учитель называет вершину, которая видна ­–
видимой (а), а другую, которая расположена за ней
– невидимой (b).
После всего построения делаем вывод:
проекция вершины на плоскость – есть всегда
точка
(независимо от расположения) – запись в
рабочих тетрадях. 
Далее рассматривается ребро АВ и его
изображения на чертеже.
После построения делаем вывод:
проекция ребра на плоскость – зависит от его
расположения Учитель предлагает ученикам
продемонстрировать (модель: отрезок – ручка,
плоскость – парта) расположение отрезка
относительно плоскости проекции.
По гиперссылке переходим на СЛАЙД 6 –
расположение ребра относительно плоскостей
проекций.
И с СЛАЙДА 6 по гиперссылкам на СЛАЙДЫ 8,9, 10, 11,
где наглядно показано расположение отрезка
относительно плоскостей проекций. С каждого из
этих слайдов по гиперссылке возвращаемся на
СЛАЙД 6. После рассмотрения всех случаев
расположения ребра относительно плоскостей
проекции по гиперссылке возвращаемся на СЛАЙД 5.

Учитель: На наглядном изображении
выделим одну из граней (стрелка указатель).
Рассмотрим изображение проекции грани на
чертеже.

После построения делаем вывод: проекция
грани на плоскость – зависит от его
расположения.
Для рассмотрения зависимости расположения
грани относительно плоскостей проекций
переходим по гиперссылке на СЛАЙД 7 и по
гиперссылкам рассматриваем СЛАЙД 12, 13 , с каждого
из этих слайдов по гиперссылке возвращаемся на
СЛАЙД 7. После рассмотрения всех случаев
расположения грани относительно плоскостей
проекции по гиперссылке возвращаемся на СЛАЙД 5.
СЛАЙД 5 рассмотрен, по гиперссылке на СЛАЙД 3 –
план изучения нового материала.

– Переходим к рассмотрению третьего вопроса
нового материала (гиперссылка на СЛАЙД 14)
выполнение задания по заданной теме.

Учащиеся выполняют эскизно чертеж детали
(заготовка габаритных рамок для вычерчивания
видов).

3. Итог урока и запись домашнего задания
(8 мин.)

Учитель оценивает выполнение практического
задания.

Проекции точек на поверхностях геометрических тел

Вы уже знаете, как построить проекции предмета или объекта. Часто при изготовлении изделий необходимо по заданным проекциям определить геометрическую форму предметов и их частей. Предмет можно рассматривать как комбинацию различных геометрических элементов: вершин, ребер, граней и т. д.

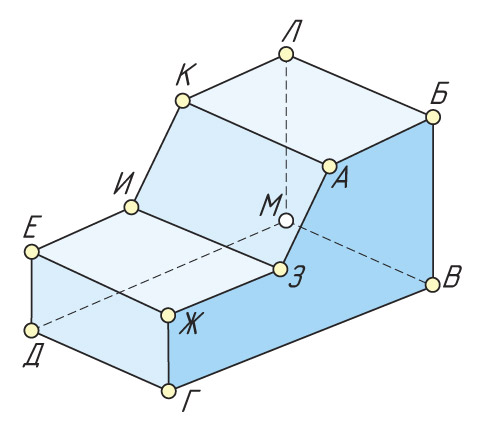
Укажите количество вершин, ребер и граней изображенного предмета.

Для точного построения изображений ряда деталей необходимо уметь находить проекции отдельных точек. Чтобы построить проекции точки, принадлежащей поверхности геометрического тела, необходимо понять, на какой поверхности или на каком элементе поверхности (ребре, вершине, грани) находится эта точка. Представив любую деталь как совокупность геометрических тел, можно легко найти проекцию точки.

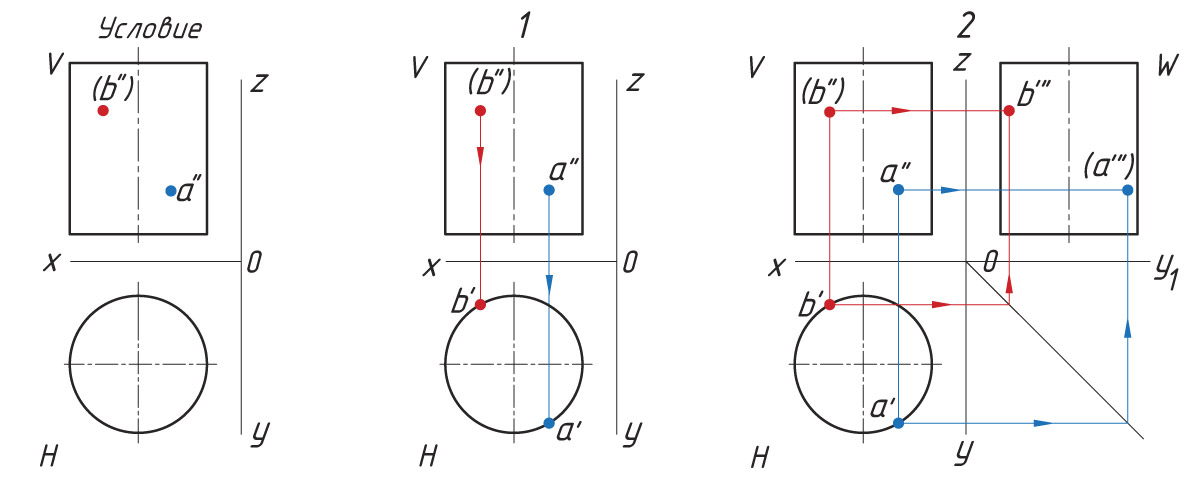
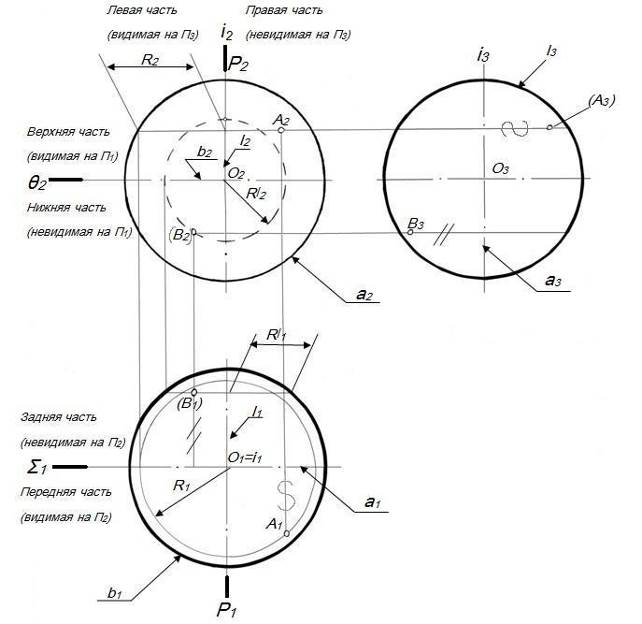
Рассмотрим проекции точки на геометрических телах. Проецирование точек на поверхности цилиндра  Последовательность проецирования точек Заданы фронтальные проекции а″ и b″ точек А и В, лежащие на боковой поверхности цилиндра. Проекция а″ находится на видимой части поверхности цилиндра (на плоскости V показана без скобок), b″ находится на невидимой части поверхности цилиндра (на плоскости V показана в скобках). 1. Находят горизонтальные проекции точек а′ и b′. Так как горизонтальная проекция боковой проекции цилиндра отображается в виде круга, то проекции точек а′ и b′ будут находиться на нем. Для их нахождения проводят вертикальные линии связи из проекций точек а″ и b″ до пересечения с окружностью. 2. Проекции точек а′″ и b′″ находят на пересечении линий проекционной связи.

Направление взгляда на плоскости проекций H, W помогает определить видимость проекций точек на горизонтальной и профильной плоскости проекций. Например, проекции а′ и b′ на плоскости H видны. Проекция а′″ на плоскости W не видна (показана в скобках), проекция b′″ видна (показана без скобок).

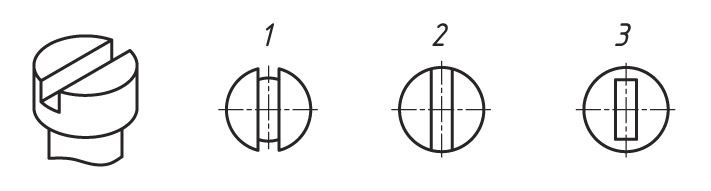
Определите, какая из горизонтальных проекций на рисунке является проекцией наглядного изображения головки винта. 

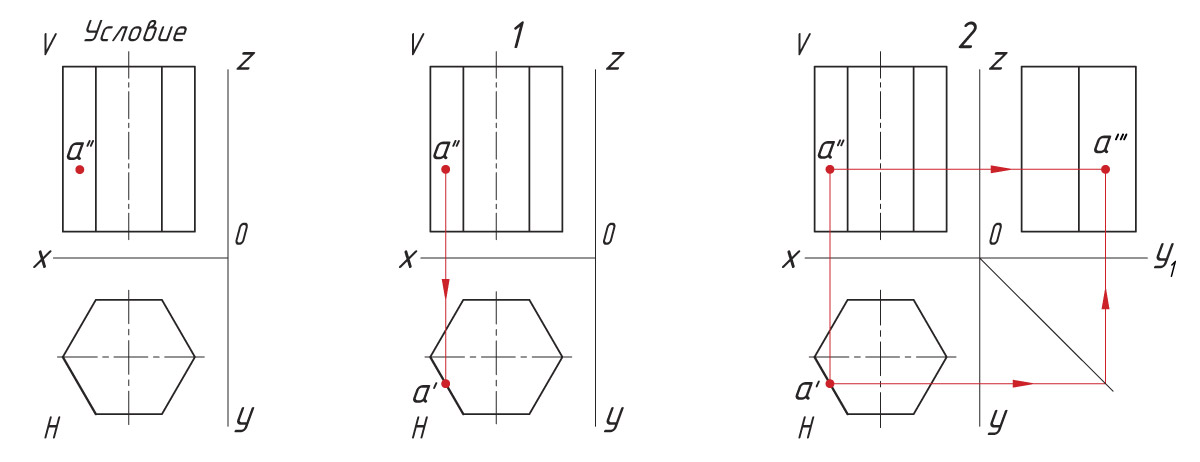
Проецирование точек на поверхности призмы  Последовательность проецирования точек Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности шестигранной призмы. 1. Находят горизонтальную проекцию точки а′. Для ее нахождения проводят вертикальную линию связи из проекции точки а″ до пересечения с шестиугольником (горизонтальная проекция призмы). 2. Проекцию точки а′″ находят на пересечении линий проекционной связи.

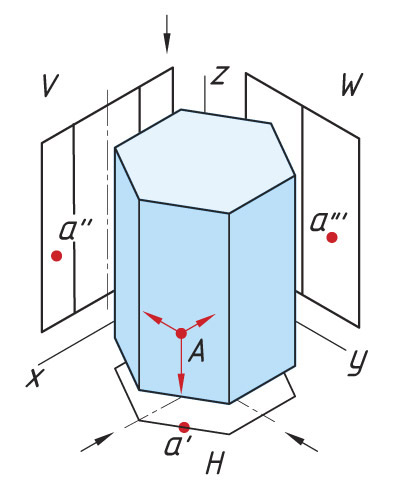Опишите последовательность проецирования точки, находящейся на ребре призмы. Выполните это построение.

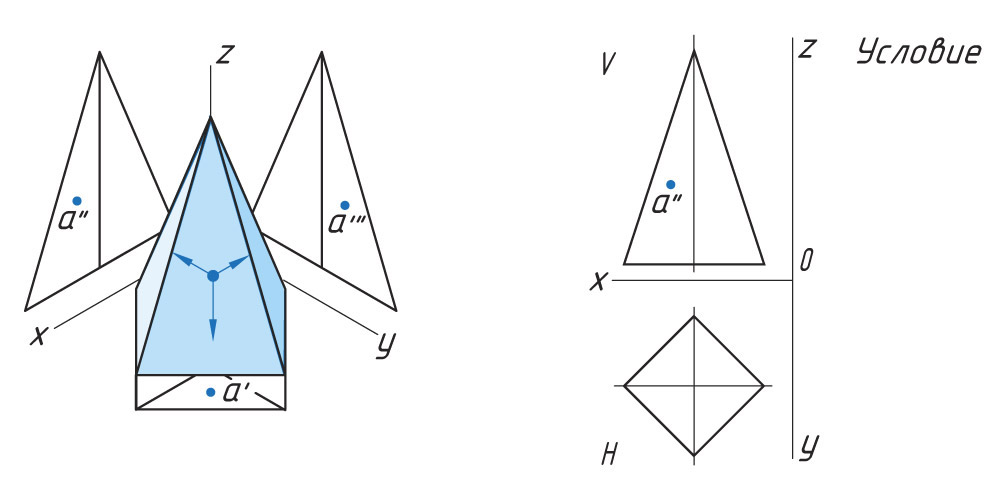
Проецирование точек на поверхности пирамиды

Построение проекции точки, лежащей на ребре
Если точка находится на ребре предмета, то сначала необходимо выполнить проекцию ребра, а затем при помощи линий проекционной связи найти проекции точки, лежащей на ребре.

Как вы считаете, можно ли таким способом спроецировать точку, находящуюся не на ребре, а на грани четырехгранной пирамиды? Свои предположения проверьте на практике.

Общий метод определения точки, лежащей на поверхности геометрического тела, заключается в следующем: через точку на поверхности проводят вспомогательную прямую, проекции которой легко определяются на данной поверхности.

Построение проекции точки, лежащей на грани
Задана фронтальная проекция а″ точки А, лежащая на боковой поверхности четырехгранной пирамиды.

Проекции точек можно определить несколькими способами. Рассмотрим каждый из них. 

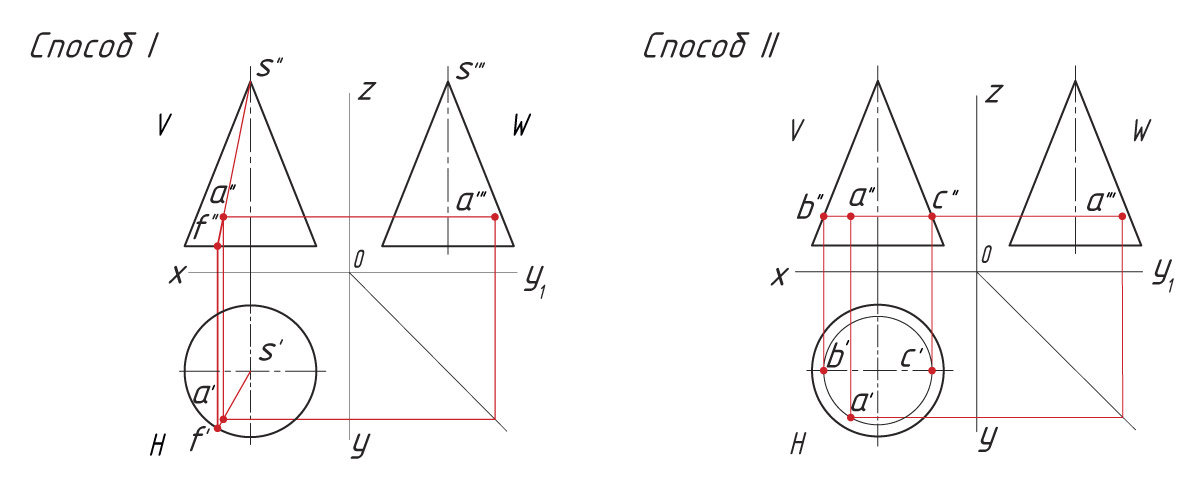
Способ I. 1. Находят горизонтальную проекцию точки а′: вспомогательной прямой соединяют заданную проекцию точки а″ с проекцией вершины пирамиды s″ и продлевают ее до пересечения с основанием в точке f″. 2. Проводят вертикальную линию связи из проекции f″ до пересечения с основанием на плоскости H в точке f′. 3. Точку f′ соединяют с вершиной пирамиды s′. На нее проводят вертикальную линию связи из проекции а″ до пересечения в точке а′. 4. Проекции точки а′″ находят на пересечении линий проекционной связи.

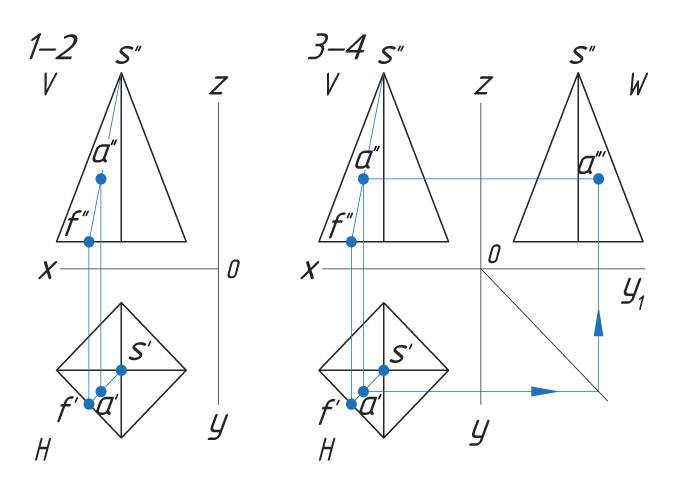Способ II. 1. Через проекцию а″ точки А проводят вспомогательную прямую и получают точки пересечения с ребрами пирамиды 1″ и 2″. 2. Опустив из точки 1″ вертикальную линию связи до пересечения с соответствующим ребром на плоскости H, получают горизонтальную проекцию точки 1′. 3. Для нахождения проекции 2′ проводят из точки 1′ вспомогательную прямую, параллельную основанию до пересечения с ребром. 4. Горизонтальную проекцию а′ определяют, опустив вертикальную линию связи из точки а″ до пересечения со вспомогательной прямой 1′2′. 5. Проекцию точки а′″ находят на пересечении линий проекционной связи.

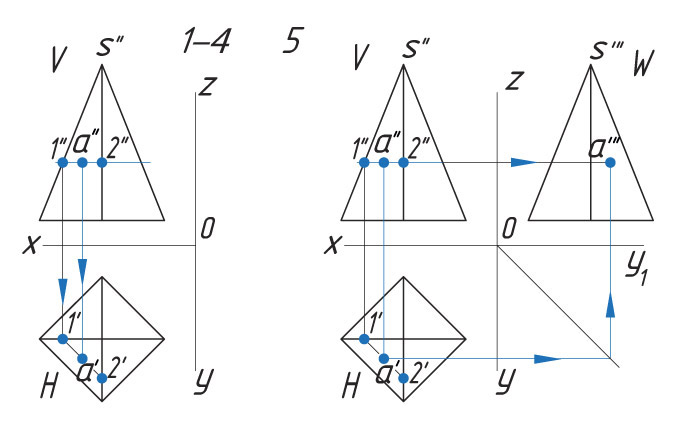На ваш взгляд, изменится ли положение проекции точки, если вспомогательную прямую провести не параллельно, а наклонно к горизонтальной плоскости?

Проецирование точек на поверхности конуса. На поверхности конуса проекции точек можно также определить двумя способами. Способ I заключается в определении проекций точки с помощью вспомогательной линии — образующей, расположенной на поверхности конуса и проведенной через точку А. В способе II через точку А проводят вспомогательную плоскость, которая пересечет конус по окружности, расположенной в плоскости, параллельной основанию конуса.

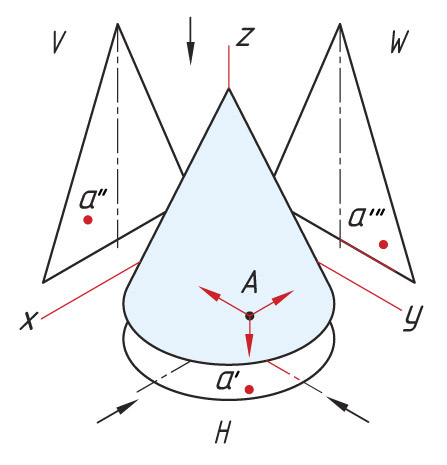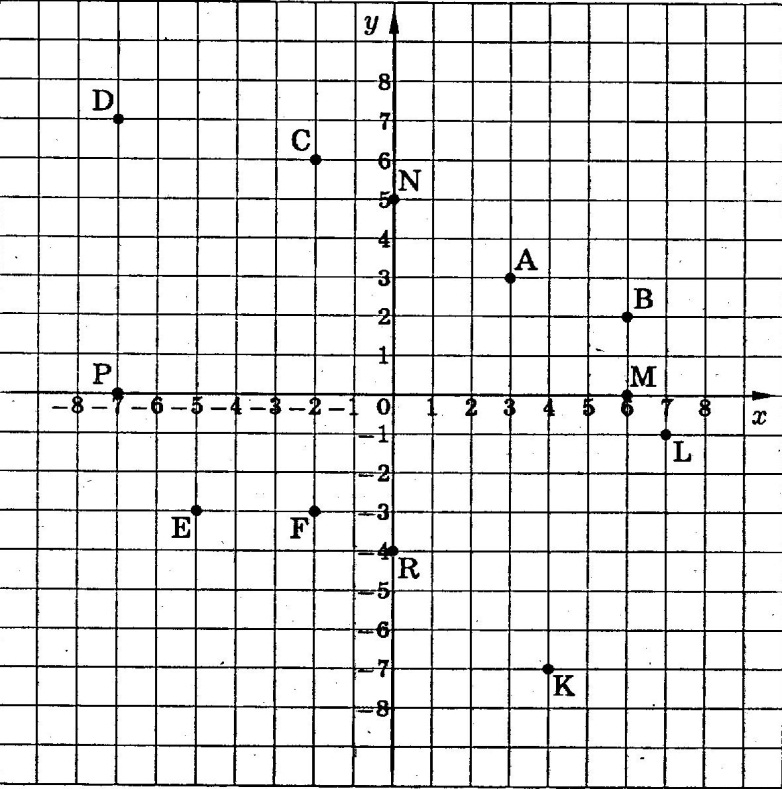
Точка – это геометрический абстрактный объект, который имеет координаты. Точки также участвуют в создании чертежа.

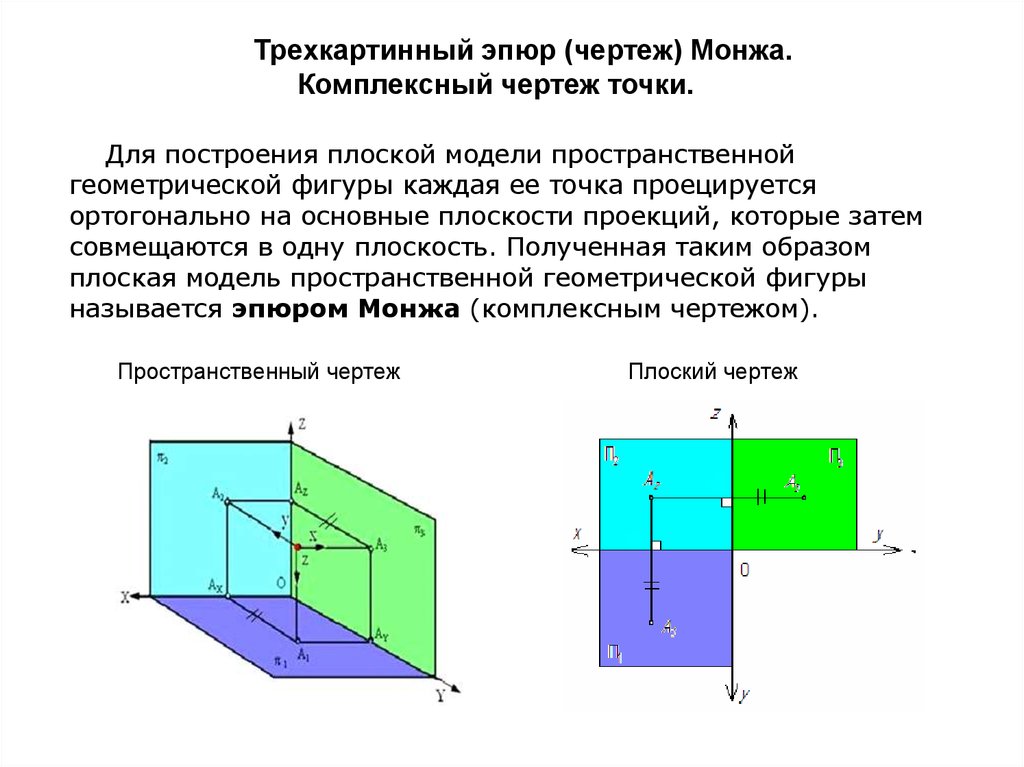
Комплексный чертеж и координаты точки

Комплексным называется чертеж, который был получен на фронтальной и горизонтальной плоскости проекции. Комплексный чертеж получается путем совмещения трех плоскостей проекций в одну.

Существует строгий порядок расположения проекций на чертеже, горизонтальная проекция должна располагаться под фронтальной, профильная проекция должна располагаться справа от фронтальной.

Как найти точки на чертеже

Рассматривая предмет как сочетание граней, вершин и ребер мы можем находить проекции отдельных точек. Для начала нужно определить, какой плоскости или грани точка принадлежит. Затем находят горизонтальные проекции точки, для этого проводят вертикальную прямую линию связи из проекции точек. Видимость проекций определяется исходя из направления взгляда.

Как правильно расставлять точки

Чтобы правильно вычертить вид детали, необходимо уметь строить проекции. С помощью проекций можно определить местоположение точки. Вспомогательные линии позволяют определить место, где ее можно поставить и используются в качестве опорных. Вспомогательные линии двух проекций пересекаются под углом в 45 градусов. В местах пересечения линий связи с проекциями поверхности расставляют точки.

Видимые и невидимые точки

Видимые проекции изображают на чертеже без скобок, а невидимые в скобках, например, А’’ относится к видимой проекции, а (B’’) к невидимой.

Точки сопряжения

В месте, где сопрягаются две линии образуется точка перехода или точка сопряжения. Для нахождения точки сопряжения линий прямого угла используется циркуль, его ставят в вершину угла и проводят дугу R до пересечения со сторонами. Чтобы найти центр сопряжения из найденных точек снова проводят окружности радиусом R, в месте их пересечения находится точка центра сопряжения, установив в нее циркуль проводят радиус сопряжения.

Опорные точки на чертеже

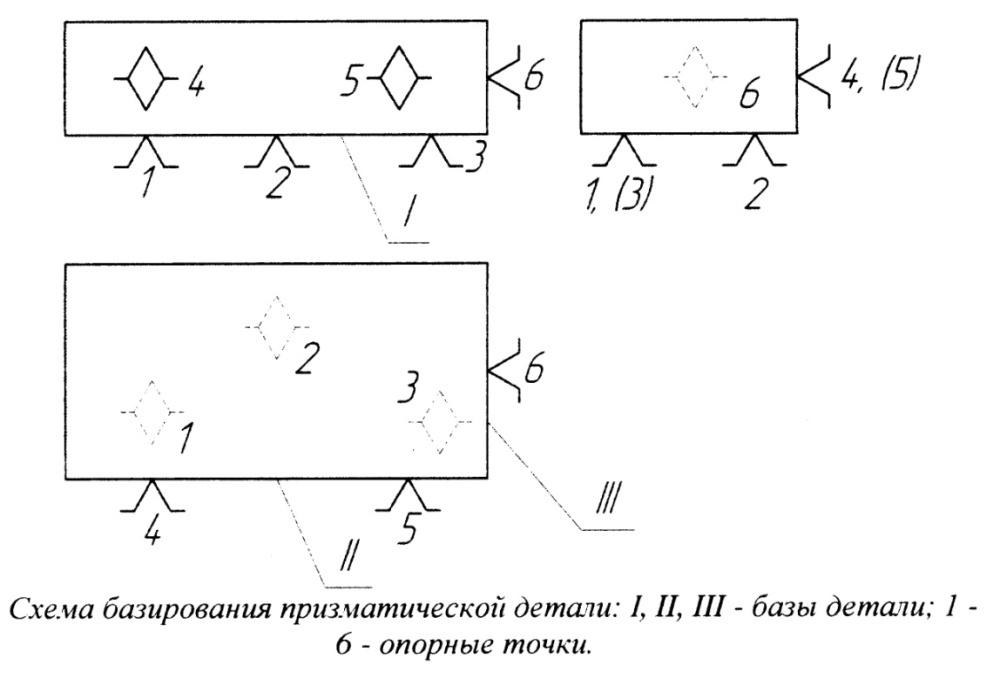
Опорные точки на схеме обозначают условными знакам согласно ГОСТ 21495-76, эти точки символизируют одну из связей заготовки иди изделия с выбранной системой координат. Нумерация опорных точек расставляется, начиная с базы, на которой расположено наибольшее число точек. Также опорные точки называют характерными, их число конечно, они выделяются своим особым положением относительно плоскости проекции и поверхности.

Сварные точки

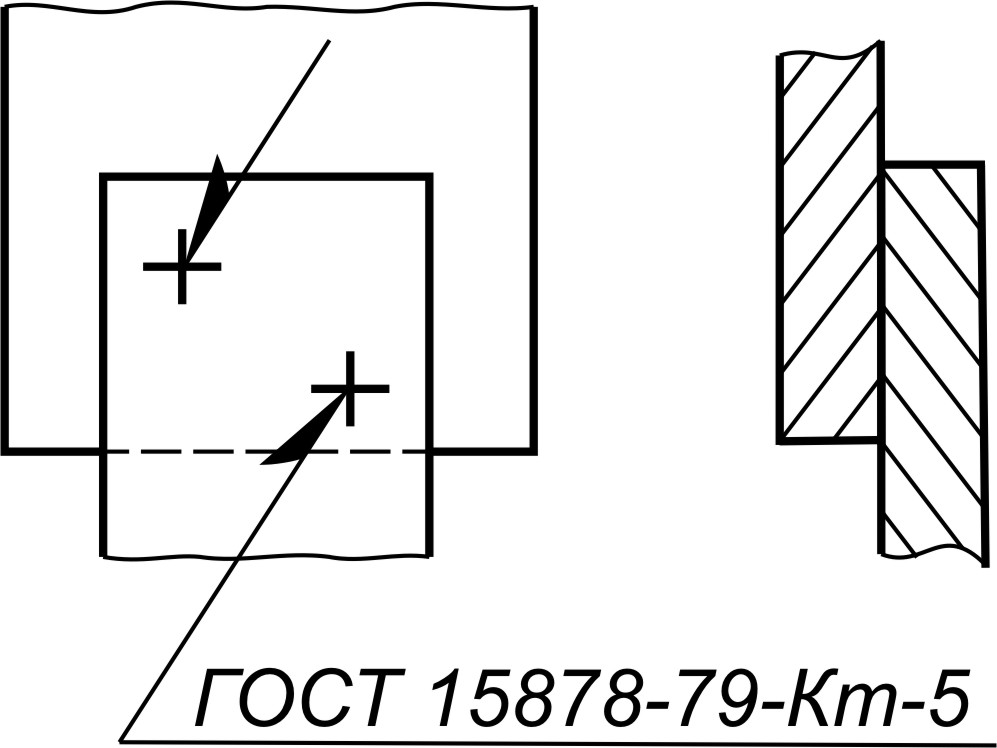
Если детали соединяются сваркой, то ее также условно изображают на чертеже. В зависимости от расположения сварки можно увидеть шов или одиночную точку. Видимую одиночную точку обозначают знаком «+», невидимые одиночные точки на чертеже не обозначают. Видимый сварной шов обозначают основной сплошной линией, а невидимый штриховой линией.

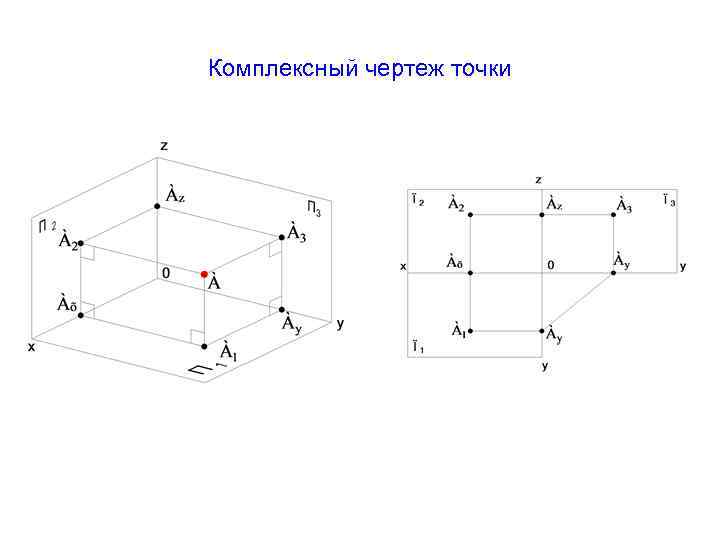
Трехкартинный чертеж точки

Трехкартинный чертеж или чертеж Монка представляет собой прямоугольник, сторонами которого являются линии связи, которые расположены перпендикулярно соответствующим осям проекции. При этом три вершины – проекции точки, а четвертая это точка перелома линии связи.

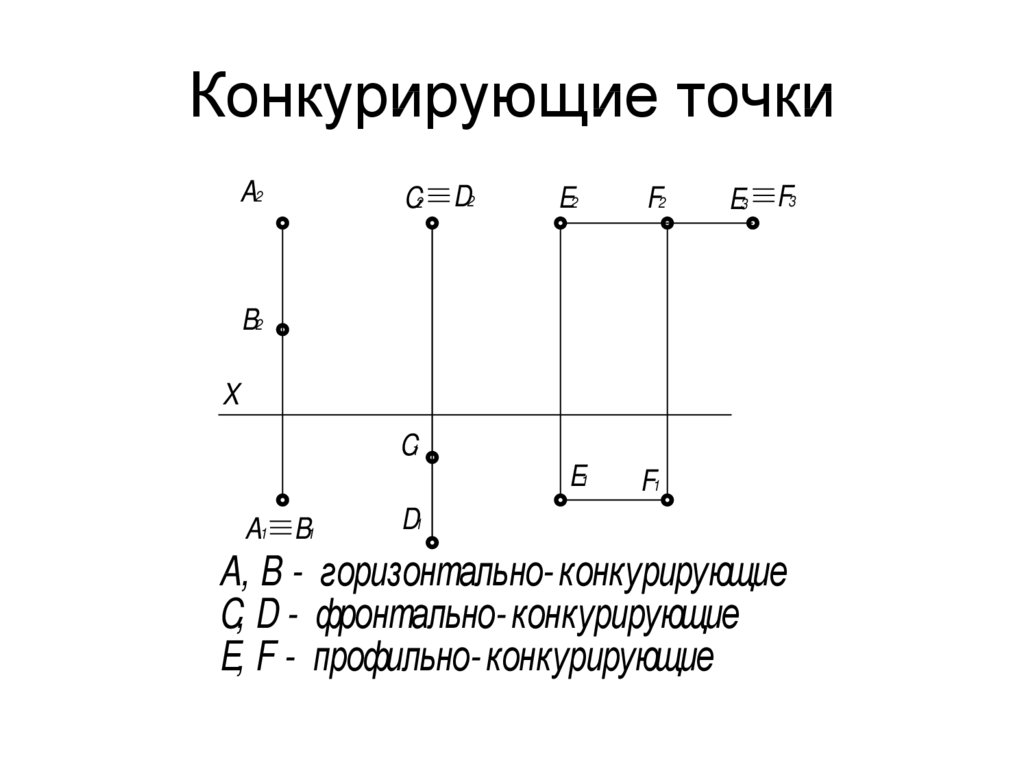
Конкурирующие точки на чертеже

Конкурирующие точки располагаются на одном проецирующем луче, таким образом для наблюдателя одна точка будет видимой, явной, а другая нет, что отразится и на чертеже.

Что такое явная точка на чертеже

Одним из важных понятий чертежа является база. Под базой понимается поверхность (точка, ось или сочетание поверхностей), принадлежащие заготовке, которая предназначена для придания изделию требуемого положения. Поверхность, используемая для базирования, может быть установочной ( лишает изделие возможностей перемещения), опорной (лишает одной степени свободы) или направляющей (лишает изделие или заготовку двух степеней свободы). По характеру базы могут быть скрытые и явные. Скрытые находятся в воображаемой плоскости или точке, а явные — в реальной поверхности или точке пересечения рисок.

Как построить комплексный чертеж точки: инструкция

Чтобы построить комплексный чертеж точки используется метод ортогональных или прямоугольных проекций, часто применяемый в инженерной графике. Проекция находится на пересечении проецирующего луча и плоскости.

Построение комплексного чертежа точки А состоит следующих этапов:

• возьмем две плоскости, которые перпендикулярны друг другу и назовем их П1 и П2;
• в результате пересечения проецирующих лучей, перпендикулярных каждой из плоскостей получаем горизонтальную и вертикальную проекцию точки А;
• координаты точки описываются с помощью расстояния до плоскостей;
• для построения плоского чертежа плоскость П1 разворачивают так, чтобы она совпадал с плоскостью П2, а прямая соединяющая А1 и А2 называется линией связи;
• третья плоскость вводится для построения профильной проекции.

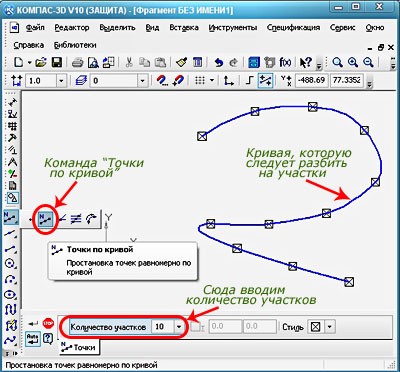
Как поставить точку на чертеже в Компасе

В меню программы Компас есть специальный инструмент «Точка», который позволяет сделать нужное действие за несколько шагов. Точку можно разместить, указав координаты, либо кликнув в месте рабочей области. Помимо основной функции команды, можно использовать расширенный список команд.

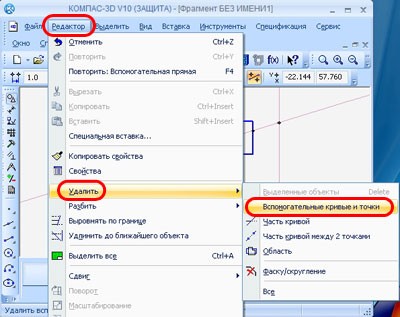
Как убрать точки на чертеже в Компасе

Убрать точки можно выделив их и нажав на клавишу «Delete», либо с помощью команды «Удалить вспомогательные кривые и точки».

Ответы на вопросы

Как правильно показать невидимую сварную точку?

Невидимые сварные точки не имеют обозначения, в отличие от швов.

Как на чертеже показать характерные точки отрезка?

Характерные точки зависят от объекта, у отрезка они находятся в начале и в конце прямой. Если какая-либо точка принадлежит прямой, то ее проекция принадлежит проекции прямой. При этом длина проекции отрезка прямой общего положения меньше длины самого отрезка.

Чем отличается двухкартинный чертеж точки от трехкартинного?

Разница состоит в количестве проекций на поверхности. В двухкартинном чертеже используются горизонтальная и фронтальная плоскости, такой чертеж вполне позволяет описать форму и размеры фигуры. В трехкартинном чертеже используется еще и третья плоскость.

Урок №27

Тема урока: Нахождение на чертеже вершин, ребер, образующих и поверхностей

Учебно-воспитательные задачи:

1.Образовательная:  Проверить уровень сформированности знаний, умений, навыков   

2.Воспитательная:   Воспитывать навыки самостоятельной работы

3.Развивающая:  Развивать память учащихся: логическую, моторную, зрительную

Ход урока

1.Вводная часть. Информация о теме и цели урока.

Опрос домашнего задания по теме «Геометрические тела, проекции многогранников, проекции тел вращения».

     а)  Назовите предметы , имеющие форму шара, цилиндра, конуса, призмы.

     б)  Какие геометрические тела вам известны?

     в)  Для чего нужен анализ геометрической формы предмета?

 2.Изложение новой темы:

Как изображают элементы предметов. Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребра, грани, кривой поверхности и т. п. (рис. 85). Поэтому изображение любого предмета сводится к изображению его вершины, ребер, граней и кривых поверхностей.

Рис. 85. Элементы поверхности предмета

Рассмотрим этот процесс на примере построения прямоугольных проекций предмета (рис. 86).

Расположим предмет в пространстве так, чтобы каждая из двух параллельных между собой граней была параллельна одной из плоскостей проекций. Тогда эти грани изобразятся на соответствующих плоскостях проекций без искажения.

Проведем через вершины предмета проецирующие лучи, перпендикулярные плоскостям проекций, и отметим точки пересечения их с плоскостями V, H и W.

Предмет так расположен относительно плоскостей проекций, что на одном проецирующем луче оказалось по две вершины, поэтому их проекции слились в одну точку. Так, вершины А и В лежат на одном луче, перпендикулярном горизонтальной плоскости проекций H. Их горизонтальные проекции а и b совпали. Вершины А и С лежат на одном луче, проецирующем эти точки на фронтальную плоскость проекций. Их фронтальные проекции а’ и с’ также совпали. На профильной плоскости проекций W в одну точку (b» и d») спроецировались вершины В и D.

Из двух совпадающих на изображении точек одна является изображением видимой вершины, другая — закрытой (невидимой). На горизонтальмой проекции будет видима та вершина, которая расположена в пространстве выше. Так, вершина А видима, вершина В невидима. На фронтальной проекции видимой будет та вершина, которая находится ближе к нам. Отсюда а’ изображение видимой вершины А, с’ — изображение невидимой вершины С, она закрывается при проецировании вершиной А. На изображении обозначение проекций невидимых точек берут иногда в скобки.

Соединив попарно точки на фронтальной, горизонтальной и профильной проекциях, получим изображения ребер предмета. Например, ас — горизонтальная проекция ребра АС, а’b’ фронтальная проекция ребра АB

Рис. 86. Изображения предмета

На рисунке 86 видно, что если ребро параллельно плоскости проекций, то оно на этой плоскости изображается без искажения, или, как говорят, в истинную (натуральную) величину. В этом случае проекция ребра и само ребро равны между собой. Например, проекция а’b’ — истинная величина ребра АВ на фронтальной, а проекция а»b»— на профильной плоскости проекций.

Если ребро перпендикулярно плоскости проекций, оно проецируется на нее в точку. Так, на фронтальную плоскость проекций в точку спроецировалось ребро АС, на горизонтальную плоскость—ребро АВ, на профильную — ребро BD и т. д.

Построив проекции ребер, видим, что на изображении они ограничивают проекции граней. Как и ребро, грань, параллельная плоскости проекций, проецируется на нее без искажения. Например, на профильную плоскость проекций без искажения спроецировалась грань, в которой лежат точки А, В и С. На горизонтальную плоскость проекций спроецировались без искажения нижняя и верхняя грани и т. д. Найдите эти грани на чертеже предмета в системе прямоугольных проекций.

Если грань перпендикулярна плоскости проекций, она проецируется на нее в отрезок прямой.

Таким образом, каждый отрезок прямой на изображении — это проекция ребра или проекция плоскости, перпендикулярной плоскости проекций. Ребра и грани предмета, наклоненные к плоскости проекций, проецируются на нее с искажением. Найдите такие ребра и грань на рисунке 86.

Строя чертеж, надо четко представлять, как изобразится на нем каждая вершина, ребро и грань предмета. Читая чертеж, надо представить, изображение какой части предмета скрыто за каждой точкой, отрезком или фигурой.

Следует помнить, что каждый вид— это изображение всего предмета, а не одной его стороны. Разница заключается лишь в том, что одни грани спроецируются в истинную фигуру, другие— в отрезки прямых.

12.2. Построение проекций точек на поверхности предмета. Теперь рассмотрим способы построения проекций точек, лежащих на поверхностях предметов.

На рисунке 91 изображена шестиугольная пирамида. На линии, являющейся проекцией ребра, задана фронтальная проекция а точки А. Как найти ее остальные проекции?

Рис. 91. Построение проекций точки, лежащей на ребре пирамиды

Рассуждают так. Точка находится на ребре предмета. Проекции точки должны лежать на проекциях этого ребра. Следовательно, нужно сначала найти проекции ребра, а затем при помощи линий связи отыскать проекции точки.

Чтобы построить профильную проекцию предмета и, в частности, профильную проекцию ребра, на котором находится точка А, удобно воспользоваться постоянной прямой. Так называют линию, которую проводят справа от вида сверху под углом 45° к рамке чертежа (рис. 91). Линии связи, идущие от вида сверху, доводят до постоянной прямой. Из точек их пересечения проводят перпендикуляры к горизонтальной прямой и строят профильную проекцию.

Рис. 92. Построение постоянной прямой

Расположение постоянной прямой определяет место строящегося вида (рис. 91). Но если три вида уже построены, как на рисунке 92, а, нужно найти точку, через которую пройдет постоянная прямая. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии. Через полученную точку k (рис. 92, б) проводят прямую под углом 45° к осям. Это и будет постоянная прямая.

Если осей симметрии на чертеже нет, то продолжают до пересечения в точке k1горизонтальную и профильную проекции граней, проецирующихся в виде отрезков прямых. Через точку k1 проводят постоянную прямую.

А теперь вернемся к рисунку 91. Проекции ребра, на котором лежит точка А, выделены голубым цветом. Горизонтальная проекция точки А должна лежать на горизонтальной проекции ребра. поэтому проводим из точки а’ вертикальную линию связи. В месте ее пересечения с проекцией ребра находится точка а — горизонтальная проекция точки А.

Профильная проекция а» точки А лежит на профильной проекции ребра. Ее можно определить и как точку пересечения линий связи.

Мы рассмотрели, как находят на чертеже проекции точек, лежащих на ребрах предметов. Однако часто приходится строить проекции точек, лежащих не на ребрах, а на гранях. Например, чтобы просверлить в детали отверстие, надо определить, где находится его центр.

Чтобы по одной проекции точки, лежащей на грани предмета, найти остальные, нужно прежде всего найти проекции этой грани. Такие упражнения вы уже выполняли (см. рис. 89). Затем при помощи линий связи надо отыскать проекции точки, которые должны лежать на проекциях грани.

Линию связи сначала проводят к той проекции, на которой грань изображается в виде отрезка прямой.

Рис. 93. Построение проекций точки, лежащей на поверхности предмета

На рисунке 93 проекции грани, содержащие проекции точки А, выделены цветом. Точка A задана фронтальной проекцией а’. Горизонтальная проекция а этой точки должна лежать на горизонтальной проекции грани. Для ее нахождения проводят вертикальную линию связи из точки а’.

Чтобы найти профильную проекцию, нужно из точки а’ провести горизонтальную линию связи. В месте ее пересечения с отрезком прямой — проекцией грани лежит точка а».

Построение проекций точки В, изданной горизонтальной проекцией b, также показано линиями связи со стрелками.

3.Заключительная часть урока.

          Итог урока: Выставление оценок

Д/З просмотреть материал урока и подготовиться к графической работе №4

Просмотр содержимого документа

«Нахождение на чертеже вершин, ребер, образующих и поверхностей »

Муниципальное бюджетное общеобразовательное учреждение

Белоберезковская средняя общеобразовательная школа №1

Трубчевский  район  Брянская область

        

Разработка урока по черчению на тему:

     

                                  Учитель ИЗО и черчения:        

  Кивалина      Елена    

                                                                                                           Владимировна

Белая Березка

Тема урока:      « Проекции вершин, ребер и граней предмета»

Цели урока:   познавательные

• общеучебные:  познакомить с понятиями вершина, ребро, грань; учить проецировать элементы поверхности предмета на плоскости;

• развивающие: развивать логическое мышление на основе мыслительных операций анализа, синтеза, сравнения; установление причинно-следственных связей;
• воспитательные: воспитывать аккуратность и точность при выполнении графических построений , внимательность, усидчивость;

                      коммуникативные

           развитие социальной компетентности:

• умение слушать и вступать в диалог,                          
• участие в коллективном обсуждении;

Тип урока: комбинированный.

Методы , приемы  проведения: беседа, объяснение, демонстрация, чтение и выполнение чертежей, упражнения, работа с учебником.

Материальное обеспечение:   таблицы-задания  « Восстанови чертеж!», «Ошибающийся ученик»;  модель детали; таблицы для устных упражнений; карточки-задания; мультимедийное оборудование.

Литература:      1. Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С.

                        Черчение: Учебник для 9 кл. общеобразоват. учрежд.М.:                      

                        Просвещение 2009.

                             2. Ботвинников А.Д., Вышнепольский И.С. Черчение в

                            средней школе:  Пособие для учителя. М.: Просвещение,1989.

                            3.Кузьменко В.И. , КосолаповМ.А. Методика преподавания        

                               черчения. М.,1981

                           4. Воротников И.А. Занимательное черчение:

                               кн. для учащихся сред. шк.М.: Просвещение,1990  

Рекомендации  к  уроку:

                   Метод проекций — тема особая. Она не имеет прямых аналогий в других предметах, изучаемых к тому времени девятиклассниками. Учителю предстоит ввести учащихся в область знания, где с помощью воображаемых лучей происходит процесс воображаемого проецирования элементов поверхности предмета на несколько плоскостей. Справиться с подобной задачей ему поможет очень важная и полезная способность, которую принято называть пространственными  представлениями. Именно эта способность, это свойство человеческого мышления, помогает учащемуся заполнить этот пробел, который возникает перед ним, когда возможности практической реализации самого процесса проецирования с помощью физических средств отсутствуют, но задачу тем не менее можно решить, прибегая к помощи пространственных представлений и воображения. Перед обучающими эти задачи целесообразно ставить так, чтобы они имели реальный характер. Желательно, чтобы точки задавались не как абстрактные понятия, а как конкретные элементы изображаемых предметов. Таким требованиям отвечают вершины предмета. Поэтому упражнения в построении проекций точек целесообразно начать с определения проекций вершин. На этом уроке обучающееся должны получить сведения о видимых и невидимых точках, о проецировании прямых ребер и граней. Своим воспитанникам необходимо помочь уяснить, что каждая точка на чертеже есть проекция какой-либо вершины предмета , либо ребра, перпендикулярного к плоскости проекций. Каждая прямая линия чертежа – это проекция ребра или другой какой-либо линии предмета, либо проекция плоскости, перпендикулярной к плоскости проекций.

                    Задания на построения изображений точек, принадлежащих заданному на чертеже предмету, являются одним из средств, способствующих сознательному усвоению проецирования элементов объекта. В таких заданиях ученику необходимо произвести анализ объекта путем установления однозначного соответствия между заданными на чертеже проекциями точек и элементами поверхности , которым должны эти точки принадлежать. Для получения ответа необходимо:

1. прочитать чертеж, т.е. получить пространственное представление о геометрической форме объекта;
2. установить по чертежу, какому элементу поверхности принадлежит точка, одна из проекций которой задана;
3. выделить этот элемент на том виде, на котором задана проекция точки;
4. найти этот элемент на всех других видах чертежа, установив характер его изображения на каждом из видов;
5. достроить на выделенных элементах предмета отсутствующие на чертеже проекции точки с помощью линий проекционной связи;
6. проверить решение.

Данный урок позволяет осуществлению решения многих задач. Это  закрепление  правил построения чертежей,  развитие приемов сравнения деталей и их чертежей, углубление понятия о проекционной связи между изображениями.

План урока:

1. Мотивация учебной деятельности.

1. Организационный момент. Рефлексия.
2. Актуализация опорных знаний.

1. Повторение пройденного материала.

1. Построение проекций предмета.
2. Виды проецирования. Параллельное, прямоугольное проецирование.
3. Виды аксонометрических проекций. Изометрия.

1. Формирование знаний, умений и навыков.

1. Сообщение темы и целей урока.
2. Изучение нового материала:

    а) знакомство с элементами поверхности предмета;

    б) повторение метода проецирования;

    в) знакомство с алгоритмом построения проекций вершин, ребер, граней  предмета.

          3.  Здоровьесберегающая пауза. Рефлексия. Решение задачи.

1. Закрепление изученного материала.

1. Практическая работа по карточкам. Взаимопроверка.
2. Игра «Ошибающийся ученик».

1. Подведение итогов.

1. Беседа с обучающимися.
2. Оценивание обучающихся.
3. Рефлексия.

1. Домашнее задание.

                                                  Ход урока:

1. Мотивация учебной деятельности

1. Организационный момент. Рефлексия.

— Здравствуйте, ребята! Проверьте свое рабочее место, всё ли на месте? Сегодня на уроке вам понадобится: тетрадь, учебник, чертежные инструменты, цветные ручки (3 цветов).

— Порядок на рабочем месте,

В уме порядок уж давно.

Понять графическое построенье

Удастся всем нам все равно!

1. Актуализация опорных знаний.

 — Ученик по ошибке порвал чертеж, на котором изображены три проекции модели. Попробуйте восстановить взаимное расположение проекций                 ( приложение 1).

1. Повторение изученного материала.

— Выбрать из представленных наглядных изображений детали ту, которая соответствует данному построению проекции (приложение 2).

• Какие плоскости проекций представлены?
• Какие виды соответствуют данным плоскостям?
• Какие виды аксонометрических проекций вы знаете?
• Какой вид аксонометрической проекции соответствует представленному наглядному изображению детали?
• Какие виды проецирования вы знаете?
• Какой вид проецирования представлен на данных проекциях?
• Приведите из жизненной практики пример центрального проецирования.
• Что значит параллельное прямоугольное проецирование?

1. Формирование знаний, умений, навыков.

               1. Сообщение темы и целей урока (по презентации).

— Ребята, изображения любых самых простых объектов окружающего нас мира состоят из простейших геометрических элементов: вершин, ребер, граней и кривых поверхностей. Изображение любого предмета сводится к изображению вершин, ребер, граней, кривых поверхностей.

— Открыли тетради. Подписали число и тему урока: «Проекции вершин, ребер, граней предмета».

— Сегодня мы познакомимся с понятиями вершина, ребро, грань предмета. Будем учиться их находить. Познакомимся со способом проецирования вершин, ребер и граней на плоскости ( приложение №3).

            2.  Изучение новой темы.

1. Знакомство с элементами поверхности предмета (по презентации).

Вершина – это точка пересечения двух и более прямых линий, образующих угол.

Ребро – это отрезок, соединяющий соседние вершины.

Грань – это многоугольник, из которого состоит поверхность предмета.

— Сколько вершин имеет данная деталь?

— Назовите ребра данной детали.

— Назовите выделенную грань.

1. Повторение метода проецирования. Объяснение нового материала.

-В чем заключается метод проецирования, когда точка  находится в пространстве?

1. Знакомство с алгоритмом построения  проекций вершин, ребер и граней предмета.

• Построение видов детали.
• Построение вершин (на трех видах) видимых и невидимых.
• Построение ребер.
• Построение граней.

Объяснение учителя сопровождается чертежом у доски. По выбору предлагается модель детали.

• Построение видов (ученик).
• Построение проекций элементов поверхности предмета (учитель).

Ученики выполняют данное задание вместе с учителем в тетради.

        Для закрепления учебного материала учитель еще раз объясняет последовательность построения проекции поверхности предмета по презентации.

1. Здоровьесберегающая пауза. Рефлексия. Решение задачи.

На дворе у дома лежали бочки и ящики. Пошел дождь. После дождя хозяин решил убрать их в сарай. После бочек и ящиков на земле остались следы. Сколько было бочек и сколько ящиков?  (приложение №4)

1. Закрепление изученного материала.

1. Практическая работа по карточкам ( приложение №5).

Взаимопроверка (по презентации).

1. Игра «Ошибающийся ученик». Найди ошибки  ( по таблице).

— Вы учились строить проекции вершин, ребер, граней предмета, соблюдая все правила построения. Но вот вам передали чертеж, где есть ошибки. Попробуйте теперь себя в роли учителя. Найдите ошибки.

1. Подведение итогов. Оценивание обучающихся.

1. Беседа с обучающимися.

– Что нового вы узнали на уроке?

—  Что понравилось,  что заинтересовало вас на  уроке?

—  Какие новые мысли, чувства у вас возникли на уроке? Что у нас на уроке было  особенно удачным, а что не получилось? Почему?

                 —  Добились ли мы поставленных целей?

—  На следующем уроке мы рассмотрим вопрос о проецировании точки , лежащей на поверхности предмета.

2. Рефлексия. Чтение  стихотворения.

• Появился в расписании замечательный предмет
  Сразу стала жизнь прекрасной и полнее спору нет .
  С чертежами всюду ходим дочертить их недосуг ,
  Всех соседей слезно просим будь то друг или не друг .
• Но сосед помочь не в силах, с чертежами ходит сам
  Зря соседа мы просили помогать придется нам
  Мы за шрифты дружно сели, не на шутку увлеклись .
  Не страшны теперь ним мели, вверх по курсу понеслись .
• Трудно было человеку десять тысяч лет назад.
  Не имел он готовален, не имел карандаша,
  Не резинки, не бумаги и не ГОСТов за душой,
  И работал он ногами, голове давал, покой.
• Хорошо теперь живется человеку на земле
  Чертежи с собою носит он повсюду и везде .
  Превратился в домоседа и не верит в чудеса
  Потому , что он изведал все сверхтайны чертежа .
• Гордо ты иди по свету, выше голову держи,
  Ведь просвета в жизни нету, коль не сделал чертежи.
  Береги же опыт скромный, пусть хоть маленький, но свой,
  Впереди нас ждет когда-то очень трудный курсовой.

1. Домашнее задание (дифференцированное).

1. п.12 (с. 69-71)- прочитать;

2. Знать элементы поверхности предмета, уметь их проецировать;

3. с. 72, упр. 21 (рис. 87-а)- в тетради;

4.* с.72, упр.21(рис. 87-б).

                                          ПРИЛОЖЕНИЕ