Как найти вертикаль прямоугольника

В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.

Стороны прямоугольника – вертикальные и горизонтальные, формула вычисления

Содержание

  • Длины прямоугольника
  • Примеры решения задач
    • Задача 1
    • Задача 2
    • Задача 3
  • Что мы узнали?

Длины прямоугольника

Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.

Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.

Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:

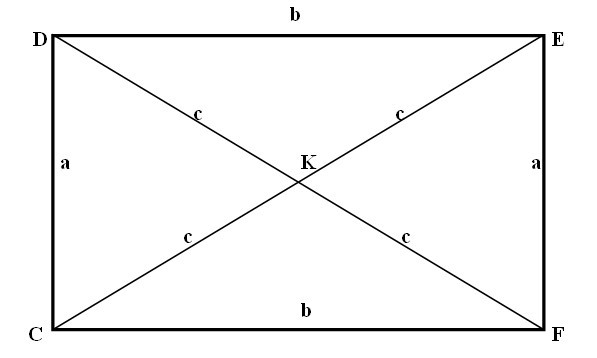
  • Диагонали прямоугольника равны.
  • Диагонали точкой пересечения делятся пополам.
  • Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.

Стороны прямоугольника – вертикальные и горизонтальные, формула вычисления

Рис. 1. Прямоугольник

Примеры решения задач

Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.

Задача 1

  • Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.

Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:

$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)

$a*b=S$ (уравнение для нахождения площади)

При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.

Продолжим решение. Выразим значение a из первого выражения системы.

  • $(а+b)*2=Р$
  • $а+b={Рover{2}}$
  • $а={Рover{2}}-b$
  • Подставим значение периметра: $а={20over{2}}-b=10-b$

Подставим получившееся выражение в уравнение нахождения площади:

$a*b=S$

$(10-b)*b=21$

$b^2-10b-21=0$

Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.

$а=10-b$

Значит, при $b=3$, $а=10-3=7$

При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.

Задача 2

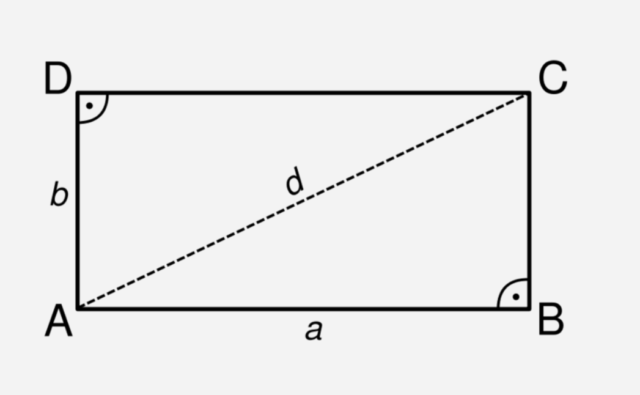
  • Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.

Стороны прямоугольника – вертикальные и горизонтальные, формула вычисления

Рис. 2. Рисунок к задаче.

Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).

Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.

$D^2=a^2+b^2$

$A^2=d^2-b^2$

$а^2=400-256=144$

Корень квадратный из 144 равен 12. Это и есть ответ к задаче.

Задача 3

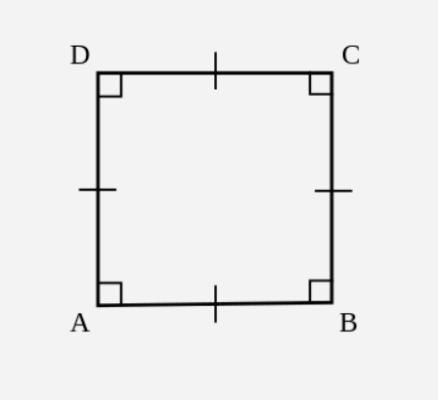
  • Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.

Стороны прямоугольника – вертикальные и горизонтальные, формула вычисления

Рис. 3. Квадрат.

У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.

Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.

$а^2=S$

$а^2=25$

$а=5$

Что мы узнали?

Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.

Предыдущая

МатематикаПорядок выполнения сложения и вычитания

Следующая

МатематикаГипотенуза треугольника – формула длины

Источник

Задача нахождения границ повернутого прямоугольника одинаково востребована, как в векторной, так и в растровой графике. При создании разного рода редакторов необходима область, описывающая фигуру, к которой применена трансформация. При обработке изображений, фото, для достижения каких-то художественных эффектов или решения сугубо технических проблем, например, для «выравнивания горизонта».

Возможно, Вы попали на эту страницу по запросу: «Поворот прямоугольника и нахождение вершин онлайн«. В этом случае имеет смысл посмотреть эту ссылку. Там прямой ответ на этот вопрос. Если требуется поворот вокруг центра прямоугольника, не забудьте установить переключатель «Вращать вокруг центра прямоугольника«.

Подобные задачи можно разделить на три группы:

  1. Нахождение описывающего прямоугольника для повернутого прямоугольника.
  2. Нахождение ширины и высоты повернутого прямоугольника, вписанного в некий прямоугольник.
  3. Нахождение вписанного прямоугольника в повернутый прямоугольник.

Повернуть прямоугольник

Чтобы повернуть прямоугольник необходимо воспользоваться аффинным преобразованием поворота, или просто применить формулы преобразования ко всем четырем вершинам прямоугольника.

Формулы преобразования поворота доказываются тут.

Давайте создадим прямоугольник и зададим угол поворота. Можно менять угол поворота зажав и перетаскивая оранжевую вершину.

Угол поворота:

Ширина:

Высота:

Get a better browser, bro…

Рис.1. Поворот прямоугольника. O(x,y) — координаты центра вращения. За оранжевую вершину можно тащить.

Чтобы посчитать координаты вершин повернутого прямоугольника, используются следующие формулы:

Latex formula
Latex formula

Если вращение происходит не вокруг центра координат, необходимо добавить координаты центра вращения, как на рисунке.1.

Немного кода:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

type

  T4PointF = array [0..3] of TPointF;

//*********************************************************************

//   Посчитать координаты массива точек повернутых на Angle радиан

//*********************************************************************

function CalcAnglePoints(const APoints: T4PointF; const ACenter: TPointF;

  const Angle: single): T4PointF;

var i: Integer;

    sn,cs: single;

begin

  SinCos(Angle, sn, cs);

  for i := 0 to Length(APoints)—1 do

  begin

    Result[i].X := (APoints[i].X—ACenter.X) * cs —

      (APoints[i].Y—ACenter.Y) * sn + ACenter.X;

    Result[i].Y := (APoints[i].X—ACenter.X) * sn +

      (APoints[i].Y—ACenter.Y) * cs + ACenter.Y;

  end;

end;

Описывающий прямоугольник повернутого прямоугольника

Краткая формулировка задачи:

Есть некий прямоугольник (a b c d), с шириной w и высотой h. К нему применен поворот на α градусов. Необходимо найти ширину W и высоту H описывающего прямоугольника.

Get a better browser, bro…

Рис.2. Описывающий прямоугольник для повернутого прямоугольника. За оранжевую вершину можно тащить.

На рисунке синий цвет угла означает направление против часовой и положительный знак угла, красный — по часовой и отрицательный.

В качестве поворачиваемого прямоугольника может выступать, допустим, картинка. Чтобы получить на выходе «необрезанное» по краям изображение, необходимо посчитать размер будущей картинки, чтобы повернутое изображение полностью входило в область.

Рис.3. Обрезанные края при повороте картинки.

Можно решить задачу следующим образом: пройтись по вершинам, найти минимальные и максимальные значения координат:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

//**************************************************************

//  Получить описывающий прямоугольник массива вершин

//**************************************************************

function GetPointsRect(const APoints: T4PointF): TRect;

var

  i: Integer;

begin

  Result := Rect(MaxInt, MaxInt, —MaxInt, —MaxInt);

  for i := 0 to Length(APoints)—1 do

  begin

    if APoints[i].X < Result.Left then

      Result.Left := Trunc(APoints[i].X);

    if APoints[i].X > Result.Right then

      Result.Right := Round(APoints[i].X);

    if APoints[i].Y < Result.Top then

      Result.Top := Trunc(APoints[i].Y);

    if APoints[i].Y > Result.Bottom then

      Result.Bottom := Round(APoints[i].Y);

  end;

end;

Это способ хороший, не особо затратный и универсальный. Если у нас число таких вершин непредсказуемо большое и отличается таким же непредсказуемым многообразием, это пожалуй, единственный способ. Но для прямоугольника есть способ лучше и проще.

Вспомним свойства прямоугольника.

— Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.

— Стороны прямоугольника являются его высотами. Середины сторон прямоугольника образуют ромб.

— Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).

— Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).

Википедия

По теме прямоугольника можно заглянуть сюда (не реклама, просто симпатично, кратко, емко).

Сейчас нас интересует попарная параллельность сторон и то, что все углы прямоугольника — прямые. На основании этого и будет строится дальнейшее рассуждение. Предполагается, что про углы у параллельных прямых все в курсе.

Get a better browser, bro…

Рис.4. Расчет ширины W и высоты H описывающего прямоугольника. За оранжевую вершину можно тащить.

Рассмотрим рисунок 4.

  • Угол β — интересующая нас часть угла α, остаток от деления на π / 2.
  • Угол γ — это дополнение угла β до π / 2, т.е. γ = π / 2 — β.

Цвет в данном случае означает попадание β в один из квадрантов. Синий — квадранты 1 и 3, красный — 2 и 4.

Внимание! Следующий текст генерируется автоматически в зависимости от угла на рисунках.

Поставив галочку ниже, в рисунках 2 и 4 будет отображаться решение. Не стал сразу выводить, ну чтоб не нарушать интригу.

Показать решение

В качестве итога. Чтобы найти высоту и ширину описывающего прямоугольника для повернутого прямоугольника всегда работают эти красивые формулы:

Latex formula

Latex formula

Где:

  • W’ — ширина описывающего прямоугольника
  • H’ — высота описывающего прямоугольника
  • w — ширина исходного прямоугольника
  • h — высота исходного прямоугольника
  • α — угол поворота

Зная координаты центра трансформации, высоту и ширину границ, нетрудно рассчитать координаты описывающего прямоугольника.

Друзья, спасибо за внимание!

Подписывайтесь на телеграм-канал.

Жду ваших комментариев. Надо ли рассказывать, как вписать повернутый прямоугольник в заданный прямоугольник? Или может про «выравнивание горизонта»?

Источник


Cтороны прямоугольника

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.

Длины прямоугольника

Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.

Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.

Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:

  • Диагонали прямоугольника равны.
  • Диагонали точкой пересечения делятся пополам.
  • Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.

Рис. 1. Прямоугольник

Примеры решения задач

Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.

Задача 1

  • Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.

Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:

$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)

$a*b=S$ (уравнение для нахождения площади)

При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.

Продолжим решение. Выразим значение a из первого выражения системы.

  • $(а+b)*2=Р$
  • $а+b={Рover{2}}$
  • $а={Рover{2}}-b$
  • Подставим значение периметра: $а={20over{2}}-b=10-b$

Подставим получившееся выражение в уравнение нахождения площади:

$a*b=S$

$(10-b)*b=21$

$b^2-10b-21=0$

Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.

$а=10-b$

Значит, при $b=3$, $а=10-3=7$

При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.

Задача 2

  • Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.

Рис. 2. Рисунок к задаче.

Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).

Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.

$D^2=a^2+b^2$

$A^2=d^2-b^2$

$а^2=400-256=144$

Корень квадратный из 144 равен 12. Это и есть ответ к задаче.

Задача 3

  • Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.

Рис. 3. Квадрат.

У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.

Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.

$а^2=S$

$а^2=25$

$а=5$

Заключение

Что мы узнали?

Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.

Тест по теме

Доска почёта

Доска почёта

Чтобы попасть сюда — пройдите тест.

    Пока никого нет. Будьте первым!

Оценка статьи

4.4

Средняя оценка: 4.4

Всего получено оценок: 200.

А какая ваша оценка?

Источник

Лучшие помощники

15 января 2023 11:47

434

Как найти высоту прямоугольника

Посмотреть ответы

Ответ:

Всё в разделе «Объяснение».

Пошаговое объяснение:

  • В прямоугольнике 4 стороны и все они являются высотами, так как высота — это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
  • В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.

==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b — высота прямоугольника).
Тогда b = P : 2 — a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b — высота прямоугольника).
Тогда b = S : a.

image

Еще вопросы по категории Математика

Все предметы

Источник

Ответ:

Всё в разделе «Объяснение».

Пошаговое объяснение:

  • В прямоугольнике 4 стороны и все они являются высотами, так как высота — это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
  • В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.

==============================================================

Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.

Рассмотрю 2 способа:

1) Можно найти, если известно:

Периметр прямоугольника P и одна из сторон прямоугольника a.

P = (a + b) * 2 (b — высота прямоугольника).

Тогда b = P : 2 — a.

2) Можно найти, если известно:

Площадь прямоугольника S и одна из сторон прямоугольника a.

S = ab (b — высота прямоугольника).

Тогда b = S : a.

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти страховой полис в электронном виде
  • Как составить отзыв на вайлдберриз
  • Как найти контакты следователя
  • Как найти толкающую силу
  • Radar pre leak 64 windows 10 как исправить