Как найти вертикальную асимптоту калькулятор - Исправление недочетов и поиск решений вместе с Examum.ru

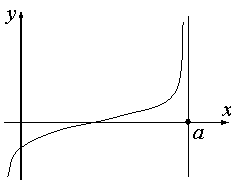
Вертикальной асимптотой
функции

называется прямая параллельная оси
y
к которой неограниченно приближается функция
при стремлении к бесконечности. Уравнение вертикальной асимптоты записывается в виде

,
где

— некоторая константа (конечное число)

Вертикальная асимптота функции

существует, если значение хотя бы одного из
пределов

или

равно
.

Стоит отметить, что представленные выше пределы используются также для проверки является ли точка

точкой разрыва
функции
.
Отсюда следует, что вертикальные асимптоты необходимо искать только в точках разрыва функции.

Воспользуйтесь нашим онлайн калькулятором, построенным на основе системы WolramAlpha, для вычисления вертикальных асимптот своей функции.

Источник

Асимптоты кривой

Прямая линия называется асимптотой кривой y=f(x), если расстояние точки кривой до этой прямой стремится к нулю при стремлении точки к бесконечности.

Назначение сервиса. Данный сервис предназначен для нахождения асимптот к графику функции в онлайн режиме. Решение оформляется в формате Word.

Решение онлайн
Видеоинструкция
Оформление Word

Правила ввода функции

Примеры

≡ x^2/(x+2)

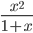
cos²(2x+π) ≡ (cos(2*x+pi))^2

≡ x+(x-1)^(2/3)

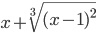
Классификация асимптот

Вертикальные асимптоты.
Горизонтальные асимптоты.
Наклонные асимптоты.

Вертикальные асимптоты

Уравнение любой вертикальной прямой, то есть прямой, параллельной оси OY, имеет вид x=a.

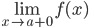
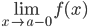
Если прямая x=a является вертикальной асимптотой графика функции y=f(x), то очевидно, что хотя бы один из односторонних пределов или равен бесконечности (+∞ или -∞).

Все функции с бесконечными разрывами (разрывы второго рода) имеют вертикальные асимптоты.

Пример 1. Найти уравнение вертикальных асимптот графика функции .

Решение. Видим, что y→∞, если x→1, точнее , , то есть прямая x=1 является вертикальной асимптотой, причем двусторонней.

Горизонтальные асимптоты

Всякая горизонтальная прямая имеет уравнение y=A.

Если прямая y=A является горизонтальной асимптотой кривой y=f(x), то .

Пример 2. Найти горизонтальные асимптоты кривой .

Решение. Найдем , то есть y→0 при x→+∞ и при x→-∞, значит прямая y=0 – горизонтальная асимптота данной кривой.

Наклонные асимптоты

Уравнения наклонных асимптот обычно ищут в виде y=kx+b. По определению асимптоты или (1)

Разделим обе части этого равенства на x:
, откуда

(2)

Теперь из (1):

(3)

Для существования наклонных асимптот необходимо существование пределов (2) и (3). Если хотя бы один из них не существует, то наклонных асимптот нет. Пределы (2) и (3) нужно находить отдельно при x→+∞ и при x→-∞, так как пределы могут быть разными (функция имеет две разные асимптоты).

Пример 4. Найти наклонные асимптоты графика функции .

Решение. По формуле (2) найдем .

Теперь найдем . Получаем уравнение наклонной асимптоты y=x+1.

Пример 5. Найти асимптоты кривой y=(x-1)²(x+3).

Решение. Вертикальных и горизонтальных асимптот нет, так как y→∞ при x→∞. Ищем наклонные:

.

Таким образом, кривая асимптот не имеет.

Пример 6. Найти асимптоты кривой .

Решение. Поскольку y→∞ при x→0 и при x→4, то прямые x=0 и x=4 являются вертикальными асимптотами. Так как , то y=2 – горизонтальная асимптота. Выясним вопрос о существовании наклонных асимптот: , следовательно, кривая наклонных асимптот не имеет (искать “b” не имеет смысла, так как горизонтальные асимптоты уже найдены).

Пример 7. Построить все виды асимптот к функции

Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:

Находим коэффициент k:

Находим коэффициент b:

Получаем уравнение наклонной асимптоты: y = -x

Найдем вертикальные асимптоты. Для этого определим точки разрыва:

Находим переделы в точке

— является вертикальной асимптотой.

Находим переделы в точке

— является вертикальной асимптотой.

Источник

Данный калькулятор предназначен для нахождения асимптот графика функции онлайн, вычислит вертикальные, горизонтальные и наклонные асимптоты.

Асимптота – это прямая, к которой бесконечно близко приближается график функции, и график при этом бесконечно удаляется от начала координат. Знание уравнения асимптоты функции может быть полезно при анализе функции и построении ее графика.
В зависимости от поведения аргумента асимптоты разделяются на вертикальные, горизонтальные и наклонные. Вертикальная асимптота – это вертикальная линия вида x=α, если .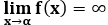

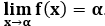
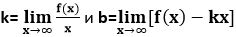
Точки разрыва функции и границы области определения являются основанием для нахождения вертикальных асимптот. Горизонтальная асимптота – горизонтальная прямая линия вида x=α, если . Наклонная асимптота – прямая вида y=kx+b; для существования наклонных асимптот, необходимо одновременное существование пределов .
Преимуществом онлайн калькулятора является то, что нет необходимости знать, как находить асимптоты графика функции. Достаточно только ввести функцию в ячейку. Основные примеры ввода функций для данного калькулятора указаны ниже.

Для получения полного хода решения нажимаем в ответе Step-by-step.

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	— twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{»}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	—
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

асимптоты:y=frac{x^2+x+1}{x}
асимптоты:f(x)=x^3
асимптоты:f(x)=ln (x-5)
асимптоты:f(x)=frac{1}{x^2}
асимптоты:y=frac{x}{x^2-6x+8}
асимптоты:f(x)=sqrt{x+3}
Показать больше

Описание

Найдите шаг за шагом вертикальные и горизонтальные асимптоты функций

function-asymptotes-calculator

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

The calculator will try to find the vertical, horizontal, and slant asymptotes of the function, with steps shown.

Solution

Your input: find the vertical, horizontal and slant asymptotes of the function $$$f(x)=frac{2 x^{3} + 15 x^{2} + 22 x — 11}{x^{2} + 8 x + 15}$$$

Vertical Asymptotes

The line $$$x=L$$$ is a vertical asymptote of the function $$$y=frac{2 x^{3} + 15 x^{2} + 22 x — 11}{x^{2} + 8 x + 15}$$$, if the limit of the function (one-sided) at this point is infinite.

In other words, it means that possible points are points where the denominator equals $$$0$$$ or doesn’t exist.

So, find the points where the denominator equals $$$0$$$ and check them.

$$$x=-5$$$, check:

$$$lim_{x to -5^+}left(frac{2 x^{3} + 15 x^{2} + 22 x — 11}{left(x + 3right) left(x + 5right)}right)=-infty$$$ (for steps, see limit calculator).

Since the limit is infinite, then $$$x=-5$$$ is a vertical asymptote.

$$$x=-3$$$, check:

$$$lim_{x to -3^+}left(frac{2 x^{3} + 15 x^{2} + 22 x — 11}{left(x + 3right) left(x + 5right)}right)=infty$$$ (for steps, see limit calculator).

Since the limit is infinite, then $$$x=-3$$$ is a vertical asymptote.

Horizontal Asymptotes

Line $$$y=L$$$ is a horizontal asymptote of the function $$$y=f{left(x right)}$$$, if either $$$lim_{x to infty} f{left(x right)}=L$$$ or $$$lim_{x to -infty} f{left(x right)}=L$$$, and $$$L$$$ is finite.

Calculate the limits:

$$$lim_{x to infty}left(frac{2 x^{3} + 15 x^{2} + 22 x — 11}{x^{2} + 8 x + 15}right)=infty$$$ (for steps, see limit calculator).

$$$lim_{x to -infty}left(frac{2 x^{3} + 15 x^{2} + 22 x — 11}{x^{2} + 8 x + 15}right)=-infty$$$ (for steps, see limit calculator).

Thus, there are no horizontal asymptotes.

Slant Asymptotes

Do polynomial long division $$$frac{2 x^{3} + 15 x^{2} + 22 x — 11}{x^{2} + 8 x + 15}=2 x — 1 + frac{4}{x^{2} + 8 x + 15}$$$ (for steps, see polynomial long division calculator).

The rational term approaches 0 as the variable approaches infinity.

Thus, the slant asymptote is $$$y=2 x — 1$$$.

Answer

Vertical asymptotes: $$$x=-5$$$; $$$x=-3$$$

No horizontal asymptotes.

Slant asymptote: $$$y=2 x — 1$$$

Источник