Как найти вертикальную длину

Была ли эта статья полезной?

Общие сведения

Фигуру с четырьмя прямыми углами, то есть равными 90 градусов, называют прямоугольником. Он состоит из четырёх отрезков, каждый из которых соединяется с двумя другими. Впервые упоминание о прямоугольнике встречается в манускриптах Древнего Египта. Но подробные признаки фигуры в III веке до н. э. дал математик Евклид.

В евклидовой геометрии достаточным условием для прямоугольника является существование трёх прямых углов в замкнутой фигуре. Если этот признак выполняется, оставшийся будет прямой в силу правила о сумме углов в простейших многоугольниках: если она не равняется 360 градусам, тело не может называться прямоугольным.

Современное правило, позволяющее отнести фигуру к прямоугольному объекту — параллелограмм называется прямоугольником, когда его 4 угла прямые. Исходя из этого определения, сюда относятся:

• квадрат;
• ромб.

Эти фигуры являются частным видом не только параллелограмма, но и прямоугольника. Для них действуют одинаковые правила и формулы. Единственно, для производных четырёхугольников существует ряд упрощений.

Углы многоугольника называют вершинами, а прямые линии, соединяющие их — гранями или сторонами. Для обозначения первых используют большие буквы латинского алфавита, чаще всего — А, B, C, D. Проставляют их по часовой стрелке начиная с нижнего левого угла. Соответственно, отрезки, соединяющие вершины, подписывают так: AB, BC, CD, AD.

Грани фигуры формируют ширину и длину. Эти названия условны для квадрата и ромба, так как их 4 стороны между собой равны.

В классической прямоугольной фигуре нижнюю грань принимают за ширину, а боковую считают длиной. Узнать их можно, просто измерив размеры или рассчитав по формулам.

В повседневности термины «длина» и «ширина» фактически обозначают пространственные оси координат, расположенные параллельно поверхности земли. За первую принимают более длинную сторону фигуры, вне зависимости от её пространственного расположения. Другими словами, это «размер по оси X» или «размер по оси Y», поэтому понятия о длине и ширине — довольно абстрактные.

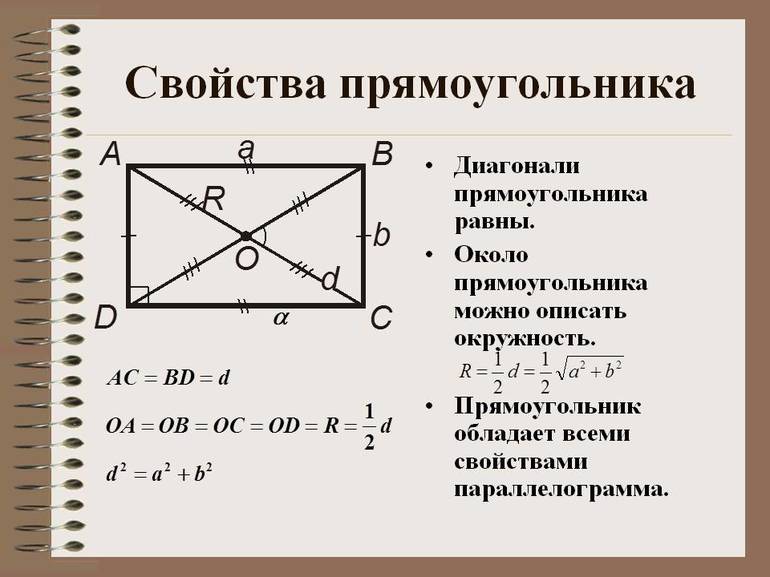
Свойства и линии

Из-за того, что прямоугольник — это параллелограмм, все свойства последнего справедливы и к нему. В первую очередь для него характерно, что противоположные стороны являются параллельными, то есть лежат на непересекающихся прямых. Отсюда следует, что фигуры отличаются друг от друга только размерами двух граней.

К основным свойствам прямоугольника относят:

• противолежащие стороны имеют равную длину: AB = CD, BC = AD;
• все углы равны 90 градусов;
• отрезки, обозначающие ширину и длину, всегда перпендикулярные друг другу: AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB;
• сумма любых двух углов фигуры равняется 180 градусов, соответственно всех четырёх — 360;
• в четырёхугольном теле можно провести 2 диагонали, длины которых будут совпадать по величине: AB = BC;
• сумма квадратов диагональных отрезков равняется удвоенной сумме квадратов сторон фигуры: AC² + BD² = 2 (AB² + BC²);
• построенная диагональ разделяет прямоугольник на 2 одинаковые фигуры — прямоугольные треугольники;
• точка пересечения прямых линий, соединяющая попарно противоположные углы, является центром фигуры и описанной окружности;
• диагонали в месте пересечения разделяются на 4 равных отрезка;
• в многоугольник, у которого длина не равна ширине, вписать окружность нельзя, поэтому её можно построить только для частных случаев прямоугольника.

На свойстве, что сложенные квадраты диагоналей можно найти как сумму квадратов всех его сторон, построено решение многих геометрических задач. Нелишним будет доказательство теоремы. Пусть имеется прямоугольник, у которого линии AC и BD — диагонали. Если изобразить многоугольник на рисунке и построить отрезки, можно увидеть, что каждая диагональ делит фигуру на 2 треугольника: ABC и BDC.

Используя теорему косинусов, можно записать: AC² = AB² + BC² — 2 * AB * BC * cos (ABC); BD² = CD² + BC² — 2 * CD * BC * cos (BCD). После сложения полученных выражений получится запись: AC² + BD² = AB² + BC² — 2 * AB * BC * cos (ABC) + CD² + BC² — 2 * CD * BC * cos (BCD).

Так как по свойству прямоугольной фигуры противоположные стороны равны, уравнение примет вид: AC² + BD² = 2AB² + 2BC² — 2 * AB * BC * cos (ABC) — 2 * AB * BC * cos (BCD). Учитывая, что сумма двух углов равняется 180⁰, полученное выражение можно переписать так: AC² + BD ² = 2 (AB ² + BC ²). Что и следовало доказать.

Формулы нахождения длины

Существует несколько способов, позволяющих найти длину. Как лучше это сделать и какой алгоритм использовать, зависит от известных данных и личных предпочтений решающего. Как показывает практика, найти величину достаточно просто, если есть значение ширины и ещё одного из параметров многоугольника.

Найти длину (BC) прямоугольника можно следующим образом:

1. Зная площадь и ширину. Так как первая величина находится из произведения сторон S = AB * BC, длина будет равняться отношению размера замкнутой плоскости к ширине: BC = S/AB.
2. По известному периметру и примыкающей стороне. Периметр прямоугольника равен сумме всех его граней: P = AB + BC + CD + AD. Так как противолежащие стороны равны, равенство можно переписать так: P = 2AB + 2BC. Отсюда следует, что BC = (P — 2AB)/2.
3. Если известна диагональ и ширина. Отрезок, соединяющий противолежащие вершины, делит многоугольник на 2 прямоугольных треугольника, поэтому можно воспользоваться теоремой Пифагора: a = √ (‎ b² + c²), где: a — гипотенуза (диагональ); b, с — катеты (ширина и длина). Отсюда: b = √ (c² — a²) = ВС = √ CA² — AB ².
4. Используя формулу радиуса описанной окружности: R = √ (AB² — BC2)/2. Для квадрата или ромба формула выглядит проще: R = a / √2 = d / 2, где d — диаметр описанного круга.

При решении задач может случиться, что исходные данные не позволяют напрямую воспользоваться формулами для нахождения длины. В этом случае приходится использовать переходные выражения.

Диагональ прямоугольника можно вычислить через радиус описанной окружности d = 2 R или используя синус угла: d = a / sin (a), то есть найти из отношения прилегающей функции к ширине. Исходя из этого, можно вывести ещё одну формулу для поиска длины: BC = CA * cos (a).

Площадь фигуры можно найти не только как произведение сторон, но и зная размер диагонали с величиной синуса острого угла: S = d² * sin (b) / 2, где b — угол между диагоналями. Приведённых формул будет достаточно для нахождения длины прямоугольника. При этом следует отметить важное свойство фигуры — высота многоугольника является шириной. Это свойство необходимо знать, так как в примерах нередко даётся размер не стороны, а именно высоты.

Решение примеров

Несмотря на то что формулы довольно простые, запомнить их простой зубрёжкой сложно. Чтобы материал закрепился, нужно научиться их применять на практике. Если понять принцип нахождения длины, многие из этих выражений можно будет вывести самостоятельно.

Вот некоторые задачи, рассчитанные на учащихся седьмых классов, рекомендуемые к самостоятельной проработке:

1. Определить длину прямоугольного многоугольника, у которого длина в 4 раза больше ширины. Периметр тела равен 20 см. Для решения задачи нужно принять сторону фигуры за х. Тогда длина будет составлять 4х. Согласно формуле, периметр равен: P = 2AB + 2 BC = 2* x + 2 * 4x. После подстановки значения P и выражения неизвестного, должно получиться следующее равенство: x = 20 / 10 = 2. Отсюда следует, что искомая длина равняется: BC = 4 * x = 4 * 2 = 8 см. Задача решена.
2. Длина прямоугольной фигуры больше её ширины на 2. Если ширина увеличится на 3 см, а длина на 8, площадь фигуры возрастёт в 3 раза. Найти длину. Чтобы решить задачу, нужно рассуждать следующим образом: пусть x ширина для первого состояния фигуры. Значит, длина этой фигуры будет x + 2. Соответственно, площадь равна: S = x * (x + 2). После трансформации ширина изменилась до значения x + 3, а длина — х + 2 + 8 = х + 10. Площадь новой фигуры равна: S = (х + 3) * (х + 10). После раскрытия скобок получится уравнение: 2 * х² — 7* х — 30 = 0. После его решения должно получиться, что x = 6 см. Отсюда длина будет равняться: 6 + 2 = 8 см.
3. Определить длину и ширину прямоугольника ABCD, в который вписаны 3 круга, если радиус каждой описанной окружности равен 5 см. Для решения примера нужно вспомнить, что ширина многоугольника равна двум радиусам круга или его диаметру. Значит, AB = 2 * 5 = 10 см. Соответственно, длина будет составлять 3 диаметра или 6 радиусов: BC = 6 * 5 = 30 см. Ответ найден.

В процессе изучения материала совсем не зазорно пользоваться так называемыми онлайн-калькуляторами. Это сайты, предлагающие своим пользователям рассчитать различные математические величины по исходным данным. Их интересность не только в том, что можно получить готовый ответ, но и в появлении возможности просмотреть подробное решение. Это как раз и позволит устранить пробелы в знании на стадии обучения.

Определение длины вертикальных отрезков

Данная тема
разбирается в п. 1.8 «Масштаб высот»
(см. Рис. 1 .17).

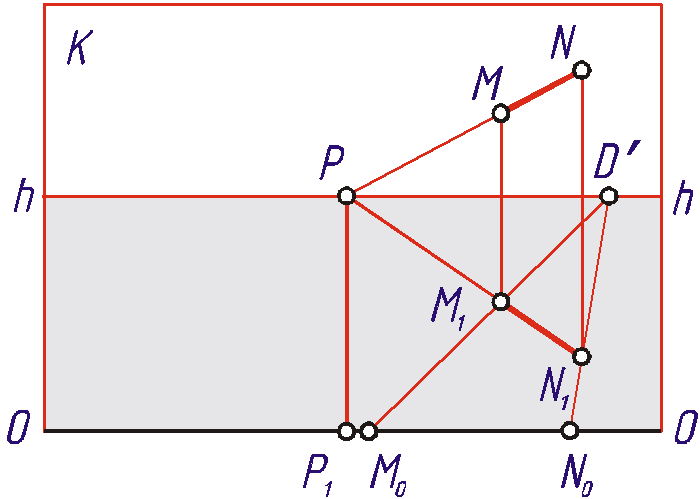
1. Определение длины отрезков, перпендикулярных к картине

Если отрезок,
перпендикулярный плоскости проекций,
косоугольно спроецировать на эту
плоскость при помощи параллельных
лучей, проведенных к плоскости под углом
45°, то длина проекции отрезка будет
равна длине самого отрезка.

Пользуясь этим
свойством косоугольной параллельной
проекции, можно определить длину заданных
в перспективе отрезков, перпендикулярных
картинной плоскости.

ПРИМЕР 1.
Определить длину отрезка AB,
лежащего в предметной плоскости и
перпендикулярного к плоскости картины
(Рис. 1 .33).

РЕШЕНИЕ.
Продолжаем отрезок AB
до пересечения с основанием картины в
точке 1.

Рис. 1.33

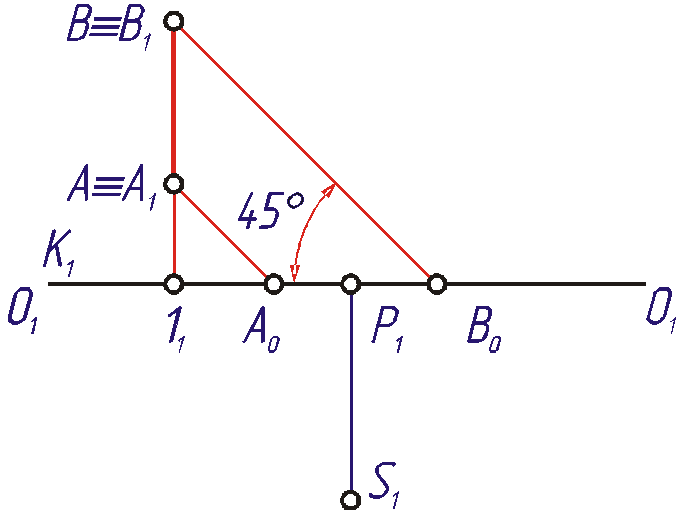
Через точки A
и B
проводим прямые под углом 45° к основанию
картины. В перспективе такие прямые
пройдут соответственно через точки A,
B и дистанционную
точку D
(Рис.  1 .34).

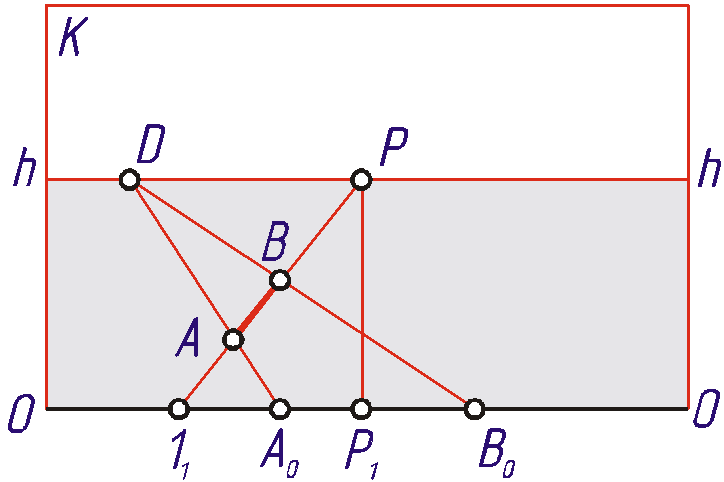
Продолженные до
основания картины, эти прямые отсекут
на ней отрезки 1₁A₀
и A₀B₀,
длины которых равны истинной длине
отрезков 1A
и AB.

Если измеряемый
отрезок, перпендикулярный картине, не
лежит в предметной плоскости, то его
длину можно определить, проецируя на
плоскость картины его горизонтальную
проекцию. Подобным образом на Рис.  1 .35
определена длина заданного отрезка MN,
равная длине отрезка M₀N₀.

1. Выбор точки зрения и положения картинной плоскости

Для получения
хорошего перспективного изображения
рекомендуется при выборе точки зрения
и положения картинной плоскости
руководствоваться следующими правилами,
выработанными практикой.

1. Положение
точки зрения
должно обеспечивать хорошую обозреваемость
предмета. Его составные части не должны
загораживать друг друга.

Угол зрения
φ —
угол между проецирующими лучами,
направленными в крайние точки плана
предмета (Рис. 1 .36), можно брать в пределах
от 18 до 53°.

Для того чтобы
предмет был ясно виден без поворота
головы, угол зрения должен быть не более
23°. Так как размеры картины всегда
немного больше размеров изображаемого
на ней предмета, то наилучшим
углом зрения для картины
считается угол φ = 28°. При этом значении
наибольший размер (00)
картины (ширина или высота) вдвое
меньше её
удаленности (d)
от точки зрения, т.е. d/00
= 2.

2. Картинную
плоскость ориентируют так, чтобы главная
точка P
оказалась в пределах средней трети
ширины картины, а горизонтальный след
К₁
картинной плоскости с одной из сторон
плана (чаще всего — с главным фасадом)
составлял угол от 25 до 35°.

Целесообразно,
кроме того, картинную плоскость совместить
с одним из ребер предмета, которое на
перспективной проекции будет изображено
в истинную величину.

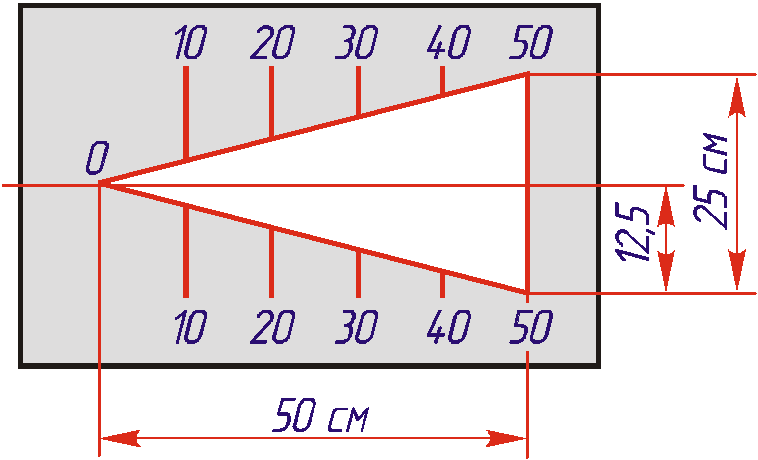
На практике для
выбора точки зрения и положения картинной
плоскости применяют шаблон, изготовленный
из листового картона по размерам,
указанным на Рис. 1 .37.

Для переноса точек
с комплексного чертежа на картину
применяют поворотную линейку, изготовленную
также из листового картона по размерам
Рис. 1 .38.

3. Высоту горизонта
обычно принимают на уровне глаз человека,
стоящего на земле, т.е. h
= 1,5-1,7 м. При
изображении застройки большого района
высоту горизонта берут равной 100 м и
более. Такую перспективу называют
перспективой «с птичьего полета».

Итак, на первом
этапе построения перспективы по заданным
прямоугольным проекциям здания или
предмета необходимо:

— выбрать положение
точки зрения относительно предмета;

— установить
направление главного луча;

— определить
положение картинной плоскости.

Рис. 1.36

Рис. 1.37

Рис. 1.38

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

На моем веб-сайте есть куча фреймов, требующих калибровки. Я использую:

x=window.innerWidth;
y=window.innerHeight;

Таким образом, я знаю, сколько пикселей я должен работать, и все отлично работает. Однако теперь я создаю прокручиваемую страницу. Мне нужно знать высоту страницы в пикселях (как в том, насколько высока будет окно, чтобы контент не прокручивался). Каким будет самый простой способ написать это с помощью javascript?