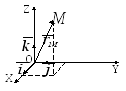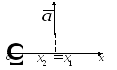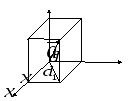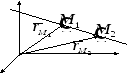Key Questions
-
Vectors can be added by adding the components individually as long as they have the same dimensions. Adding two vectors simply gives you a resultant vector.
What that resultant vector means depends on what quantity the vector represents. If you are adding a velocity with a change of velocity, then you would get your new velocity. If you are adding 2 forces, then you would get a net force.
If you are adding two vectors that have the same magnitude but opposite directions, your resultant vector would be zero. If you are adding two vectors that are in the same direction, then the result is in the same direction with a magnitude that is the sum of the 2 magnitudes.
-
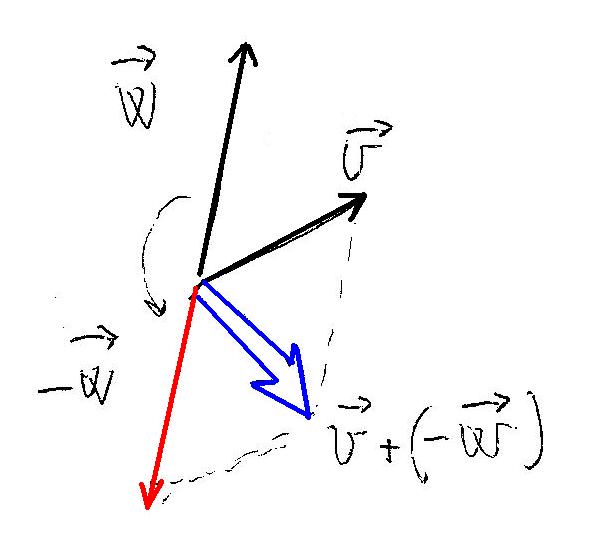
Given two vectors #vecv# and #vecw# you have:
#vecv-vecw=vecv+(-vecw)#Graphically we can use the Parallelogram Law:
If you have the vectors in components form you again use:
#vecv-vecw=vecv+(-vecw)# operating on each set of corresponding components.For example:
#vecv=4veci+2vecj-5veck# and:
#vecw=-2veci+4vecj+veck##vecv-vecw=vecv+(-vecw)=[4+(2)]veci+[2+(-4)]vecj+[-5+(-1)]veck=#
#=6veci-2vecj-6veck# -
The formula for the vertical component of a vector ai + bj is as follows:
#v_y = ||A|| sin(θ)#
First, calculate the magnitude of the vector A which is #||A||#:
||A|| = #sqrt(a^2 + b^2)#Next, determine #theta#
If you draw a triangle where a is the x axis and b is the y axis, you get a right triangle. The angle #theta# has the following measurement below:
#tan(theta) = b/a#
#theta = artcan(b/a)#Finally, we have the vertical component formula:
#v_y = ||A|| sin(θ)#For calculator assistance, use the component button here:
http://www.mathcelebrity.com/vector.php
-
Consider a vector #vecv#, for example, in space:
If you want to describe it to, say, a friend you can say that has a «modulus» (=length) and direction (you may use, for example, North, South, East, west…etc.).There is also another way to describe this vector.
You must take your vector into a reference frame to have some numbers related to it and then you take the coordinates of the tip of the arrow…your COMPONENTS !
You can now write your vector as: #vecv=(a,b)#
For Example: #vecv=(6,4)#
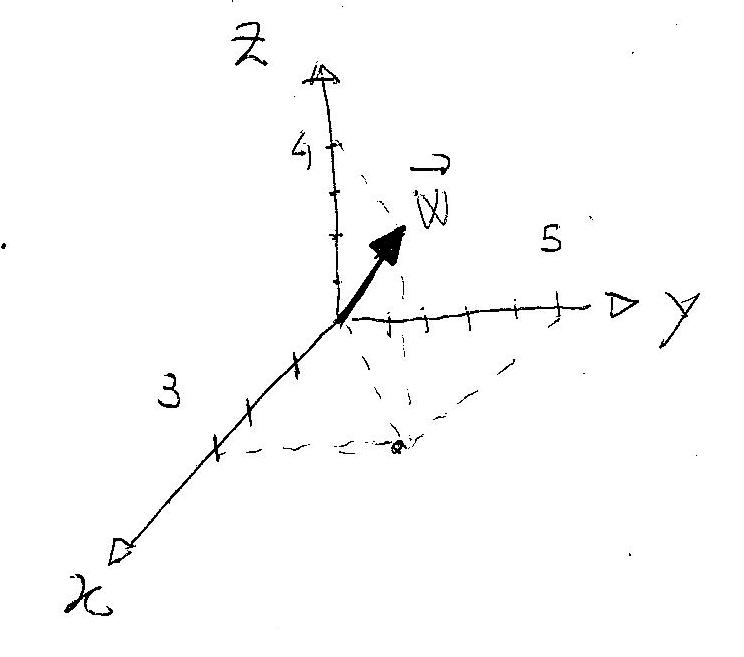
In 3 dimensions you simply add a third component on the #z# axis.
For example: #vecw=(3,5,4)#
ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ ВЕКТОРА ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
Земля имеет форму эллипсоида вращения. Если пренебречь ее сплющенностью (разность радиусов на экваторе и полюсах составляет 21 км), Землю можно принять за шар. Вращающийся земной шар намагничен и обладает магнитным полем. Магнитное поле шара практически совпадает с полем стержнеобразного магнита или диполя, расположенного в его центре. Поэтому Землю можно рассматривать как гигантский магнит, который смещен примерно на 400 км от центра планеты в сторону Тихого океана и наклонен к оси вращения Земли приблизительно под
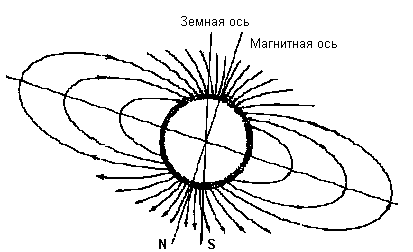
углом 12 0 . Точки на поверхности Земли, в которые проектируется ось такого диполя, называются геомагнитными полюсами. Следует иметь в виду, что в северном полушарии расположен южный магнитный полюс, а в южном — северный.
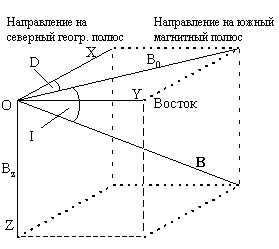
Если подвесить магнитную стрелку так, чтобы она могла свободно вращаться вокруг центра тяжести, то она установится по направлению касательной к силовой линии магнитного поля в данной точке Земли. Геомагнитные полюса не совпадают с географическими. Угол между географическим и магнитным меридианами в любой точке планеты (кроме полюсов) называется магнитным склонением D. Если стрелка компаса отклоняется к востоку, то склонение считается положительным, если — к западу, то — отрицательным.
Стрелка укрепленная на вертикальной оси, расположенной перпен-дикулярно к географическому меридиану, наклоняется под некоторым углом к горизонтальной поверхности. Этот угол получил название магнитного наклонения I. Оно положительно, если северный конец стрелки направлен внутрь Земли, и наоборот.
Вектор индукции магнитного поля Земли 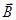
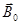

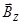
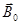
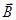
4 ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1 Тангенс — гальванометр.
5 Четырехполюсный переключатель.
7 Источник питания.
Рассмотрим круговой проводник (тангенс-гальванометр) из n вит-ков, достаточно плотно прилегающих друг к другу, расположенных вертикально в плоскости магнитного меридиана. В центре проводника поместим магнитную стрелку, вращающуюся вокруг вертикальной оси. Пока ток по катушке не пропускается, стрелка располагается в плоскости магнитного меридиана (в плоскости катушки). Если по катушке пропустить ток I, то в окружающем катушку пространстве возникает магнитное поле, вектор индукции которого 
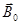

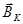
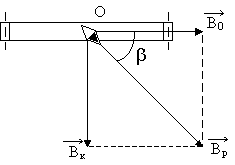
Векторы магнитной индукции этих полей взаимно перпендикулярны. Стрелка устанавливается по направлению результирующего вектора 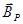
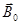
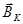
На рисунке 3 показано сечение катушки горизон-тальной плоскостью. Вектор 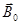
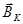
На основании закона Био-Савара-Лапласа значение вектора индукции в центре кругового витка с током вычисляется по формуле:
Вк = 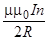
где m — магнитная проницаемость среды (для воздуха m= 1);
m0 = 4p 10 -7 Гн/м — магнитная постоянная;
n — число витков в катушке;
R — радиус витка .
Приравняв правые части выражений (1) и (2), получим
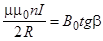
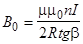
Таким образом, зная величину тока, протекающего по катушке, ра-диус витков и, измерив отклонение магнитной стрелки, можно определить горизонтальную составляющую вектора индукции магнитного поля Земли.
5 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1 Занести в отчет данные электроизмерительных приборов: систему, класс точности, диапазон, число делений шкалы.
2 Выбрать диапазон амперметра. Рассчитать цену деления амперметра. 3 Найти приборную погрешность 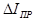
4 Проверить электрическую цепь на соответствие ее схеме (рисунок 4).
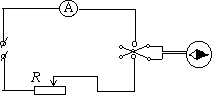
5 С помощью реостата установить следующие значения углов отклонения стрелки компаса: 30 0 , 45 0 .
6 Снять показания амперметра и занести их в таблицу 1.
7 Поменять полярность подаваемого на тангенс-гальванометр напряжения с помощью четырехполюсного переключателя.
8 С помощью реостата установить значения углов отклонения стрелки компаса: -30 0 , -45 0 . Показания амперметра занести в таблицу 1.
9 Вычислить В0 — величину горизонтальной составляющей вектора ин-дукции магнитного поля Земли по формуле (3) для каждого из углов.
10 С целью уменьшения систематической ошибки[1] найти средние арифметические значения вектора магнитной индукции для каждой пары углов 30 0 и -30 0 , 45 0 и — 45 0 соответственно. Средние значения занести в таблицу.
11 Определить абсолютную погрешность
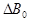
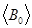
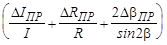
9 Найти относительную ошибку результата для каждой пары углов по формуле
e 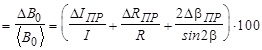
где 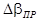
10 Выбрать из рассчитанных значений 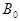
| b | Dbпр | I | D I пр | B0 | DB0 | e = DB/B0 | |
| рад | дел. | мA | мA | Тл | Тл | Тл | ´100% |
| 30 0 | |||||||
| -30 0 | |||||||
| 45 0 | |||||||
| -45 |
[1] ) Определяющей ошибкой при расчете горизонтальной составляющей вектора индукции магнитного поля Земли методом тангенс-гальванометра является систематическая ошибка, которая может быть связана как с некоторыми недостатками конструкции измерительной установки, так и с несовершенством измерительных приборов. Так например, на стрелку компаса могут оказывать влияние окружающие посторонние железные предметы, отклоняющие стрелку от положения магнитного меридиана. Размер стрелки и ее положение относительно плоскости кольца должны быть такими, чтобы она целиком помещалась в однородной части магнитного поля колец (для этого ее длина не должна превышать 0.1 R колец). Учитывая эти замечания в работе предлагается рассчитать приборную ошибку результата и сделать это для каждого угла отклонения стрелки компаса.
| | | следующая лекция ==> | |
| ГРАДУИРОВКА ТЕРМОПАРЫ С ПОМОЩЬЮ ВОЛЬТМЕТРА | | | ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ЗАРЯДА ЭЛЕКТРОНА К ЕГО МАССЕ МЕТОДОМ МАГНЕТРОНА |
Дата добавления: 2016-01-03 ; просмотров: 12737 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Компоненты вектора
Вектор – геометрическое представление величины и направления, выражающиеся стрелками в двух-трех измерениях.
Задача обучения
- Константы двумерных и трехмерных векторов.
Основные пункты
- Векторы разделяются на два компонента: величина и направление.
- Если принимать вектор как гипотенузу, то горизонтальные и вертикальные составляющие можно найти, заполнив треугольник. Нижний край – горизонталь, а противоположная углу сторона – вертикаль.
- Угол, созданный с горизонталью, можно применить для поиска длины двух компонентов.
Термины
- Координаты – числа, указывающие на позицию относительно оси. Например, х и у демонстрируют положение относительно одноименных осей.
- Величина – число вектора, указывающее на его длину.
- Ось – воображаемая линия, вокруг которой объект вращается или расположен симметрично.
Обзор
Вектор – геометрическое отображение величины и направления, которые чаще всего отмечаются прямыми стрелками, начиная с одной точки на координатной оси и заканчивая на другой. Все векторы наделены длиной, при помощи которого один вектор сравнивают с другим. Векторы со стрелками также обладают направлением. Это главное отличие от скаляров, выступающих простыми числами без направления.
Какие есть составляющие вектора? Вектор характеризуется величиной и позицией относительно оси координат. Полезно анализировать векторы, чтобы разложить на составные части. Если мы говорим о двумерных векторах, то это вертикальные и горизонтальные компоненты. В случае с трехмерными все остается прежним, но теперь мы имеем еще одно направление: x, y, z.
Разложение вектора
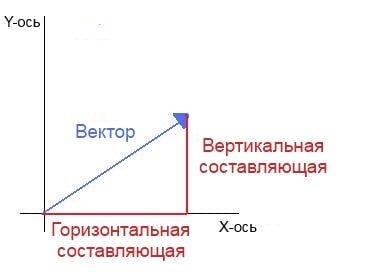
Чтобы визуально разложить вектор на составляющие, начните с системы координат. Далее проведите прямую линию от оси х и продолжайте ее, пока не выровняется с кончиком вектора. Это горизонтальный компонент. Для поиска вертикального, проведите линию от конца горизонтального вектора, пока не дойдете до кончика вектора. В итоге, получите правильный треугольник, в котором вектор играет роль гипотенузы.
Исходный вектор, определенный относительно множества осей. Горизонтальный компонент простирается от начала вектора и до координаты х. Вертикальный тянется от х к самой вертикальной точке. Вместе формируют правильный треугольник
Разделение на горизонталь и вертикаль – удобный способ разобраться в физической проблеме. Как только замечаете движение под углом, вы обязаны воспринимать его как перемещение по горизонтали и вертикали одновременно. Это помогает намного проще отслеживать движение объектов.
Определение напряженности магнитного поля при помощи земного индуктора
Страницы работы
Содержание работы
Министерство образования РФ
Санкт- Петербургский государственный горный институт им. Г.В. Плеханова
Кафедра общей и технической физики.
ЛАБОРАТОРНАЯ РАБОТА № 6
«ОПРЕДЕЛЕНИЕ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ПРИ ПОМОЩИ ЗЕМНОГО ИНДУКТОРА»
Цель работы — измерить горизонтальную и вертикальную составляющие вектора напряженности магнитного поля Земли, оценить погрешность выполненных измерений и сопоставить полученные результаты со справочными данными о величине напряженности магнитного поля Земли на широте Санкт-Петербурга.
Общие сведения
Известно, что магнитные полюса Земли не совпадают с ее географическими полюсами. В первом приближении магнитное поле Земли (геомагнитное поле) можно рассматривать как поле шара, ось намагниченности которого, отклонена от оси вращения Земли приблизительно на 11,5°. Напряженность геомагнитного поля убывает от магнитных полюсов к магнитному экватору со «скоростью» 34¸55 А/м. Существование геомагнитного поля объясняется наличием электрических токов в ядре Земли.
Магнитная стрелка, способная свободно вращаться вокруг вертикальной и горизонтальной осей, установится по направлению вектора напряженности магнитного Земли, то есть по касательной к силовой линии магнитного поля. В любой точке М земной поверхности задан вектор напряженности магнитного поля Земли. Вертикальная плоскость проведенная через этот вектор называется плоскостью магнитного меридиана в данной точкеземной поверхности (рис.1): через точку М земной поверхности проходит магнитный меридиан KL, плоскость Р — плоскость магнитного меридиана, а N — горизонтальная плоскость. Вектор напряженности магнитного поля H в точке М можно разложить на горизонтальную (Hг) и вертикальную (Hв) координаты в плоскости магнитного меридиана P.
Измерения Hг и Hв удобно проводить с помощью земного индуктора (рис.2), представляющего собой плоскую катушку на которую в несколько слоев намотана проволока, концы которой присоединены к зажимам баллистического гальванометра G. Индуктор закреплен в кардановом подвесе, позволяющем вращать его вокруг и вертикальной, и горизонтальной осей.
Поток магнитной индукции, пронизывающий плоскость одного витка равен:
,
где Вn – составляющая вектора магнитной индукции, перпендикулярная плоскости витка; Hг – горизонтальная составляющая магнитного поля Земли, S – площадь катушки, m — магнитная проницаемость среды, окружающей катушку, m0 — магнитная постоянная. Если же катушка имеет N витков, то потокосцепление магнитной индукции, сцепленной со всеми витками, вычисляется по формуле:
.
При вращении индуктора поток магнитной индукции поля Земли, пронизывающий плоскость катушки, меняется и в обмотке индуктора возбуждается индукционный ток. Если это изменение произошло за время dt , то по закону электромагнитной индукции в катушке должна возникнуть ЭДС индукции eин=—dy/dt. Согласно закону Ома индукционный ток
,
http://v-kosmose.com/fizika/komponentyi-vektora/
http://vunivere.ru/work4361
Любой вектор можно представить как сумму нескольких векторов. Например, перемещение тела можно представить как результат нескольких последовательных перемещений, переводящих тело из того же начального в то же конечное положение. Замену одного вектора векторной суммой нескольких других называют разложением вектора на составляющие. Составляющие вектора, конечно, тоже векторы. Разложение вектора на составляющие можно произвести бесконечным числом способов. Можно, например, разложить вектор по двум данным направлениям. Тогда разлагаемый вектор будет служить диагональю параллелограмма, а с заданными направлениями составляющих совпадут стороны параллелограмма (рис. 43).

Рис. 43. Разложение скорости самолета, набирающего высоту, на вертикальную и горизонтальную составляющие
Если задать направление только одной составляющей, то задача о разложении вектора не будет иметь определенного ответа; на рис. 44 мы видим, что можно построить сколько угодно параллелограммов с заданной диагональю (разлагаемый вектор) и заданным направлением одной стороны (направление одной из составляющих).
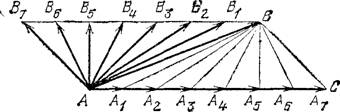
Рис. 44. Разложение вектора
, в котором задано только направление
одной составляющей. Вектор
может быть представлен как суммы векторов
и
,
и
,
и
и т. д.
Задача:
24.1. Самолет должен приземлиться в пункте А, лежащем в 300 км к юго-западу от аэродрома вылета, но предварительно он должен сбросить вымпел над аэродромом В, лежащим в 400 км к юго-востоку от аэродрома вылета, Чему равен модуль перемещения
?
Чаще всего производят разложение векторов по направлениям осей какой-либо прямоугольной системы координат (рис. 45, а). На рис. 45, б изображен вектор (a) (он же
). Проведем из точек А и В перпендикуляры к осям
и
.Точка пересечения перпендикуляра с осью называется проекцией соответствующей точки (A или В) на данную ось (
или
). На рисунке указаны координаты этих проекций. Разность
обозначается
и называется проекцией вектора (a) на ось
; аналогично, разность
обозначается
и называется проекцией вектора (a) на ось
. Проекции называют также компонентами вектора по координатным осям (
— компонента вектора (a) по оси
и т. д.). Проекции (компоненты) являются скалярами.
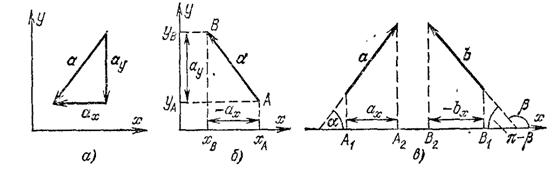
Рис. 45. а) Пример разложения вектора на составляющие, параллельные координатным осям. б) и в) Проекции вектора на координатные оси
Для вектора, изображенного на рис. 45, б,
, вследствие чего проекция на ось
отрицательна
; поскольку
, проекция на ось
положительна
. На рис. 45, б показаны длины отрезков, заключенных между проекциями на ось начала и конца вектора. Эти длины должны выражаться положительными числами. Поэтому значение длины отрезка между проекциями точек А и В на ось
указано в виде
(само
). Отметим, что проекция вектора (a), изображенного на рис. 45, в, положительна, а проекция вектора (b) отрицательна.
Дадим еще одно определение проекции вектора. На рис. 45, в показаны векторы (a) и (b) и их проекции на произвольную ось
. Проекция вектора (a) (т. е.
) равна длине отрезка
, взятой со знаком плюс (так как
); проекция вектора (b) (т. е.
) равна длине отрезка
, взятой со знаком минус (так как
). Напомним, что на рисунке проставлена длина отрезка
, которая выражается положительным числом, равным
.
Из рис. 45, в видно, что длина отрезка
(т. е.
) равна длине отрезка, изображающего вектор (a) (т. е. модулю вектора (a) ), умноженной на косинус угла
между направлением оси
и направлением вектора. Следовательно,
. Длина отрезка
равна длине отрезка, изображающего вектор (b) (т. е. модулю вектора (b) ), умноженной на косинус угла
. Проекция вектора (b) равна этой длине, взятой со знаком минус. Следовательно,
.
Таким образом, независимо от того, какой угол образует направление вектора с направлением оси
, проекция вектора на ось определяется формулой
. (24.1)
Если
, то
, если
, то
. При
проекция вектора равна нулю.
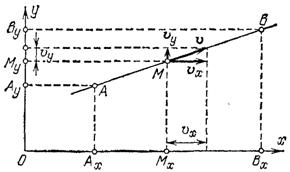
Рис. 46. Проектирование движения точки М на оси координат
Очевидно, что модуль и направление вектора (а следовательно, и сам вектор) полностью определяются заданием проекций вектора на координатные оси. В частности, для векторов, лежащих в плоскости
, модуль определяется формулой
. «Длины» и знаки проекций определяют направление вектора.
Пусть какая-либо точка движется по прямой. Выберем какую-нибудь систему координат
и спроектируем движущуюся точку на оси координат (рис. 46). На рисунке показаны проекции
и
точки, занимающей в данный момент положение
. При движении точки будут двигаться и ее проекции. Если точка
совершила перемещение
, то за то же время ее проекции совершили перемещения
,
по соответственным осям. Из построения видно, что проекции перемещения движущейся точки
равны перемещениям ее проекций
и
по осям координат. Если точка двигалась равномерно, то проекции также двигались равномерно. Разделив перемещения точки и ее проекций на время
движения точки, найдем скорости
и
точки
и ее проекций
и
.
Можно показать, что проекция скорости точки равна скорости движения ее проекции. Точно так же можно показать, что при неравномерном движении точки по прямой проекции ее мгновенной скорости и ускорения равны мгновенным скоростям и ускорениям ее проекций. Обратно, если известны перемещения, скорости или ускорения проекций движущейся точки на оси координат, то можно найти перемещение, скорость или ускорение, складывая получившиеся составляющие искомого вектора по правилу параллелограмма.
Таким образом, вместо того чтобы рассматривать движение точки в произвольном направлении, мы всегда можем рассматривать движение только вдоль определенных прямых — осей координат. В ряде случаев выбор осей подсказывается самими условиями задачи. Например, изучая движение брошенного тела, удобно выбрать ось координат по вертикали и но горизонтали.
Загрузить PDF
Загрузить PDF
Разложение вектора на перпендикулярные составляющие помогает при сложении и вычитании векторов. Эта статья расскажет вам, как разложить вектор на составляющие.
Шаги
-
1
Определите угол между вектором и либо осью Х, либо осью Y.
-
2
Найдите длину вектора (в соответствующих единицах).
-
3
Найдите составляющие вектора по следующим формулам: Составляющая1 = длина * sin (уол) Составляющая2 = длина * cos (угол). Первая формула дает составляющую, противолежащую углу, а вторая – составляющую, прилежащую к углу.
Реклама
Об этой статье
Эту страницу просматривали 10 345 раз.
Была ли эта статья полезной?
|
Пусть на оси |
|
|
1 |
Вектор
|
|
2 |
Вектор
|
|
3 |
Так как
|
|
Составляющая |
2.4. Координаты вектора в дск
|
Вектор
т.е. Z
называется x |
|
Замечания:
1) векторы
образом: |
2.5. Радиус-вектор точки. Координаты точки в пространстве
|
Определение. Координатами |
2.6. Координаты
вектора
|
|
Пусть в базисе
Тогда
|
|
|
Чтобы найти |
||
 Замечание 1. Замечание 1.Проекцией вектора
Аналогино: |
||
|
|
|
|
|
|
|
|
2.7. Линейные
операции над векторами
Если в пространстве
задан базис и в нём векторы
и
,
то выполнение линейных операций над
векторами сводится к выполнению тех же
операций над
их координатами:

если
действительное
число, то
.
2.8. Модуль вектора
через координаты
|
Пусть |
|
|
|
Тогда вектор
Пифагора, получим: |
2
.9. Расстояное между двумя точками
|
|
Пусть заданы
Вектор
|
2.10. Деление
отрезка в данном отношении
|
Пусть на прямой
|
||
|
Если
тогда координаты |
||
|
Если |
-
Условие
коллинеарности двух векторов
Условие
коллинеарности двух векторов записывается
в виде
.
Если в пространстве
задан базис и в нём векторы
и
,
то
что равносильно записи:

равенства, получим

т.е. условие коллинеарности векторов:
Замечание.
Если два вектора, заданные своими
координатами,
и
линейно зависимы, то
,
то их координаты пропорциональны, т.е.
то векторы линейно зависимы.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
15.06.201410.37 Mб58Краткий курс высшей математики_Демидович Б.П_2001 -656с.djvu




 .
. .
. .
. ОА=x,
ОА=x,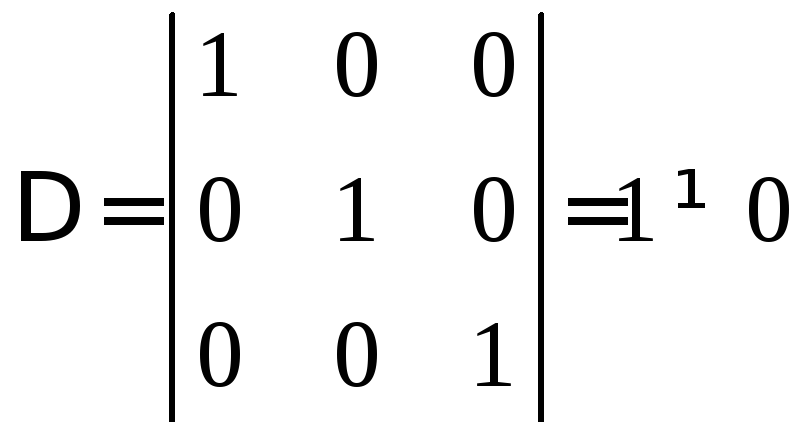 .
.