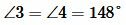Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
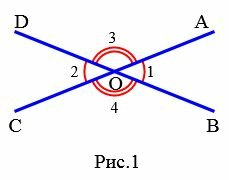
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Следовательно 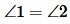
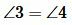
Задачи и решения
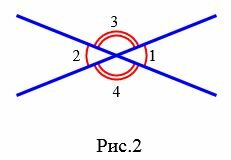
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
Решение. Так как углы 1 и 2 вертикальны, то 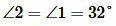
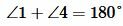
Углы 3 и 4 вертикальные. Тогда
Ответ. 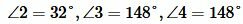
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
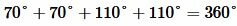
Ответ. 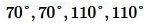
Треугольник. Формулы определения и свойства треугольников.
В данной статье мы расскажем о классификаци и свойствах основной геометрической фигуры — треугольника. А также разберем некоторе примеры решения задач на треугольники.
Содержание:
Определение треугольника
Треугольник — это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. В геометрических задачах треугольник обычно изображают специальным симовлом — △, после которго пишут названия вершин треугольника напр. △ABC.
Треугольник ABC (△ABC)
- Точки A, B и C — вершины треугольника. Принято писать их большими буквами.
- Отрезки AB, BC и СА — стороны треугольника. Обычно сторонам присваивают свои названия маленькими буквами. Имя выбирают по первой вершине каждой стороны. Напр. у стороны AB первая вершина А поэтому эта сторона называется а. Тоесть AB = a, BC = b, CА = c.
- Стороны треугольника в местах соединения образуют три угла, которым обычно дают названия буквами греческого алфавита α, β, γ. Причем напротив стороны a лежит угол α, b — β, с — γ.
Углы треугольника, также, можно обозначать специальным символом — ∠. После которого пишут вершины треугольника в таком порядке чтобы вершина обозначающегося угла была в серединке. Например:
Классификация треугольников
Все треугольники можно разделить на несколько видов, различающихся между собой величиной углов или длинами сторон. Такая классификация позволяет выделить особенности каждого из них.
1.Разносторонний – треугольник, у которого все стороны имеют разную длину.
2. Равнобедренный – треугольник, у которого длины двух сторон равны. Они называются боковыми сторонами AB и BC. Третья сторона называется основание СА. В данном треугольнике углы при основании равны ∠ α = ∠ β
3.Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
4.Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°
5.Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
6. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и BC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (CА).
Свойства треугольника
1.Свойства углов и сторон треугольника.
- Сумма всех углов треугольника равна 180°:
- Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
- В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
2.Теорема синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c |
| sin α | sin β | sin γ |
3. Теорема косинусов.
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема о проекциях
Для остроугольного треугольника:
Медианы треугольника
Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
1. Медианы треугольника пересекаются в одной точке O. (Точка пересечения медиан называется центроидом)
2. В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
| AO | = | BO | = | CO | = | 2 |
| OD | OE | OF | 1 |
3. Медиана треугольника делит треугольник на две равновеликие по площади части
4. Треугольник делится тремя медианами на шесть равновеликих треугольников.
5. Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны:
Вертикальные треугольники в геометрии
Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.
Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).
Биссектриса — луч, который выходит из вершины угла и делит его пополам.
Виды углов. Измерение углов
- Развернутый угол — угoл, стороны которого лежат на одной прямой.
- Прямой угoл — угoл, который равен половине развернутого угла.
- Острый угол — угoл меньше прямого угла.
- Тупой угoл — угoл больше прямого, но меньше развернутого.
Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.
Смежные и вертикальные углы
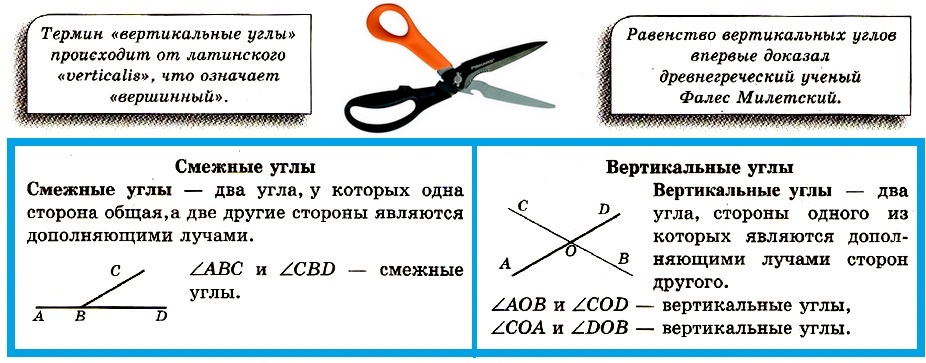
Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.
Теорема. Сумма смежных углов равна 180°.
Теорема. Вертикальные углы равны.
Свойства смежных и вертикальных углов
Углы при пересечении двух прямых секущей
Вы смотрели конспект по геометрии «Угол. Смежные и вертикальные углы». Использованы цитаты из учебных пособий:
Цитирование указанных пособий произведено в учебных целях (часть 1 статьи 1274 Гражданского кодекса РФ) с указанием авторства, источника заимствования и ссылки на покупку учебного пособия в крупнейшем книжном Интернет-магазине. Выберите дальнейшие действия:
http://binary2hex.ru/triangle.html
Вертикальные углы в геометрии
19 июня 2022
В двух словах: вертикальные углы возникают при пересечении двух прямых, не имеют общих сторон и всегда равны друг другу.
Содержание
- Определение и примеры
- Основная теорема
- Комбинированные задачи
1. Определение и примеры
Определение. Два угла называются вертикальными, если стороны одного из них являются продолжениями сторон другого.
На рисунке ниже пересекаются две прямые: $AB$ и $MN$:
В результате образуются две пары вертикальных углов: $angle ASM$ и $angle BSN$, а также $angle ASN$ $angle BSM$.
Обратите внимание: вертикальные углы образуются только в точке пересечении прямых. Например, углы $ASM$ и $BSN$ на картинке ниже — не вертикальные, даже если они равны:
Если в одной точке пересекается более двух прямых, то вертикальных углов становится очень много:
Я не случайно пометил вертикальные углы одинаковыми дугами. Дело в том, что верна следующая теорема.
2. Основная теорема
Теорема 1. Вертикальные углы всегда равны друг другу.
Доказательство. Рассмотрим «синие» вертикальные $ASN$ и $BSM$. Каждый из них является смежным с углом $BSN$:
Но сумма смежных углов равна 180°, и если $angle BSN=color{red}{x}$, то
[begin{align}angle ASN&={180}^circ -color{red}{x} \ angle BSM&={180}^circ -color{red}{x} end{align}]
Итак, вертикальные углы равны одной и той же величине. Т.е. они равны между собой.
Эта теорема позволяет решать огромное количество задач — от самых простых до весьма нетривиальных. Начнём с простых.
Задача 1. Найдите углы 2, 3 и 4, если $angle 1={134}^circ $.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle 3=angle 1={134}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle 1+angle 2&={180}^circ \ angle 2&={180}^circ -angle 2= \ &={180}^circ -{134}^circ ={46}^circ end{align}]
Углы 2 и 4 вертикальные, поэтому они равны: $angle 4=angle 2={46}^circ $.
Из всех чертежей видно, что при пересечении двух прямых обычно возникает два острых угла и два тупых. Причём острый и тупой угол всегда будут смежными.
Если предположить, что острый угол равен $color{red}{x}$ градусов, то тупой равен $180-color{red}{x}$ градусов.
Задача 2. Найдите углы, образованные при пересечении двух прямых, если разность двух из них равна 68°.
Решение. Пусть острые углы содержат $color{red}{x}$ градусов. Тогда смежные с ними тупые углы содержат по ${180}^circ -color{red}{x}$ градусов.
По условию задачи, разность двух углов равна 68°. Очевидно, речь идёт о смежных углах. Потому что разность вертикальных углов была бы равна нулю. Вычитаем из тупого угла острый и получаем:
[begin{align}{180}^circ -color{red}{x} -color{red}{x} &={68}^circ\ 2color{red}{x}&={112}^circ\ color{red}{x}&={56}^circend{align}]
Итак, острые углы содержат по 56°. Тогда тупые углы содержат по 124°.
Единственный случай, когда все вертикальные углы равны — это когда прямые перпендикулярны, т.е. пересекаются под углом 90°.
Задача 3. На рисунке прямые $a$ и $b$ перпендикулярны, $angle color{red}{1}={36}^circ $. Найдите углы 2, 3 и 4.
Решение.
Углы 1 и 3 вертикальные, поэтому они равны: $angle color{red}{3}=angle color{red}{1}={36}^circ $.
Углы 1 и 2 смежные, поэтому их сумма равна 180°:
[begin{align}angle color{red}{1}+angle color{blue}{2}&={180}^circ \ angle color{blue}{2}&={180}^circ -angle color{red}{1}= \ &={180}^circ -{36}^circ ={144}^circ end{align}]
Углы 3 и 4 вместе образуют прямой угол, поэтому их сумма равна 90°:
[begin{align}angle color{red}{3}+angle color{green}{4}&={90}^circ \ angle color{green}{4}&={90}^circ -angle color{red}{3}= \ &={90}^circ -{36}^circ ={54}^circ end{align}]
Перед тем как переходить к более сложным задачам, рассмотрим ещё одно интересное свойство вертикальных углов.
Теорема 2. Биссектрисы вертикальных углов лежат на одной прямой.
Доказательство. В самом деле, пусть $SC$ и $SD$ — биссектрисы вертикальных углов $ASM$ и $BSN$ соответственно.
Допустим, градусные меры углов $ASM$ и $BSN$ равны $2color{red}{x}$. Тогда градусные меры всех маленьких углов $ASC$, $BSD$ и т.д. равны $color{red}{x}$. Но тогда
[begin{align}angle CSD&=angle CSA+angle ASN+angle NSD= \ &=2color{red}{x}+angle ASN end{align}]
С другой стороны, углы $ASN$ и $ASM=2color{red}{x}$ смежные, поэтому
[2color{red}{x}+angle ASN={180}^circ ]
Итак, угол $angle CSD={180}^circ $, т.е. является развёрнутым. А это как раз и означает, что лучи $SC$ и $SD$ являются дополнительными друг другу и образуют прямую.
3. Комбинированные задачи
Рассмотрим несколько более сложных задач. Тут встречаются вертикальные углы, смежные углы, а также перпендикуляры.
Задача 4. Найдите углы, образованные при пересечении двух прямых, если:
- Сумма двух из них равна 110°.
- Сумма трёх из них равна 308°.
Решение. Для обоих пунктов будем использовать один и тот же чертёж. Пусть острые вертикальные углы содержат по $color{red}{x}$ градусов, тогда два других угла содержат по ${180}^circ -color{red}{x}$ градусов:
1. Если сумма двух углов равна 110°, то, очевидно, речь идёт о вертикальных углах. Потому что сумма смежных углов всегда равна 180°, а не 110°.
Кроме того, это явно острые углы, иначе их сумма была бы больше 180°. Поэтому
[begin{align}color{red}{x}+color{red}{x}&={110}^circ\ 2color{red}{x}&={110}^circ\ color{red}{x}&={55}^circend{align}]
Итак, острые вертикальные углы содержат по 55°. Следовательно, смежные с ними тупые вертикальные углы содержат по 125°.
2. Сумма трёх углов всегда содержит два вертикальных и один смежный с ними. Например, так:
Зелёным пунктиром обозначены три угла, участвующие в сумме. Следовательно, эта сумма равна
[begin{align}left( {180}^circ -color{red}{x} right)+color{red}{x}+left( {180}^circ -color{red}{x} right)&={308}^circ \ {360}^circ -color{red}{x}&={308}^circ\ color{red}{x}&={52}^circend{align}]
Итак, углы равны 52° и 128°.
Эту задачу можно решить по-разному. Взгляните ещё раз на чертёж:
Мы знаем, что «большой зелёный угол» содержит 308°. А «полный оборот» содержит 360°. Но чтобы получить полный оборот, нужно добавить к зелёному сектору небольшой угол $color{red}{x}$. Поэтому
[begin{align}{308}^circ +color{red}{x}&={360}^circ\ color{red}{x}&={52}^circend{align}]
Возможно, такой подход покажется вам более простым и «очевидным».
Заметьте: благодаря введённым обозначениям нам даже не потребовались буквы для обозначения углов.:)
Задача 5. Сумма двух углов, образованных при пересечении двух прямых, равна 250°. Докажите, что эти углы вертикальные.
Решение. Пусть тупой угол $ACN$ содержит $color{blue}{x}$ градусов. Тогда смежный с ним угол $BCN$ содержит ${180}^circ -color{blue}{x}$ градусов, а вертикальный угол $BCM$ тоже равен $color{blue}{x}$ градусов:
Но тогда
[angle ACN+angle BCN={180}^circ ne {250}^circ ]
И это вполне логично, поскольку сумма смежных углов всегда равна 180°. То же самое можно сказать, например, про углы $ACN$ и $ACM$ — они тоже смежные.
Остаётся лишь вариант вертикальных углов $ACN$ и $BCM$. Но эти углы вертикальные, что и требовалось доказать.
В последнем задании мы построили чертёж исходя из следующих соображений. Если искомые углы вертикальные (а именно это мы и пытаемся доказать), то они равны, и каждый из них будет равен 125°. Следовательно, речь идёт о тупых углах, поэтому именно тупые углы мы обозначили за $x$.
Помните: в геометрии важно построить правильный чертёж. И чем сложнее задачи, тем выше требования к качеству чертежей. Иначе на можно просто «не увидеть» алгоритм решения задачи.
Кроме того, в следующих уроках мы будем всё чаще отождествлять углы и их градусные меры. Абсолютно нормально писать и говорить «угол $ABC$ равен $x$» вместо «угол $ABC$ содержит $x$ градусов» — все прекрасно поймут, о чём речь.
Смотрите также:
- Перпендикулярные прямые — определение и свойства
- Что такое смежные углы
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- Метод координат в пространстве
- Интегрирование по частям
- Как формулы приведения работают в задаче B11
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Тогда
Следовательно 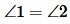
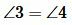
Задачи и решения
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
Решение. Так как углы 1 и 2 вертикальны, то 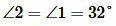
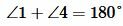
Углы 3 и 4 вертикальные. Тогда
Ответ. 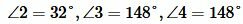
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
Ответ. 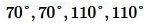
Треугольник – это геометрическая фигура, состоящая из трех отрезков, попарно соединенных между собой. (показать на рисунке с обозначением)
Элементами треугольника являются – медиана, высота и биссектриса. (все показать на рисунке)
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной высоты.
Все три медианы любого треугольника пересекаются в одной точке.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину с противоположной стороной.
Все три биссектрисы любого треугольника пересекаются в одной точке.
Высота треугольника – это перпендикуляр, опущенный из вершины треугольника на противоположную сторону, или ее продолжение.
Все три высоты, или их продолжения любого треугольника пересекаются в одной точке.
2. Теорема об угле в 300 в прямоугольном треугольнике.


1. Приложим к DАВС, равный ему DАВD, так чтобы вершины С и D оказались по разные стороны от прямой АВ.
2. Рассмотрим DDCB: ÐВDС = 900 — ÐDВА = 900 – 300 = 600 (из DАВD по теореме о сумме острых углов пр/уг D) ÐСВD = 300 + 300 = 600 ÞDDCB – р/б и ÞDС = ВС.
3. Но АС= DС и так как DC = ВС (из п.2) Þ АС= ВС (ч.т.д.)
Билет №6.
Измерение отрезков и углов.
Отрезок – это часть прямой ограниченная двумя точками, включает в себя граничные точки.
— Каждый отрезок имеет определенную длину, большую нуля. (привести пример с рисунком)
— Равные отрезки имеют равные длины. (привести пример с рисунком)
— Меньший отрезок имеет меньшую длину. (привести пример с рисунком)
— Длина отрезка, на котором отмечена точка, равна сумме длин отрезков, на которые делит его эта точка.
Угол – это геометрическая фигура, состоящая из двух лучей, исходящих из одной точки.
— Углы измеряются в градусах.
— Равные углы имеют равные градусные меры. (привести пример с рисунком)
— Градусная мера меньшего угла меньше градусной меры большего угла. (привести пример с рисунком)
— Если луч делит угол на два угла, то градусная мера всего угла равна сумме градусных мер этих углов. (привести пример с рисунком)
Теорема о двух прямых перпендикулярных к третьей.

1. Предположим, что прямые а и b пересекаются, тогда они будут иметь одну общую точку О.
2. Тогда получим, что из точки О на прямую с опущены два перпендикуляра a^c и b^c.
3. Но по теореме о существовании и единственности перпендикуляра к прямой этого быть не может.
4. Мы получили противоречие, значит наше предположение неверно и прямые а и b не будут пересекаться. (ч.т.д.)
Билет №7.
Смежные и вертикальные углы.
Смежными углами – это два угла, у которых одна сторона общая, а две другие являются дополнительными лучами. (показать на рисунке)
Свойство смежных углов: сумма смежных углов равна 1800.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого. (показать на рисунке)
Свойство вертикальных углов: вертикальные углы равны.
Свойство углов равнобедренного треугольника.
В равнобедренном треугольнике, углы при основании равны.
1. Мысленно скопируем DАВС и перевернем копию – получим DСВА.
2. Наложим DСВА на DАВС, так чтобы вершина В копии совместилась с вершиной В DАВС.
3. Так как ÐВ копии равен ÐВ треугольника Þ они при наложении совпадут.
4. Отрезок ВС копии наложится на луч ВА треугольника и так как АВ = ВС (по условию)Þ ВС и ВА – совпадут.
5. Отрезок ВА копии наложится на луч ВС треугольника и так как АВ = ВС (по условию)Þ ВА и ВС – совпадут.
6. Таким образом отрезок СА копии совместится с отрезком АС треугольника и треугольники при наложении совпадут Þ ÐА совпадет с ÐС и значит: ÐА=ÐС (ч.т.д.)
Билет №8.
Рекомендуемые страницы:
lektsia.com
Треугольник как магический символ
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека.
Треугольник — символ триединой природы вселенной: Небо, Земля, Человек; отец, мать, дитя; человек как тело, душа и дух; мистическое число три; тройка, первая из плоских фигур. Отсюда символ поверхности вообще. Поверхность состоит из треугольников (Платон).
Равносторонний треугольник символизирует завершение.
На Древнем Востоке почитали треугольник как символ природы всего сущего. Треугольник с вершиной, соединенной с такой же геометрической фигурой, аптеки использовали в качестве эмблемы временного цикла.
Герменевтической традиции известно множество видов треугольников, имеющих различные толкования.
Янтра Тары
Треугольник, обращенный вершиной вниз, является лунным и имеет символику женского начала, матки, воды, холода, природы, тела, йони, шакти. Символизирует Великую Мать как родительницу. Горизонтальная линия — это земля; ее цвет — белый. В символике горы и пещеры гора — это мужской, обращенный вверх треугольник, а пещера — треугольник женский, обращенный вершиной вниз. Во многих янтрах богинь в середине помещен треугольник вершиной вниз с точкой.
Треугольник, обращенный вершиной вверх, является солнечным и имеет символику жизни, огня, пламени, жара (отсюда горизонтальная линия, символизирующая воздух), мужское начало, лингам, шакта, духовный мир; это также троица любви, истины и мудрости. Означает королевское величие и имеет в качестве символа красный цвет.
Гексаграмма. При его наложении на описанный выше знак женского начала мы получим индуистскую эмблему объединения созидающего и порождающего начал — гексаграмму.
В индийской традиции такой символ толковался также и как знак любви богов ко всему земному. В Европе же данная геометрическая фигура была известна как звезда Давида.
Треугольник, вписанный в окружность, олицетворяет собой мир форм, заключенный в круге вечности. Плутарх, описывая эту геометрическую фигуру, называл пространство, ограниченное сторонами треугольника, равниной истины, на которой расположены образы всего, что было и будет. Треугольники могут выступать и в качестве лунного символа, тогда они располагаются горизонтально и соприкасаются своими вершинами. Общая точка этих треугольников символически обозначает смерть и новолуние.
В буддийской традиции два смыкающихся треугольника олицетворяют чистое пламя и Три Драгоценности Будды.
Троица и треугольник
Начиная с ранних христиан треугольник был символом Святой Троицы. Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.
Печать Соломона
Печать Соломона — другое название звезды Давида, образованной наложением друг на друга двух треугольников, т.е. гексаграммы. По преданию, царь Соломон с помощью этого знака управлял духами, заключенными в медный сосуд. Считается, что печать Соломона является мощным амулетом, способным защитить своего обладателя от влияния злых духов.
Треугольник Кеплера
В начале XVII в. знаменитый астроном Кеплер составил диаграмму соединения планет Сатурна и Юпитера. Так в астрономии называют расположение планет, при котором для земного наблюдателя эклиптические долготы равны нулю, а сами небесные тела находятся близко друг к другу или даже перекрываются. Кеплер представил это явление в виде треугольника, который вращается по зодиакальному кругу, совершая полный оборот за 2400 лет.
Треугольник в античной архитектуре
В античной традиции треугольник, обращенный вершиной вверх, символизировал стремление материи к духу. Поэтому фронтоны древнегреческих храмов в самой глубокой древности делали треугольными и всячески украшали. В отличие от поздних, более северных европейских построек наличие двускатной крыши не было вызвано климатическими условиями. В Древней Греции был теплый климат и снега зимой не было.
Треугольники на сосудах
В эпоху неолита у ранних земледельческих народов треугольники в орнаментах символизировали воздух, землю и огонь. Они — одни из самых древних символов, связанных с сельскохозяйственными работами, природой и ее календарными циклами.
Созвездие Треугольника
Точное происхождение названия этого созвездия неизвестно. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.
Глаз в треугольнике
Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII веке. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов. В XIX веке он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.
Треугольник в круге означает мир форм, заключенный в круге вечности. Область внутри такого треугольника есть общий центр их всех и именуется Равниной Истины, на которой находятся причина, формы и образы всего, что было и что будет; они пребывают там в покое, который не может быть нарушен, и Вечность окружает их; и отсюда время, как струя фонтана, стекает вниз в миры (Плутарх).
Три соединенных треугольника обозначают ненарушимое единство трех лиц Троицы.
Двойной треугольник, шестиконечная звезда, Печать Соломона, Могун Давид, говорит о том, что каждая истинная аналогия должна быть употребима обратно, что вверху, то и внизу. Это союз противоположностей, мужского и женского, положительного и отрицательного, причем верхний треугольник белый, а нижний черный, огонь и вода, эволюция и инволюция, взаимопроникновение, все является образом другого, гермафродит, совершенное равновесие взаимодополняющих сил, андрогинное проявление божества, человек, всматривающийся в свою собственную природу, двойственные силы творения, синтез всех стихий, при обращенном вверх треугольнике как небесном символе, и обращенном вниз — как символе земном, а вместе — символ человека, как объединяющего эти два мира. Как Печать Соломона это изображение Сохраняющего; оно дает духовную власть над материей и является повелителем джиннов.
Два треугольника, лежащие горизонтально и соприкасающиеся вершинам, — это лунный символ, растущая и убывающая Луна, вечное возвращение, смерть и жизнь, умирание и воскрешение. Точка соприкосновения — это новолуние и смерть. У алхимиков два треугольника — сущность и субстанция, forma и materia, дух и душа, сера и ртуть, стабильное и изменчивое, духовная сила и телесное существование.
Треугольники, символизирующие стихии, таковы:
огонь (обращенный вершиной вверх),
воду (обращенный вершиной вниз),
воздух (обращенный усеченной вершиной вверх),
землю (обращенный усеченной вершиной вниз).
У китайцев треугольник с подвешенными мечами символизирует восстановление.
У христиан равносторонний треугольник или треугольник, образованный тремя пересекающимися кругами, символизирует Троицу в единении и равенстве трех составляющих ее лиц. Треугольное сияние — атрибут Бога-Отца.
У египтян треугольник символизирует Триаду. Они сравнивают вертикальную сторону (прямоугольного треугольника) с мужчиной, горизонтальную — с женщиной, а гипотенузу — с их потомком: Озирис как начало, Изида как середина или хранилище и Гор как завершение (Плутарх). Рука Египтян — это союз огня и воды, мужчины и женщины. Фигура из трех двойных треугольников, окруженная концентрическими кругами, символизирует Кхуй, Страну Духов.
У греков дельта символизирует дверь жизни, женское начало, плодородие.
У индийцев обращенные вершинами вверх и вниз треугольники — это шакта и шакти, лингам и йони, Шива и его Шакти.
У пифагорейцев равносторонний треугольник символизирует Афину как богиню мудрости.
Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла, о Треугольник в сочетании с крестом образует алхимический знак Серы. В перевернутом виде он означает завершенное Великое Делание.
Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу — Отца, Сына и Святого Духа.
У масонов треугольник символизирует Тройственность космоса, а его стороны — Свет, Тьму и Время (основание).
Увиденный во сне треугольник символизирует материнское лоно космоса.
В Древнем Китае треугольник является «символом женского начала», однако не играет значительной роли в умозрительных рассуждениях. В тибетском тантризме комбинация двух равносторонних треугольников в виде гексаграммы представляет собой «проникновение в женственное мужского огня».
Символический знак «Сердце Хрунгнира» из трех переплетенных треугольников. Времена викингов. Остров Готланд .
В иудаизме и христианстве треугольник — знак Бога. Бог христианской Троицы иногда представлен глазом внутри треугольника или фигурой с треугольным нимбом. Алхимики использовали треугольники с вершинами, направленными вверх и вниз, в качестве знаков огня и воды. В более общем смысле линейные треугольники или композиции, имеющие форму треугольника, могут обозначать триады богов или другие тройственные понятия.
Магический треугольник христианских теософов есть знаменитая «абракадабра», которому они приписывали необыкновенные свойства. Употребляясь в качестве магической формулы, это слово обычно вписывалось в или выстраивалась как перевернутый треугольник .
Сань цзяо фу, или «Треугольное Заклинание», представляет собой листок бумаги, на котором написаны заклинания, сложенный в форме треугольника.
Амулеты гностиков были разнообразны по форме: треугольные, прямоугольные, огонь — Теджас — красный — зеленый — треугольник.
Символы союза — все парные оппозиции, совершенный круг, пересекающиеся круги, двойной треугольник, андрогин, деревья с перевившимися ветвями, рог единорога, инь-ян, лингам и йони.
Важную роль в архитектуре играет геометрическая символика космоса: все круглые формы выражают идею неба, квадрат — это земля, треугольник- символизирует взаимодействие между землей и небом.
Готическая архитектура имеет в своей основе треугольник — символ Троицы. Пламенеющая готическая арка — задает тему огня и развивает апокалиптическую тему.
Источник
shuwany.rs
Треугольники
Задача
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K.
Найти площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 10.
Дано: ABCD — параллелограмм,
AK, BK — биссектрисы углов BAD и ABC,
AK∩BK=K, KF⊥AB,
KF=10, BC=19
Найти: SABCD
Читать далее
Параллелограмм
Задача
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.
Найти стороны треугольника ABC.
Дано: ΔABC,
AD — медиана, BE — биссектриса,
AD=BE=8, AD⊥BE
Найти: AB, BC, AC
Читать далее
Решение треугольников
Задача
Боковые стороны AB и CD трапеции ABCD равны соответственно16 и 34, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB.Найти площадь трапеции.
Дано: ABCD — трапеция, AD || BC, BC=2,
AB=16, CD=34, DF — биссектриса ∠ADC, F — середина AB
Найти: SABCD
Решение:
Читать далее
Трапеция
Задача
На стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.
Найти AH.
Читать далее
Подобие треугольников
Задача
В треугольнике ABC известны длины сторон AB=28, AC=56, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найти CD.
Читать далее
Подобие треугольников
Задача
В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найти радиус окружности, описанной около треугольника ABC, если BC=12.
Решение:
Пусть биссектриса угла A пересекает высоту BD треугольника ABC в точке F.
По условию, BF:FD=5:4.
Рассмотрим треугольник ABD, ∠ADB=90°.
Читать далее
Элементы треугольника
Задача
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=5 и MB=10. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найти CD.
Дано: ΔABC вписан в окр.(O;R),
CM — биссектриса ∠ACB, CD — касательная к окр.(O;R),
AM=5, MB=10, CD∩AB=D
Найти: CD
Читать далее
Решение треугольников
www.treugolniki.ru
Треугольник, все про треугольники
Определение треугольника
В любом треугольнике три угла и три стороны.
Против большего угла треугольника лежит большая сторона.
Виды треугольников
Треугольники бывают
Треугольник называется
Основные линии треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектрисой угла треугольника называется луч, исходящий из вершины треугольника и делящий его пополам.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону (или ее продолжение).
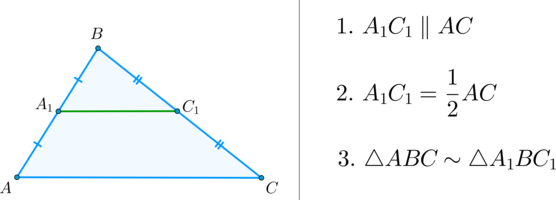
Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника и параллельный третьей стороне.
В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.
Два треугольника называются равными, если у них равны соответствующие стороны и соответствующие углы.
Признаки равенства треугольников
I признак (по двум сторонам и углу между ними). Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак (по стороне и прилежащим углам). Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак (по трем сторонам). Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Подробнее про признаки равенства треугольников читайте по ссылке.
Признаки подобия треугольников
Треугольники называются подобными, если их стороны пропорциональны.
I признак. Если два угла одного треугольника раны двум углам другого треугольника, то такие треугольники подобны.
II признак. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то такие треугольники подобны.
III признак. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Подробнее про признаки подобия треугольников читайте по ссылке.
Теоремы треугольников
Для любого треугольника справедливы следующие теоремы.
Подробнее про теорему косинусов читайте по ссылке.
Подробнее про теорему синусов читайте по ссылке.
Примеры решения задач
ru.solverbook.com
Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия
2. Вникай в доказательства
Готовиться с нами — ЛЕГКО!
Эффективное решение существует!
Вы ищете теорию и формулы для ЕГЭ по математике? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.
Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить, выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Факт 1.
(bullet) Смежные углы — два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.
Смежные углы: (angle AOB) и (angle BOC).
Теорема: Сумма смежных углов равна (180^circ): (angle
AOB+angle BOC=180^circ).
Факт 2.
(bullet) Вертикальные углы — два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).
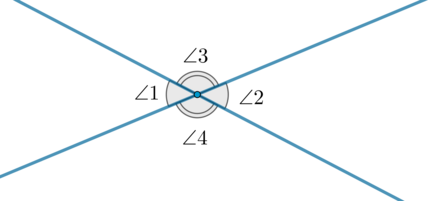
Вертикальные углы: (angle 1) и (angle 2), (angle 3) и (angle 4).
Теорема: Вертикальные углы равны: (angle 1=angle 2) и (angle 3=angle 4).
Факт 3.
(bullet) Сумма углов (angle A, angle B, angle C) треугольника (ABC) равна (180^circ).
(bullet) Внешний угол (angle BCD) треугольника (ABC) равен сумме двух углов треугольника, не смежных с ним.
Факт 4.
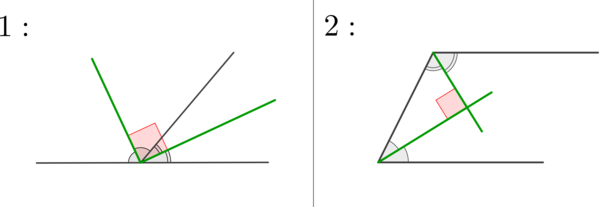
(bullet) Биссектрисы смежных углов взаимно перпендикулярны.
(bullet) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
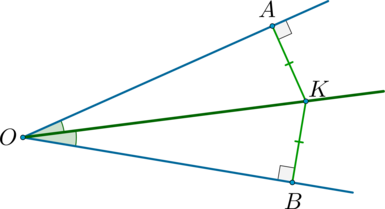
(bullet) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
(bullet) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
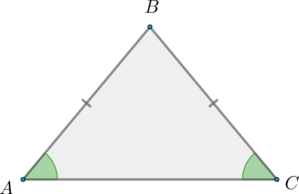
(bullet) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
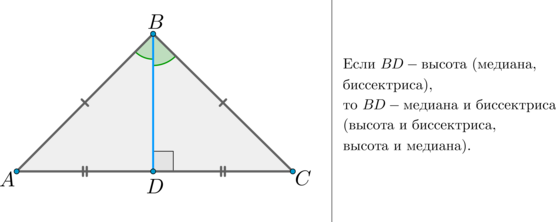
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
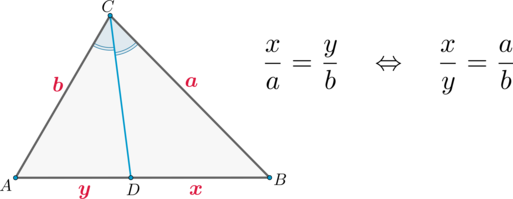
(bullet) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 8.
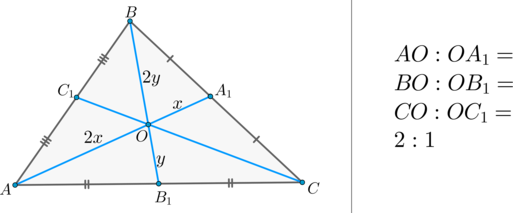
(bullet) Медианы в треугольнике точкой пересечения делятся в отношении (2:1), считая от вершины.
Факт 9.
(bullet) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
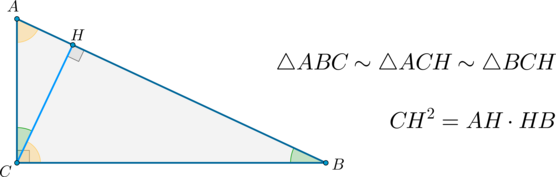
(bullet) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
(bullet) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.
Факт 11.
(bullet) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
(bullet) 1. Средняя линия треугольника параллельна третьей стороне.
(bullet) 2. Средняя линия треугольника равна половине третьей стороны.
(bullet) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект. Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.

УСТАЛ? Просто отдохни