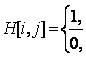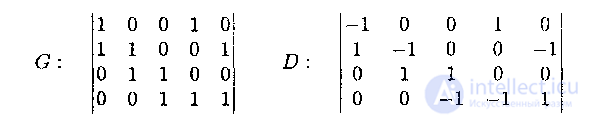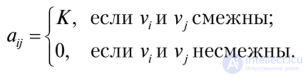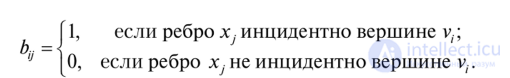Иногда
дугам графа G
сопоставляются
(приписываются) числа — дуге
ставится
в соответствие некоторое число
,
называемое
весом,
или
длиной,
пли
стоимостью
(ценой) дуги.
Тогда граф G
называется
графом
со взвешенными дугами. Иногда
веса (числа vi)
приписываются
вершинам xi
графа,
и тогда получается граф со
взвешенными вершинами. Если
в графе веса приписаны и дугам, и вершинам,
то он называется просто взвешенным.
При
рассмотрении пути
,
представленного последовательностью
дугза еговес
(или
длину,
или
стоимость)
принимается
число
,
равное сумме весов всех дуг, входящих
в,
т.е.
Таким образом,
когда слова «длина», «стоимость», «цена»
и «вес» применяются к дугам, то они
эквивалентны по содержанию, и в каждом
конкретном случае выбирается такое
слово, которое
Рис. 1.3.
ближе
подходит по смыслу и совпадает с принятым
в литературе.
Длиной
(или
мощностью) пути
называется число дуг, входящих в него.
3. Петли, ориентированные циклы и циклы
Петлей
называется
дуга, начальная и конечная вершины
которой совпадают. На рис. 1.3, например,
дуги
являются петлями.
Путь
называетсязамкнутым,
если
в нем начальная вершина дуги
совпадает
с конечной вершиной дуги
.
Так, например, в
графе, приведенном на рис. 1.3,
последовательности дуг
(1.7)
(1.8)
(1.9)
являются замкнутыми
путями.
Пути
(1.7) и (1.9) являются замкнутыми простыми
орцепями (контурами,
или
простыми
орциклами), поскольку
в них одна и та же вершина используется
только один раз (за исключением начальной
и конечной вершин, которые совпадают),
а путь (1.8) не является контуром,
так
как вершина х1
используется
в нем дважды. Контур, проходящий через
все вершины графа, имеет особое значение
и называется гамильтоновым
контуром.
Конечно, не все графы обладают
гамильтоновыми контурами. Так, например,
контур (1.9) является гамильтоновым
контуром графа, приведенного на рис.
1.3, а граф на рис. 1.2 не имеет гамильтоновых
контуров, поскольку не существует такой
дуги, для которой х1
была бы конечной вершиной.
Замкнутый
маршрут является
неориентированным двойником замкнутого
пути. Таким образом, замкнутый маршрут
является маршрутом
в
котором совпадают начальная и конечная
вершины, т. е. в котором
.
На рис. 1.3 маршруты
(1.10)
и
(1.11)
4. Степени вершины
Число
дуг, которые имеют вершину xi
своей
начальной вершиной, называется
полустепенью
исхода вершины
xi,
и, аналогично, число дуг, которые имеют
xi
своей
конечной вершиной, называется полустепенью
захода вершины
xi.
Таким
образом, на рис. 1.3 полустепень исхода
вершины x6,
обозначаемая через
,
равна,
и полустепень захода вершиныx6,
обозначаемая через
,
равна.
Совершенно
очевидно, что сумма полустепеней захода
всех вершин графа, а также сумма
полустепеней исхода всех вершин равны
общему числу дуг графа G,
т.
е.
(1.12)
где п
—
число вершин и т
—
число дуг графа G.
Для
неориентированного графа G=(X,
Г)
степень
вершины
xi
определяется
аналогично — с помощью соотношения
,
и когда не может возникнуть недоразумений,
мы будем обозначать степень вершиныxi
через
di.
Соседние файлы в папке Прикладная теория графов
- #
21.04.2015645.12 Кб65L1.doc
- #
21.04.2015629.25 Кб78L2.doc
- #
21.04.2015350.72 Кб86L3.doc
- #
- #
21.04.2015860.67 Кб61L5.doc
- #
21.04.2015468.48 Кб59L6.doc
страницы: 1 2 3 4
Содержание
- Содержание
- Ориентированные графы
- Взвешенные графы
- Способы представления графов
- Матрица смежности
- Примечания
Ориентированные графы
Орграф — это граф, все рёбра которого имеют направление. Такие направленные рёбра называются дугами. На рисунках дуги изображаются стрелочками (см. рис. 11.6).
Рис. 11.6. Орграф
В отличие от рёбер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из неё исходит), вторая — концом дуги (дуга в неё входит). Можно сказать, что любое ребро — это пара дуг, направленных навстречу друг другу.
Если в графе присутствуют и рёбра, и дуги, то его называют смешанным.
Все основные понятия, определённые для неориентированных графов (инцидентность, смежность, достижимость, длина пути и т. п.), остаются в силе и для орграфов — нужно лишь заменить слово «ребро» словом «дуга». А немногие исключения связаны с различиями между рёбрами и дугами.
Степень вершины в орграфе — это не одно число, а пара чисел: первое характеризует количество исходящих из вершины дуг, а второе — количество входящих дуг.
Путь в орграфе — это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причём каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 11.6 нет пути, ведущего из вершины 2 в вершину 5. «Двигаться» по орграфу можно только в направлениях, заданных стрелками.
Таблица 11.2. Примеры ориентированных графов
| Орграф | Вершины | Дуги |
|---|---|---|
| Чайнворд | Слова | Совпадение последней и первой букв (возможность связать два слова в цепочку) |
| Стройка | Работы | Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) |
| Обучение | Курсы | Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Ada, и т. п.) |
| Одевание ребенка | Предметы гардероба | Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т. п.) |
| Европейский город | Перекрёстки | Узкие улицы с односторонним движением |
| Организация | Сотрудники | Иерархия (начальник — подчинённый) |
Взвешенные графы
Взвешенный (другое название: размеченный) граф (или орграф) — это граф (орграф), некоторым элементам которого (вершинам, рёбрам или дугам) сопоставлены числа. Наиболее часто встречаются графы с помеченными рёбрами. Числа–пометки носят различные названия: вес, длина, стоимость.
Замечание: Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все рёбра которого имеют одинаковый вес 1.
Длина пути во взвешенном (связном) графе — это сумма длин (весов) тех рёбер, из которых состоит путь. Расстояние между вершинами — это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображённом на рис. 11.7, равно 6.
Рис. 11.7. Взвешенный граф
N–периферия вершины v — это множество вершин, расстояние до каждой из которых (от вершины v) не меньше, чем N.
Таблица 11.3. Примеры взвешенных графов
| Граф | Вершины | Вес вершины | Рёбра (дуги) | Вес ребра (дуги) |
|---|---|---|---|---|
| Таможни | Государства | Площадь территории | Наличие наземной границы | Стоимость получения визы |
| Переезды | Города | Стоимость ночёвки в гостинице | Дороги | Длина дороги |
| Супер–чайнворд | Слова | — | Совпадение конца и начала слов (возможность «сцепить» слова) | Длина пересекающихся частей |
| Карта | Государства | Цвет на карте | Наличие общей границы | — |
| Сеть | Компьютеры | — | Сетевой кабель | Стоимость кабеля |
Способы представления графов
Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.
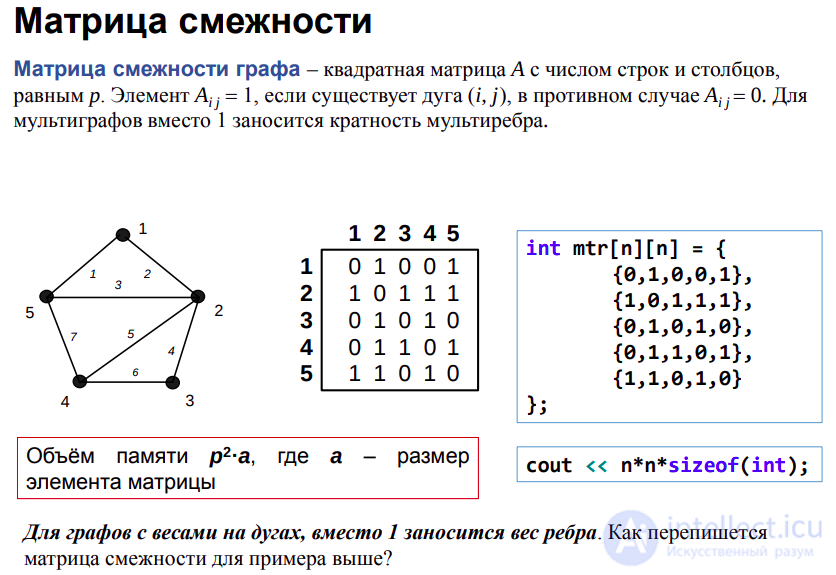
Матрица смежности
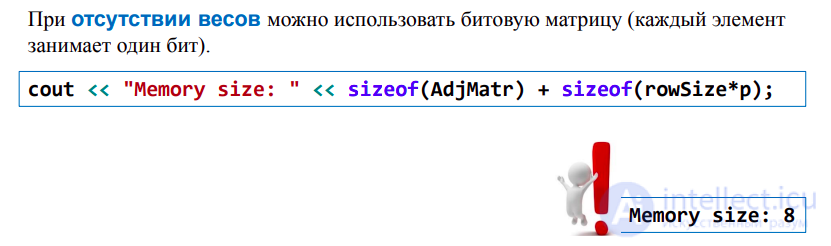
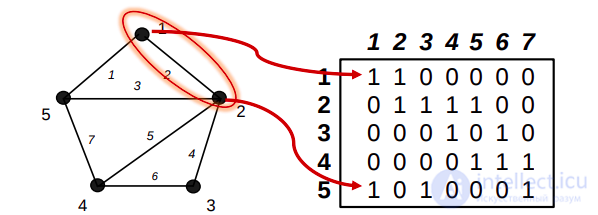
Матрица смежности Sm — это квадратная матрица размером NxN (N — количество вершин в графе), заполненная единицами и нулями по следующему правилу:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u, v] = 1, в противном случае Sm[u, v] = 0.
Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа — несимметричной.
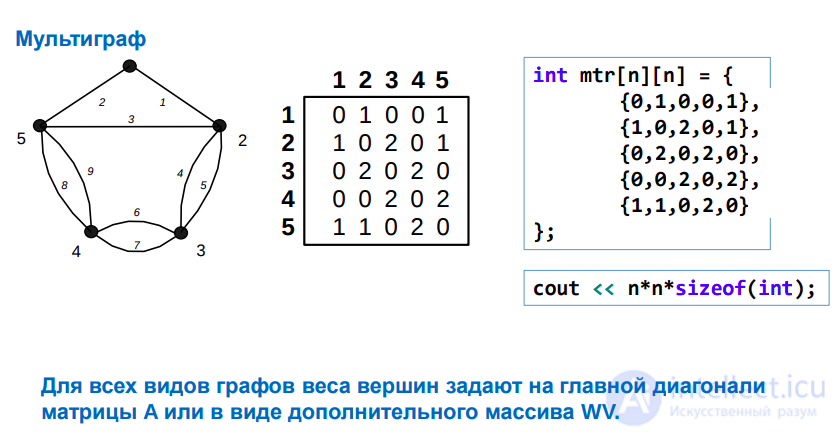
Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = ves(e), в противном случае Sm[u,v] = 0.
Это хорошо согласуется с замечанием, сделанным в предыдущем пункте: невзвешенный граф можно интерпретировать как взвешенный, все рёбра которого имеют одинаковый вес 1.
Небольшое затруднение возникнет в том случае, если в графе разрешаются рёбра с весом 0. Тогда придётся хранить два массива: один с нулями и единицами, которые служат показателем наличия рёбер, а второй — с весами этих рёбер.
В качестве примера приведём матрицы смежности для трёх графов, изображённых на рис. 11.5, рис. 11.6 и рис. 11.7 (см. рис. 11.8).
Таблица 11.8. Примеры матриц смежности
| a | b | c | d | f | 1 | 2 | 3 | 4 | 5 | a | b | c | d | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | a | 0 | 1 | 10 | 0 |
| b | 1 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | b | 1 | 0 | 2 | 10 |
| c | 1 | 1 | 0 | 1 | 1 | 3 | 1 | 1 | 0 | 0 | 1 | c | 10 | 2 | 0 | 3 |
| d | 0 | 1 | 1 | 0 | 1 | 4 | 0 | 0 | 1 | 0 | 0 | d | 0 | 10 | 3 | 0 |
| f | 0 | 1 | 1 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на её использовании. А неудобство — в несколько завышенном требовании к памяти: если граф далёк от полного, то в массиве, хранящем матрицу смежности, оказывается много «пустых мест» (нулей). Кроме того, для «общения» с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.
страницы: 1 2 3 4
Примечания
Привет, сегодня поговорим про представление графов в памяти компьютера, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
представление графов в памяти компьютера, описание бержа графа , список дуг графа, массив дуг графа, списки смежности, матрица инциденций, матрица смежности, хранение графов в памяти эвм , настоятельно рекомендую прочитать все из категории Структуры данных.
Для начала разберемся, что же такое граф и какие они бывают. Граф — множество V вершин и набор E неупорядоченных и упорядоченных пар вершин. Говоря проще, граф — это множество точек (вершин) и соединяющих их путей (дуг или ребер). Граф может быть ориентированным и неориентированным. В ориентированном графе пути (дуги) имеют направление, а в неориентированном — не имеют. Пути в неориентированном графе называются ребрами.
Взвешенным называется такой граф, для каждого ребра(дуги) которого определена некоторая функция. А эта функция называется весовой.
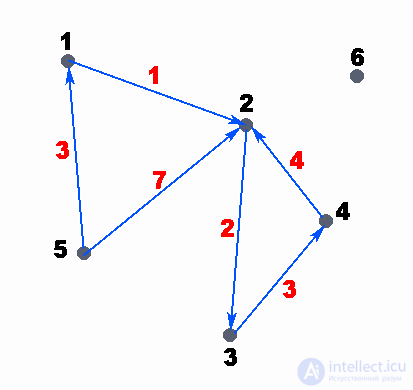
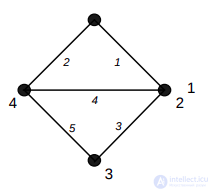
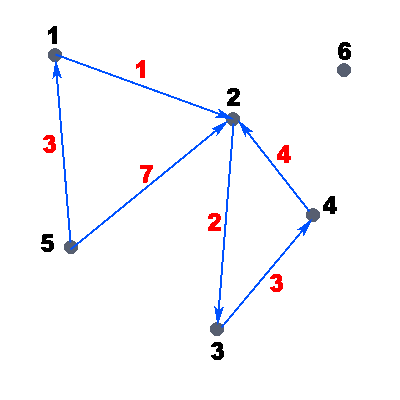
Рассмотрим пример ориентированного взвешенного графа:
Пример ориентированного взвешенного графа
На рисунке точками обозначены вершины графа, стрелками — дуги, черные числа — номера вершин графа, а красные — веса дуг. Вес дуги можно представить также как стоимость. Т.е. например: дан граф, нужно дойти от вершины i до вершины j, заплатив минимальное количество денег/потратив наименьшее количество времени. Пусть в нашем графе, который представлен на рисунке, нам нужно пройти из вершины 5 в вершину 2, а вес дуг — стоимость прохода по данному ребру. В данном примере очевидно, что выгоднее пройти через вершину 1 и только потом прийти в вершину 2, так мы заплатим всего 4 единицы денег, иначе, если пойти напрямую, мы заплатим целых 7 единиц.
Рисунок 1.
На рисунке все смотрится красиво, все задачи вроде бы решаются легко… Но, если граф будет действительно большим, например на 1000 вершин? Да, такой граф на бумажке рисовать очень долго и неприятно… Пускай лучше все это делает за нас компьютер!
Проблема правильного хранения графа в памяти компьютера(ЭВМ) действительно актуальна в сегодняшние дни.
Очертанием графа считается любая топологически связанная область, ограниченная ребрами графа. Для многих приложений все узлы графа должны совпадать с узлами технологической сетки. В этом случае ребра графа могут представлять собой кривые линии, дуги или ломаные линии, состоящие из отрезков прямых.
Важно помнить, что сеть может быть изображена многими различными способами; например, сети, приведенные на рис. 8.20, изоморфные.
Рис. 8.20. Способы изображения сети
Графы в ПЭВМ можно представить тремя способами: матрицей смежности, матрицей инцидентности и вектором смежности.
Требования к представлению графов в памяти
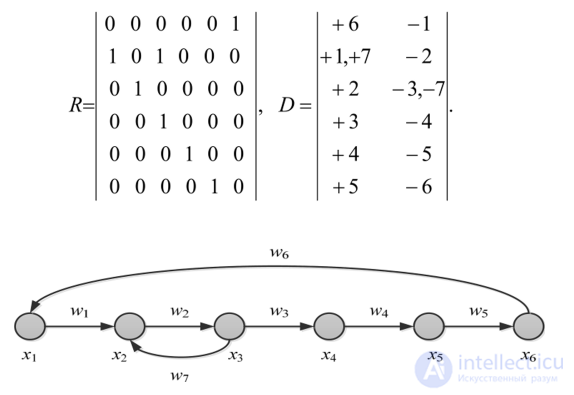
Известны различные способы представления графов в памяти компьютера, кото рые различаются объемом занимаемой памяти и скоростью выполнения oneраций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики n(р, q) — объема памяти для каждого представления. Здесь р — число вершин, a q — число ребер.
ЗАМЕЧАНИЕ Указанные представления пригодны для графов и орграфов, а после некоторой модификации также и для псевдографов, мультиграфов и гиперграфов.
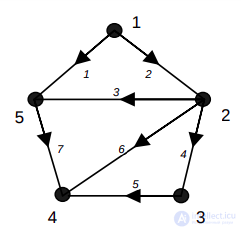
Представления иллюстрируются на конкретных примерах графа G и орграфа D диаграммы которых представлены на рис. 2.
Рисунок 2. Диаграммы графа (слева) и орграфа (справа), используемых в качестве примеров
матрица смежности
Представление графа с помощью квадратной булевской матрицы
М : array [l..p, l..p] of 0..1,
отражающей смежность вершин, называется матрицей смежности, где
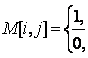
если вершины vi и vj не смежны.
Для матрицы смежности n(p,q) = О(р2)
Пример
Кроме большого количества требуемой памяти и медленной работы на разреженных графах (графах, у которых E << V2) у матрицы смежности есть еще один важный недостаток. Иногда в задачах нужно выводить не номера вершин, а номера дуг (ребер) на вводе. Хранить эти номера матрица смежности «не умеет». Нужно реализовывать восстановление номера дуги (ребра) как-то иначе, а это совсем неудобно.
Приведем расчеты временной сложности хранения графа матрицей смежности:
Операция Временная сложность
Проверка смежности вершин x и y О(1)
Перечисление всех вершин смежных с x О(V)
Определение веса ребра (x, y) О(1)
Перечисление всех ребер (x, y) О(V2)
Перечисление ребер, инцидентных вершине x Номера ребер не хранятся
Перечисление вершин, инцидентных ребру s Номера ребер не хранятся
Определение веса вершины x О(1)
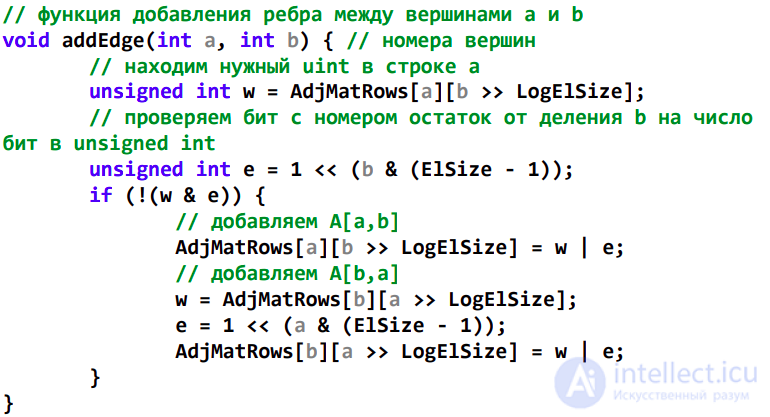
Вариант реализации матрицы смежности через битовую матрицу
Выделение памяти под битовую матрицу
Добавления ребра… Куда поставить 1?
Функция печати битовой матрицы
расширение функции main()
На практических занятиях самостоятельно:
1) запустите код и протестируйте его для матриц смежности графов с 32 и более вершинами.
2) допишите функцию удаления ребра между вершинами a и b
матрица инциденций
Матрица инциденций графа – прямоугольная матрица В с числом строк p и числом столбцов q . Об этом говорит сайт https://intellect.icu . Каждый столбец соответствует одному из ребер. Столбец, соответствующий ребру e = {i, j} содержит 1 в i-й и j-й строке, в остальных строках содержатся нули. Столбец, соответствующий петле, содержит единственную 1. Для орграфа начало и конец дуги задаются разными числами (например, –1 – начало, 1 – конец). Для мультиграфа можно либо рассматривать каждое ребро в составе мультиребра как отдельное (с записью в отдельный столбец), либо записывать значение кратности ребра вместо 1.
Представление занимает объем памяти, равный p*q*a, где a – размер элемента матрицы.
Представление графа с помощью матрицы Н : array [l..p, l..q] of 0..1 (для орграфов H : array [l..p,l..q] of -1..1), отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа
если вершина vi инцидентна ребру ej
в противном случае,
а для ориентированного графа

если вершина vi и ребро ej не инцидиентны,
если вершина vi инцидентна ребру ej и является его началом.
Для матрицы инциденций n(p,q)=O(pq).
Примеры матриц инциденций
Пример
Пространственная сложность этого способа O(N*M).
Временные сложности сведены в таблицу
- Операция Временная сложность
- Проверка смежности вершин x и y T(M*N)
- Перечисление всех вершин смежных с x T(M*N)
- Определение веса ребра (x, y) T(M*N)
- Определение веса вершины x Вес вершины не хранится
- Перечисление всех ребер (x, y) T(M)
- Перечисление ребер, инцидентных вершине x T(M)
- Перечисление вершин, инцидентных ребру s T(N)
Матрица инцидентности лучше всего подходит для операции «перечисление ребер, инцидентных вершине x».
Массив ребер
Массив ребер графа – прямоугольная матрица C с двумя строками и числом столбцов q. Каждый столбец соответствует одному из ребер. В столбце, соответствующем ребру e = {i, j} первый элемент содержит i, а второй – j.
Дополнения
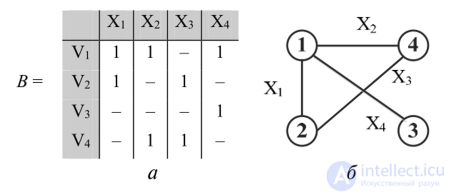
Матрица смежности. Любой граф G = (V, Е) с М вершинами может быть представлен матрицей размера М х М при условии, что вершинам G приписаны произвольные метки. Если вершины G обозначены Vv V2,…, VM, то матрица смежности Л определяется следующим образом:
Здесь К — вес ребра, соединяющего данные вершины. На рис. 8.21 представлены граф и матрица смежности, описывающая его.
Рис. 8.21. Матрица смежности (а) для графа (б)
Матрица смежности неориентированного графа является симметричной.
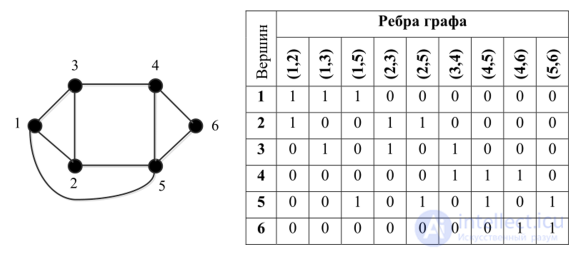
Матрица инцидентности. Если вершины графа обозначены vp v2, …, vM, а ребра — метками ер е2,…, eN, то матрица инцидентности Мх Мопределяется следующим образом:
Часто в матрицах смежности и инцидентности вместо нуля ставят « — » (для наглядности). Единицы в матрицах (рис. 8.22) могут быть заменены целыми числами, характеризующими веса ребер, такая матрица называется матрицей оценки (весов).
Рис. 8.22. Матрица инцидентности (инциденций) (а) для графа (б)
На рис. 8.23, 8.24 приведены матрицы инциденций для ориентированного и неориентированного графов.
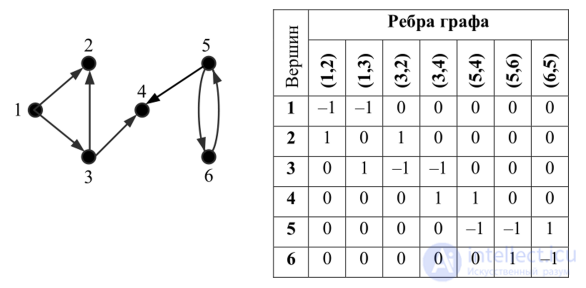
Модель системы часто представляется ориентированным графом G = (V, Е) с множеством вершин V = vp …., vn и множеством дуг Е — упорядоченных пар номеров смежных вершин [/, у], Е = [ipjVn,jnl Общее число таких пар обозначим как Q. Одним из способов представления топологии является матрица изо- морфности D, в строках которой помещены номера входящих (с плюсом) и выходящих (с минусом) дуг.
Рис. 8.23. Ориентированный граф и его матрица инциденций
Рис. 8.24. Неориентированный граф и его матрица инциденций
Для графа, приведенного на рис. 8.25, матрицы смежности и изо- морфности имеют вид
Рис. 8.25. Модель системы в форме графа
Избыточность хранимой информации в матрице смежности (нулевые значения) компенсируется простотой вычислительных алгоритмов и скоростью получения требуемой информации из матрицы.
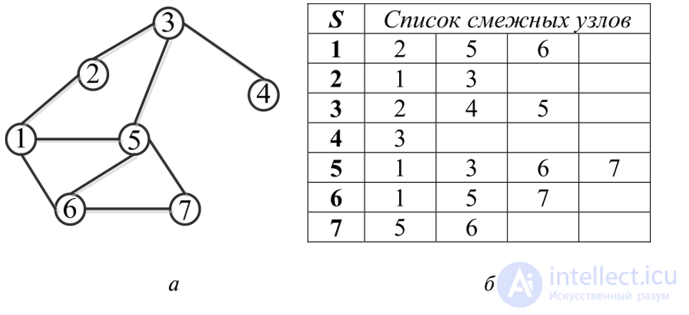
Другой способ представления графа — вектор смежности, выдающий списки узлов, с которыми данный узел связан непосредственно. Для графа, изображенного на рис. 8.26, такое описание можно представить в виде структуры (таблицы). В столбце S представлены
Рис. 8.26. Граф (а), представленный вектором смежности (б)
номера узлов, далее в строке таблицы следует список соседних узлов. По этой причине число столбцов в каждой из строк различно.
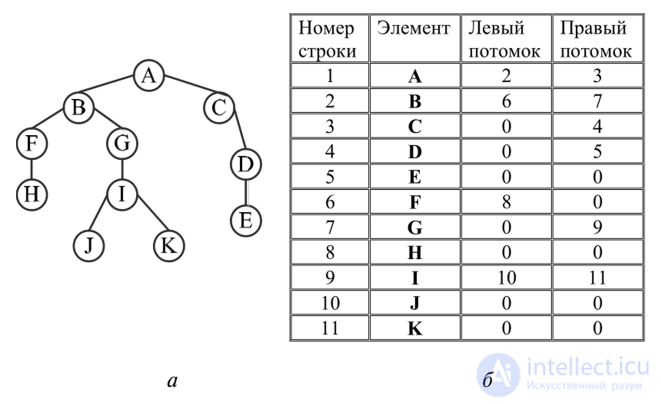
Представление древовидных структур. При представлении в машинной памяти древовидных структур в виде связного списка каждый элемент списка может содержать три поля, в одном из которых хранятся данные, соответствующие элементу (базовый тип), а в двух оставшихся полях — указатели левого и правого потомков узла (рис. 8.27).
Рис. 8.27. Представление древовидной структуры: а — дерево; б — табличное представление
списки смежности
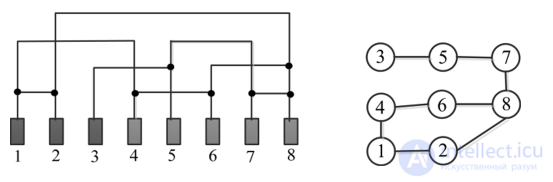
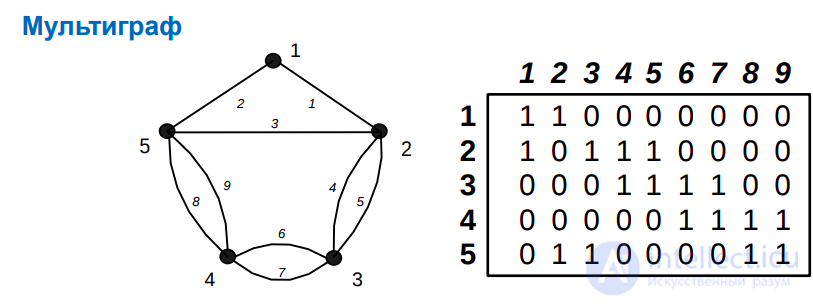
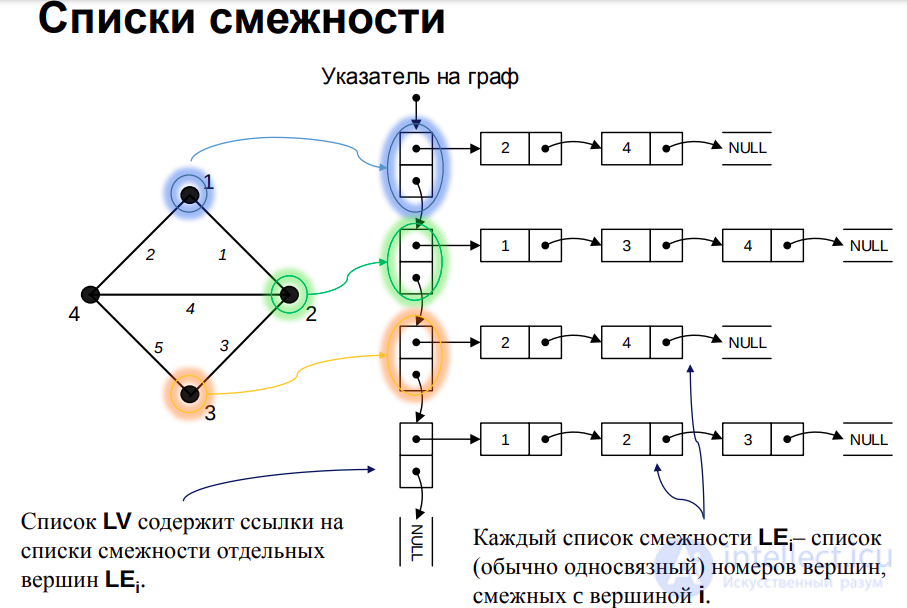
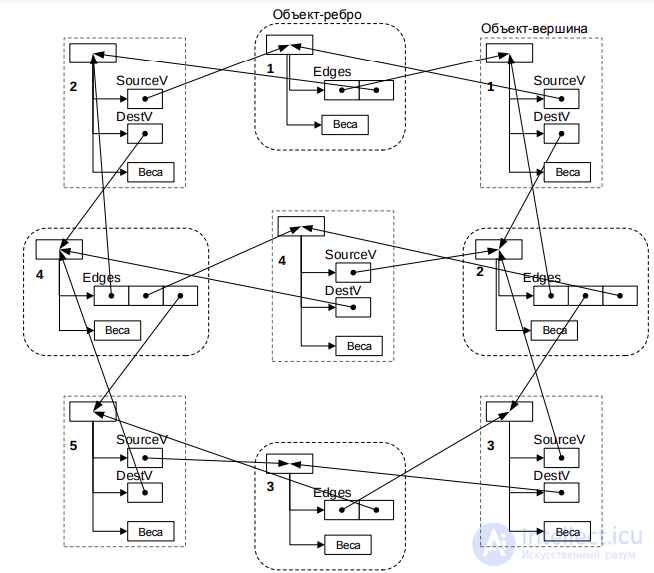
Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей Г : array [l..p] of N на списки смежных вершин (элемент списка представлен структурой N : record v : l..p; n : N endrecord), называется списком смежности. В случае представления неориентированных графов списками смежности n(p,q) = O(p + 2q), а в случае ориентированных графов n(р, q) = О(р + q).
Пример
Списки смежности для графа G и орграфа D представлены на рис. 3
Рисунок 3 . Списки смежности для графа G (слева) и орграфа D (справа)
Приведем расчеты временной сложности хранения графа списками смежных вершин:
- Операция Временная сложность
- Проверка смежности вершин x и y О(E)
- Перечисление всех вершин смежных с x О(E)
- Определение веса ребра (x, y) О(E)
- Перечисление всех ребер (x, y) О(E)
- Поиск i-ой дуги О(1)
Времена у всех операций, вроде бы, такие же, как и у списка ребер. Однако, большинство из них реально намного меньше. Например, проверка смежности вершин x и y и перечисление всех вершин смежных с x в списке ребер гарантированно будет выполнятся О(Е) операций, т.к. нам обязательно нужно пробежать весь список, а в списке смежности мы бежим только по вершинам, смежным с х.
Кроме того, мы экономим колоссальное количество памяти.
Реализация списков смежности на C++
Односвязные списки, построенные при помощи структур
Список дуг(массив дуг) графа
Следующий тип хранения графа в памяти компьютера — список дуг. Чаще всего это двумерный массив размером 3*E, в первой строке которого хранится информация, из какой вершины начинается дуга, во второй — в какой кончается, а в третьей строке — вес дуги. Опять же разберемся на примере
1 2 3 4 5 6
1 1 2 3 4 5 5
2 2 3 4 2 1 2
3 1 2 3 4 3 7
Мы четко видим, что почти вся таблица заполнена «нужными» значениями, а не нулями. Это уже хорошо, значит, память экономится.
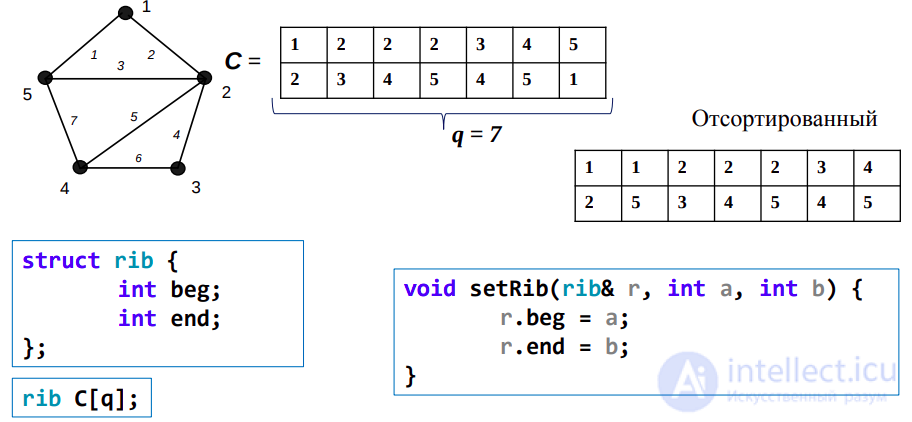
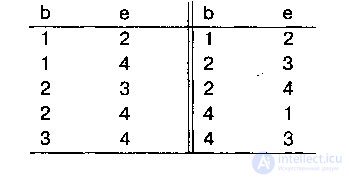
Представление графа с помощью массива структур E: array [1..p] of record b,e: 1..p endrecord, отражающего список пар смежных верщин, называется массивом ребер (или, для орграфов, массивом дуг). Для массива ребер (или дуг) n(p,q)=O(2q).
Пример
Представление с помощью массива ребер (дуг) показано в следующей таблице (для графа G слева, а для орграфа D справа).
Приведем расчеты временной сложности хранения графа списком дуг:
Операция Временная сложность
Проверка смежности вершин x и y О(E)
Перечисление всех вершин смежных с x О(E)
Определение веса ребра (x, y) О(E)
Перечисление всех ребер (x, y) О(E)
Поиск i-ой дуги О(1)
Как видно, этот способ, в отличие от матрицы смежности, хранит информацию о номере дуги. Также ясно, что этот способ нам выгоден, если чаще всего нам нужно будет узнать что-то (вес, вершины начала или конца) о i-ой дуге. Однако, такие задачи в практическом программировании встречаются довольно редко.
Если в предыдущих представлениях одно ребро мы заменяли двумя дугами, то список дуг может хранить или дуги или ребра (в зависимости от реализации). Это довольно удобно и может требовать в 2 раза меньше памяти.
описание бержа графа
Для того чтобы ускорить работу матрицы смежности на разреженных графах, можно использовать другой тип хранения графа — описание Бержа. Для каждой вершины хранится список смежных вершин. Чаще всего для этого используется двумерный массив размером V в квадрате, в строке u которого хранятся номера вершин, смежных с u. В нулевой элемент строки u вписывается количество вершин, хранящихся в данной строке. Теперь попробуем представить наш граф при помощи описания Бержа на примере:
0 1 2 3 4 5 6
1 1 2 0 0 0 0 0
2 1 3 0 0 0 0 0
3 1 4 0 0 0 0 0
4 1 2 0 0 0 0 0
5 2 1 2 0 0 0 0
6 0 0 0 0 0 0 0
В нулевом столбце хранятся «длины» строк. Однако, вес дуг никак не хранится, а если его хранить отдельно, то нужно заводить еще один массив размером V в квадрате…
Временные сложности сведены в таблицу:
- Операция Временная сложность
- Проверка смежности вершин x и y О(V)
- Перечисление всех вершин смежных с x О(V)
- Определение веса ребра (x, y) Вес не хранится
- Перечисление всех ребер (x, y) О(Е)
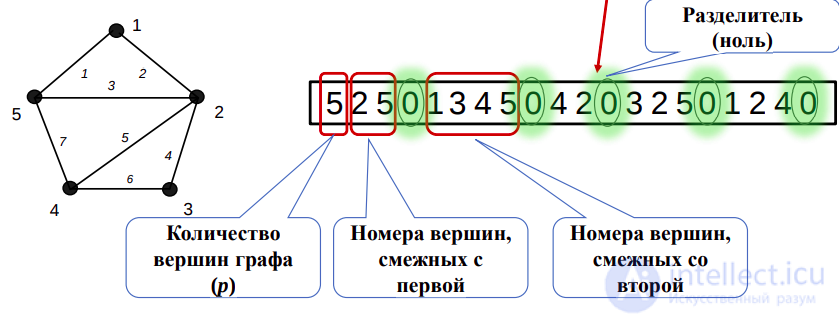
FO и FI-представления
Для неориентированных графов определено только FO-представление, реализуемое одним одномерным массивом.
Длина массива FO: 1 + 2·q + p, где q – количество ребер, а p – количество вершин графа
Если нумерация вершин начинается с нуля, роль разделителя играет другой символ, например -1.
пример реализации на C++
Варианты для орграфа:
1. для каждой вершины записываются номера вершин, в которые из этой вершины исходят дуги (FO-представление),
2. Для каждой вершины записываются номера вершин, из которых исходят дуги в эту вершину (FI-представление)
Длина массивов FO и FI равна 1 + q + p.
Задание на 5 минут: Напишите FO и FI представления для этого орграфа. В качестве разделителя используйте ноль
Ответ
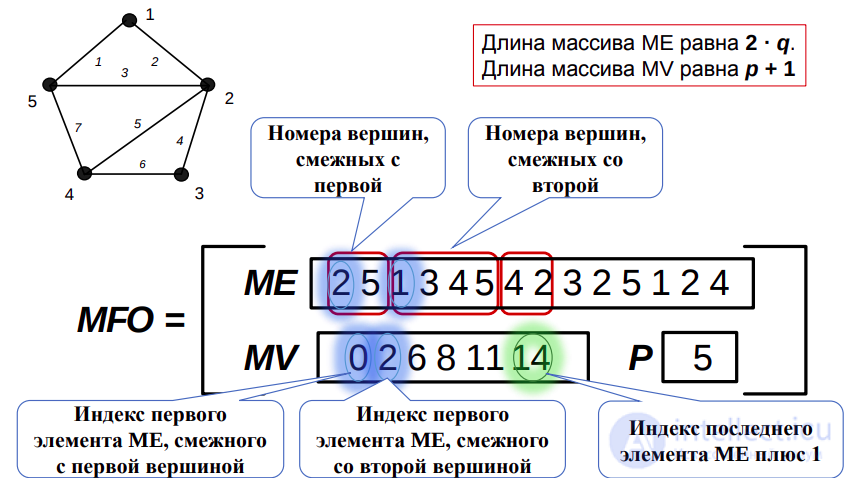
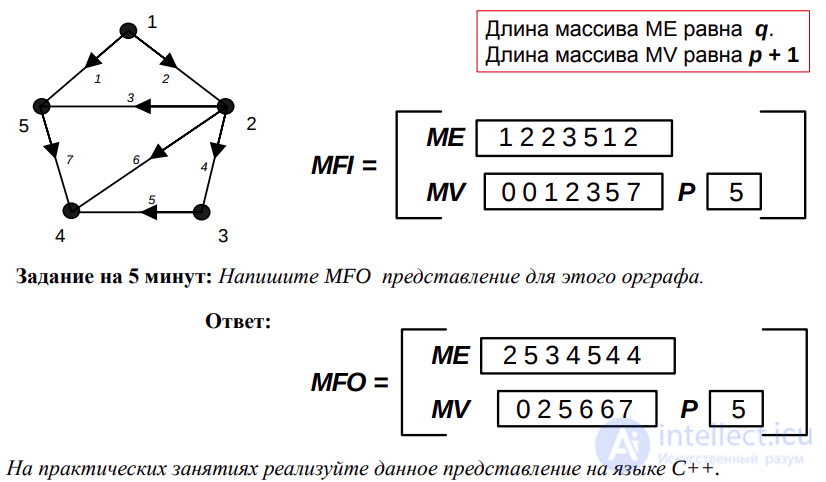
MFO и MFI-представления
Для неориентированных графов определено только MFO-представление.
Длина массива ME равна 2 · q.
Длина массива MV равна p + 1
Пример реализации
Варианты для орграфа:
1. FO-представление записывается в виде двух массивов (выходящие ребра)
2. FI-представление записывается в виде двух массивов (входящие ребра)
На чем можно сэкономить и как можно оптимизировать?
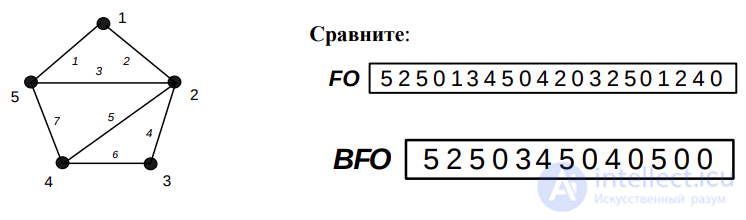
Для неориентированных графов допустимы сокращенные FO- и MFO представления (BFO и BMFO)
В массивы FO и ME для каждой вершины записываются только те номера вершин, которые не меньше (или не больше) номера этой вершины.
Это позволяет уменьшить размер массива FO c (1+2*q+p) до (1+q+p), а массива ME – с 2*q до q.
пример
Объектно-ориентированные представления графа
Объектно-ориентированная библиотека для работы с графами
Boost Graph Library (BGL). Graph interface
Заключение и рекомендации по применению представлений и хранеия в памяти графов
Найти универсальный способ хранения графа в памяти компьютера, который бы хранил максимально много информации о графе, работал с любыми графами и работал бы быстроне простая задача, универсального способа нет. Для различных задач и графов оптимальны различные представления. Конечно, наиболее мощным и универсальным способом хранения является список смежности. зачастую он работает быстрее и все еще требует не так уж и много памяти. Однако, если количество дуг приближается к квадрату количества вершин, то лучше матрицы смежности способа не найти, т.к. тогда скорость работы и количество памяти даже списка смежности приближается к матрице смежности, если не требует больше… Конечно, можно написать и список смежности, однако пишется он дольше матрицы смежности, да и работать с матрицей смежности намного проще.
Применение матрицы смежности является оправданным, когда:
1) число вершин невелико (p <=1000), а число ребер велико (стандартная оценка для обыкновенного графа: > p(p-1)/4);
2) когда необходимо иметь быстрый доступ к произвольным ребрам графа;
3) когда часто необходимо добавлять и удалять ребра при неизменном числе вершин.
Когда трансформация графа не требуется, хорошим компромиссом для графов общего вида является MFO-представление и его варианты (списки смежности
и др.).
Матрица инциденций – самое невыгодное с алгоритмической точки зрения представление графа.
Сравнение сложностей базовых операций при различных представлениях графа
Вау!! 😲 Ты еще не читал? Это зря!
- вектор как структура данных , представление вектора в памяти ,
- представление разреженного массива в виде массива указателей ,
- разреженные массивы , методы хранения разреженных данных ,
- хранение отношений в памяти ,
- способы хранения множеств , булеан ,
Напиши свое отношение про представление графов в памяти компьютера. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое представление графов в памяти компьютера, описание бержа графа , список дуг графа, массив дуг графа, списки смежности, матрица инциденций, матрица смежности, хранение графов в памяти эвм
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Структуры данных
Если Вы хоть немного знакомы с теорией графов, Вам наверняка интересно, как же правильно хранить граф в памяти компьютера. В этой статье рассмотрено 4 способа, как это сделать. Также проведён полный их анализ и размышления на эту тему.
Содержание:
- Введение
- Матрица смежности
- Описание Бержа
- Список дуг
- Список смежности
- Оптимизация к списку смежности
- Заключение
Введение
Для начала разберёмся, что же такое граф и какие они бывают.
Граф — множество V вершин и набор E неупорядоченных и упорядоченных пар вершин. Говоря проще, граф — это множество точек (вершин) и соединяющих их путей (дуг или рёбер). Граф может быть ориентированным и неориентированным. В ориентированном графе пути (дуги) имеют направление, а в неориентированном — не имеют. Пути в неориентированном графе называются рёбрами.
Взвешенным называется такой граф, для каждого ребра(дуги) которого определена некоторая функция. А эта функция называется весовой.
Рассмотрим пример ориентированного взвешенного графа:
На рисунке точками обозначены вершины графа, стрелками — дуги, чёрные числа — номера вершин графа, а красные — веса дуг. Вес дуги можно представить также как стоимость. Т.е. например: дан граф, нужно дойти от вершины i до вершины j, заплатив минимальное количество денег/потратив наименьшее количество времени. Пусть в нашем графе, который представлен на рисунке, нам нужно пройти из вершины 5 в вершину 2, а вес дуг — стоимость прохода по данному ребру. В данном примере очевидно, что выгоднее пройти через вершину 1 и только потом прийти в вершину 2, так мы заплатим всего 4 единицы денег, иначе, если пойти напрямую, мы заплатим целых 7 единиц.
Ну вот мы и разобрались, что такое граф. На рисунке всё смотрится красиво, все задачи вроде бы решаются легко… Но! А если граф будет действительно большим, например на 1000 вершин? Да, такой граф на бумажке рисовать очень долго и неприятно… Пускай лучше всё это делает за нас компьютер!
Теперь осталось только научить компьютер работать с графами. Сам я довольно часто участвую в олимпиадах по информатике, а там очень любят давать задачи на графы. От того, как хранить граф в той или иной задаче очень много зависит… После того, как я придумал полное решение, но, написав его, получил только половину баллов, я задумался, а правильно ли я хранил граф?
Проблема правильного хранения графа в памяти компьютера действительно актуальна в сегодняшние дни. Я решил выяснить, так какой же из способов всё-таки лучше.
Матрица смежности
Один из самых распространённых способов хранения графа — матрица смежности. Она представляет из себя двумерный массив. Если в клетке i,j установлено значение ПУСТО, то дуги, начинающейся в вершине i и кончающейся в вершине j, нет. Иначе дуга есть. Чаще всего за значение ПУСТО берут 0, а в клетки, которые обозначают наличие дуги, вписывают вес этой дуги. Если граф не взвешенный, то вес дуги считается равным единице. Нарисуем матрицу смежности для нашего графа:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 2 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 3 | 0 | 0 |
| 4 | 0 | 4 | 0 | 0 | 0 | 0 |
| 5 | 3 | 7 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 |
Я намеренно употреблял слово “дуга”, т.к. матрица смежности приспособлена ТОЛЬКО для ориентированных графов. Очень много способов хранения приспособлены только для ориентированных графов. Однако почти во всех задачах ребро можно заменить двумя дугами, т.е. если у нас есть ребро (1,3), то мы можем заменить его на дуги (1,3) и (3,1) — так мы сможем пройти в любом направлении в любое время.
Как вы уже заметили, в матрице смежности нам часто нужно хранить большое количество нулей. Например, в нашей матрице “нужных” значений только 6, а остальные 30 — нули, не представляющие для нас почти никакой нужной информации.
Для представления графа матрицей смежности нужно V в квадрате (где V — количество вершин). Если граф почти полный, т.е. Е почти развно V в квадрате (где Е — количество дуг), этот способ хранения графа наиболее выгоден, т.к. его очень просто реализовывать и память будет заполнена “нужными” значениями.
Кроме большого количества требуемой памяти и медленной работы на разреженных графах у матрицы смежности есть ещё один важный недостаток. Иногда в задачах нужно выводить не номера вершин, а номера дуг(рёбер) на вводе. Хранить эти номера матрица смежности не умеет. Нужно реализовывать восстановление номера дуги(ребра) как-то иначе, а это совсем неудобно.
Временные сложности сведены в таблицу:
| Операция | Временная сложность |
|---|---|
| Проверка смежности вершин x и y | О(1) |
| Перечисление всех вершин смежных с x | О(V) |
| Определение веса ребра (x, y) | О(1) |
| Перечисление всех ребер (x, y) | О(V2) |
Описание Бержа
Для того чтобы ускорить работу матрицы смежности на разреженных графах, можно использовать другой тип хранения графа — описание Бержа. Для каждой вершины хранится список смежных вершин. Чаще всего для этого используется двумерный массив размером V в квадрате, в строке u которого хранятся номера вершин, смежных с u. В нулевой элемент строки u вписывается количество вершин, хранящихся в данной строке. Теперь попробуем представить наш граф при помощи описания Бержа на примере:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 3 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 4 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | 1 | 2 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В нулевом столбце хранятся “длины” строк. Однако, вес дуг никак не хранится, а если его хранить отдельно, то нужно заводить ещё один массив размером V в квадрате…
Временные сложности сведены в таблицу:
| Операция | Временная сложность |
|---|---|
| Проверка смежности вершин x и y | О(V) |
| Перечисление всех вершин смежных с x | О(V) |
| Определение веса ребра (x, y) | Вес не хранится |
| Перечисление всех ребер (x, y) | О(Е) |
Список дуг
Следующий тип хранения графа в памяти компьютера — список дуг. Чаще всего это двумерный массив размером 3*E, в первой строке которого хранится информация, из какой вершины начинается дуга, во второй — в какой кончается, а в третьей строке — вес дуги. Опять же разберёмся на примере:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 5 | 0 | 0 |
| 2 | 2 | 3 | 4 | 2 | 1 | 2 | 0 | 0 |
| 3 | 1 | 2 | 3 | 4 | 3 | 7 | 0 | 0 |
Мы чётко видим, что почти вся таблица заполнена “нужными” значениями, а не нулями. Это уже хорошо, значит, память экономится.
Временные сложности сведены в таблицу:
| Операция | Временная сложность |
|---|---|
| Проверка смежности вершин x и y | О(E) |
| Перечисление всех вершин смежных с x | О(E) |
| Определение веса ребра (x, y) | О(E) |
| Перечисление всех ребер (x, y) | О(E) |
| Поиск i-ой дуги | О(1) |
Как видно, этот способ, в отличие от матрицы смежности и описания Бержа, хранит информацию о номере дуги. Также ясно, что этот способ нам выгоден, если чаще всего нам нужно будет узнать что-то (вес, вершины начала или конца) о i-ой дуге. Однако, такие задачи в практическом программировании встречаются довольно редко.
Если в предыдущих представлениях одно ребро мы заменяли двумя дугами, то список дуг может хранить или дуги или рёбра (в зависимости от реализации). Это довольно удобно и может требовать в 2 раза меньше памяти.
Список смежности
И последний способ, про который я вам расскажу — список смежности. Он представляет из себя два массива: vert и adj.
Из каждой вершины может выходить 0, 1 и более дуг, причём вершин будет V или менее. Если из вершины i не выходит дуг (т.е. количество дуг равно нулю), то в массиве vert в i-ой клетке будет храниться значение ПУСТО. Если из вершины i выходит хотя бы одна дуга, то в массиве vert в i-ой клетке будет храниться номер элемента массива adj, в котором хранится конечная вершина дуги. Также в массиве adj хранится вес дуги, и указатель на следующую “конечную” вершину дуги, которая начинается в вершине i. Поначалу может показаться, что этот способ очень запутан, т.к. один массив указывает на другой, другой сам на себя, при чём много раз. Однако это не совсем так, т.к. следует лишь несколько раз самому попробовать реализовать хранение графа таким способом, и он кажется очень мощным, полезным и несложным. Давайте сами попробуем разобраться на примере.
На вход нам подаются следующие данные:
6 6
5 1 3
1 2 1
4 2 4
2 3 2
3 4 3
5 2 7
Так выглядит массив vert:
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| 2 | 4 | 5 | 3 | 1 | 0 |
А вот так массив adj:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2 | 3 | 4 | 2 | 0 | 0 |
| 2 | 3 | 1 | 4 | 2 | 3 | 7 | 0 | 0 |
| 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В массиве adj первая строка — конечная вершина дуги, вторая — её вес, а третья — ссылка на следующую.
В этом примере я специально вводил дуги не по порядку, чтобы можно было лучше разобраться, и было видно, что позиции могут быть совершенно различными. Например, первая конечная вершина дуги, начинающейся в вершине 5, лежит в массиве adj на первой позиции, а не на пятой.
Рассмотрим временные сложности:
| Операция | Временная сложность |
|---|---|
| Проверка смежности вершин x и y | О(E) |
| Перечисление всех вершин смежных с x | О(E) |
| Определение веса ребра (x, y) | О(E) |
| Перечисление всех ребер (x, y) | О(E) |
| Поиск i-ой дуги | О(1) |
Времена у всех операций, вроде бы, такие же, как и у списка рёбер. Однако, большинство из них реально намного меньше. Например, проверка смежности вершин x и y и перечисление всех вершин смежных с x в списке рёбер гарантированно будет выполнятся О(Е) операций, т.к. нам обязательно нужно пробежать весь список, а в списке смежности мы бежим только по вершинам, смежным с х.
Оптимизация к списку смежности
UPD: Данная оптимизация не актуальна. Лучше вместо хранения ссылки на следующий элемент хранить ссылку на предыдущий.
Когда я первый раз пытался разобраться, что такое список смежности, меня очень смутила процедура добавления дуги. Для того, чтобы добавить дугу (i,j) мы должны начать из вершины i и пройти по всем вершинам, смежными с нею. И так каждый раз! А что если вершине х инцидентны E рёбер? Тогда сложность добавления O(E в квадрате) ! Это совсем не годится.
А почему бы нам не добавлять ребро сразу туда, куда надо? Конечно, при считывании, мы сразу записываем данные в нужную нам ячейку (в конец получившегося списка). Но ведь на эти данные нужно сделать указатель. Самое тяжёлое — найти место, где делать указатель. Поиск этого места и занимает основу драгоценного времени. А что, если хранить указатель не только на первую конечную вершину дуги, но и на последнюю? Тогда наша проблема решена! Добавление занимает О(1) времени, но требует дополнительно О(V) памяти…
Рассмотрим данную оптимизацию на примере. Изменится только вид массива vert, поэтому рассмотрим только его:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 5 | 3 | 1 | 0 |
| 2 | 2 | 4 | 5 | 3 | 6 | 0 |
Здесь в первой строке массива vert хранится указатель на первую конечную вершину, во второй — на последнюю. В данном примере польза от этой оптимизации почти не заметна, т.к. максимальное вершин, исходящих из одной дуги, равно 2, что очень мало. Если дуг, инцидентных одной вершине, будет много, то и ускорение будет довольно большое и “лишняя” выделенная память окупится.
Возможно, о данной оптимизации к списку смежности где-то уже было написано до меня, но ни в интернете, ни в печатных источниках я этого не встречал.
Заключение
Я пытался найти универсальный способ хранения графа в памяти компьютера, который бы хранил максимально много информации о графе, работал с любыми графами и работал бы быстро. Однако, универсального способа нет. Для различных задач и графов оптимальны различные представления. Конечно, наиболее мощным и универсальным способом хранения является список смежности. С моей оптимизацией он работает быстрее и всё ещё требует не так уж и много памяти. Однако, если количество дуг приближается к квадрату количества вершин, то лучше матрицы смежности способа не найти, т.к. тогда скорость работы и количество памяти даже списка смежности приближается к матрице смежности, если не требует больше… Конечно, можно написать и список смежности, однако пишется он дольше матрицы смежности, да и работать с матрицей смежности намного проще.
Конечно, мною были рассмотрены не все способы представления графов в памяти компьютера. Я старался рассмотреть лишь те, которые смогут реально помочь в олимпиадном программировании, т.е. пишутся наиболее быстро, быстро работают, и требуют немного памяти. Я рассмотрел только статические способы представления графа в памяти компьютера. Есть ещё различные динамические способы хранения графов, они занимают меньше памяти, иногда быстрее работают. Однако и пишутся они намного сложнее. Например, элементарная работа с графом, хранящимся в структуре Вирта, еле-еле влазит в 250 строк кода на паскале…
Конечно, в профессиональном программировании лучше использовать динамические методы, однако и старые добрые статические способы от них не так уж и далеко отстают! 
Другие Алгоритмы:
- Алгоритмы · Структура данных бинарная куча
- Алгоритмы · Способы хранения графов в памяти компьютера
- Алгоритмы · Длинная арифметика: сложение
- Delphi · Создание градиентной заливки
Аннотация: Рассматриваются взвешенные пути и маршруты в графах. Дается понятие веса и длины пути. Приводятся сведения о орциклах и циклах и их особенностях. Цель лекции: Дать представление о путях и циклах в графах и весе и длине пути.
Пути и маршруты
Путем в орграфе называется последовательность дуг, в которой конечная вершина всякой дуги, кроме последней, является начальной вершиной следующей дуги.
Например, для графа на
рис.
8.1 последовательности дуг
M1: a6, a5, a9, a8, a4 ,
M2: a1, a6, a5, a9, a7 ,
M3: a1, a6, a5, a9, a10, a6, a4
являются путями. Пути могут быть различными.
Рис.
8.1.
Орграф
Орцепью (или простым путем) называется такой путь, в котором каждая дуга используется не более одного раза.
Так пути M1
и M2
являются орцепями, а M3
нет, поскольку дуга a6
используется дважды.
Простой орцепью (или элементарным путем) называется путь, в котором каждая вершина используется не более одного раза.
Простой орцепью является путь M2
.
Для неориентированного графа понятия маршрута, цепи и простой цепи аналогичны понятиям пути, орцепи и простой орцепи в орграфе. (В определениях следует заменить слово «дуга» на слово «ребро«).
Путь или маршрут можно изображать также последовательностью вершин. Так путь M1
можно представить последователь-ностью вершин х2, х5, х4, х3, х5, х6
, и такое представление часто оказывается более полезным.
Вес и длина пути
Иногда дугам графа сопоставляют числа ai -> сi
, называемые весом или длиной, или стоимостью или ценой. В каждом конкретном случае выбирается то слово, которое ближе подходит по смыслу задачи.
Граф G, описываемый тройкой вида
G = (X, A, С),
где Х = { хi }, i =1, 2, 3, …, n – множество вершин,
А = { ai }, i = 1, 2, 3, …, m – множество дуг,
С = {Ci}, i = 1, 2, 3, …, m – множество характеристик дуг, называется графом со взвешенными дугами.
Пример такого графа приведен на
рис.
8.2,а. При рассмотрении пути M, представленного последовательностью дуг (a1, a2, …, aq), за его вес (или длину, или стоимость) принимается число L(M), равное сумме весов всех дуг, входящих в путь, т. е.
для всех 
Длиной (или мощностью ) пути называется число дуг, входящих в него. Чаще всего термин «длина» употребляется, когда все дуги, входящие в путь, имеют веса, равные 1, т. е. когда вес пути совпадает с его длиной (мощностью).
Рис.
8.2.
Взвешенные графы: а – граф со взвешенными дугами; б – граф со взвешенными вершинами; в – взвешенный граф
Граф со взвешенными вершинами – это граф, описываемый тройкой
G = ( X, А, V ),
где Х = { хi }, i = 1, 2, …, n – множество вершин графа;
А = { ai }, i = 1, 2, …, m – множество дуг графа;
V ={ vi }, i = 1, 2, …, n – множество характеристик вершин.
В качестве характеристик вершин могут выступать «стоимость«, «мощность«, «вес» и т. п. Пример такого графа приведен на
рис.
8.2,б. Для графа со взвешенными вершинами в случае представления пути последовательностью вершин весом пути является сумма весов, входящих в этот путь вершин.
И наконец, взвешенный граф определяется четверкой вида G = (Х, А, V, С), т. е. и дуги, и вершины этого графа имеют некоторые характеристики.
Область применения взвешенных графов в качестве моделей довольно обширна: транспортные задачи, задачи оптимизации сети связи и системы перевозок и др. Одной из известнейших оптимизационных задач является нахождение кратчайших путей в графе со взвешенными дугами.