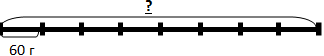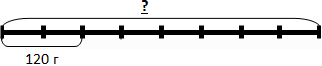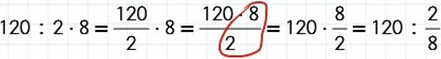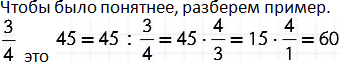Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем 

Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой 
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)





Тогда масса:
2. Масса цилиндра




Тогда масса:
3. Масса шара



Тогда масса:
4. Масса сегмента шара




Тогда масса:
5. Масса конуса




Для круглого конуса: 


Масса круглого конуса:
6. Масса усеченного конуса










Отсюда масса:
7. Масса пирамиды




Для пирамиды с прямоугольным основанием: 



Тогда масса пирамиды:
8. Масса усеченной пирамиды






Исчеркав половину тетрадного листа, получаем: 





И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: 
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (

Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-
1
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-
2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-
4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-
1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-
2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-
3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-
1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-
2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 770 раз.
Была ли эта статья полезной?
Мы уже научились находить часть от числа (см. здесь).
А сегодня мы поговорим о том, как найти число по его части (число по его дроби). Эти умения необходимы при решении задач.
Обратимся опять же к пицце.
1. Пиццу разрезали на 8 кусков. Один кусок весит 60 г. Надо узнать вес пиццы. Мы знаем, что пиццу разрезали на 8 частей, т.е. 1 кусок – это 1/8 от целого.
Изобразим это на схеме:
Если 1 кусок весит – 60 г, значит, вся пицца весит в 8 раз больше и надо 60 г умножить на 8.
В дроби 1/8 – знаменатель 8. Итак, чтобы найти целое – надо вес 1 части умножить на знаменатель.
2. Рассмотрим другой пример:
2 куска пиццы весят 120 г. Надо узнать вес целой пиццы.
Как поступим в этом случае?
Вес целой пиццы мы узнавали в предыдущем случае: вес одного куска умножали на число кусков. Значит, надо узнать вес одного куска. Для этого 120 : 2 = 60 (г)
А потом 60 умножим на 8 (как в примере 1).
Итак: 2/8 = 120
данное число 120 разделили на 2 (это числитель дроби), а потом умножили на 8 (это знаменатель дроби):
120 : 2 х 8
Заменим деление на дробь:
Итак, для того чтобы было легко найти целое по его дроби и дробь от целого, используйте памятку.
Похожие статьи
Наибольшие трудности при изучении физики
учащиеся испытывают при решении задач, т.е. когда
требуется применить знания. Эти трудности
представляются ребятам настолько большими, что
многие из них отказываются даже от попыток
решать задачи. Отказ от решения задач еще как-то
«проходил» во времена устных экзаменов по
физике. Но теперь – как при прохождении
Государственной итоговой аттестации, выполнении
заданий Единого государственного экзамена или
тестирования при поступлении – проверяют именно
умение применять полученные знания, а не
декларировать их.
Понимание смысла физических законов – главная
цель школьного курса физики, но понимание этих
законов может родиться только в осознанной
деятельности по применению этих законов.
Школьникам же часто предлагают алгоритмы
решения задач, которые провоцируют бездумное,
автоматическое применение физических формул.
Преодолеть эту принципиальную трудность можно,
только неоднократно применяя законы физики в
тщательно отобранных простейших ситуациях,
когда смысл этих законов кристально ясен.
В школьном курсе физики тысячи задач. Однако,
если посмотреть на все множество этих задач «с
высоты птичьего полета», то нетрудно заметить,
что подавляющее их большинство группируются
вокруг нескольких десятков типичных учебных
ситуаций. Эти ситуации можно назвать ключевыми.
А овладение ключевыми ситуациями «даст ключи» к
решению задач.
Ключевые ситуации – важнейшая связь между
«теорией» и «задачами». Без этой связи теория
мертва для школьника, а задачи представляются
ему случайной россыпью неинтересных загадок.
Однако пока еще некоторые учителя «дают» своим
ученикам «теорию» отдельно, а «задачи» отдельно.
После такого разрезания по живому от живой
физики остаются только мертвые формулы-шаблоны
для примитивных задач на подстановку.
Изучение ключевых ситуаций – это живой мост
между «теорией» и «задачами», причем мост с
двухсторонним движением. С одной стороны, задачи
рождаются при изучении ключевых ситуаций, в
которых наглядно проявляется действие
физических законов, с другой стороны, благодаря
решению задач на основе ключевой ситуации теория
осознается, т.е. становится действенной силой, а
не пассивным набором фактов и формул.
И еще одна очень важная роль ключевых ситуаций.
Дело в том, что результатом изучения школьного
курса физики должен быть не набор решенных задач
(это быстро забывается), а понимание физических
законов и физическая интуиция, которая может
развиваться именно при рассмотрении ключевых
ситуаций.
Приложение 1.
Фрагмент урока с выделением ключевой ситуации по
теме «Плотность».
Приложение 2. Фрагмент
урока с выделением ключевой ситуации по теме
«Полые тела».
Приложение 3.
Дополнительный материал по теме «Сплавы».
Приведем фрагмент урока с выделение ключевой
ситуации по теме «Сплавы».
Фрагмент урока по теме «СПЛАВЫ»
Учитель. Тема урока зашифрована
ребусом. Кто первый раскроет секрет?
Ученики. …
Учитель. Тема урока «Сплавы».
Сплав — макроскопически однородная смесь двух
или большего числа химических элементов с
преобладанием металлических компонентов.
Основной или единственной фазой сплава, как
правило, является твёрдый раствор легирующих
элементов в металле, являющемся основой сплава.
Сплавы имеют металлические свойства, например:
металлический блеск, высокие электропроводность
и теплопроводность. Иногда компонентами сплава
могут быть не только химические элементы, но и
химические соединения, обладающие
металлическими свойствами. Например, основными
компонентами твёрдых сплавов являются карбиды
вольфрама или титана. Макроскопические свойства
сплавов всегда отличаются от свойств их
компонентов, а макроскопическая однородность
многофазных (гетерогенных) сплавов достигается
за счёт равномерного распределения примесных
фаз в металлической матрице.
Сплавы обычно получают с помощью смешивания
компонентов в расплавленном состоянии с
последующим охлаждением. При высоких
температурах плавления компонентов, сплавы
производятся смешиванием порошков металлов с
последующим спеканием (так получаются, например,
многие вольфрамовые сплавы).
Сплавы являются одним из основных
конструкционных материалов. Среди них
наибольшее значение имеют сплавы на основе
железа и алюминия. В состав многих сплавов могут
вводиться и неметаллы, такие как углерод,
кремний, бор и др. В технике применяется более 5
тыс. сплавов.
Цель нашего урока –
научиться решать задачи для определения
плотности, массы или объема сплавов или веществ
входящих в их состав.
Рассматривая сплавы, обычно предполагают, что
объем сплава равен сумме объемов
составляющих его веществ. В таком случае
плотность сплава ,
где индексы 1 и 2 относятся к двум компонентам
сплава.
Если заданы или требуется найти массы
компонентов известной плотности ρ1 и ρ2, то объемы
компонентов надо выразить через их массы и
плотности, в результате чего формула для
плотности сплава примет вид 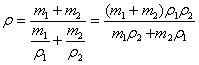
Часто в задаче дано или требуется найти
соотношение масс компонентов сплава. Обозначим . Тогда
. Эта формула связывает
плотность сплава ρ и массовое отношение
компонент . Из
нее при следует:
. Приведенные
формулы позволяют по заданному значению одной из
величин ( или ρ)
найти значение другой.
Запишите в тетрадях:
Примечание.
1. Задача первого уровня предназначена для
применения основной формулы: .
2. Задачи второго уровня похожи, поэтому
целесообразно применить разные способы решения.
3. Задачи третьего уровня предусмотрены для
закрепления способов решения задач предложенных
ранее с добавлением дополнительных вычислений
(объема и процентного отношения).
РЕШЕНИЕ ЗАДАЧ
Задачи по теме «СПЛАВЫ»:
УРОВЕНЬ 1
Найдите плотность бронзы, для изготовления
которой взяли 100 г меди и 30 г олова, считая, что
объем сплава равен сумме объемов входящих в него
металлов.
УРОВЕНЬ 2
1. Кусок сплава из свинца и олова массой 664 г
имеет плотность 8,3 г/см3. Определите массу
свинца в сплаве. Принять объем сплава равным
сумме объемов его составных частей.
2. В куске кварца содержится небольшой
самородок золота. Масса куска 100 г, а его
плотность 8 г/см3. Определите массу
золота, содержащегося в кварце. Принять, что
плотность кварца и золота соответственно равны
2,65 и 19,36 г/см3.
УРОВЕНЬ 3
1. Сплав золота и серебра массой 400 г имеет
плотность 14·103 кг/м3. Полагая объем сплава
равным сумме объемов его составных частей,
определите массу, объем золота и процентное
содержание его в сплаве.
2. В чистой воде растворена кислота. Масса
раствора 240 г, а его плотность 1,2 г/см3.
Определите объем кислоты в растворе и его
процентное содержание, если плотность кислоты 1,8
г/см3. Принять объем раствора равным сумме
объемов его составных частей.
Выходной контроль:
Установите соответствие:
Ответы: 1-Д, 2-Ж, 3-А, 4-Б, 5-В. 6-Г, 7-Е.
Домашнее задание:
Дополнительный материал.
Сплавы различаются по своему предназначению.
Конструкционные сплавы: стали, чугуны,
дюралюминий.
Конструкционные со специальными свойствами
(например, искробезопасность, антифрикционные
свойства): бронзы, латуни.
Для заливки подшипников: баббит.
Для измерительной и электронагревательной
аппаратуры: манганин, нихром.
Для изготовления режущих инструментов:
победит.
Подготовьте сообщение о каком-нибудь сплаве.
Расскажите о веществах, которые в него входят, о
их процентном вхождении в сплав и т.д.
Задачи:
1. Найдите плотность стали (сталь —
деформируемый (ковкий) сплав железа с углеродом),
для изготовления которой взяли 100 г железа и 2 г
углерода (углекислого газа), считая, что объем
сплава равен сумме объемов входящих в него
веществ.
2. Чтобы получить латунь, сплавили куски меди
массой 178 кг и цинка массой 355 кг. Какой плотности
была получена латунь? Объем сплава равен сумме
объемов его составных частей.
3. Сплав золота и серебра массой 500 г имеет
плотность 11 г/см3. Полагая объем сплава равным
сумме объемов его составных частей, определите
массу, объем золота и процентное содержание его в
сплаве.
Ответы: 1. 0,098 г/см3, 2. 8540 кг/м3, 3. 50 г, 2,59
см3, 10%.
Подведение итогов урока. Рефлексия
На полях рабочей тетради изобрази схематически
один из рисунков, который соответствует степени
усвоения материала на уроке. Солнце – мне все
понятно, туча – материал интересный, но надо еще
поработать, луна – я все проспал.
Литература
- Материалы курса «Как научить решать задачи по
физике (основная школа). Подготовка к ГИА: лекции
1-4. – М.: Педагогический университет «Первое
сентября», 2010. -80с. - Сборник задач по физике: Учеб. Пособие для
учащихся 7-8 классов средней школы. – 6-е изд.,
перераб. – М.: Просвещение, 1994. – 191 с.: ил. - Физическая олимпиада в 6-7 классах средней школы:
Пособие для учащихся. – 2-е изд, перераб. И доп. –
М.: Просвещение, 1987. – 192 с: ил.
На чтение 7 мин Просмотров 124к.
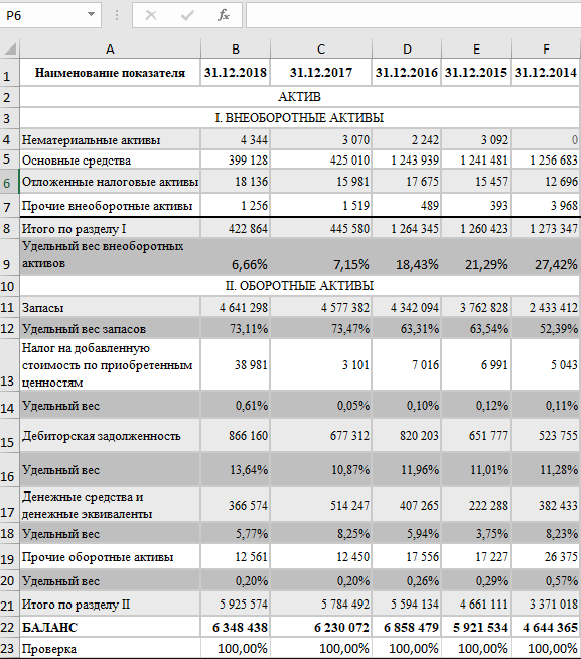
Удельный вес представляет собой относительную часть одной составляющей предмета к целому. Расчет показателя производится во многих сферах жизни, в том числе, в экономике. На предприятии чаще всего определяют удельный вес активов, затрат, выработки, доходов и расходов.
Содержание
- Удельный вес в экономике простыми словами
- Что показывает удельный вес
- Предмет удельного веса в экономике
- Методика определения удельного веса в экономике
- Формула для расчета удельного веса
- Определение удельного веса в Excel
- Пример расчета удельного веса
- Расчет удельного веса активов
- Расчет удельного веса затрат
Удельный вес в экономике простыми словами
Удельный вес в экономике рассчитывается для определения влияния одной части инструмента на весь предмет. Если говорить простыми словами, то на предприятии при помощи показателя определяют, как тот или иной фрагмент влияет на общее состояние. Например, если определяется удельный весь затрат, то все расходы классифицируют, а затем выявляют, на что компания тратит больше всего средств.
Удельный вес рассчитывают и при проведении анализа общей финансово-хозяйственной деятельности предприятия. При этом к учету принимаются расходы и доходы компании. Зачастую для выявления значения показателя используют бухгалтерский баланс. Удельный вес принято измерять только в процентах. Причем целый предмет всегда будет равен 100%.
Что показывает удельный вес
Как уже было сказано, удельный вес показывает влияние одной части на целый предмет. Например, если рассчитывается показатель расходов на производство продукции, при помощи него можно понять, на что предприятие потратило больше средств в ходе изготовления товаров.
Показатель применяется и при выявлении выработки на одного сотрудника, на бригаду и на цех. Для этого количество произведенной продукции единицей расчета (работником, группой специалистов или отделом) делят на общее число изготовленных товаров и умножают на 100. В таком случае удельный вес отражает качество работы сотрудника, бригады или цеха.
Удельный вес помогает определить:
- качество распределения МПЗ;
- эффективность работы предприятия;
- целесообразность расходования средств;
- основные источники доходов и расходов и т.д.
Для выявления динамики удельного веса в сфере экономического развития предприятия его рассчитывают для каждого показателя по годам. Таким образом можно понять, как менялась структура активов и обязательств фирмы.
Предмет удельного веса в экономике
Предметом удельного веса в экономике является любой показатель, который можно выделить в виде части от целого. В качестве предмета выступают:
- Доходы. Компания принимает поступления от разных видов деятельности. Чтобы понять, какое направление приносит больше прибыли, рассчитывают удельный вес.
- Расходы. Предприятие расходует средства не только на производство продукции, но и на иные нужды. Показатель выявляют с целью определения уровня затрат на то или иное направление деятельности и эффективности расходования денежных средств по каждому пункту.
- Активы. К ним относят финансовые инструменты, при помощи которых компания получает прибыль. Как правило, расчет удельного веса активов необходим для выявления достаточности оснащения предприятия и для прослеживания динамики.
- Обязательства. В их число включают денежные долги компании, в том числе, перед поставщиками и покупателями, заказчиками и кредиторами. Удельный вес обязательств рассчитывают для выявления значимости каждого из них и степени их влияния на расходы предприятия.
- Выработка. Для определения рентабельности работы сотрудника, цеха и отдела рассчитывают удельный вес.
Важно! Удельный вес можно выявить практически для каждого экономического показателя деятельности фирмы.
Методика определения удельного веса в экономике
В экономике удельный вес рассчитывается при помощи формул. Проводить вычисления можно двумя методами: вручную или при помощи компьютерных программ. В первом случае бухгалтер формирует таблицу с экономическими показателями, составляющими одно целое, например, группирует все активы. На следующем этапе он вычисляет удельный вес для каждого признака и заносит в соответствующее окно. В результате, каждый показатель имеет свой удельный вес, выраженный в процентном соотношении к общему объему.
Важно! Чтобы проверить правильность вычислений, достаточно сложить все результаты удельного веса. Если получилось 100%, значит, расчеты проведены верно.
Намного легче выявить удельный вес при помощи специализированных компьютерных программ. Сегодня существует множество электронных сервисов, созданных специально для бухгалтеров. Однако часто их приобретают за плату. Чтобы избежать лишних расходов и сократить время на вычисление удельного веса, можно использовать стандартную программу Excel.
Формула для расчета удельного веса
Для расчета удельного веса в экономике используют общую формулу:
УдВ = Ч / Ц * 100,
где УдВ – удельный вес;
Ч – часть целого предмета;
Ц – целый предмет.
Формулу применяют для расчета удельного веса всех экономических показателей, подстраивая ее под каждый из них. Например, выражение для определения удельного веса доходов компании выглядит следующим образом:
УдВД = Вд / ОСД * 100,
где УдВД — удельный вес доходов;
Вд – сумма поступлений по одному виду деятельности;
ОСД – общая сумма выручки компании по всем видам деятельности.
Чтобы применить формулу для расчета удельного веса других экономических показателей, необходимо поменять делимое на определяемый фактор целого предмета и делитель — на общую сумму инструмента.
Определение удельного веса в Excel
Для выявления удельного веса экономических показателей деятельности предприятия можно использовать стандартную компьютерную программу Excel. Она поможет облегчить и ускорить процесс расчета. Кроме того, снижается риск допущения ошибок.
Для использования таблицы Excel с целью выявления удельного веса достаточно обладать базовыми познаниями в области программирования.
Пример расчета удельного веса
Для лучшего понимания процесса определения удельного веса экономических показателей компании, разберем пример на основе компании ООО «МегаЛенд»:
| Экономический показатель | Сумма на начало отчетного периода, в тыс. руб. | Сумма на конец отчетного периода, в тыс. руб. |
| Актив | ||
| Раздел 1: Внеоборотные активы | ||
| НМА | 56,3 | 58,2 |
| ОС | 125,63 | 125,63 |
| Долгосрочные финансовые вложения | 87,36 | 98,32 |
| Прочие внеоборотные активы | 12,3 | 15,6 |
| Всего по разделу: | 281,59 | 297,75 |
| Раздел 2: Оборотные активы | ||
| МПЗ | 98,3 | 106,3 |
| НДС | 12,1 | 14,5 |
| Дебиторская задолженность | 25,9 | 24,2 |
| Денежные средства | 45,36 | 58,96 |
| Прочие оборотные активы | 14,6 | 12,3 |
| Всего по разделу: | 196,26 | 216,26 |
| Итого: | 477,85 | 514,01 |
| Пассив | ||
| Раздел 3: Капитал и резервы | ||
| Уставный капитал | 88,3 | 88,3 |
| Добавочный капитал | 36,1 | 32,1 |
| Резервный капитал | 55,3 | 34,2 |
| Нераспределенная прибыль | 56,2 | 65,3 |
| Всего по разделу: | 235,9 | 219,9 |
| Раздел 4: Долгосрочные обязательства | ||
| Заемные средства | 65,2 | 74,63 |
| Всего по разделу: | 65,2 | 74,63 |
| Раздел 5: Краткосрочные обязательства | ||
| Кредиты и займы | 96,3 | 125,69 |
| Кредиторская задолженность | 80,45 | 93,79 |
| Всего по разделу: | 176,45 | 219,48 |
| Итого: | 477,85 | 514,01 |
Важно! Доходы предприятия в бухгалтерском балансе отражаются как актив, расходы – как пассив.
Расчет удельного веса активов
В первую очередь, определим удельный вес оборотных (УдВОА) и внеоборотных активов (УдВВА) на начало и конец отчетного периода:
УдВОА на начало отчетного периода = 196,26 / 477,85 * 100 = 41,07%:
УдВОА на конец отчетного периода = 216,26 / 514,01 * 100 = 42,07%;
УдВВА на начало отчетного периода = 281,59 / 477,85 * 100 = 58,93%;
УдВВА на конец отчетного периода = 297,75 / 514,01 * 100 = 57,93%.
Теперь найдем удельный вес для каждого актива:
| Экономический показатель | Сумма на начало отчетного периода, в тыс. руб. | Сумма на конец отчетного периода, в тыс. руб. | Уд. вес на начало отчетного периода, в % | Уд. вес наконец отчетного периода, в % |
| Раздел 1: Внеоборотные активы | ||||
| НМА | 56,3 | 58,2 | 11,78 | 11,32 |
| ОС | 125,63 | 125,63 | 26,29 | 24,38 |
| Долгосрочные финансовые вложения | 87,36 | 98,32 | 18,28 | 19,13 |
| Прочие внеоборотные активы | 12,3 | 15,6 | 2,57 | 3,03 |
| Всего по разделу: | 281,59 | 297,75 | ||
| Раздел 2: Оборотные активы | ||||
| МПЗ | 98,3 | 106,3 | 20,57 | 20,68 |
| НДС | 12,1 | 14,5 | 2,53 | 2,82 |
| Дебиторская задолженность | 25,9 | 24,2 | 5,42 | 4,71 |
| Денежные средства | 45,36 | 58,96 | 9,49 | 11,47 |
| Прочие оборотные активы | 14,6 | 12,3 | 3,05 | 2,39 |
| Всего по разделу: | 196,26 | 216,26 | ||
| Итого: | 477,85 | 514,01 | 100 | 100 |
При вычислении удельного веса зачастую результат представляется в виде нецелого числа. Его нужно округлять до сотых. Если после сотой число больше 6, последнюю цифру показателя увеличиваем на 1.
Расчет удельного веса затрат
Найдем удельный вес каждого раздела пассива баланса:
Капитал и резервы на начало года = 235,9 / 477,85 * 100 = 49,37%;
Капитал и резервы на конец года = 219,9 / 514,01 * 100 = 42,78%;
Долгосрочные обязательства на начало года = 65,2 / 477,85 * 100 = 13,64%;
Долгосрочные обязательства на конец года = 74,63 / 514,01 * 100 = 14,52%;
Краткосрочные обязательства на начало года = 176,45 / 477,85 * 100 = 36,9%;
Краткосрочные обязательства на конец года = 219,48 / 514,01 * 100 = 42,7%.
Теперь найдем удельный вес для каждой статьи пассива баланса:
| Экономический показатель | Сумма на начало отчетного периода, в тыс. руб. | Сумма на конец отчетного периода, в тыс. руб. | Уд. вес на начало отчетного периода, в % | Уд. вес на конец отчетного периода, в % |
| Раздел 3: Капитал и резервы | ||||
| Уставный капитал | 88,3 | 88,3 | 18,48 | 17,18 |
| Добавочный капитал | 36,1 | 32,1 | 7,55 | 6,24 |
| Резервный капитал | 55,3 | 34,2 | 11,57 | 6,53 |
| Нераспределенная прибыль | 56,2 | 65,3 | 11,76 | 12,7 |
| Всего по разделу: | 235,9 | 219,9 | ||
| Раздел 4: Долгосрочные обязательства | ||||
| Заемные средства | 65,2 | 74,63 | 13,64 | 14,52 |
| Всего по разделу: | 65,2 | 74,63 | ||
| Раздел 5: Краткосрочные обязательства | ||||
| Кредиты и займы | 96,3 | 125,69 | 20,15 | 24,45 |
| Кредиторская задолженность | 80,45 | 93,79 | 16,83 | 18,25 |
| Всего по разделу: | 176,45 | 219,48 | ||
| Итого: | 477,85 | 514,01 | 100 | 100 |
Динамика удельного веса пассивов предприятия показывает, что на конец года компания взяла краткосрочный кредит, из-за чего показатель значительно увеличился. Также уменьшился резервный капитал, что может говорить об ухудшающемся экономическом положении фирмы, из-за чего руководству пришлось израсходовать резервные средства.