Из-за притяжения Земли все тела имеют вес.
Сила, с которой тело давит на опору или растягивает подвес, называют весом.
Рис. (1). Тело на опоре, тело на подвесе
Вес тела обозначают (P) и измеряют в ньютонах ((H)).
Вес неподвижного тела равен
P=mg
.
Формула определения веса неподвижного тела точно такая же, как и формула силы тяжести (см. предыдущую тему «Сила. Сила тяжести»). Однако вес тела и сила тяжести — не одно и то же.
Рис. (2). Сила тяжести и вес тела
Например, сила тяжести свободно падающего трёхкилограммового кирпича приблизительно составляет (30) (H), ((F = mg)), а его вес (P) в момент падения равен (0) (H) (так как кирпич находится в состоянии невесомости).
Если помещённое на опору или подвешенное тело неподвижно по отношению к Земле или находится в равномерном движении вверх или вниз, тогда вес тела не меняется.
Вес меняется, когда тело перемещается вверх или вниз с ускорением.
Во время поездки в лифте, если мы двигаемся с ускорением вверх, наш вес увеличивается, хотя сила тяжести остаётся неизменной.
Состояние невесомости — это состояние, когда тело не давит на опору и не растягивает подвес. Такое происходит, когда тело свободно падает под воздействием только силы гравитации.
Почему в космическом корабле есть состояние невесомости?
Потому что космический корабль, обращаясь вокруг Земли, находится в свободном падении (он всё время как бы падает на Землю, но пролетает мимо). Это происходит, когда космический корабль достигает 1-й космической скорости — 7,9 км/с.
Если скорость космического корабля была бы меньше, он упал бы на Землю, а если корабль достиг бы 2-й космической скорости — 11,2 км/с, он стал бы искусственным спутником Солнца.
Если скорость космического корабля достигнет 3-й космической скорости — 16,7 км/с, тогда корабль направится из Солнечной системы к другим звёздам.
К сожалению, до ближайшей звёздной системы Альфа Центавра нужно лететь (18000) лет, так как она находится на расстоянии (4) световых лет.
Интересно, что для того, чтобы достичь Луны, ракета должна развить скорость, равную (0,992) от второй космической скорости.
Источники:
Рис. 1. Тело на опоре, тело на подвесе. © ЯКласс.
Рис. 2. Сила тяжести и вес тела. © ЯКласс.
Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-
1
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-
2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-
4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-
1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-
2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-
3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-
1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-
2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 870 раз.
Была ли эта статья полезной?
Вес тела

4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
Обновлено 16 Июля, 2021
4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
Обновлено 16 Июля, 2021
Понятие «вес тела» очень часто используется в повседневной жизни. Многие продукты и материалы покупаются, исходя из измеренного веса. Как правило, в быту понятие веса отождествляется с понятием массы тела. Однако в физике это не одно и то же. Более того, эти величины не равны. Рассмотрим эту тему подробнее, приведём определение и формулу веса тела.
Вес тела
Чтобы понять физическую природу веса тела, достаточно вспомнить, как происходит взвешивание на пружинных весах. На чашку весов укладывается тело, под действием силы тяжести оно сжимает пружину, и по степени этого сжатия можно судить о том, сколько весит тело.
То есть сила, с которой тело воздействует на опору, называется весом.
Найдём величину этой силы. На тело, имеющее опору, действует сила тяжести $m overrightarrow {mathrm{g}}$ и сила реакции опоры $ overrightarrow {N}$.
По третьему закону Ньютона, тело также действует на опору с равной силой $ overrightarrow {P}= – overrightarrow {N}$ (противоположной по направлению). Эта сила и есть вес тела.
Если опора (и тело вместе с ней) движется вверх с ускорением $ overrightarrow {a}$, то по второму закону Ньютона имеем:
$$overrightarrow {N}+ m overrightarrow {mathrm{g}} = m overrightarrow {a}$$
Учитывая равенство веса и его противоположную направленность относительно реакции опоры, после проецирования на ось координат, направленную вниз, можно записать:
$$P = m (mathrm{g} – a)$$
Это и есть формула веса тела массой $m$, существующего в условиях гравитации (ускорение свободного падения $mathrm{g}$), имеющего опору, которая двигается вверх с ускорением $a$.
Свойства веса тела
Из вышесказанного можно сделать важные выводы.
- Во-первых, как физическая величина, вес является силой. Поэтому единица измерения веса в физике — ньютон.
- Во-вторых, вес — фактически, это проявление сил упругости. Вес появляется в результате взаимодействия тела с опорой.
- В-третьих, вес зависит от ускорения, с которым движется опора. Если опора неподвижна (или движется равномерно и прямолинейно), то вес равен силе тяжести.
Последнее свойство показывает, что вес — это величина непостоянная, и может быть как меньше, так и больше силы тяжести, в зависимости от движения опоры.
Невесомость и перегрузки
Таким образом, вес без опоры не существует. Говорят, что тело, у которого нет опоры, находится в состоянии невесомости.
Обратите внимание, состояние невесомости не зависит от того, действует ли на тело гравитационная сила или нет. Предмет во время свободного падения, кабина лифта в момент начала спуска, когда натяжение троса исчезло, человек во время прыжка — всё это примеры состояния невесомости, которое появляется, несмотря на действие силы тяжести.
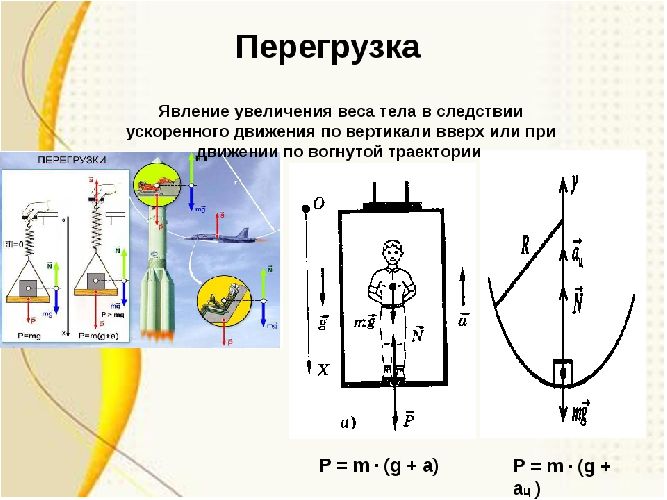
Из формулы веса тела следует, что если опора движется с ускорением, у тела появляется вес, который может быть даже больше, чем сила тяжести. В этом случае говорят о возникновении перегрузок.
Поскольку в формулу веса входит масса и сумма ускорения, перегрузку можно измерять в единицах $mathrm{g}$. Для нахождения перегрузки используется формула:
$$k= {m(mathrm{g} + a) over mmathrm{g}}=1+{aover mathrm{g}}$$
Фактически перегрузка показывает, во сколько раз вес тела больше силы тяжести, действующей на тело на Земле. Перегрузка $k=1$ означает обычный вес тела, перегрузка $k=2$ означает, что вес тела вдвое больше, чем сила тяжести и так далее.
Что мы узнали?
Вес тела — это сила, с которой тело действует на опору. Фактически это проявление силы упругости. Тело, у которого нет опоры, находится в состоянии невесомости. Если опора тела двигается с ускорением, тело испытывает перегрузки.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 101.
А какая ваша оценка?
На предыдущих уроках мы узнали определение понятия силы, познакомились с силой тяжести и силой упругости.
Возможно, вы заметили, что рассматривая примеры и сравнивая тела с разными массами, мы избегали выражения “одно тело весит больше другого”. В повседневном жизни же мы часто используем подобные фразы, как и само слово “вес”.
На данном уроке мы узнаем о понятии веса со стороны физики.
Что такое вес?
Вспомним опыт, когда мы ставим тело (гирю) на опору (рисунок 1).
Мы уже говорили, что на гирю действует сила тяжести. Из-за этого начинает прогибаться доска — происходит ее деформация.
Возникает сила упругости, направленная вертикально вверх. Доска перестает прогибаться, когда сила тяжести и сила упругости уравновешивают друг друга.
Обратите внимание, что гиря и доска взаимодействуют друг с другом, но:
- Cила тяжести — это результат взаимодействия гири с Землей, а не с доской
- по всем изученным нами принципам должна быть еще одна сила, которая возникает со стороны гири
Подобная ситуация происходит в случае, если мы будем рассматривать тело, подвешенное на нити. Возникает некая сила, действующая на подвес.
Эта сила и называется весом тела.
Что называют весом тела?
Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Характеристики веса
- Вес тела — это векторная физическая величина и обозначается буквой $vec{P}$
- Модуль веса тела обозначается буквой $P$
- Вес тела численно равен силе тяжести, если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно.
$P=F_{тяж}$
- Вес тела приложен к опоре или подвесу и направлен перпендикулярно опоре или вдоль подвеса (рисунки 2, 3).
Сравните с изображением силы тяжести (рисунок 4). Следует помнить, что сила тяжести приложена к самому телу.
Вес как частный случай силы упругости
Когда мы ставим тело на опору — оно деформирует ее. Когда мы подвешиваем тело — оно деформирует подвес. Не всегда эта деформация видна как в наших предыдущих опытах.
Когда вы кладёте учебник на парту, что происходит? Учебник (тело) деформирует парту (опору). Но такая деформация не видна невооруженным глазом. Тем не менее, она существует. Если бы деформация не происходила, то не возникала бы сила упругости. Тогда ничего бы не препятствовало движению вашего учебника к самому центру Земли.
Так, парта в свою очередь деформирует учебник, что тоже незаметно.
Давайте рассмотрим опыт, где деформация тела будет заметна. Взгляните на рисунок 5.
У нас есть штатив и резиновый шнур длиной $l_0$ (рисунок 5, а). На шнур мы подвешиваем небольшой мешок с песком (рисунок 5, б).
Шнур растягивается и останавливается, когда сила тяжести становится равна возникшей в шнуре силе упругости. Длина шнура изменилась и стала равна $l$.
У нас провзаимодействовали два тела: шнур и мешок. Оба тела деформировались.
Теперь мы отрежем прикрепленный шнур (рисунок 5, в). Во время падения на мешок с песком действует только сила тяжести, он восстанавливает свою форму. Шнурок также восстанавливает свою форму.
Когда же мешок падает на рабочую поверхность (рисунок 5, г), то он снова деформируется. Теперь взаимодействует опора и тело.
В данном случае не видно, как деформируется опора, но, если бы мы подставили доску на брусьях, она бы прогнулась. Так мы наглядно показали, что при взаимодействии происходит деформация обоих тел.
Под действием опоры или подвеса происходит деформация тела. Опора сжимает нижнюю часть тела, а подвес растягивает его верхнюю часть.
Именно эта деформация тела вызывает появление в теле силы упругости. В данном случае сила упругости и будет весом тела.
Чем отличается вес тела от силы тяжести?
Вы уже знаете, что вес тела будет равен силе тяжести, если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно. Также сила тяжести приложена к центру тела, а вес — к опоре или подвесу.
Но важнее помнить, из-за чего возникают эти две силы. Сила тяжести возникает из-за взаимодействия физического тела и Земли. А вес возникает в результате взаимодействия тела и опоры (подвеса). А это взаимодействие возникает тоже из-за взаимодействия тела и Земли. При этом тела деформируются, что приводит к возникновению силы упругости.
Сила тяжести. Вес
- Движение тел вблизи поверхности Земли
- Сила тяжести
- Вес тела
- Невесомость
- Задачи
- Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
п.1. Движение тел вблизи поверхности Земли
Вблизи поверхности Земли все тела, предоставленные самим себе, падают вниз, независимо от направления начальной скорости.
Такое движение тел называют свободным падением.
п.2. Сила тяжести
Многочисленные эксперименты показали, что в свободном падении все тела вблизи поверхности Земли падают с одинаковым ускорением (overrightarrow{g}), которое направлено вниз, к центру Земли.
В системе отсчета, связанной с Землей, на любое тело массой (m) действует сила тяжести $$ overrightarrow{F_{text{тяж}}}=m overrightarrow{g} $$
 |
Сила тяжести прямо пропорциональна массе тела. Точка приложения силы тяжести – центр масс тела. Сила тяжести всегда направлена вертикально вниз, к центру Земли. |
 |
Измерения показывают, что на средних географических широтах ускорение свободного падения (gapprox 9,81 text{м/с}^2). Т.е., скорость при падении увеличивается на (9,81 text{м/с}) каждую следующую секунду.
В общем случае, ускорение свободного падения зависит от широты рассматриваемого места, высоты над уровнем моря, времени суток и ещё нескольких более «тонких» факторов. В школьных задачах, если другое не оговорено, для вычислений используют приблизительное значение (gapprox 10 text{м/с}^2). |
п.3. Вес тела
Если подвесить тело или положить его на опору, сила тяжести, действующая на тело, будет уравновешена силой, которую называют силой реакции подвеса или силой реакции опоры.
Т.к. силы уравновешивают друг друга, выполняется соотношение $$ moverrightarrow{g}=-overrightarrow{N} $$ где (moverrightarrow{g}) — сила тяжести, (overrightarrow{N}) — реакция подвеса или опоры.
По третьему закону Ньютона, если подвес или опора действуют на тело с силой (overrightarrow{N}), то и тело действует на подвес или опору с силой (overrightarrow{P}=-overrightarrow{N})
Вес тела – это сила, с которой тело действует на подвес или опору.
Получаем, что (overrightarrow{P}=moverrightarrow{g}), вес и сила тяжести равны по величине и направлению, но приложены к разным точкам: сила тяжести – к центру масс тела, вес – к подвесу или опоре.
По своей природе реакции подвеса или опоры являются силами упругости: под действием веса тела подвес или опора деформируются, и силы упругости стремятся восстановить их форму и размеры.
Равенство (overrightarrow{P}=moverrightarrow{g}) выполняется, если подвес или опора покоятся или движутся относительно Земли прямолинейно и равномерно.
Если движение подвеса или опоры равноускоренное с ускорением (overrightarrow{a}ne 0), то (overrightarrow{P}ne moverrightarrow{g}), вес будет больше (при (overrightarrow{a}) направленном вверх) или меньше (при (overrightarrow{a}) направленном вниз) силы тяжести. Подробней этот случай будет рассмотрен в курсе физики для 9 класса.
п.4. Невесомость
Если опора свободно падает вместе с телом, то под действием силы тяжести каждая частица опоры и тела двигается вниз с одним и тем же ускорением (overrightarrow{g}). Ни в опоре, ни в теле не возникают сжатия или растяжения, нет сил упругости, а значит, вес тела равен нулю.
Состояние, при котором в свободно падающих телах исчезают деформации и взаимные давления частиц тел друг на друга, называют невесомостью.
Состояние невесомости можно испытать, если подпрыгнуть – с момента отрыва от земли до момента приземления. В первые моменты прыжка до раскрытия парашюта, парашютисты также находятся в состоянии невесомости.
Движение космического корабля по орбите вокруг Земли представляет собой непрерывное свободное падение, поэтому космонавты испытывают состояние невесомости в течение всего полета, кроме тех моментов, когда передвигаются по кораблю или включают двигатели для маневрирования.
п.5. Задачи
Задача 1. Какой вес имеет человек массой 65 кг, который стоит на земле?
Дано:
(m=65 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(P-?)
Вес равен силе тяжести (P=mg) $$ Papprox 65cdot 10=650 (text{Н}) $$ Ответ: 650 Н
Задача 2. Парашютист равномерно опускается на землю. Сила сопротивления воздуха 900 Н. Масса парашюта 15 кг. Найдите массу парашютиста.
Дано:
(F_{text{сопр}}=900 text{Н})
(m_1=15 text{кг})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)
На раскрытый парашют действуют две силы: сила сопротивления воздуха, направленная вверх, и суммарный вес (парашюта и парашютиста), направленный вниз.
Т.к. движение равномерное, ускорение (a=0). Значит, вес равен силе тяжести, и begin{gather*} F_{text{сопр}}=P=F_{text{т}}=(m_1+m_2)g\[6pt] m_1+m_2=frac{F_{text{сопр}}}{g}Rightarrow m_2=frac{F_{text{сопр}}}{g}-m_1 end{gather*} Подставляем $$ m_2=frac{900}{10}-15=75 (text{кг}) $$ Ответ: 75 кг.
Задача 3. На сколько сантиметров растянется пружина жесткостью k=267 Н/м, если подвесить к ней медный брусок размерами 5 см х 6 см х 10 см. Плотность меди 8900 кг/м3.
Дано:
(V=5 text{см}times 6 text{см}times 10 text{см}=300 text{см}^3=3cdot 10^{-4} text{м}^3)
(rho=8900 text{кг/м}^3)
(k=1000 text{Н/м})
(gapprox 10 text{м/с}^2)
__________________
(m_2-?)
Вес бруска равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow Delta l=frac{mg}{k}, m=rho V\[6pt] Delta l=frac{rho Vg}{k} end{gather*} Получаем: $$ Delta l=frac{8900cdot 3cdot 10^{-4}cdot 10}{267}=0,1 (text{м}=10 (text{см}) $$ Ответ: 10 см.
Задача 4*. При подвешивании гирьки массой 450 г пружина динамометра растягивается до 8 см. А при подвешивании гирьки массой 300 г – до 6 см. Найдите длину пружины динамометра без груза (ответ запишите в см).
Дано:
(m_1=450 text{г}=0,45 text{кг})
(l_1=8 text{см}=0,8 text{м})
(m_2=300 text{г}=0,3 text{кг})
(l_2=6 text{см}=0,6 text{м})
__________________
(l_0-?)
Вес гирьки равен силе тяжести и уравновешивается силой упругости: begin{gather*} mg=F_{text{упр}}=kDelta lRightarrow k=frac{mg}{Delta l} end{gather*} где (Delta l=l-l_0) – растяжение пружины.
Жесткость пружины begin{gather*} k=frac{m_1g}{Delta l_1}=frac{m_1g}{l_1-l_0}, k=frac{m_2g}{Delta l_2}=frac{m_2g}{l_2-l_0}\[6pt] frac{m_1g}{l_1-l_0}=frac{m_2g}{l_2-l_0} Rightarrow frac{m_1}{l_1-l_0}=frac{m_2}{l_2-l_0} Rightarrow m_2(l_2-l_0)=m_2(l_1-l_0)\[6pt] m_1l_2-m_1l_0=m_2l_1-m_2l_0 Rightarrow m_1l_2-m_2l_1=(m_1-m_2)l_0\[6pt] l_0=frac{m_1l_2-m_2l_1}{m_1-m_2} end{gather*} Получаем $$ l_0=frac{0,45cdot 0,06-0,3cdot 0,08}{0,45-0,3}=frac{0,027-0,024}{0,15}=0,02 (text{м}=2 (text{см}) $$ Ответ: 2 см.
п.6. Лабораторная работа №7. Градуирование шкалы динамометра и измерение силы тяжести
Цель работы
Исследовать зависимость силы упругости от величины деформации. Изготовить шкалу динамометра. Измерить силу тяжести для двух тел неизвестной массы; рассчитать их массу.
Теоретические сведения
 |
При подвешивании груза на пружину, его вес уравновешивается силой упругости. Для неподвижной пружины вес равен силе тяжести. Получаем $$ P=F_{text{т}}=mg=F_{text{упр}} =kDelta l $$ Удлинение пружины $$ Delta l=frac gk m $$ При постоянном ускорении свободного падения (g) и постоянной жесткости (k), удлинение прямо пропорционально массе подвешенного груза. |
В данной работе считаем, что грузу массой 100 г соответствует показание динамометра (F=1 text{Н}), т.е. (overline{g}=frac{1 text{Н}}{100 text{г}}=10frac{text{Н}}{ text{кг}}=10frac{ text{м}}{ text{с}^2}). Более точное стандартное значение (g_0=9,80665frac{ text{м}}{ text{с}^2})
Ошибка метода, связанная с величиной (g) $$ delta_g=frac{|overline{g}-g_0|}{g_0}approx 0,02=2text{%} $$ Тогда грузу массой 200 г соответствует показание 2 Н, 300 г – 3 Н и т.д.
После градуирования в целых значениях Н на динамометре наносятся промежуточные деления с ценой деления (d=0,1 text{Н}).
Ошибка градуирования определяется как степень отклонения от равномерности шкалы, (delta_{text{шк}}).
Теперь с помощью полученного прибора можно непосредственно измерять силу тяжести, действующую на тела. Ошибка метода при определении сил равна сумме (delta=delta_g+delta_{text{шк}}).
Т.к. шкала изготовлена для (overline{g}=10frac{ text{м}}{ text{с}^2}), массу тел находим по формуле (m=frac{F}{overline{g}}), где (F) — показание динамометра. При этом ошибка метода равна (delta=delta_{text{шк}}), т.к. ошибка (delta_g) нивелируется за счет пропорциональности массы и растяжения пружины.
Таким образом, за счет сокращения (overline{g}), полученный прибор позволяет точнее измерять массы по сравнению с измерениями сил.
Приборы и материалы
Лабораторный динамометр на 5Н со шкалой, закрытой чистой бумагой; набор грузиков по 100 г; линейка; карандаш; 2 тела неизвестной массы.
Ход работы
1. Закрепите динамометр в штативе.
2. Подвесьте грузик массой 100 г, сделайте отметку 1Н на шкале.
3. Сделайте отметки 2Н, 3Н, 4Н и 5Н для грузов 200 г, 300 г, 400 г и 500 г соответственно.
4. Снимите динамометр со штатива и проверьте с помощью линейки, насколько равномерной получилась шкала. Оцените относительную ошибку (delta_{text{шк}})
5. С помощью линейки нанесите по 10 промежуточных делений между основными делениями шкалы.
6. Снова закрепите динамометр в штативе и проведите измерения силы тяжести для двух тел неизвестной массы. Найдите абсолютную и относительную погрешность измерений.
7. Рассчитайте массы для обоих тел. Найдите абсолютную и относительную погрешность расчетов. 8. Сделайте выводы.
Результаты измерений и вычислений
Расчетная таблица для оценки равномерности шкалы
| Отрезок шкалы | Длина отрезка, мм | (|x-x_{text{ср}}|) |
| 0-1 Н | 25 | 0 |
| 1-2 Н | 25 | 0 |
| 2-3 Н | 26 | 1 |
| 3-4 Н | 24 | 1 |
| 4-5 Н | 25 | 0 |
| Всего | 125 | 2 |
Средняя длина отрезка $$ x_{text{ср}}=frac{125}{5}=25 (text{мм}) $$ Среднее линейное отклонение $$ Delta =frac 25=0,4 (text{мм}) $$ Цена деления линейки (d_{text{л}}=1 text{мм}), абсолютная погрешность измерений (Delta_{text{л}}=0,5 text{мм})
Т.к. (Delta_{text{л}}gt Delta), принимаем погрешность равномерности шкалы (Delta=Delta_{text{л}}=0,5 text{мм})
Относительная погрешность равномерности шкалы $$ delta_{text{шк}}=frac{0,5}{25}=0,02=2text{%} $$
Относительная погрешность равномерности шкалы
| Показание динамометра (F, text{Н}) |
Ошибка метода (delta=delta_g+delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta F=deltacdot F, text{Н}) |
|
| 1-е тело | 2,7 | 4% | 0,11 ≈ 0,1 |
| 2-е тело | 1,9 | 4% | 0,08 ≈ 0,1 |
Цена деления динамометра (d=0,1 text{Н}); погрешность прямых измерений (Delta_0=frac d2=0,05 text{Н})
Полученные абсолютные погрешности больше (Delta_0).
Сила тяжести для первого тела (F_1=(2,7pm 0,1) text{Н}, delta=4text_%)
Сила тяжести для второго тела (F_2=(1,9pm 0,1) text{Н}, delta=4text_%)
Расчет массы $$ m=frac{F}{10} (text{кг})=100F (text{г}) $$
| Масса (m=100F, text{г}) |
Ошибка метода (delta=delta_{text{шк}}, text{%}) |
Абсолютная погрешность (Delta m=deltacdot m, text{г}) |
|
| 1-е тело | 270 | 2% | 5 |
| 2-е тело | 190 | 2% | 4 |
Масса первого тела (m_1=(270pm 5) text{г}, delta=2text{%})
Масса второго тела (m_2=(190pm 4) text{г}, delta=2text{%})
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для градуирования динамометра в ньютонах использовалось значение $$ overline{g}=10 frac{text{м}}{text{с}^2} $$
По сравнению со стандартным значением (g_0=9,80665 text{м/с}^2) это приводит к вкладу в ошибку метода (delta_gapprox 2text{%}).
При градуировании равномерность шкалы дала составляющую ошибки метода (delta_{text{шк}}=2text{%}).
При определении силы тяжести с помощью полученного динамометра ошибка метода равна сумме (delta+delta_g+delta_{text{шк}}=4text{%}).
Для двух тел неизвестной массы были получены следующие значения сил тяжести: $$ F_1=(2,7pm 0,1) text{Н}, F_2=(1,9pm 0,1) text{Н}, delta=4text{%} $$
При расчете массы по формуле (m=frac Fg), ошибка (delta_g) нивелируется за счет пропорциональности растяжения пружины. Ошибка метода уменьшается (delta=delta_{text{шк}}=2text{%}).
Получаем следующие значения масс: $$ m_1=(270pm 5) text{г}, m_2=(190pm 4) text{г}, delta=2text{%} $$ Таким образом, полученный в ходе работы динамометр позволяет измерять силы тяжести в интервале от 0 до 5 Н с погрешностью 4% и рассчитывать массы тел в интервале от 0 до 500 г с погрешностью 2%.