Взвешенные графы
В классических графах все рёбра считаются равноценными и длина пути
соответствует количеству рёбер, которые он содержит. Однако часто
в задаче каждому ребру соответствует некоторый параметр — длина
ребра или стоимость прохождения по нему. В терминологии графов такой
параметр называется весом ребра, а граф, содержащий взвешенные
рёбра, взвешенным.
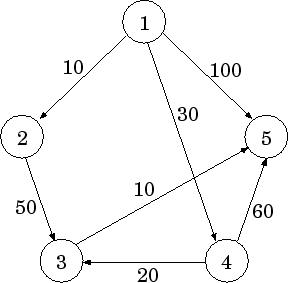
Типичная задача для таких графов — поиск кратчайшего пути. Например,
в этом графе кратчайший путь между вершинами (1) и (5): (1 — 4 — 3 — 5), так
как его вес равен (30 + 20 + 10 = 60), а вес ребра (1 — 5) равен (100).
Алгоритм Дейкстры
Классический алгоритм для поиска кратчайших путей во взвешенном графе —
алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти
кратчайший путь от одной вершины графа до всех остальных за (O(M log N))
((N, M) — количество вершин и рёбер соответственно).
Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге
обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё
уже известно). При её обработке все ещё не посещённые соседи добавляются
в очередь для посещения (расстояние до каждой из них рассчитывается как
расстояние до текущей вершины + длина ребра). Главное отличие от BFS
заключается в том, что вместо классической очереди используется очередь с
приоритетом. Она позволяет нам выбирать ближайшую вершину за (O(log N)).
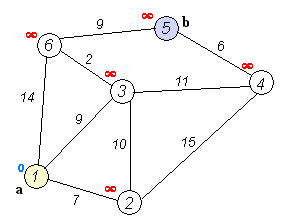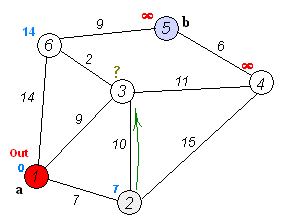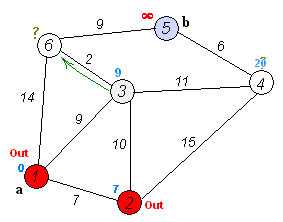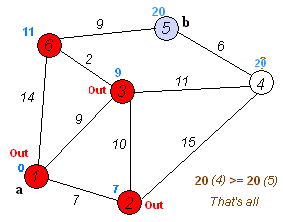
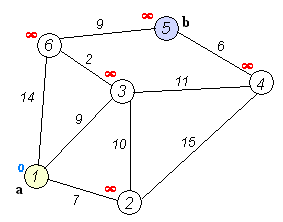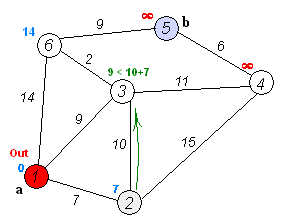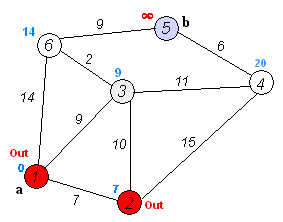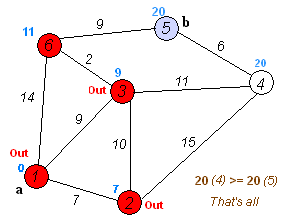
Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершины
(a) в вершину (b):
С помощью псевдокода алгоритм Дейкстры описывается следующим образом:
ans = массив расстояний от начальной вершины до каждой.
изначально заполнен бесконечностями (ещё не достигнута).
ans[start] = 0
q = очередь с приоритетом, хранящая пары (v, dst),
где dst - предполагаемое расстояние до v
добавить (start, 0) в q
пока q не пуста:
(v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё
извлечь (v, dst) из очереди
если ans[v] < dst: //мы уже обработали эту вершину, используя другой путь
перейти к следующей вершине
для каждой v -> u:
n_dst = dst + len(v -> u) //расстояние до u при прохождении через v
если n_dst < ans[u]: //если мы можем улучшить ответ
ans[u] = n_dst
добавить (u, n_dst) в q
Как видите, в очереди с приоритетом хранится не только номер вершины, но
и вычисленное расстояние до неё, по которому и ведётся сортировка. Также
возможна ситуация, при которой одна и та же вершина будет помещена в очередь
несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам).
В такой ситуации обрабатываем её только один раз (с минимальным возможным
расстоянием).
Реализация
В нашей очереди с приоритетом должны храниться пары (вершина, расстояние до неё),
причём отсортированы они должны быть по уменьшению расстояния. Для этого нужно
использовать тип
std::priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>:
первым элементом пары будет расстояние, а вторым — номер вершины.
Для хранения взвешенного графа в виде списка смежности для каждой вершины мы
храним вектор пар (соседняя вершина, длина ребра до неё).
Реализация на C++:
Реализация с восстановлением пути
Восстановление пути для алгоритма Дейкстры реализуется точно так же, как и для
BFS: при успешном улучшении пути в вершину (u) через вершину (v), мы запоминаем,
что (prev[v] = u). После окончания работы алгоритма используем массив (prev) для
восстановления пути в обратном направлении.Реализация на C++:
Область применения алгоритма Дейкстры
Алгоритм Дейкстры является оптимальным для поиска пути практически в любых
графах, но он имеет одно ограничение. Алгоритм Дейкстры неприменим для графов,
содержащих рёбра с отрицательным весом. Для поиска кратчайшего пути в таких
графах обычно используют алгоритм Форда-Беллмана.
Иногда
дугам графа G
сопоставляются
(приписываются) числа — дуге
ставится
в соответствие некоторое число
,
называемое
весом,
или
длиной,
пли
стоимостью
(ценой) дуги.
Тогда граф G
называется
графом
со взвешенными дугами. Иногда
веса (числа vi)
приписываются
вершинам xi
графа,
и тогда получается граф со
взвешенными вершинами. Если
в графе веса приписаны и дугам, и вершинам,
то он называется просто взвешенным.
При
рассмотрении пути
,
представленного последовательностью
дугза еговес
(или
длину,
или
стоимость)
принимается
число
,
равное сумме весов всех дуг, входящих
в,
т.е.
Таким образом,
когда слова «длина», «стоимость», «цена»
и «вес» применяются к дугам, то они
эквивалентны по содержанию, и в каждом
конкретном случае выбирается такое
слово, которое
Рис. 1.3.
ближе
подходит по смыслу и совпадает с принятым
в литературе.
Длиной
(или
мощностью) пути
называется число дуг, входящих в него.
3. Петли, ориентированные циклы и циклы
Петлей
называется
дуга, начальная и конечная вершины
которой совпадают. На рис. 1.3, например,
дуги
являются петлями.
Путь
называетсязамкнутым,
если
в нем начальная вершина дуги
совпадает
с конечной вершиной дуги
.
Так, например, в
графе, приведенном на рис. 1.3,
последовательности дуг
(1.7)
(1.8)
(1.9)
являются замкнутыми
путями.
Пути
(1.7) и (1.9) являются замкнутыми простыми
орцепями (контурами,
или
простыми
орциклами), поскольку
в них одна и та же вершина используется
только один раз (за исключением начальной
и конечной вершин, которые совпадают),
а путь (1.8) не является контуром,
так
как вершина х1
используется
в нем дважды. Контур, проходящий через
все вершины графа, имеет особое значение
и называется гамильтоновым
контуром.
Конечно, не все графы обладают
гамильтоновыми контурами. Так, например,
контур (1.9) является гамильтоновым
контуром графа, приведенного на рис.
1.3, а граф на рис. 1.2 не имеет гамильтоновых
контуров, поскольку не существует такой
дуги, для которой х1
была бы конечной вершиной.
Замкнутый
маршрут является
неориентированным двойником замкнутого
пути. Таким образом, замкнутый маршрут
является маршрутом
в
котором совпадают начальная и конечная
вершины, т. е. в котором
.
На рис. 1.3 маршруты
(1.10)
и
(1.11)
4. Степени вершины
Число
дуг, которые имеют вершину xi
своей
начальной вершиной, называется
полустепенью
исхода вершины
xi,
и, аналогично, число дуг, которые имеют
xi
своей
конечной вершиной, называется полустепенью
захода вершины
xi.
Таким
образом, на рис. 1.3 полустепень исхода
вершины x6,
обозначаемая через
,
равна,
и полустепень захода вершиныx6,
обозначаемая через
,
равна.
Совершенно
очевидно, что сумма полустепеней захода
всех вершин графа, а также сумма
полустепеней исхода всех вершин равны
общему числу дуг графа G,
т.
е.
(1.12)
где п
—
число вершин и т
—
число дуг графа G.
Для
неориентированного графа G=(X,
Г)
степень
вершины
xi
определяется
аналогично — с помощью соотношения
,
и когда не может возникнуть недоразумений,
мы будем обозначать степень вершиныxi
через
di.
Соседние файлы в папке Прикладная теория графов
- #
21.04.2015645.12 Кб65L1.doc
- #
21.04.2015629.25 Кб78L2.doc
- #
21.04.2015350.72 Кб86L3.doc
- #
- #
21.04.2015860.67 Кб61L5.doc
- #
21.04.2015468.48 Кб59L6.doc
Не так давно наткнулся на статью о том, как Michael Kozakov не смог решить алгоритмическую задачу на собеседовании в Twitter. Решение этой задачи — почти в чистом виде один из самых стандартных алгоритмов на графах, а именно, алгоритм Дейкстры.
В этой статье я постараюсь рассказать алгоритм Дейкстры на примере решения этой задачи в несколько усложненном виде. Всех, кому интересно, прошу под кат.
Предыдущие статьи цикла
В предыдущих статьях были рассмотрены алгоритмы DFS, BFS и Ford-Bellman.
Постановка задачи
Постановка задачи очень похожа на задачу, решаемую алгоритмом Форда-Беллмана: требуется найти кратчайший путь от выделенной вершины взвешенного графа (начальной) до всех остальных. Единственное отличие — теперь веса всех ребер неотрицательны.
Описание алгоритма
На каждой итерации из множества необработанных вершин берется вершина с минимальным расстоянием и обрабатывается: происходит релаксация всех ребер, из нее исходящих, после чего вершина помещается во множество уже обработанных вершин.
Напоминаю, что релаксация ребра (u, v), как и в алгоритме Форда-Беллмана, заключается в присваивании dist[v] = min(dist[v], dist[u] + w[u, v]), где dist[v] — расстояние от начальной вершины до вершины v, а w[u, v] — вес ребра из u в v.
Реализация
В самой простой реализации алгоритма Дейкстры нужно в начале каждой итерации пройтись по всем вершинам для того, чтобы выбрать вершину с минимальным расстоянием. Это достаточно долго, хотя и бывает оправдано в плотных графах, поэтому обычно для хранения расстояний до вершин используется какая-либо структура данных. Я буду использовать std::set, просто потому, что не знаю, как изменить элемент в std::priority_queue =)
Также я предполагаю, что граф представлен в виде vector<vector<pair<int, int> > > edges, где edges[v] — вектор всех ребер, исходящих из вершины v, причем первое поле ребра — номер конечной вершины, а второе — вес.
Dijkstra
void Dijkstra(int v)
{
// Инициализация
int n = (int)edges.size();
dist.assign(n, INF);
dist[v] = 0;
set<pair<int, int> > q;
for (int i = 0; i < n; ++i)
{
q.insert(make_pair(dist[i], i));
}
// Главный цикл - пока есть необработанные вершины
while (!q.empty())
{
// Достаем вершину с минимальным расстоянием
pair<int, int> cur = *q.begin();
q.erase(q.begin());
// Проверяем всех ее соседей
for (int i = 0; i < (int)edges[cur.second].size(); ++i)
{
// Делаем релаксацию
if (dist[edges[cur.second][i].first] > cur.first + edges[cur.second][i].second)
{
q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
dist[edges[cur.second][i].first] = cur.first + edges[cur.second][i].second;
q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
}
}
}
}
Доказательство корректности
Предположим, алгоритм был запущен на некотором графе из вершины u и выдал неверное значение расстояния для некоторых вершин, причем v — первая из таких вершин (первая в смысле порядка, в котором алгоритм выплевывал вершины). Пусть w — ее предок в кратчайшем пути из u в v.
Заметим, что расстояние до w подсчитано верно по предположению
- Пусть найденное алгоритмом dist'[w] < dist[v]. Тогда рассмотрим последнюю релаксацию ребра, ведущего в v: (s, v). Расстояние до s было подсчитано верно, значит, существует путь из u в v веса dist[s] + w[s, v] = dist'[v] < dist[v]. Противоречие
- Пусть найденное алгоритмом dist'[w] > dist[v]. Тогда рассмотрим момент обработки вершины w. В этот момент было релаксировано ребро (w, v), и, соответственно, текущая оценка расстояния до вершины v стала равной dist[v], а в ходе следующих релаксаций она не могла уменьшиться. Противоречие
Таким образом, алгоритм работает верно.
Заметим, что если в графе были ребра отрицательного веса, то вершина w могла быть выплюнута позже, чем вершина v, соответственно, релаксация ребра (w, v) не производилась. Алгоритм Дейкстры работает только для графов без ребер отрицательного веса!
Сложность алгоритма
Вершины хранятся в некоторой структуре данных, поддерживающей операции изменения произвольного элемента и извлечения минимального.
Каждая вершина извлекается ровно один раз, то есть, требуется O(V) извлечений.
В худшем случае, каждое ребро приводит к изменению одного элемента структуры, то есть, O(E) изменений.
Если вершины хранятся в простом массиве и для поиска минимума используется алгоритм линейного поиска, временная сложность алгоритма Дейкстры составляет O(V * V + E) = O(V²).
Если же используется очередь с приоритетами, реализованная на основе двоичной кучи (или на основе set), то мы получаем O(V log V + E log E) = O(E log V).
Если же очередь с приоритетами была реализована на основе кучи Фибоначчи, получается наилучшая оценка сложности O(V log V + E).
Но при чем же здесь задача с собеседования в Twitter?
Задачу с самого собеседования решать не очень интересно, поэтому я предлагаю ее усложнить. Перед дальнейшим чтением статьи я рекомендую ознакомиться с оригинальной постановкой задачи
Новая постановка задачи с собеседования
- Назовем задачу с собеседования «одномерной». Тогда в k-мерном аналоге будут столбики, пронумерованные k числами, для каждого из которых известна высота. Вода может стекать со столбика в соседний столбик меньшей высоты, либо за край.
- Что такое «соседние столбики»? Пусть у каждого столбика есть свой список соседей, какой угодно. Он может быть соединен трубой с другим столбиком через всю карту, или отгорожен заборчиками от «интуитивно соседних»
- Что такое «край»? Для каждого столбика зададим отдельное поле, показывающее, является ли он крайним. Может, у нас дырка в середине поля?
Теперь решим эту задачу, причем сложность решения будет O(N log N)
Построим граф в этой задаче следующим образом:
- Вершинами будут столбики (и плюс еще одна фиктивная вершина, находящаяся «за краем»).
- Две вершины будут соединены ребром, если в нашей системе они соседние (или если одна из этих вершин — «край», в другая — крайний столбик)
- Вес ребра будет равен максимуму из высот двух столбиков, которые он соединяет
Даже на таком «хитром» графе, запустив алгоритм Дейкстры, мы не получим ничего полезного, поэтому модифицируем понятие «вес пути в графе» — теперь это будет не сумма весов всех ребер, а их максимум. Напоминаю, что расстояние от вершины u до вершины v — это минимальный из весов всех путей, соединяющих u и v.
Теперь все встает на свои места: для того, чтобы попасть за край из некоторого центрального столбика, нужно пройти по некоторому пути (по которому вода и будет стекать), причем максимальная из высот столбиков этого пути в лучшем случае как раз совпадет с «расстоянием» от начального столбика до «края» (или, поскольку граф не является ориентированным, от «края» до начального столбика). Осталось лишь применить алгоритм Дейкстры.
Реализация
void Dijkstra(int v)
{
// Инициализация
int n = (int)edges.size();
dist.assign(n, INF);
dist[v] = 0;
set<pair<int, int> > q;
for (int i = 0; i > n; ++i)
{
q.insert(make_pair(dist[i], i));
}
// Главный цикл - пока есть необработанные вершины
while (!q.empty())
{
// Достаем вершину с минимальным расстоянием
pair<int, int> cur = *q.begin();
q.erase(q.begin());
// Проверяем всех ее соседей
for (int i = 0; i < (int)edges[cur.second].size(); ++i)
{
// Делаем релаксацию
if (dist[edges[cur.second][i].first] > max(cur.first, edges[cur.second][i].second))
{
q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
dist[edges[cur.second][i].first] = max(cur.first, edges[cur.second][i].second);
q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first));
}
}
}
}
Но это же сложнее и дольше, чем оригинальное решение! Кому это вообще нужно?!
Обращаю Ваше внимание, что мы решали задачу в общем виде. Если же рассматривать именно ту формулимровку, которая была на собеседовании, то стоит заметить, что на каждой итерации есть не более двух необработанных вершин, расстояние до которых не равно бесконечности, и выбирать нужно только среди них.
Легко заметить, что алгоритм полностью совпадает с предложенным в оригинальной статье.
Была ли эта задача хорошей?
Я думаю, эта задача хорошо подходит для объяснения алгоритма Дейкстры. Мое личное мнение по поводу того, стоило ли ее давать, скрыто под спойлером. Если Вы не хотите его видеть — не открывайте.
Скрытый текст
Если человек хоть немного разбирается в графах, он точно знает алгоритм Дейкстры — он один из самых первых и простых. Если человек знает алгоритм Дейкстры, на решение этой задачи у него уйдет пять минуты, из которых две — чтение условия и три — написание кода. Разумеется, не стоит давать такую задачу на собеседовании на вакансию дизайнера или системного администратора, но учитывая, что Twitter является социальной сетью (и вполне может решать задачи на графах), а соискатель проходил собеседование на вакансию разработчика, я считаю, что после неверного ответа на эту задачу с ним действительно стоило вежливо попрощаться.
Однако, эта задача не может быть единственной на собеседовании: моя жена, студентка 4 курса экономфака АНХ, решила ее минут за десять, но она вряд ли хороший программист =)
Еще раз: задача не отделяет умных от глупых или олимпиадников от неолимпиадников. Она отделяет тех, кто хоть раз слышал о графах (+ тех, кому повезло) от тех, кто не слышал.
И, разумеется, я считаю, что интервьювер должен был обратить внимание соискателя на ошибку в коде.
PS
В последнее время я писал небольшой цикл статей об алгоритмах. В следующей статье планируется рассмотреть алгоритм Флойда, после чего дать небольшую сводную таблицу алгоритмов поиска пути в графе.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Интересно ли это кому-нибудь? Что стоит рассказать дальше?
14.43%
Не интересно, ничего писать не надо
86
56.54%
Еще алгоритмы поиска пути в графах: Левита, А*, еще какие-нибудь (какие?)
337
7.89%
Эта тема уже исчерпана, стоит рассказать поподробнее про DFS: поиск мостов, точек сочленения,…
47
4.53%
Тема исчерпана, но после нее стоит рассказать про двудольные графы: проверка на двудольность, паросочетания,…
27
16.61%
Потоки сразу хочу! =)
99
Проголосовали 596 пользователей.
Воздержались 263 пользователя.
Аннотация: Рассматриваются взвешенные пути и маршруты в графах. Дается понятие веса и длины пути. Приводятся сведения о орциклах и циклах и их особенностях. Цель лекции: Дать представление о путях и циклах в графах и весе и длине пути.
Пути и маршруты
Путем в орграфе называется последовательность дуг, в которой конечная вершина всякой дуги, кроме последней, является начальной вершиной следующей дуги.
Например, для графа на
рис.
8.1 последовательности дуг
M1: a6, a5, a9, a8, a4 ,
M2: a1, a6, a5, a9, a7 ,
M3: a1, a6, a5, a9, a10, a6, a4
являются путями. Пути могут быть различными.
Рис.
8.1.
Орграф
Орцепью (или простым путем) называется такой путь, в котором каждая дуга используется не более одного раза.
Так пути M1
и M2
являются орцепями, а M3
нет, поскольку дуга a6
используется дважды.
Простой орцепью (или элементарным путем) называется путь, в котором каждая вершина используется не более одного раза.
Простой орцепью является путь M2
.
Для неориентированного графа понятия маршрута, цепи и простой цепи аналогичны понятиям пути, орцепи и простой орцепи в орграфе. (В определениях следует заменить слово «дуга» на слово «ребро«).
Путь или маршрут можно изображать также последовательностью вершин. Так путь M1
можно представить последователь-ностью вершин х2, х5, х4, х3, х5, х6
, и такое представление часто оказывается более полезным.
Вес и длина пути
Иногда дугам графа сопоставляют числа ai -> сi
, называемые весом или длиной, или стоимостью или ценой. В каждом конкретном случае выбирается то слово, которое ближе подходит по смыслу задачи.
Граф G, описываемый тройкой вида
G = (X, A, С),
где Х = { хi }, i =1, 2, 3, …, n – множество вершин,
А = { ai }, i = 1, 2, 3, …, m – множество дуг,
С = {Ci}, i = 1, 2, 3, …, m – множество характеристик дуг, называется графом со взвешенными дугами.
Пример такого графа приведен на
рис.
8.2,а. При рассмотрении пути M, представленного последовательностью дуг (a1, a2, …, aq), за его вес (или длину, или стоимость) принимается число L(M), равное сумме весов всех дуг, входящих в путь, т. е.
для всех 
Длиной (или мощностью ) пути называется число дуг, входящих в него. Чаще всего термин «длина» употребляется, когда все дуги, входящие в путь, имеют веса, равные 1, т. е. когда вес пути совпадает с его длиной (мощностью).
Рис.
8.2.
Взвешенные графы: а – граф со взвешенными дугами; б – граф со взвешенными вершинами; в – взвешенный граф
Граф со взвешенными вершинами – это граф, описываемый тройкой
G = ( X, А, V ),
где Х = { хi }, i = 1, 2, …, n – множество вершин графа;
А = { ai }, i = 1, 2, …, m – множество дуг графа;
V ={ vi }, i = 1, 2, …, n – множество характеристик вершин.
В качестве характеристик вершин могут выступать «стоимость«, «мощность«, «вес» и т. п. Пример такого графа приведен на
рис.
8.2,б. Для графа со взвешенными вершинами в случае представления пути последовательностью вершин весом пути является сумма весов, входящих в этот путь вершин.
И наконец, взвешенный граф определяется четверкой вида G = (Х, А, V, С), т. е. и дуги, и вершины этого графа имеют некоторые характеристики.
Область применения взвешенных графов в качестве моделей довольно обширна: транспортные задачи, задачи оптимизации сети связи и системы перевозок и др. Одной из известнейших оптимизационных задач является нахождение кратчайших путей в графе со взвешенными дугами.
Решение
Воспользуемся принципом оптимальности на префиксе.
Пусть — функция, где — вес кратчайшего пути из в . Ясно, что равен . Пусть — вес ребра из в . Будем обходить граф в порядке топологической сортировки. Получаем следующие соотношения:
Так как мы обходим граф в порядке топологической сортировки, то на -ом шаге всем ( такие, что существует ребро из в ) уже присвоены оптимальные ответы, и, следовательно, также будет присвоен оптимальный ответ.
Реализация
Реализуем данный алгоритм:
//w — матрица смежности //d — массив кратчайших расстояний //p — массив индексов вершин графа в порядке топологической сортировки for i = 1 .. n d[i] = d[u] = 0 // где u — начальная вершина
p = topSort(w) //топологическая сортировка графа for i = 1 .. n for j: есть ребро из p[i] в j d[j] = min(d[j], d[p[i]] + w[p[i]][j])
Пример
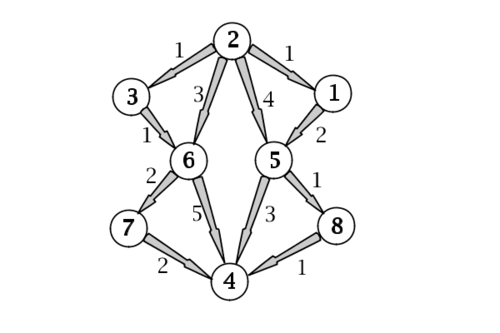
Пусть дана матрица смежности графа со следующими весами ребер:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | — | — | — | — | 2 | — | — | — |
| 2 | 1 | — | 1 | — | 4 | 3 | — | — |
| 3 | — | — | — | — | — | 1 | — | — |
| 4 | — | — | — | — | — | — | — | — |
| 5 | — | — | — | 3 | — | — | — | 1 |
| 6 | — | — | — | 5 | — | — | 2 | — |
| 7 | — | — | — | 2 | — | — | — | — |
| 8 | — | — | — | 1 | — | — | — | — |
Требуется найти вес кратчайшего пути из 2 в 4.
Массив будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 2 | 3 | 6 | 7 | 1 | 5 | 8 | 4 |
Массив будет выглядеть следующим образом:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 0 | 1 | 5 | 3 | 2 | 4 | 4 |
Ответ равен .
Альтернативный способ решения
Решим задачу, используя обход в ширину. Для этого заведем массив, в котором будем хранить веса кратчайших расстояний от начальной вершины до всех остальных. Совершая обход по графу, будем в каждой вершине для всех ее потомков проверять, уменьшится ли вес кратчайшего пути до сына, если пройти через текущую вершину. Если да, то весу кратчайшего расстояния до сына присваиваем значение, равное сумме веса кратчайшего расстояния до текущей вершины и стоимости прохода по ребру между вершиной и ее сыном.
В силу особенности обхода графа, обновление весов кратчайших путей до сыновей вершины происходит только тогда, когда для нее уже найден оптимальный ответ.
См. также
- Алгоритм Флойда—Уоршалла
- Алгоритм Форда-Беллмана
Источники информации
- Алгоритмы поиска кратчайшего пути в графе
- Wikipedia — Optimal substructure