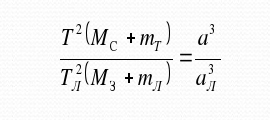Содержание
- Как узнать, какая версия Windows установлена на вашем компьютере?
- Способ 1: Использование команды «winver»
- Способ 2: Использование окна «Свойства»
- Как узнать полную информацию о компьютере в Windows 10?
- Узнаём базовую информацию с помощью стандартного приложения «Параметры»
- Стандартная подпрограмма «Сведения о системе» даёт более детальную информацию
- Информация о системе в Командной строке
- Диспетчер устройств в Windows 10
- Как узнать версию «DirectX»
- Как узнать размер файла или папки
- Содержание:
- Единицы измерения размера файла
- Как определить размер файла или папки
- Как определить суммарный размер нескольких файлов и папок
- Как определить размер пространства диска или флешки
- Как наглядно увидеть, какие папки и файлы на компьютере занимают больше всего места?
- Введение
- Примерная оценка занятого файлами места на дисках через встроенный проводник Windows
- Наглядная и понятная оценка занятого файлами места на дисках при помощи программы WinDirStat
- Загрузка и установка программы
- Использование программы
- Анализ занимаегого объёма при помощи «дерева» файлов и папок
- Анализ занимаемого места файлами по их типам
- Заключение
- 4 комментария
Как узнать, какая версия Windows установлена на вашем компьютере?
Шесть способов узнать версию, сборку и разрядность Windows, которая установлена на вашем ПК.Этот вопрос очень часто задают многие пользователи по электронной почте и в комментариях, поэтому сегодня мы решили опубликовать руководство о том, как узнать информацию об установленной версии операционной системы «Windows» на любом компьютере.
Последнее время очень часто можно приобрести персональный компьютер или ноутбук с уже предустановленной операционной системой «Windows». Это удобно, так как система полностью настроена и проверена на отсутствие ошибок. Но можно приобрести компьютер и без установленной операционной системы. Тогда пользователю приходится дополнительно обращаться в специальную службу для установки операционной системы или пользоваться услугами своих друзей и знакомых. При этом большинство пользователей, использующих операционную систему «Windows», абсолютно не задумываются о ее параметрах и характеристиках. Но когда появляется необходимость установки дополнительного программного обеспечения или приложений, то возникает вопрос совместимости таких программ и операционной системы «Windows», установленной у пользователя. Вот тогда у пользователя появляются разные вопросы о характеристиках операционной системы, установленной на его компьютере или ноутбуке.
В этом руководстве мы постарались ответить на такие вопросы об операционной системе:
Существует много способов получить ответы на эти вопросы об операционной системе «Windows», установленной на вашем компьютере. Мы покажем разные методы, подходящие для различных операционных систем «Windows», вы сможете опробовать их все и выбрать наиболее подходящие для вас.
Способ 1: Использование команды «winver»
Этот метод очень простой и позволяют быстро узнать информацию об установленной версии операционной системы «Windows» с помощью простой команды «winver». Это универсальный метод, и он подходит для любой версии «Windows».
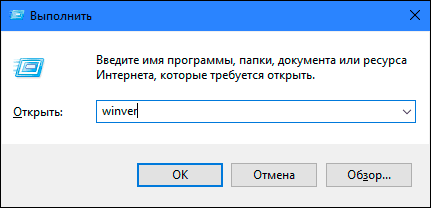
Нажмите вместе сочетание клавиш «Windows + R», чтобы открыть диалоговое окно «Выполнить». В поле командной строки введите «winver» и нажмите кнопку «ОК» или клавишу «Enter» на клавиатуре для выполнения команды.
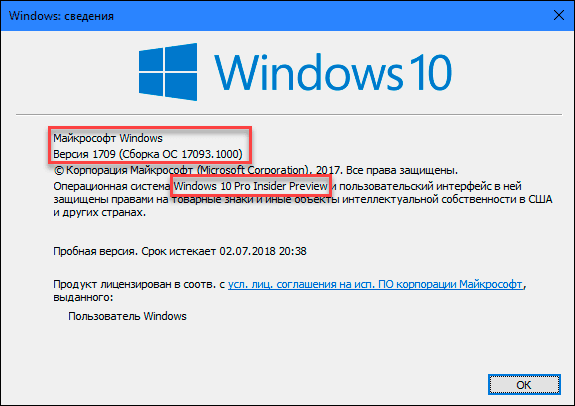
Команда запустит диалоговое окно «Windows: сведения».
В окне отражается основная информация об установленной операционной системе «Windows», показана ее версия, номер сборки системы, пакет обновления и т.д. Вы также можете узнать, на какое имя пользователя или какую организацию она зарегистрирована.
Способ 2: Использование окна «Свойства»
Во всех версиях «Windows» по умолчанию включен стандартный набор приложений, в котором обязательно присутствует приложение «Система». Оно содержит большой массив полезной и подробной информации о версии установленной операционной системы «Windows», и ее всегда можно легко просмотреть.
Вы можете открыть окно «Система» разными способами, но мы покажем только два из них.
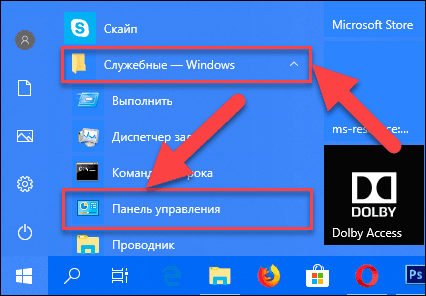
Способ 1: В левом нижнем углу экрана на «Панели задач» нажмите кнопку «Пуск» и откройте главное меню. Опустите бегунок установленных программ и приложений вниз к разделу «Служебные – Windows» и выберите раздел «Панель управления».
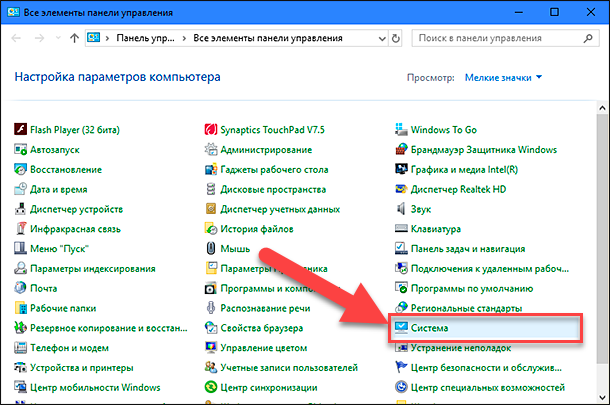
В окне «Все элементы панели управления» выберите раздел «Система».
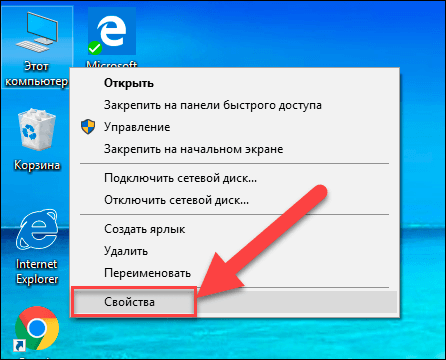
Способ 2: Найдите на рабочем столе вашего компьютера или ноутбука значок «Этот компьютер» (значок «Компьютер» или «Мой компьютер» для более ранних версий «Windows»), щелкните на нем правой кнопкой мыши и выберите во всплывающем меню раздел «Свойства».
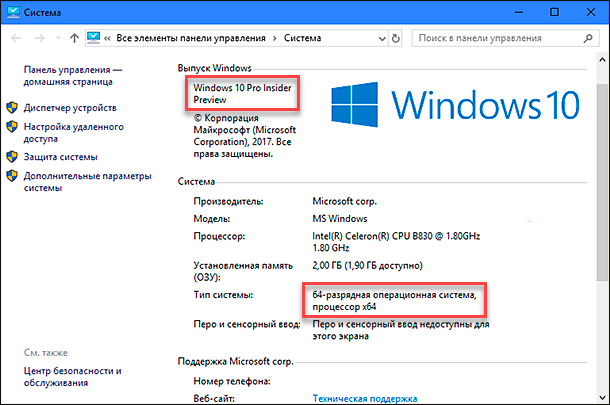
В окне «Система» отражена вся основная информация. Вы сможете увидеть, какая версия «Windows» («XP», «Vista», «7», «8 / 8.1» или «10») установлена на вашем компьютере, а также определить выпуск операционной системы «Windows» («Home», «Professional», «Home Basic», «Home Premium» и т.д.), проверить, установлен ли пакет обновления или нет.
В пункте «Тип системы» вы сможете определить разрядность операционной системы «Windows» (32-разрядная (x86) или 64-разрядная (x64)), установленной у вас на компьютере.
Так же в перечень основных параметров компьютера, указанных в окне «Система», входит информация о процессоре, установленной памяти (ОЗУ), имени компьютера, идентификаторе продукта и т.д. Здесь вы легко сможете найти всю необходимую информацию о вашей операционной системе «Windows».
Полную версию статьи со всеми дополнительными видео уроками читайте в нашем блоге.
Источник
Как узнать полную информацию о компьютере в Windows 10?
Читайте, где в Windows 10 посмотреть полную информацию о компьютере и его устройствах. Какие стандартные приложения или сторонние утилиты для этого использовать.Иногда вам может понадобиться быстро найти информацию о конфигурации вашего компьютера, операционной системе, установленных драйверах и поддерживаемых технических модулях, например, точную модель сетевой карты, версию «BIOS» или «UEFI», или какая версия «DirectX» установлена на вашем ПК.
В данной статье, я расскажу о некоторых стандартных инструментах операционной системы, которые предоставляют эту системную информацию, как общую, так и более детализированную.
Узнаём базовую информацию с помощью стандартного приложения «Параметры»
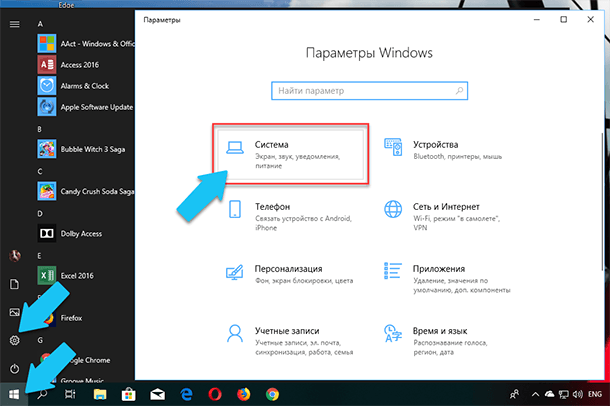
Если вы хотите посмотреть базовый обзор вашей системы, то его можно найти в стандартном приложении «Параметры», как Windows 8 так и Windows 10. Чтобы открыть приложение, нажмите «Пуск» и далее кликните на кнопке «Параметры» (иконка в виде шестерёнки) в левом нижнем углу окна, или нажмите сочетание клавиш «Windows + I». Далее в приложении щелкните по значку «Система».
После этого, на открывшейся странице, перейдите на вкладку «О системе» в меню слева.
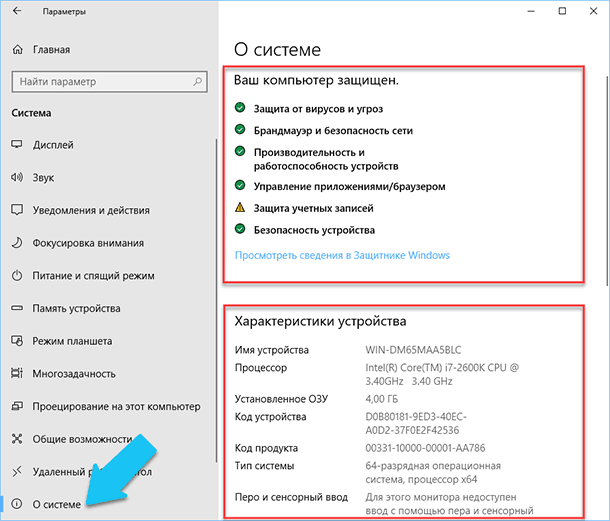
В правой части окна будут выведены три раздела с информацией. В первом, будет показана информация о защите вашего ПК в реальном времени, в разделе «Характеристики устройства» приведены основные сведения о конфигурации вашего ПК, модель процессора, объем оперативной памяти, идентификаторы устройства и продукта, а также тип используемой системы (32-разрядной или 64-разрядной).
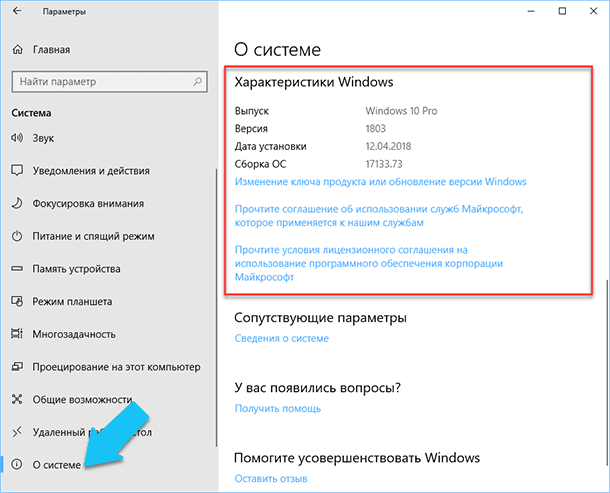
В разделе «Характеристики Windows» указаны название и версия вашей операционной системы, дата установки и номер сборки Windows. Также в этом окне можно перейти по ссылкам: обновление ключа и переактивация ОС, прочитать лицензионное соглашение и соглашение об использовании служб «Microsoft».
Стандартная подпрограмма «Сведения о системе» даёт более детальную информацию
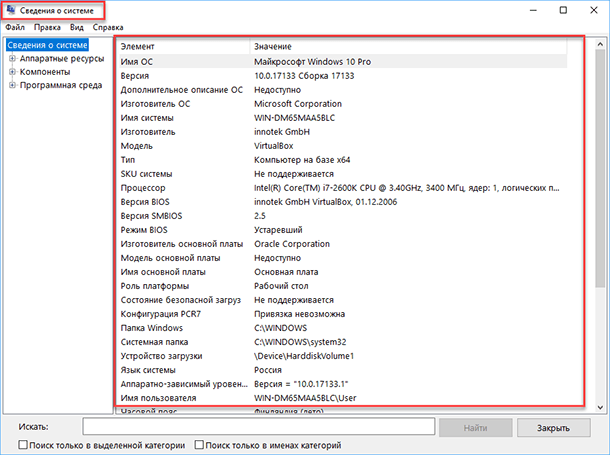
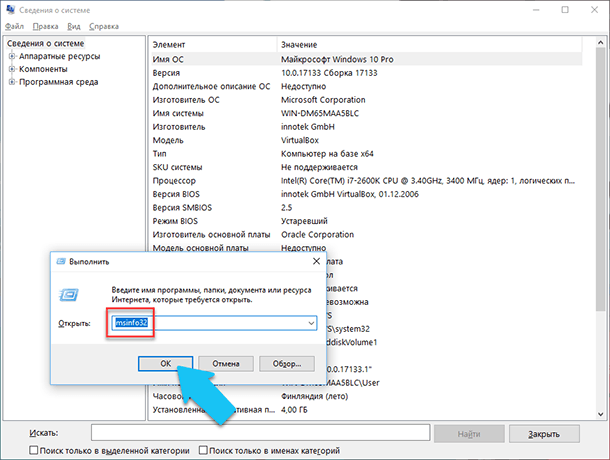
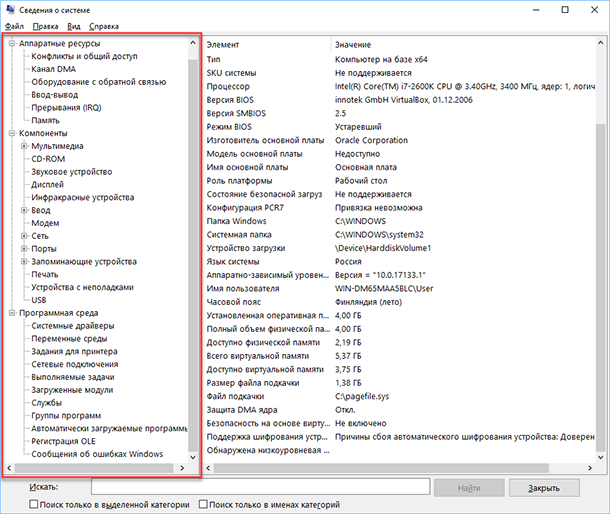
Приложение «Сведения о системе» (System Information) было добавлено ещё в Windows XP. С его помощью можно посмотреть гораздо более подробный обзор как системной информации, так и сведений об используемом оборудовании, намного информативней чем предыдущий способ.
Чтобы открыть окно «Сведения о системе», нажмите сочетание «Windows + R», и в открывшемся диалоге «Выполнить» введите «msinfo32» и кликните «Enter».
Главная страница сразу предоставит гораздо больше информации, чем мы видели в приложении «Параметры». Здесь она указана более подробно, изготовитель вашего ПК, детальная информация о конфигурации, версия BIOS, модель материнской платы, установленная оперативная память и т. д.
Но это только начало. Разверните дерево вкладок в меню слева, и перед вами откроется настоящий функционал данного приложения. Большая часть этой информации пригодится, наверное, только разработчикам программного обеспечения и системным администраторам, но в тоже время, здесь имеются почти все необходимы данные о системе.
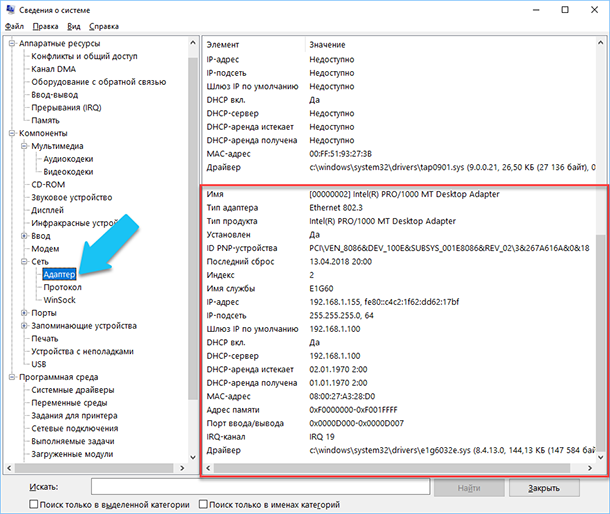
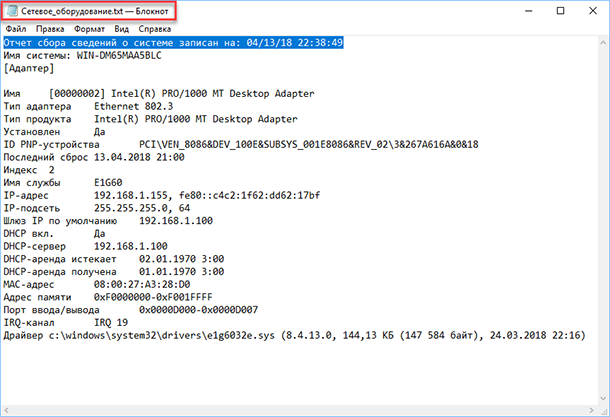
Например, в разделе «Компоненты» кликните по полю «Сеть» и далее «Адаптер» и программа выдаст полную информацию об устройстве: название, модель вашей сетевой карты, производитель, версии драйвера, текущее состояние, а также все связанные с ней настройки, которые используются в данный момент.
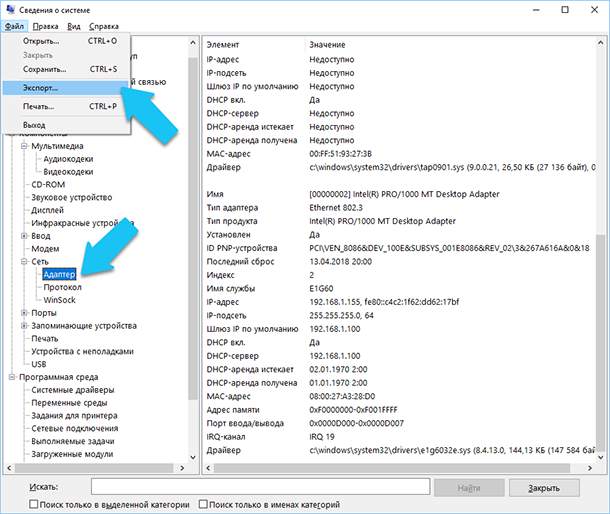
Есть еще одна превосходная функция данного программного обеспечения – это возможность экспортировать интересующую вас информацию в текстовый файл. Эта опция крайне полезна, когда вам понадобится отправить данные о своей системе или о возникающих ошибках оборудования другому пользователю, например, в службу поддержки, или если вы просто захотите сохранить копию вашей конфигурации и настроек системы на всякий случай.
Сначала необходимо выбрать нужный раздел или подраздел, информацию из которого вы хотите экспортировать. Если вы выберете раздел «Сведения о системе», то экспортируемый файл будет содержать данные из всех разделов, которые доступны в приложении. Но также можно выбрать любой отдельный раздел или подраздел, чтобы сохранить только конкретную информацию.
Затем откройте меню «Файл» и кликните на команду «Экспорт».
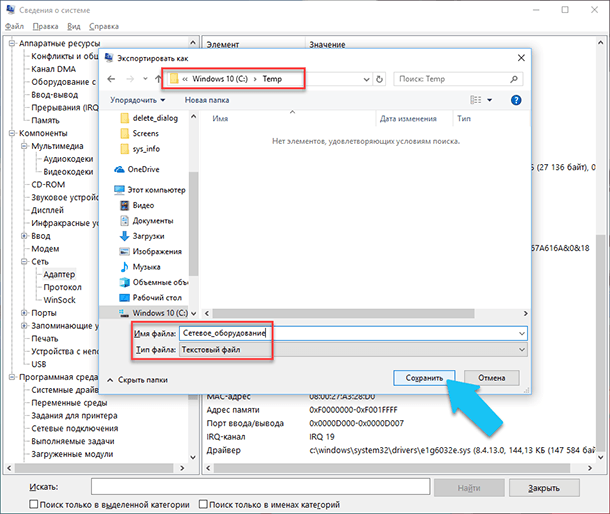
Откроется стандартный диалог сохранения файла в Windows, просто перейдите в нужный каталог и введите названия нового отчёта и нажмите кнопку «Сохранить».
Теперь в любое время, вы сможете без проблем открыть данный файл и просмотреть все, интересующие вас, сведения и настройки.
Информация о системе в Командной строке
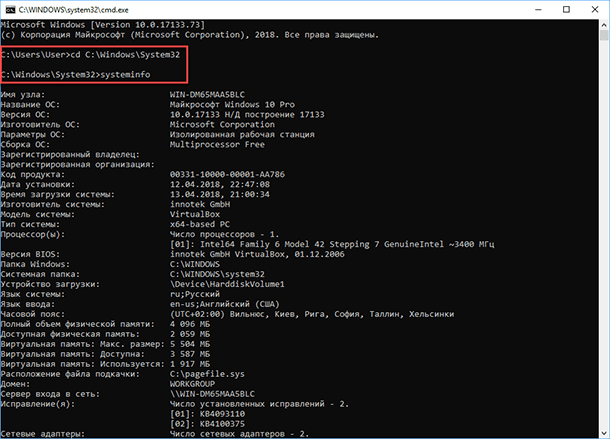
Если Windows не загружается в нормальном рабочем режиме, то для получения сведений о системе можно использовать специальную команду для «Командной строки». Используя этот вариант, вы не сможете получить столь детальную информацию, как в приложении «Сведения о системе», и, возможно, данный вариант является более сложным, по сравнению с обычным приложением, но все же эта команда будет крайне полезной в случае, когда операционная система начинает «выделываться» и перестаёт нормально загружаться.
После стандартного приглашения командной строки, нужно перейти в каталог, где расположена данная программа, ведите следующую команду «cd C:WindowsSystem32». Далее введите команду «systeminfo» и нажмите «Enter». После небольшого анализа, программа выведет несколько строк нужной вам информации о сборке и версии ОС, процессоре, версии BIOS, загрузочном диске, памяти и сведениях о сети.
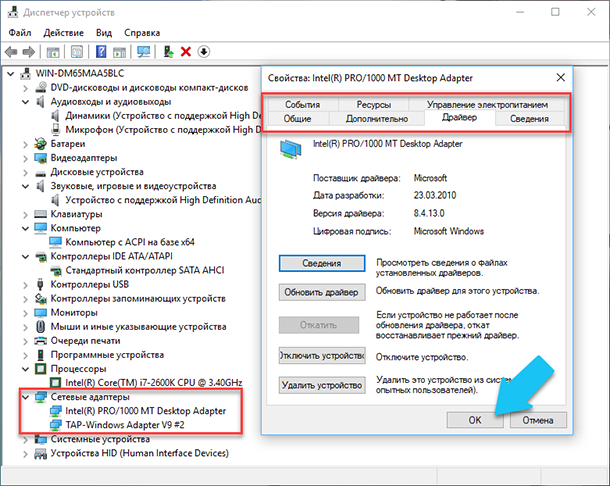
Диспетчер устройств в Windows 10
Диспетчер устройств – это стандартный компонент операционной системы, который предоставляет информацию обо всех устройствах, подключенных и используемых в данный момент. Также является единственным инструментом управления драйверами для каждого установленного устройства, управляет выделенными им ресурсами (запросами на прерывания, каналами DMA, областями памяти, портами ввода-вывода). Ещё предоставляет большой объём дополнительной информации.
Открыть «Диспетчер устройств» в Windows 10 можно несколькими способами, самый простой через поиск, для этого кликните на иконку «Поиск» и начните вводить выражение «Диспетчер устройств», наш вариант будет в самом верху списка результатов поиска.
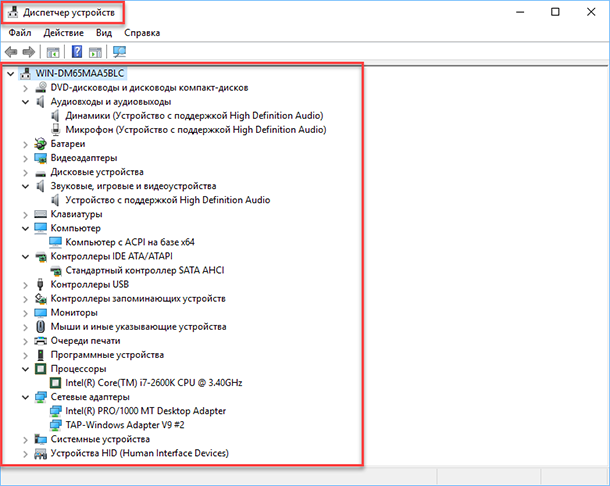
В открывшемся окне, будут представлены все установленные устройства на вашем ПК.
Перейдите в любой раздел, например, «Сетевые адаптеры» и щёлкните на строке с названием устройства.
Сразу откроется окно свойств данного оборудования, вверху вы увидите несколько закладок: события связанные с работой устройства, ресурсы, которые оно использует, управление электропитанием, общие сведения об устройстве и управление драйверами. Собственно, здесь собран весь функционал управления данным устройством, вы можете обновить драйвер, удалить устройство, отключить его и так далее.
Как узнать версию «DirectX»
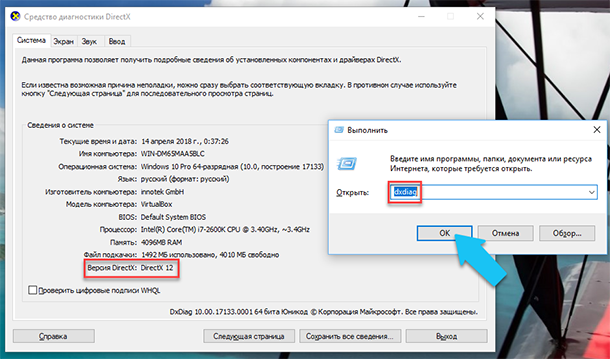
«DirectX» – это специальный набор готовых графических элементов, процедур и функций, которые операционная система Windows предоставляет для использования внешними программами. «DirectX» специально разработан компанией «Microsoft» для облегчения разработки графических приложений под Windows, большинство программ, так или иначе, но используют его для визуализации всевозможных данных. Чаще всего его используют для написания компьютерных игр. И если вы установили игру, которой для нормальной работы нужна более новая версия «DirectX», чем та которая установлена на вашем ПК. То, узнав какая версия установлена, вы сможете понять нужно его обновлять или нет.
Самый простой способ сделать это, запустив стандартную утилиту ОС. Для этого нажмите сочетание клавиш «Windows + R», и в появившемся окне «Выполнить» введите «dxdiag» и нажмите «Enter».
В результате запустится утилита «Средство диагностики DirectX». На первой вкладке окна программы будут выведены некоторые сведения о ПК и информация о версии «DirectX». На самом деле, данная надпись говорит лишь о том какая версия программы активна и используется в данный момент, а не какая последняя установлена на ваш ПК. После обновления «Windows 10 Fall Creators Update» в этом окне, утилита всегда показывает версию 12. Но тут встаёт вопрос, о том, что не каждая видеокарта может поддерживать этот «DirectX». Версию программы, которую поддерживает ваше устройство можно найти в разделе «Экран» стандартного приложения «Параметры» Windows.
Источник
Как узнать размер файла или папки
В статье подробно описан порядок определения размера файлов и папок, а также объема свободного и занятого пространства запоминающих устройств.
Содержание:
Единицы измерения размера файла
В одной из наших предыдущих статей мы уже говорили о том, что каждый файл или папка имеет определенный размер, который автоматически определяется компьютером в зависимости от их содержания. Размер файла зависит от количества информации, которую он содержит. Размер папки равен сумме размеров находящихся в ней файлов.
Количество информации, а соответственно и размер файла, измеряется в специальных единицах, называемых байтами (сокращенно обозначается латинской буквой b или русской Б).
Байт – это очень маленькое количество информации. На практике чаще встречаются более крупные единицы, а именно:
— килобайт (равен 1024 байтам, сокращенно – kb или КБ);
— мегабайт (равен 1024 килобайтам, сокращенно – mb или МБ);
— гигабайт (равен 1024 мегабайтам, сокращенно – gb или ГБ);
— терабайт (равен 1024 гигабайтам, сокращенно – tb или ТБ).
Есть и еще более крупные единицы, но они в повседневной жизни встречаются редко.
Все запоминающие устройства (постоянные запоминающие устройства компьютеров, портативные носители типа флешек и др.) имеют определенное пространство. Оно не безгранично и также измеряется в байтах.
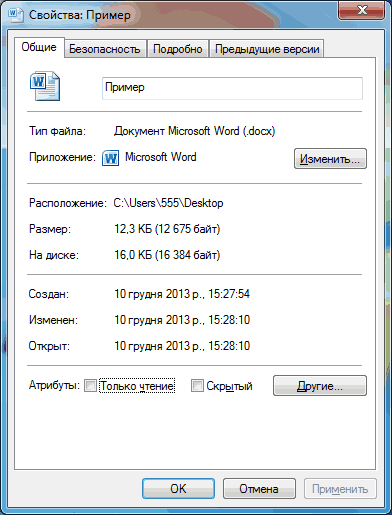
Как определить размер файла или папки
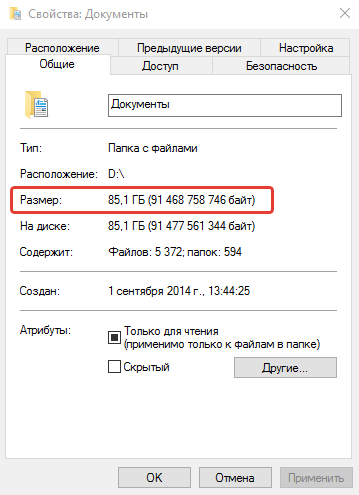
Чтобы узнать размер файла или папки необходимо щелкнуть по нему правой кнопкой мышки и в открывшемся контекстном меню выбрать пункт «Свойства». Откроется окно «Свойства…», в котором и будет отображена необходимая информация.
На рисунке видно, что размер созданного автором статьи файла составляет 12,3 kb (или 12675 байт). В Вашем случае, естественно, размеры будут другими.
Если создать папку и поместить в нее файл, то можно убедиться, что размер такой папки будет равен размеру находящегося в ней файла. Указанным выше способом можно узнать размер любого файла или папки.
Как определить суммарный размер нескольких файлов и папок
Чтобы определить суммарный размер нескольких файлов и папок, можно указанным выше способом узнать размер каждого из них и затем сложить все полученные числа. В то же время, такой способ будет связан с большими затратами времени, особенно, если речь идет о значительном числе файлов.
Операционная система Windows позволяет решать подобные задачи значительно проще. Но для этого необходимо овладеть навыком выделения нескольких файлов и папок.
Откройте любую имеющуюся на компьютере папку с файлами и выделите один из них указанным способом. После щелчка мышки вокруг значка выделенного файла появится специальная рамка ( см. изображение ).
Если щелкнуть по другому файлу – рамка выделения перейдет на него, а выделение с предыдущего файла автоматически снимется.
Чтобы выделение с предыдущего файла не снималось, на клавиатуре нужно постоянно удерживать нажатой кнопку «Ctrl».
Чтобы овладеть навыком выделения нескольких файлов необходимо немного попрактиковаться, что я вам и рекомендую сделать. Подробнее основные операциях с файлами, которые можно осуществить при помощи мышки, рассмотрены в этой нашей статье.
А для того, чтобы быстро узнать суммарный размер нескольких файлов (папок), необходимо выделить их указанным выше способом, после чего щелкнуть по любому из них правой кнопкой мышки и в открывшемся контекстном меню выбрать пункт «свойства». Откроется окно, в котором будет отображаться уже обобщенная информация ( см.изображение ниже ).

На рисунке видно, что общий размер выделенных 2 файлов и 1 папки составляет 24,7 килобайт (или 25350 байт).
Как определить размер пространства диска или флешки
Если речь идет о съемном устройстве (флешка, портативный жесткий диск и т.д.), его необходимо сначала подключить к компьютеру.
Затем нужно открыть раздел «Компьютер» (дважды щелкнуть левой кнопкой мышки по соответствующему значку на рабочем столе), щелкнуть правой кнопкой мышки по значку этого запоминающего устройства и выбрать пункт «Свойства».
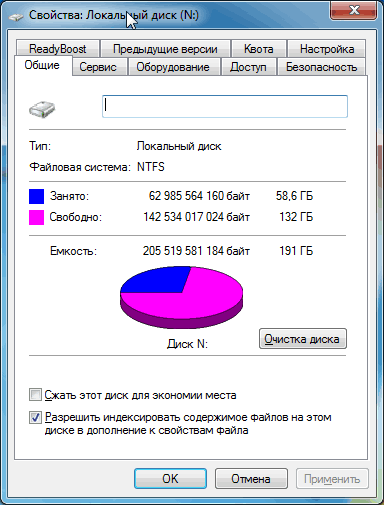
Откроется окно, в котором об этом устройстве будет отображена вся необходимая информация ( см. изображение ):
Емкость – общий размер запоминающего устройства (в байтах);
Занято – какая часть общего размера устройства уже занята (в байтах);
Свободно – сколько байт свободного пространства осталось на запоминающем устройстве.
На примере видно, что локальный диск компьютера имеет:
— общий объем 191 гигабайт (что равно 205534017024 байтам, или 200716813,5 килобайтам, или 196012,5 мегабайтам);
— из этих 191 gb занято 58,6 gb (что равно 62985564160 байтам, или 61509340 килобайтам, или 60067,7 мегабайтам);
— остальное пространство свободно – 132 гигабайта (что равно 142534017024 байтам, или 139193376 килобайтам, или 135931 мегабайтам).
Пользователь, произведя не сложные математические расчеты, всегда может определить, сколько и каких файлов и папок можно сохранить на носителе.
Если этот носитель полностью очистить (стереть все уже находящиеся на нем файлы), то на нем можно будет сохранить 191 гигабайт файлов и папок.
Источник
Как наглядно увидеть, какие папки и файлы на компьютере занимают больше всего места?
Введение
Очень знакомая многим ситуация. Мы качаем регулярно много всего из интернете — фильмы, видюхи, музыку, игрушки и прочее. В итоге многим всегда лень заняться чисткой своего компьютера от ненужной информации, хранящейся на жёстком диске, либо всегда некогда 🙂 В итоге жёсткие диски компьютера набиваются так, что в проводнике Windows объём оставшегося свободного места уже отмечен красной полоской, т. е. место подходит к концу. И хорошо когда всё ненужное накапливается где-нибудь в одной папке (к примеру папка «Загрузки» для скачивания файлов из интернете). Но обычно много больших по объёму файлов пачками разбросаны по всему жёсткому диску и тогда определять, что именно занимает больше всего места и где это расположено в компьютере, становится очень неудобно. Стандартные средства Windows не позволяют быстро оценить, где больше всего хранится данные на компьютере, но для такой цели есть специальные сторонние программы, одна из которых — WinDirStat, являющаяся бесплатной. При помощи неё наглядно видно, какие файлы и в каком объёме, где именно располагаются на жёстком диске, что позволяет легко проанализировать, что из этого нам уже не нужно и можно сразу же удалить! Итак, в этой статье я покажу как легко оценить, что и сколько места занимает на вашем жёстком диске, а также где это располагается.
Примерная оценка занятого файлами места на дисках через встроенный проводник Windows
Начну с того, покажу как через встроенный проводник Windows можно было хотя бы примерно оценить, где и что у нас отнимает место. Для этого нужно открыть проводник Windows и в нём, в первую очередь раздел «Компьютер» (или «Мой компьютер», если Windows XP).
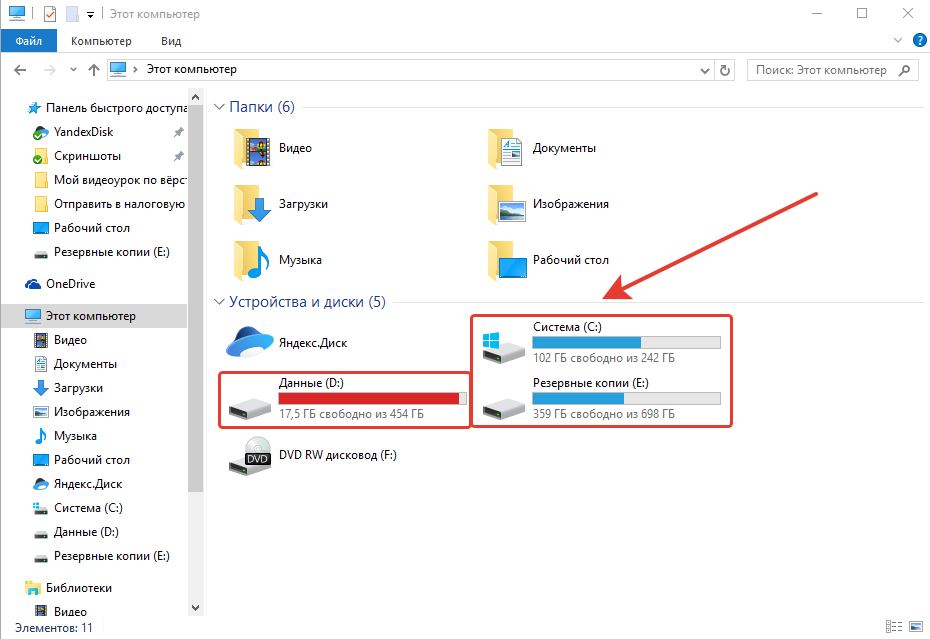
В этом разделе отображаются все локальные диски, на которых могут быть ваши данные. Локальный диск — это как раздел на вашем жёстком диске, т. е. его часть. К примеру у меня имеется 3 локальных диска (см.изображение выше), т. е. весь жёсткий диск поделён на 3 части.
Подробную информацию о том, что вообще такое жёсткий диск, как он выглядит и о других устройствах компьютера, вы сможете узнать в отдельной статье — вот здесь.
В этом окне сразу видно, сколько места занято на каждом из локальных дисков и сколько там всего объём. Если места остаётся маловато, то полоса под диском станет красной. Например, у меня сильно забит раздел «D», который я использую именно для хранения всяких личных данных. Программы и сама Windows у меня хранятся на диске «C:».
Итак, переходим в диск, где больше всего занято свободного места. Теперь остаётся только ходить по папкам и вручную оценивать объём каждой. Windows почему то не показывает через соответствующий столбец проводника «Размер», сколько места занимает та или иная папка. Показывает только размер файлов, имеющихся в открытой папке. Чтобы увидеть, сколько места занимает папка, нужно навести на неё курсор мыши и не щёлкая, подержать курсор на папке около 3-х секунд. В итоге во сплывающем окне появится информаци, где будет пункт «Размер».
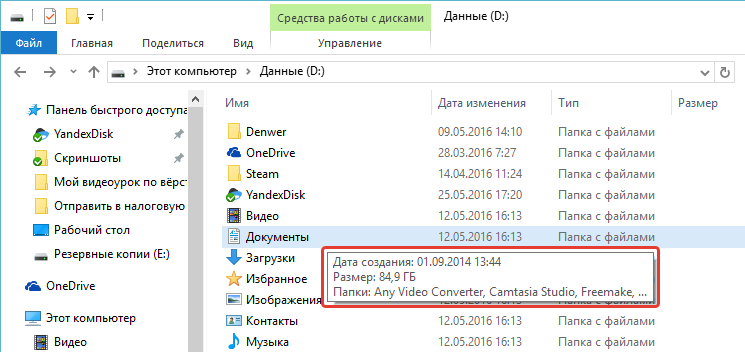
Это и есть объём на диске, который занимает данная папка.
Либо можно щёлкнуть правой кнопкой мыши (далее «ПКМ») по папке, затем выбрать «Свойства» из контекстного меню.
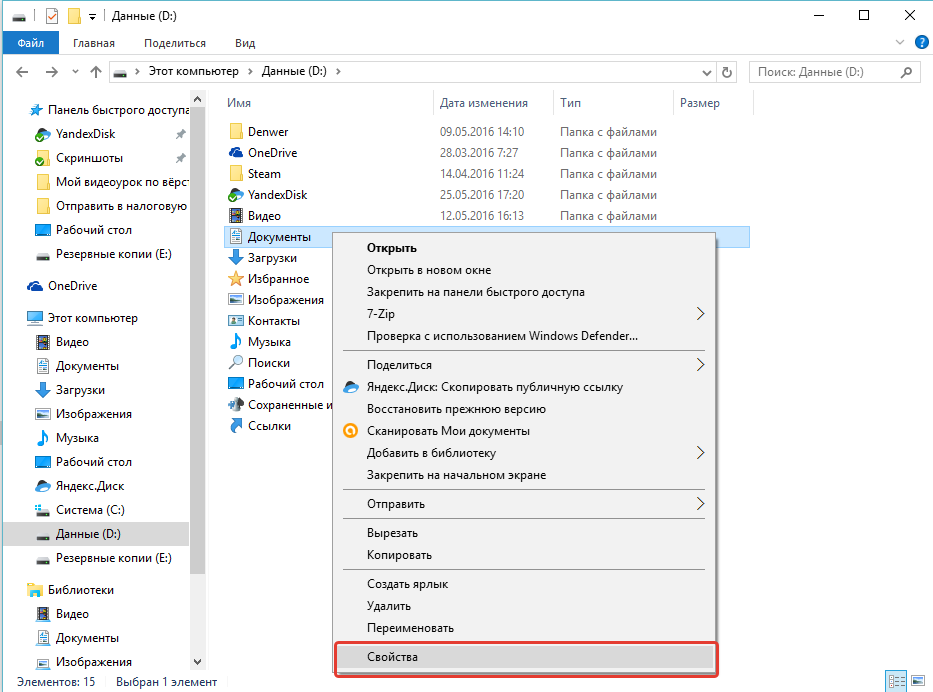
В открывшемся окне увидим размер папки:
И таким образом, открывая самые крупные папки друг за другом, мы в итоге увидим ту папку, где хранятся самые крупные файлы, которые больше всего занимают места на диске. Но если таких мест много? Например, фильмы в разном количества разбросаны по разным папкам + игры и всякие другие файлы. Тогда поиск получится уже затруднительным, неудобным. Проще когда пользователь сам примерно помнит, куда они что складывал и всё аккуратно раскладывает по папкам, например, фильмы и видюхи в «Видео», фотки в «Изображения». И даже в этом случае не сразу оценишь, что, где и как обстоит с файлами, особенно при больших по объёму жёстких дисках, 1.5 Тб и более.
Наглядная и понятная оценка занятого файлами места на дисках при помощи программы WinDirStat
Программа WinDirStat позволит сразу наглядно увидеть, какие папки и файлы, сколько места занимают на всех локальных дисках. При этом можно сразу отсортировать по объёму, чтобы в первую очередь отображались файлы и папки, занимающие больше всего места на дисках. Также можно посмотреть наглядно, какие именно это файлы по формату (видео, или ещё что-то, например), а также ещё много полезных функций.
Загрузка и установка программы
Программа ставится очень просто и никаких спец.настроек во время установки не требует.
Подробнее об установке программ для Windows вы можете почитать в статье — вот здесь.
Официальный сайт программы, откуда её можно скачать:
Даю прямую ссылку на скачивание:
скачать программу (если работать перестанет, пользуйтесь ссылкой с официального сайта). Размер программы меньше 1 Мб.
После загрузки программы, запускаем скачанный файл для установки.
В первом окне соглашаемся с условиями (1) и нажимаем Next.
В следующем окне ничего настраивать не нужно и просто нажимаем Next:
В последующих двух окнах тоже просто нажимаем «Next».
В последнем окне нажимаем «Close» для завершения установки:
После завершения установки, программа будет запущена автоматически.
Использование программы
Пользоваться программой очень просто. При запуске программы предлагается выбрать, какие имеющиеся разделы жёсткого диска (локальные диски) будут анализироваться. Если вы храните практически всё на какому-то одном диске, то выберите «Индивидуальные диски», отметьте нужный диск и нажмите «ОК». Но если данные могут быть разбросаны по разным дискам, то лучше отметить «Все локальные диски» (1) и нажать «ОК».
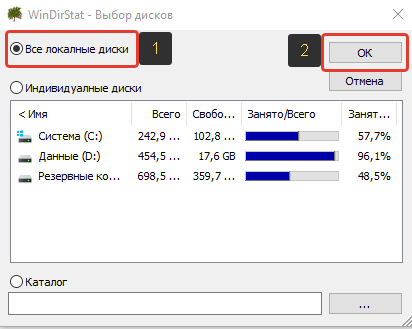
Затем программа начнёт анализ выбранных разделов жёсткого диска для того чтобы вывести полную «картину», что и где отнимает у вас место с указанием форматов файлов. Процесс сканирования будет отображаться в виде бегающих жёлтеньких пакменов (как из старой игры на компьютер):
В первый раз процесс анализа может занять несколько минут, а при повторных запусках программы он будет проходить в разы быстрее. После того как анализ будет завершён, окно программы примет вот такой вид:
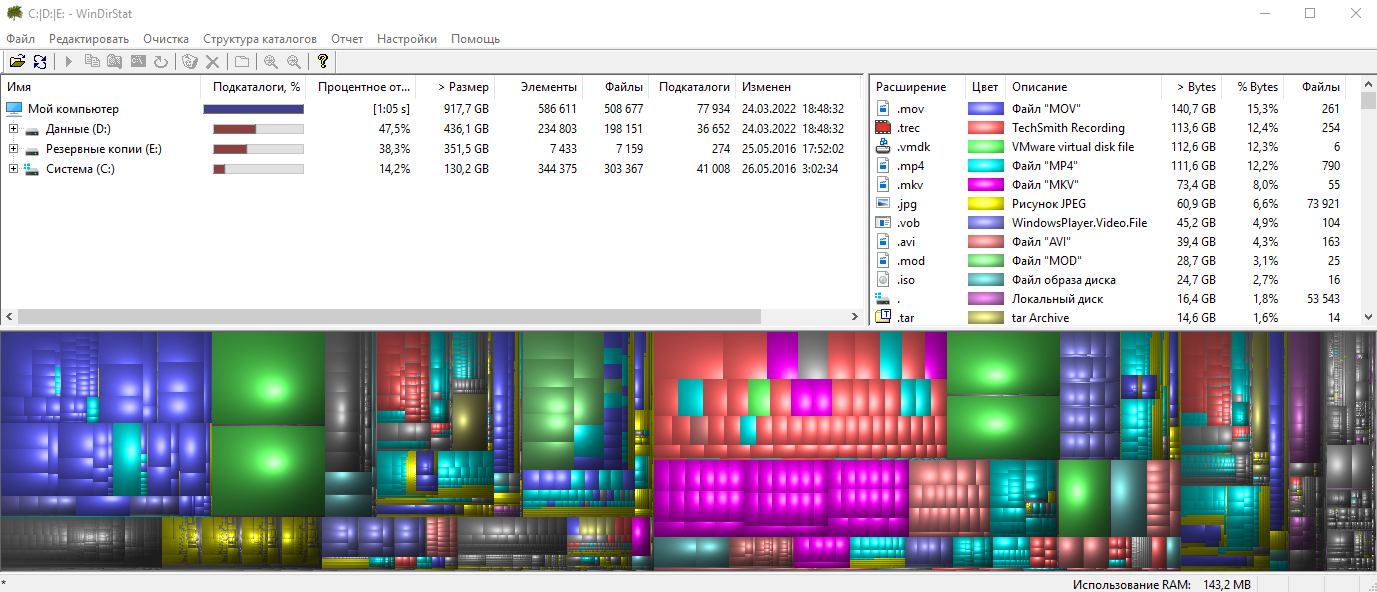
В столбце слева вверху отображаются непосредственно ваши выбранные разделы жёсткого диска с указанием занятого пространства на каждом, количества папок, файлов и др. информации. В столбце справа имеется информация о типах файлов, которые у вас имеются на компьютере также с указанием общего размера по каждому типу файлов, их количеству и при этом за каждым типом файлов закреплён определённый цвет. Эти цвета позволяют наглядно видеть в окне внизу, сколько места занимает тот или иной тип файла.
Анализ занимаегого объёма при помощи «дерева» файлов и папок
Рассмотрим для начала главное окне, т. е. расположенное слева вверху.
Здесь в основном имеет смысл обращать внимание на столбец «Размер», который упорядочивает изначально все ваши диски и папки в них по занимаемому объёму на компьютере, в порядке убывания.
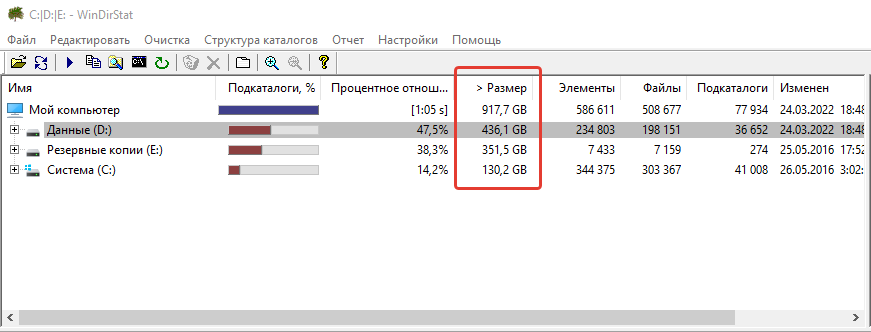
Например, в моём примере видно, что общее занятое место на всех дисках равно 917.7 Гб. При этом больше всего занято места на диске «D»: 436.1 Гб. Это также видно по столбцу «Процентное отношение», т. е. столбец показывает, сколько место занято на том или ином диске от общего занятого пространства на всех.
Щёлкнув дважды по диску, мы открываем его содержимое подобно проводнику Windows.
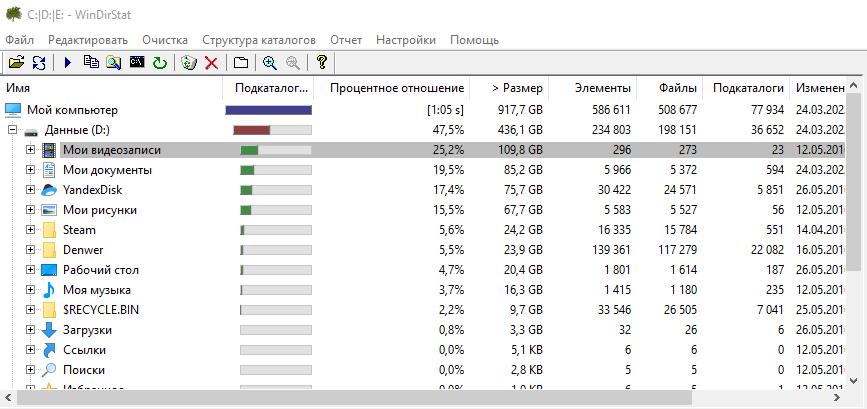
Здесь мы уже может с лёгкостью оценить, сколько места занимает каждая из папок внутри, ориентируясь на те же столбцы «Размер» и «Процентное отношение». И опять же, самые ёмкие папки будут располагаться изначально вверху для удобства. В самом низу, соответственно, будут папки, занимающие минимум свободного пространства на диске. Цветовое обозначение в столбце «Процентное отношение» означает количество имеющихся внутри данной папки. Чем больше полоска, тем больше папок внутри по отношению к кол-ву файлов. В принципе это не тот показатель, на котором стоит заострять внимание.
Если в какой-то папке имеются файлы, то они для удобства группируются как «Файлы», чтобы можно было открыть эту группу и сразу увидеть все файлы, а не в перемешку с папками.
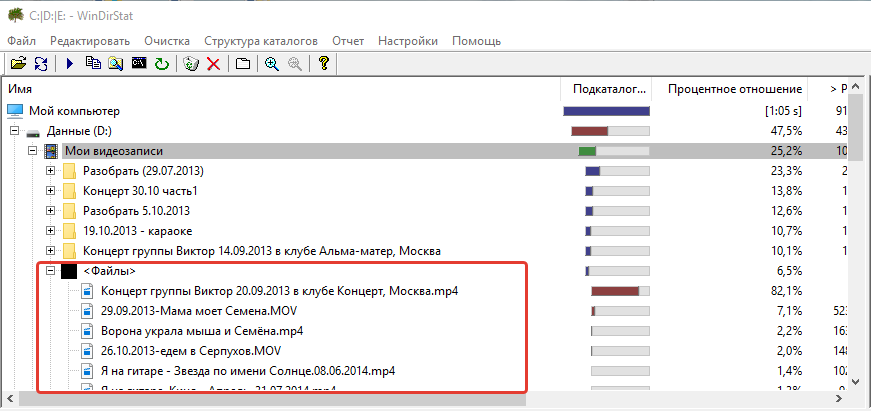
Таким образом вы можете быстро оценить, какие диски и папки на них отнимают больше всего места на компьютере и проанализировать, что именно в них находиться, а затем удалить то, что вам не нужно. Чтобы удалить какой-то элемент, нужно кликнуть по нему ПКМ и выбрать один из вариантов «Удалить (в корзину)», либо «Удалить (без возможности восстановления)».
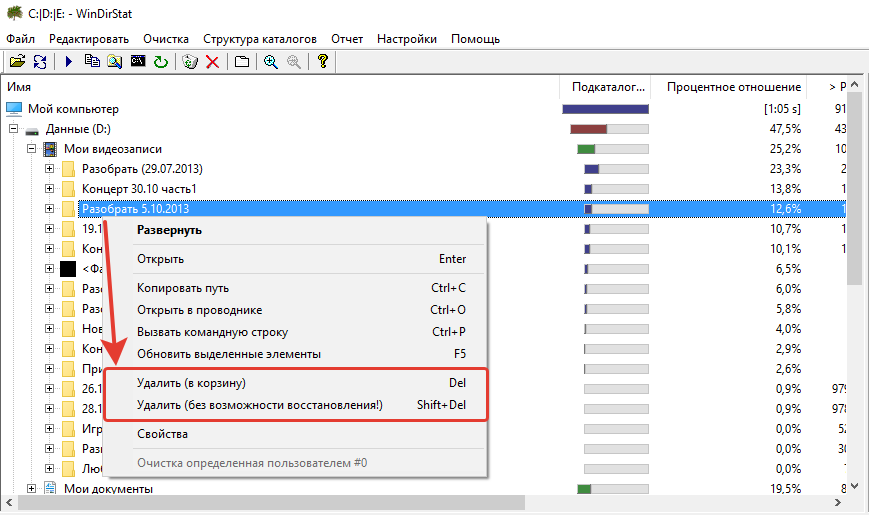
В первом случае элементы (папки или файлы) удаляются, как нам привычно, в корзину и оттуда затем их можно, если потребуется, вернуть. Во втором же случае файлы удаляются на всегда, минуя корзину и восстановить их получится, разве что специальными программами для восстановления, например «R.Saver» или платным аналогом «R-Studio».
Анализ занимаемого места файлами по их типам
При помощи окна справа в связке с окном внизу, вы можете наглядно оценить, какие именно файлы (по их типу) отнимают больше всего места на дисках. Типы файлов также будут упорядочены по занимаемому размеру в порядке убывания, т. е. вверху те файлы, которые занимают больше всего пространства. Правда здесь, чтобы ориентироваться, следует знать, что представляет собой каждый из перечисленных типов файлов, для чего он служит и какой программой открывается.
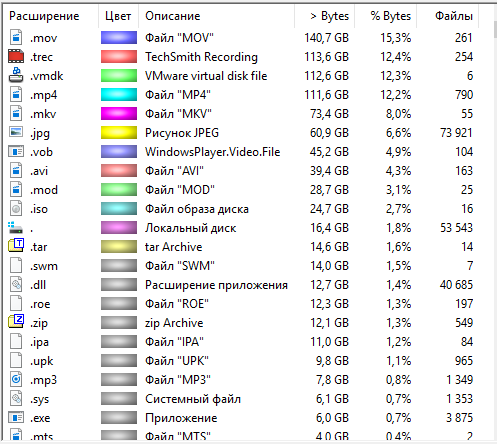
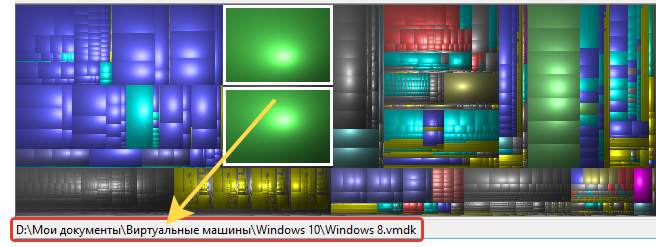
Например, на моём изображении видно, что больше всего места отнимают файлы формата «MOV» (.mov), затем файлы «TechSmith Recording» (.trec), «Vmware virtual disk file» (.vmdk) и т. д.
Файлы «.mov», к примеру — это один из форматов видеофайлов, которые могут получаться при записи видео с фотоаппарата или камеры. Открываются, в принципе, любым видео проигрывателем. Файлы «.trec» — это видео, записанные через программу Camtasia Studio (для записи с экрана, монтажа видео). «.vmdk» — это файлы виртуальных машин для бесплатной программы, позволяющей создавать и запускать виртуальные машины WMWare Player (или для платного аналога WMWare Workstation». Такие форматы новичкам, веротяно, не известны, но зато большинство понимает, к примеру, что за форматы такие «JPG» (изображения), «AVI» (видео), «MP3» (аудио).
Кликнув по одному из форматов файлов, внизу в программе станет наглядно видно, как эти файлы распределены по жёстким дискам, какое их количество и общий объём по сравнению с другими. Для этого у каждого формата файла задан свой цвет. Например, справа я выбрал формат «.mov» (1). и внизу в графическом видео данные файлы стали подсвечиваться (2).
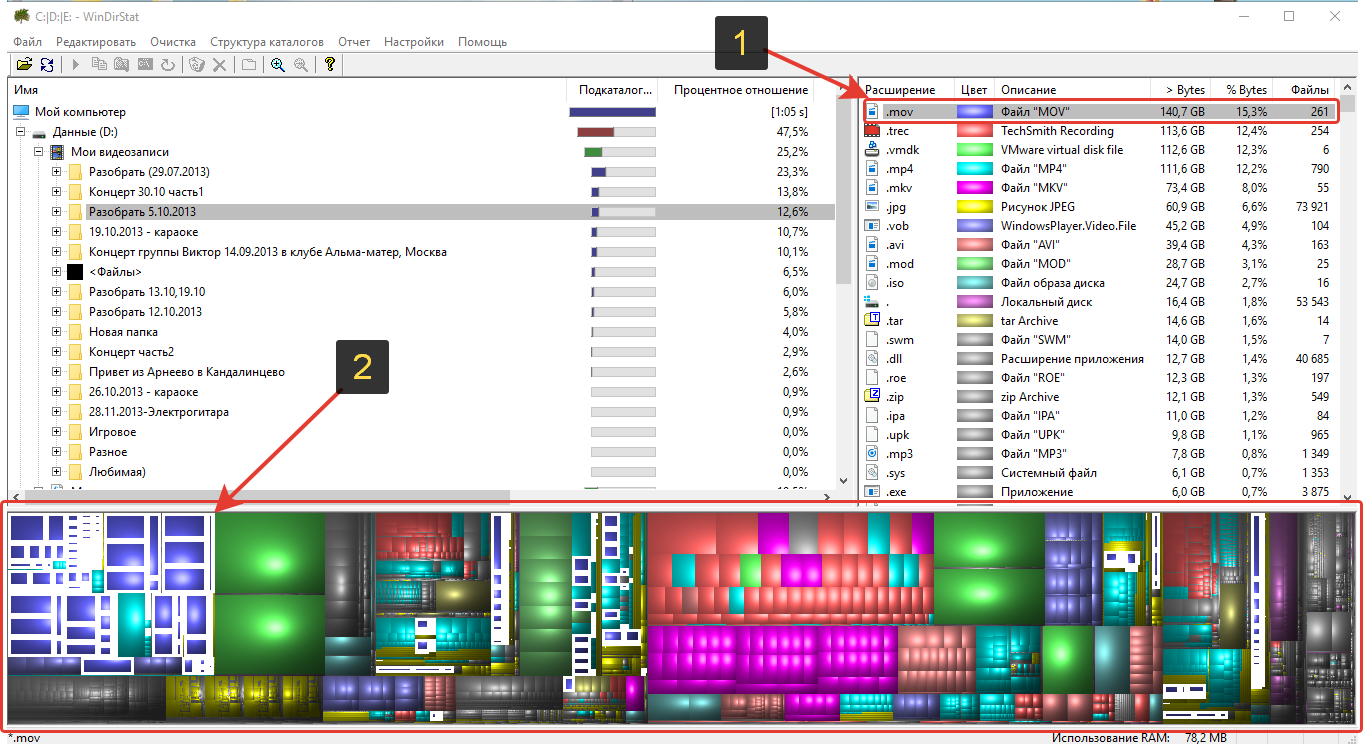
Наглядно видно, что таких файлов у меня на дисках много и все они такого среднего размера. Для сравнения: зелёным цветом отображаются гораздо большего размера квадратики, но зато их по количеству меньше.

Это файлы созданных виртуальных машин «.vmdk». Большие квадраты потому что эти файлы сами по себе намного больше по объёму, чем файлы видео «.mov» у меня на компьютере, но зато их меньше по количеству, поскольку число зелёных квадратов куда меньше.
Наведя на один из квадратов, внизу окна программы отобразится путь к файлу, который обозначается этим квадратом, что тоже очень удобно. К примеру, сразу видно, где расположены самые огромные файлы в моём компьютере.
Заключение
Я думаю, каждый, у кого очень активно используется компьютер, регулярно заполняется какими-то данными, оценит удобство анализа дисков через программу «WinDirStat». Как на крути, встроенные средства Windows такого удобного представления расположенных в компьютере файлов и папок, дать не могут. Зато через WinDirStat видно всё очень наглядно, а главное понятно буквально сразу, т. е. разбираться в программе долго не приходится. А самое классное то, что программу и настраивать не нужно, потому что по умолчанию всё настроено, на мой взгляд, идеально, т. е. отображается вся нужная информация.
Хорошего вам дня и отличного настроения! 🙂
Сделай репост – выиграй ноутбук!
Каждый месяц 1 числа iBook.pro разыгрывает подарки.
—> LENOVO или HP от 40-50 т.р., 8-16ГБ DDR4, SSD, экран 15.6″, Windows 10
4 комментария
Спасибо большое! Все просто и ясно. Мне отлично помогло разобраться в причинах перегруженности диска.
Автор: Владимир Белев
Рад помочь и спасибо за комментарий! 🙂
Спасибо огромное за инфу и ссылку на скачивание.
У меня папка с видео курсами очень много места занимает.
Источник
Масса системы. Центр масс.
Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему
.
В однородном поле тяжести, для которого , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:
,
,
. (1)
В полученные равенства входят только массы материальных точек (частиц), образующих тело, и координаты
этих точек. Следовательно, положение точки С (xC, yC, zC) действительно характеризует распределение масс в теле или в любой механической системе, если под
,
понимать соответственно массы и координаты точек этой системы.
Лекция «Тема 4. ВИДЫ ГОРЕНИЯ» также может быть Вам полезна.
Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.
Положение центра масс определяется его радиус-вектором
,
где — радиус-векторы точек, образующих систему.
Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.
Движение
системы, кроме действующих сил, зависит
также от её суммарной массы и распределения
масс. Масса
системы равна
арифметической сумме масс всех точек
или тел, образующих систему
.
В
однородном поле тяжести, для которого
,
вес любой частицы тела будет пропорционален
ее массе. Поэтому о распределении масс
в теле можно судить по положению его
центра тяжести. Преобразуем формулы,
определяющие координаты центра тяжести:
,
,
. (1)
В
полученные равенства входят только
массы
материальных
точек (частиц), образующих тело, и
координаты
этих
точек. Следовательно, положение
точки С (xC, yC, zC)
действительно характеризует
распределение масс в теле или в любой
механической системе, если
под
,
понимать
соответственно массы и координаты точек
этой системы.
Геометрическая
точка С,
координаты которой определяются
указанными формулами, называется
центром масс или центром
инерции системы.
Положение
центра масс определяется его
радиус-вектором
,
где
— радиус-векторы
точек, образующих систему.
Хотя
положение центра масс совпадает с
положением центра тяжести тела,
находящегося в однородном поле тяжести,
понятия эти не являются тождественными.
Понятие о центре тяжести, как о точке,
через которую проходит линия действия
равнодействующей сил тяжести, по
существу имеет смысл только для твердого
тела, находящегося в однородном поле
тяжести. Понятие же о центре масс, как
о характеристике распределения масс в
системе, имеет смысл для любой системы
материальных точек или тел, причем, это
понятие сохраняет свой смысл независимо
от того, находится ли данная система
под действием каких-нибудь сил или нет.
48. Теорема о движении центра масс.
В
ряде случаев для определения характера
движения системы (особенно твердого
тела), достаточно знать закон движения
ее центра масс. Например, если бросить
камень в цель, совсем не нужно знать как
он будет кувыркаться во время полета,
важно установить попадет он в цель или
нет. Для этого достаточно рассмотреть
движение какой-нибудь точки этого тела.
Чтобы
найти этот закон, обратимся к уравнениям
движения системы и сложим почленно их
левые и правые части. Тогда получим:
.
Преобразуем
левую часть равенства. Из формулы для
радиус-вектора центра масс имеем:
.
Беря
от обеих частей этого равенства вторую
производную по времени и замечая, что
производная от суммы равна сумме
производных, найдем:
или
.
где
—
ускорение центра масс системы. Так как
по свойству внутренних сил системы
, то,
подставляя все найденные значения,
получим окончательно:
(4)
Уравнение
и выражает теорему о движении центра
масс системы: произведение
массы системы на ускорение ее центра
масс равно геометрической сумме всех
действующих на систему внешних
сил. Сравнивая
с уравнением движения материальной
точки, получаем другое выражение
теоремы: центр
масс системы движется как материальная
точка, масса которой равна массе всей
системы и к которой приложены все внешние
силы, действующие на систему.
Проектируя
обе части равенства на
координатные оси, получим:
Эти
уравнения представляют собою дифференциальные
уравнения движения центра масс в
проекциях
на оси декартовой системы координат.
Значение
доказанной теоремы состоит в следующем.
1)
Теорема дает обоснование методам
динамики точки. Из уравнений видно,
что решения,
которые мы получаем, рассматривая
данное тело как материальную точку,
определяют закон движения центра масс
этого тела, т.е.
имеют вполне конкретный смысл.
В
частности, если тело движется поступательно,
то его движение полностью определяется
движением центра масс. Таким образом,
поступательно движущееся тело можно
всегда рассматривать как материальную
точку с массой, равной массе тела. В
остальных случаях тело можно
рассматривать как материальную точку
лишь тогда, когда практически для
определения положения тела достаточно
знать положение его центра масс.
2)
Теорема позволяет при определении закона
движения центра масс любой системы исключать
из рассмотрения все наперед неизвестные
внутренние силы. В этом состоит ее
практическая ценность.
Так
движение автомобиля по горизонтальной
плоскости может происходить только под
действием внешних сил, сил трения,
действующих на колеса со стороны дороги.
И торможение автомобиля тоже возможно
только этими силами, а не трением между
тормозными колодками и тормозным
барабаном. Если дорога гладкая, то как
бы не затормаживали колеса, они будут
скользить и не остановят автомобиль.
Или
после взрыва летящего снаряда (под
действием внутренних сил) части, осколки
его, разлетятся так, что центр масс их
будет двигаться по прежней траектории.
Теоремой
о движении центра масс механической
системы следует пользоваться для решения
задач механики, в которых требуется:
—
по силам, приложенным к механической
системе (чаще всего к твердому телу),
определить закон движения центра масс;
—
по заданному закону движения тел,
входящих в механическую систему, найти
реакции внешних связей;
—
по заданному взаимному движению тел,
входящих в механическую систему,
определить закон движения этих тел
относительно некоторой неподвижной
системы отсчета.
С
помощью этой теоремы можно составить
одно из уравнений движения механической
системы с несколькими степенями свободы.
При
решении задач часто используются
следствия из теоремы о движении центра
масс механической системы.
Следствие
1. Если главный вектор внешних сил,
приложенных к механической системе,
равен нулю, то центр масс системы
находится в покое или движется равномерно
и прямолинейно. Так
как ускорение центра масс равно нулю,
.
Следствие
2. Если
проекция главного вектора внешних сил
на какую-нибудь ось равна нулю, то центр
масс системы или не изменяет своего
положения относительно данной оси, или
движется относительно нее равномерно.
Например,
если на тело начнут действовать
две силы, образующие пару сил (рис.38), то
центр масс С его
будет двигаться по прежней траектории.
А само тело будет вращаться вокруг
центра масс. И неважно, где приложена
пара сил.
Кстати,
в статике мы доказывали, что действие
пары на тело не зависит от того, где она
приложена. Здесь мы показали, что вращение
тела будет вокруг центральной оси С.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
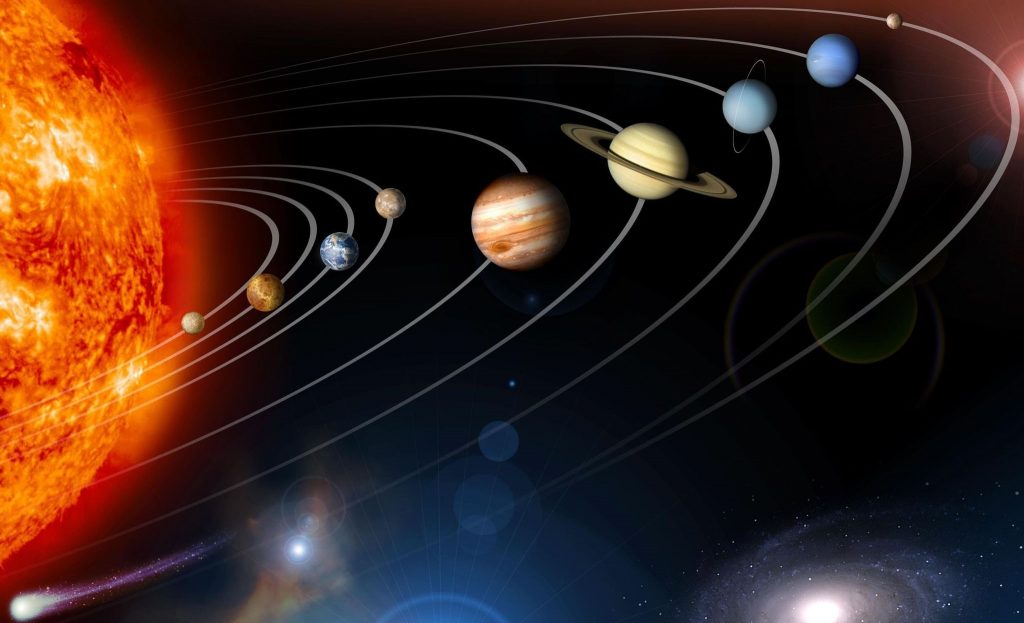
Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
Содержание:
- Динамика механической системы
- Геометрия масс
- Механическая система. Центр масс механической системы
- Порядок решения задач на определение центра масс механической системы
- Примеры решения задач на тему: Определение центра масс механической системы
- Моменты инерции твердого тела относительно оси
- Моменты инерции некоторых однородных тел
- Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
- Теорема о движении центра масс механической системы
- Закон сохранения движения центра масс
- Порядок решения задач на применение теоремы о движении центра масс
- Примеры решения задач на тему: Теорема о движении центра масс механической системы
- Теорема об изменении количества движения точки и механической системы
- Импульс силы
- Теорема об изменении количества движения точки и системы
- Закон сохранения количества движения системы
- Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
- Теорема об изменении момента количества движения точки и механической системы
- Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
- Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
- Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
- Теорема об изменении кинетической энергии механической системы
- Кинетическая энергия механической системы
- Определение кинетической энергии твердого тела в различных случаях его движения
- Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
- Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Динамика механической системы – изучает движение совокупности материальных точек и твердых тел, объединяемых общими законами.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика механической системы
В предыдущей главе рассматривались задачи, связанные с движением материальной точки, которая находится под действием приложенных к ней сил. Однако часто приходится встречаться с такими случаями, когда движение одной точки невозможно рассматривать изолированно от движения других материальных точек. Это заставляет нас перейти к изучению движения совокупности материальных точек, или механических систем.
В механике под механической системой материальных точек или тел имеют в виду такую их совокупность, в которой положение или движение каждой точки (или тела) зависит от положения или движения всех других.
Совокупность тел, между которыми отсутствуют силы взаимодействия и движение которых никаким образом не связано друг с другом, механическую систему не создают. Механические системы бывают свободными и несвободными.
Система материальных точек, движение которых не ограничено никакими связями, а определяется только действующими на эти точки силами, называется системой свободных точек.
Система материальных точек, движение которых ограничивается наложенными на точки связями, называется системой несвободных точек.
Решение задач динамики механической системы базируется на теоремах динамики и некоторых принципах, которые будут рассмотрены в данной главе.
Геометрия масс
Геометрия точки масс, в просторечии известная как точки масс , является проблемой геометрии — метод решения , который применяет физический принцип центра масс к геометрическим задачам, включающим треугольники и пересекающиеся чевианы . Все задачи, которые могут быть решены с использованием геометрии материальных точек, также могут быть решены с использованием аналогичных треугольников, векторов или соотношений площадей, но многие студенты предпочитают использовать массовые точки.
Механическая система. Центр масс механической системы
В механике под механической системой подразумевают совокупность взаимодействующих между собой материальных точек или тел.
Частным случаем механической системы является абсолютно твердое тело.
Массой механической системы называется сумма масс всех точек, входящих в систему:
где 


Центром масс (центром инерции) механической системы называется точка 

где 


Декартовы координаты центра масс системы материальных точек определяются по зависимостям:
Здесь 

Для твердого тела центр масс совпадает с центром тяжести.
Порядок решения задач на определение центра масс механической системы
Решение задач, в которых необходимо определить положение центра масс и уравнение его траектории, рекомендуется проводить в следующей последовательности:
Выбрать систему координат.
Записать координаты центров тяжести каждой из масс системы, выразив их в виде функций времени:
Определить координаты центра масс системы по формулам (5.1), при этом 
Для нахождения уравнений траектории центра масс надо с последних выражений (пункт 3) исключить время.
Примеры решения задач на тему: Определение центра масс механической системы
Задача № 1
Определить положение центра масс центробежного регулятора, изображенного на рис.5.2, если вес каждого из шаров 






Решение. Система координат, относительно которой необходимо определить положение центра масс, изображена на рис.5.2.
Для определения положения центра масс системы надо определить его координаты по формулам (5.1):
где




Следовательно,
Находим координаты центров масс:
пули 
пули 
муфты 
Тогда:
поскольку
Ответ:
Задача № 2
Найти уравнение движения центра масс шарнирного параллелограмма 


Решение. Начало системы координат свяжем с шарниром 





Поскольку звенья 1,2,3 параллелограмма однородны, то центры масс их лежат посередине звеньев (точки 
Из размеров звеньев вытекает:
Определим координаты центров масс звеньев механизма как функции угла поворота 
Для определения координат центра масс шарнирного параллелограмма 
Для определения уравнения траектории центра масс (точки 

Сложим, соответственно, левые и правые части этих уравнений:
Таким образом, траекторией центра масс шарнирного параллелограмма является окружность:
с радиусом, равным 

Ответ: 
Задача № 3
Определить траекторию центра масс механизма эллипсографа (рис.5.4), который состоит из муфт 






Считать, что линейка и кривошип есть однородные стержни, а муфты — точечные массы.
Решение. Механизм состоит из 4 подвижных звеньев. Для удобства решения задачи пронумеруем звенья соответственно рис.5.4.
Система координат, относительно которой будет определяться траектория центра масс механизма показана на рисунке.
Сначала определим координаты центров масс всех звеньев механизма:
Для определения координат центра масс механизма эллипсографа воспользуемся формулой (5.1):
Следовательно, координаты центра масс эллипсографа имеют значения:
Для нахождения уравнения траектории центра масс в явном виде необходимо из этих уравнений исключить угол 


Траекторией центра масс является окружность с центром в точке 

Ответ:
Задача № 4
Определить зависимость от угла поворота кривошипа 





Решение. Выберем систему координат 



Применяя формулу (5.1), получим:
где 

С рис.5.5 находим:
Масса всей системы в данном случае равна:
Подставляя в выражения (1) и (2) значения координат центров масс тел механической системы и величину массы системы 
Ответ:
Задача № 5
Определить уравнение траектории центра масс кулисного механизма (рис.5.6), если вес кривошипа 









Будем считать, что в начальный момент ползун 
Решение. Выберем оси декартовых координат, как показано на рисунке, где положение кулисного механизма соответствует моменту времени 
Для определения положения центра масс системы 


Поскольку механическая система состоит из трех тел — кривошипа 


Индекс 1 соответствует кривошипу, индекс 2 — ползуну 
Из рисунка видно:
Подставим значения 


Исключим время 
Для этого решим оба уравнения относительно 

Возведем эти уравнения к квадрату и добавим:
Таким образом, траекторией центра масс кулисного механизма является эллипс с полуосями 
Центр эллипса лежит на оси 

Ответ: 
Моменты инерции твердого тела относительно оси
Влияние собственных свойств тела на вращательное движение значительно сложнее, чем в поступательном движении.
Также как масса тела является мерой инертности тела при его поступательном движении, так и момент инерции тела относительно данной оси является мерой инертности тела при его вращательном движении.
Как мера инертности тела момент инерции входит во все формулы вращательного движения. Не зная момента инерции тела, не умея его определить, нельзя решать задачи, которые связаны с вращательным или сложным движением тела, частью которого является вращательное движение.
Момент инерции тела (системы) относительно оси, например 

Моментом инерции тела относительно оси, например 
Если тело сплошное, то под 

где 

Этот интеграл берется по всей массе тела. Очевидно, что величина момента инерции зависит от размеров и формы тела , а также от закона распределения массы в теле.
Момент инерции измеряется в системе СИ — в 

Для тел правильной геометрической формы определение моментов инерции делается с помощью интегрального вычисления. Если тело имеет неправильную форму, то момент инерции его определяется либо приблизительно, путем разбития тела на несколько тел, которые имеют правильную геометрическую форму, либо экспериментально.
Для однородного тела, при плотности 
где интеграл берется по всему объему тела.
Для однородной материальной поверхности:
где 
Для однородной материальной линии:
где 

Для одной материальной точки, которая находится на расстоянии 
Иногда при определении момента инерции тела пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси, например 

где 
Следовательно, радиус инерции определяет расстояние от оси 

Момент инерции системы относительно начала координат равен
Моменты инерции относительно координатных осей (осевые моменты) выражаются зависимостями:
Существует простая зависимость между моментами инерции тела относительно параллельных осей, одна из которых проходит через его центр масс (теорема Гюйгенса-Штейнера).
Момент инерции тела относительно любой оси равен моменту инерции тела относительно оси, проходящей через центр масс тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями:
где 


Из выражения (5.4) вытекает, что наименьшим момент инерции тела будет относительно той оси, которая проходит через центр его масс.
Моменты инерции некоторых однородных тел
| Форма тела. | Схема тела. | Момент инерции. |
| Тонкий прямолинейный стержень |  |
 |
| -„- |  |
 |
| Круглая пластинка малой толщины |  |
 |
| Кольцо (материальная окружность) |  |
 |
| Круглый цилиндр |  |
 |
| Прямоугольный параллелепипед |  |
 |
| Полый шар со стенками малой толщины |  |
 |
| Шар |  |
 |
Примеры решения задач на тему: Моменты инерции твердого тела относительно оси
Задача №1
Маятник, изображенный на рис. 5.7, состоит из тонкого однородного стержня длиной 


Определить момент инерции 


Решение. Маятник состоит из двух тел: стержня и диска, поэтому
где 


Момент инерции стержня равен (см. 5.5):
Момент инерции диска найдем по формуле (5.4):
где 



Итак
Пользуясь выражениями для моментов инерции стержня (2) и диска (3), найдем момент инерции маятника относительно оси 
После подстановки в выражение (4) числовых данных, получим:
Ответ:
Задача №2.
Определить момент инерции 


Решение. Для определения момента инерции стального вала относительно оси 
где 



Тогда
Ответ:
Задача № 3
Определить осевые моменты инерции 


Решение. Определим момент инерции пластинки относительно оси 


Момент инерции этой тонкой полоски относительно оси 
где 
Масса полоски равна:
где 

Тогда:
а момент инерции всей пластинки будет равен сумме моментов инерции всех полосок, на которые можно разбить пластинку:
При предельном переходе, то есть, когда
Итак,
Вычислим массу пластинки:
Таким образом
Момент инерции пластинки относительно оси 
Ответ:
Задача №4
Определить момент инерции относительно оси 


Решение. Выделим элементарный параллелепипед со сторонами основания 





Момент инерции элементарного параллелепипеда относительно оси 
где: 
Тогда,
а момент инерции всего параллелепипеда
При предельном переходе, то есть при 
Вычислим двойной интеграл:
Масса параллелепипеда:
Следовательно,
Ответ:
Задача №5
Определить момент инерции относительно оси 



Решение. Проведем на пластинке (рис.5.11) две прямые, параллельные оси 

Вычислим момент инерции относительно оси 
где 
Здесь 

Итак,
Из уравнения 
Таким образом
Момент инерции пластинки относительно оси 
Масса пластинки
где площадь пластинки
Тогда
Следовательно,
Ответ:
Задача №6
Определить для тонкого равнобедренного треугольника 



Решение. С серединой 




Для определения момента инерции треугольника относительно основания (относительно оси 


Момент инерции этой полоски относительно оси 
где 

Тогда момент инерции элементарной полоски относительно основания будет равен:
Найдем зависимость между координатой 




откуда
Подставив (2) у (1’), получим:
а момент инерции треугольника 
или
В интеграле (3) границы координаты 


Высчитаем интеграл (3):
Выразим момент инерции 


Преобразуем выражение (4):
или
Перейдем к определению момента инерции треугольника 

Поскольку у треугольника 


где 



Расчетная схема для определения момента инерции 
Выделим элементарную полоску на расстоянии 



Определим момент инерции этой полоски относительно оси 
где 
Определим зависимость между длиной полоски 




откуда
Подставив (6) у (5), получим:
Момент инерции треугольника 


или
Определим интеграл (7):
Окончательно,
Тогда, момент инерции треугольника 

Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 34.9, 34.12, 34.16 [2].
Теорема о движении центра масс механической системы
Силы, действующие на механическую систему, можно условно поделить на внешние и внутренние.
Силы, которые действуют на точки данной механической системы со стороны точек или тел, не входящих в эту систему, называются внешними.
Силы, действующие на точки механической системы со стороны точек данной системы, называются внутренними.
Внешние силы обозначаются верхним индексом 



Внутренние силы обладают следующими свойствами:
а) геометрическая сумма (главный вектор) внутренних сил равна нулю:
б) геометрическая сумма моментов (главный момент) всех внутренних сил относительно любого центра 
Теорема о движении центра масс механической системы формулируется следующим образом:
Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех внешних сил, действующих на систему.
где 


Из сравнения приведенной выше формулы со вторым законом динамики, который, как известно, записан для материальной точки:
можно сделать следующий вывод:
Центр масс механической системы движется как материальная точка, в которой сосредоточено массу всей системы и к которой приложены те же внешние силы, действующие на систему.
Теорема о движении центра масс системы, если ее записать в проекциях на оси декартовой системы координат, имеет вид:
где 
Из приведенных уравнений следует, что внутренние силы непосредственно не влияют на движение центра масс. Теорема позволяет исключить из рассмотрения все ранее неизвестные внутренние силы.
Задачи динамики поступательного движения твердого тела решаются с помощью теоремы о движении центра масс системы материальных точек.
Действительно, применив эту теорему, мы определим уравнение траектории, скорость и ускорение центра тяжести твердого тела. При поступательном движении твердого тела траектории всех его точек одинаковы, одинаковы и их скорости и ускорения.
Закон сохранения движения центра масс
Из теоремы о движении центра масс вытекает несколько следствий:
а) если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.
Пусть 


Если изначально центр масс был в покое, то он и останется в покое. Если же начальная скорость не равна нулю, то центр масс движется прямолинейно и равномерно с этой скоростью;
б) если геометрическая сумма внешних сил, действующих на систему, не равна нулю, но сумма их проекций на какую-нибудь ось (например, ось 
Если 


Если при этом равна нулю начальная скорость, то есть 

Таким образом видим, что в этом случае координата центра масс 
При 

Все эти результаты выражают законы сохранения движения центра масс системы.
Порядок решения задач на применение теоремы о движении центра масс
Рекомендуется такая последовательность решения задач:
Изобразить на рисунке все внешние силы, действующие на систему;
Выбрать систему координат;
Записать теорему о движении центра масс в векторной форме;
Спроектировать это векторное уравнение на оси координат;
Высчитать суммы проекций всех внешних сил на оси координат и подставить их в проекции уравнения движения;
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема о движении центра масс механической системы
Задача № 1
Определить главный вектор внешних сил, действующих на колесо весом 


Решение. Покажем внешние силы, которые действуют на колесо: силу тяжести 


Запишем теорему о движении центра масс в векторной форме:
Выбираем систему координат 


Поскольку 



Найдем проекцию ускорения центра масс на ось 
Итак,
Ответ:
Задача №2
Колесо весом 



Определить скорость центра масс колеса, если в начальный момент оно находилось в покое. Коэффициент трения скольжения равен 
Решение. На колесо действуют внешние силы: 




Запишем теорему о движении центра масс колеса в векторной форме:
где 
Спроектируем это уравнение на оси координат 
Во время движения колеса 

Поскольку при качении колеса со скольжением сила трения достигает своего максимального значения, то
Подставим (3) в первое из уравнений (1) и получим:
Поскольку
то
Согласно начальным условиям при 
Итак, закон изменения скорости центра масс колеса 
Ответ:
Задача №3
На однородную призму 



Определить длину 



Решение. Рассмотрим движение механической системы, состоящей из 2-х призм 



Для решения этой задачи применим теорему о движении центра масс.
На систему действуют внешние силы: тяжести 




Таким образом, все внешние силы системы вертикальны. Внутренние силы системы (давление призмы 



Введем систему координат 


Поскольку внешние силы перпендикулярны оси 
Тогда
где 
В начальный момент времени система находилась в состоянии покоя, то есть скорость центра масс 
Из этого следует, что 
Запишем выражение для определения координаты центра масс в начале движения:
где 



Выражение для определения координаты центра масс системы, когда призма 

где 



Поскольку 
или
Перепишем это уравнение следующим образом:
Найдем перемещение центров масс призм 

Присутствие слагаемого (



Подставим значение перемещений в уравнение (1):

Решим это уравнение относительно 

Ответ:
Задача №4
Три груза (рис.6.4), весом 









Решение. Изобразим все внешние силы, которые приложены к материальной системе, состоящей из пирамиды и трех грузов (рис.6.4). Внешними силами являются: 


горизонтальной плоскости. Направим ось 
Поскольку все внешние силы перпендикулярны оси 
Следовательно,
тогда
В начальный момент времени система была в состоянии покоя, то есть 
Поскольку
то
Таким образом, абсцисса центра масс системы не зависит от перемещений грузов, входящих в систему, и остается неизменной относительно неподвижной системы координат 
Запишем выражение для определения 
где 

Если груз 1 опустится на величину 









Грузы 1,2 и 3 вместе с пирамидой также переместятся влево на расстояние 
Запишем выражение для определения положения абсциссы центра масс для нового положения системы:
Поскольку 
После приведения подобных получим:
или
Окончательно
После подстановки числовых величин, получим:
Ответ:
Задача № 5
Электрический двигатель весом 
На валу электродвигателя (рис.6.5) под прямым углом закреплен одним концом однородный стержень 





Определить:
Закон горизонтального движения электродвигателя;
Угловую скорость вала электродвигателя, при которой электродвигатель будет «подскакивать» над фундаментом;
Наибольшее горизонтальное усилие 
Решение. Будем рассматривать электромотор, стержень и груз как одну механическую систему. Внешними силами, которые действуют на эту систему, являются: сила тяжести электродвигателя 




Начало неподвижной системы координат возьмем в точке 
Поскольку проекция на ось 

где 
В нашем случае 
Тогда дифференциальное уравнение движения центра масс (1) приводится к виду:
откуда
Предполагая, что в начальный момент скорость центра масс системы равна нулю, то есть, при пуске электродвигателя он был неподвижным, получим
Следовательно, 

Поскольку в начальный момент времени центр масс системы находится на оси 

При вращении стержня координаты центров масс электрического двигателя, стержня и груза 
Предположим, что в некоторый момент времени 




Поскольку все время 
где 

Тогда
откуда
и, следовательно:
Таким образом, центр электродвигателя совершает гармонические колебания вдоль оси 
и периодом
Определим угловую скорость вала, при которой электродвигатель будет «подскакивать» над фундаментом.
Для этого составим дифференциальное уравнение движения центра масс системы вдоль оси 
или
где 
Значение 
поскольку
Последнее уравнение перепишем в виде:
Возьмем из обеих частей равенства вторую производную по времени
Из уравнений (2) и (3) вытекает, что
итак,
Минимальное значение реакции фундамента будет при 
Если 
откуда
В завершение определим наибольшее горизонтальное усилие 
На рис.6.5 штрих-пунктирными линиями показаны оси болтов и горизонтальные реакции болтов 

В этом случае дифференциальное уравнение движения центра масс системы вдоль оси 
Значение 
или
Тогда
При этом уравнение (4) принимает вид:
Из последнего уравнения выходит:
Таким образом, максимальное горизонтальное усилие, действующее на болты, будет при 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 35.1; 35.6; 35.10; 35.20 [2].
Теорема об изменении количества движения точки и механической системы
Теорема об изменении количества движения (импульса) системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает количество движения с импульсом внешних сил, действующих на тела, составляющие систему.
Импульс силы
Для характеристики действия силы за некоторый промежуток времени вводится понятие импульса силы.
Если сила 

Направление импульса силы 

Единица измерения импульса в системе СИ — 

Если сила 

Импульс силы — сложная физическая величина, которая одновременно учитывает влияние модуля, направления и времени действия силы на изменение состояния движения тела.
Модуль импульса силы можно определить через его проекции на оси координат:
где 

Углы между вектором 
Теорема об изменении количества движения точки и системы
Одной из мер движения точки является количество ее движения.
Количеством движения точки называется вектор 



Понятие количества движения было введено в механику Декартом и положено в основу механики Ньютоном.
Единица измерения количества движения в системе СИ — 

Если спроектировать вектор количества движения на оси координат, то ее проекции определяются следующим образом:
Теорема об изменении количества движения точки в дифференциальной форме имеет вид:
Производная по времени от количества движения материальной точки равна геометрической сумме всех сил, действующих на эту точку.
Теорема об изменении количества движения точки в интегральной форме:
Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех сил, которые приложены к точке.
Векторному уравнению (7.1) соответствуют три уравнения в проекциях на оси координат:
Большинство практических задач решается с использованием выражения (7.2).
Количеством движения механической системы называется векторная величина 
Найти 
Замыкающая сторона векторного многоугольника будет представлять собой вектор 
Величина 

Формулу (7.3) можно записать в виде:
где 

Из этой формулы следует, что количество движения системы равно нулю, когда скорость центра масс равна нулю. Например, если тело вращается вокруг неподвижной оси, которая проходит через его центр масс, то количество движения тела равно нулю.
В случае, когда колесо катится, вектор 
Теорема об изменении количества движения системы в дифференциальной форме выразится формулой:
где 
Производная по времени от количества движения механической системы равна геометрической сумме всех действующих на точки системы внешних сил.
В проекциях на оси координат уравнение (7.5) соответствует уравнениям:
В интегральной форме теорема об изменении количества движения системы имеет вид:
где 

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, которые действуют на систему за тот же промежуток времени.
Векторному уравнению (7.7) соответствуют три уравнения в проекциях на оси координат:
Практическая ценность теоремы заключается в том, что она позволяет исключить из рассматривания неизвестные внутренние силы.
Закон сохранения количества движения системы
Выводы из теоремы об изменении количества движения системы, которые еще имеют название законов сохранения количества движения:
1. Если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы не меняется:
если
то 
2. Если сумма проекций внешних сил на какую-либо ось, например 
если
то 
Эти результаты выражают законы сохранения количества движения системы. Из них вытекает, что внутренние силы не могут изменить количество движения системы.
Порядок решения задач на применение теоремы об изменении количества движения точки и механической системы
Для материальной точки:
Изобразить на рисунке все силы, приложенные к материальной точке, то есть активные силы и реакции связей.
Выбрать систему координат.
Записать теорему об изменении количества движения точки в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Для механической системы:
Изобразить на рисунке все внешние силы.
Выбрать систему координат.
Записать теорему об изменении количества движения системы в векторной форме.
Спроектировать это векторное уравнение на оси выбранной системы координат.
Решить полученные уравнения и определить искомые величины.
Примеры решения задач на тему: Теорема об изменении количества движения точки и механической системы
Задача № 1
Железнодорожный поезд движется по горизонтальному и прямолинейному участку пути (рис.7.2). Во время торможения до полной остановки развивается сила сопротивления, равная 

Определить время 

Решение. Изобразим силы, действующие на поезд во время торможения: сила тяжести поезда 


Выберем систему координат. Поскольку движение прямолинейное и горизонтальное, достаточно рассмотреть движение по направлению оси 
Запишем теорему об изменении количества движения поезда (рассматривая его как материальную точку) в интегральной форме:
где 





Спроектируем векторное уравнение (1) на ось 
Проекции импульсов сил 




Сила сопротивления 
Скорость в конце участка торможения равна нулю, то есть
Окончательно, уравнение импульсов (2) в проекции на ось 
или
откуда
С учетом числовых значений величин 

Путь торможения определим из формулы для равнопеременного движения:
В этом случае ускорение поезда определяется из формулы:
то есть,
Тогда
Ответ:
Задача № 2
По шероховатой наклонной плоскости, которая составляет с горизонтом угол 
Определить время 



Решение. Во время движения на тело действуют сила тяжести тела 


Направим ось 
Спроектируем ровность (1) на ось 
Проекция импульса нормальной реакции 



Учитывая, что во время движения сила тяжести 

Кроме того
Итак, уравнение импульса (2) примет вид:
Вычислим силу трения:
Тогда уравнение (3) примет вид:
или
откуда
Поскольку
то
Используя полученную зависимость, сначала подсчитаем ускорение тела, а после этого — время движения.
Поскольку
то

Из формулы 

Из этой формулы находим время движения 
Ответ:
Задача № 3
На полигоне пушка, которая наклонена под углом 



Определить скорость 
Решение. В задаче рассматривается движение материальной системы, состоящей из ствола и снаряда (рис.7.4).
На систему действуют внешние силы: тяжести ствола 


Применим теорему об изменении количества движения системы:
где 




Ось 


Спроектируем уравнение (1) на ось 
Поскольку проекции сил 





Таким образом, проекция количества движения системы на ось 
В начальный момент времени (до выстрела) снаряд и ствол были неподвижны, следовательно, их количества движения равнялись нулю и
В момент вылета снаряда проекция количества движения системы на ось равна:
или
Поскольку
то
откуда

С учетом числовых значений:
Знак минус показывает, что скорость ствола направлена в сторону, противоположную скорости снаряда.
Ответ:
Задача № 4
Буксирный пароход весом 


Определить общую скорость парохода и баржи 




Решение. Для определения скорости 
На систему, которая состоит из парохода и баржи, действуют внешние силы: силы тяжести 





Внутренняя сила — натяжение буксирного каната 
Ось 
Запишем теорему об изменении количества движения данной системы в интегральной форме:
где 


Спроектируем уравнение (1) на ось 
Поскольку по условиям 

Кроме того, проекции на ось 




Подсчитаем количество движения парохода и баржи в начальный момент времени, когда скорость парохода равна 

Совместимое движение парохода и баржи происходит с одинаковой скоростью 
Поскольку
то
Отсюда имеем
Ответ:
Задача № 5
Механическая система состоит из грузов 1 и 2 массами 















Определить зависимость 
Решение. Рассмотрим механическую систему в произвольном положении (рис.7.6).
Изобразим все внешние силы, действующие на систему: силы тяжести 



Проведем координатные оси 



Определим 


Поскольку все внешние силы, действующие на систему, вертикальны, то 


где 


Определим количества движения 

где
Выразим координаты 


С рис.7.6 видно, что в произвольный момент времени абсцисса первого груза
а абсцисса второго груза
Тогда
Подставляя полученные выражения для 

Поскольку 
В соответствии с (1), выражения (2) и (4) равны, то есть:
Отсюда окончательно получим:
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 28.3; 28.7; 36.9; 36.11; 36.16 [2].
Теорема об изменении момента количества движения точки и механической системы
Наряду с количеством движения, как векторной меры поступательного движения, для вращательного движения можно ввести момент количества движения.
Для материальной точки массой 



Вектор момента количества движения прикладывается в точке 
Кинетическим моментом 
Подобно тому, как количество движения системы является характеристикой поступательного движения, кинетический момент является характеристикой вращательного движения системы.
Кинетический момент твердого тела, которое вращается относительно оси 

Производная по времени от момента количества движения точки, взятого относительно любого неподвижного центра 
Спроектировав это уравнение на оси координат, получим:
Если рассматривать движение системы, на которую действуют внешние 

Проектируя обе части уравнения на неподвижные оси 
Теорема об изменении кинетического момента позволяет изучать вращательное движение твердого тела вокруг оси и точки, или вращательную часть движения тела в общем случае движения свободного твердого тела.
Практическая ценность теоремы заключается еще и в том, что она позволяет при изучении движения системы исключить из рассмотрения неизвестные внутренние силы.
Из теорем об изменении кинетического момента системы (8.7)-(8.8) вытекают важные выводы:
Если сумма моментов относительно центра 

если 

Если сумма моментов всех внешних сил, действующих на систему, относительно некоторой оси, например 
если 

Дифференциальное уравнение вращательного движения тела вокруг неподвижной оси
Кинетический момент тела относительно оси вращения по уравнению (8.4) , если ось 
Следовательно,
Сумма моментов внешних сил 
Таким образом, дифференциальное уравнение вращательного движения тела имеет вид:
Из (8.9) следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение тела равно вращательному моменту
Это уравнение позволяет решать следующие задачи:
— если заданы уравнения вращения тела 

— если заданы внешние силы, приложенные к телу, начальные условия вращения 



— определить момент инерции тела 


Из уравнения 
1. Если 



2. Если 



Порядок решения задач на применение теоремы об изменении момента количества движения точки и механической системы
Задачи, которые относятся к этой теме, можно разделить на следующие четыре основных типа:
Вычисление кинетического момента.
Изучение движения конкретной точки механической системы, если эта точка участвует во вращательном движении системы.
Изучение вращательного движения твердого тела.
Изучение движения механической системы, в которую входят тела, совершающие как поступательные, так и вращательные движения.
Задачи первого типа могут быть решены с помощью общих формул (8.4), (8.5).
Порядок решения задач второго типа может быть следующим:
- Выбрать систему координат.
- Изобразить все внешние силы, приложенные к материальной точке; в случае произвольной точки к этим силам добавить реакции внешних связей.
- Записать в скалярной форме выражение теоремы об изменении момента количества движения точки.
- Высчитать сумму моментов сил, которые приложены к материальной точке.
- Определить количество движения материальной точки и его момент относительно осей.
- Подставить данные пунктов 4 и 5 в уравнения (8.6) теоремы об изменении момента количества движения материальной точки.
- Решить, в соответствии с условием, прямую или обратную задачу динамики точки.
При решении задач третьего типа сохранять рекомендации первых двух пунктов, а далее делать следующим образом:
- Записать дифференциальное уравнение вращательного движения тела вокруг неподвижной оси (8.9).
- Определить момент инерции твердого тела относительно неподвижной оси.
- Подсчитать сумму моментов всех внешних сил относительно оси вращения.
- Величины, полученные в п. п. 4 и 5, подставить в уравнение (8.9).
- Записать начальные условия.
- Решить уравнение п. 6 в зависимости от условия, как прямую или обратную задачу.
При решении задач четвертого типа необходимо предварительно расчленить заданную систему на отдельные твердые тела, и к каждому из них, в зависимости от характера движения, применить одну из теорем: об изменении количества движения – в случае поступательного движения тел расчлененной системы; об изменении кинетического момента – при наличии тел, которые совершают вращательные движения.
Примеры решения задач на тему: Теорема об изменении момента количества движения точки и механической системы
Задача №1
Однородный круглый диск весом 

Определить главный момент количеств движения диска 

Решение. Главный момент количеств движения системы (кинетический момент) относительно оси вращения равен (8.6):
где 

В данном случае кинетический момент относительно оси, проходящей через центр диска 
Ответ:
Задача №2
Во время вращения барабана 1 весом 



Определить главный момент количества движения (кинетический момент) системы относительно оси 

Решение. В состав механической системы входят два твердых тела: барабан 1 и груз 2.
Следовательно, кинетический момент системы равен:
где 


Кинетический момент барабана равен (8.5):
где
тогда
Главный момент количества движения груза, который движется поступательно, определяется как момент количества движения материальной точки, то есть:
поскольку
то
Окончательно
Ответ:
Задача №3
Шарик 








Определить, через какой промежуток времени 

Решение. Ось 







Все силы указаны на рисунках, направления сил 

Запишем дифференциальное уравнение вращательного движения шарика относительно оси 
где момент инерции шарика
Поскольку момент силы тяжести 






Следовательно, дифференциальное уравнение вращательного движения имеет вид:
или
Разделим переменные и проинтегрируем:
Произвольную постоянную 

Следовательно,
Высчитаем, через какой промежуток времени 

Откуда:
Для определения числа оборотов, которые сделает стержень с шариком за промежуток времени 


Следовательно,
Разделим переменные и проинтегрируем это дифференциальное уравнение:
Произвольную постоянную 

Итак закон изменения угла поворота 
или
При 

Поскольку за 1 оборот шарик обернется на 

Ответ:
Задача №4
Для определения момента трения в цапфах, на вал насажен маховик весом 



Определить момент трения 
Решение. Направим ось 




Запишем теорему об изменении кинетического момента относительно оси вращения:
Поскольку мы рассматриваем вращение твердого тела, то
Найдем вращательный момент внешних сил относительно оси вращения 




Таким образом
Высчитаем величины, которые входят в это уравнение:
где 


Поскольку 
С учетом значений 

Ответ:
Задача №5
Однородный цилиндр (рис.8.6) радиусом 


Определить, как изменится угловая скорость 

Решение. На цилиндр действует сила тяжести 
Запишем теорему об изменении кинетического момента цилиндра:
где 

Поскольку сила 

Итак, 
где 



По теореме Гюйгенса-Штейнера
где 
Из формулы (1) получим:
Вычислим 

Следовательно,
Угловая скорость уменьшилась в три раза, поскольку в три раза увеличился момент инерции.
Ответ:
Задача №6
Молотильный барабан начинает вращаться из состояния покоя (
Определить, пренебрегая трением, частоту вращения барабана после того, как он начнет вращаться и сделает 
Решение. Для определения угловой скорости барабана воспользуемся формулой:
где 


Из (1) вытекает:

Следовательно,
Таким образом, для определения угловой скорости необходимо знать угловое ускорение 
Для определения 
где 
На барабан действуют следующие внешние нагрузки: 





С учетом действующих сил уравнение (2) будет иметь вид:
При этом 




Тогда,
Ответ:
Задача №7
Груз весом 
Определить угловое ускорение барабана 


Решение. Для определения углового ускорения 


Если применить теорему об изменении кинетического момента системы относительно оси, то натяжение каната, являющегося внутренней силой, в уравнение не войдет.
Относительно оси, которая проходит через точку 
На систему действуют следующие внешние силы: 



Силы 




Итак,
Определим кинетический момент системы относительно оси вращения 
где 

где 

поскольку
Тогда кинетический момент системы равен:
Подставим полученные результаты в уравнение (1):
Знак момента силы 

Решаем уравнение (2) и определяем угловое ускорение 
Выносим из под знака дифференциала в левой части уравнения (2) постоянные величины:
или
С учетом числовых значений угловое ускорение 
Ответ:
Теорема об изменении кинетической энергии механической системы
Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему.
Кинетическая энергия механической системы
Кинетической энергией 
Кинетической энергией 
Кинетическая энергия системы не зависит от направлений скоростей точек.
Кинетическая энергия может равняться нулю, если скорости всех точек системы равны нулю.
Кинетическая энергия системы характеризует и поступательное, и вращательное движения системы. Поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Единицей кинетической энергии в системе СИ является Джоуль (Дж).
Определение кинетической энергии твердого тела в различных случаях его движения
Поступательное движение твердого тела:
При поступательном движении твердого тела скорости всех его точек (в том числе скорость 

Кинетическая энергия твердого тела при поступательном движении равна половине произведения массы тела 
Вращательное движение твердого тела:
Скорость любой точки твердого тела, которое вращается с угловой скоростью 
где 
Тогда кинетическая энергия тела определяется согласно зависимости:
Поскольку
то
Следовательно кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости тела.
Плоскопараллельное движение твердого тела:
При плоскопараллельном движении скорости всех точек тела в каждый момент времени распределены так, будто тело вращается вокруг оси, которая перпендикулярна плоскости движения и которая проходит через мгновенный центр скоростей 
В этом случае кинетическую энергию тела можно определить по формуле:
где 
Поскольку (согласно теореме Штейнера-Гюйгенса)
где 
Поскольку 
Таким образом,
в случае плоскопараллельного движения тела кинетическая энергия состоит из кинетических энергий поступательного движения вместе со скоростью центра масс и вращательного движения вокруг оси, которая проходит через центр масс перпендикулярно плоскости движения.
Теорема об изменении кинетической энергии механической системы:
Дифференциальная форма:
Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему:
Производная по времени от кинетической энергии механической системы равна сумме мощностей всех внешних и внутренних сил, действующих на систему:
Интегральная форма:
Изменение кинетической энергии механической системы при конечном перемещении ее из положения (1) в положение (2) равно сумме работ на этом перемещении всех внешних и внутренних сил, действующих на эту систему
Если механическая система неизменна, то сумма работ внутренних сил равна нулю и теорема запишется так:
Порядок решения задач на использование теоремы об изменении кинетической энергии механической системы
Решение задач с помощью теоремы об изменении кинетической энергии в интегральной форме рекомендуется проводить в следующей последовательности:
а) изобразить на рисунке все внешние силы системы;
б) высчитать сумму работ всех внешних сил на перемещении точек системы;
в) вычислить кинетическую энергию системы материальных точек в начальном и конечном ее состояниях;
г ) пользуясь результатами подсчетов по пунктам б) и в) записать теорему об изменении кинетической энергии механической системы и определить искомую величину.
Примеры решения задач на тему: Теорема об изменении кинетической энергии механической системы
Задача № 1
Механизм эллипсографа (рис.10.1) состоит из ползунов 









Определить кинетическую энергию механизма эллипсографа, полагая, что линейка 



Решение. Заданная механическая система состоит из четырех тел: кривошипа 1 и линейки 2, ползунов 3 и 4.
Кинетическая энергия всей системы равна:
где 


Кривошип 

Тогда
Линейка 2 движется плоскопараллельно. Ее кинетическая энергия равна
где 




Для определения угловой скорости 


С другой стороны, точка 
Тогда, учитывая, что 
Момент инерции линейки относительно оси 
С учетом полученных значений 
Подсчитаем кинетическую энергию ползунов 3 и 4, которые двигаются поступательно:

Скорости точек 
Тогда
Подставляя найденные выражения (2), (4), (5) в (1), получим:
Ответ:
Задача № 2
На рисунке 10.2 изображен подъемный механизм лебедки. Груз 






где 
Определить скорость груза 




Решение. Изобразим на рисунке все внешние силы, действующие на барабан 








Запишем теорему об изменении кинетической энергии системы:
где 





Поскольку в начальный момент времени система находилась в состоянии покоя, то
В связи с тем, что трос не растягивается и при движении системы находится в натянутом состоянии, сумма работ внутренних сил системы равна нулю, следовательно
При поднятии груза 

Поскольку точки приложения сил 

Работа силы 
Работа вращательного момента в случае, когда он не меняется
где 
Поскольку в нашем случае вращательный момент меняется, то его работа определится следующим образом:
Определим угол 



Следовательно,
Таким образом,
Перейдем к подсчету кинетической энергии системы в конечном положении:
где 





Груз 
Диск 
где 

Поскольку диск 

где 
Поскольку линейная скорость обода диска равна скорости груза, угловая скорость вращения 
Итак,
Кинетическая энергия барабана 
Поскольку масса барабана 
Угловую скорость барабана высчитаем из условия равенства линейных скоростей на ободах диска и барабана:
Откуда
Таким образом
Кинетическая энергия системы в конечном положении равна
Итак, теорема об изменении кинетической энергии системы имеет вид:
Решая это уравнение относительно 


Ответ:
Задача № 3
Груз 








Определить скорость груза 

В начальный момент система находилась в состоянии покоя.
Решение. Изобразим внешние силы, которые действуют на систему: силы тяжести 




Запишем теорему об изменении кинетической энергии системы:
В начальный момент времени система находилась в покое, следовательно, 
Сумма работ внешних сил при перемещении системы в конечное положение составляет:
Работа сил 

Итак,
Работа силы 


Работу силы тяжести 











Таким образом,
Груз 


Итак,
Вычислим кинетическую энергию системы в конечном положении:
Груз 
где 

Блок 
Кинетическая энергия поступательного движения блока 
Поскольку точка 




Тогда
Таким образом,
Кинетическая энергия вращательного движения блока 
где 



Тогда
Таким образом, кинетическая энергия блока 
Блок 
то есть
Груз 


Следовательно, кинетическая энергия системы 
Таким образом, теорема об изменении кинетической энергии системы имеет вид:
Находим скорость груза 

Ответ:
Задача № 4
Прямоугольная пластинка 






Определить, сколько оборотов сделает пластинка к тому мгновению, когда ее угловая скорость станет вдвое меньше начальной?
Решение. Поскольку силы сопротивления, приложенные к пластинке, не постоянные, а зависят от скорости, то для решения задачи воспользуемся теоремой об изменении кинетической энергии системы в дифференциальной форме:
Высчитаем дифференциал кинетической энергии пластинки. Поскольку пластинка вращается вокруг неподвижной оси, то ее кинетическая энергия равна:
откуда:
где 

Перейдем к определению суммы элементарных работ внешних сил, которые действуют на пластинку. Это такие силы (рис.10.4):
— сила тяжести пластинки 
— реакции в опорах 



— сила сопротивления воздуха 
Итак,
где 



Работы реакций 


Таким образом,
Для вычета работы сил сопротивления воспользуемся формулой для работы сил, которые приложены к вращающемуся твердому телу:
где 

Чтобы определить 


и
Следовательно,
или
и

Таким образом, уравнение (1) принимает вид:
Разделим переменные и проинтегрируем:
Момент инерции пластинки составляет:
Тогда
Откуда находим:
Число оборотов 
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки