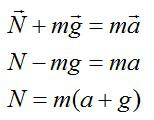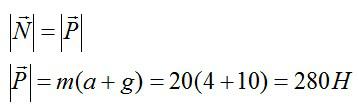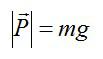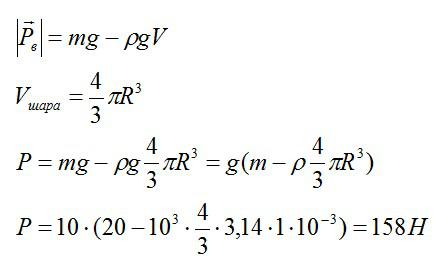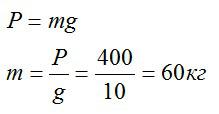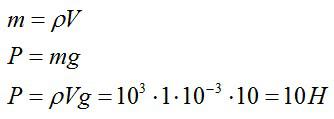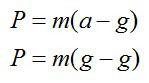Задачи на силу тяжести
и вес тела с решениями
Формулы, используемые на уроке «Задачи на силу тяжести и вес тела»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = F / g |
Вес тела |
P |
H |
P = m *g |
Сила тяжести |
Fтяж |
H |
Fтяж = mg |
Постоянная (сила тяжести, действующая на тело массой 1 кг) |
g = 10 H/кг |
H/кг |
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.
Задача № 2.
Какова масса свинцового шара, если он весит 600 Н?
Задача № 3.
Масса футбольного мяча 400 г. Вычислите вес мяча и силу тяжести, действующую на него.
Задача № 4.
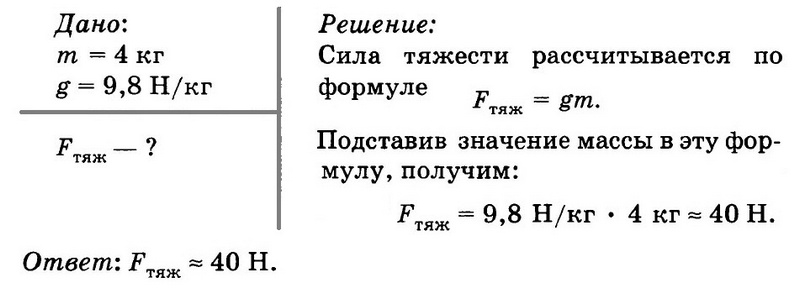
Чему равна сила тяжести тела, масса которого 4 кг?
Задача № 5.
Какой вес имеет вода объемом 3 дм3?
Задача № 6.
Подвешенная к потолку люстра действует на потолок с силой 49 Н. Какова масса люстры?
Задача № 7.
Изобразите графически силу тяжести и вес гири массой 1 кг.
Задача № 8.
Изобразите графически силы, действующие на шар, висящий на нити.
Решение. На шар, висящий на нити, действуют несколько сил: сила тяжести, приложенная к шару, сила упругости нити, приложенная к нити, и вес тела, приложенный к подвесу. Шар неподвижен, поэтому численно эти силы равны, следовательно, длина стрелок, изображающих силы, будет одинакова.
Задача № 9 (повышенной сложности).
Как изменяются сила тяжести, действующая на космонавта, и его вес, когда он перемещается с Земли на орбитальную станцию?
ОТВЕТ: сила тяжести — незначительно, а вес будет равен нулю.
РЕШЕНИЕ: Сила тяжести уменьшается незначительно (менее чем на 10% при высоте орбиты 300 км), так как она зависит только от массы тела и расстояния до центра Земли, которое при перемещении на орбитальную станцию изменяется всего на несколько процентов. Если бы не сила притяжения к Земле, орбитальная станция покинула бы околоземную орбиту и улетела далеко в космическое пространство. А вот вес космонавта в орбитальной станции равен нулю, поскольку космонавт вместе со станцией находится в состоянии свободного падения на Землю.
Краткая теория к задачам на силу тяжести и вес тела
Конспект урока «Задачи на силу тяжести и вес тела с решениями».
Следующая тема: «Задачи на давление твердых тел».
Сегодняшняя тема – задачи на вес и невесомость. Разберем несколько примеров и вопросов, которые нужно знать при решении таких задач.
Больше разнообразной и полезной информации для учащихся ежедневно ждет вас на нашем телеграм-канале.
Задачи на вес и невесомость с решениями
Задача №1. Задача на расчет веса тела, движущегося с ускорением
Условие
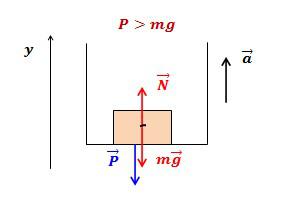
Груз массой 20 кг лежит на полу лифта, который движется вверх с ускорением а=4 м/с^2. Найти вес тела.
Решение
По второму закону Ньютона (в векторной форме и в проекции на ось y):
По третьему закону Ньютона:
Ответ: 280 Ньютонов
Задача №2. Задача на вычисление веса тела в жидкости
Условие
Шар радиусом 10 сантиметров имеет массу 20 килограмм. Сколько она будет весить в воде?
Решение
Вес шара в воздухе:
На тело, погруженное в жидкость, действует сила Архимеда:
Ответ: P=158 Н.
Задача №3. Нахождение веса тела при известной массе
Условие
Тело весит 400 Ньютонов. Какова его масса?
Решение
Ответ: 60 кг.
Задача №4. Вычисление веса жидкости
Условие
Какой вес имеет вода, полностью заполнившая литровую бутылку?
Решение
Зная объем воды и взяв из справочника ее плотность, вычислим массу воды:
Ответ: Р=10 Н.
Задача №5. Нахождение веса при свободном падении. Невесомость на Земле
Условие
Лифт с человеком срывается в шахте и свободно падает вниз, пока не сработает система безопасности. Чему в момент падения равен вес человека.
Решение
Лифт и человек движутся с ускорением a=g. Согласно второму и третьему законам Ньютона, вес человека в этом случае будет вычисляться по формуле:
Другими словами, человек никак не действует на опору, так она падает одновременно с ним. Типичный пример, когда вес равен нулю.
Ответ: P=0 Н.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Вопросы на тему «вес и невесомость»
Вопрос 1. В каком случае вес тела равен силе тяжести, действующей на него?
Ответ. Вес равен силе тяжести, если тело покоится или движется равномерно и прямолинейно (с нулевым ускорением).
Вопрос 2. В каких еще случаях можно испытывать состояние невесомости?
Ответ. Состояние невесомости также достигается при свободном падении.
Вопрос 3. Вредно ли длительное воздействие невесомости на здоровье?
Ответ. Длительное пребывание в невесомости влечет адаптивные изменения в сердечно-сосудистой и опорно-двигательной системах. Поэтому, по прибытии на Землю, космонавтам необходима реабилитация.
Вопрос 4. Где вес 100-киллограммового тела будет больше: на Земле, на Марсе или на Сатурне?
Ответ. Вес тела будет больше на Сатурне, так как там сильнее гравитационное взаимодействие.
Вопрос 5. От чего зависит вес тела?
Ответ. Вес зависит от ускорения, с которым движется тело, а также от физической среды, в которой тело находится. Например, в воде вес будет меньше, так как на тело действует выталкивающая сила Архимеда, которая частично компенсирует силу тяжести.
Все мы слышали слово «перегрузка». Перегрузка – противоположность невесомости. Это значит, что вес тела увеличивается из-за ускоренного движения опоры или подвеса.
Вес и невесомость: что есть что
Понятие веса широко используется в повседневной жизни. Но, решая задачи по физике, очень важно различать вес и массу.
Вес – это сила, к которой тело действует на опору или подвес вследствие притяжения к Земле.
Обозначается латинской буквой P, как и любая механическая сила, измеряется в Ньютонах. Вес – векторная физическая величина.
Не путайте вес с массой а также с силой тяжести! Это важно при решении задач.
Невесомость – отсутствие веса, то есть состояние тела, когда сила взаимодействия с опорой или подвесом отсутствует.
Космонавты на орбите испытывают состояние невесомости. Но не следует путать невесомость с отсутствием гравитации.
Примеры проявления невесомости:
- автомобиль подскакивает на ухабе и отрывается колесами от дороги;
- самолет проваливается в воздушную яму;
- десантник свободно падает, прежде чем раскрыть парашют;
- космонавт находится в космическом корабле, который движется по орбите с выключенным двигателем.
Нужна помощь в решении задач и выполнении других заданий? Обращайтесь в профессиональный студенческий сервис.
Загрузить PDF
Загрузить PDF
Вес — сила, с которой тело действует на опору (или другой вид крепления), возникающая в поле силы тяжести. Масса связана с энергией и импульсом тела и эквивалентна энергии его покоя. Масса не зависит от силы тяжести (точнее от ускорения свободного падения). Поэтому тело, на Земле имеющее массу 20 кг, на Луне будет иметь массу 20 кг, но совсем другой вес (потому что ускорение свободного падения на Луне в 6 раз меньше, чем на Земле).
-
1
Для вычисления веса используйте формулу
. Вес — это сила, с которой тело действует на опору, и его можно рассчитать, зная массу тела. В физике используется формула
.[1]
-
2
Определите массу тела. Так как ускорение свободного падения — это стандартная величина, то необходимо знать массу тела, чтобы найти его вес. Масса должна быть выражена в килограммах.
-
3
Узнайте величину ускорения свободного падения. На Земле, как уже было сказано выше, g = 9,8 м/с2. В других местах Вселенной эта величина меняется.[3]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
- Ускорение свободного падения на Солнце приблизительно равно 274,0 м/с2 (примерно в 28 раз больше, чем на Земле). Поэтому ваш вес на Солнце будет в 28 раз больше вашего земного веса (если, конечно, вы выживете на Солнце, что еще не факт!).[5]
- Ускорение свободного падения на поверхности Луны приблизительно равно 1,622 м/с2 (примерно в 6 раз меньше, чем на поверхности Земли). Поэтому ваш вес на Луне будет в 6 раз меньше вашего земного веса.[4]
-
4
Подставьте значения в формулу
. Теперь, когда вы знаете массу
и ускорение свободного падения
, подставьте их значения в формулу
. Так вы найдете вес тела (измеряется в ньютонах, Н).
Реклама
-
1
Задача № 1. Найдите вес тела массой 100 кг на поверхности Земли.
-
2
Задача № 2. Найдите вес тела массой 40 кг на поверхности Луны.
-
3
Задача № 3. Найдите массу тела, которое на поверхности Земли весит 549 Н.
Реклама
-
1
Не путайте массу и вес. Самая распространенная ошибка — перепутать вес и массу (что немудрено, ведь в повседневной жизни мы обычно называем массу весом). Но в физике все не так. Запомните, масса — это постоянное свойство объекта, то, сколько в нем вещества (килограммов), где бы он ни находился. Вес — это сила, с которой объект всеми своими килограммами давит на поверхность, и эта сила на разных небесных телах будет различной.
- Масса измеряется в килограммах или граммах. Запомните, что в этих словах, как и в слове «масса», есть буква «м».
-
2
Используйте правильные единицы измерения. В задачах по физике вес или силу измеряют в ньютонах (Н), ускорение свободного падения — в метрах на секунду в квадрате (м/с2), а массу — в килограммах (кг). Если для какой-либо из этих величин вы возьмете не ту единицу измерения, воспользоваться формулой будет нельзя. Если масса в условиях задачи указана в граммах или тоннах, не забудьте перевести ее в килограммы.
Реклама
Приложение: вес, выраженный в кгс
- Ньютон — это единица измерения силы в международной системе единиц СИ. Нередко сила выражается в килограмм-силах, или кгс (в системе единиц МКГСС). Эта единица очень удобна для сравнения весов на Земле и в космосе.
- 1 кгс = 9,8166 Н.
- Разделите вес, выраженный в ньютонах, на 9,80665.
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне.
- Международная система единиц СИ — система единиц физических величин, которая является наиболее широко используемой системой единиц в мире.
Советы
- Самая трудная задача — уяснить разницу между весом и массой, так как в повседневной жизни слова «вес» и «масса» используются как синонимы. Вес — это сила, измеряемая в ньютонах или килограмм-силах, а не в килограммах. Если вы обсуждаете ваш «вес» с врачом, то вы обсуждаете вашу массу.
- Ускорение свободного падения также может быть выражено в Н/кг. 1 Н/кг = 1 м/с2.
- Плечевые весы измеряют массу (в кг), в то время как весы, работа которых основана на сжатии или расширении пружины, измеряют вес (в кгс).
- Вес космонавта, который «весит» 101 кг (то есть его масса равна 101 кг), составляет 101,3 кгс на Северном полюсе и 16,5 кгс на Луне. На нейтронной звезде он будет весить еще больше, но он, вероятно, этого не заметит.
- Единица измерения «Ньютон» применяется намного чаще (чем удобная «кгс»), так как можно найти множество других величин, если сила измеряется в ньютонах.
Реклама
Предупреждения
- Выражение «атомный вес» не имеет ничего общего с весом атома, это масса. В современной науке оно заменено на выражение «атомная масса».
Реклама
Об этой статье
Эту страницу просматривали 113 770 раз.
Была ли эта статья полезной?
В окружающем нас мире на различные тела действуют множество сил. Вы уже познакомились с несколькими из них: весом тела, силой тяжести и силой упругости.
- Сила тяжести действует на все тела находящиеся на Земле и всегда направлена вертикально вниз:
$F_{тяж} = gm$,
где $m$ — масса тела, $g$ — ускорение свободного падения ($g = 9.8 frac{Н}{кг}$) - Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Вес тела приложен всегда к опоре или подвесу.
Если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно, то вес будет численно равен силе тяжести, действующей на это тело:
$P = F_{тяж}$ - Сила упругости возникает в теле в результате его деформации и стремится вернуть тело в исходное положение.
Закон Гука определяет зависимость этой силы от деформации тела:
$F_{упр} = k Delta l$,
где $k$ — коэффициент упругости (жесткость тела), $Delta l$ — изменение длины тела
В данном уроке мы рассмотрим задачи и их подробные решения, чтобы вы научились уверенно использовать новые понятия и вычислять изученные силы.
Задача №1
Вычислите силу тяжести, действующую на тело массой: $1.5 space кг$; $500 space г$; $2.5 space т$; $20 space г$.
Дано:
$m_1 = 1.5 space кг$
$m_2 = 500 space г$
$m_3 = 2.5 space т$
$m_4 = 20 space г$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_2 = 0.5 space кг$
$m_3 = 2500 space кг$
$m_4 = 0.02 space кг$
$F_{тяж1}, F_{тяж2}, F_{тяж3}, F_{тяж4} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле $F_{тяж} = gm$.
Для того чтобы получить верный ответ при таких простых вычислениях, всегда обращайте внимание на единицы измерения данных величин. Мы уже перевели единицы массы в $кг$. Если бы мы этого не сделали, то получили бы неверные ответы.
Рассчитаем силу тяжести, действующую на каждое тело:
- $F_{тяж1} = gm_1$,
$F_{тяж1} = 9.8 frac{Н}{кг} cdot 1.5 space кг = 14.7 space Н$ - $F_{тяж2} = gm_2$,
$F_{тяж2} = 9.8 frac{Н}{кг} cdot 0.5 space кг = 4.9 space Н$ - $F_{тяж3} = gm_3$,
$F_{тяж3} = 9.8 frac{Н}{кг} cdot 2500 space кг = 24 space 500 space Н = 24.5 space кН$ - $F_{тяж4} = gm_4$,
$F_{тяж4} = 9.8 frac{Н}{кг} cdot 0.02 space кг = 0.196 space Н$
Ответ: $F_{тяж1} = 14.7 space Н$, $F_{тяж2} = 4.9 space Н$, $F_{тяж3} = 24.5 space кН$, $F_{тяж1} = 0.196 space Н$.
Задача №2
Банка объемом $5 space дм^3$ заполнена водой. Какой вес имеет вода?
Дано:
$V = 5 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
Показать решение и ответ
Скрыть
Решение:
У нас в задаче не сказано, что банка каким-либо образом движется, поэтому мы будем считать, что она неподвижна. Если банка неподвижна, то и вода в ней тоже. Тогда вес воды мы можем рассчитать следующим способом:
$P = F_{тяж} = gm$.
Массу воды выразим через ее плотность и объем банки, который она заполняет:
$m = rho V$.
Подставим в нашу формулу и рассчитаем вес воды:
$P = g rho V$,
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 49 space Н$.
Ответ: $P = 49 space Н$.
Задача №3
Два кубика изготовлены из одного материала. Объем первого кубика в 12.2 раза больше, чем второго. На какой кубик действует большая сила тяжести и во сколько раз?
Дано:
$V_1 = 12.2 V_2$
$rho_1 = rho_2 = rho$
$frac{F_{тяж1}}{F_{тяж2}} — ?$
Показать решение и ответ
Скрыть
Решение:
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Выразим массу кубиков через их объем и плотность:
$m_1 = rho V_1 = rho 12.2 V_2$,
$m_2 = rho V_2$.
Мы видим, что масса первого кубика в 12.2 раза больше массы второго. Это означает, что и сила тяжести, действующая на него, будет в 12.2 раза больше, чем сила тяжести, действующая на второй кубик:
$frac{F_{тяж1}}{F_{тяж2}} = frac{rho 12.2 V_2}{rho V_2} = 12.2$.
Ответ: на первый, в 12.2 раза.
Задача №4
Какой вес имеет человек, имеющий массу $65 space кг$ и находящийся на Земле?
Дано:
$m = 65 space кг$
$g = 9.8 frac{Н}{кг}$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Если человек находится на Земле неподвижно или движется равномерно и прямолинейно, то его вес будет равен силе тяжести, действующей на него:
$P = F_{тяж} = gm$,
$P = 9.8 frac{Н}{кг} cdot 65 space кг = 637 space Н$.
Ответ: $P = 637 space Н$.
Задача №5
Стальная проволока удлиняется на $2 space мм$ при действии на нее груза в $320 space Н$. Вычислите коэффициент жесткости проволоки.
Дано:
$Delta l = 2 space мм$
$F_{упр} = 320 space Н$
СИ:
$Delta l = 2 cdot 10^{-3} space м$
$k — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда коэффициент жесткости проволоки и рассчитаем его:
$k = frac{F_{упр}}{Delta l}$,
$k = frac{320 space Н}{2 cdot 10^{-3} space м} = 160 cdot 10^3 frac{Н}{м} = 160 frac{кН}{м}$.
Ответ: $k = 160 frac{кН}{м}$.
Задача №6
Под действием груза в $200 space Н$ пружина динамометра удлинилась на $0.5 space см$. Каково удлинение пружины под действием груза в $700 space Н$?
Дано:
$Delta l_1 = 0.5 space см$
$F_{упр1} = 200 space Н$
$F_{упр2} = 700 space Н$
$Delta l_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Закон Гука описывает силу упругости, возникающую в пружине при ее удлинении:
$F_{упр1} = k Delta l_1$.
Выразим отсюда жесткость пружины и рассчитаем ее:
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{200 space Н}{0.5 space см} = 400 frac{Н}{см}$.
Используя тот же закон Гука рассчитаем удлинение пружины при другой силе упругости, измерений динамометром:
$F_{упр2} = k Delta l_2$,
$Delta l_2 = frac{F_{упр2}}{k}$,
$Delta l_2 = frac{700 space Н}{400 frac{Н}{см}} = 1.75 space см$.
Ответ: $Delta l_2 = 1.75 space см$.
Под действием силы давления вагона $50 space кН$ буферные пружины между вагонами сжимаются на $1 space см$. С какой силой давит вагон, если пружины сжались на $4 space см$?
Дано:
$F_{упр1} = 50 space кН$
$Delta l_1 = 1 space см$
$Delta l_2 = 4 space см$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Вследствие давления вагона, буферные пружины сжимаются и в них возникает сила упругости, равная $50 space кН$. Найдем жесткость этих пружин:
$F_{упр1} = k Delta l_1$,
$k = frac{F_{упр1}}{Delta l_1}$,
$k = frac{50 space кН}{1 space см} = 50 frac{кН}{см}$.
Рассчитаем силу, с которой давит вагон, (силу упругости, возникающую в пружинах под таким давлением), если изменение длины пружин составило $4 space см$:
$F_{упр2} = k Delta l_2$,
$F_{упр2} = 50 frac{кН}{см} cdot 4 space см = 200 space кН$.
Ответ: $F_{упр2} = 200 space кН$.
Задача №8
Пружина без нагрузки длиной $20 space см$ имеет коэффициент жесткости $20 frac{Н}{м}$. Какой станет длина растянутой пружины под действием силы $2 space Н$?
Дано:
$l = 20 space см$
$k = 20 frac{Н}{м}$
$F_{упр1} = 2 space Н$
СИ:
$l = 0.2 space м$
$F_{упр2} — ?$
Показать решение и ответ
Скрыть
Решение:
Для того чтобы узнать длину растянутой пружины, нам нужно вычислить ее изменение длины — длину, на которую она растянется:
$l_1 = l + Delta l$.
Если бы пружина сжималась под действием силы, то мы бы отнимали удлинение от первоначальной длины.
Рассчитаем удлинение пружины:
$F_{упр} = k Delta l$,
$Delta l = frac{F_{упр}}{k}$,
$Delta l = frac{2 space Н}{20 frac{Н}{м}} = 0.1 space м$.
Теперь рассчитаем длину растянутой пружины:
$l_1 = 0.2 space м + 0.1 space м = 0.3 space м = 30 space см$.
Ответ: $l_1 = 30 space см$.
Задача №9
На рисунке 1 изображен график зависимости модуля силы упругости от удлинения пружины. Найдите жесткость пружины.
Показать решение и ответ
Скрыть
Решение:
Для того чтобы определить коэффициент жесткости нам нужно силу упругости разделить на удлинение пружины:
$k = frac{F_{упр}}{Delta l}$.
Пользуясь графиком, вы можете выбрать любую удобную для вас точку. График демонстрирует линейную зависимость силы упругости от удлинения, коэффициент жесткости при этом — величина постоянная.
Мы выберем точку, в которой сила упругости равна $4 space Н$. Этому значению силы соответствует удлинение пружины, равное $0.4 space м$.
Рассчитаем коэффициент жесткости:
$k = frac{4 space Н}{0.4 space м} = 10 frac{Н}{м}$.
Ответ: $k = 10 frac{Н}{м}$.
Задача №10
Круглый стальной брус диаметром $2 space см$, длиной $16 space м$ растягивается силой, равной $36 space кН$. Найдите удлинение этого бруса.
Дано:
$d = 2 space см$
$l = 16 space м$
$F_{упр} = 36 space кН$
$E = 200 cdot 10^9 space Па$
$Delta l — ?$
Модуль упругости $E$ — это физическая величина, характеризующая способность материала сопротивляться растяжению или сжатию.
Модуль упругости является характеристикой материала, для стали он равен $200 cdot 10^9 space Па$.
Он связан с коэффициентом упругости $k$:
$k = frac{ES}{l}$,
где $S$ — площадь поперечного сечения,
$l$ — длина.
Показать решение и ответ
Скрыть
Решение:
Запишем закон Гука:
$F_{упр} = k Delta l$.
Выразим отсюда удлинение стального бруса:
$Delta l = frac{F_{упр}}{k}$.
Коэффициент упругости $k$ мы можем выразить через модуль упругости $E$:
$k = frac{ES}{l}$.
Площадь поперечного сечения $S$ выразим через диаметр:
$S = frac{pi d^2}{4}$.
Подставим эти формулы в закон Гука:
$Delta l = frac{F_{упр}}{frac{ES}{l}} = frac{F_{упр} l}{E frac{pi d^2}{4}} = frac{4 F_{упр} l}{E pi d^2}$.
Рассчитаем удлинение бруса:
$Delta l = frac{4 cdot 36 cdot 10^3 space Н cdot 16 space м}{200 cdot 10^9 space Па cdot 3.14 cdot 0.02^2 space м^2} = frac{2304 cdot Н cdot м}{251 space 200 space Н} approx 0.009 space м approx 9 space мм$.
Ответ: $Delta l = 9 space мм$.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вес тела
Вес тела — это сила, с которой тело действует на опору или подвес. Вес приложен не к телу, а к опоре или подвесу.
Рассмотрим два стандартных случая:
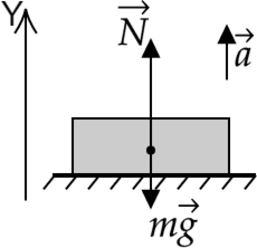
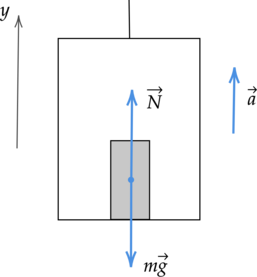
1) Тело массы (m) вместе с опорой движется с ускорением (a), направленным вертикально вверх. Найдите вес тела.
Направим ось (Y) вертикально вверх, как показано на рисунке.
Запишем второй закон Ньютона: [mvec{a}=mvec{g}+vec{N}] Перейдём к проекциям на ось (Y): [ma=N-mg] Отсюда [N = mg + ma = m(g + a)] Следовательно, вес тела находится по формуле [P = m(g + a)] Как видим, вес тела больше силы тяжести. Такое состояние называется перегрузкой.
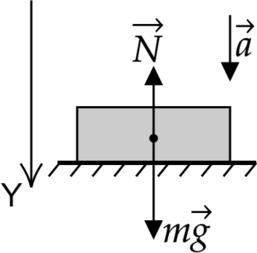
2) Тело массы m вместе с опорой движется с ускорением (displaystyle a<g), направленным вертикально вниз. Найдите вес тела.
Направим ось (Y) вертикально вниз, как показано на рисунке.
Запишем второй закон Ньютона: [mvec{a}=mvec{g}+vec{N}] Перейдём к проекциям на ось (Y): [ma=mg-N] Отсюда [N = mg — ma = m(g — a)] Следовательно, вес тела находится по формуле [P = m(g — a)] Как видим, вес тела меньше силы тяжести. При (displaystyle a=g) вес тела обращается в нуль. Такое состояние называется невесомостью, при нем тело не давит на опору или не растягивает подвес.
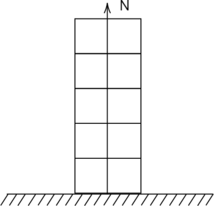
Пять одинаковых ящиков массой 10 кг, расположенных на горизонтальном столе, лежат друг на друге (см. рис.). На сколько изменится (в Н) сила реакции опоры, действующая на первый ящик со стороны стола, если снять три верхних ящика?
Вес тела – сила, с которой тело действует на опору или подвес. Исходя из третьего закона Ньютона: [vec{N}=-vec{P}] Условие равновесия: [N=5mg] Пусть масса одного ящика – m. Можно заменить 5 ящиков массой m на один большой ящик массой 5m, очевидно, что сила реакции опоры из-за этого не изменится. Так же после снятия трех ящиков остается груз массой 2m. Значит, [Delta P=5mg-2mg=3mg=3 cdot 10 cdot 10 = 300 text{ Н }]
Ответ: 300
В лифте, двигающемся вверх с ускорением 3 м/(c^{2}), стоит человек массой 70 кг. Найдите вес человека в лифте (в Н).
По третьему закону Ньютона (в модульной форме): [P=N] На человека в лифте действуют две силы – (vec{N}), направленная вверх (сила реакции опоры), и сила тяжести (mvec{g}), направленная вниз.
Запишем второй закон Ньютона: [mvec{a}=vec{N}+mvec{g} Rightarrow N=m(a+g)=70 cdot 13 = 910 text{ Н }] Заметим, что переход из векторного выражения к скалярному справедлив, так как все силы, приложенные к телу, действуют вдоль одной прямой (оси).
Ответ: 910
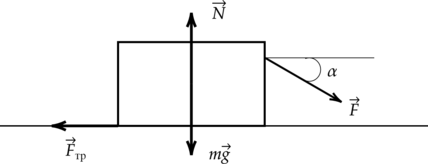
По горизонтальной шероховатой поверхности равномерно толкают ящик массой 20 кг, прикладывая к нему силу, направленную под некоторым углом к горизонтали (сверху вниз). Модуль этой силы равен 100 H, а модуль силы, с которой ящик давит на поверхность, равен 250 Н. Чему равен угол между силой и горизонталью? (Ответь дать в градусах).
Запишем второй закон Ньютона в проекции на вертикальную ось: [0=N-mg-Fsinalpha] Где N – сила, с которой ящик давит на поверхность, mg – сила тяжести, F – сила, прикладываемая к ящику.
Таким образом, синус угла между силой и горизонталью составляет: [sinalpha=dfrac{N-mg}{F}=dfrac{250text{ H}-200text{ H}}{100text{ H}}=0,5] Следовательно, угол ( alpha ) равен (30^{circ}).
Ответ: 30
Первая сферическая планета радиусом 2000 км равномерно вращается вокруг своей оси. Угловая скорость её вращения равна 121 радиан за земные сутки. Вторая сферическая планета имеет радиус 3500 км, также равномерно вращается вокруг своей оси. Ее угловая скорость вращения составляет 81 радиан за земные сутки. При этом тела, находящиеся на экваторе обоих планет, испытывают состояние невесомости. Чему равно отношение первого ускорения свободного падения ко второму? Ответ округлите до десятых долей.
Тела на экваторе планеты испытывают состояние невесомости, следовательно, на экваторе ускорение свободного падения равно центростремительному ускорению. Тогда отношение центростремительных ускорений принимает следующий вид: [{a_text{ц1}=omega^2_1 R_1=(dfrac{121}{24cdot3600text{ c}})^2cdot2cdot10^6text{ м}}approx3,9 text{ м/с$^2$}] [{a_text{ц2}=omega^2_2 R_2=(dfrac{81}{24cdot3600text{ с}})^2cdot3,5cdot10^6text{м}}approx3,1text { м/с$^2$}] Где (omega) – угловая скорость, R – радиус планеты.
Теперь найдем отношение центростремительных ускорений: [dfrac{a_text{ц1}}{a_text{ц2}}=dfrac{3,9text{ м/с$^2$}}{3,1text{ м/с$^2$}}approx1,3]
Ответ: 1,3

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды