Как найти вес тела в окружности

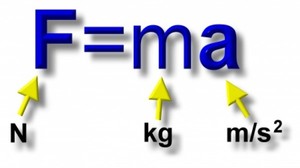
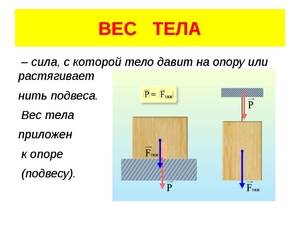
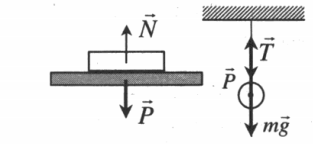
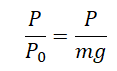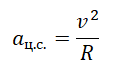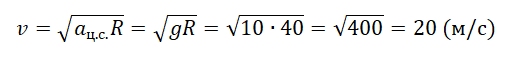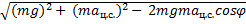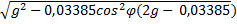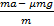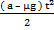Формула для измерения веса тела

Мы часто употребляем фразы наподобие: «Пачка конфет весит 250 грамм» или «я вешу 52 килограмма». Использование таких предложений происходит автоматический. Но что такое вес? Из чего он складывается и как его посчитать?

Для начала нужно понять, что неправильно говорить: «Этот предмет весит Х килограмм». В физике существует два разных понятия – масса и вес. Масса измеряется в килограммах, граммах, тонах и так далее, а вес тела рассчитывается в ньютонах. Поэтому, когда мы говорим, например, что мы весим 52 килограмма, мы на самом деле имеем в виду массу, а не вес.

Вес в физике

Масса – это мера инертности тела. Чем тело обладает большей инертностью, тем больше времени понадобится, чтобы придать ему скорость. Грубо говоря, чем выше значение массы, тем тяжелее сдвинуть предмет. В международной системе единиц массу измеряют в килограммах. Но её также измеряют и в других единицах, например;

• унция;
• фунт;
• стоун;
• американская тонна;
• английская тонна;
• грамм;
• миллиграмм и так далее.

Когда мы говорим один, два, три килограмма, мы сравниваем массу с эталонной массой (прообраз которой находится во Франции в МБМВ). Масса обозначается m.

Вес – это сила, которая действует на подвес или опору за счёт предмета, притягиваемого силой тяжести. Это векторная величина, а значит у него есть направление (как и у всех сил), в отличие от массы (скалярная величина). Направление всегда идёт в центр Земли (из-за силы тяжести). Например, если мы сидим на стуле, сиденье которого располагается параллельно Земле, то вектор силы направлен строго вниз. Вес обозначается P и рассчитывается в ньютонах [Н].

Если тело находится в движении или покое, то сила тяжести (Fтяж), действующая на тело, равна весу. Это справедливо, если движение происходит вдоль прямой линии относительно Земли, и оно имеет постоянную скорость. Вес действует на опору, а сила тяжести на само тело (которое располагается на опоре). Это разные величины, и независимо от того, что они равны в большинстве случаев, не стоит их путать.

Сила тяжести – это результат притяжения тела к земле, вес – воздействие тела на опору. Так как тело изгибает (деформирует) опору своим весом, возникает ещё одна сила, она называется сила упругости (Fупр). Третий закон Ньютона гласит, что тела взаимодействуют друг с другом с одинаковыми по модулю силами, но разными по вектору. Из этого следует, что для силы упругости должна быть противоположная сила, и эта она называется – сила реакции опоры и обозначается N.

По модулю |N|=|P|. Но так как эти силы разнонаправленные, то, раскрывая модуль, мы получим N= — P. Именно поэтому вес можно измерить динамометром, который состоит из пружинки и шкалы. Если подвесить груз на это устройство, пружинка растянется до определённой отметки на шкале.

Как измерить вес тела

Второй закон Ньютона гласит, что ускорение равно силе, делённой на массу. Таким образом, F=m*a. Так как Fтяж равна P (если тело находится в покое или движется по прямой (относительно Земли) с одинаковой скоростью), то и Р тела будет равняться произведению массы и ускорения (P=m*a).

Мы знаем, как найти массу, и знаем, что такое вес тела, осталось разобраться с ускорением. Ускорение – это физическая векторная величина, которая обозначает изменение скорости тела за единицу времени. Например, объект движется первую секунду со скоростью 4 м/с, а на второй секунде его скорость увеличивается до 8 м/с, значит, его ускорение равняется 2. По международной системе единиц ускорение рассчитывается в метрах на секунду в квадрате [м/с 2 ].

Если поместить тело в специальную среду, где будет отсутствовать сила сопротивления воздуха – вакуум, и убрать опору, то объект начнёт лететь равноускоренно. Название этого явления — ускорение свободного падения, которое обозначается g и рассчитывается в метрах на секунду в квадрате [м/с 2 ].

Интересно, что ускорение не зависит от массы тела, а значит если мы кинем листок бумажки и гирю на Земле в специальных условиях, при которых отсутствует воздух (вакуум), то эти предметы приземлятся в одно и то же время. Так как листок имеет большую площадь поверхности и относительно маленькую массу, то для того чтобы упасть, ему приходятся сталкиваться с большим сопротивлением воздуха. В вакууме такого не происходит, и поэтому перо, листок бумаги, гиря, пушечное ядро и другие предметы будут лететь с одной и той же скоростью и упадут в одно время (при условии, что они начнут лететь в одно и то же время, и их первоначальная скорость будет равняться нулю).

Так как Земля имеет форму геоида (или по-другому эллипсоида), а не идеального шара, то и ускорение свободного падения в разных участках Земли разное. Например, на экваторе оно равно 9,832 м/с 2 , а на полюсах 9,780 м/с 2 . Это происходит потому, что на некоторых участках Земли расстояние до ядра больше, а на некоторых меньше. Чем ближе объект находится к центру, тем сильнее он притягивается. Чем объект дальше, тем сила тяжести меньше. Обычно, в школе округляют это значение до 10, это делается для удобства расчётов. Если же необходимо измерить более точно (в инженерном или военном деле и так далее), то берут конкретные значения.

Таким образом, формула для расчёта веса телу будет выглядеть следующим образом P=m*g.

Примеры задач для расчёта веса тела

Первая задача. На стол положили груз массой 2 килограмма. Каков вес груза?

Для решения этой задачи нам понадобится формула по расчёту веса P=m*g. Мы знаем массу тела, а ускорение свободного падения примерно составляет 9,8 м/с 2 . Подставляем эти данные в формулу и получим P=2*9,8=19,6 Н. Ответ: 19,6 Н.

Вторая задача. На стол положили парафиновый шарик, объёмом 0,1 м 3 . Каков вес шарика?

Эту задачу необходимо решать в следующей последовательности;

1. Для начала нам надо вспомнить формулу веса P=m*g. Ускорение нам известно – 9,8 м/с 2 . Осталось найти массу.
2. Масса рассчитывается по формуле m=p*V, где p – это плотность, а V – объём. Плотность парафина можно посмотреть в таблице, объём нам известен.
3. Необходимо подставить значения в формулу, для нахождения массы. m=900*0,1=90 кг.
4. Теперь подставляем значения в первую формулу, для нахождения веса. P=90*9,9=882 Н.

Видео

В этом видео уроке разбирается тема — сила тяжести и вес тела.

Вес тела

О чем эта статья:

Невесомость: что это такое

Невесомость — это состояние, при котором тело не давит на опору или подвес.

Само слово «невесомость» как бы подсказывает нам, что веса здесь быть не должно. При этом непонятно, что с ним тогда происходит. Давайте разбираться.

Вес тела

Вес — это сила, с которой тело действует на опору или подвес. Измеряется вес, как и любая другая сила, в Ньютонах.

«Но погодите! Вес же измеряют в килограммах — я вот вешу 50»

Это не совсем верно. В быту мы часто подменяем понятие «масса» понятием «вес» и говорим: вес чемодана — десять килограммам. В физике это два совершенно разных понятия, которые при этом взаимосвязаны.

Если у вас неподалеку есть весы — приглашаем в эксперимент! Один нюанс: наша затея сработает именно с механическими весами, но не с электронными. Поехали!

Шаг 1. Если встать на весы ровно и не двигаться — ваш вес будет высчитываться по формуле:

P = mg

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Здесь может возникнуть два возражения:

Это же сила тяжести, а не вес. Формула такая же!

На весах масса отображается в килограммах. И если я свою массу умножу на ускорение свободного падения, то явно получу число почти в 10 раз больше, чем показывают весы.

Точка приложения силы. Эта формула и правда аналогична силе тяжести. Вес тела в состоянии покоя численно равен массе тела, разница состоит лишь в точке приложения силы.

Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.

Весы измеряют силу. Весы работают таким образом, что измеряют вес тела — силу, с которой мы на них действуем, а показывают — массу. Можно сделать вывод, что весы — это динамометр (прибор, измеряющий силу).

Шаг 2. Теперь пошалим и резко встанем на носочки! Стрелка резко отклонилась влево, а потом вернулась на место. Вы придали себе ускорение, направленное вверх — в то время, как ускорение свободного падения всегда направлено к центру Земли (вниз).

Теперь вес тела вычисляем по формуле:

P = m (g − a)

g — ускорение свободного падения [м/с 2 ]

a — ваше ускорение [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Шаг 3. Последняя часть эксперимента — резко опуститься на пятки. Теперь вы сильнее давите на весы, потому что придали ускорение, направленное вниз. Стрелка весов отклонится вправо и вернется на место, когда вы придете в состояние покоя.

Формула веса примет вид:

P = m (g + a)

g — ускорение свободного падения [м/с 2 ]

a — ваше ускорение [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Кстати, если ровно стоять на весах, но взвешиваться в лифте — все будет работать наоборот. Если лифт едет вверх, то он как будто давит весами на человека, стоящего на них, а это как раз ситуация с увеличением веса. А если вниз — весы как будто бы от вас «убегают», чтобы показать меньшее значение.

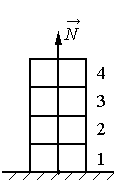
Этот случай мы можем описать через 2 закон Ньютона. Возьмем лифт, который едет вниз. Обозначим силы на рисунке.

N – сила реакции опоры [Н];

mg – сила тяжести [Н];

a – ускорение, с которым движется лифт [м/с 2 ].

При проецировании на ось y, направленную вниз, мы получаем:

А теперь нам понадобится третий закон Ньютона — по нему сила реакции опоры равна весу тела:

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Снова невесомость

Ну что, с весом разобрались. А теперь давайте сделаем так, чтобы его не стало и получилась та самая невесомость.

Чтобы привыкнуть к ощущению невесомости в космосе, космонавты тренируется в специальных самолетах-лабораториях:

Он взлетает и начинает просто падать, чтобы ускорение самолета было равно ускорению свободного падения. В этот момент, в формуле веса из g вычитается равное ему значение и получается 0:

P = m (g − a) = m (9,8 − 9,8) = 0

Вот мы и в невесомости!

Если они летят вокруг Земли, то да. Как писал Дуглас Адамс в книге «Автоспом по галактике»: «Летать просто. Нужно просто промахнуться мимо Земли».

Когда космический корабль обращается вокруг Земли, он просто пытается на нее упасть, но промахивается. Такой процесс происходит, когда корабль движется с первой космической скоростью, равной 7.9 км/с. Это та скорость, с которой корабль становится искусственным спутником Земли.

Кстати, есть еще вторая и третья космические скорости. Вторая космическая скорость — это минимальная скорость, с которой должно двигаться тело, чтобы оно могло без затрат дополнительной работы преодолеть влияние поля тяготения Земли, т. е. удалиться на бесконечно большое расстояние от Земли. А тело, которое двигается с третьей космической скоростью, и вовсе вылетит за пределы Солнечной системы. Такие дела. 🙂

Вес тела

теория по физике 🧲 динамика

Вес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.

Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P . Измеряется динамометром. Единица измерения — Н (Ньютон).

Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P ↑↓ N или P ↑↓ T .

Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:

Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:

Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.

Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.

Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:

P = mg = 16,38∙10 = 163,8 (Н)

Перегрузка

Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.

Перегрузка определяется отношением:

Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.

Вес тела в движущейся равноускоренно системе

Вес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:

1. Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a ↑↑ g —P a ↑↓ g —P > P₀.
2. Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 —P = P₀.

Применение законов Ньютона для определения веса тела

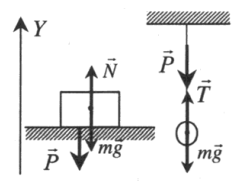
Опора или подвес неподвижны

Второй закон Ньютона в векторной форме:

N + m g = m a или T + m g = m a

Проекция на ось ОУ:

N – mg = 0 или T — mg = 0

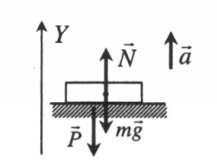
Ускорение опоры направлено вверх

Второй закон Ньютона в векторной форме:

Проекция на ось ОУ:

P = N = ma + mg = m(a + g)

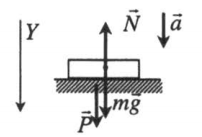
Ускорение опоры направлено вниз

Второй закон Ньютона в векторной форме:

Проекция на ось ОУ:

P = N = mg – ma = m(g – a)

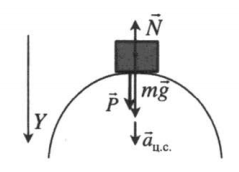
Вершина выпуклого моста

Второй закон Ньютона в векторной форме:

Проекция на ось ОУ:

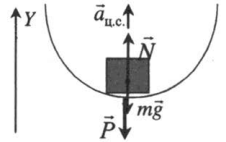
Нижняя точка вогнутого моста

Второй закон Ньютона в векторной форме:

Проекция на ось ОУ:

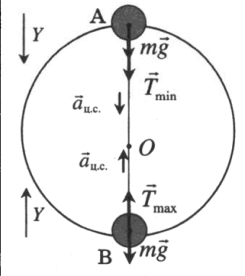
Полный оборот на подвесе

Второй закон Ньютона в векторной форме:

Проекция на ось ОУ в точке А:

Вес тела в точке А:

Проекция на ось ОУ в точке В:

Вес тела в точке В:

Важно! Центростремительное ускорение всегда направлено к центру окружности.

Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?

Вес тела в верхней точке выпуклого моста равен:

Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:

Масса не может быть нулевой, поэтому:

Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:

Отсюда скорость автомобиля в верхней точке моста должна быть равна:

Четыре одинаковых кирпича массой m каждый сложены в стопку (см. рисунок). Если убрать два верхних кирпича, то модуль силы N, действующей со стороны горизонтальной опоры на первый кирпич, уменьшится на…

Решение задач повышенной сложности на движение в НСО

 Пример задачи

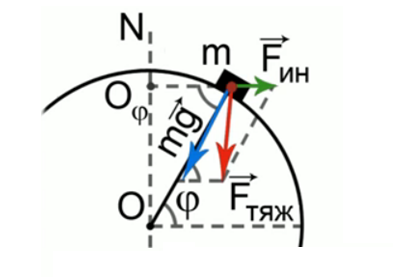
Найти вес тела на ши­ро­те φ (рис. 1).

Рис. 1. При­мер ре­ше­ния за­да­чи

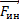
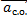
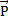
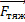
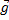
P_φ – ?  = -m;  =  = m + 

a_c.o. = a_ц.с. = 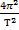 R_зcosφ

F_тяж = 

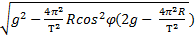
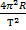
F_тяж = m ;  = a_э = 0,03385 м/с²

F_тяж = m

Мы при­вык­ли, что вес тела – mg, но Земля со­вер­ша­ет свое дви­же­ние во­круг своей оси и яв­ля­ет­ся неинер­ци­аль­ной си­сте­мой от­сче­та.

Рас­смот­рим тело, ко­то­рое на­хо­дит­ся на по­верх­но­сти Земли на ши­ро­те φ. Ши­ро­та опре­де­ля­ет­ся на­прав­ле­ни­ем на эту точку зем­ной по­верх­но­сти, и угол, ко­то­рый она со­став­ля­ет с эк­ва­то­ри­аль­ной плос­ко­стью, как раз и яв­ля­ет­ся ши­ро­той места.

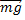
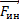
На тело в неинер­ци­аль­ной си­сте­ме от­сче­та кроме силы гра­ви­та­ци­он­но­го при­тя­же­ния дей­ству­ет еще сила инер­ции , ко­то­рая на­прав­ле­на в сто­ро­ну, про­ти­во­по­лож­ную уско­ре­нию си­сте­мы от­сче­та, и чис­лен­но равна про­из­ве­де­нию массы на уско­ре­ние этой си­сте­мы от­сче­та. А уско­ре­ние си­сте­мы от­сче­та – уско­ре­ние про­тив зем­ной по­верх­но­сти на ши­ро­те φ, тогда сила тя­же­сти, ко­то­рая и равна весу тела, равна сумме этих двух сил. Это век­тор­ная сумма и сила тя­же­сти на­прав­ле­на не к цен­тру Земли, а немнож­ко мимо цен­тра. Уско­ре­ние про­тив зем­ной по­верх­но­сти на ши­ро­те φ со­став­ля­ет от­но­ше­ние 4π² на пе­ри­од об­ра­ще­ния Земли во­круг оси в квад­ра­те, умно­жен­ное на ра­ди­ус окруж­но­сти, ко­то­рую опи­сы­ва­ет дан­ная точка. В дан­ном слу­чае цен­тром окруж­но­сти яв­ля­ет­ся О_φ и ра­ди­ус окруж­но­сти – это ра­ди­ус Земли, умно­жен­ный на ко­си­нус ши­ро­ты места, тогда по тео­ре­ме ко­си­ну­сов на­хо­дим силу тя­же­сти как сто­ро­ну тре­уголь­ни­ка, у ко­то­ро­го из­вест­ны две дру­гие сто­ро­ны и угол между ними.

Под­став­ляя вы­ра­же­ние для цен­тро­стре­ми­тель­но­го уско­ре­ния, по­лу­ча­ем силу тя­же­сти, в фор­му­ле ко­то­рой мы видим уско­ре­ние точек зем­ной по­верх­но­сти на эк­ва­то­ре – а_э. При вы­чис­ле­нии по­лу­чим а_э = 0,03385 м/с², и, под­став­ляя в вы­ра­же­ние для силы тя­же­сти, мы можем опре­де­лить ее в любой точке по­верх­но­сти для необ­хо­ди­мых ши­ро­ты и массы тел.

Для кон­тро­ля най­дем силу тя­же­сти тела мас­сой 10 кг на эк­ва­то­ре, на ши­ро­те 60⁰ и на по­лю­се, срав­ним по­лу­чен­ные зна­че­ния.

Ответ: при φ = 0⁰F_тяж1 = 94,62 (H),

φ =60⁰ F_тяж2 = 96,33 (H),

φ = 90⁰F_тяж3 = 98 (H).

Есте­ствен­но, самое ма­лень­кое зна­че­ние будет на эк­ва­то­ре, самое боль­шое – на по­лю­се.

 Задача 1

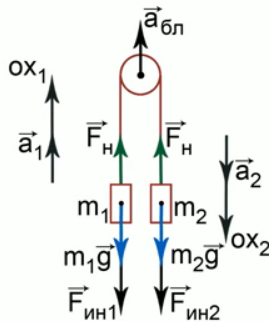
Грузы мас­сой 2 кг и 8 кг под­ве­ше­ны к кон­цам нити, пе­ре­ки­ну­той через блок, ко­то­рый под­ни­ма­ет­ся вер­ти­каль­но с уско­ре­ни­ем 5 м/с². Найти силу на­тя­же­ния нити.

Слож­но­сти при ре­ше­нии этой за­да­чи свя­за­ны с тем, что ранее го­во­ри­лось о при­ме­не­нии за­ко­нов Нью­то­на толь­ко в инер­ци­аль­ных си­сте­мах от­сче­та и рас­смат­ри­ва­лось дви­же­ние этих гру­зов от­но­си­тель­но Земли. От­но­си­тель­но Земли уско­ре­ние гру­зов раз­ное, по­это­му за­да­ча и стала для мно­гих слож­ной.

Ре­шать такие за­да­чи необ­хо­ди­мо в си­сте­ме от­сче­та «Блок» (рис. 2), ко­то­рая яв­ля­ет­ся неинер­ци­аль­ной, и в этой си­сте­ме от­сче­та ко всем силам, ко­то­рые обыч­но при­ло­же­ны к телам, до­бав­ля­ет­ся сила инер­ции.

К при­ме­ру, когда ав­то­бус резко тор­мо­зит, нас тол­ка­ет вниз сила инер­ции. Здесь при дви­же­нии блока на­верх к каж­до­му из тел до­бав­ля­ет­ся сила, про­ти­во­по­лож­ная уско­ре­нию блока и на­прав­лен­ная вниз.

Рис. 2. Си­сте­ма от­сче­та «Блок»

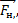
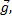
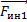
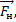
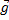
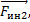
Эйн­штейн до­ка­зал, что эта сила инер­ции в прин­ци­пе неот­ли­чи­ма от силы гра­ви­та­ци­он­но­го при­тя­же­ния. В дан­ном слу­чае на пер­вое тело дей­ству­ет сила на­тя­же­ния нити  на­прав­лен­ная вверх, сила гра­ви­та­ци­он­но­го при­тя­же­ния m₁ на­прав­лен­ная вниз, и сила инер­ции . На вто­рое тело точно так же дей­ству­ет  на­прав­лен­ная вверх, сила гра­ви­та­ци­он­но­го при­тя­же­ния m₂ и сила инер­ции  на­прав­лен­ные вниз.

У нас си­сте­ма свя­зан­ных тел, для каж­до­го из тел ось необ­хо­ди­мо на­пра­вить в свою сто­ро­ну по уско­ре­нию. Оче­вид­но, что пер­вое тело, ко­то­рое легче, будет дви­гать­ся от­но­си­тель­но блока вверх, а вто­рое тело будет дви­гать­ся вниз. По­это­му ось ох₁на­прав­ля­ем вверх, ох₂ на­прав­ля­ем вниз.

За­пи­шем крат­кое усло­вие за­да­чи и ре­ше­ние.

Ответ: F_н = 48 H.

Урав­не­ние в про­ек­ции на ось ох₁ будет иметь вид -m₁g — m₁а_бл + F_н = m₁а.

На ось ох₂ будет m₂g + m₂а_бл — F_н = m₂а.

Ре­ше­ние си­сте­мы урав­не­ний до­сти­га­ет­ся сло­же­ни­ем, при сло­же­нии сразу уби­ра­ем про­ти­во­по­лож­ные зна­че­ния силы на­тя­же­ния и по­лу­ча­ем вы­ра­же­ние, из ко­то­ро­го можем за­пи­сать уско­ре­ние и вы­чис­лить его. Далее его зна­че­ние можно под­ста­вить в любое из урав­не­ний и опре­де­лить силу на­тя­же­ния.

 Задача 2

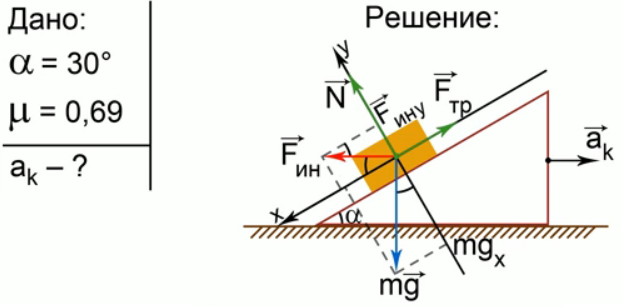
На на­клон­ной по­верх­но­сти клина с углом 30⁰ по­ко­ит­ся бру­сок при ко­эф­фи­ци­ен­те тре­ния 0,69. С каким ми­ни­маль­ным уско­ре­ни­ем нужно пе­ре­ме­щать по го­ри­зон­та­ли клин, чтобы бру­сок стал сколь­зить вниз по его по­верх­но­сти?

Вы­пол­ня­ем крат­кое усло­вие за­да­чи, ри­су­нок и ре­ше­ние (рис. 3).

Рис. 3. Ре­ше­ние за­да­чи 2

 = — m; m +  +  + = m; a ≥ 0

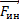
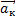
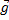
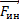
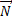
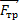
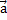
по ох: mgsinα + ma_кcosα — F_тр ≥ 0

по оу: -mgcosα + ma_кsinα + N = 0

N = mgcosα — ma_кsinα F_тр = μN = μmgcosα — μma_кsinα

mgsinα + ma_кcosα — μmgcosα + μma_кsinα ≥ 0

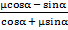
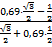
a_к ≥  g a_к ≥  · 10 a_к ≥ 0,8 (м/с²)

Ответ: a_к ≥ 0,8 м/с².

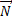
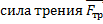
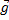
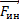
Сила, ко­то­рая за­став­ля­ет бру­сок про­скаль­зы­вать, – это mgsinα, но sinα = 0,5 при μ = 0,69, мы видим, что сила тре­ния боль­ше силы, со­став­ля­ю­щей mg. Ре­ша­ем за­да­чу в си­сте­ме от­сче­та «Клин». К тем силам, ко­то­рые обыч­но при­ло­же­ны к брус­ку, – сила ре­ак­ции опоры ,  и сила тя­же­сти m – до­бав­ля­ет­ся сила инер­ции , на­прав­лен­ная про­тив уско­ре­ния клина. За­пи­шем вто­рой закон Нью­то­на для брус­ка и вы­бе­рем оси, ось х в сто­ро­ну воз­мож­но­го на­прав­ле­ния и ось у пер­пен­ди­ку­ляр­но по­верх­но­сти клина. По­лу­ча­ем: по оси х mg про­еци­ру­ет­ся через sinα, это про­ти­во­ле­жа­щий катет, сила инер­ции про­еци­ру­ет­ся через cosα и минус сила тре­ния, так как она на­прав­ле­на в про­ти­во­по­лож­ную сто­ро­ну, будет боль­ше или равно нулю. Когда уско­ре­ние равно нулю, то сила инер­ции при­ни­ма­ет ми­ни­маль­ное зна­че­ние, со­от­вет­ствен­но, уско­ре­ние клина тоже ми­ни­маль­но.

По оси у mg будет со зна­ком минус, так как она на­прав­ле­на про­тив оси у. Урав­не­ние по оси у необ­хо­ди­мо, чтобы вы­ра­зить силу ре­ак­ции опоры 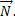 Под­став­ляя зна­че­ния силы ре­ак­ции опоры и силы тре­ния, мы по­лу­чим урав­не­ние, из ко­то­ро­го и на­хо­дим вы­ра­же­ние для уско­ре­ния клина. Под­став­ляя зна­че­ния, мы видим, что уско­ре­ние, с ко­то­рым нужно дви­гать клин в го­ри­зон­таль­ном на­прав­ле­нии, будет боль­ше или рав­ным 0,8 м/с².

При на­хож­де­нии мак­си­маль­но­го уско­ре­ния его необ­хо­ди­мо на­пра­вить в про­ти­во­по­лож­ную сто­ро­ну.

 Задача 3

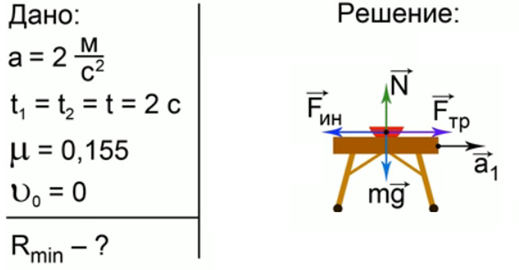
В цен­тре круг­ло­го стола по­ме­сти­ли ма­лень­кое блю­деч­ко. Ко­эф­фи­ци­ент тре­ния между ним и сто­лом μ = 0,155. Стол дви­га­ли пря­мо­ли­ней­но с уско­ре­ни­ем 2 м/ с² в те­че­ние 2 с, а затем оста­но­ви­ли с тем же по ве­ли­чине уско­ре­ни­ем. При каком ми­ни­маль­ном ра­ди­у­се стола блю­деч­ко с него не упа­дет?

За­пи­шем крат­кое усло­вие за­да­чи, схему и ре­ше­ние (рис. 4).

Рис. 4. Ре­ше­ние за­да­чи 3

F_ин = ma = 2m; F_тр = μmg = 1,55m

1.      t = t₁

a₁ =  =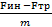 

a₁ = a — μg V₁ = ( a — μg ) t S₁ = 

2.      t = t₂

 = —  => F_ин ↑↑ F_трa₂ = -(a + μg)

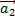
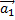
V₀₂ = V₁ V₂ = 0

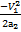
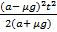
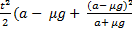
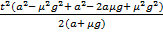
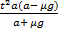
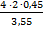
S₂ =  = ; S = S₁ + S₂; S = )

S =  =  =  = 1,01 (м)

Ответ: R_min = 1,01 м.

На­чаль­ная ско­рость блю­деч­ка равна нулю, оно лежит в цен­тре стола. Когда стол на­чи­на­ет дви­гать­ся с уско­ре­ни­ем, он ста­но­вит­ся неинер­ци­аль­ной си­сте­мой от­сче­та и ко всем силам, ко­то­рые были при­ло­же­ны к блю­деч­ку, до­бав­ля­ет­ся сила инер­ции, на­прав­лен­ная про­тив уско­ре­ния стола и рав­ная по ве­ли­чине про­из­ве­де­нию массы на уско­ре­ние блю­деч­ка. Сила тре­ния сразу будет ме­шать блю­деч­ку дви­гать­ся. При под­ста­нов­ке из­вест­ных ве­ли­чин мы видим, что сила тре­ния мень­ше силы инер­ции, блю­деч­ко на­чи­на­ет дви­гать­ся по по­верх­но­сти стола.

Пер­вое усло­вие за­да­чи – стол дви­жет­ся с уско­ре­ни­ем, в этом слу­чае сила инер­ции на­прав­ле­на в про­ти­во­по­лож­ную сто­ро­ну силы тре­ния, но боль­ше нее. Опре­де­лим уско­ре­ние, с ко­то­рым дви­жет­ся блю­деч­ко, по вто­ро­му за­ко­ну Нью­то­на. За это время ско­рость блю­деч­ка уве­ли­чи­ва­ет­ся с этим уско­ре­ни­ем и до­сти­га­ет зна­че­ния V₁, а путь – S₁.

При вто­ром про­ме­жут­ке вре­ме­ни уско­ре­ние стола ме­ня­ет­ся на про­ти­во­по­лож­ное, со­от­вет­ствен­но, и сила инер­ции при­ни­ма­ет про­ти­во­по­лож­ное на­прав­ле­ние, в дан­ном слу­чае она будет сов­па­дать с силой тре­ния, то есть и сила инер­ции, и сила тре­ния тор­мо­зят дви­же­ние блю­деч­ка. На­чаль­ная ско­рость к мо­мен­ту тор­мо­же­ния будет равна V₁, а ко­неч­ная ско­рость в ре­зуль­та­те тор­мо­же­ния будет равна нулю. По­это­му за время тор­мо­же­ния блю­деч­ко прой­дет путь S₂, так как уско­ре­ние у нас от­ри­ца­тель­ное, то знак минус уйдет из вы­ра­же­ния.

Общий путь, ко­то­рый прой­дет блю­деч­ко, со­став­ля­ет сумму двух по­лу­чен­ных вы­ра­же­ний S₁ и S₂. Про­ве­дя ал­геб­ра­и­че­ские пре­об­ра­зо­ва­ния и под­став­ляя чис­ло­вые зна­че­ния, мы по­лу­чим, что блю­деч­ко прой­дет путь 1,01 метра, то есть ра­ди­ус стола от цен­тра до края дол­жен быть не мень­ше этого зна­че­ния, иначе блю­деч­ко со­скольз­нет.

 Заключение

Как мы уви­де­ли на при­ме­рах ре­ше­ния задач, при учете сил инер­ции вто­рой закон Нью­то­на будет спра­вед­лив для любой си­сте­мы от­сче­та и ряд задач лучше ре­ша­ет­ся в неинер­ци­аль­ной си­сте­ме от­сче­та.

Была ли эта статья полезной?

Вес тела. Калькулятор онлайн.

Калькулятор вычисления веса тела, вычислит вес тела, массу, ускорение свободного падения и даст подробное решение.

Калькулятор содержит:
Калькулятор вычисления веса тела, если известны масса тела и ускорение свободного падения.
Калькулятор вычисления массы тела, если известны вес тела и ускорение свободного падения.
Калькулятор вычисления ускорения свободного падения, если известны вес тела и его масса.

В данной таблице приведены значения ускорения свободного падения для планет Солнечной системы и их спутников.

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Масса

Масса обозначается символом (m ), является скалярной величиной и в СИ измеряется в килограммах.

Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:

[ large boxed{ begin{matrix} m = left( text{тонны} right) cdot 10^{3} left( text{кг}right) \ m = left( text{центнеры} right) cdot 10^{2} left( text{кг}right) \ m = left( text{граммы} right) cdot 10^{-3} left( text{кг}right) \ m = left( text{миллиграммы} right) cdot 10^{-6} left( text{кг}right) \ end{matrix}} ]

• ( large text{(тонны)} ) – подставьте количество тонн вместо этой скобки;
• ( large text{(центнеры)} ) – вместо этой скобки подставьте количество сотен килограммов;
• ( large text{(граммы)} ) – подставьте количество граммов вместо этой скобки;
• ( large text{(миллиграммы)} ) – вместо этой скобки подставьте количество миллиграммов;

От массы зависят инерционные и гравитационные свойства физических тел.

Масса в природе проявляет себя двумя способами. Поэтому, выделяют:

1. массу инертную и
2. массу гравитационную.

Инертная масса

Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.

Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».

Гравитационная масса

Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.

Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.

Так же, масса входит в формулы для расчета импульса и механической энергии.

Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.

Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.

Сила тяжести

Сила тяжести — это сила, с которой Земля притягивает к себе тело.

(large vec{F_{text{тяж}}} left(Hright) ) — сила тяжести, она действует на тело со стороны планеты (или другого крупного небесного тела, например, астероида, или звезды).

[large vec{F_{text{тяж}}} = m cdot vec{g}]

(large m left(text{кг}right) ) — масса тела;

(large vec{g} left(frac{text{м}}{c^{2}}right) ) — ускорение свободного падения, это не постоянная величина, она может меняться. Читайте подробнее о ускорении свободного падения .

Вес

Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.

Является векторной величиной и обозначается символом (vec{P} ).

(vec{P} left(Hright) ) – вес тела, как любая сила в СИ измеряется в Ньютонах.

Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.

Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу (large vec{N}). Как только мы найдем реакцию опоры (large vec{N}), мы найдем вес тела, давящего на эту опору.

Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.

Чем вес отличается от силы тяжести

Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.

Что такое невесомость

Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.

Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.

Как изменяется вес тела лифте

Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.

Если скорость лифта не изменяется

Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.

Примечание: «неизменной», также, значит «постоянной», или «одной и той же».

По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.

Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.

Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:

[ large N – m cdot g = 0 ]

А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).

Прибавив к обеим частям уравнения величину ( m cdot vec{g} ), получим

[ large N = m cdot g ]

По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.

Воспользуемся тем, что ( left|vec{N} right|= left|vec{P} right|), получим

[ large boxed{ P = m cdot g }]

То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен ( mg ). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета.

Если скорость лифта изменяется

Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2).

Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах.

Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так:

[ large N – m cdot g = m cdot a ]

А для рисунка 2б, так:

[ large N – m cdot g = — m cdot a ]

Прибавим теперь к обеим частям уравнений величину ( m cdot g ), получим:

( large N = m cdot a + m cdot g ) – для случая рис. 2а;

( large N = — m cdot a + m cdot g ) – для рис. 2б;

Вынесем массу за скобки

( large N = m cdot left( a + g right) ) – для рис. 2а;

( large N = m cdot left( -a + g right) ) – для рис. 2б;

Учтем, что ( left|vec{N} right|= left|vec{P} right|), окончательно запишем

Для рисунка 2а — движение лифта вверх с ускорением:

[ large boxed{ P = m cdot left( g + a right) }]

Вес тела в движущемся с ускорением вверх лифте, будет равен ( m cdot left( g + a right) ), то есть, превышает величину ( m cdot g ).

Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается:

[ large boxed{ P = m cdot left( g — a right) }]

Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен ( m cdot g ).

Вес тела в движущемся вниз с ускорением лифте, равен ( m cdot left( g — a right) ), это меньше величины ( m cdot g ).

А если при движении вниз ускорение лифта ( vec{a} ) сравняется с ускорением ( vec{g} ), то груз перестанет давить на опору и наступит состояние невесомости, вес тела будет равен нулю.

Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать!

Что такое перегрузка

Когда вес тела больше силы тяжести, говорят, что возникает перегрузка.

[ large boxed{ P > m cdot g }]

Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения (large vec{g}).

Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз.

Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…».

Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить.

Подведем итоги

(P = m cdot g ) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте.

( P = m cdot left( g + a right) ) — вес, когда лифт движется с ускорением вверх;

( P = m cdot left( g — a right) ) — вес в движущемся вниз с ускорением;

Если ускорение лифта при его движении вниз ( a = g ), наступит невесомость, вес тела исчезнет ( P = 0 ).