-
Основные
определения
Дерево
– связный граф без циклов. Лес
(или ациклический
граф) – неограф без циклов. Компонентами
леса являются деревья.
Теорема 14.1.
Для неографа G
с n
вершинами без петель следующие условия
эквивалентны:
-
G
– дерево; -
G
– связной граф, содержащий n
– 1
ребро; -
G
– ациклический граф, содержащий n
– 1
ребро; -
Любые две
несовпадающие вершины графа G
соединяет единственная цепь; -
G
– ациклический граф, такой, что если в
него добавить одно ребро, то в нем
появится ровно один цикл.
Теорема 14.2.
Неограф G
является лесом тогда и только тогда,
когда коранг графа v(G)=0.
Висячая вершина
в дереве – вершина степени 1. Висячие
вершины называются листьями,
все остальные – внутренними
вершинами.
Если в дереве особо
выделена одна вершина, называемая
корнем,
то такое дерево называется корневым,
иначе – свободным.
Корневое дерево
можно считать орграфом с ориентацией
дуг из корня или в корень. Очевидно, что
для любой вершины корневого дерева,
кроме корня,
.
Для корня,
для листьев.
Вершины дерева,
удаленные на расстояние k
(в числе дуг) от корня, образуют k-й
ярус (уровень) дерева. Наибольшее значение
k
называется высотой
дерева.
Если из какой-либо
вершины корневого дерева выходят дуги,
то вершины на концах этих дуг называют
сыновьями
(в английской литературе – дочери
(daughter)).
-
Центроид дерева
Ветвь
к вершине v
дерева – это максимальный подграф,
содержащий v
в качестве висячей вершины. Вес
вершиныk
– наибольший размер ее ветвей. Центроид
(или центр масс) дерева C
– множество вершин с наименьшим весом:
C
= {v|
c(v)
=
}.
Вес любого листа
дерева равен размеру дерева. Высота
дерева с корнем, расположенным в
центроиде, не больше наименьшего веса
его вершин.
Свободное дерево
порядка n
с двумя центроидами имеет четное
количество вершин, а вес каждого центроида
равен n/2.
Теорема 14.3
(Жордана).
Каждое дерево имеет центроид, состоящий
из одной или двух смежных вершин.
Пример 14.1.
Найти наименьший вес вершин дерева,
изображенного на рис. 14.1, и его центроид.
Рис. 14.1
Решение.
Очевидно, что вес каждой висячей вершины
дерева порядка n
равен n
– 1. Висячие вершины не могут составить
центроид дерева, поэтому исключим из
рассмотрения вершины 1, 2, 4, 6, 12, 13 и 16. Для
всех остальных вершин найдем их вес,
вычисляя длину (размер) их ветвей.
Число ветвей
вершины равно ее степени. Вершины 3, 5 и
8 имеют по две ветви, размеры которых
равны 1 и 14. К вершине 7 подходят четыре
ветви размером 1, 2, 2 и 10. Таким образом,
ее вес
.
Аналогично вычисляются веса других
вершин:,
,
.
Минимальный вес вершин равен 8,
следовательно, центроид дерева образуют
две вершины с таким весом: 11 и 15.
-
Десятичная
кодировка
Деревья представляют
собой важный вид графов. С помощью
деревьев описываются базы данных,
деревья моделируют алгоритмы и программы,
их используют в электротехнике, химии.
Одной из актуальных задач в эпоху
компьютерных и телекоммуникационных
сетей является задача сжатия информации.
Сюда входит и кодировка деревьев.
Компактная запись дерева, полностью
описывающая его структуру, может
существенно упростить как передачу
информации о дереве, так и работу с ним.
Существует множество
способов кодировки деревьев. Рассмотрим
одну из простейших кодировок помеченных
деревьев с выделенным корнем – десятичную.
Кодируя дерево,
придерживаемся следующих правил.
-
Кодировка начинается
с корня и заканчивается в корне. -
Каждый шаг на одну
дугу от корня кодируется единицей. -
В узле выбираем
направление на вершину с меньшим
номером. -
Достигнув листа,
идем назад, кодируя каждый шаг нулем. -
При движении назад
в узле всегда выбираем направление на
непройденную вершину с меньшим номером.
Кодировка в такой
форме получается достаточно компактной,
однако она не несет в себе информации
о номерах вершин дерева. Существуют
аналогичные кодировки, где вместо единиц
в таком же порядке проставляются номера
или названия вершин.
Есть деревья, для
которых несложно вывести формулу
десятичной кодировки. Рассмотрим,
например, графы-звезды
,
являющиеся полными двудольными графами,
одна из долей которых состоит из одной
вершины. Другое обозначение звезд –.
На рис. 14.2 показаны
звезды, а также приведены их двоичные
и десятичные кодировки. Корень дерева
располагается в центральной вершине
звезды. Легко получить общую формулу:
. (14.1)
Рис. 14.2
Если корень
поместить в любой из висячих вершин, то
код
такого дерева будет выражаться большим
числом. Более того, существует зависимость.
Аналогично рассматриваются и цепи (рис.
14.3). Цепи обозначаются как.
Рис. 14.3
В звездах только
два варианта расположения корня с
различными десятичными кодировками. В
цепи же число вариантов кодировок в
зависимости от положения корня растет
с увеличением n.
Рассмотрим самый простой вариант,
расположив корень в концевой вершине
(листе). Для
получим двоичную кодировку 10 и десятичную
2, для– 1100 и 12, для
– 111000 и 56, для
– 11110000 и 240. Общая формула для десятичной
кодировки цепи с корнем в концевой
вершине имеет вид
. (14.2)
Пример
14.2. Записать
десятичный код дерева, изображенного
на рис. 14.4, с корнем в вершине 3.
Рис. 14.4
Решение.
На основании правила кодировки, двигаясь
по дереву, проставим в код единицы и
нули. При движении из корня 3 к вершине
7 проходим четыре ребра. В код записываем
четыре единицы: 1111. Возвращаясь от
вершины 7 к вершине 2 (до ближайшей
развилки), проходим три ребра. Записываем
в код три нуля: 000. От вершины 2 к 5 и далее
к 8 (меньший номер): 11; от 8 назад к 5 и от
5 к 9: 01; от 9 к корню 3: 000.
И, наконец, от 3 к
6 и обратно: 10. В итоге, собирая все вместе,
получим двоичный код дерева:
1 111 000 110 100 010.
Разбивая число
на тройки, переводим полученное двоичное
представление в восьмеричное. Получаем
.
Затем переводим это число в десятичное:.
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Взвешенные графы
В классических графах все рёбра считаются равноценными и длина пути
соответствует количеству рёбер, которые он содержит. Однако часто
в задаче каждому ребру соответствует некоторый параметр — длина
ребра или стоимость прохождения по нему. В терминологии графов такой
параметр называется весом ребра, а граф, содержащий взвешенные
рёбра, взвешенным.
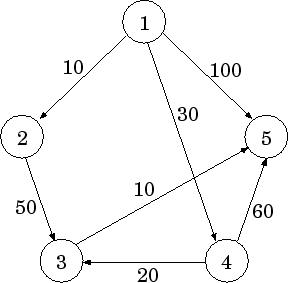
Типичная задача для таких графов — поиск кратчайшего пути. Например,
в этом графе кратчайший путь между вершинами (1) и (5): (1 — 4 — 3 — 5), так
как его вес равен (30 + 20 + 10 = 60), а вес ребра (1 — 5) равен (100).
Алгоритм Дейкстры
Классический алгоритм для поиска кратчайших путей во взвешенном графе —
алгоритм Дейкстры (по имени автора Эдгара Дейкстры). Он позволяет найти
кратчайший путь от одной вершины графа до всех остальных за (O(M log N))
((N, M) — количество вершин и рёбер соответственно).
Принцип работы алгоритма напоминает принцип работы BFS: на каждом шаге
обрабатывается ближайшая ещё не обработанная вершина (расстояние до неё
уже известно). При её обработке все ещё не посещённые соседи добавляются
в очередь для посещения (расстояние до каждой из них рассчитывается как
расстояние до текущей вершины + длина ребра). Главное отличие от BFS
заключается в том, что вместо классической очереди используется очередь с
приоритетом. Она позволяет нам выбирать ближайшую вершину за (O(log N)).
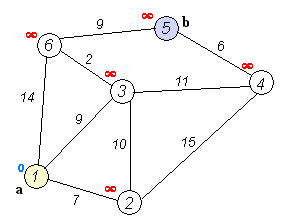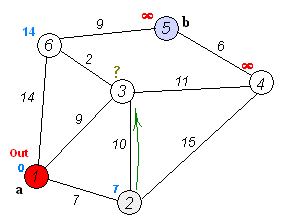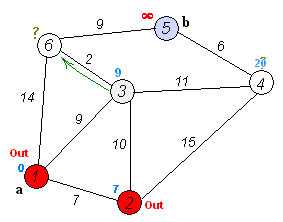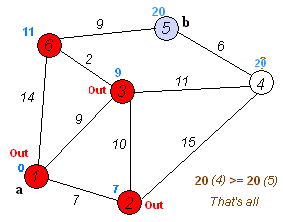
Анимация выполнения алгоритма Дейкстры для поиска кратчайшего пути из вершины
(a) в вершину (b):
С помощью псевдокода алгоритм Дейкстры описывается следующим образом:
ans = массив расстояний от начальной вершины до каждой.
изначально заполнен бесконечностями (ещё не достигнута).
ans[start] = 0
q = очередь с приоритетом, хранящая пары (v, dst),
где dst - предполагаемое расстояние до v
добавить (start, 0) в q
пока q не пуста:
(v, dst) = первая вершина в очереди (с минимальным расстоянием), и расстояние до неё
извлечь (v, dst) из очереди
если ans[v] < dst: //мы уже обработали эту вершину, используя другой путь
перейти к следующей вершине
для каждой v -> u:
n_dst = dst + len(v -> u) //расстояние до u при прохождении через v
если n_dst < ans[u]: //если мы можем улучшить ответ
ans[u] = n_dst
добавить (u, n_dst) в q
Как видите, в очереди с приоритетом хранится не только номер вершины, но
и вычисленное расстояние до неё, по которому и ведётся сортировка. Также
возможна ситуация, при которой одна и та же вершина будет помещена в очередь
несколько раз с разным расстоянием (так как она достижима по нескольким рёбрам).
В такой ситуации обрабатываем её только один раз (с минимальным возможным
расстоянием).
Реализация
В нашей очереди с приоритетом должны храниться пары (вершина, расстояние до неё),
причём отсортированы они должны быть по уменьшению расстояния. Для этого нужно
использовать тип
std::priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>:
первым элементом пары будет расстояние, а вторым — номер вершины.
Для хранения взвешенного графа в виде списка смежности для каждой вершины мы
храним вектор пар (соседняя вершина, длина ребра до неё).
Реализация на C++:
Реализация с восстановлением пути
Восстановление пути для алгоритма Дейкстры реализуется точно так же, как и для
BFS: при успешном улучшении пути в вершину (u) через вершину (v), мы запоминаем,
что (prev[v] = u). После окончания работы алгоритма используем массив (prev) для
восстановления пути в обратном направлении.Реализация на C++:
Область применения алгоритма Дейкстры
Алгоритм Дейкстры является оптимальным для поиска пути практически в любых
графах, но он имеет одно ограничение. Алгоритм Дейкстры неприменим для графов,
содержащих рёбра с отрицательным весом. Для поиска кратчайшего пути в таких
графах обычно используют алгоритм Форда-Беллмана.
Ориентированные графы
Орграф — это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками (см. рис. 11.6).
Рис.
11.6.
Орграф
В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги ( дуга из нее исходит ), вторая — концом дуги ( дуга в нее входит ). Можно сказать, что любое ребро — это пара дуг, направленных навстречу друг другу.
Если в графе присутствуют и ребра, и дуги, то его называют смешанным.
Все основные понятия, определенные для неориентированных графов ( инцидентность, смежность, достижимость, длина пути и т.п.), остаются в силе и для орграфов — нужно лишь заменить слово » ребро » словом » дуга «. А немногие исключения связаны с различиями между ребрами и дугами.
Степень вершины в орграфе — это не одно число, а пара чисел: первое характеризует количество исходящих из вершины дуг, а второе — количество входящих дуг.
Путь в орграфе — это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причем каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 11.6 нет пути, ведущего из вершины 2 в вершину 5. «Двигаться» по орграфу можно только в направлениях, заданных стрелками.
| Орграф | Вершины | Дуги |
|---|---|---|
| Чайнворд | Слова | Совпадение последней и первой букв (возможность связать два слова в цепочку) |
| Стройка | Работы | Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) |
| Обучение | Курсы | Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Delphi, и т.п.) |
| Одевание ребенка | Предметы гардероба | Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т.п.) |
| Европейский город | Перекрестки | Узкие улицы с односторонним движением |
| Организация | Сотрудники | Иерархия (начальник — подчиненный) |
Взвешенные графы
Взвешенный (другое название: размеченный ) граф (или орграф ) — это граф ( орграф ), некоторым элементам которого ( вершинам, ребрам или дугам ) сопоставлены числа. Наиболее часто встречаются графы с помеченными ребрами. Числа-пометки носят различные названия: вес, длина, стоимость.
Замечание: Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.
Длина пути во взвешенном (связном) графе — это сумма длин (весов) тех ребер, из которых состоит путь. Расстояние между вершинами — это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 11.7, равно 6.
Рис.
11.7.
Взвешенный граф
N — периферия вершины v — это множество вершин, расстояние до каждой из которых (от вершины v ) не меньше, чем N.
| Граф | Вершины | Вес вершины | Ребра (дуги) | Вес ребра (дуги) |
|---|---|---|---|---|
| Таможни | Государства | Площадь территории | Наличие наземной границы | Стоимость получения визы |
| Переезды | Города | Стоимость ночевки в гостинице | Дороги | Длина дороги |
| Супер-чайнворд | Слова | — | Совпадение конца и начала слов(возможность «сцепить» слова) | Длина пересекающихся частей |
| Карта | Государства | Цвет на карте | Наличие общей границы | — |
| Сеть | Компьютеры | — | Сетевой кабель | Стоимость кабеля |
Способы представления графов
Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.
Матрица смежности
Матрица смежности Sm — это квадратная матрица размером NxN ( N — количество вершин в графе ), заполненная единицами и нулями по следующему правилу:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = 1, в противном случае Sm[u,v] = 0.
Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа — несимметричной.
Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = ves(e), в противном случае Sm[u,v] = 0.
Это хорошо согласуется с замечанием, сделанным в предыдущем пункте: невзвешенный граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.
Небольшое затруднение возникнет в том случае, если в графе разрешаются ребра с весом 0. Тогда придется хранить два массива: один с нулями и единицами, которые служат показателем наличия ребер, а второй — с весами этих ребер.
В качестве примера приведем матрицы смежности для трех графов, изображенных на рис. 11.5, рис. 11.6 и рис. 11.7 (см. рис. 11.8).
| a | b | c | d | f | 1 | 2 | 3 | 4 | 5 | a | b | c | d | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | a | 0 | 1 | 10 | 0 |
| b | 1 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | b | 1 | 0 | 2 | 10 |
| c | 1 | 1 | 0 | 1 | 1 | 3 | 1 | 1 | 0 | 0 | 1 | c | 10 | 2 | 0 | 3 |
| d | 0 | 1 | 1 | 0 | 1 | 4 | 0 | 0 | 1 | 0 | 0 | d | 0 | 10 | 3 | 0 |
| f | 0 | 1 | 1 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство — в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много «пустых мест» (нулей). Кроме того, для «общения» с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.
Scapegoat-tree — сбалансированное двоичное дерево поиска, обеспечивающее наихудшее время поиска — , и амортизирующее время вставки и удаления элемента — .
В отличие от большинства других самобалансирующихся бинарных деревьев поиска, которые обеспечивают худшем случае время поиска, Scapegoat деревья не требуют дополнительной памяти в узлах по сравнению с обычным двоичным деревом поиска: узел хранит только ключ и два указателя на своих потомков.
Содержание
- 1 Операции
- 1.1 Обозначения и Определения
- 1.2 Структура вершины
- 1.3 Поиск элемента
- 1.4 Вставка элемента
- 1.4.1 Тривиальный способ перебалансировки
- 1.4.2 Получение списка
- 1.4.3 Построение дерева
- 1.4.4 Перестроение дерева
- 1.4.5 Более сложный способ перебалансировки
- 1.4.6 Псевдокод
- 1.5 Удаление элемента
- 1.5.1 Псевдокод
- 2 Сравнение с другими деревьями
- 2.1 Достоинства Scapegoat дерева
- 2.2 Недостатки Scapegoat дерева
- 3 См. также
- 4 Источники информации
Операции
| Операции | Insert | Delete | Search | Память | |||
|---|---|---|---|---|---|---|---|
| Среднее | Худшее | Среднее | Худшее | Среднее | Худшее | Среднее | Худшее |
| Scapegoat-tree | Амортизировано | Амортизировано |
Обозначения и Определения
Квадратные скобки в обозначениях означают, что хранится это значение явно, а значит можно взять за время . Круглые скобки означают, что значение будет вычисляться по ходу дела то есть память не расходуется, но зато нужно время на вычисление.
— обозначение дерева,
— корень дерева ,
— левый сын вершины ,
— правый сын вершины ,
— брат вершины (вершина, которая имеет с общего родителя),
— глубина вершины (количество рёбер от нее до корня),
— глубина дерева (глубина самой глубокой вершины дерева ),
— вес вершины (количество всех её дочерних вершин плюс — она сама),
— размер дерева (количество вершин в нём),
— максимальный размер дерева (максимальное значение, которое параметр принимал с момента последней перебалансировки, то есть если перебалансировка произошла только что, то
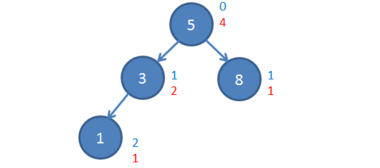
Синим цветом обозначены глубины вершин, а красным — их веса.
Считается вес вершины следующим образом: для новой вершины вес равен . Для её родителя (вес новой вершины) (вес самого родителя) .
Возникает вопрос — как посчитать ? Делается это рекурсивно. Это займёт время . Понимая, что в худшем случае придётся посчитать вес половины дерева — здесь появляется та самая сложность в худшем случае, о которой говорилось в начале. Но поскольку совершается обход поддерева -сбалансированного по весу дерева можно показать, что амортизированная сложность операции не превысит .
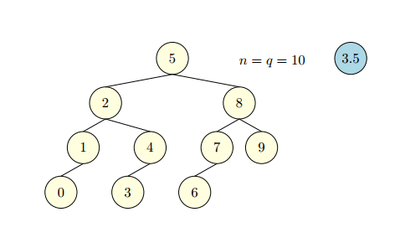
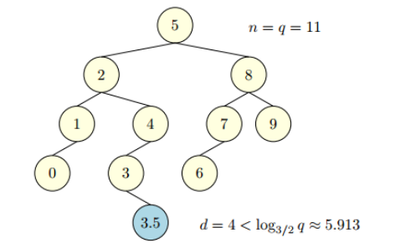
В данном Scapegoat-дереве ,
Коэффициeнт — это число в диапазоне от , определяющее требуемую степень качества балансировки дерева.
| Определение: |
| Некоторая вершина называется -сбалансированной по весу, если и . |
Перед тем как приступить к работе с деревом, выбирается параметр в диапазоне . Также нужно завести две переменные для хранения текущих значений и и обнулить их.
Структура вершины
struct Node: T key //значение в вершине Node left //левый ребенок вершины Node right //правый ребенок вершины Node height //высота поддерева данной вершины Node depth //глубина вершины Node parent //ссылка на родителя Node sibling //ссылки на "братьев" данной вершины
Поиск элемента
Пусть требуется найти в данном Scapegoat дереве какой-то элемент. Поиск происходит так же, как и в обычном дереве поиска, поскольку не меняет дерево, но его время работы составляет .
Таким образом, сложность получается логарифмическая, но! При близком к мы получаем двоичный (или почти двоичный) логарифм, что означает практически идеальную скорость поиска. При близком к единице основание логарифма стремится к единице, а значит общая сложность стремится к .
- — корень дерева или поддерева, в котором происходит поиск.
- — искомый ключ в дереве.
Search(root, k):
if root = or root.key = k:
return root
else if k root.left.key:
return Search(root.left, k)
else:
return Search(root.right, k)
Вставка элемента
Классический алгоритм вставки нового элемента: поиском ищем место, куда бы подвесить новую вершину, ну и подвешиваем. Легко понять, что это действие могло нарушить -балансировку по весу для одной или более вершин дерева. И вот теперь начинается то, что и дало название нашей структуре данных: требуется найти Scapegoat-вершину — вершину, для которой потерян -баланс и её поддерево должно быть перестроено. Сама только что вставленная вершина, хотя и виновата в потере баланса, Scapegoat-вершиной стать не может — у неё ещё нет потомков, а значит её баланс идеален. Соответственно, нужно пройти по дереву от этой вершины к корню, пересчитывая веса для каждой вершины по пути. Может возникнуть вопрос — нужно ли хранить ссылки на родителей? Поскольку к месту вставки новой вершины пришли из корня дерева — есть стек, в котором находится весь путь от корня к новой вершине. Берутся родители из него. Если на этом пути от нашей вершины к корню встретится вершина, для которой критерий -сбалансированности по весу нарушился — тогда полностью перестраивается соответствующее ей поддерево так, чтобы восстановить -сбалансированность по весу.
Сразу появляется вопрос — как делать перебалансировку найденной Scapegoat-вершины?
Есть способа перебалансировки, — тривиальный и чуть более сложный.
Тривиальный способ перебалансировки
- совершается обход всего поддерева Scapegoat-вершины (включая её саму) с помощью in-order обхода — на выходе получается отсортированный список (свойство In-order обхода бинарного дерева поиска).
- Находится медиана на этом отрезке и подвешивается в качестве корня поддерева.
- Для «левого» и «правого» поддерева рекурсивно повторяется та же операция.
Данный способ требует времени и столько же памяти.
Получение списка
- — корень дерева, которое будет преобразовано в список.
FlattenTree(root, head):
if root = :
return head
root.right = FlattenTree(root.right, head)
return FlattenTree(root.left, root)
Построение дерева
- — число вершин в списке.
- — первая вершина в списке.
BuildHeightBalancedTree(size, head):
if size = 1 then:
return head
else if size = 2 then:
(head.right).left = head
return head.right
root = (BuildHeightBalancedTree(⌊(size − 1)/2⌋, head)).right
last = BuildHeightBalancedTree(⌊(size − 1)/2⌋, root.right)
root.left = head
return last
Перестроение дерева
- — число вершин в поддереве.
- — вершина, которая испортила баланс.
RebuildTree(size, scapegoat):
head = FlattenTree(scapegoat, )
BuildHeightBalancedTree(size, head)
while head.parent
head = head.parent
return head
Более сложный способ перебалансировки
Время работы перебалансировки вряд ли улучшится — всё-таки каждую вершину нужно «подвесить» в новое место. Но можно попробовать сэкономить память. Давайте посмотрим на способ алгоритма внимательнее. Выбирается медиана, подвешивается в корень, дерево делится на два поддерева — и делится весьма однозначно. Никак нельзя выбрать «какую-то другую медиану» или подвесить «правое» поддерево вместо левого. Та же самая однозначность преследует и на каждом из следующих шагов. То есть для некоторого списка вершин, отсортированных в возрастающем порядке, будет ровно одно порождённое данным алгоритмом дерево. А откуда же берется отсортированный список вершин? Из in-order обхода изначального дерева. То есть каждой вершине, найденной по ходу in-order обхода перебалансируемого дерева соответствует одна конкретная позиция в новом дереве. И можно эту позицию рассчитать и без создания самого отсортированного списка. А рассчитав — сразу её туда записать. Возникает только одна проблема — этим затирается какая-то (возможно ещё не просмотренная) вершина — что же делать? Хранить её. Где? Ответ прост: выделять для списка таких вершин память. Но этой памяти нужно будет уже не , а всего лишь .
Представьте себе в уме дерево, состоящее из трёх вершин — корня и двух подвешенных как «левые» сыновья вершин. In-order обход вернёт нам эти вершины в порядке от самой «глубокой» до корня, но хранить в отдельной памяти по ходу этого обхода нам придётся всего одну вершину (самую глубокую), поскольку когда мы придём во вторую вершину, мы уже будем знать, что это медиана и она будет корнем, а остальные две вершины — её детьми. То есть расход памяти здесь — на хранение одной вершины, что согласуется с верхней оценкой для дерева из трёх вершин — .
Таким образом, если нужно сэкономить память, то способ перебалансировки дерева — лучший вариант.
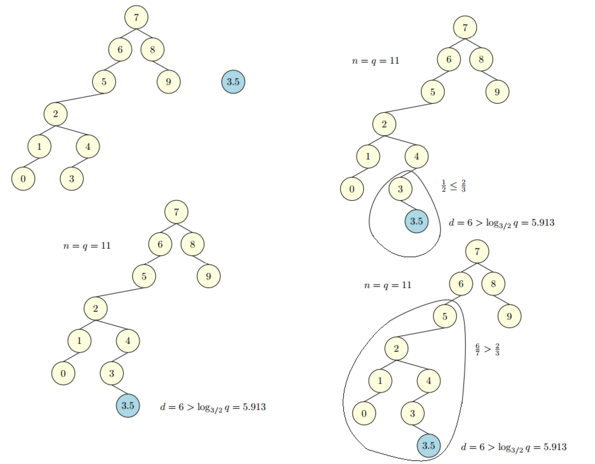
|
Вставка без нарушения баланса 1 |
Вставка без нарушения баланса 2 |
Вставка с нарушением баланса. Вершина 5 стала Scapegoat, будет запущена перебалансировка
Псевдокод
- — узел дерева. Обычно, процедура вызывается от только что добавленной вершины.
FindScapegoat(n):
size = 1
height = 0
while n.parent :
height = height + 1
totalSize = 1 + size + n.sibling.size()
if height :
return n.parent
n = n.parent
size = totalSize
Сама вставка элемента:
- — ключ, который будет добавлен в дерево.
Insert(k):
height = InsertKey(k)
if height = −1:
return false;
else if height > T.hα:
scapegoat = FindScapegoat(Search(T.root, k))
RebuildTree(n.size(), scapegoat)
return true
Удаление элемента
Удаляется элемент из дерева обычным удалением вершины бинарного дерева поиска (поиск элемента, удаление, возможное переподвешивание детей).
Далее следует проверка выполнения условия:
- ;
Если оно выполняется — дерево могло потерять -балансировку по весу, а значит нужно выполнить полную перебалансировку дерева (начиная с корня) и присвоить:
- ;
Псевдокод
Функция удаляет элемент, аналогично удалению в бинарном дереве, и возвращает глубину удаленного элемента.
- — ключ, который будет удален.
Delete(k):
deleted = DeleteKey(k)
if deleted:
if T.size < (T.α · T.maxSize):
RebuildTree(T.size, T.root)
Сравнение с другими деревьями
Достоинства Scapegoat дерева
- По сравнению с такими структурами, как Красно-черное дерево, АВЛ-дерево и Декартово дерево, нет необходимости хранить какие-либо дополнительные данные в вершинах (а значит появляется выигрыш по памяти).
- Отсутствие необходимости перебалансировать дерево при операции поиска (а значит гарантируется максимальное время поиска , в отличии от структуры данных Splay-дерево, где гарантируется только амортизированное )
- При построении дерева выбирается некоторый коэффициент , который позволяет улучшать дерево, делая операции поиска более быстрыми за счет замедления операций модификации или наоборот. Можно реализовать структуру данных, а дальше уже подбирать коэффициент по результатам тестов на реальных данных и специфики использования дерева.
Недостатки Scapegoat дерева
- В худшем случае операции модификации дерева могут занять времени (амортизированная сложность у них по-прежнему , но защиты от плохих случаев нет).
- Можно неправильно оценить частоту разных операций с деревом и ошибиться с выбором коэффициента — в результате часто используемые операции будут работать долго, а редко используемые — быстро, что не очень хорошо.
См. также
- Поисковые структуры данных
- АВЛ-дерево
- Декартово дерево
- Splay-дерево
- Красно-черное дерево
Источники информации
- Википедия — Scapegoat tree
- Хабрахабр — Scapegoat деревья
- Scapegoat Tree Applet by Kubo Kovac
страницы: 1 2 3 4
Содержание
- Содержание
- Ориентированные графы
- Взвешенные графы
- Способы представления графов
- Матрица смежности
- Примечания
Ориентированные графы
Орграф — это граф, все рёбра которого имеют направление. Такие направленные рёбра называются дугами. На рисунках дуги изображаются стрелочками (см. рис. 11.6).
Рис. 11.6. Орграф
В отличие от рёбер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из неё исходит), вторая — концом дуги (дуга в неё входит). Можно сказать, что любое ребро — это пара дуг, направленных навстречу друг другу.
Если в графе присутствуют и рёбра, и дуги, то его называют смешанным.
Все основные понятия, определённые для неориентированных графов (инцидентность, смежность, достижимость, длина пути и т. п.), остаются в силе и для орграфов — нужно лишь заменить слово «ребро» словом «дуга». А немногие исключения связаны с различиями между рёбрами и дугами.
Степень вершины в орграфе — это не одно число, а пара чисел: первое характеризует количество исходящих из вершины дуг, а второе — количество входящих дуг.
Путь в орграфе — это последовательность вершин (без повторений), в которой любые две соседние вершины смежны, причём каждая вершина является одновременно концом одной дуги и началом следующей дуги. Например, в орграфе на рис. 11.6 нет пути, ведущего из вершины 2 в вершину 5. «Двигаться» по орграфу можно только в направлениях, заданных стрелками.
Таблица 11.2. Примеры ориентированных графов
| Орграф | Вершины | Дуги |
|---|---|---|
| Чайнворд | Слова | Совпадение последней и первой букв (возможность связать два слова в цепочку) |
| Стройка | Работы | Необходимое предшествование (например, стены нужно построить раньше, чем крышу, т. п.) |
| Обучение | Курсы | Необходимое предшествование (например, курс по языку Pascal полезно изучить прежде, чем курс по Ada, и т. п.) |
| Одевание ребенка | Предметы гардероба | Необходимое предшествование (например, носки должны быть надеты раньше, чем ботинки, и т. п.) |
| Европейский город | Перекрёстки | Узкие улицы с односторонним движением |
| Организация | Сотрудники | Иерархия (начальник — подчинённый) |
Взвешенные графы
Взвешенный (другое название: размеченный) граф (или орграф) — это граф (орграф), некоторым элементам которого (вершинам, рёбрам или дугам) сопоставлены числа. Наиболее часто встречаются графы с помеченными рёбрами. Числа–пометки носят различные названия: вес, длина, стоимость.
Замечание: Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все рёбра которого имеют одинаковый вес 1.
Длина пути во взвешенном (связном) графе — это сумма длин (весов) тех рёбер, из которых состоит путь. Расстояние между вершинами — это, как и прежде, длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображённом на рис. 11.7, равно 6.
Рис. 11.7. Взвешенный граф
N–периферия вершины v — это множество вершин, расстояние до каждой из которых (от вершины v) не меньше, чем N.
Таблица 11.3. Примеры взвешенных графов
| Граф | Вершины | Вес вершины | Рёбра (дуги) | Вес ребра (дуги) |
|---|---|---|---|---|
| Таможни | Государства | Площадь территории | Наличие наземной границы | Стоимость получения визы |
| Переезды | Города | Стоимость ночёвки в гостинице | Дороги | Длина дороги |
| Супер–чайнворд | Слова | — | Совпадение конца и начала слов (возможность «сцепить» слова) | Длина пересекающихся частей |
| Карта | Государства | Цвет на карте | Наличие общей границы | — |
| Сеть | Компьютеры | — | Сетевой кабель | Стоимость кабеля |
Способы представления графов
Существует довольно большое число разнообразных способов представления графов. Однако мы изложим здесь только самые полезные с точки зрения программирования.
Матрица смежности
Матрица смежности Sm — это квадратная матрица размером NxN (N — количество вершин в графе), заполненная единицами и нулями по следующему правилу:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u, v] = 1, в противном случае Sm[u, v] = 0.
Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа — несимметричной.
Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = ves(e), в противном случае Sm[u,v] = 0.
Это хорошо согласуется с замечанием, сделанным в предыдущем пункте: невзвешенный граф можно интерпретировать как взвешенный, все рёбра которого имеют одинаковый вес 1.
Небольшое затруднение возникнет в том случае, если в графе разрешаются рёбра с весом 0. Тогда придётся хранить два массива: один с нулями и единицами, которые служат показателем наличия рёбер, а второй — с весами этих рёбер.
В качестве примера приведём матрицы смежности для трёх графов, изображённых на рис. 11.5, рис. 11.6 и рис. 11.7 (см. рис. 11.8).
Таблица 11.8. Примеры матриц смежности
| a | b | c | d | f | 1 | 2 | 3 | 4 | 5 | a | b | c | d | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | a | 0 | 1 | 10 | 0 |
| b | 1 | 0 | 1 | 1 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | b | 1 | 0 | 2 | 10 |
| c | 1 | 1 | 0 | 1 | 1 | 3 | 1 | 1 | 0 | 0 | 1 | c | 10 | 2 | 0 | 3 |
| d | 0 | 1 | 1 | 0 | 1 | 4 | 0 | 0 | 1 | 0 | 0 | d | 0 | 10 | 3 | 0 |
| f | 0 | 1 | 1 | 1 | 0 | 5 | 0 | 0 | 0 | 0 | 0 |
Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на её использовании. А неудобство — в несколько завышенном требовании к памяти: если граф далёк от полного, то в массиве, хранящем матрицу смежности, оказывается много «пустых мест» (нулей). Кроме того, для «общения» с пользователем этот способ представления графов не слишком удобен: его лучше применять только для внутреннего представления данных.
страницы: 1 2 3 4