Баканина Л.П. Задачи о воздушных шарах // Квант
Баканина Л.П. Задачи о воздушных шарах // Квант. — 1975. — № 1. — С. 60-63.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В наш век самолетов и ракет, для которых доступны любые высоты над поверхностью Земли, воздушные шары, громоздкие, ненадежные и неуправляемые, уже отошли в прошлое, хотя когда-то именно они дали человеку возможность подняться в воздух. Впрочем, в некоторых случаях воздушные шары очень удобны, они используются и сейчас. Например, с аэростата удобно обучать прыжкам с. парашютом, а метеорологи исследуют давление, температуру и воздушные потоки в атмосфере с помощью шаров-зондов.
Задачи о воздушных шарах даются иногда на вступительных экзаменах. Обычно их можно разделить на два типа:
1) задачи, в которых нужно найти связь между габаритами и наполнением шара и подъемной силой, действующей на шар у поверхности Земли;
2) задачи, в которых нужно определить максимальную высоту подъема шара; при этом задается какая-нибудь модель атмосферы, то есть закон изменения давления и температуры с высотой.
По существу, задачи обоих типов – это задачи на статику. Для их решения нужно уметь применять уравнение состояния газов и найти условие равновесия шара, на который действует сила притяжения Земли и выталкивающая сила со стороны окружающего шар воздуха. Если выталкивающая сила больше силы притяжения (разность этих сил называют подъемной силой), шар поднимается вверх. Но по мере подъема уменьшается плотность окружающего воздуха, а, следовательно, уменьшается и выталкивающая сила, по закону Архимеда равная
где ρ — плотность воздуха, а V — объем шара. На некоторой высоте выталкивающая сила окажется равной силе притяжения – это и будет максимальной высотой подъема шара.
Разберем теперь несколько конкретных задач, которые в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Сферическая оболочка воздушного шара сделана из материала, квадратный метр которого имеет массу b = 1 кг/м 2 . Шар наполнен гелием при нормальном атмосферном давлении. При каком минимальном радиусе шар поднимает сам себя? Температура гелия и температура окружающего воздуха одинаковы и равны 0 ºС. Молекулярная масса воздуха 29 кг/кмоль, молекулярная масса гелия 4 кг/кмоль.
При увеличении радиуса шара выталкивающая сила растет пропорционально кубу радиуса, а вес оболочки – пропорционально квадрату радиуса. Следовательно, выталкивающая сила растет быстрее и, начиная с какого-то значения радиуса, станет больше, чем вес оболочки. Тогда шар начнет подниматься. Обозначим этот радиус оболочки через r. При этом
Плотности воздуха ρв и гелия ρНе при данных условиях найдем с помощью закона Менделеева–Клапейрона :
Задача 2. Объем воздушного шара равен V = 230 м 3 , масса оболочки М = 145 кг. Шар наполнен горячим воздухом при нормальном атмосферном давлении. Какую температуру должен иметь воздух внутри оболочки, чтобы шар начал подниматься? Температура наружного воздуха t0 = 0 о С.
При нагревании воздуха его плотность уменьшается, так как (см. задачу 1). Шар начнет подниматься, если (ρ0 – плотность наружного воздуха). Подставляя выражения для плотности наружного воздуха и воздуха внутри шара ρ, получаем
Задача 3. Для удержания на поверхности Земли метеорологического шара-зонда с массой М = 20 кг необходимо приложить силу F = 1000 Н. Шар поднимается до такой высоты, где его объем увеличивается в два раза. Температура воздуха, измеренная на этой высоте с помощью зонда, оказалась равной t = –43 ºС. Вычислить давление воздуха на этой высоте, если на поверхности Земли давление р0 = 754 мм рт. ст., а температура t0= +17 °С.
Условие равновесия шара у поверхности Земли записывается так:
где V — объем шара у поверхности Земли, а — плотность воздуха. При этом масса шара М включает в себя массу оболочки, приборов и газа, заключенного внутри оболочки. Из условия известно, что объем шара при подъеме увеличивается. Следовательно, оболочка шара мягкая и герметичная. Объем увеличивается потому, что при мягкой оболочке давление газа внутри должно быть таким же, как давление окружающего воздуха, которое уменьшается с высотой. Если оболочка герметичная, масса шара не изменяется при подъеме и максимальная высота его подъема определяется условием
где . Решая совместно уравнения (1) и (2), находим
Задача 4. Шар-зонд, наполненный водородом, имеет герметичную оболочку постоянного объема V = 50 м 3 . Масса шара вместе с водородом М = 5 кг. Определить, на какую максимальную высоту он сможет подняться, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура в стратосфере t = –60 ºС. Молекулярная масса воздуха 29 кг/кмоль. Давление у поверхности Земли р0 = 1 атм.
На максимальной высоте выталкивающая сила равна весу шара- зонда:
Выразив плотность окружающего воздуха через давление и температуру, получим
Таким образом, давление воздуха на этой высоте равно
Посмотрим теперь, во сколько раз давление р меньше давления у поверхности Земли р0: .
Из условия известно, что давление падает в два раза через каждые 5 км подъема, то есть , где Н — высота подъема, a h = 5 км. В нашем случае
Задача 5. Нерастяжимая оболочка шара-зонда объема V = 75 м 3 имеет в нижней части небольшое отверстие. Масса оболочки t = 7 кг. Шар наполнен водородом. Определить, на какую максимальную высоту сможет подняться этот шар-зонд, если известно, что атмосферное давление уменьшается в два раза через каждые h = 5 км высоты. Температура воздуха в стратосфере t = –60 °С, температура водорода равна температуре окружающего воздуха. Давление у поверхности Земли р0 = 1 атм.
Эта задача отличается от предыдущей тем, что оболочка шара не герметична, а имеет отверстие. Следовательно, давление внутри шара все время равно давлению в атмосфере, и по мере увеличения высоты подъема шара водород вытекает из отверстия. Будем, считать, что подъем происходит достаточно быстро и можно пренебречь диффузией воздуха внутрь оболочки, тогда условие равновесия шара на максимальной высоте
Плотности водорода и воздуха можно найти из уравнения Менделеева-Клапейрона:
Таким образом, давление на максимальной высоте
Отношение , и, следовательно, высота подъема Н = 20 км (см. решение предыдущей задачи).
Высота подъема в задаче 5 получилась такая же, как для герметичного шара в задаче 4, но не следует забывать, что мы рассматривали разные шары, с разными объемами и массами. А если оба шара совершенно одинаковы и отличаются только тем, что у одного оболочка герметичная, а у другого имеет отверстие, — какой из шаров поднимется выше в этом случае?
Выталкивающая сила будет одинакова для обоих шаров, так как их объемы равны. Если начальные массы шаров были одинаковы, то после подъема шар с отверстием окажется легче, так как часть наполняющего его газа вытечет при подъёме. Следовательно, шар с отверстием сможет подняться на большую высоту.
Обычно человеку, впервые задумавшемуся над этим вопросом, такой результат кажется странным. Часто задают вопрос: «Как вообще в шаре с отверстием возникает подъемная сила? Ведь снизу, там, где отверстие, воздух и газ внутри шара находятся в равновесии».
Давайте рассмотрим верхнюю точку шара. Если в нижней точке шара давление воздуха и газа равно р0, в верхней точке давление воздуха , а давление газа (h — высота шара). Если , то и, следовательно, на оболочку снизу действует большая сила, чем сверху — возникает подъемная сила. Легко убедиться (вы сможете это сделать сами для тела достаточно простой формы), что именно эта разница давлений и дает результирующую выталкивающую силу, определяемую законом Архимеда. Недоумение часто возникает потому, что при расчетах плотности газа внутри шара обычно считают давление в шаре всюду одинаковым. Не нужно забывать, что это всего лишь приближение. Если мы определяем саму величину
то, так как h мало — всего несколько метров, , и мы можем считать . Если же нас интересует разность
то здесь оба члена одинаковы по порядку величины, и учитывать их надо оба. Кстати сказать, то, что мы считаем ρв и ρг постоянными, — тоже приближение, на самом деле они уменьшаются с высотой по мере уменьшения давления. Но учет этого обстоятельства дал бы значительно меньшую поправку к выталкивающей силе, этой поправкой можно пренебречь.
1. Определить подъемную силу воздушного шара, в котором находится t г водорода. Оболочка шара герметичная и сделана из легкого неупругого материала, который может свободно растягиваться.
2. На сколько градусов надо нагреть воздух внутри сообщающегося с атмосферой воздушного шара, сферическая оболочка которого имеет диаметр 10 м и весит 10 кг, для того чтобы шар взлетел? Атмосферное давление 735 мм. рт. ст., температура окружающего воздуха +27 °С.
3. Воздушный шар представляет собой баллон постоянного объема, наполненный гелием. Через отверстие в нижней части шар сообщается с атмосферой. Как изменится максимальная высота подъема шара, если гелий нагреть до температуры t1? Температуру атмосферы считать постоянной и равной t0, а давление изменяющимся по закону , где а — постоянная, h — высота подъема, р0 — давление у поверхности Земли.
Как вычислить массу шара
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 40 114.
Шар является одним из наиболее простых трехмерных тел. Чтобы найти массу шара, необходимо знать его объем и плотность. Объем можно вычислить по радиусу, длине окружности или диаметру. Можно также погрузить шар в воду и найти объем по количеству вытесненной им воды. После того как вы определите объем, умножьте его на плотность, и вы получите массу шара.
Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем 


Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)




Тогда масса:
2. Масса цилиндра



Тогда масса:
3. Масса шара


Тогда масса:
4. Масса сегмента шара



Тогда масса:
5. Масса конуса



Для круглого конуса: 

Масса круглого конуса:
6. Масса усеченного конуса






Отсюда масса:
7. Масса пирамиды



Для пирамиды с прямоугольным основанием: 


Тогда масса пирамиды:
8. Масса усеченной пирамиды








И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим:
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,666 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,992 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Незнайка → ЕГЭ → Физика → Вариант 18 → Задание 4
Задание № 24758
Объём воздушного шара-гиганта 8500 м3. Чему равен вес этого шара вместе с наполняющим его тёплым воздухом и кабиной, если он поднялся и неподвижно висит над землёй? Плотность воздуха 1,2 кг/м3.
Ответ: _____ H
Решать другие задания по теме: Статика. Гидростатика. Колебания и волны
Показать ответ
Комментарий:
Посчитаем вес шара по формуле силы Архимеда: [math]P=rho Vg=8500ast1,2ast10=102000;Н[/math].
Ответ: 102000
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Как найти вес воздуха
В обыденной жизни значения слов «масса» и «вес» совпадают – например, говорится, что предмет весит 10 килограммов. Однако в науке эти понятия различны. Масса тела — это физическая величина, характеризующая свойства тела, прямо пропорциональная объёму и плотности. Единица измерения — килограмм. Её величина неизменна и на Земле, и в невесомости. Вес тела прямо пропорционален массе тела и ускорению. Воздух, как и любое другое вещество, имеет вес.

Вам понадобится
- — объём воздуха;
- — плотность воздуха;
- — барометр-анероид;
- — термометр;
- — манометр.
Инструкция
Существует понятие Международной стандартной атмосферы. За нулевую точку отсчета принят воздух, имеющий барометрическое давление 760 мм рт. ст., температуру +15 гр. С, плотность 1,225 кг/м3.Масса тела вычисляется по формуле: m=Vρ,где V – объём вещества, м3;ρ – плотность вещества, кг/м3.Плотность воздуха примите 1,225 кг/м3. Зная объем воздуха, найдите его массу.
Вес тела описывается формулой: G=mc,где G – вес тела, измеряется в Ньютонах;m – масса тела, кг; с – ускорение, м/с2.Если в условии воздух не двигается и находится в земных условиях, ускорение равно ускорению свободного падения: G=mg. Подставьте в формулу значение массы воздуха и найдите его вес.
Если температура и плотность воздуха отличается от принятых за стандарт, массу заданного объема сухого воздуха рассчитайте из уравнения состояния идеального газа Менделеева- Клайперона, где M – молярная масса газа (для воздуха равна 29*10-3 кг/моль);R – универсальная газовая постоянная. R=8.314472 м2кг с-2 К-1 Моль-1 ;T – температура газа, К;p — абсолютное давление, Па.
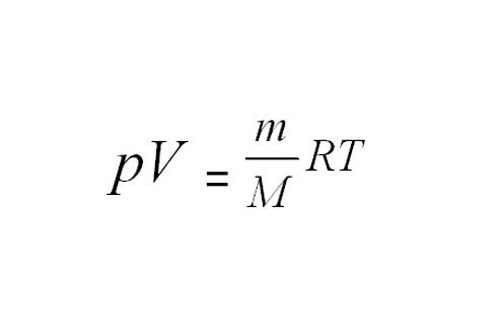
Для расчета требуется знать давление и температуру воздуха. Давление измерьте с помощью барометра-анероида, температуру – термометром. Переведите температуру из градусов Цельсия в Кельвины, прибавив к значению температуры 273. Давление переведите из мм рт. ст. в паскали, 1 мм рт.ст.=133,3 Па. Если воздух заключен в сосуд и находится под давлением, избыточное давление измерьте манометром. Сложите величины избыточного и атмосферного давлений, и вы получите значение абсолютного давления: p=pатм+pизб.
Подставив найденные величины в уравнение Менделеева-Клайперона, решите его и найдите массу воздуха для заданного объёма воздуха.Зная массу, рассчитайте вес воздуха по формуле из шага 2.
Обратите внимание
Формула Менделеева-Клайперона действительна только для сухого воздуха.
Источники:
- как найти объём воздуха
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

