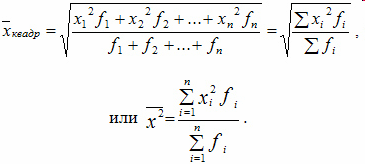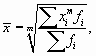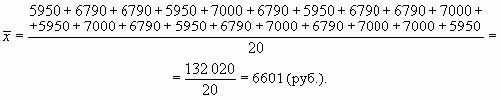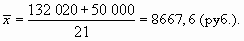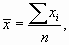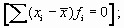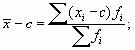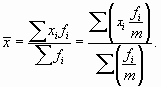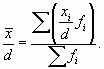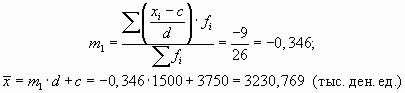Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):
(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
- Средняя арифметическая взвешенная формула 8.9.
(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
|
Желаемый размер заработной платы, тыс.руб хi |
Количество работников fi | хifi |
| 1 | 2 | 3 |
|
50 100 200 350 500 |
6
10 20 9 5 |
300
1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):
Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:
(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле
(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:
Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.
- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12
(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13
(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)
8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)
(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.
Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Средней
величиной
называется статистический показатель,
который дает обобщенную характеристику
варьирующего признака однородных единиц
совокупности в конкретных условиях
места и времени. Величина средней дает
характеристику всей совокупности и
характеризует ее в отношении одного,
данного признака.
Средняя
величина
отражает то общее, что присуще всем
единицам исследуемой совокупности.
Так,
например, средняя заработная плата дает
обобщающую количественную характеристику
состояния оплаты труда рассматриваемой
совокупности работников.
Сущность
средней
заключается в том, что в ней взаимопогашаются
случайные отклонения значений признака
и учитываются изменения, вызванные
основным фактором.
Статистическая
обработка методом средних величин
заключается в замене индивидуальных
значений варьирующего признака
некоторой уравновешенной средней
величиной Х .
Например,
индивидуальная выработка у 5 операционистов
коммерческого банка за день составила
136, 140, 154 и 162 операции. Чтобы получить
среднее число операций за день, выполненных
одним операционистом, необходимо сложить
эти индивидуальные показатели и
полученную сумму разделить на количество
операционистов:
Как
видно из приведенного примера, среднее
число операций не совпадает ни с одним
из индивидуальных, так как ни один
операционист не сделал 150 операций. Но
если мы представим себе, что каждый
операционист сделал по 150 операций, то
их общая сумма не изменится, а будет
также равна 750. Таким образом, мы пришли
к основному свойству средних величин:
сумма индивидуальных значений признака
равна сумме средних величин.
Это
свойство еще раз подчеркивает, что
средняя величина является обобщающей
характеристикой всей статистической
совокупности.
Виды средних величин
Средние
величины делятся на два больших класса:
Степенные
средние:
•
Арифметическая
•
Гармоническая
•
Геометрическая
•
Квадратическая
Структурные
средние:
•
Мода
•
Медиана
Самым
распространенным видом средней является
средняя арифметическая:
•
Средняя
арифметическая простая
•
Средняя
арифметическая взвешенная
•
Средняя
арифметическая для интервального ряда.
Простая
среднеарифметическая величина
представляет
собой среднее слагаемое, при определении
которого общий объем данного признака
в совокупности данных поровну
распределяется между всеми единицами,
входящими в данную.
Так,
среднегодовая выработка продукции на
одного работающего — это такая величина
объема продукции, которая приходилась
бы на каждого работника, если бы весь
объем выпущенной продукции в одинаковой
степени распределялся между всеми
сотрудниками организации. Среднеарифметическая
простая величина исчисляется по формуле:
Равна
отношению суммы индивидуальных значений
признака к количеству признаков в
совокупности

Пример
1.
Бригада
из 6 рабочих получает в месяц 3 3,2 3,3 3,5
3,8 3,1 тыс.руб.
Найти
среднюю заработную плату
Решение:
(3
+ 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 (тыс. руб.)
Средняя
арифметическая взвешенная
Если объем совокупности данных большой
и представляет собой ряд распределения,
то исчисляется взвешенная среднеарифметическая
величина. Так определяют средневзвешенную
цену за единицу продукции: общую стоимость
продукции (сумму произведений ее
количества на цену единицы продукции)
делят на суммарное количество продукции.
Представим
это в виде следующей формулы:
— цена
за единицу продукции;
— количество (объем) продукции.
Средняя
арифметическая взвешенная
равна отношению (суммы произведений
значения признака к частоте повторения
данного признака) к (сумме частот всех
признаков).Используется, когда варианты
исследуемой совокупности встречаются
неодинаковое количество раз.
Пример
2.
Найти
среднюю заработную плату рабочих цеха
за месяц

Средняя
заработная плата может быть получена
путем деления общей суммы заработной
платы на общее число рабочих:

Ответ:
3,35 тыс.руб.
Средняя
арифметическая для интервального ряда
При расчете средней
арифметической для интервального
вариационного ряда
сначала определяют среднюю для каждого
интервала, как полусумму верхней и
нижней границ, а затем — среднюю всего
ряда. В случае открытых интервалов
значение нижнего или верхнего интервала
определяется по величине интервалов,
примыкающих к ним.
Средние,
вычисляемые из интервальных рядов
являются приближенными.
Пример
3.
Определить средний возраст студентов
вечернего отделения.


Средние,
вычисляемые из интервальных рядов
являются приближенными. Степень их
приближения зависит от того, в какой
мере фактическое распределение единиц
совокупности внутри интервала приближается
к равномерному.
При
расчете средних в качестве весов могут
использоваться не только абсолютные,
но и относительные величины (частость):

Средняя
гармоническая
Используется в тех случаях когда
известны индивидуальные значения
признака Х и произведение Х*f , а частоты
f неизвестны.
В
примере ниже Х — урожайность известна,
f — площадь неизвестна (хотя её можно
вычислить делением валового сбора
зерновых на урожайность), Х*f — валовый
сбор зерна известен.
Среднегармоническую
величину можно определить по следующей
формуле:
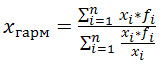
Пример4.
Вычислить
среднюю урожайность по трем фермерским
хозяйствам


В
тех случаях, когда произведение Х*f
одинаково или равно 1 (z = 1) для расчета
применяют среднюю гармоническую простую,
вычисляемую по формуле:
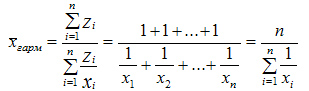
Средняя
гармоническая простая —
показатель, обратный средней арифметической
простой, исчисляемый из обратных значений
признака.
Средняя
геометрическая простая
дает возможность сохранять в неизменном
виде не сумму, а произведение индивидуальных
значений данной величины. Ее можно
определить по следующей формуле:
Средние
геометрические величины наиболее часто
используются при анализе темпов роста
экономических показателей, исчисляемых
из обратных значений признака.
Для
расчетов средней геометрической простой
используется формула:

где:
— цепной
коэффициент роста
n
— число этих коэффициентов роста
П—
знак произведения
m
— количество уровней ряда
— значение
начального уровня ряда
— значение
конечного уровня ряда .
Средняя
квадратическая
Средние диаметры колес, труб, средние
стороны квадратов определяются при
помощи средней квадратической.
Среднеквадратические
величины используются для расчета
некоторых показателей, например
коэффициента вариации, характеризующего
ритмичность выпуска продукции. Он
определяет среднеквадратическое
отклонение от планового выпуска продукции
за определенный период по следующей
формуле:
Эти
величины точно характеризуют изменение
экономических показателей по сравнению
с их базисной величиной, взятое в его
усредненной величине.
Средняя
квадратическая простая вычисляется по
формуле:
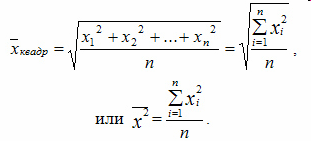
Средняя
квадратическая взвешенная:
В
статистике могут применяться также
степенные средние 3-го и более высоких
порядков.
Кроме
степенных средних в статистике для
относительной характеристики величины
варьирующего признака и внутреннего
строения рядов распределения пользуются
структурными средними, которые
представлены ,в основном, модой
и медианой.
Мода
— это наиболее часто встречающийся
вариант ряда.
Мода
применяется, например, при определении
размера одежды, обуви, пользующейся
наибольшим спросом у покупателей.
Модой
для дискретного ряда является варианта,
обладающая наибольшей частотой.
При
вычислении моды для интервального
вариационного ряда необходимо сначала
определить модальный интервал (по
максимальной частоте), а затем — значение
модальной величины признака по формуле:
где:
— значение
моды
— нижняя
граница модального интервала
h —
величина интервала
— частота
модального интервала
— частота
интервала, предшествующего модальному
— частота
интервала, следующего за модальным.
Медиана
—
это значение признака, которое лежит в
основе ранжированного ряда и делит этот
ряд на две равные по численности части.
Для
определения медианы
в дискретном ряду при наличии
частот
сначала вычисляют полусумму частот
,
а
затем определяют, какое значение варианта
приходится на нее. (Если отсортированный
ряд содержит нечетное число признаков,
то номер медианы вычисляют по формуле:
Ме
= (n(число признаков в совокупности) +
1)/2, в случае четного числа признаков
медиана будет равна средней из двух
признаков, находящихся в середине ряда).
При
вычислении медианы для
интервального вариационного ряда
сначала определяют медианный интервал,
в пределах которого находится медиана,
а затем — значение медианы по формуле:

где:
— искомая
медиана
— нижняя
граница интервала, который содержит
медиану
— величина
интервала
— сумма
частот или число членов ряда
—
сумма
накопленных частот интервалов,
предшествующих медианному
— частота
медианного интервала.
Пример
5.
Найти моду и медиану.

Решение:
В
данном примере модальный интервал
находится в пределах возрастной группы
25-30 лет, так как на этот интервал приходится
наибольшая частота (1054).
Рассчитаем
величину моды:
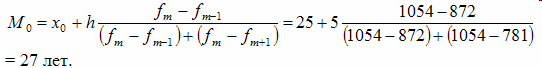
Это
значит что модальный возраст студентов
равен 27 годам.
Вычислим
медиану. Медианный интервал находится
в возрастной группе 25-30 лет, так как в
пределах этого интервала расположена
варианта, которая делит совокупность
на две равные части (Уfi/2 = 3462/2 = 1731). Далее
подставляем в формулу необходимые
числовые данные и получаем значение
медианы:

Это
значит что одна половина студентов
имеет возраст до 27,4 года, а другая свыше
27,4 года.
Кроме
моды и медианы могут быть использованы
такие показатели, как квартили, делящие
ранжированный ряд на 4 равные части,
децили -10 частей и перцентили — на 100
частей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Начиная рассуждать о средних величинах, чаще всего вспоминают, как заканчивали школу и поступали в учебное заведение. Тогда по аттестату рассчитывался средний балл: все оценки (и хорошие, и не очень) складывали, полученную сумму делили на их количество. Так вычисляется самый простой вид средней, которая называется средняя арифметическая простая. На практике в статистике применяются различные виды средних величин: арифметическая, гармоническая, геометрическая, квадратическая, структурные средние. Тот или иной их вид используется в зависимости от характера данных и целей исследования.
Средняя величина является наиболее распространенным статистическим показателем, с помощью которого дается обобщающая характеристика совокупности однотипных явлений по одному из варьирующих признаков. Она показывает уровень признака в расчете на единицу совокупности. С помощью средних величин проводится сравнение различных совокупностей по варьирующим признакам, изучаются закономерности развития явлений и процессов общественной жизни.
В статистике применяются два класса средних: степенные (аналитические) и структурные. Последние используются для характеристики структуры вариационного ряда и будут рассмотрены далее в гл. 8.
К группе степенных средних относят среднюю арифметическую, гармоническую, геометрическую, квадратическую. Индивидуальные формулы для их вычисления можно привести к виду, общему для всех степенных средних, а именно
где m — показатель степенной средней: при m = 1 получаем формулу для вычисления средней арифметической, при m = 0 — средней геометрической, m = -1 — средней гармонической, при m = 2 — средней квадратической;
xi — варианты (значения, которые принимает признак);
fi — частоты.
Главным условием, при котором можно использовать степенные средние в статистическом анализе, является однородность совокупности, которая не должна содержать исходных данных, резко различающихся по своему количественному значению (в литературе они носят название аномальных наблюдений).
Продемонстрируем важность этого условия на следующем примере.
Пример 6.1. Вычислим среднюю заработную плату сотрудников малого предприятия.
Таблица
6.1.
Заработная плата работников
| № п/п | Заработная плата, руб. | № п/п | Заработная плата, руб. |
|---|---|---|---|
| 1 | 5 950 | 11 | 7 000 |
| 2 | 6 790 | 12 | 5 950 |
| 3 | 6 790 | 13 | 6 790 |
| 4 | 5 950 | 14 | 5 950 |
| 5 | 7 000 | 5 | 6 790 |
| 6 | 6 790 | 16 | 7 000 |
| 7 | 5 950 | 17 | 6 790 |
| 8 | 7 000 | 18 | 7 000 |
| 9 | 6 790 | 19 | 7 000 |
| 10 | 6 790 | 20 | 5 950 |
Для расчета среднего размера заработной платы необходимо просуммировать заработную плату, начисленную всем работникам предприятия (т.е. найти фонд заработной платы), и разделить на число работающих:
А теперь добавим в нашу совокупность всего лишь одного человека (директора этого предприятия), но с окладом в 50 000 руб. В таком случае вычисляемая средняя будет совсем другая:
Как видим, она превышает 7000 руб., т.д. она больше всех значений признака за исключением одного-единственного наблюдения.
Для того чтобы таких случаев не происходило на практике, и средняя не теряла бы своего смысла (в примере 6.1 она уже не выполняет роль обобщающей характеристики совокупности, которой должна быть), при расчете средней следует аномальные, резко выделяющиеся наблюдения либо исключить из анализа и тем самым сделать совокупность однородной, либо разбить совокупность на однородные группы и вычислить средние значения по каждой группе и анализировать не общую среднюю, а групповые средние значения.
6.1. Средняя арифметическая и ее свойства
Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина.
При расчете средней заработной платы по данным таблицы примера 6.1 мы сложили все значения признака и поделили на их количество. Ход наших вычислений запишем в виде формулы средней арифметической простой
где хi — варианты (отдельные значения признака);
п — число единиц в совокупности.
Пример 6.2. Теперь сгруппируем наши данные из таблицы примера 6.1, т.д. построим дискретный вариационный ряд распределения работающих по уровню заработной платы. Результаты группировки представлены в таблице.
Таблица
6.2.
Распределение работников предприятия по уровню заработной платы
| Заработная плата, руб. | Численность работников |
|---|---|
| 5 950 | 6 |
| 6 790 | 8 |
| 7 000 | 6 |
| Итого | 20 |
Запишем выражение для вычисления среднего уровня заработной платы в более компактной форме:
В примере 6.2 была применена формула средней арифметической взвешенной
где fi — частоты, показывающие, сколько раз встречается значение признака хi y единиц совокупности.
Расчет средней арифметической взвешенной удобно проводить в таблице, как это показано ниже (табл. 6.3):
Таблица
6.3.
Расчет средней арифметической в дискретном ряду
| Исходные данные | Расчетный показатель | |
| заработная плата, руб. | численность работающих, чел. | фонд заработной платы, руб. |
| xi | fi | xifi |
| 5 950 | 6 | 35 760 |
| 6 790 | 8 | 54 320 |
| 7 000 | 6 | 42 000 |
| Итого | 20 | 132 080 |
Следует отметить, что средняя арифметическая простая используется в тех случаях, когда данные не сгруппированы или сгруппированы, но все частоты равны между собой.
Часто результаты наблюдения представляют в виде интервального ряда распределения (см. таблицу в примере 6.4). Тогда при расчете средней в качестве xi берут середины интервалов. Если первый и последний интервалы открыты (не имеют одной из границ), то их условно «закрывают», принимая за величины данного интервала величину примыкающего интервала, т.д. первый закрывают исходя из величины второго, а последний — по величине предпоследнего.
Пример 6.3. По результатам выборочного обследования одной из групп населения рассчитаем размер среднедушевого денежного дохода.
В приведенной таблице середина первого интервала равна 500. Действительно, величина второго интервала — 1000 (2000-1000); тогда нижняя граница первого равна 0 (1000-1000), а его середина — 500. Аналогично поступаем с последним интервалом. За его середину принимаем 25 000: величина предпоследнего интервала 10 000 (20 000-10 000), тогда его верхняя граница — 30 000 (20 000 + 10 000), а середина, соответственно, — 25 000.
Таблица
6.4.
Расчет средней арифметической в интервальном ряду
| Среднедушевой денежный доход, руб. в месяц | Численность населения к итогу, % fi |
Середины интервалов xi |
xifi |
|---|---|---|---|
| До 1 000 | 4,1 | 500 | 2 050 |
| 1 000-2 000 | 8,6 | 1 500 | 12 900 |
| 2 000-4 000 | 12,9 | 3 000 | 38 700 |
| 4 000-6 000 | 13,0 | 5 000 | 65 000 |
| 6 000-8 000 | 10,5 | 7 000 | 73 500 |
| 8 000-10 000 | 27,8 | 9 000 | 250 200 |
| 10 000-20 000 | 12,7 | 15 000 | 190 500 |
| 20 000 и выше | 10,4 | 25 000 | 260 000 |
| Итого | 100,0 | — | 892 850 |
Тогда среднедушевой размер месячного дохода составит
Средняя арифметическая величина обладает рядом математических свойств. Приведем основные из них:
- если хi = с, где с — постоянная величина, то средняя арифметическая будет равна с;
- сумма отклонений значений признака от его средней арифметической равна 0, т.е.
- если из всех значений признака вычесть постоянную величину с, то средняя арифметическая уменьшится на эту величину с:
- от уменьшения или увеличения частот fi каждого значения признака в m раз величина средней арифметической не изменится:
- если все индивидуальные значения признака уменьшить или увеличить в d раз, то величина средней арифметической также уменьшится или увеличится в d раз:
На изложенных свойствах средней арифметической базируется один из методов ее расчета — способ моментов, или метод отсчета от условного нуля, который используется в случае вариационных рядов с равными интервалами. Согласно этому методу среднюю арифметическую взвешенную можно вычислить по следующей формуле: x = mi * d + c
где 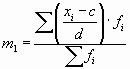
За d, как правило, принимают величину интервалов, а за с — значение середины интервала, находящегося в центре ряда (если количество интервалов нечетное), или середину интервала с наибольшей частотой также из центра ряда (при четном количестве интервалов в центре ряда будут находиться два интервала).
Пример 6.4. Рассчитаем среднюю прибыль по группе банков способом моментов.
Рис.
6.13.
Расчет средней арифметической способом моментов



 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.





 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.