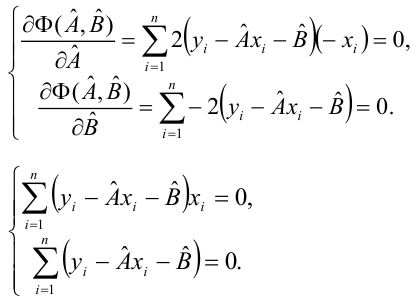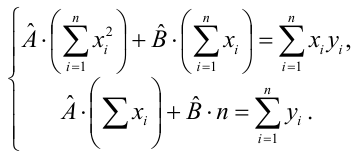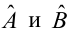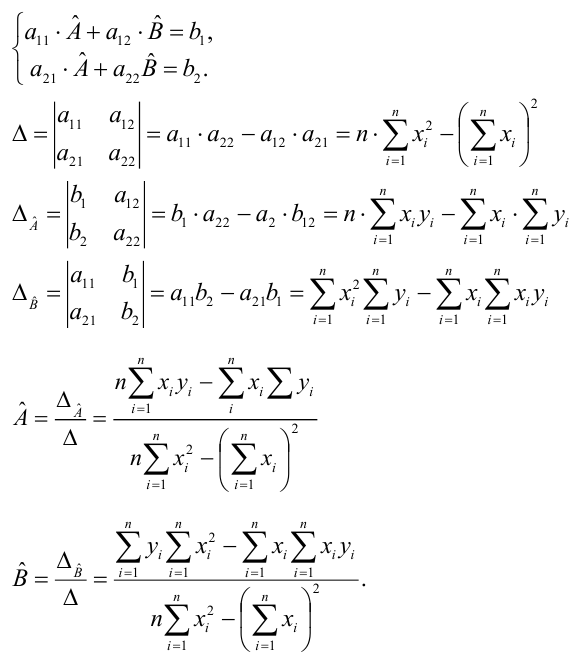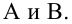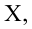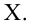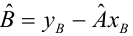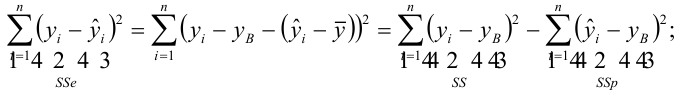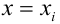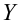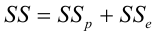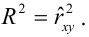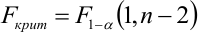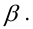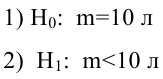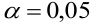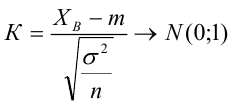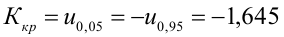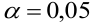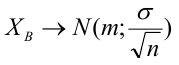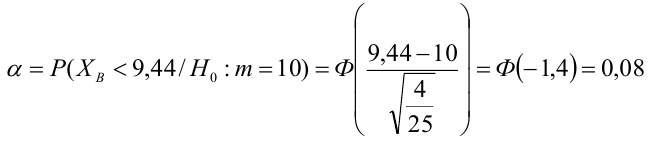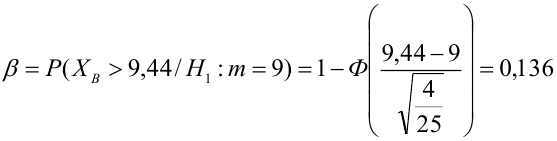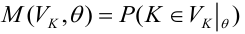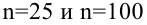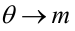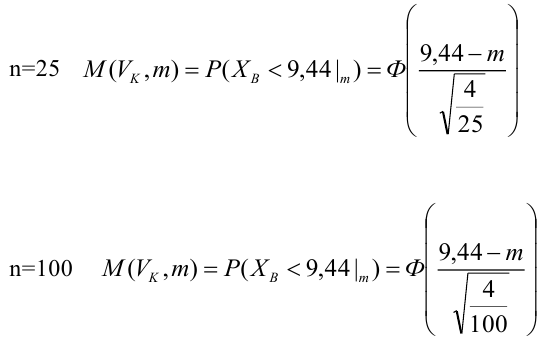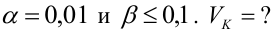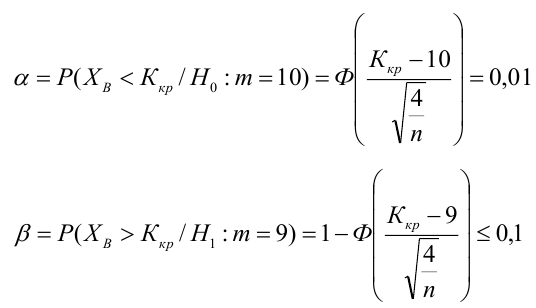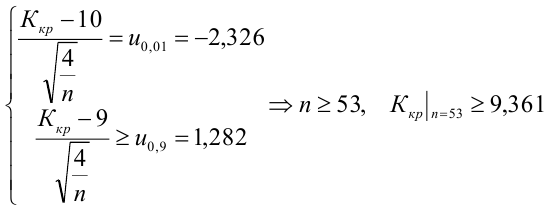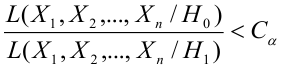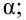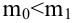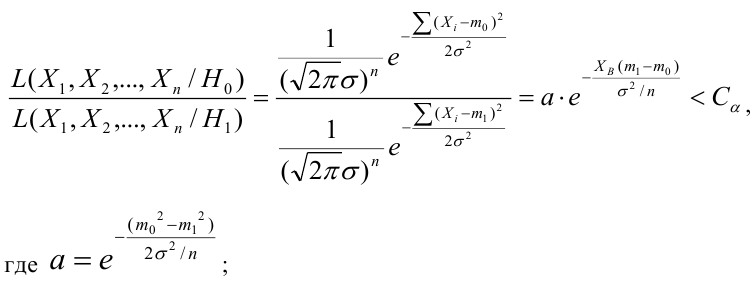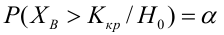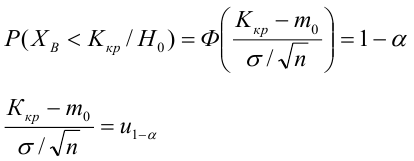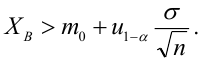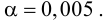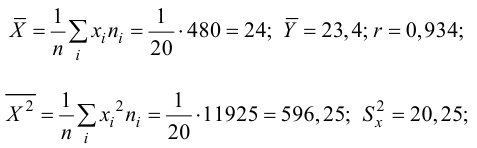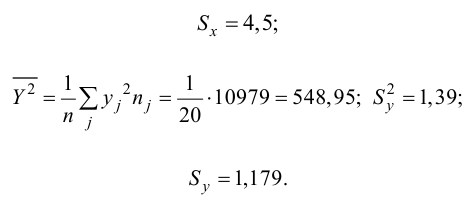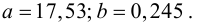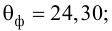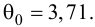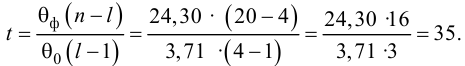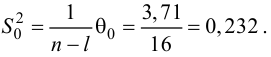Изучение
корреляционных зависимостей основывается
на исследовании таких связей между
переменными, при которых значение одной
переменной, которую можно применять за
зависимую переменную «в среднем»
изменяется в зависимости от того, какие
значения принимает другая переменная,
рассматриваемая, как причина по отношению
к зависимой переменной.
Изучение зависимостей
ведёт к поиску аналитических связей в
виде формул (т.е. функций, который
записываются составлением уравнений
регрессии).
А на графическом
поле строится теоретическая
линия регрессии
– это та
линия, вокруг которой группируются
точки корреляционного поля и которая
указывает основное направление, основную
тенденцию связи.
Наиболее часто
для характеристики связей экономических
явлений используются такие типы функций:
Линейную:
Гиперболическую:
Показательную:
Степенную:
13.5. Корреляционно-регрессивные модели (крм),
их применение
в анализе и прогнозе
На практике чаще
всего изменение изучаемого признака
зависит от действия нескольких причин.
В таких случаях изменение корреляционной
связи не может ограничиться парными
зависимостями, и в анализ необходимо
включить другие признаки-факторы
существенно влияющие на изучаемую
переменную.
Отбор факторов
для построения многофакторных моделей
производится на основе качественного
и количественного анализа
социально-экономических явлений с
использованием статистических критериев.
Корреляционно-регрессивной
моделью
системы
взаимосвязанных признаков является
такое уравнение регрессии, которое
включает основные факторы.
Построение
многофакторных регрессионных моделей
позволяет дать количественное описание
основных закономерностей изучаемых
явлений, выделить существенные факторы,
обуславливающие изменение экономических
показателей, и оценить их влияние.
Полученные модели
в основном используются в двух
направлениях:
-
Для сравнительного
анализа -
В прогнозировании
Возможность
применения методов корреляционно-регрессивного
анализа ещё в недалёком прошлом
сдерживалась высокой трудоёмкостью
необходимых расчётов. Сегодня широкое
распространение получили пакеты
прикладных программ по статистике,
ликвидировав эти ограничения.
С целью расширения
возможностей экономического анализа
используют коэффициент эластичности:
,
где
— среднее значение
факторного признака
— среднее значение
результативного признака
—
коэффициент регрессии при соответствующем
факторном признаке.
Показывает на
сколько процентов в среднем изменится
значение результативного признака при
изменении факторного признака.
— устанавливают
как справочную величину.
Следует различать
функциональные и корреляционные связи.
В отличие от функциональной зависимости,
при которой каждому значению одной
переменной строго соответствует одно
определённое значение другой переменной,
зависимость, при которой одному значению
переменной (х)
может соответствовать (в силу наслоения
действия других причин) множество
значений другой переменной (y),
называют корреляционной. Корреляционная
зависимость проявляется лишь на основе
массового наблюдения.
Примером
корреляционной зависимости может
служить зависимость производительности
труда от стажа работы рабочих, зависимость
урожайности от срока сева, зависимость
годового удоя коров от количества отёлов
и т.п.
Наиболее простым
случаем корреляционной зависимости
является парная
корреляция, т.е. зависимость между двумя
признаками (результативными и одним из
факторных).
Основными задачами
при изучении корреляционных зависимостей
являются:
-
отыскание
математической формулы, которая бы
выражала эту зависимость y
от x -
измерение тесноты
такой зависимости.
Решение первой
задачи, т.е. определение формы связи с
последующим отысканием параметров
уравнения, называется нахождением
уравнения связи (уравнения регрессии).
Показатели, рассматриваемые как функция
х,
обозначают
(читается: «игрек, выровненный по икс»).
Возможны различные
формы связи:
-
прямолинейная:
-
криволинейная в виде:
а)
параболы второго порядка
(или высших порядков)
б) гиперболыв)
показательной функциии т.д.
Параметры для всех
уравнений связи чаще всего определяют
из так называемой системы
нормальных уравнений,
отвечающих
требованию «метода наименьших квадратов»
(МНК). Это требование можно записать как
или, при линейной зависимости,
т.е.
требуется определить, при каких значениях
параметрови
сумма квадратов отклоненийy
от
будет минимальной. Найдя частные
производные указанной суммы пои
и приравняв их к нулю, легко записать
систему уравнений, решение которой и
дают параметры искомой функции, т.е.
уравнения регрессии.
Так, система
нормальных уравнений при линейной
зависимости имеет вид:
Если связь выражена
параболой второго порядка
,
то система нормальных
уравнений для отыскания параметров
,
,
выглядит следующим образом:
Вторая задача –
измерение тесноты зависимости – для
всех форм связи может быть решена с
помощью исчисления теоретического
корреляционного отношения
:
где
— дисперсия в ряду
выравненных значений
результативного
показателя
;
— дисперсия в ряду
фактических значений
y.
Так как дисперсия
отражает вариацию в ряду
только за счёт вариации фактораx,
а дисперсия
отражает вариациюy
за счёт всех факторов, то их отношение,
именуемое теоретическим
коэффициентом детерминации,
показывает, какой удельный вес в общей
дисперсии ряда y
занимает дисперсия, вызываемая вариацией
фактора х.
квадратный корень из отношения этих
дисперсий даёт нам теоретическое
корреляционное отношение. Если
=
,
то это означает, что роль других факторов
в вариацииy
сведена на нет, и отношение:
означает полную
зависимость вариации y
от х.
Если
=0,
то это означает, что вариациях
никак не влияет на вариацию y,
и в этом случае
.
Следовательно,
максимальное значение, которое может
принимать корреляционное отношение,
равно 1, минимальное значение – 0.
Математически
легко доказывается, что в случае линейной
зависимости корреляционное отношение
может быть заменено выражением
которое называют линейным коэффициентом
корреляции
и обозначают
r,
т.е.
где
— коэффициент регрессии в уравнении
связи,и
— соответственно среднее квадратическое
отклонение в рядуx
и в ряду y.
Линейный коэффициент
корреляции можно выразить и другими
формулами, тождественными первой, в
частности:
или
а также
Линейный коэффициент
корреляции может принимать по модулю
значения от 0 до 1 (знак «+» при прямой
зависимости и знак «-» при обратной
зависимости).
Рассмотрим решение
задачи по этой теме.
Задача 1
Пусть по 10 однотипным
предприятиям имеются следующие данные
о выпуске продукции (х)
в тыс. ед. и о расходе условного топлива
(y)
в тоннах (графы 1 и 2 таблицы).
Требуется найти
уравнение зависимости расхода топлива
от выпуска продукции (или уравнение
регрессии y
по x)
и измерить тесноту зависимости между
ними.
Решение.
А.
рассматривая
уравнение регрессии в форме линейной
функции вида
,
параметры данного уравнения (и
)
найдём из системы нормальных уравнений
|
X |
y |
x2 |
xy |
|
y2 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
5 6 8 8 10 10 14 20 20 24 |
4 4 6 5 7 8 8 10 12 16 |
25 36 64 64 100 100 196 400 400 576 |
20 24 48 40 70 80 112 200 240 384 |
3,9 4,4 5,5 5,5 6,6 6,6 8,8 12,1 12,1 14,3 |
16 16 36 25 49 64 64 100 144 156 |
|
125 |
80 |
1961 |
1218 |
80 |
770 |
Необходимые для
решения суммы
,
,
рассчитаны выше в таблице. Подставляем
их в уравнения и решаем систему:
Отсюда
Подставляя в это
уравнение последовательно значения
х=5,6,8,10
и т.д., получаем выравненные (теоретические)
значения результативного показателя
(графа 5 таблицы).
Поскольку параметры
уравнения регрессии являются оценочными,
то для каждого из них рассчитывается
средняя ошибка, т.е.
.
Конкретный расчёт
ошибок для
и
по данным нашего примера приведён далее.
Б. Для измерения
тесноты зависимости между y
и x
воспользуемся прежде всего линейным
коэффициентом корреляции (поскольку
зависимость рассматривалась линейно):
а) применяем формулу
.
Находим
Определяем
,
предварительно найдяи
Отсюда
Значение линейного
коэффициента корреляции
(т.е. близкое к единице) характеризует
не только меру тесноты зависимости
вариацииy
от вариации
x,
но и степень близости этой зависимости
к линейной;
б) воспользуемся
ещё одной формулой линейного коэффициента
корреляции:
т.е. результат тот
же.
При расчёте
коэффициента корреляции очень важно
оценить его значимость. Оценка значимости
(существенности) линейного коэффициента
корреляции основана на сопоставлении
значения r
с его средней квадратической ошибкой
().
Средняя ошибка
коэффициента корреляции при n>50
рассчитывается приближённо по формуле
Если при этом
коэффициент корреляции r
превышает
свою среднюю ошибку
больше чем в 3 раза, т.е. если
то он считается значимым, а связь —
реальной.
При n<30
значимость коэффициента корреляции
проверяется на основе t-критерия
Стьюдента. Для этого рассчитывается
фактическое (расчётное) значение
критерия:
Которое сопоставляется
с
определяемым по Приложению 9, для числа
степеней свободыи заданного уровня значимости (обычно
).
Если
>
r
считается
значимым, а связь – реальной. Если
<
то
считается, что связь междуx
и y
отсутствует и значение r,
отличное от нуля, получено случайно.
В рассматриваемом
примере средняя ошибка коэффициента
корреляции
а
По таблице приложений
находим, что при числе степеней свободы
и уровне
табличное (критическое, пороговое)t
равно 2,306, т.е.
=2,306.
Поскольку фактическое
(расчётное) t
больше
табличного, т.е.
>
то
линейный коэффициент корреляцииr=0,96
считается
значимым, а связь между x
и y
– реальной.
Контрольные
вопросы к теме:
-
Какие признаки
являются результативными, факторными. -
Какие два основных
вида связей между явлениями различают.
Объясните их суть. -
Расскажите
классификацию взаимосвязей. -
В чем заключаются
задачи статистики при изучении связей
между явлениями.
5. Расскажите,
какие вы знаете методы выявления наличия
корреляционной связи между двумя
признаками.
6. При помощи,
каких показателей дается характеристика
силы воздействия одних факторов на
другие.
7. Расскажите о
коэффициенте множественной корреляции.
8. Что такое
«корреляционно-регрессивные модели»
и каково их применение в анализе и
прогнозе.
9. Расскажите о
линейном коэффициенте корреляции.
10. В чем суть метода
наименьших квадратов.
Библиографический
список
-
Елисеева И.И.,
Юзбашев М.М. Общая теория статистики:
Учебник / Под ред. И.И. Елисеевой. 5-е
изд., перераб. и доп. М.: Финансы и
статистика, 2004. -
Ефимова М.Р.,
Петрова Е.В., Румянцева В.Н. Общая теория
статистики: Учебник. – 2-е изд., испр. и
доп. – М.: ИНФРА-М, 2000. – 416 с. -
Общая теория
статистики: Учебник / Под ред. О.Э.
Башиной, А.А. Спирина, 5-е изд. М., 1999. -
Практикум по
теории статистики: Учеб. пособие / Под
ред. Р.А. Шмойловой. М.: Финансы и
статистика, 1999. -
Сиденко А.В., Попов
Г.Ю., Матвеева В.М. Статистика: Учебник.
М., 2000. -
Социальная
статистика: Учебник / Под ред. И.И.
Елисеевой. 3-е изд., перераб. и доп. М.:
Финансы и статистика, 2003. -
Статистика товаров
и услуг: Учебник / Под ред. И.К. Белявского.
М., 2002. -
Статистика: Учебник
/ Под ред. В.С. Мхитаряна. М.: Экономист,
2005 -
Теория статистики:
Учебник/Под ред. профессора Г.Л. Громыко.
– М.: ИНФРА-М, 2000. – 414 с. -
Экономика и
статистика фирм / Под ред. С.Д. Ильенковой.
М., 2000
24
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
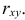
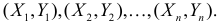
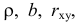
Неизвестная нам линия регрессии 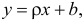

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 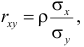
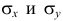
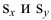
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 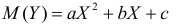
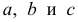
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 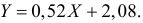
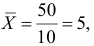
Аналогично, 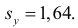
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 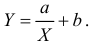
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 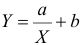
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 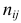
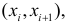
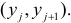
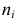
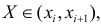
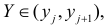
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 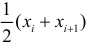
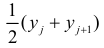
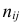
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 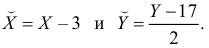
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 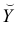
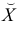
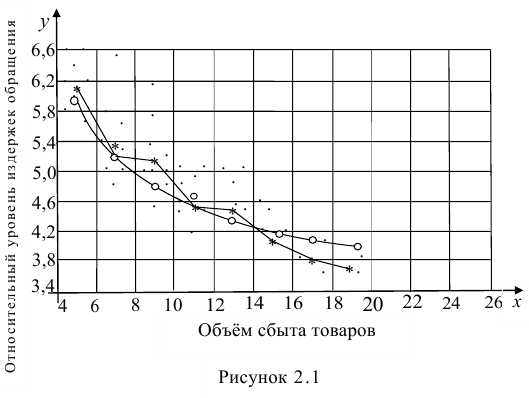
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
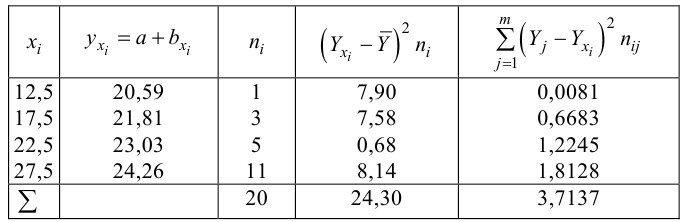
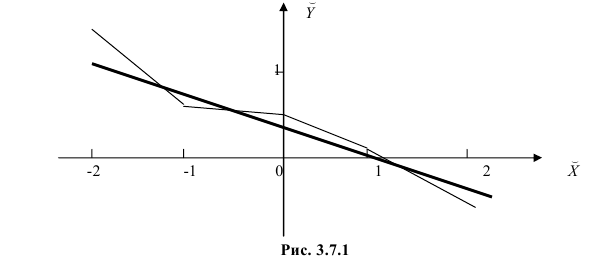
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 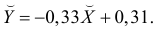
Для оценки 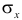
Подобным же образом можно оценить 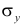
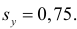
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 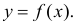
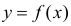
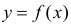
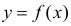
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 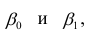
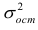
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей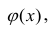
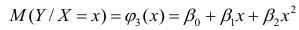
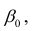
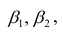
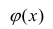
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 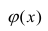
по переменным. Оценки параметров модели (2.1) 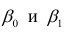
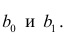
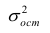
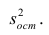
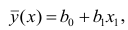
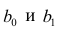
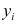
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно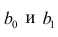
Остаётся получить оценку параметра 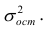
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы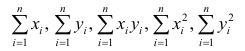
где 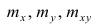
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
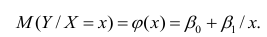
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 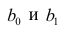
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 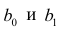
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 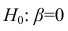
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 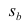
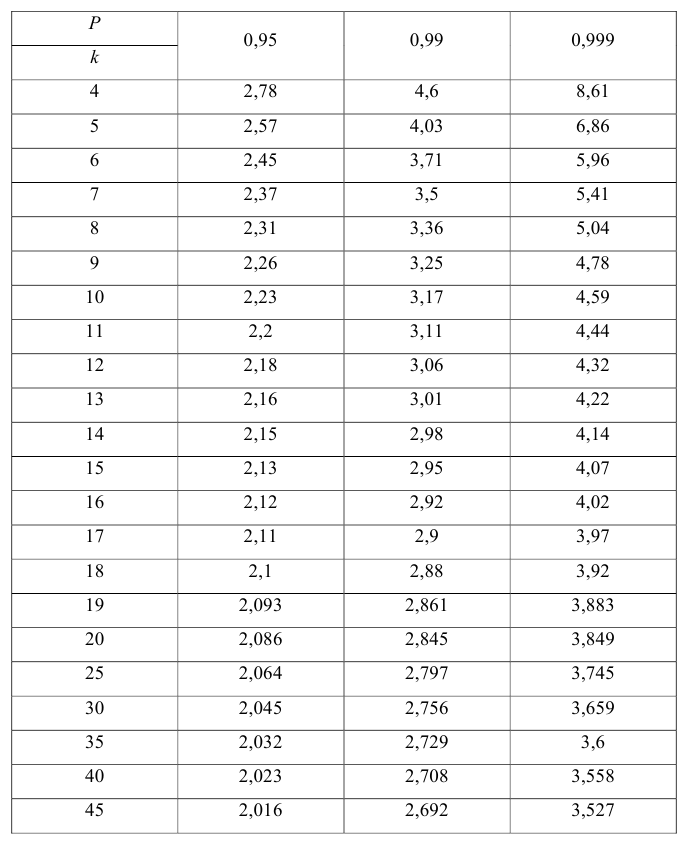
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение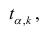
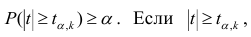
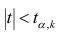
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 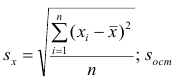
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 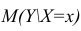
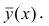
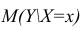
построить доверительный интервал в точке
Известно, что 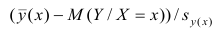
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
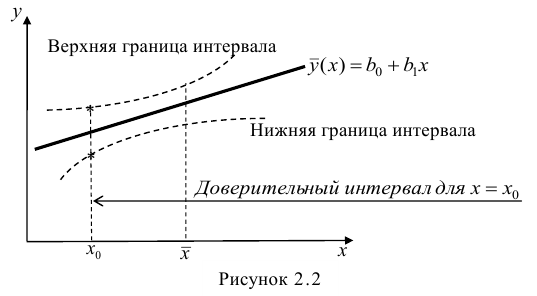
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 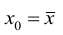
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 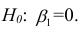
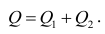
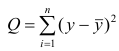
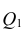
X) и 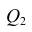
Для проверки нулевой гипотезы вычисляют статистику 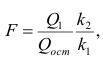
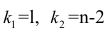
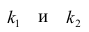
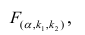
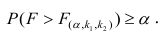
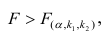
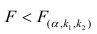
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 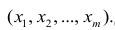
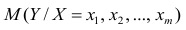
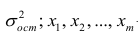
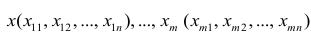
Оценке подлежат параметры 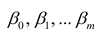
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 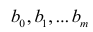

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 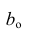
Подставим в остальные уравнения системы вместо 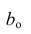
Пусть С — матрица коэффициентов при неизвестных параметрах 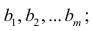
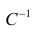
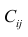
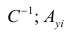
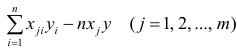
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии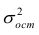
где 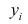
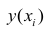
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику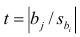
где 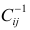
го столбца;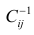
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 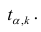
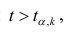
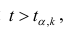
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: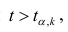
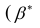
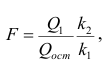
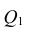
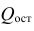
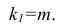
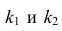
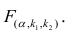
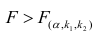
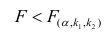
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 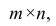
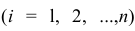
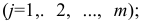
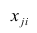
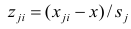
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 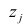
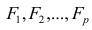
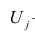
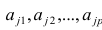
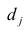
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 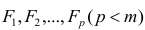
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков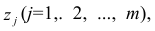
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 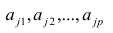
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 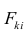
Дисперсию признака 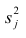
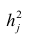
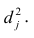
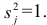
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 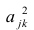
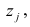
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где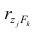
м фактором;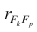
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
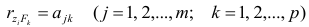
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 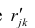
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 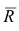
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции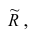
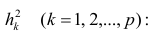
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 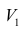
где 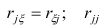
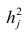
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора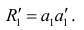
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 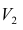
где 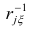
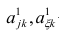
Факторный анализ учитывает суммарную общность. Исходная суммарная общность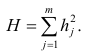
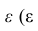
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 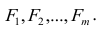
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 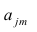
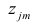
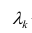
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 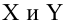
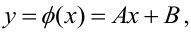
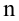
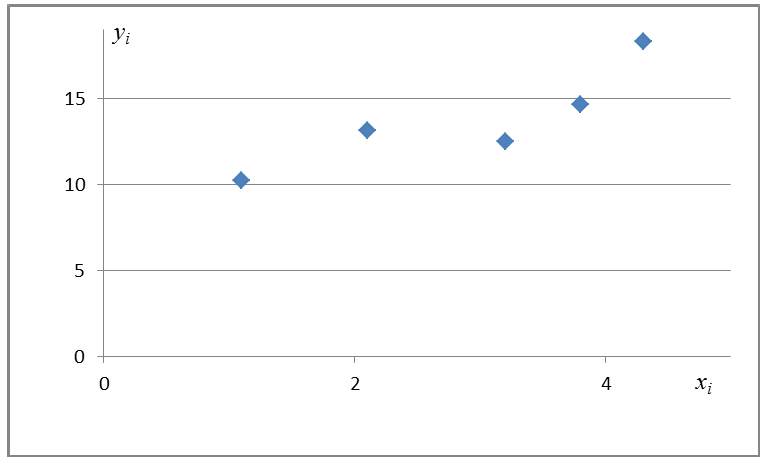
Диаграмма рассеяния (разброса, рассеивания)
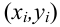
Выборочное уравнение прямой линии регрессии 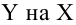
Задача: подобрать 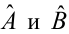
Для того, что бы провести прямую 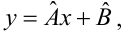
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 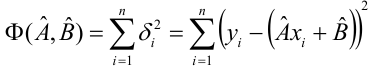
Решив систему, получим искомые значения
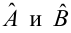
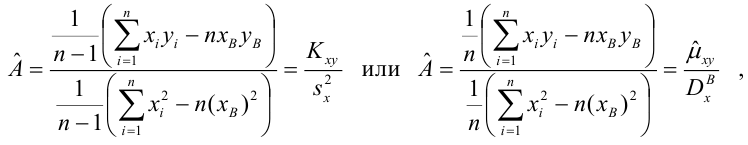
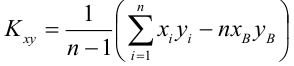
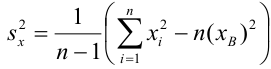
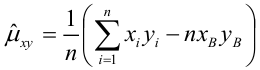
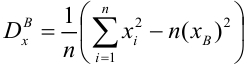
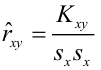
Коэффициент детерминации
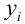
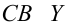
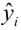
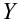
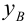
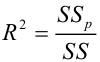
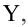
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
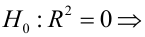
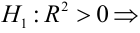
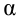
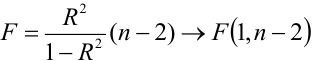
Критическая область — правосторонняя;
Если 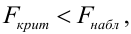
Мощность статистического критерия. Функция мощности
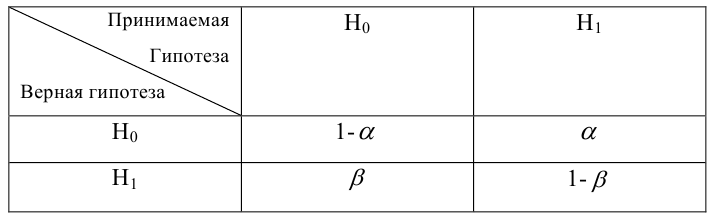
Определение. Мощностью критерия 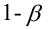
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 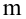
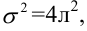
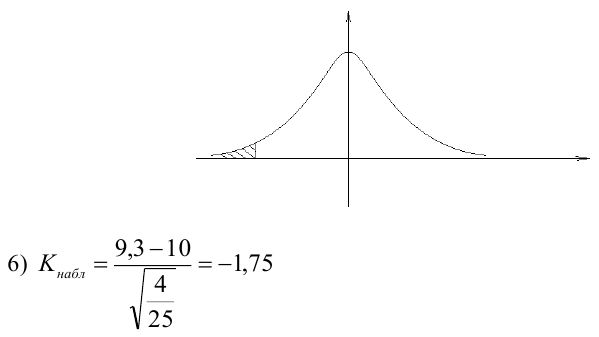
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
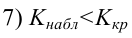
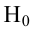
Пример:
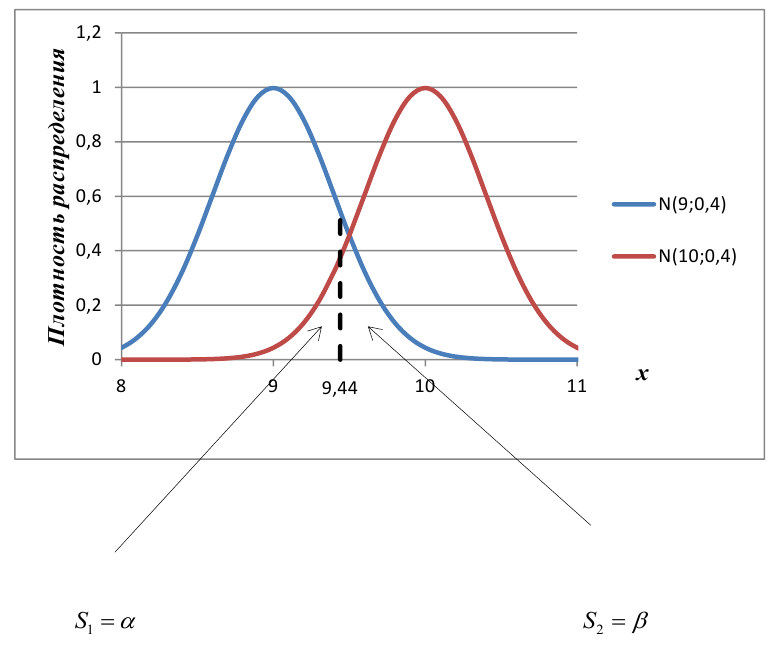
В условиях примера 1 предположим, что наряду с 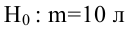
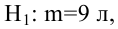
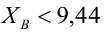
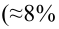
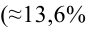
Определение. Пусть проверяется 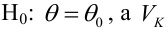
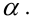
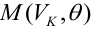
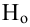
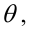
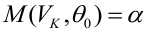
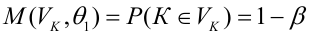
Пример:
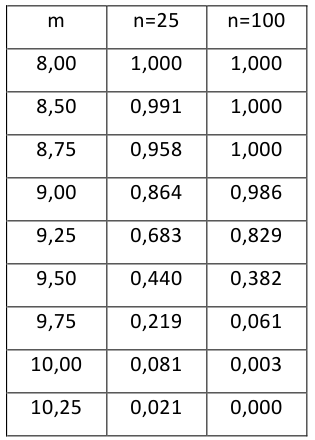
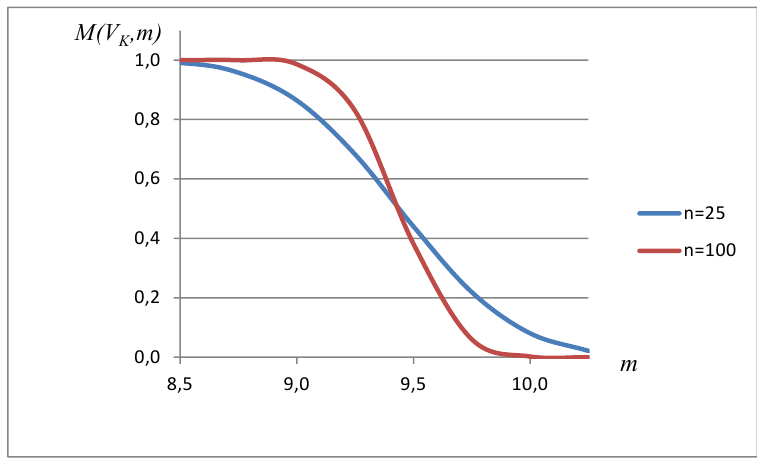
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 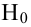
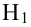
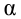
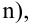
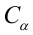
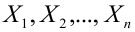
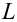
Пример:
Случайная величина 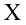
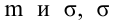
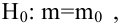
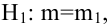
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости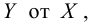
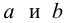
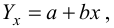
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 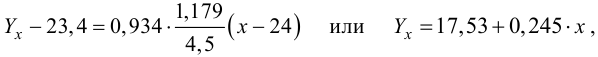
Для выяснения значимости уравнения регрессии вычислим суммы 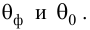
Из (27) и (28) по данным таблицы получим
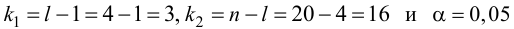
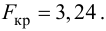
Вычислим статистику
Так как 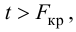
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Основы линейной регрессии
Время на прочтение
13 мин
Количество просмотров 123K
Здравствуй, Хабр!
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Содержание
- Введение
- Метод наименьших квадратов
- Математический анализ
- Статистика
- Теория вероятностей
- Мультилинейная регрессия
- Линейная алгебра
- Произвольный базис
- Заключительные замечания
- Проблема выбора размерности
- Численные методы
- Реклама и заключение
Введение
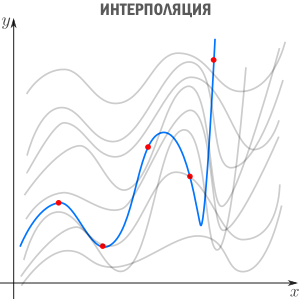
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.
Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.
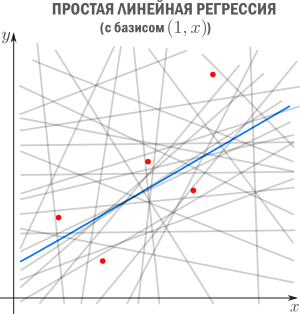
В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию
(которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
Метод наименьших квадратов
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости
и мы ищем такую аффинную функцию

.
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого
поэтому измерять нужно вдоль оси
.
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц
. Простейший вариант — сумма модулей отклонений
приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
Метод наименьших квадратов (по англ. OLS) — линейная регрессия c
в качестве функции потерь.
Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу
.
Математический анализ
Простейший способ найти
— вычислить частные производные по
и
, приравнять их нулю и решить систему линейных уравнений
Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям
которые легко решить
Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.
Статистика
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего
, вариации
(стандартного отклонения), ковариации
и корреляции
Перепишем
как
где
это нескорректированное (смещенное) стандартное выборочное отклонение, а
— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
и запишем
Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения
отклоняется от своего среднего значения меньше чем
, потому что
. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации
. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.
, равный
, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что
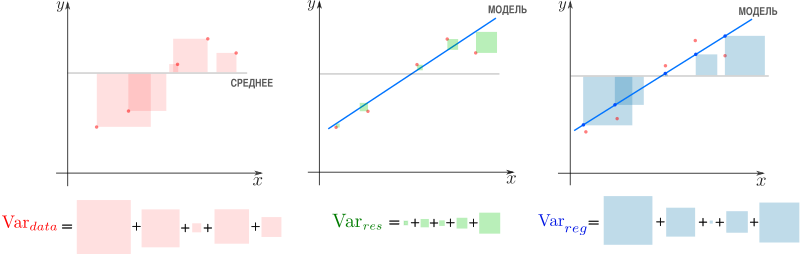
показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
— вариация исходных данных (вариация точек
).
— вариация остатков, то есть вариация отклонений от регрессионной модели — от
нужно отнять предсказание модели и найти вариацию.
— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках
(обратите внимание, что среднее предсказаний модели совпадает с
).
Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)
или
Как видим, стандартные отклонения образуют прямоугольный треугольник.
Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует
, равный единице минус доля вариации ошибок в суммарной вариации
или доле объясненной вариации (доля вариации регрессии в полной вариации)
равен косинусу угла в прямоугольном треугольнике
. Кстати, иногда вводят долю необъясненной вариации
и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
Теория вероятностей
Ранее мы пришли к функции потерь
из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть
независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например
и
). Для этого нужно вычислить вероятность получить
датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
Вернемся к задаче простой регрессии. Допустим, что значения
нам известны точно, а в измерении
присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
где
— нормально распределенная случайная величина
Исходя из предположений выше, запишем функцию правдоподобия
и ее логарифм
Таким образом, максимум правдоподобия достигается при минимуме
что дает основание принять ее в качестве функции потерь. Кстати, если
мы получим функцию потерь LAD регрессии
которую мы упоминали ранее.
Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
Мультилинейная регрессия
До сих пор мы рассматривали задачу регрессии для одного скалярного признака
, однако обычно регрессор — это
-мерный вектор
. Другими словами, для каждого измерения мы регистрируем
фич, объединяя их в вектор. В этом случае логично принять модель с
независимыми базисными функциями векторного аргумента —
степеней свободы соответствуют
фичам и еще одна — регрессанту
. Простейший выбор — линейные базисные функции
. При
получим уже знакомый нам базис
.
Итак, мы хотим найти такой вектор (набор коэффициентов)
, что
Знак «
» означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
Последнее уравнение можно переписать более удобным образом. Для этого расположим
в строках матрицы (матрицы информации)
Тогда столбцы матрицы
отвечают измерениям
-ой фичи. Здесь важно не запутаться:
— количество измерений,
— количество признаков (фич), которые мы регистрируем. Систему можно записать как
Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь
которую мы намерены минимизировать
Продифференцируем финальное выражение по
(если забыли как это делается — загляните в Matrix cookbook)
приравняем производную к
и получим т.н. нормальные уравнения
Если столбцы матрицы информации
линейно независимы (нет идеально скоррелированных фич), то матрица
имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
где
псевдообратная к
. Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
Напомню, что обратить
и найти
можно только если столбцы
линейно независимы. Впрочем, если столбцы
близки к линейной зависимости, вычисление
уже становится численно нестабильным. Степень линейной зависимости признаков в
или, как говорят, мультиколлинеарности матрицы
, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе
к вырожденной и неустойчивее вычисление псевдообратной.
Линейная алгебра
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор
, образ которого
ближе остальных к
. Напомню, что множество образов или колоночное пространство
— это линейная комбинация вектор-столбцов матрицы
—
-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов
. Итак, если
принадлежит
, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
Если в дополнение к векторам
мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из
разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай
, тогда
равен нулю в том и только в том случае, если
перпендикулярен всем
, а значит и целому
. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все
. Иногда это обозначают c помощью символа ортогональной прямой суммы
где
. В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.
Теперь представим
в виде разложения
Если мы ищем решение
, то естественно потребовать, чтобы
была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
но поскольку, выбрав подходящий
, я могу получить любой вектор колоночного пространства, то задача сводится к
а
останется в качестве неустранимой ошибки. Любой другой выбор
сделает ошибку только больше.
Если теперь вспомнить, что
, то легко видеть
что очень удобно, так как
у нас нет, а вот
— есть. Вспомним из предыдущего параграфа, что
имеет обратную при условии линейной независимости признаков и запишем решение
где
уже знакомая нам псевдообратная матрица. Если нам интересна проекция
, то можно записать
где
— оператор проекции на колоночное пространство.
Выясним геометрический смысл коэффициента детерминации.
Заметьте, что фиолетовый вектор
пропорционален первому столбцу матрицы информации
, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
Так как этот треугольник прямоугольный, то по теореме Пифагора
Это геометрическая интерпретация уже известного нам факта, что
Мы знаем, что
а значит
Красиво, не правда ли?
Произвольный базис
Как мы знаем, регрессия выполняется на базисных функциях
и её результатом есть модель
но до сих пор мы использовали простейшие
, которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей
. Как можно было заметить, на самом деле ни вид
, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки
ложатся на параболу, а не на прямую, то стоит выбрать базис
. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
записываем функцию потерь
и находим её минимум, например с помощью псевдообратной матрицы
или другим методом.
Заключительные замечания
Проблема выбора размерности
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что
монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
где
— размер выборки,
— количество независимых переменных. Следя за
, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
Вторая группа подходов — регуляризации, самые известные из которых Ridge(
/гребневая/Тихоновская регуляризация), Lasso(
регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов
неограниченно расти и тем самым воспрепятствуют переобучению
где
и
— параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента
Численные методы
Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Реклама и заключение
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
- все материалы должны быть доступны студентам с первой пары;
- лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
- конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
- наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.

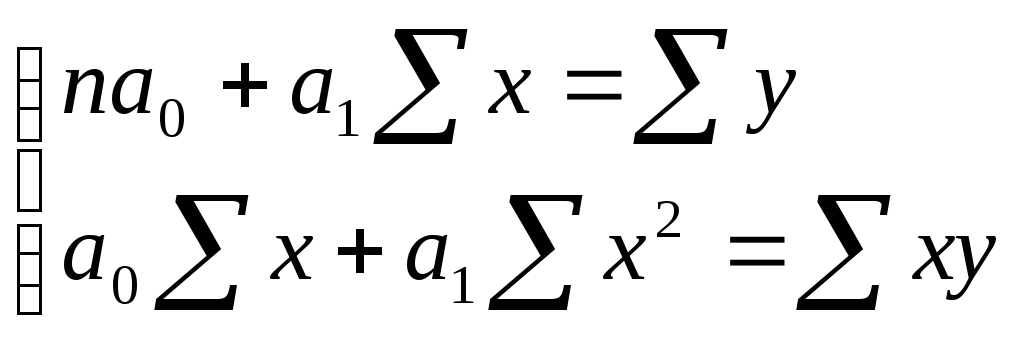
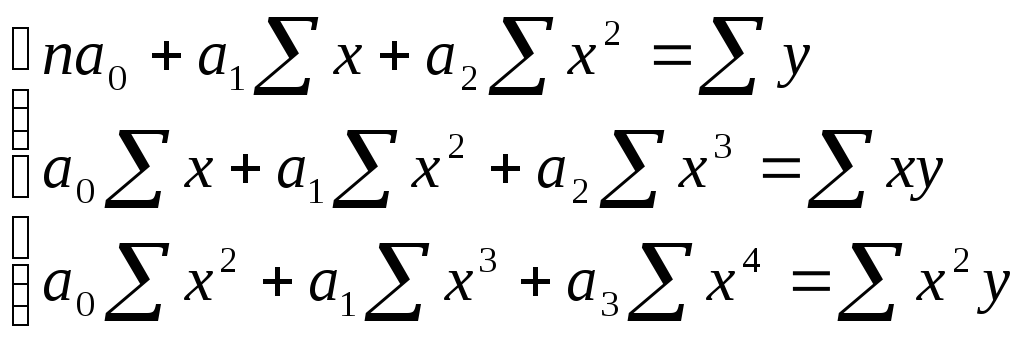
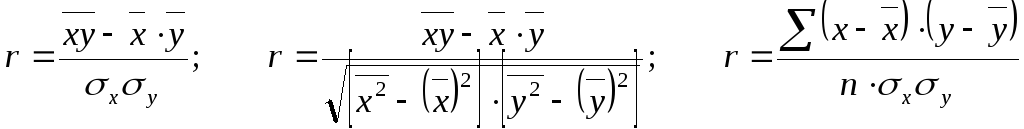
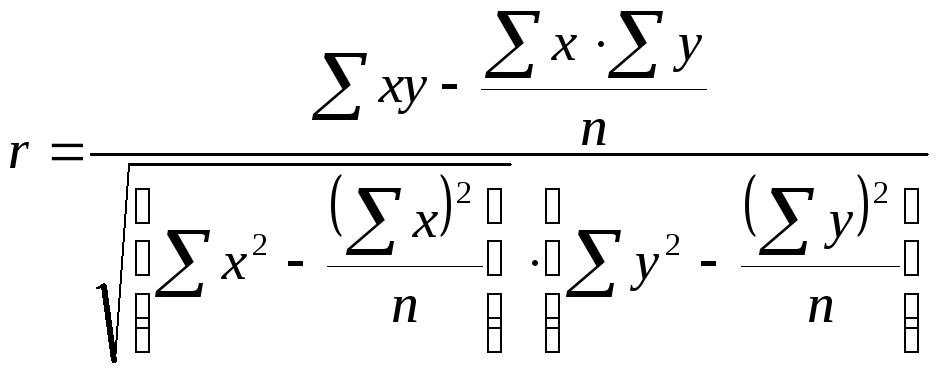
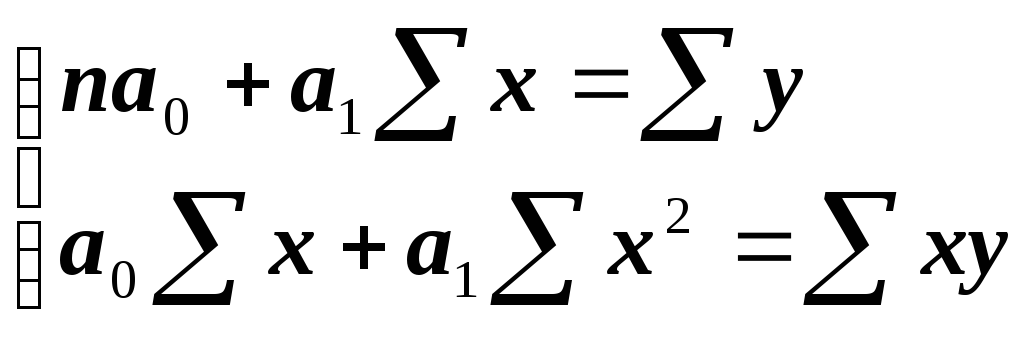
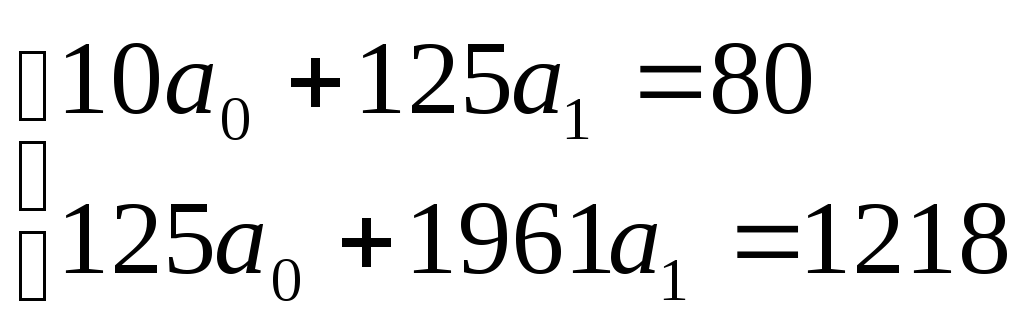
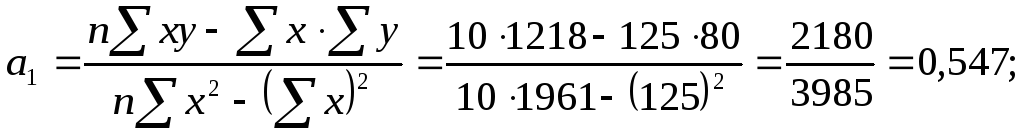
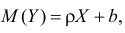
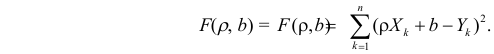
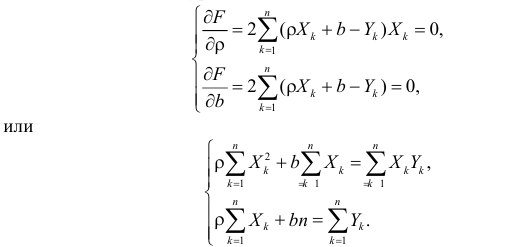
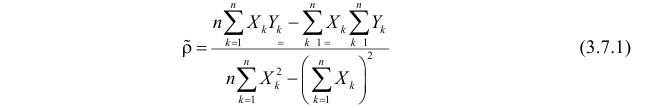
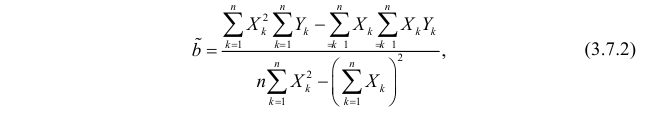
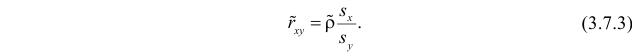
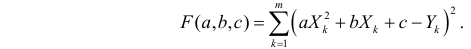

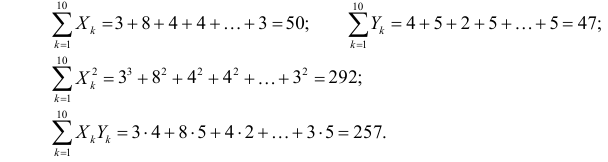
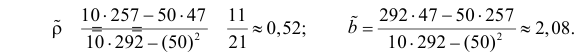
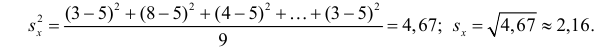
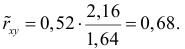
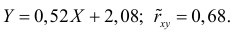

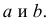
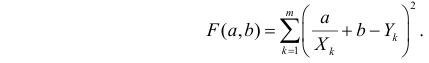
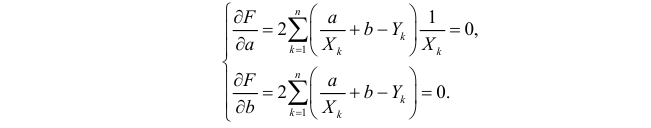
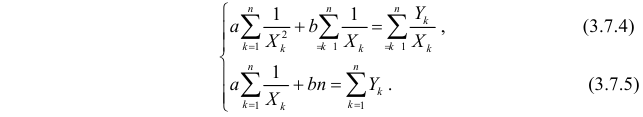
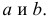
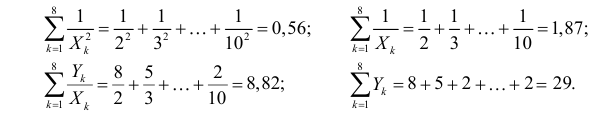
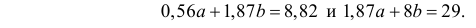
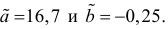
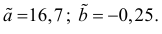

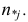



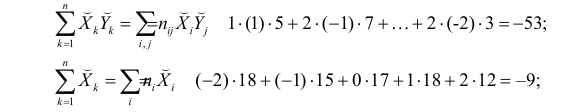
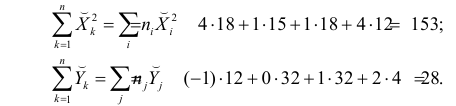
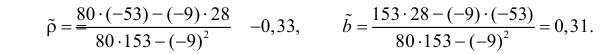
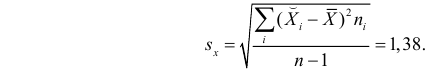
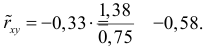
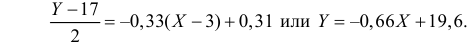
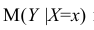 можно представить в виде
можно представить в виде 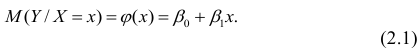
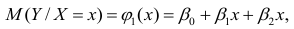
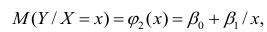
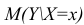 можно представить в виде (2.1).
можно представить в виде (2.1).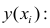
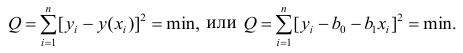
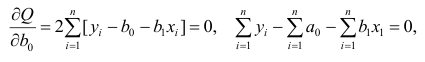
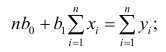
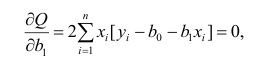
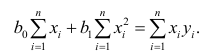
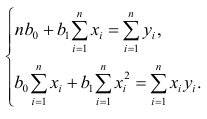
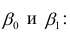
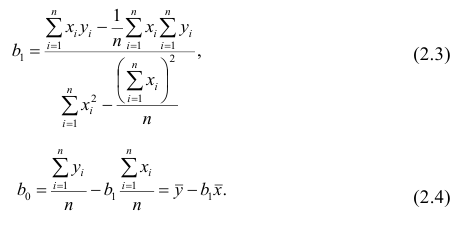
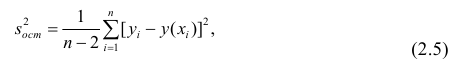
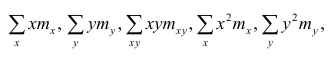
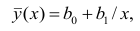
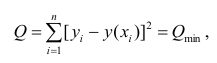
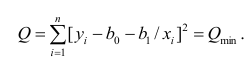
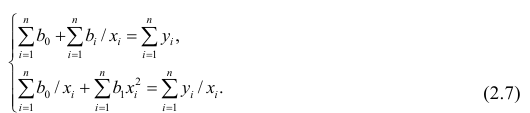
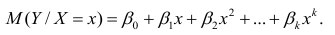
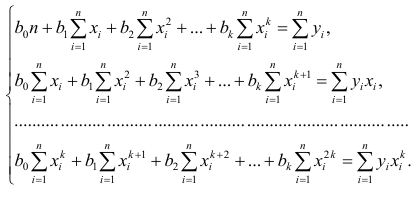

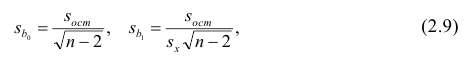
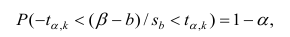

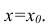
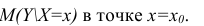
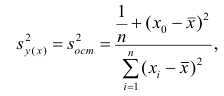
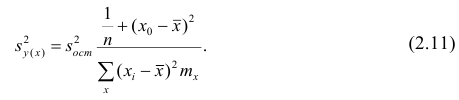
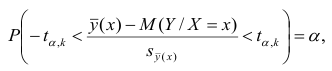
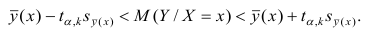
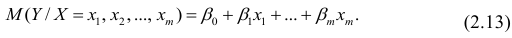
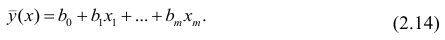
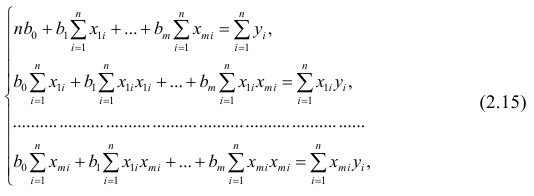
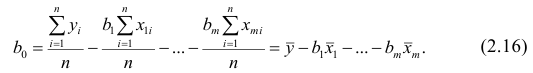
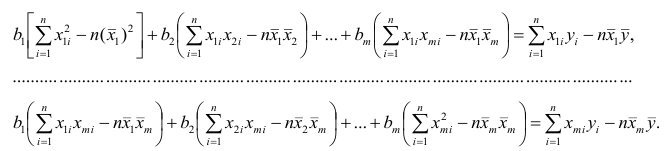
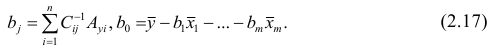
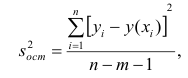
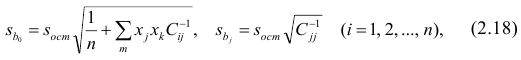
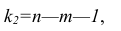
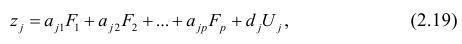
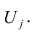
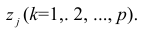
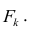
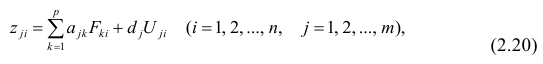
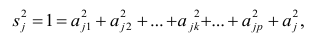
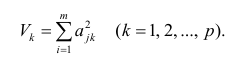
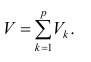
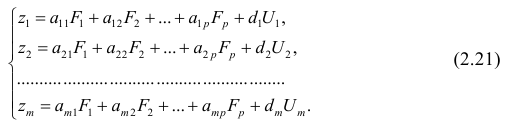
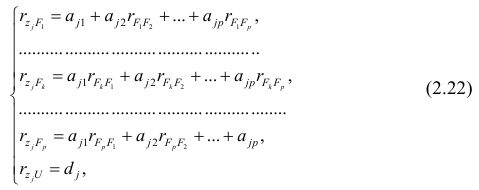
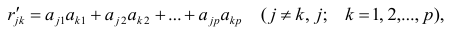
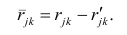
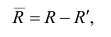

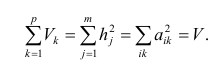
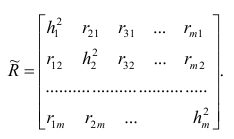


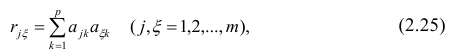

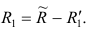

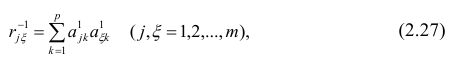
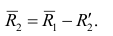
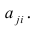
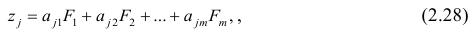
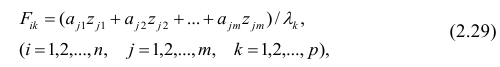
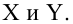
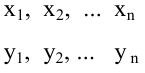
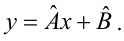
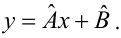
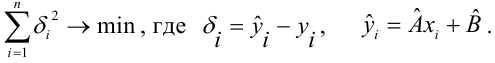
 подчинены нормальному закону распределения.
подчинены нормальному закону распределения.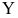 постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.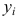 в разных точках независимы.
в разных точках независимы.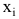 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.