Как найти видимость прямой на чертеже - Исправление недочетов и поиск решений вместе с Examum.ru

Пересечение прямой линии с плоскостью. Определение видимости прямой

6 февраля, 2014 Анна Веселова

Здравствуйте друзья! Сегодня разбираем тему из начертательной геометрии – пересечение прямой линии с плоскостью и определение видимости прямой.

Задание берем из сборника Боголюбова, 1989 год, стр. 63, вар. 1. Нам требуется по заданным координатам построить комплексный чертеж треугольника ABC и прямой MN. Найти точку встречи (пересечения) прямой с непрозрачной плоскостью ABC.Определить видимые участки прямой.

Пересечение прямой линии с плоскостью

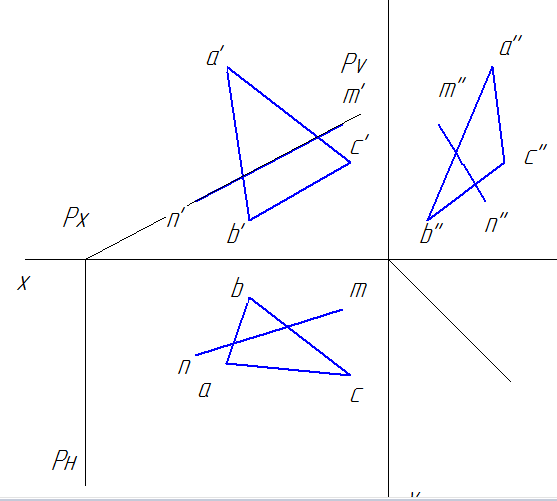
1. По координатам точек A, B и C строим комплексный чертеж треугольника и прямой NM. Начинаем чертить с горизонтальной проекции. Координаты точек проекции находим при помощи вспомогательных прямых.

2. Получаем вот такой комплексный чертеж.

3. Для определения координат точки пересечения прямой и плоскости выполним следующее.

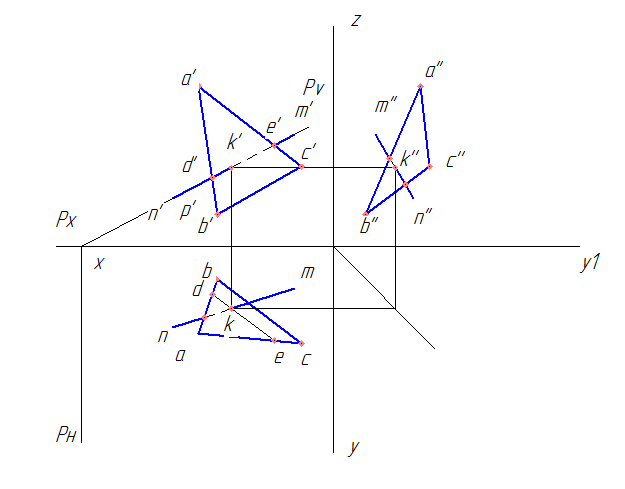
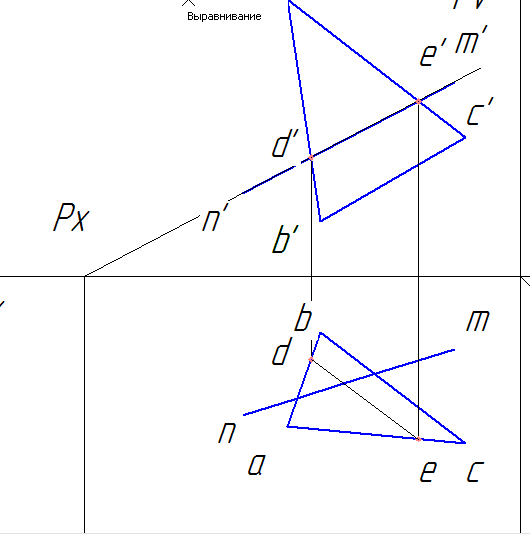
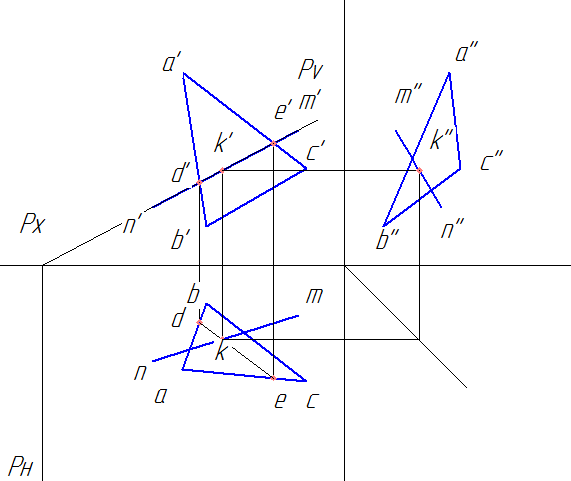
a) Через прямую NM проводим вспомогательную плоскость Р, т.е. на фронтальной проекции проводим след плоскости Pv, на горизонтальную плоскость опускаем перпендикуляр Рн – горизонтальный след плоскости Р.

b) Находим фронтальную проекцию линии пересечения следа плоскости Р с треугольником АВС. Это отрезок d’e’. Горизонтальную проекцию находим по линиям связи до пересечения со сторонами ab (т. d) и ac (т. e) треугольника. Точки d и e соединяем.

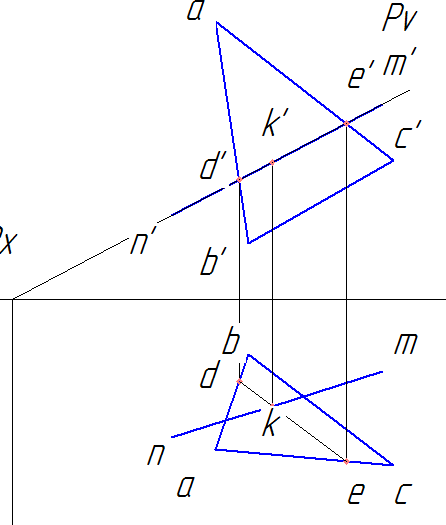
c) Вместе пересечения de и nm будет находиться горизонтальная проекция искомой точки пересечения прямой линии с плоскостью k.

d) Проводим линию связи из k до пересечения с d’e’, получаем фронтальную проекцию точки k’.

e) по линиям связи находим профильную проекцию точки k’’.

Координаты точки пересечения прямой и плоскости К найдены. Эта точка также называется точкой встречи прямой и плоскости.

Определение видимости прямой

Для определения видимости прямой воспользуемся методом конкурирующих точек.

Конкурирующие точки – это точки, расположенные на одной проекционной прямой и имеющие одинаковые одноименные координаты.

Применительно к нашему чертежу конкурирующими будут точки:

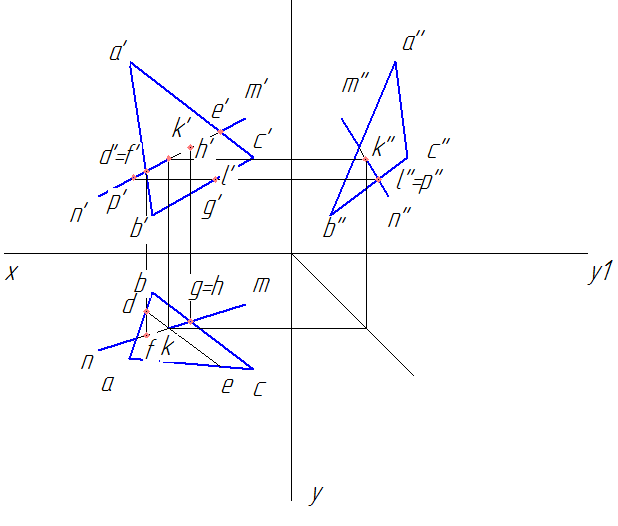
— точки: d’ принадлежащая a’b’ и e’ принадлежащая n’m’ (фронтально конкурирующие),

— точки: g принадлежащая bc и h принадлежащая nm (горизонтально конкурирующие),

— точки: l’’ принадлежащая b’’c’’ и p’’ принадлежащая n’’m’’ (профильно конкурирующие).

Из двух конкурирующих точек видимой будет та, высота которой будет больше. Граница видимости ограничена точкой К.

Для пары точек d’ и e’ видимость определяем так: опускаем перпендикуляр до пересечения с ab и nm на горизонтальной проекции, находим точки d и f. Видим, что координата по y для точки f больше, чем у d → точка f видима → видима прямая nm на участке f’k’, а на участке k’m’ невидима.

Аналогично рассуждаем и для пары точек g и h: на фронтальной проекции координата по z у точки h’ больше, чем у g’ → точка h’ видима, g’ – нет → прямая nm на отрезке hk видима, а на участке kn невидима.

И для пары точек l’’p’’: на фронтальной проекции координата по x больше у точки p’, а значит она закрывает собой точку l’’ на профильной проекции → р’’ видима, l’’ нет → отрезок прямой n’’k’’ видим, k’’m’’ невидим.

Заменяем в нужных местах линию nm на невидимую. На этом определение видимости прямой NM на комплексном чертеже треугольника АВС завершено.

Окончательно чертеж выглядит следующим образом.

Еще полезные материалы по начертательной геометрии

Как построить линию пересечения поверхностей двух взаимно перпендикулярных цилиндров?

Все о построении усеченных цилиндра и призмы, а также разверток этих геометрических тел.

Подробно весь процесс построения и определения видимости прямой описан в видеоуроке.

Скачать чертеж бесплатно можно здесь

Теперь у вас не вызовет затруднений нахождение точки пересечения прямой линии с плоскостью и определение видимости прямой на проекциях чертежа.

The following two tabs change content below.

Bio
Latest Posts

Рада приветствовать Вас в своем блоге! Я создала его с целью помочь всем желающим освоить программу Компас 3d. Мы пройдем весь путь от азов черчения до создания серьезных сборок. Присоединяйтесь!

Понравился материал? Подпишись на обновления!

Вы можете пропустить чтение записи и оставить комментарий. Размещение ссылок запрещено.

Источник

Определение видимости точек, прямых и плоских фигур.

Видимость
— это изображение на чертеже только
тех точек, прямых и поверхностей
(плоскостей) предметов, которые расположены
ближе к наблюдателю. Изображение
предметов с учетом видимости улучшает
восприятие их формы и размещения в
пространстве.

Определение
видимости — это определение точек
предмета, лежащих на одном луче
проецирования (называемых конкурирующими),
и обозначение на чертеже только тех из
них, которые расположены по этому лучу
ближе к наблюдателю.

F’

С’

Рис. 3.16

Если
необходимо указать невидимые точки, их
обозначения на плоскости проекций, где
проекции точек совпадают, заключают в
круглые скобки. Невидимые линии
изображаются на чертеже штриховыми
линиями.

Определение
видимости осуществляется как при
центральном, так и при параллельном
проецировании.

Граничными точками
видимости называются точки, разделяющие
зоны видимости и невидимости прямых и
поверхностей (плоскостей).

На
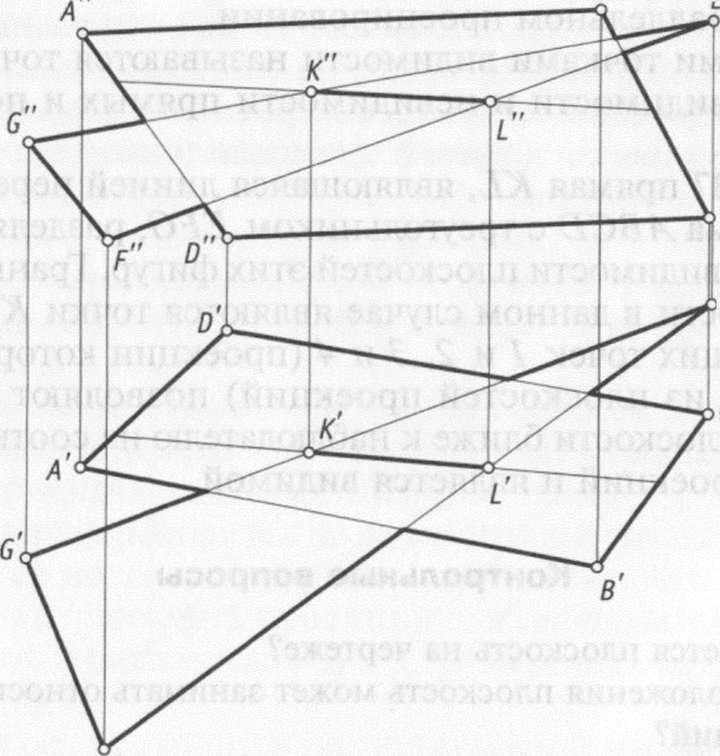
рис. 3.17 прямая АХ, являющаяся линией
пересечения параллелограмма ABCD с
треугольником EFG, разделяет зоны видимости
и невидимости плоскостей этих фигур.
Граничными точками видимости в данном
случае являются точки К и L, а пары
конкурирующих точек 1 и 2, 3 и 4 (проекции
которых совпадают на одной из
плоскостей проекций) позволяют определить,
какая часть плоскости ближе к наблюдателю
на соответствующей плоскости проекций
и является видимой.

Контрольные
вопросы

Как задается
плоскость на чертеже?
Какие
положения плоскость может занимать
относительно плоскостей проекций?
Как определить
на чертеже восходящую и нисходящую
плоскости общего положения?
Какие положения
занимают горизонтально-проецирующая,
фрон- тально-проецирующая и
профильно-проецирующая плоскости?
Как определить
углы между проецирующими плоскостями
и плоскостями проекций?
Где располагается
проекция любой точки, находящейся в
проецирующих плоскостях?
Какие положения
занимают плоскости уровня?
Как определяются
углы наклона плоскости уровня к
плоскостям проекций?
Каково условие
принадлежности точки плоскости?
Дайте определения
горизонтали, фронтали и профильной
прямой плоскости.
Каковы условия
параллельности прямой и плоскости?
Как могут
располагаться две плоскости относительно
друг друга?

Глава 4. Способы преобразования чертежа

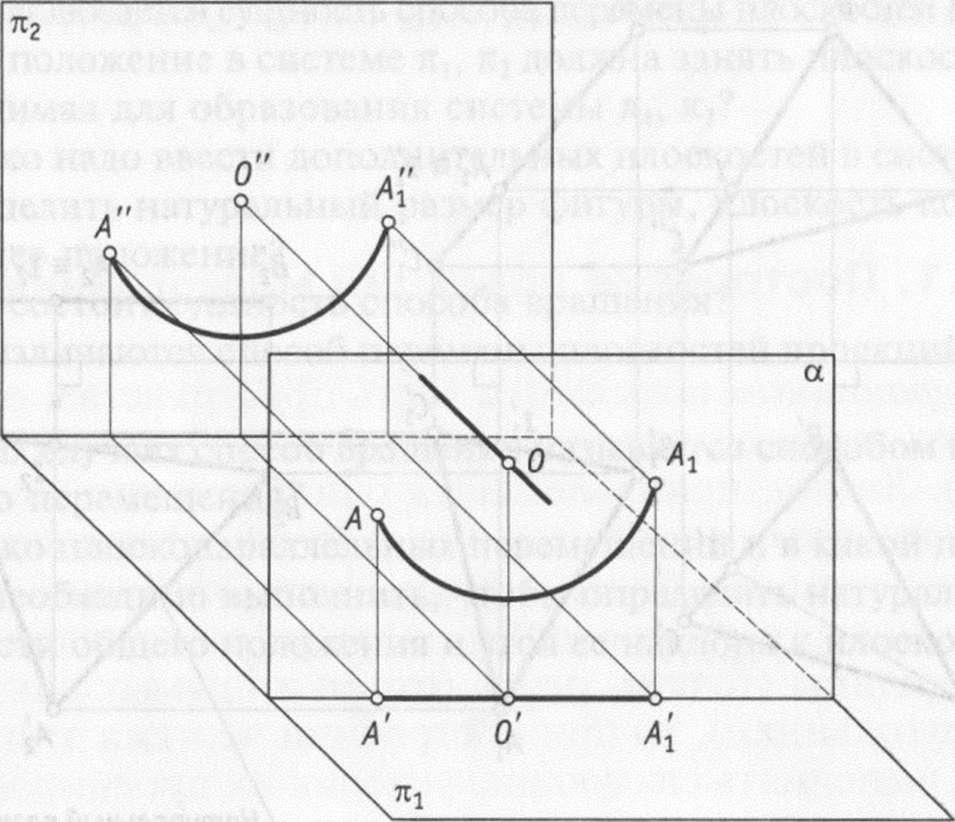
Использование
частных положений прямых линий и плоских
фигур относительно плоскостей проекций
значительно упрощает построение чертежа
и позволяет отобразить натуральные
размеры прямых линий, плоских фигур,
расположенных на одной плоскости
проекций, и расстояний между ними. Для
такого преобразования чертежа используют:

введение
дополнительных плоскостей проекций
таким образом, чтобы прямая линия или
плоская фигура, не изменяя своего
положения в пространстве, оказалась в
каком-либо частном положении в новой
системе плоскостей проекций — способ
перемены плоскостей проекций;
изменение
положения прямой линии или плоской
фигуры посредством поворота вокруг
некоторой оси таким образом, чтобы
прямая или плоская фигура оказалась в
частном положении относительно
неизменной системы плоскостей проекций
— способ вращения.

Преобразование
чертежа (для достижения необходимого
результата) при определении натуральных
размеров отрезков и углов может
осуществляться многократно одним или
разными способами.

Способ
перемены плоскостей проекций.
При использовании способа перемены
плоскостей проекций (рис. 4.1) положение
точек, линий, плоских фигур, поверхностей
в пространстве остается неизменным, а
система щ, п2 дополняется плоскостями,
образующими с щ или п2, или между собой
системы двух взаимно-перпендикулярных
плоскостей, принимаемых за плоскости
проекций.

Рис. 4.1

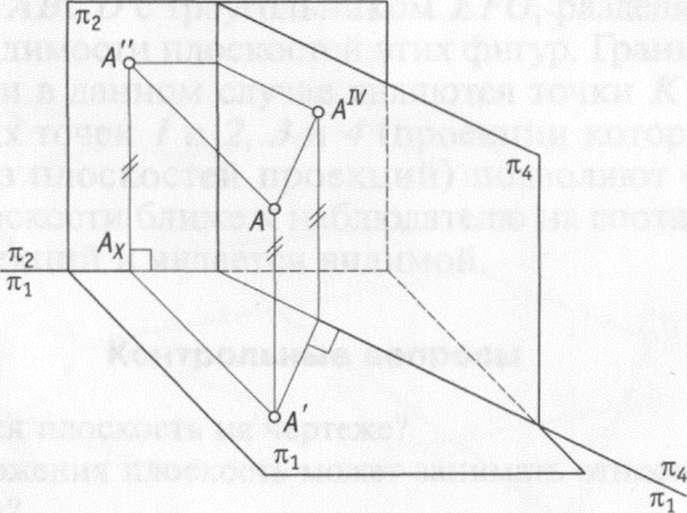
При введении
дополнительной плоскости проекций
проводят новую ось системы проекций
(рис. 4.2), разделяющую две плоскости
проекций в новой системе проекций. При
этом новую ось проводят либо параллельно,
либо перпендикулярно проекциям прямых,
чтобы получить частное положение этих
прямых в новой системе проекций.

При построении в
новой системе плоскостей следует
соблюдать те же условия положения
наблюдателя, которые были установлены
в первоначальной системе проекций.

Если новая ось
проводится на горизонтальной плоскости,
значит, изменяется положение фронтальной
плоскости проекций и дополнительная
плоскость проекций для наблюдателя
становится фронтальной. Наблюдатель
при этом перемещается в горизонтальной
плоскости.

Если
новая ось проводится на фронтальной
плоскости, значит, изменяется положение
горизонтальной плоскости проекций и
дополнительная плоскость проекций для
наблюдателя становится горизонтальной.
Наблюдатель при этом перемещается в
фронтальной плоскости.

Таким образом,
наблюдатель может рассматривать предметы
с любой стороны.

Дополнительные
плоскости по мере построения обозначают
тг4, 7с5и т.д. Обозначения дополнительных
плоскостей представляют собой как бы
числитель и знаменатель дроби,
разделительной чертой которой является
ось проекций, причем их обозначения
располагаются по ту сторону оси, где
должны размещаться соответствующие
проекции.

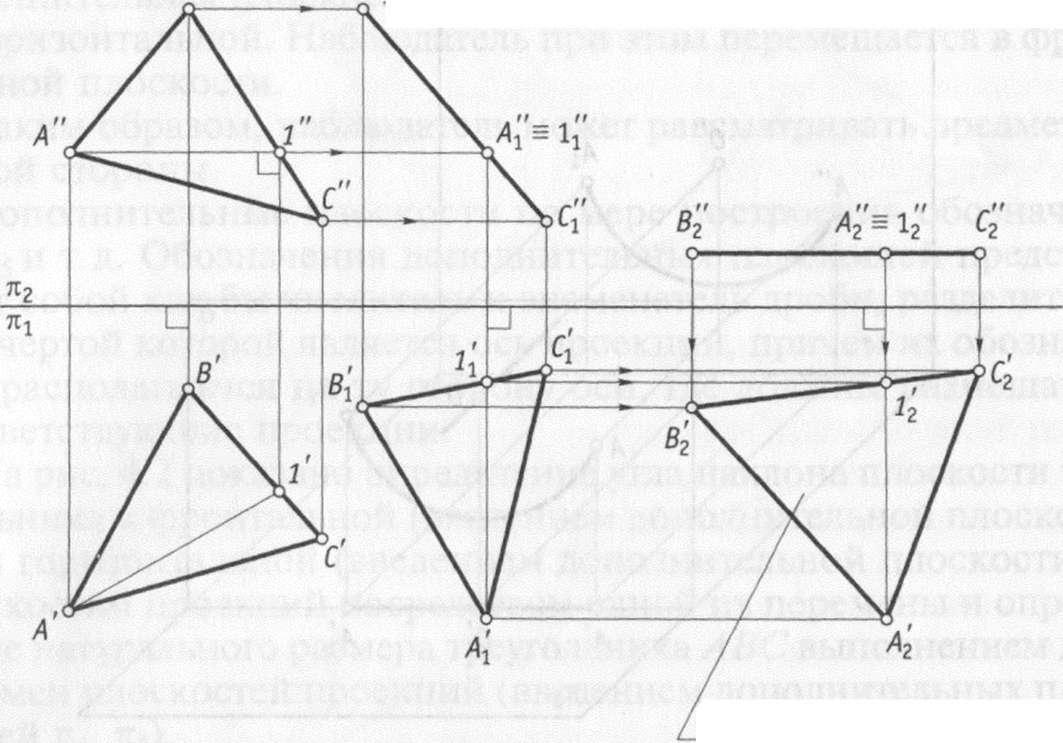
На
рис. 4.2 показано определение угла наклона
плоскости треугольника к фронтальной
(введением дополнительной плоскости
я6) и горизонтальной (введением
дополнительной плоскости я4) плоскостям
проекций посредством одной их перемены
и определение натурального размера
треугольника ЛВС выполнением двух
перемен плоскостей проекций (введением
дополнительных плоскостей я4, тс5).

Способ
вращения.
При вращении вокруг некоторой неподвижной
прямой — оси вращения — каждая точка
вращаемой фигуры перемещается в
плоскости, перпендикулярной этой оси
(т.е. плоскости вращения).

Точка
вращаемой фигуры перемещается по
окружности, центр которой находится в
точке пересечения оси вращения этой
фигуры с плоскостью вращения, называемой
центром вращения, а радиус этой окружности
равен расстоянию от вращаемой точки до
центра вращения и называется радиусом
вращения.

Если какая-либо
из точек данной системы находится на
оси вращения, то при ее вращении эта
точка считается неподвижной.

Ось
вращения может быть задана или выбрана.
В последнем случае ее выгодно располагать
перпендикулярно одной из плоскостей
проекций, так как при этом упрощаются
построения.

Действительно,
если ось вращения перпендикулярна,
например, плоскости тс2, то плоскость,
в которой происходит вращение точки,
параллельна плоскости п2. Следовательно,
траектория этой точки на плоскость п2
проецируется в виде окружности без
искажения, а на плоскость 7Cj — в виде
отрезка прямой линии (рис. 4.3).

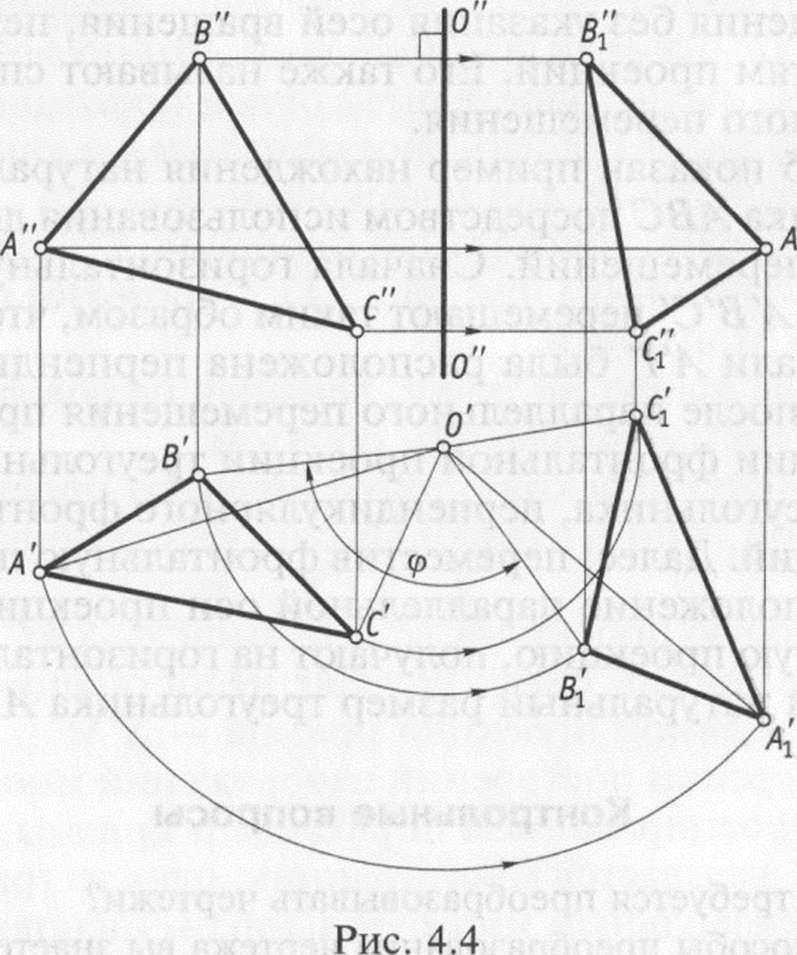
На
рис. 4.4 показан поворот треугольника
ABC вокруг выбранной оси О на угол ср.

Если
вращать отрезок прямой линии или плоскую
фигуру вокруг оси, перпендикулярной
плоскости проекций, то проекция на эту
плоскость не изменится ни по виду, ни
по размеру, изменится лишь положение
этой проекции относительно оси проекций.
Что же касается проекции на плоскость,
параллельную оси вращения, все ее точки
(за исключением, конечно, точек, проекции
которых расположены на оси вращения)
перемещаются по прямым, параллельным
оси проекций, и, следовательно, изменяются
ее форма и размер. В этом случае можно
не указывать проек цию оси вращения, не
устанавливать радиус вращения, а, не
изменяя вид и размер одной из проекций
заданной плоской фигуры, переместить
ее в требуемое положение и построить
другую проекцию с помощью линий,
параллельных оси проекций.

Рис. 4.3

Натуральный размер

Рис. 4.5

Данный
способ преобразования чертежа получил
название способа вращения без указания
осей вращения, перпендикулярных
плоскостям проекций. Его также называют
способом плоскопараллельного перемещения.

На
рис. 4.5 показан пример нахождения
натурального размера треугольника ABC
посредством использования двух
плоскопараллельных перемещений. Сначала
горизонтальную проекцию треугольника
А’В’С’ перемещают таким образом, чтобы
проекция его горизонтали AT была
расположена перпендикулярно оси
проекций, и после параллельного
перемещения проекций точек при построении
фронтальной проекции треугольника
получают плоскость треугольника,
перпендикулярного фронтальной плоскости
проекций. Далее, переместив фронтальную
проекцию треугольника в положение
параллельной оси проекций и построив
горизонтальную проекцию, получают на
горизонтальной плоскости проекций
натуральный размер треугольника ЛВС.

Контрольные
вопросы

Для чего требуется
преобразовывать чертежи?
Какие способы
преобразования чертежа вы знаете?
В чем заключается
сущность способа перемены плоскостей
проекции?
Какое
положение в системе щ9 к2 должна занять
плоскость я3 проекций, вводимая для
образования системы я4, Я|?
Сколько
надо ввести дополнительных плоскостей
в систему яь тс2, чтобы определить
натуральный размер фигуры, плоскость
которой занимает общее положение?
В чем состоит
сущность способа вращения?
Чем различаются
способ перемены плоскостей проекций
и способ вращения?
В каких случаях
способ вращения называется способом
плоскопараллельного перемещения?
Сколько
плоскопараллельных перемещений и в
какой последовательности необходимо
выполнить, чтобы определить натуральный
размер плоскости общего положения и
угол ее наклона к плоскостям проекций?

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Определение видимости в начертательной геометрии с примерами

Определение видимости:

Точки, расположенные на одной проецирующей прямой, называются конкурирующими.

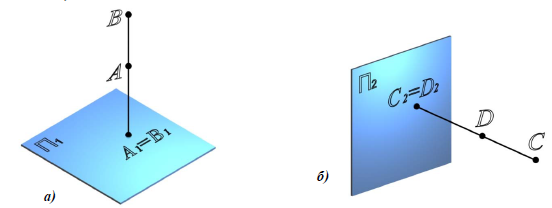
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).

Рис. 7.1. Конкурирующие точки:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций

Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D — невидима).

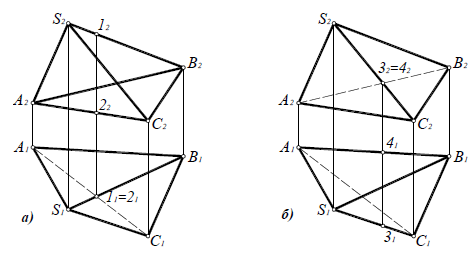
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).

Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а — относительно горизонтальной плоскости проекций;
б — относительно фронтальной плоскости проекций

Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П₁, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П₁, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П₁.

Заказать чертежи

Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П₂.

Конструктивное отображение пространства
Чертежи точки, отрезка прямой
Чертежи плоскости
Взаимное положение двух плоскостей, прямой линии и плоскости
Пересечение поверхностей вращения плоскостью
Виды, разрезы, сечения
Геометрические тела
Комплексный чертеж

Источник

Определение видимости в начертательной геометрии с примерами

Определение видимости:

Точки, расположенные на одной проецирующей прямой, называются конкурирующими.

Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Конструктивное отображение пространства
Чертежи точки, отрезка прямой
Чертежи плоскости
Взаимное положение двух плоскостей, прямой линии и плоскости
Пересечение поверхностей вращения плоскостью
Виды, разрезы, сечения
Геометрические тела
Комплексный чертеж

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Определение видимости на чертеже.

В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.

Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.

Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В²С² и М²N², фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3¢, лежащая на проекции прямой M¢N¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой В¢С¢, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М²N² будет закрывать проекцию В²С². Границей видимости является проекция точки пересечения К².

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢С¢ и M¢N¢, горизонтальные проекции которых пересекаются в точках 4¢ и 5¢. По фронтальной проекции определяем, что проекция точки 5², лежащая на проекции прямой М²N², будет закрывать проекцию точки 4², лежащую на проекции прямой А²С², т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M¢N¢ будет закрывать проекцию А¢С¢. Границей видимости является проекция точки пересечения К¢.

Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.

Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).

Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение

Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.

(KL) ‑ линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.

Задача 4. Построение линии пересечения двух плоскостей общего положения.

Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.

Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.

Алгоритм решения задачи:

1. Определяют первую точку линии пересечения двух треугольников – точку М.

1.1. Фронтально-проецирующая плоскость a проведена через сторону DК и задана на чертеже фронтальным следом a_V.

1.2. Плоскость a пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.

1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М² и М¢.

2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.

2.1. Горизонтально-проецирующая плоскость b проведена через сторону АВ и задана на чертеже горизонтальным следом b_Н.

2.2. Плоскость b пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.

2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N² и N¢.

Плоскости треугольников АВС и DЕК пересекаются по прямой MN.

Рис. 4. Построение линии пересечения двух треугольников

3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.

Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D²K² и A²B², фронтальные проекции которых пересекаются в точках 1² и 5². По горизонтальной проекции определяем, что проекция точки 5¢, лежащая на проекции прямой D¢K¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой А¢В¢, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D²K² будет закрывать проекцию A²B². Границей видимости является проекция линии пересечения M²N².

Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢В¢ и D¢Е¢, горизонтальные проекции которых пересекаются в точках 3¢ и 6¢. По фронтальной проекции определяем, что проекция точки 3², лежащая на проекции прямой D²Е², будет закрывать проекцию точки 6², лежащую на проекции прямой A²B², т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D¢Е¢ будет закрывать проекцию А¢В¢. Границей видимости является проекция линии пересечения N¢M¢.

Задача 5. Построить две проекции линии пересечения плоскости a ‑ общего положения, заданной следами и плоскости b ‑ общего положения, заданной параллельными прямыми а и b.

Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.

Графическое решение задачи приведено на рис. 5.

Рис. 5. Построение линии пересечения двух плоскостей

Вспомогательная горизонтальная плоскость-посредник γ задана следом γ_V и пересекает плоскость a по горизонтали, проходящей через точку 3, а плоскость b по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям a и b. Вторая точка N, общая для двух плоскостей a и b, определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δ_V). Искомая прямая (КN) является линией пересечения двух плоскостей a и b.

ПРИЛОЖЕНИЕ 1

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.

2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.

3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.

источники:

http://poisk-ru.ru/s25018t12.html

http://student-com.ru/%D0%BF%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BB%D0%B8%D0%BD%D0%B8%D0%B8-%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F-%D0%B4%D0%B2%D1%83%D1%85-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2.html

Источник

Построение точки пересечения прямой и плоскости

Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h_0α, f_0α.

Алгоритм

Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h_0γ, f_0γ.
Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h_0α ∩ h_0γ, A» = f_0α ∩ f_0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».

Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П₂на разное расстояние.
Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П₂ на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П₁на разное расстояние.
Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П₁ на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.

Дополнительные материалы:

Построение линии пересечения двух плоскостей
Способы задания плоскости на чертеже

Источник

Пересечение прямой линии с плоскостью. Определение видимости прямой

Пересечение прямой линии с плоскостью

Определение видимости прямой

Понравился материал? Подпишись на обновления!

Определение видимости точек, прямых и плоских фигур.

Глава 4. Способы преобразования чертежа

Определение видимости в начертательной геометрии с примерами

Определение видимости в начертательной геометрии с примерами

Определение видимости на чертеже.

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях. Определить натуральную величину треугольника ABC.

Построение точки пересечения прямой и плоскости

Видимость прямой a относительно плоскости α. Метод конкурирующих точек

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.