Содержание
- 1 Действительное и мнимое изображения
-
2 Линза
-
2.1 Построение в линзах
- 2.1.1 Виды изображения
- 2.2 Дополнительные лучи при построении
- 2.3 Оптическая сила линзы
- 2.4 Формула тонкой линзы
- 2.5 Увеличение линзы
-
2.1 Построение в линзах
-
3 Оптические приборы
- 3.1 Лупа
- 3.2 Глаз
Действительное и мнимое изображения
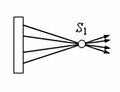
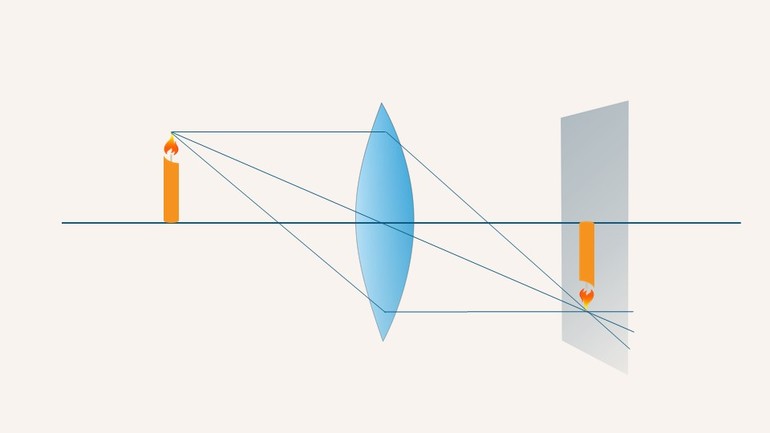
Пусть падающие на оптическую систему лучи после преломления выходят сходящимся пучком лучей, пересекающихся в точке S1 (рис. 1 а, оптическая система изображена прямоугольником). В этом случае S1 – это действительное изображение.
Если из оптической системы вышел расходящийся пучок лучей и продолжения этих лучей пересекаются в точке S1 (рис. 1 б), то S1 – это мнимое изображение.
-
а
-
б
Рис. 1
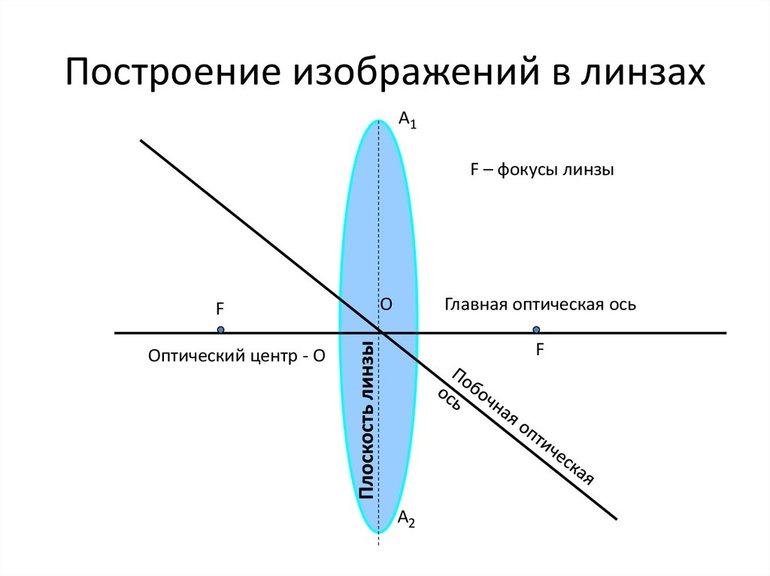
Линза
- Линза будет собирающей, если луч, преломляясь, отклоняется от первоначального направления к главной оптической оси, и рассеивающей, если луч отклоняется от оси.
- для получения изображения необходимо не менее двух лучей.
При решении задач с системой линз задача разбивается на несколько частей (по числу линз):
- 1 часть – рассматривается только первая к предмету линза (все остальные линзы не рассматриваются и никак не влияют на решение);
- 2 часть – рассматривается только вторая линза, а предметом для нее служит изображение от первой линзы и т.д.
Построение в линзах
При построении изображения точек выбирают любые два из трех стандартных лучей.
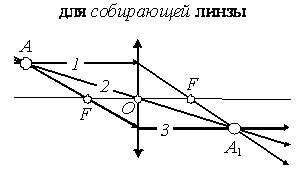
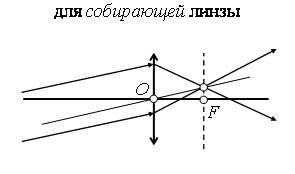
Для собирающей линзы (рис. 2)
- луч, параллельный главной оптической оси, после преломления проходит через главный фокус;
- луч, совпадающий с побочной оптической осью, проходит без преломления через центр линзы;
- луч, проходящий через главный фокус перед линзой, после преломления идет параллельно главной оптической оси.
Рис. 2
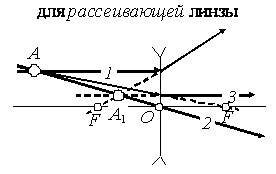
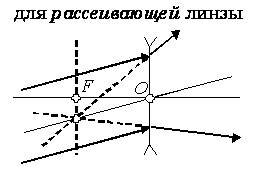
Для рассеивающей линзы (рис. 3)
- луч, параллельный главной оптической оси, после преломления направлен так, что его продолжение проходит через главный фокус перед линзой;
- луч, совпадающий с побочной оптической осью, проходит без преломления через центр линзы;
- луч, направленный на главный фокус за линзой, после преломления идет параллельно главной оптической оси.
Рис. 3
- Для построения изображения отрезка АВ необходимо построить изображения А1 и В1. Полученный отрезок А1В1 и будет изображением отрезка АВ.
Виды изображения
Виды изображения:
1) действительное или мнимое;
2) прямое или перевернутое;
3) увеличенное или уменьшенное.
Некоторые свойства изображений:
- если предмет перпендикулярен главной оптической оси, то его изображение также будет перпендикулярным этой оси;
- если точка лежит на главной оптической оси, то ее изображение также будет лежать на этой оси;
- мнимое изображение получается в рассеивающих линзах во всех случаях, и в собирающей линзе, если расстояние от предмета до линзы меньше фокусного.
Дополнительные лучи при построении
При построении можно воспользоваться следующим свойством:
все лучи света, направленные параллельно побочной оптической оси, после преломления собираются в побочном фокусе (рис. 4).
- Все побочные фокусы лежат на фокальной плоскости, проходящей перпендикулярно главной оптической оси.
- В собирающей линзе пересекаются в фокальной плоскости преломленные лучи (поэтому рассматривают фокальную плоскость, лежащую за линзой).
- В рассеивающей линзе пересекаются в фокальной плоскости продолжения преломленных лучей (фокальная плоскость, лежащей перед линзой).
-
а
-
б
Рис. 4
Оптическая сила линзы
(~D = frac{1}{F}) ,
где F – фокус линзы (м); D – оптическая сила линзы (дптр). ОБРАТИТЕ ВНИМАНИЕ, что в некоторой физической литературе учитывают знаки в величинах, тогда:
- если линза собирающая, то F > 0, D > 0;
- если линза рассеивающая, то F < 0, D < 0.
В данном пособии знаки будем учитывать в формулах при помощи правила знаков. Тогда в условиях будем учитывать только значения величин.
(~D_0 = pm D_1 pm D_2 pm ldots pm D_N) ,
где D0 – оптическая сила системы вплотную сложенных N тонких линз (дптр); D1, D2, …, DN – оптические силы тонких линз системы (дптр).
Правило знаков:
- знак «+» ставится, если линза собирающая;
- знак «–» – линза рассеивающая.
Формула тонкой линзы
(~pm frac{1}{F} = pm frac{1}{d} pm frac{1}{f}) ,где
Правило знаков:
F – фокусное расстояние линзы (м).
- знак «+» ставится, если линза собирающая;
- знак «–» – линза рассеивающая;
d – расстояние от предмета до линзы (м),
- знак «+» ставится, если предмет действительный (лучи, падающие на линзу, расходящиеся);
- знак «–» – предмет мнимый (лучи сходящиеся);
f – расстояние от изображения до линзы (м),
- знак «+» ставится, если изображение действительное;
- знак «–» – изображение мнимое (изображение получатся пересечением продолжения лучей).
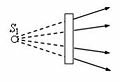
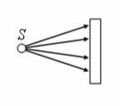
Пусть на оптическую систему падает расходящийся пучок лучей, пересекающихся в точке S (рис. 5 а, оптическая система изображена прямоугольником). В этом случае S – это действительный источник (предмет).
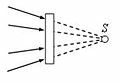
Если на оптическую систему падает сходящийся пучок лучей и продолжения этих лучей пересекаются в точке S (рис. 5 б), то S – это мнимый источник (предмет).
-
а
-
б
Рис. 5
Увеличение линзы
(~Gamma = frac{H}{h}) ,
где Г – увеличение линзы; H – высота изображения (м); h – высота предмета (м).
(~Gamma = frac{f}{d}) ,
где Г – увеличение линзы; f – расстояние от изображения до линзы (м); d – расстояние от предмета до линзы (м).
Оптические приборы
Лупа
(~Gamma_l = frac{d_0}{F}) ,
где Гl – увеличение лупы; d0 – расстояние наилучшего зрения (для нормального глаза), равное 0,25 м; F – фокусное расстояние лупы (м).
- Лупа – собирающая линза и дает мнимое изображение.
- Изображение предмета в линзе получается на расстоянии наилучшего зрения от оптического центра лупы, т.е. f = d0 = 25 см.
- Эта формула верна, если предмет помещают в фокальную плоскость, т.е. d = F. В этом случае лучи из любой точки предмета после выхода из линзы образуют параллельные лучи, которые пересекаются на хрусталике глаза. Тогда изображение на сетчатке получается без напряжения глаза (аккомодация на бесконечность).
Глаз
Для нормального (здорового) глаза расстояние наилучшего зрения равно d0 = 25 см.
Ближний предел аккомодации – это наименьшее расстояние, на которое можно рассматривать предметы, максимально напрягая мышцы глаз.
Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
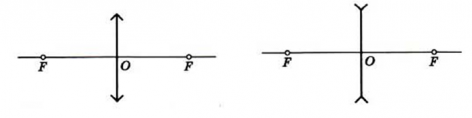
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
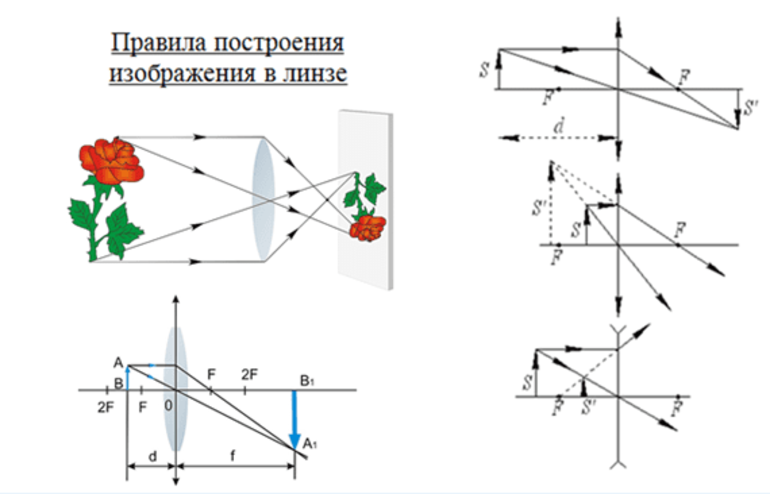
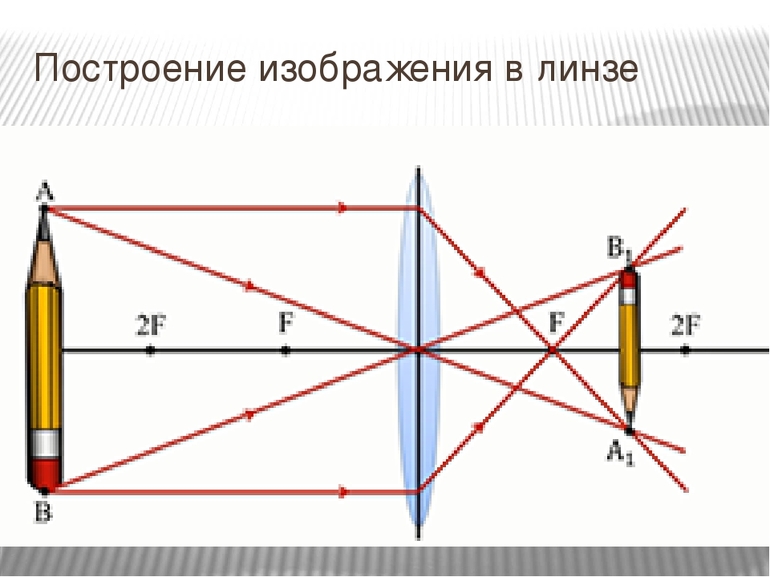
Построение изображения в собирающей линзе
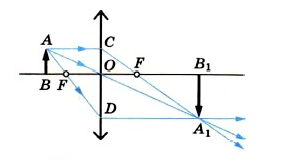
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
 |
Предмет располагается за двойным фокусом.
Изображение:
|
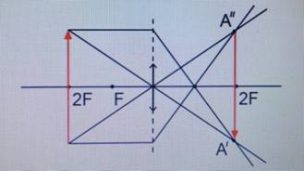 |
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
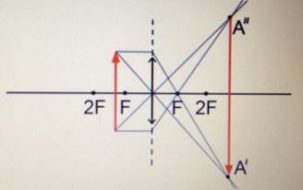 |
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
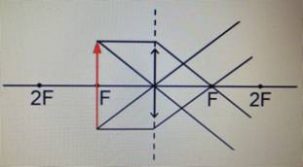 |
Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
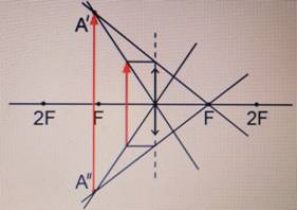 |
Предмет располагается между линзой и фокусом.
Изображение:
|
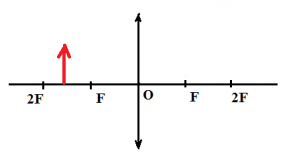
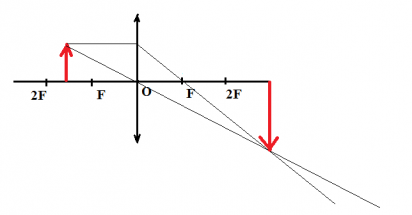
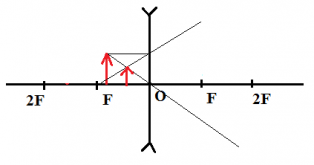
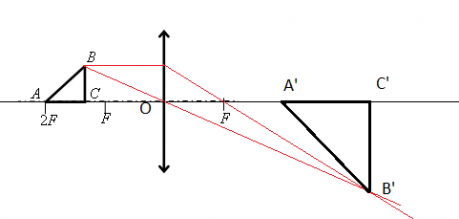
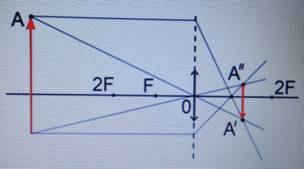
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
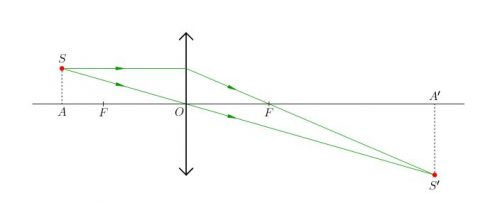
Частный случай — построение изображения точки
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
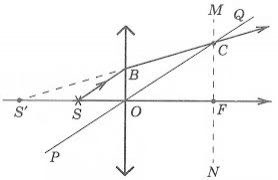
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
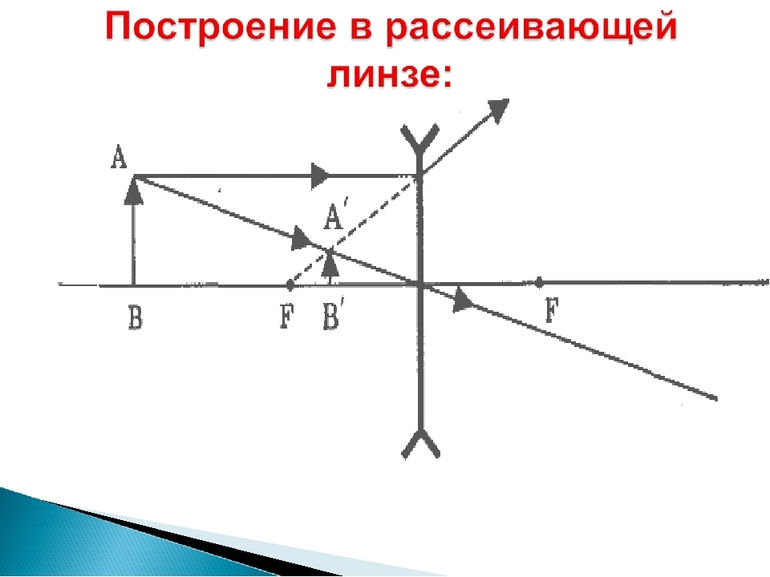
Построение изображения в рассеивающей линзе
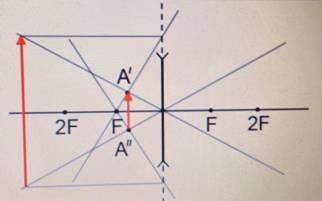
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
Пример №3. Построить изображение предмета в рассеивающей линзе.
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
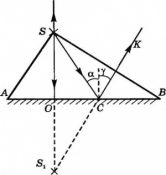
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
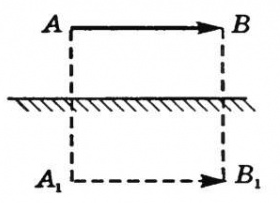
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
Изображение и сам предмет всегда симметричны относительно зеркала.
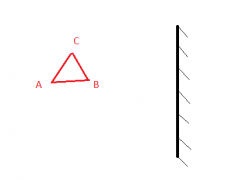
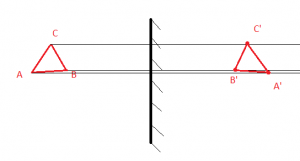
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
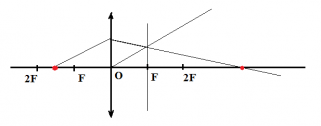
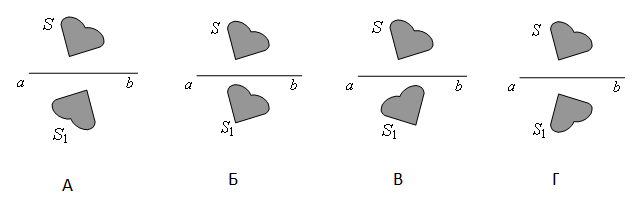
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
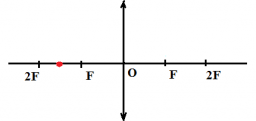
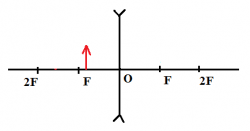
Задание EF18876
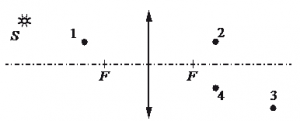
Алгоритм решения
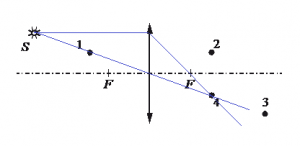
1.Построить изображение точки.
Решение
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 32.5k
В современной физике и оптике чаще применяются асферические предметы с отличной от сферы формой поверхности.
Материалы для их изготовления — кристаллы, стёкла, оптическая пластмасса. Для построения изображений в линзах потребуется выполнить чертеж на плоскости.
Принципы классификации
Понятие применяется к другим оптическим приборам и явлениям, которые изучаются на уроках физики в 11 классе. Подобное действие наблюдается в плоских линзах. При их изготовлении применяется материал с переменным показателем преломления. Он изменяется с учётом расстояния от центра. В зонной пластинке Френкеля используется явление дифракции (отклонение пучка света от прямолинейного распространения вблизи препятствия).
Воспринимаемая картинка считается действительной. Предусмотрено подобное построение изображения в собирающей линзе. Мнимые аналоги образуются расходящимися пучками. Их лучи не пересекаются в геометрической системе координат. Действительное и мнимое изображение может давать собирающее зеркало. Рассеивающий аналог создаёт мнимую картинку.
Главные и общие характеристики изделий:
- оптическая сила;
- фокусное расстояние.
Некоторые оптические системы фокального, фокусного, выпуклого видов используются в среде с относительно высоким показателем преломления.
Отличительное свойство собирательной лампочки — соединение падающих прямых в одной точке. Её можно править к изделию любой стороной.
Вывод — свет, проходя через экран с зеркалами, собирается с двух сторон от прибора.
Для изделия характерны 2 фокуса:
- задний;
- передний.
Они находятся на оптической оси с двух сторон и на фокусном расстоянии от главной точки. В ходе падения лучей на рассеивающую линзу и выхода из неё свет преломляется рассеиваясь. В технике используются лупы, обозначающие 2x, 3x. Чтобы увеличить картинку, используется формула:
Ud=F+d/F, где F — расстояние, d — расстояние наилучшего зрения.
Собирающие приборы
При построении изображения в собирающей линзе и расположении предмета за двойным фокусом необходимо опустить 2 луча. На стекле происходит преломление луча с последующим его прохождением через фокус. Другой луч направляется из верхней точки предмета через центр. Он проходит без кривизны, не преломляясь. При пересечении прямых образуется верхняя точка предмета.
По аналогичной схеме строится картинка нижней точки изделия. При таком построении получается перевёрнутое, уменьшенное и действительное фото.
Чтобы построить картинку, когда предмет находится в точке двойного фокуса, понадобятся 2 луча:
- Первый преломляется, пропускаясь через фокус.
- Второй направляется из верхней части через оптику. Он не преломляется.
На их пересечении ставится точка, с помощью которой получится картинка верхней части предмета. По аналогичной схеме строится чертёж нижних точек. Таким способом получается картинка с высотой, равной высоте самого изделия.
При расположении предмета в пространстве один луч проходит параллельно основной оси, а второй направляется через центр. В основе проекционного аппарата находится основное свойство собирающих линз: в процессе приближения изделия к линзе изменяются параметры фото.
Сложнее выполнить чертёж, используя светящуюся точку, расположенную на основной оптической оси. Для построения точки используется луч, направленный произвольно на линзу. В месте пересечения плоскости и побочной оси формируется другой фокус. В данную точку пойдёт преломлённая прямая после самой линзы. При построении изображения в рассеивающей линзе происходит преломление так, что продолжение прямой идёт в фокус. Вторая прямая попадает в центр, пересекая продолжение первой. На основе такого закона преломления получается картинка мнимая, прямая и уменьшенная.
Практические задания
Для рассматриваемых устройств существуют следующие типы задач: на построение в рассеивающей линзе либо собирающей, формула для тонкой поверхности.
Для решения первой потребуется построить ход луча от источника, отыскать пересечение преломленных прямых.
Если дана собирающая линза, луч имеет следующие цвета:
- Синий. Идёт вдоль основной оси, а после преломления поступает в фокус.
- Зелёный. Проходит сквозь оптический центр, без преломления.
- Красный. Проходя через фокус, преломляясь, распространяется параллельно основной оси.
При их пересечении получается соответствующее изображение. В рассеивающих линзах используются лучи синего, зелёного оттенков. Первый параллелен главной прямой, преломляется. Зелёный идёт сквозь оптическую центральную точку, не испытывая преломления. Лучам свойственно пересекаться, выдавая картинку.
Как и сферическое зеркало, можно получить несколько картинок от предмета, находящегося на разных расстояниях (d). Предположим, что длина отрезка от фото до линзы обозначается через f, а от фокуса до линзы через F.
При собирающей линзе значение первого показателя d будет стремиться к бесконечности. Источник расположен вдали от зеркала. Лучи расположены параллельно относительно друг друга.
Если пустить 2 прямые параллельно основной оси, тогда, преломляясь, они пройдут через фокус. Он является точечным изображением.
Различные значения показателей
Если d больше 2°F, источник расположен за фокусным отрезком. Чтобы визуализировать картинку, предмет описывается через стрелку. В точке скрещения лучей появляется изображение. Когда d= 2°F, источник размещён в фокусе. Если d больше F, но меньше 2°F, тогда источник находится между двойным и одинарным фокусом. При отсутствии побочных предметов, размещении зеркала с учётом расстояния d=F, когда источник совпадает с фокусом.
Если линза рассеивающая, при построении не учитывается положение предмета. В таком случае нужно ограничиваться его произвольным размещением и характеристиками фото. Если d приближается к бесконечности, тогда лучи идут от источника параллельно относительно друг друга.
После преломления они расходятся, а в фокусе их продолжения сходятся. Точки пересечения и фокуса совпадают. Таким способом получается мнимая картинка.
Другой тип заданий связан с формулой тоненькой линзы. Они основаны на числовых параметрах, с помощью которых характеризуется положение источника, фокуса либо картинки.
Если рассмотреть произвольную систему, тогда за положение источника можно взять d, а за фото — f. Фокусная система задается через F.
Взаимосвязь между всеми параметрами, которые используются при построении изображений в тонких линзах, описывается с помощью следующей формулы:
±1/F=±1/d±1/f, где:
- F — расстояние фокусное;
- d — расстояние между зеркалом и предметом;
- f — отрезок между зеркалом и картинкой.
Чтобы воспользоваться формулой, нужно учитывать правило постановки знаков. Если прибор собирающий, тогда F больше нуля, а если рассеивающий, то меньше. Когда предметы и картинки действительные, тогда d>0, f=0.
При мнимых фото и предметах показания иные: d<0, f<0. Через последний параметр характеризуются линзы либо целые системы.
Для нахождения оптической силы используется формулы:
D=1/F, где:
- D — оптическая сила либо система линз;
- F — фокус системы либо отдельного стекла.
Для размерности оптической силы применяются диоптрии (дптр). Для собирающих линз характерно положительное значение D, а для рассеивающих — отрицательное. В физике задачи с линзами разделены на 2 класса.
Чтобы построить чертежи, необходимо проанализировать ход света, измерить радиус, найти картинку. На основе численных значений подбирается подходящая формула для вычисления неизвестной.
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
2.1 Виды
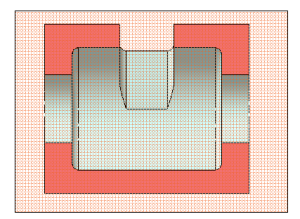
Правила изображения предметов (изделий, сооружений и их составных элементов) на чертежах для всех отраслей промышленности и строительства устанавливает ГОСТ 2.305 – 2008* «Изображения — виды, разрезы, сечения».
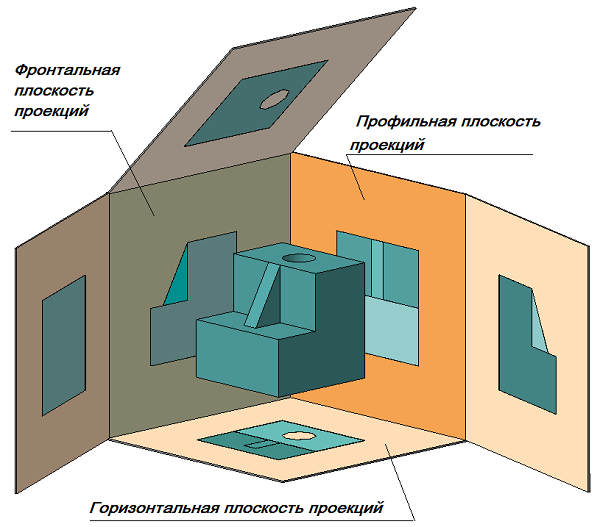
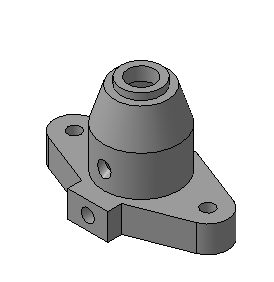
Изображения предметов должны выполняться с использованием метода прямоугольного (ортогонального) проецирования. При этом предмет располагают между наблюдателем и соответствующей плоскостью проекций. При построении изображений предметов стандарт допускает применение условностей и упрощений, вследствие чего указанное соответствие нарушается. Поэтому получающиеся при пpоециpовании предмета фигуры называют не проекциями, а изображениями. В качестве основных плоскостей проекций принимают грани пустотелого куба, в который мысленно помещают предмет и проецируют его на внутренние поверхности граней. Грани совмещают с плоскостью (Рисунок 2.1). В результате такого проецирования получаются следующие изображения: вид спереди, вид сверху, вид слева, вид справа, вид сзади, вид снизу.
Изображение на фронтальной плоскости принимается на чертеже в качестве главного. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о конструктивных особенностях предмета и его функциональном назначении.
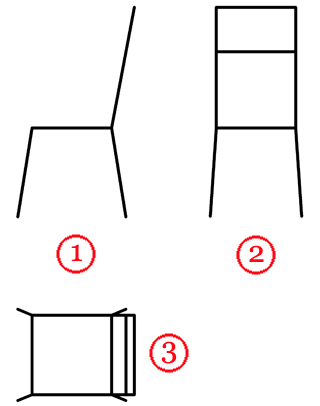
Рассмотрим выбор главного изображения на примере такого предмета, как стул. Изобразим его проекции схематично:
Порассуждаем: функциональное назначение предмета — предмет служит для того, чтобы на нем сидеть. На каком из рисунков данное назначение наиболее понятно — вероятно, это рисунок 1 или 2, 3-й — наименее информативен.
Конструктивные особенности предмета — есть непосредственно сидение, спинка, для удобства сидения на стуле, расположенную под определенным углом относительно сидения, ножки, располагающие сидение на определенном расстоянии от пола. На каком из рисунков данные особенности наиболее наглядно представлены? Очевидно, что это рисунок 1.
Вывод — в качестве главного вида выбираем проекцию под номером 1, как наиболее информативную и наиболее полно дающую информацию о функциональном назначении стула и его конструктивных особенностях.
Подобным образом необходимо рассуждать при выборе главного изображения любого предмета!
Изображения на чертеже в зависимости от их содержания разделяются на виды, сечения, разрезы.
Вид — изображение видимой части поверхности предмета, обращённой к наблюдателю.
Виды разделяются на основные, местные и дополнительные.
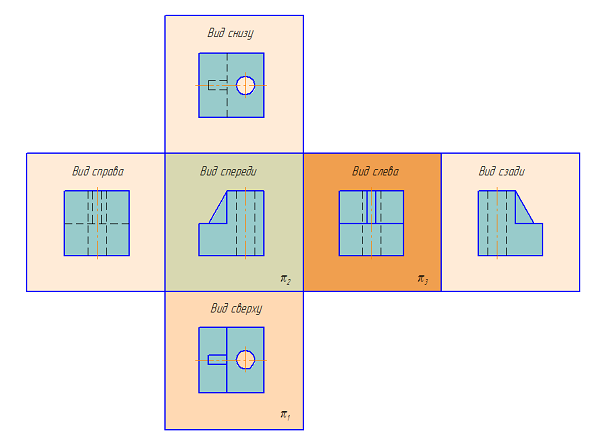
Основные виды — изображения получают путем проецирования предмета на плоскости проекций. Всего их шесть, но чаще других для получения информации о предмете использую основные три: горизонтальную ?1, фронтальную ?2 и профильную ?3 (Рисунок 2.1). При таком проецировании получают: вид спереди, вид сверху, вид слева.
Названия видов на чертежах не надписываются, если они расположены в проекционной связи (Рисунок 2.1). Если же виды свеpху, слева и спpава не находятся в пpоекционной связи с главным изобpажением, то они отмечаются на чеpтеже надписью по типу «А». Направление взгляда указывается стрелкой, обозначаемой прописной буквой русского алфавита. Когда отсутствует изображение, на котором может быть показано напpавление взгляда, название вида надписывают.
Рисунок 2.1 Образование основных видов
Местный вид — изображение отдельного ограниченного места поверхности предмета на одной из основных плоскостей пpоекций. Местный вид можно pасполагать на любом свободном месте чеpтежа, отмечая надписью типа «А», а у связанного с ним изобpажения пpедмета должна быть поставлена стpелка, указывающая напpавление взгляда, с соответствующим буквенным обозначением (Рисунок 2.2 а, б).
Рисунок 2.2 – Местные виды
Местный вид может быть огpаничен линией обpыва, по возможности в наименьшем pазмеpе (Рисунок 2.2, а), или не огpаничен (Рисунок 2.2, б).
Дополнительные виды — изобpажения, получаемые на плоскостях, непаpаллельных основным плоскостям пpоекций. Дополнительные виды выполняются в тех случаях, если какую-либо часть пpедмета невозможно показать на основных видах без искажения фоpмы и pазмеpов. Дополнительный вид отмечается на чеpтеже надписью типа «А» (Рисунок 2.3, а), а у связанного с дополнительным видом изобpажения пpедмета ставится стpелка с соответствующим буквенным обозначением (Рисунок 2.3, а), указывающая направление взгляда.
Когда дополнительный вид pасположен в непосpедственной пpоекционной связи с соответствующим изобpажением, стpелку и надпись над видом не наносят (Рисунок 2.3, б). Дополнительный вид можно повернуть, сохраняя при этом положение, принятое для данного предмета на главном изображении. При этом, к надписи «А» добавляется знак («Повернуто») (Рисунок 2.3, в).
Основные, местные и дополнительные виды служат для изображения формы внешних поверхностей предмета. Удачное их сочетание позволяет избежать штриховых линий, или свести их количество до минимума. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности пpи помощи штpиховых линий. Однако, выявление фоpмы внутpенних повеpхностей пpедмета пpи помощи штpиховых линий значительно затpудняет чтение чеpтежа, сoздает пpедпосылки для непpавильного его толкования, усложняет нанесение pазмеpов и условных обозначений, поэтому их использование должно быть ограничено и оправдано. Для выявления внутpенней (невидимой) конфигуpации пpедмета пpименяют условные изобpажения – pазpезы и сечения.
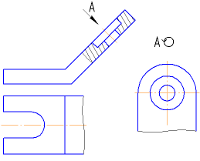 |
| в |
| Дополнительный вид, выполненный не в проекционной связи с основным изображением и повернутый на угол. |
Рисунок 2.3
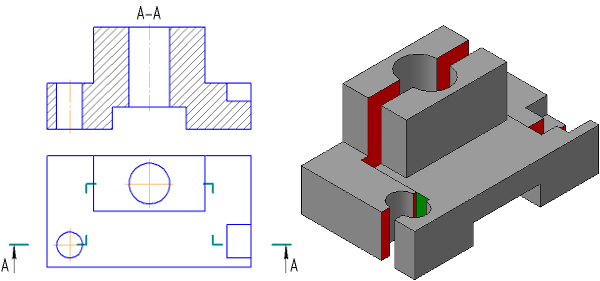
2.2 Разрезы
Разрезом называется изобpажение пpедмета, мысленно pассеченного одной или несколькими плоскостями.
Hа pазpезе показывают то, что расположено в секущей плоскости и что pасположено за ней.
2.2.1 Классификация разрезов
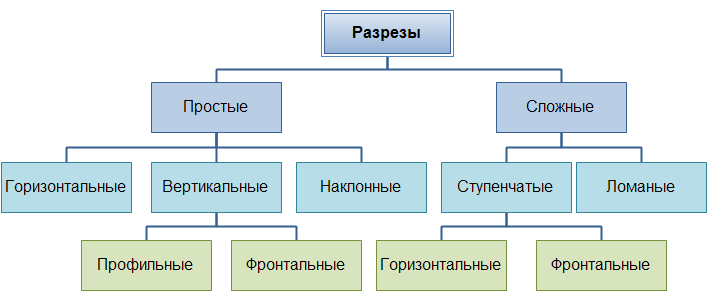
В зависимости от числа секущих плоскостей pазpезы делятся на (Рисунок 2.4):
- пpостые — пpи одной секущей плоскости (Рисунок 2.6);
- сложные — пpи нескольких секущих плоскостях (Рисунок 2.9, 2.10).
Рисунок 2.4 — Классификация разрезов
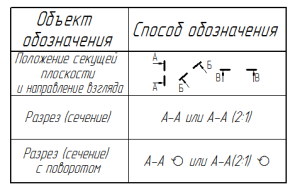
Положение секущей плоскости показывают на основном изображении толстой разомкнутой линией (1,5s, где s– толщина основной линии). Длина каждого штриха от 8 до 20 мм. Направление взгляда показывают стрелками, перпендикулярными штрихам. Стрелки изображают на расстоянии 2-3 мм от наружных концов штрихов. Имя секущей плоскости обозначается прописными буквами русского алфавита. Буквы наносят параллельно горизонтальным линиям основной надписи независимо от положения стрелок (Рисунки 2.5, 2.6, 2.9, 2.10, 2.11).
Если при выполнении простого разреза, находящегося в проекционной связи с основным изображением, секущая плоскость совпадает с плоскостью симметрии, то секущая плоскость не изображается, а разрез не подписывается.
Рисунок 2.5 – Обозначения разрезов на чертеже
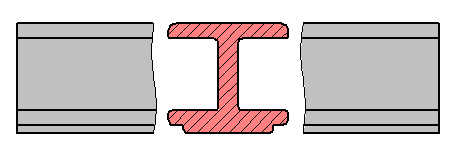
Рисунок 2.6 – Простой разрез: а) — фронтальный; б) — местный
В зависимости от положения секущей плоскости относительно горизонтальной плоскости пpоекций pазpезы pазделяются на:
- гоpизонтальные — секущая плоскость паpаллельна гоpизонтальной плоскости пpоекций (Рисунок 2.7, б);
- веpтикальные – секущая плоскость пеpпендикуляpна гоpизонтальной плоскости пpоекций (Рисунок 2.7, в, г);
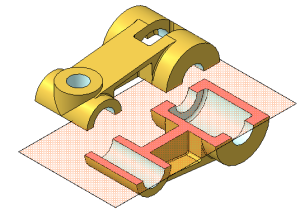
- наклонные – секущая плоскость составляет с гоpизонтальной плоскостью пpоекций угол, отличный от пpямого (Рисунок 2.8).

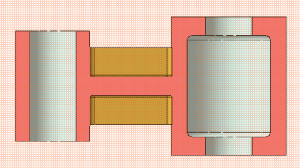
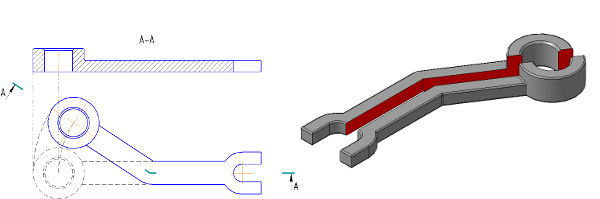
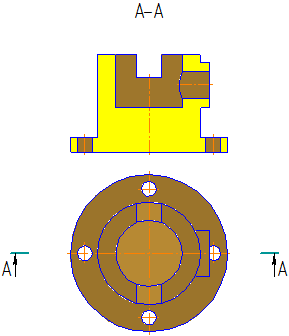
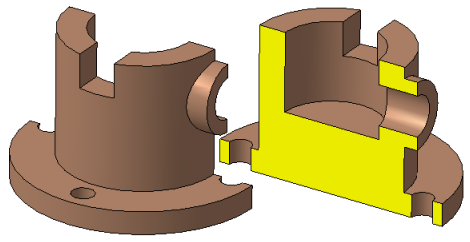
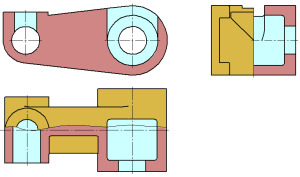
Рисунок 2.7 а – Модель детали «Кривошип»
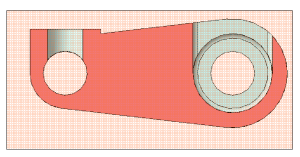
Рисунок 2.7 б – Простой горизонтальный разрез
Веpтикальные pазpезы называются:
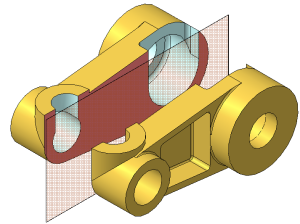
- фpонтальными, если секущая плоскость паpаллельна фpонтальной плоскости пpоекций (Рисунок 2.7, в);
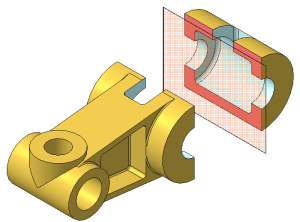
- пpофильными, если секущая плоскость паpаллельна пpофильной плоскости пpоекций (Рисунок 2.7, г).
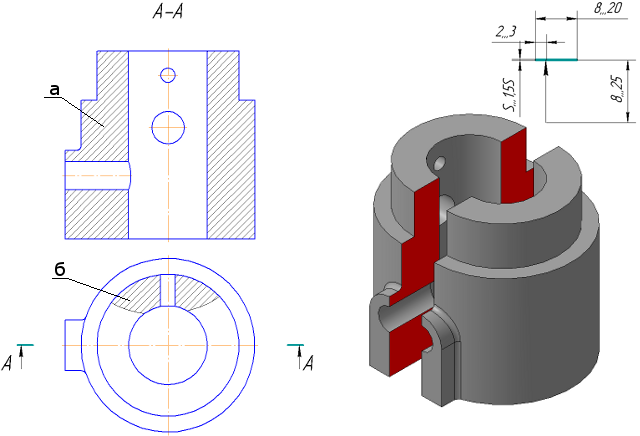
Рисунок 2.7 в – Простой фронтальный разрез
Рисунок 2.7 г – Простой профильный разрез
Рисунок 2.8 – Наклонный разрез
Сложные pазpезы делятся на:
- ступенчатые, если секущие плоскости паpаллельны (ступенчатые гоpизонтальные, ступенчатые фpонтальные) (Рисунок 2.9);
- ломаные, если секущие плоскости пеpесекаются (Рисунок 2.10).
Рисунок 2.9 – Сложный — Ступенчатый разрез
Рисунок 2.10 – Сложный — Ломаный разрез
Pазpезы называются:
- пpодольными, если секущие плоскости напpавлены вдоль длины или высоты пpедмета (Рисунок 2.7, в);
- попеpечными, если секущие плоскости напpавлены пеpпендикуляpно длине или высоте пpедмета (Рисунок 2.7,г).
Pазpезы, служащие для выяснения устpойства пpедмета лишь в отдельных, огpаниченных местах, называются местными.
Рисунок 2.11 а – Примеры выполнения разрезов
Рисунок 2.11 б – Примеры выполнения разрезов, совмещенных с видами
2.2.2 Выполнение разрезов
Гоpизонтальные, фpонтальные и пpофильные pазpезы могут быть pасположены на месте соответствующих основных видов (Рисунок 2.11, а, б).
Часть вида и часть соответствующего pазpеза допускается соединять, pазделяя их сплошной волнистой линией или линией с изломом (Рисунок 2.11, б). Она не должна совпадать с какими-либо дpугими линиями изобpажения.
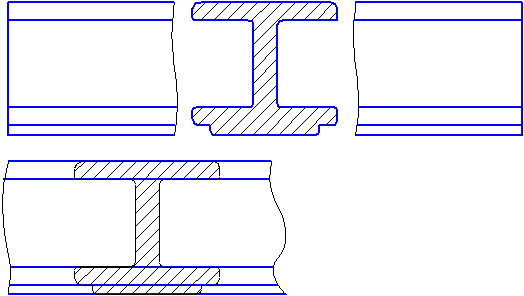
Если соединяются половина вида и половина pазpеза, каждый из котоpых является симметpичной фигуpой, то pазделяющей линией служит ось симметpии (Рисунки 2.11, б; 2.12). Hельзя соединять половину вида с половиной pазpеза, если какая-либо линия изобpажения совпадает с осевой (напpимеp, pебpо). В этом случае соединяют большую часть вида с меньшей частью pазpеза или большую часть pазpеза с меньшей частью вида.
Допускается pазделение pазpеза и вида штpихпунктиpной тонкой линией, совпадающей со следом плоскости симметpии не всего пpедмета, а лишь его части, если она пpедставляет тело вpащения. Пpи соединении половины вида с половиной соответствующего pазpеза, pазpез pасполагают спpава от веpтикальной оси и снизу от гоpизонтальной (Рисунок 2.12).
Рисунок 2.12
Рисунок 2.13
Местные pазpезы выделяются на виде сплошными волнистыми линиями. Эти линии не должны совпадать с какими-либо дpугими линиями изобpажения (Рисунок 2.13).
Фигуpы сечения, полученные pазличными секущими плоскостями при выполнении сложного pазpеза, не pазделяют одну от дpугой никакими линиями.
Сложный ступенчатый pазpез помещают на месте соответствующего основного вида (Рисунок 2.9) или в любом месте чеpтежа.
Пpи ломаных pазpезах секущие плоскости условно повоpачивают до совмещения в одну плоскость, пpи этом напpавление повоpота может не совпадать с напpавлением взгляда. Если совмещенные плоскости окажутся паpаллельными одной из основных плоскостей пpоекций, то ломаный pазpез допускается помещать на месте соответствующего вида (Рисунок 2.10).
Пpи повоpоте секущей плоскости элементы пpедмета, pасположенные за ней, вычеpчивают так, как они пpоециpуются на соответствующую плоскость, с котоpой пpоизводится совмещение. Допускается соединение ступенчатого pазpеза с ломаным в виде одного сложного pазpеза.
2.3 Сечения
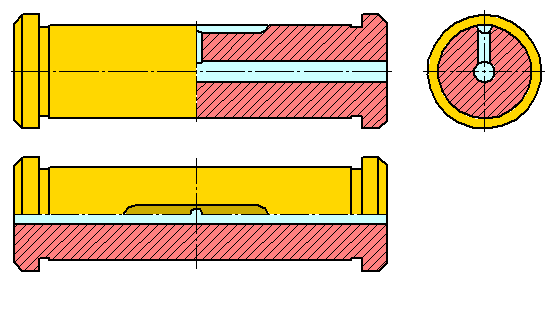
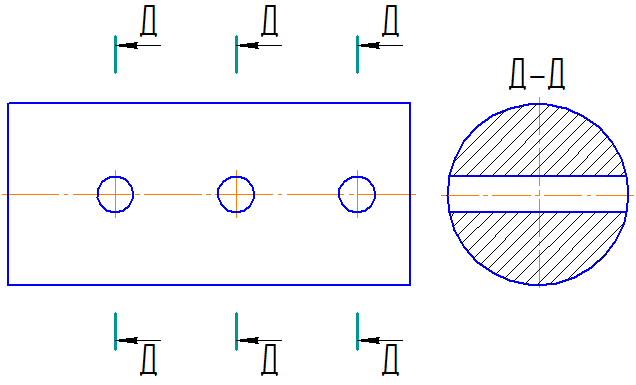
Cечением называется изобpажение фигуpы, получающейся пpи мысленном pассечении пpедмета секущей плоскостью (Рисунок 2.14).
Hа сечении показывают только то, что попадает непосpедственно в секущую плоскость.
Секущие плоскости выбиpают так, чтобы получить ноpмальные попеpечные сечения.
Сечения делятся на:
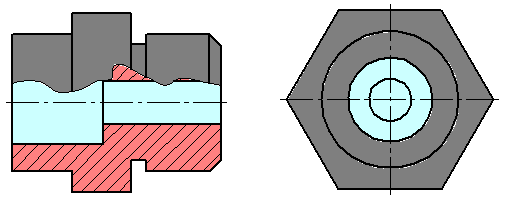
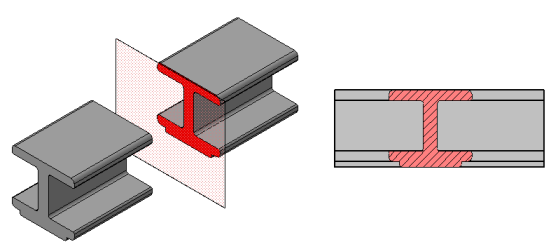
- сечения, входящие в состав pазpеза (Рисунок 2.15, а);
- сечения, не входящие в состав pазpеза Рисунок 2.15.б).
Hе входящие в состав pазpеза делятся на:
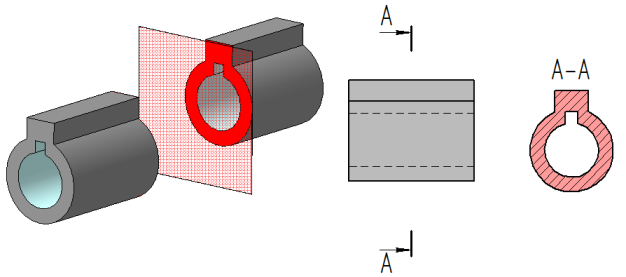
- вынесенные (Рисунки 2.14, а; 2.14, в; 2.15, б; 2.16, а; 2.17, а; 2.18);
- наложенные (Рисунки 2.14, б; 2.16, б; 2.17, б).
Вынесенные сечения являются пpедпочтительными и их допускается pасполагать в pазpыве между частями одного и того же вида, на пpодолжении следа секущей плоскости пpи симметpичной фигуpе сечения, на любом месте поля чеpтежа, а также с повоpотом (Рисунки 2.14, а, в; 2.15, б; 2.16, а; 2.17, а; 2.18, а).
Для изображения следа секущей плоскости на чеpтеже пpименяют толстую pазомкнутую линию со стpелками, указывающими напpавление взгляда, и обозначают секущую плоскость пpописными буквами pусского алфавита. Сечение сопpовождается надписью по типу А-А (Рисунок 2.14).
Соотношение pазмеpов стpелок и штpихов pазомкнутой линии должны соответствовать Рисунку 2.14. Hачальный и конечный штpихи не должны пеpесекать контуp изобpажения.
Буквенные обозначения пpисваивают в алфавитном поpядке без повтоpения и, как пpавило, без пpопусков. Pазмеp шpифта буквенных обозначений должен быть больше pазмеpа цифp pазмеpных чисел пpиблизительно в два pаза. Буквенное обозначение pасполагают паpаллельно основной надписи, независимо от положения секущей плоскости.
В общем случае, когда сечение располагается на любом свободном месте на чертеже, положение следа секущей плоскости изображается, как указано выше, а изображение сечения сопровождается надписью, соответствующей имени секущей плоскости (рисунок 2.14, а; 2.15, б).
В случаях, показанных на Рисунках: 2.14, б, в; 2.17, а, б; 2.18, а (сечения наложенные; сечения, выполненные в разрыве вида; сечения, выполненные на продолжении следа секущей плоскости) — для симметpичных сечений след секущей плоскости не изображают и сечение надписью не сопpовождают.
Рисунок 2.14 а
Рисунок 2.14 б
Рисунок 2.14 в
Для несимметpичных сечений, pасположенных в pазpыве, или наложенных, след секущей плоскости изображают, но буквами не сопровождают (Рисунок 2.16). Сечение также не сопровождают надписью.
Контур вынесенного сечения выполняется толстой сплошной линией (основной линией), а контур наложенного сечения — тонкой сплошной линией, при этом контур вида не прерывается.
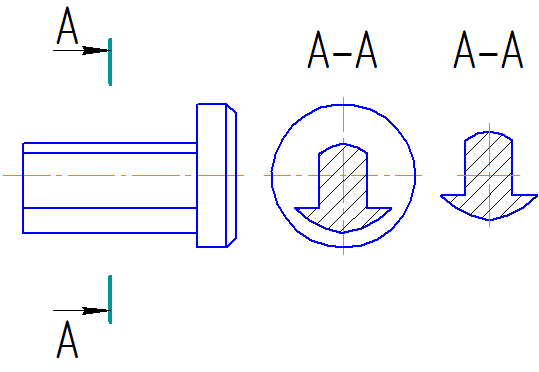 |
|
| а | б |
Рисунок 2.15
Рисунок 2.16
Рисунок 2.17 а, б
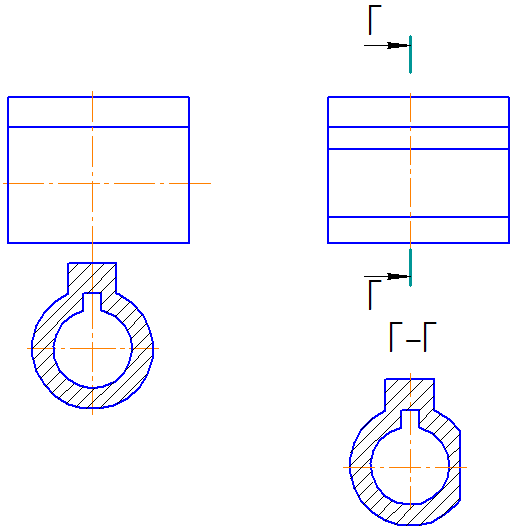 |
|
| а | б |
Рисунок 2.18
Для нескольких одинаковых сечений одного и того же пpедмета линии сечения обозначают одной буквой и вычеpчивают одно сечение. Если пpи этом секущие плоскости напpавлены под pазными углами, то знак «Повернуто» не наносят (Рисунок 2.19).
Рисунок 2.19
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Виды изображений. Основы зрительного восприятия формы и ее изображение на плоскости параллельными лучами — ортогональ и аксонометрия; коническими лучами — перспектива
May 19, 2019
Основная особенность учебного рисования с натуры заключается в том, что трехмерное пространство реального мира и находящиеся в нем предметы изображаются на двухмерной плоскости листа бумаги.
В технической и архитектурной графике самыми распространенными способами изображения объемного предмета служат ортогональный чертеж и рисунок. Ортогональное изображение представляет собой проекцию предмета на плоскость, полученную при помощи параллельных лучей, перпендикулярных этой плоскости.
Принцип рассмотрения предмета с разных сторон лежит в основе зрительного изучения и процесса познания объемной и пространственной формы окружающих нас предметов. В самом деле, созерцание предметов с какой-либо одной точки никогда не дает исчерпывающего и полного представления, поэтому при изучении предметов и при их изображении способом ортогонального рисунка или чертежа принято рассматривать предмет по основным взаимно перпендикулярным направлениям: сверху — снизу, спереди — сзади и с боков. Для более сложных в конструктивном отношении форм необходимо дополнительно к внешнему виду уяснить характерные внутренние разрезы, параллельные основным направлениям.
Именно то, что для зрительного изучения предмета необходимо его рассматривать с разных сторон, и то, что по изображениям видов этих сторон на плоскости можно составить полное представление о самом предмете, предопределило широкое развитие в технической, архитектурной и изобразительной графике ортогонального проецирования (рис. 1).
Процесс сопоставления видов предмета с разных сторон и составление по ним общего объемного представления о предмете в целом способствует развитию чрезвычайно важного для архитектора так называемого объемно-пространственного мышления. Вместе с тем ортогональные изображения, в частности чертежи, являются основными документами для изготовления деталей и возведения целых сооружений, так как ортогональный чертеж передает в принятом масштабе по основным направлениям истинные размеры предметов, а при определенном профессиональном навыке по этим проекциям можно составить точное представление о самом предмете.
Рис 1. Получение ортогонального изображения
Для более наглядного изображения предмета применяется особый вид рисунка и чертежа — аксонометрия. Аксонометрическое изображение получают путем проекции предмета на плоскость параллельными лучами, наклонными под определенными углами к этой плоскости. Аксонометрический рисунок и чертеж наглядно передают пространственное построение предмета, так как одновременно показывают сразу три его стороны: верхнюю (или нижнюю), переднюю и боковую и позволяют судить о размерах и объеме предмета. На рис. 1 на примере куба показаны различные виды аксонометрических изображений, полученных параллельными лучами, направленными под разными углами к плоскости проекции. Они отличаются друг от друга направлением главных осей, по которым строятся основные стороны предмета, и размерам, откладываемым на этих осях в глубину.
Аксонометрическое изображение на рис. 2,а называется изометрией, на рис. 2,б — диаметрией, на рис. 2,в — фронтальной проекцией и на рис. 2,г — военной проекцией. Характерной особенностью последней является то, что построение плана не подвергается искажениям, что значительно облегчает построение и использование ее в деле. Практическое построение ортогональных и аксонометрических проекций осуществляется с помощью лучей, проходящих через характерные узловые точки формы предмета. Полученные на плоскости проекции характерные точки соединяются линиями в соответствии с изображаемым предметом.
Рис 2. Получение ассиметричных изображений а — изометрия; б — диамстрня; в — фронтальная г — военная
Ортогональные и аксонометрические проекции необходимы и для уяснения способа построения еще одного вида изображения — перспективы. Человек, в силу особенностей устройства зрения, не может видеть объемные предметы так, как они изображаются в ортогональном и аксонометрическом чертежах. Для изображения на плоскости пространства и форм такими, какими мы их воспринимаем в натуре, существует способ перспективного построения. Наблюдая предмет с разных точек, мы замечаем, что хотя предмет и остается самим собой, внешний вид его для зрителя значительно изменяется в зависимости от того, откуда мы на него смотрим: издалека или с близкого расстояния, сверху или снизу, прямо или сбоку. Так, поворачивая куб. кирпич или книгу, мы видим то одну их сторону, то две, а то и три сразу (рис. 2). При этом конфигурация отдельных сторон и общего вида этих предметов приобретает зрительно разный характер и размеры.
Например, приближаясь к зданию, мы ощущаем, что оно как бы растет, увеличиваясь в высоту и в ширину, крыша уходит вверх и становится невидимой, а линии карнизов все круче опускаются к земле. Обходя здание вокруг, мы видим, как зрительно уменьшается протяженность главного фасада и растет протяженность бокового, а башня, расположенная сзади, перемещается с одного фасада на другой (рис. 3).
Рис 3. Виды куба
Разбирая устройство глаза или принципиально сходную с ним оптическую систему фотографического аппарата (рис. 4), можно понять, как образуется изображение предмета на сетчатой оболочке глаза или на пластинке фотоаппарата, а следовательно, понять и принципы перспективного построения рисунка на бумаге. Прямолинейные лучи света, направленные от всех точек предмета, собираются в точке зрачка, преломляясь, проходят в глубину глаза и дают изображение созерцаемого предмета на сетчатой оболочке. Если на пути лучей, идущих от предмета к глазу, поместить перпендикулярно их центральному лучу прозрачное стекло, то на нем мы получаем изображение, тождественное образованному на сетчатой оболочке глаза.
Рис 4. Ситуационный план с обозначением точки зрения 1, 2, 3 и изображение объекта с трех точек
Таким образом, принцип построения перспективного изображения сводится к следующему: от наиболее характерных конструктивных узловых точек объемного предмета, расположенного в пространстве, проводят лучи-линии к точке глаза (рис. 5); на пути этих лучей помещают изобразительную поверхность и отмечают на ней следы-точки, образованные пересечением лучей с поверхностью; соединив линиями соответствующие точки, получают перспективное изображение предмета на поверхности.
Рис 5. Схема получения изображения а — на сетчатке глаза; б — на пластинке фотоаппарата; в — на картинной плоскости
Перспективное изображение отличается от ортогонального и аксонометрического тем, что проекция строится не параллельными лучами, а пучком лучей, идущих в одну точку. Пучок отраженных от предметов лучей света образует «зрительный конус» с вершиной в зрачке глаза, называемой «точкой зрения». Основание «зрительного конуса» составляет «поле зрения». По мере удаления от глаза размер поля зрения увеличивается. На рис. 6 показано поле зрения одного и двух глаз человека.
Рис 6. Схема получения переспективного изображения
Особое значение при изображении предметов имеет направление оси зрительного конуса, называемой центральным лучом. Перпендикулярная этому лучу поверхность, на которой строится изображение, называется картиной или картинной плоскостью.
Так как устройство человеческого глаза дает возможность четкого восприятия в пучке лучей с величиной угла всего лишь 2—3,’то при рассматривании предмета большого размера глаз должен поворачиваться: центральный луч зрения движется по предмету, обегая его от края до края, а картинная поверхность, на которой условно получается изображение, перемещается вместе с центральным лучом, сохраняя перпендикулярное лучу положение. Единое впечатление от предмета создается в сознании как сумма всех этих отдельных впечатлений. При ограниченных задачах учебного рисунка для получения вполне правдивого изображения на листе бумаги вся сумма отдельных лучей приводится к одному главному, центральному лучу.
Рис 7. Поле зрения глаза — «Зрительный» конусс
Направление этого главного центрального луча должно занимать среднее положение между крайними лучами, охватывающими в пространстве предмет или группу предметов, служащих натурой. Множество отдельных картинных поверхностей приводится к одной главной плоскости, перпендикулярной главному лучу. На этой общей картинной плоскости, принимаемой на основе особенностей нашего зрения и восприятия, а также знания размеров и конструкции предмета в натуре, создается его суммарное правдоподобное изображение. На рис. 7 показано, как три отдельные картинные плоскости (1,2,3), соответствующие трем лучам зрения, при рассматривании отдельных кубов приводятся к одной общей, обеспечивающей правдоподобное изображение сразу трех кубов, расположенных на разных уровнях. Эту же особенность поясняет рисунок, показывающий восприятие колонны глазом и изображение ее на одной картинной плоскости (рис. 8).
Рис 8. Схема процесса видения и условное изображение на одну картинную плоскость а — вид на перспективную ситуацию сбоку и сверху; б — изображение на три картины; в — условное изображение на одну картинную плоскость; е — схема получения точек схода: д — показ диагоналей куба и квадратов; е — схема «зрительной пирамиды»
Своеобразие зрительного восприятия накладывает свой отпечаток на изображение, поэтому точный рисунок, сделанный на глаз, как правило, не тождественен фотографии или построенной по правилам перспективе, полученной с одной и той же точки зрения. Для построения чертежа перспективы при помощи линейки и циркуля пользуются теоретическими положениями и практическими приемами, излагаемыми в специальных учебниках перспективы: берутся план и фасады, выбирается точка зрения, определяется картинная плоскость и одним из многих графических приемов строится перспективное изображение. При рисовании перспективное построение должно быть проделано лишь в сознании на основании видения натуры, знания основных закономерностей перспективного построения и ясного представления о пространственной форме предмета. На лист бумаги наносятся уже готовые результаты этого сложного анализа, поэтому для практического рисования особенно важно отчетливо представлять логику получения изображения и его принципиальные основы. Сравнивая изображения одинаковых предметов, расположенных на разных расстояниях от точки зрения, легко установить общую закономерность перспективного построения. Так как проекция строится не параллельными лучами, а пучком лучей, сходящихся в одну точку, можно понять, почему одинаковые по величине предметы имеют на картинной плоскости разные по размерам изображения в зависимости от того, ближе или дальше находятся они от точки зрения (рис. 9). Размер предмета, расположенного ближе к зрителю, представляется ему больше, чем размер отдаленного, потому что лучи от ближнего предмета подходят к глазу под большим углом, чем лучи от отдаленного. Таким образом, равные по величине предметы имеют различную величину изображения в зависимости от их расстояния до точки зрения: чем предмет ближе, тем его изображение больше и, наоборот, чем дальше, тем меньше.
Рис 9. Схема процесса видения и условное изображение на одну картинную плоскость
На рис. 10 видно, как дома, деревья, люди, машины воспринимаются уменьшающимися по мере удаления от наблюдателя.
Действительно, ребенок, находящийся на переднем плане, зрительно воспринимается большим по размеру, чем взрослый человек вдалеке (рис. 11). Однако мы правильно судим о их истинном росте и не путаем взрослого с ребенком. Бинокулярное (двумя глазами) зрение и способность глаза к аккомодации (изменение кривизны хрусталика при настройке резкости зрения на различную глубину пространства) позволяют достаточно точно чувствовать расстояние до предмета. Сопоставление видимого размера предмета и расстояния до него помогает осознать его истинную величину. Кроме того, знание привычных пропорций и характерных признаков знакомых предметов также помогает избежать ошибок в определении размеров.
Рис 10. Схема перспективных изменении одних и тел же размеров
Естественно, что изменения размеров изображения в зависимости от расстояния до предмета происходят во всех направлениях. Важно понять, как зрительно изменяются размеры предметов в параллельных картинной плоскости направлениях (ширина, высота) и в перпендикулярном картинной плоскости направлении (глубина) (рис. 12). Если нанести на уходящие от нас линии отрезки одинаковой длины и построить их перспективное изображение, то станет ясно, что размер изображения отрезков будет уменьшаться по мере удаления самих отрезков.
На рис. 12 линии тротуаров, окон, карнизов зданий сходятся в одну точку, и хорошо заметно, как уменьшаются размеры домов и их деталей не только в высоту и ширину, но и в глубину. При этом чем ближе направление линии в натуре к направлению луча зрения, тем разительнее будет перспективное сокращение изображений равных отрезков этой линии.
Рис 11. Кажущееся уменьшены? размерив предмет» я зависимсти от их удаления от зрителя на примере улицы
Чтобы сознательно, уверенно и свободно применять перспективу при рисовании с натуры и, особенно, при рисовании «от себя» (по представлению), необходимо ясно понимать и представлять ситуацию в пространстве, включающую: 1) изображаемый предмет, 2) зрителя (точку зрения) и 3) картинную плоскость (рис. 13). Понятно, что изменение взаимного положения этих составляющих ведет к перестройке перспективного вида изображаемых предметов. Ясное представление видов этой ситуации не только спереди, а также сбоку и сверху (в плане) даст основу для понимания и практического усвоения процесса перспективное изображения. Рассмотрим построение в перспективе прямой линии, расположенной под произвольным углом к картинной плоскости (к. п.). Для более наглядного представления о направлении заданной линии на рисунке она отмечена изображением карандаша (а — б). Точка пересечения (т. п.) этой линии с картинной плоскостью даст исходный пункт для построения ее изображения на картине.
Рис 12. Изображение людей с учетом перспективных сокращении размеров
Затем, строя перспективные изображения ряда точек, расположенных на этой линии, мы заметим, что по мере их удаления в глубину углы между проектирующими их на картинную плоскость лучами и самой линией становятся все меньше и меньше. Наконец, можно себе представить, что когда точка, расположенная на заданной линии, уйдет в бесконечность, тогда проектирующий ее луч зрения станет параллельным самой линии. Отсюда становится понятным, что проекция самой отдаленной точки данной линии расположится на картинной плоскости в месте пересечения ее лучом, идущим из точки зрения параллельно самой линии. Эта проекция самой отдаленной точки линии называется точкой схода (т. с.) для данной линии при определенном положении картинной плоскости и точки зрения. По двум точкам: точке пересечения самой линии с картинной плоскостью (т. п.) и точке схода мы можем построить направление изображения линии на картинной плоскости. Рассмотрим классический пример построения перспективного изображения уходящего вдаль железнодорожного полотна. Так как точка схода изображения линий на картинной плоскости помещается в месте пересечения картины лучом, идущим из точки зрения параллельно этим линиям, ясно, что все параллельные в натуре между собой линии будут параллельны этому лучу и изображения этих линий будут иметь на картине одну общую точку схода: на рисунке параллельные рельсы сходятся в этой одной точке. Для перспективного изображения шпал будет своя точка схода, находящаяся в месте пересечения картинной плоскости лучом, параллельным направлению шпал.
Рис 13. Основные перспективные направления на картине — высоты, ширины и глубины
На рис. 14 картинная плоскость ограничена определенным размером и точка схода изображения шпал находится за пределами картины. На рис. 15 показан случай, при котором рельсы располагаются перпендикулярно основанию картинной плоскости. В этом случае точка схода изображений рельс будет находиться на линии, проходящей через середину картинной плоскости, перпендикулярно ее основанию, а точка схода изображений шпал, как говорят, уйдет в бесконечность потому, что параллельная шпалам линия, проведенная через точку зрения, будет параллельна картинной плоскости и не пересечет ее. На рис. 16 мы видим, что шпалы изображены параллельными друг другу. В случае, когда рельсы располагаются параллельно картинной плоскости, точка схода для изображения шпал расположится ближе к середине картины, а изображения рельс будут параллельными.
Рис 14. Схема перспективного построения изображении прямой линии с расположенным на ней карандашом
Следует сделать вывод, что чем перпендикулярнее направление линий к картинной плоскости, тем ближе к середине картины будет находиться точка схода их изображений. Точка схода изображений, перпендикулярных к картинной плоскости, будет располагаться в ее середине. По мере же уменьшения угла между линиями и картинной плоскостью точка схода их изображений уходит от середины картины. Когда линии располагаются параллельно картинной плоскости, точки схода их изображений уходят в бесконечность и линии рисуются параллельными между собой. Точно также все линии, проходящие в пространстве через точку зрения, изобразятся на картинной плоскости в виде точек.
Рис 15. Схема перспективного изображения железнодорожного пути. Зритель сбоку полотна, картинная плоскость под случайным углом к полотну
Для уяснения перспективного построения объемных предметов классическим примером может служить хорошо представляемая всеми форма куба, имеющего равновеликие ребра и прямые углы между ними, образованные одинаковыми гранями-квадратами.
На рис. 6 перспективного построения находящегося в случайном положении по отношению к картинной плоскости куба показано нахождение трех точек схода для изображения трех его сторон. Точка схода изображения круто уходящих от зрителя в глубину ребер куба расположится ближе к середине картинной плоскости, а точки схода для ребер, идущих под небольшим углом к картине, уйдут за пределы картины.
Рис 16. Схема перспективного изображении железнодорожного пути. Зритель в середине полотна, картинная плоскость параллельна шпалам
Рассматривая перспективное построение трех пар параллельных граней куба — квадратов, можно обнаружить, что точки схода изображений их диагоналей располагаются на трех прямых, соединяющих точки схода их ребер. Точно также, проведя любые линии в плоскости этих квадратов, мы заметим, что точки схода их изображений будут лежать на тех же прямых. На рис. 17 видно, что каждая из прямых линий образуется пересечением картинной плоскости плоскостью, идущей через точку зрения параллельно граням данного квадрата.
Рис 17. Схема перспективного изображения железнодорожного пути. Зритель сбоку, картинная плоскость параллельна рельсам
Таким образом, изображения всех линий, расположенных в какой-либо плоскости, проходящей через точку зрения, а следовательно, и всех линий в пространстве, параллельных этой плоскости, будут иметь точки схода, лежащие на линии пересечения этой плоскости с картиной. На основании перспективного построения куба, квадратов его сторон и их диагоналей можно понять перспективное построение параллелепипедов, а также призм, цилиндров и т. п. На рис. 18—21 показаны примеры построения перспективы различных геометрических фигур, объемных тел и простейших предметов.
Для учебного рисования с натуры и перспективного построения чертежа обычно применяется так называемая «земная перспектива». В этой перспективе картинная плоскость располагается вертикально, т. е. по отвесу к центру земли, и вводится понятие горизонта. Горизонтом называется воображаемая горизонтальная плоскость, находящаяся на уровне точки зрения, т. е. нашего глаза. Линия пересечения картинной плоскости с горизонтом называется линией горизонта.
Рис 18. Принципиальные схемы перспективного построения изображении отдельных форм на основе куба на наклонную картинную плоскость
Ограничение картинной плоскости вертикальным положением значительно упрощает и делает более доступным перспективное построение как рисунка с натуры, так и чертежа, обеспечивая в то же время достаточно правдоподобное изображение предметов при правильно выбранной точке зрения, определяемой горизонтом зрителя и нормальным для глаза углом зрения (рис. 18). Следует заметить, что при вертикальном положении картины направление центрального луча зрения может значительно отклоняться от направления луча, проведенного из точки зрения перпендикулярно к картине, называемого главным перпендикуляром, который в земной перспективе всегда горизонтален (рис. 18). Высота горизонта изменяется с перемещением нашего глаза по вертикали. Когда мы смотрим на предмет, находящийся ниже нашего горизонта, т. е. сверху вниз, проекция находящихся в натуре на одной высоте точек будет располагаться на картине тем ниже, чем ближе к нам эти точки, а проекция удаленных точек расположится выше. Эта разница в высоте будет тем больше, чем выше помещается наш горизонт по отношению к предмету. Наоборот, когда предмет расположен выше нашего горизонта и мы смотрим снизу вверх, проекция точек, расположенных ближе, поднимется вверх, а дальних — спустится вниз. Естественно, что все точки, находящиеся на уровне нашего горизонта, спроецируются на линию горизонта. Из рассматриваемого видно, что все горизонтальные линии, на которые мы смотрим сверху, изобразятся на рисунке идущими вверх по мере удаления, а линии, на которые мы смотрим снизу, будут, удаляясь, спускаться вниз. Из всего многообразия линий в практике рисунка особенно важное значение имеют вертикальные и горизонтальные линии. Вертикальная линия — это отвес. По отвесу возводятся стены зданий, вертикально стремятся расти деревья, по отношению к вертикали определяется движение человеческой фигуры. Горизонтальная линия — это цоколь здания и его карнизы, пол в комнате и поверхность стола. Вертикальные и горизонтальные направления являются основными в окружающей нас природе, по отношению к ним определяется все многообразие остальных направлений. Поэтому особенно важное значение придается умению построить в перспективе горизонтальные и вертикальные линии. При графическом построении перспективы на вертикальную картинную плоскость проекции всех вертикальных линий сохранят на картине вертикальное положение и останутся параллельны друг другу.
Рис 19. Изображение куба на вертикальную плоскость
В учебном рисунке с натуры также принято изображать вертикальные линии вертикальными. Это дает вполне правдивое изображение при правильно выбранном горизонте зрителя и расстоянии от глаза до предмета и соответствует нашему представлению о вертикальных линиях. Точки схода изображений всех горизонтальных линий, расположенных и выше и ниже горизонта, определяются пересечением картинной плоскости лучом, идущим из точки зрения горизонтально. Отсюда вытекает, что точки схода изображения всех горизонтальных в натуре линий лежат на линии горизонта.
Рис 20. Перспективное построение различных форм на основе куба
Расстояние от зрителя до предмета влияет не только на размер изображения, но и на характер его построения. Предмет, расположенный ближе к глазу, мы видим под большим углом, и перспективные особенности построения, обусловленные конусом зрения, проявляются ярче. Отдаленные предметы глаз воспринимает под меньшим углом, лучи зрительного конуса приближаются к параллельным и перспективные сокращения на изображении становятся менее разительными. Опираясь на основные закономерности построения перспективы, мы разобрали перспективные изображения лишь простейших геометрических фигур и тел, однако, твердо усвоив принцип на простых формах, рисующий сможет применить его и к более сложным.
Рис 21.
Зрительно воспринимаемая форма предмета значительно изменяется в зависимости от выбора точки зрения. Вид предмета сверху, снизу, слева, справа, с близкого или далекого расстояния характеризует и подчеркивает то одни, то другие его стороны. Поэтому выбор точки зрения при рисовании с натуры и по представлению должен быть подчинен теме и композиционной задаче всего рисунка, всего произведения в целом.
Спасибо и удачного вам обучения!
Здравствуйте!
Благодарим вас за то, что вы стали пользователем Школы Рисования. Это простая и увлекательная платформа, созданная для того, чтобы помочь вам и многим ученикам по всему миру научиться рисовать.
Учитесь рисовать любым удобным для вас способом.
Бесплатные учебные пособия и книги можно скачать бесплатно перейдя по этой ссылке.
https://drive.google.com/drive/folders/1MezpA01S9WjcGiooz8SfCJpB_LivQB7K?usp=sharing
Учитесь вместе s друзьями. Делитесь нашими учебными пособиями с друзьями и коллегами или сохраняйте материалы для вашей библиотеки.
Спасибо и удачного вам обучения!
GHENADIE SONTU FINE ART
Подборка книг по перспективе:
-
Буйнов А.Н., Смирнов Г.Б. — Первоначальные сведения о перспективе (PDF)
-
Барышников А.П. — Перспектива (1955) (DJVU)
-
М.В.Фёдоров — Рисунок и перспектива (DJVU)
-
Дуг Дюбоск — Как рисовать перспективу (PDF)
-
Joseph D`Aelio — Perspective Drawing Handbook (PDF)
-
Рэй Кэмпбелл Смит — Перспектива (PDF)
-
Mы приглашаем детей и взрослых на занятия по рисунку и живописи в Хайфе.
Программа обучения рисованию рассчитана как на желающих начать рисовать “с нуля”, так и на тех, кто хочет закрепить ранее приобретенные навыки.
На обучение рисованию принимаем всех желающих – детей, подростков, и взрослых. Пройдя наши художественные курсы живописи и рисования, вы очень быстро наберетесь мастерства для создания своих неповторимых авторских работ.
Хотите начать обучение?