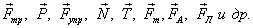I. Механика
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как 
, измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом 
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
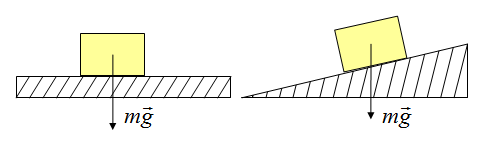
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
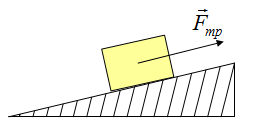
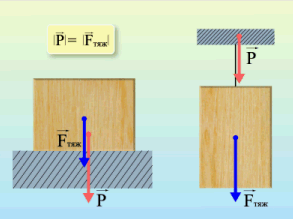
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой 
, но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как 
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой 
.
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
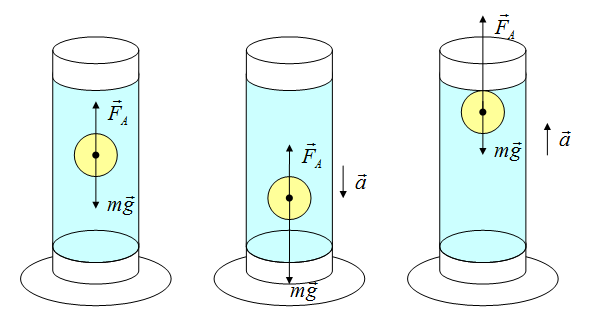
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
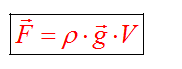
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
Внешние
силы — это такие силы, которые действуют
только на поверхность предмета, но не
проникают внутрь его. К этим силам
относятся все силы, развиваемые
материальным объектом.
Внутренние
силы — это такие силы, которые действуют
сразу на все атомы передвигаемого
предмета независимо от того, где они
находятся: на поверхности или в середине
предмета. К этим силам относятся силы
инерции и силы поля: гравитационного,
электрического, магнитного. И происходит
это потому, что поле и носитель инерции
физвакуум свободно проникают внутрь
любого тела.
В механике
внешними силами по отношению к данной
системе материальных точек (т. е. такой
совокупности материальных точек, в
которой движение каждой точки зависит
от положений или движений всех остальных
точек) называются те силы, к-рые
представляют собою действие на эту
систему других тел (других систем
материальных точек), не включенных нами
в состав данной системы.
Внутренними
силами являются силы взаимодействия
между отдельными материальными точками
данной системы. Подразделение сил на
внешние и внутренние является совершенно
условным: при изменении заданного
состава системы некоторые силы, ранее
бывшие внешними, могут стать внутренними,
и обратно. Так, например, при рассмотрении
PRIMER
движения системы, состоящей из земли и
ее спутника луны, силы взаимодействия
между этими телами будут внутренними
силами для этой системы, а силы притяжения
солнца, остальных планет, их спутников
и всех звезд будут внешними силами по
отношению к указанной системе. Но если
изменить состав системы и рассматривать
движение солнца и всех планет как
движениеодной общей системы, то внешн.
силами будут только силы притяжений,
оказываемых
Если
нагруженное тело находится в равновесии,
то внутренние силы равны по значению
внешним силам и противоположны им по
направлению. Очевидно, что они препятствуют
развитию деформации.Работа внутренних
сил (U), с учетом их направления по
отношению к деформации, всегда является
отрицательной.
Работа
внешних сил равна взятой с обратным
знаком работе внутренних сил:
.
Пусть
элемент стержня длиной 
испытывает
растяжение (рис. 15.3, а).
Действие
отброшенных частей стержня на
рассматриваемый элемент заменим
продольными силами N. Эти усилия показаны
на рисунке штриховыми линиями. По
отношению к элементу они являются как
бы внешними. Вызываемое ими удлинение
элемента равно: 
.
Действие
рассматриваемого элемента на отброшенные
части показано на рисунке сплошными
линиями. Элементарная работа внутренних
продольных сил, постепенно увеличивающихся,
и противодействующих развитию удлинения,
согласно теореме Клапейрона, выразится
формулой: 
.
ЭЛЕМЕНТАРНАЯ
РАБОТА ВНУТРЕННИХ ПОПЕРЕЧНЫХ СИЛ (
)
ПРИ ЧИСТОМ СДВИГЕ (РИС. 15.3, Б)
При чистом
сдвиге касательные напряжения равномерно
распределены по всему сечению и
определяются по формуле: 
.
Абсолютный
сдвиг правого сечения элемента по
отношению к левому сечению, с учетом
закона Гука, равен: 
,
тогда 
.
При поперечном
изгибе касательные напряжения распределены
по сечению неравномерно. В этом случае
выражение для элементарной работы
внутренних перерезывающих сил может
быть представлено в виде: 
,
где k – коэффициент, зависящий от формы
поперечного сечения стержня. Например,
для прямоугольного поперечного сечения 
.
ЭЛЕМЕНТАРНАЯ
РАБОТА ВНУТРЕННИХ УСИЛИЙ ПРИ КРУЧЕНИИ
Поворот
правого сечения элемента по отношению
к левому сечению, происходящий под
действием внешних по отношению к нему
крутящих моментов (
),
показанных (см. рис. 15.3, в) штриховыми
линиями, равен: 
.
Тогда работа
внутренних крутящих моментов (они на
рисунке не показаны) на этом угле поворота
определяется по формуле: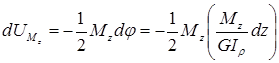 
.
Пусть теперь
элемент стержня испытывает изгиб. И
пусть его правое поперечное сечение
повернется на угол поворота 
по
отношению к левому сечению (см. рис.
15.3, г).
Тогда
внутренние изгибающие моменты, показанные
(см. рис. 15.3, г) сплошными линиями, совершат
на этом угле поворота работу:
.
При
одновременном растяжении, кручении и
прямом поперечном изгибе стержня (с
учетом того, что работа каждого из
внутренних усилий на перемещениях,
вызываемых остальными усилиями, равна
нулю) получим следующее выражение для
элементарной работы внутренних сил
упругости:
.
Интегрируя
выражение по всей длине стержня,
окончательно получим формулу работы
внутренних сил:
.
Соседние файлы в папке Динамика билеты
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Внешние и внутренние силы — две основные категории сил. Внешние силы далее подразделяются на контактные и бесконтактные.
Как следует из самого названия, внешняя сила — это сила, которая воздействует на систему через окружение. Системе требуется сила, чтобы ускориться или изменить ее кинетическую энергию, окружение обеспечивает эту внешнюю силу для системы. Давайте подробно обсудим примеры внешних сил.
Примеры внешних сил
- Сила трения
- Нормальная сила
- Сила натяжения
- Приложенная сила
- Сопротивление воздуха
- Подъемная сила
Сила трения
Когда два движущихся тела совершают движение относительно друг друга, и поверхности этих двух тел входят в контакт, возникает трение. Это трение оказывает некоторую силу на оба тела и пытается остановить их движение или помогает им двоим ускориться.
Трение — это саморегулирующаяся внешняя сила, поэтому она регулируется в зависимости от потребности в движении. Трение — это неуравновешенная сила, которую в основном делят на два типа.
- Статическое трение — это трение между поверхностями двух тел, когда тела не движутся относительно друг друга. Статическое трение в основном зависит от характера характера и нормальной силы. Если поверхность гладкая, статическое трение минимально, а грубое статическое трение максимально.
- Кинетическое трение – это трение между двумя телами, когда они находятся в движении. Когда внешняя сила превышает значение трения покоя, тело начинает двигаться, а трение между поверхностью и телом уменьшается; это уменьшенное трение является кинетическим. Величина кинетическое трение меньше статического трение.
Нормальная сила
Нормальная сила — это сила, с которой цветок действует на тело, стоящее над этим цветком. величина нормальной силы равна весу тела, а направление перпендикулярно поверхности, над которой стоит тело. Рассмотрим брусок массы М на горизонтальной поверхности, направление нормальная сила перпендикулярна поверхности, а величина силы, действующей на этот брусок, равна
Здесь N — нормальная сила на блоке.
M- Масса блока
g — ускорение под действием силы тяжести Земли
Сила натяжения
Чтобы создать натяжение струны, мы натягиваем струну, веревку или трос за два конца. Напряжение играет решающую роль в подтягивании тяжелого веса или подвешивании веса на определенной высоте. Напряжение – это контактная сила который передается по веревке или кабелю и тянет или удерживает объект.
Когда мы тянем определенный объект с помощью веревки или троса, мы можем изменить направление приложенной силы с помощью шкива, и в этой системе натяжение с обеих сторон струны одинаковое. Если груз подвешен к потолку с помощью двух веревок и находится в устойчивом состоянии, то по этой причине натяжение струны можно рассчитать с помощью теоремы Лами; в противном случае для расчета натяжения используется второй закон движения Ньютона.
Приложенная сила
Это внешняя сила, непосредственно приложенная к телу человеком или другим телом. Эта сила отвечает за ускорение тела, и эта сила неконсервативна. Рассмотрим деревянный брусок массы M, стоящий на горизонтальной поверхности. Блоку требуется некоторая внешняя сила, чтобы переместиться из своего положения, поэтому, когда мы прикладываем силу к блоку, он начинает ускоряться в направлении силы.
В повседневной жизни мы используем эту силу в основном для того, чтобы сдвинуть или сдвинуть вещи с их места. Мы можем получить механическое преимущество, используя простые механизмы, такие как рычаг и осевое колесо.
Где, м- масса объекта
а- ускорение объекта
Сопротивление воздуха
Что произойдет, если мы уроним перо с определенной высоты? Почему он падает медленнее, чем камень того же веса? Почему он не может упасть прямо на землю? Ответ на все эти вопросы сопротивление воздуха или лобовое сопротивление. Всякий раз, когда объект падает с определенной высоты или движется с определенной скоростью, воздух прикладывает силу сопротивления к объекту в направлении, противоположном движению. его сила сопротивления называется воздухом сопротивление
Сопротивление воздуха также является внешней силой, поэтому по своей природе это неконсервативная и диссипативная сила. Небоскребы, такие как Бурдж-Халифа, также сталкиваются с сопротивлением воздуха, поэтому, чтобы избежать этого сопротивления, конструкции строятся таким образом, чтобы сопротивление воздуха было минимальным.
Для расчета сопротивления воздуха используются следующие формулы:
Где c — силовая постоянная
V — скорость объекта
Подъемная сила
Вы когда-нибудь задумывались, почему в воде нам легче, чем на земле? Это происходит потому, что вода оказывает давление на поверхность тела. По мере того, как мы погружаемся в воду, давление начинает расти. Давление на нижнюю часть погружаемого тела выше, чем на верхнюю часть, и из-за этой разницы давлений корпус толкается к поверхности воды.
выражение для выталкивающая сила является,
Где ρ- плотность жидкости
g- ускорение свободного падения
Vf-объем вытесненной жидкости
Часто задаваемые вопросы
Что такое внутренняя сила?
Силы делятся на внутренние и внешние на основе их взаимодействия с системой.
Сила, которая действует на систему изнутри и вызывает изменение в системе или противодействует изменению в системе посредством внешней силы, называется внутренней силой. внутренние силы создаются внутри системы, и они не могут вызвать внешние изменения в системе, такие как ускорение системы или изменение кинетической энергии системы.
Почему внешние силы неконсервативны?
Причина внешних сил, также называемых неконсервативными силами, заключается в следующем.
Внешние силы зависят от пути, по которому происходит движение системы, поэтому они не имеют потенциальной энергии. Точно так же внешние силы являются диссипативными, что означает, что в течение определенного периода система теряет энергию, поэтому энергия системы не сохраняется. Поэтому их еще называют неконсервативными силами.
Гравитация — это внешняя сила?
Компания внутренняя и внешняя сила зависит от изучаемой системы
Гравитационная сила — это сила притяжения между двумя частицами системы. В гравитационной силе мы изучаем взаимодействие между двумя или более частицами. Кроме того, полная энергия сохраняется в гравитационной силе. Следовательно, гравитация внутренняя сила.
2.2 Работа внешних сил. Потенциальная энергия
Определим работу силы F, статически приложенной к некоторой упругой системе (рис.20, а), материал которой следует закону Гука.
Рис. 20
При малых деформациях к этой системе применим принцип независимости действия сил, следовательно, перемещения отдельных точек и сечений конструкции прямо пропорциональны вызывающей их нагрузке:
, (2.2)
где 
— перемещение по направлению силы F; 
— некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на 
.
Составим выражение элементарной работы внешней силы на перемещении , отбрасывая при этом бесконечно малые величины второго порядка малости: 
.
Заменим , используя (2.2):
Рекомендуемые материалы
.
Интегрируя это выражение в пределах полного изменения силы от нуля до ее конечного значения, получим формулу для определения работы, совершаемой статически приложенной внешней силой F:
или, с учетом(2.2):
, (2.3)
то есть работа внешней силы при статическом действии ее на любое упругое сооружение равна половине произведения значения этой силы на величину соответствующего ей перемещения.
Для обобщения полученного вывода под силой понимают любое воздействие, приложенное к упругой системе, то есть не только сосредоточенную силу, но и момент или равномерно распределенную нагрузку; под перемещением понимают тот его вид, на котором данная сила производит работу: сосредоточенной силе соответствует линейное перемещение, сосредоточенному моменту – угловое, равномерно распределенной нагрузке – площадь эпюры перемещений на участке действия нагрузки.
При статическим действии на конструкцию группы внешних сил работа этих сил равна половине суммы произведений каждой силы на величину соответствующего ей перемещения, вызванного действием всей группы сил. Например, при действии на балку (рис.20,б) сосредоточенных сил F1, F2 и сосредоточенных моментов М1 и М2 работа внешних сил:
(2.4)
Работу внешних сил на вызванных ими перемещения можно выразить и иначе – через внутренние силовые факторы (изгибающие моменты, продольные и поперечные силы), возникающие в поперечных сечениях системы.
Выделим из прямолинейного стержня двумя сечениями, перпендикулярными его оси (рис.21, а), бесконечно малый элемент dz.
Стержень состоит из бесконечно большого числа таких элементов. К каждому элементу dz в общем случае плоской задачи приложены продольная сила Nz, изгибающий момент Мх и поперечная сила Qy.
Для выделенного элемента dz усилия N, M, Q являются внешними силами, поэтому работу 
можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz.
Рассмотрим элемент dz, находящийся только под действием продольных сил N (рис.21,б). Если его левое сечение считать неподвижным, то правое сечение под влиянием продольной силы переместится вправо на величину 
. На этом перемещении сила N совершит работу:
(2.5)
Рис. 21
Если неподвижно закрепить левое сечение элемента dz, находящегося под действием только изгибающих моментов М (рис.22,а), то взаимный угол поворота торцевых сечений элемента будет равен углу поворота 
его правого сечения:
.
На этом перемещении момент М совершит работу:
(2.6)
Рис. 22
Закрепим левое сечение элемента dz, находящегося под действием только поперечных сил Q (рис.22,б,в), а к правому приложим касательные усилия 
, равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения 
равномерно распределены по всей площади А поперечного сечения, то есть 
, тогда перемещение 
определяется в виде:
,
а работа силы Q на этом перемещении будет:
(2.7)
В действительности касательные напряжения распределены по площади поперечного сечения неравномерно, что учитывается введением в (2.7) поправочного коэффициента 
.
Обратите внимание на лекцию «15 лекция».
Суммируя (2.5) – (2.7), получим полное значение работы:
(2.8)
Интегрируя выражение 
в пределах длины L каждого участка всех стержней и суммируя результаты, получим:
(2.9)
Из формулы (2.9) следует, что работа внешних сил на вызванных ими перемещениях всегда положительна.
На основании закона сохранения энергии работа внешних сил переходит в потенциальную энергию деформации, то есть 
.