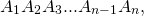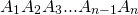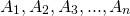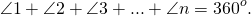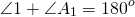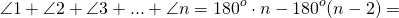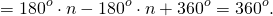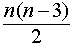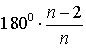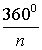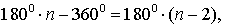Углы правильного многоугольника делятся на :
- центральный угол;
- внутренний угол;
- внешний угол.
Сумма внутреннего и внешнего угла равна (180°).
Сумма внутренних углов правильного многоугольника с (n) сторонами равна:
((n — 2)180°)
Для нахождения внутреннего угла используют формулу:
(alpha = frac{{{{180}^o}(n — 2)}}{n})
(n)— число сторон
Для нахождения внешнего угла используют формулу:
(varphi = frac{{{{360}^o}}}{n})
(n)— число сторон
Для нахождения центрального угла используют формулу:
(beta = frac{{{{360}^o}}}{n})
(n)— число сторон
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие правильного многоугольника
Определение 1
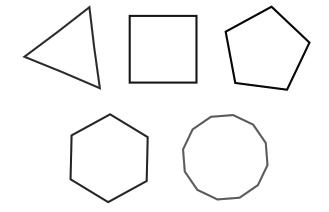
Правильный многоугольник — выпуклый многоугольник, у которого все стороны и все углы равны между собой (Рис. 1).
Рисунок 1. Правильные многоугольники
Как мы знаем, сумма углов многоугольника находится по формуле$(n-2)cdot {180}^0$
Значит, градусная мера одного угла правильного многоугольника равняется
Теорема об описанной около правильного многоугольника окружности
Доказательство.
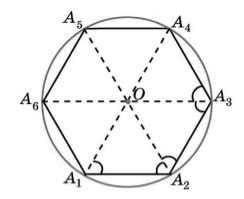
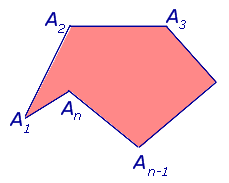
Существование. Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть биссектрисы углов $A_1 и A_2$ пересекаются в точке $O$. Соединим с этой точкой все остальные вершины правильного многоугольника (Рис. 2).
Рисунок 2. Описанная вокруг правильного многоугольника окружность
Так как углы $A_1 и A_2$ равны и $A_1O и A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $angle O{A_2A}_1=angle O{A_2A}_3$ и сторона $A_2O$ — общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны. Следовательно, $OA_2=OA_3$.
Аналогично доказывают другие равенства. В результате, будем иметь
То есть точка $O$ равноудалена от всех вершин многоугольника, а, значит, точка $O$ — центр описанной вокруг правильного многоугольника окружности.
Единственность. Рассмотрим три вершины многоугольника. Очевидно, что через них проходит только одна окружность, следовательно, вокруг правильного многоугольника можно описать только одну окружность.
«Правильные многоугольники» 👇
Теорема доказана.
Теорема вписанной в правильный многоугольник окружности
Теорема 2
В любой правильный многоугольник можно вписать единственную окружность.
Доказательство.
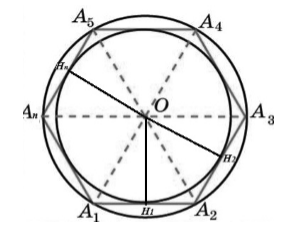
Пусть нам дан правильный многоугольник $A_1A_2A_3dots A_n$. Пусть точка $O$ — центр описанной вокруг данного многоугольника окружности (Рис. 3).
Рисунок 3. Вписанная в правильный многоугольник окружность
Так как углы $A_1 и A_2$ равны и $A_1O и A_2O$ — биссектрисы, то угол $OA_1A_2$ равен углу $O{A_2A}_1$. Следовательно, треугольник $OA_1A_2$ равнобедренный, и, значит, $A_1O=A_2O$.
Так как $A_1A_2=A_2A_3$, $angle O{A_2A}_1=angle O{A_2A}_3$ и сторона $A_2O$ — общая, то треугольники $O{A_2A}_1$ и $O{A_2A}_3$ равны.
Аналогично доказывается равенство других треугольников. То есть, мы получим
Значит и высоты этих треугольников равны между собой
Тогда окружность с центром в точке $O$ и радиусом, равным ${OH}_1$ проходит через точки $H_1, H_2,dots ,H_n$, то есть касается всех сторон данного многоугольника. Следовательно. Является вписанной для правильного многоугольника.
Единственность. Предположим противное. Пусть существует еще одна вписанная в этот многоугольник окружность. Обозначим её центр $O’$. Тогда $O’$ равноудалена от всех сторон многоугольника, а значит лежит в точке пересечения биссектрис его углов. Но тогда точка $O’$ совпадает с точкой $O$ и, следовательно, эти окружности также совпадают.
Теорема доказана.
Из этих двух теорем можно сформулировать следующие следствия:
Следствие 1: Вписанная в правильный многоугольник окружность касается его в серединах его сторон.
Следствие 2: Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.
Формулы для правильного многоугольника
Дадим теперь несколько формул, относящихся к понятию правильного многоугольника (без их вывода).
Введем следующие обозначения. Пусть $S$ — площадь правильного многоугольника, $P$ — периметр правильного многоугольника, $a$ — сторона правильного многоугольника, $r$ — радиус вписанной в правильный многоугольник окружности, $R$ — радиус описанной около правильного многоугольника окружности. Тогда
Пример задачи на понятие правильного многоугольника
Пример 1
Чему равна сумма внешних углов правильного $n$-угольника. Если при каждой вершине взят только один внешний угол.
Решение.
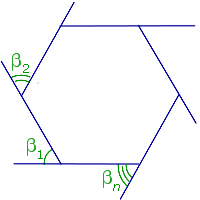
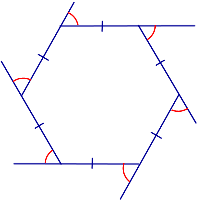
Очевидно, что все внешние углы будут равны между собой и их количество равно $n$. Найдем один из них. Внешний угол $beta $ многоугольника будет смежным с внутренним углом многоугольника. Используя формулу нахождения угла правильного $n$-угольника $alpha =frac{{180}^0(n-2)}{n}$, получим
[beta ={180}^0-frac{{180}^0(n-2)}{n}={180}^0left(1-frac{n-2}{n}right)=frac{{360}^0}{n}]
Значит, сумма всех внешних углов равна
[frac{{360}^0}{n}cdot n={360}^0]
Ответ: ${360}^0.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
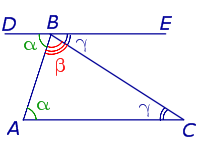
Внутренний угол многоугольника – это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.
Внешний угол многоугольника – это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.
Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
где s – это сумма углов, 2d – два прямых угла (то есть 2 · 90 = 180°), а n – количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
где s – это сумма внешних углов, 4d – четыре прямых угла (то есть 4 · 90 = 360°).
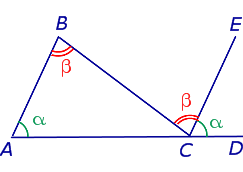
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
Что такое внешний угол многоугольника? Сколько внешних углов у многоугольника? Чему равна сумма внешних углов многоугольника?
Внешним углом многоугольника называется угол, смежный с его внутренним.углом.

так как он смежный с его внутренним углом A2A1An.
Угол 2 также является смежным углу A2A1An.
А значит, ∠2 — внешний угол при вершине A1.
Таким образом, при каждой вершине многоугольника есть два равных между собой внешних угла.
У n-угольника n вершин, значит, всего внешних углов у n-угольника 2n.
Поскольку оба внешних угла при одной вершине равны, говоря о сумме внешних углов n-угольника, рассматривают внешние углы, взятые по одному при каждой вершине.
(о сумме внешних углов выпуклого многоугольника)
Сумма внешних углов выпуклого многоугольника, взятых по одному при каждой вершине, равна 360º.

∠1, ∠2, ∠3, …, ∠n — внешние углы при вершинах
Аналогично, сумма внешнего и внутреннего углов при каждой вершине n — угольника равна 180º.
Значит, сумма всех внутренних углов многоугольника и всех его внешних углов (взятых по одному при каждой вершине) равна 180º∙n.
Следовательно, сумма всех внешних углов
Что и требовалось доказать .
Вроде бы ошибка в написании условия.Вы хотите доказать,что сумма внешних углов = 180 градусов.
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
Определение 1 . Ломаной линией с n звеньями называют фигуру L , составленную из отрезков (1), то есть фигуру, заданную равенством
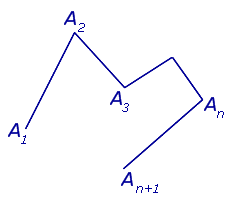
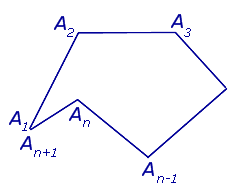
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
Определение 2 . Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию ( звенья ), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Определение 3 . Многоугольник называют n – угольником , если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником , многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром .
Диагонали n — угольника
Число диагоналей n – угольника равно
| Фигура | Рисунок | Описание |
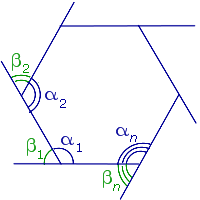
| Диагональ многоугольника |
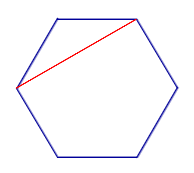 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
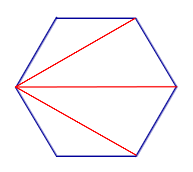 |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
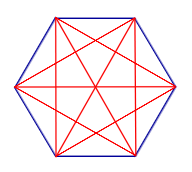 |
| Диагональ многоугольника |
 |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника
Число диагоналей n – угольника равно
Внешний угол многоугольника
Определение 5 . Два угла называют смежными , если они имеют общую сторону, и их сумма равна 180° (рис.1).
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Свойства углов треугольника
Сумма углов треугольника равна 180°
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
| Углы треугольника |
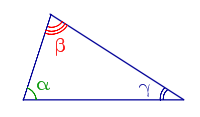 |
Сумма углов треугольника равна 180°
Внешний угол треугольника
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
Свойства углов многоугольника
Фигура
Рисунок
Формулировка теоремы
Углы
n – угольника
Сумма углов многоугольника равна
Внешние углы
n – угольника
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Углы n – угольника
Сумма углов многоугольника равна
Внешние углы n – угольника
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Свойства углов правильного n – угольника
Фигура
Рисунок
Формулировка теоремы
Углы правильного
n – угольника
Все углы правильного n – угольника равны
Внешние углы
правильного
n – угольника
Все внешние углы правильного
n – угольника равны
Углы правильного n – угольника
Все углы правильного n – угольника равны
Внешние углы правильного n – угольника
Все внешние углы правильного
n – угольника равны
Доказательства свойств углов многоугольника
Теорема 1 . В любом треугольнике сумма углов равна 180° .
Доказательство . Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE . Поскольку углы ABD , ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180° . Теорема доказана.
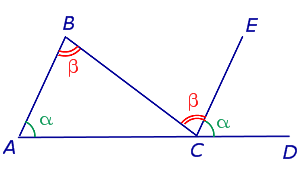
Теорема 2 . Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство . Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные . Поэтому внешний угол BCD равен сумме углов BAC и ABC . Теорема доказана.
Замечание . Теорема 1 является следствием теоремы 2.
Теорема 3 . Сумма углов n – угольника равна
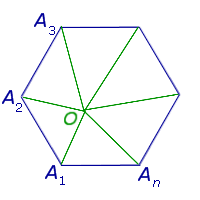
Доказательство . Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Получим n треугольников:
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O . Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
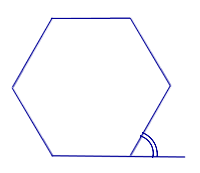
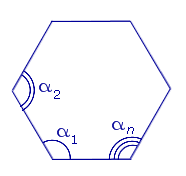
Теорема 4 . Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° .
Доказательство . Рассмотрим рисунок 6.
В соответствии рисунком 6 справедливы равенства
Инфоурок
›
Математика
›Другие методич. материалы›Таблица значений сторон, внешних и внутренних углов правильного многоугольника
Таблица значений сторон, внешних и внутренних углов правильного многоугольника
Скачать материал
Скачать материал




- Сейчас обучается 139 человек из 43 регионов


- Сейчас обучается 49 человек из 26 регионов


Краткое описание документа:
С помощью таблицы учитель составляет задачи нахождения сторон, внешних и внутренних углов правильного многоугольника.
Уважаемые коллеги
Предлагаю вам таблицу, которая поможет вам легко составить задачи на
нахождение сторон, внутренних и внешних углов правильного многоугольника.
Для решения задач нужны формулы:
формула нахождения внутреннего угла правильного многоугольника
формула нахождения внешнего угла правильного многоугольника
An и Bn cмежные углы, поэтому An+ Bn= 1800
Количество сторон правильного многоуголь- ника
n
Внутренний угол правильного многоуголь- ника
An
Внешний угол правиль-
ного многоуголь
ника Bn
Зависимость внешнего и внутреннего угла правильного многоугольника
An и Bn
Зависимость внешнего и внутреннего угла правильного многоугольника
An и Bn
3
600
1200
An< Bn на 600
An < Bn в 2 раза
4
900
900
Bn = An
An = Bn
5
1080
720
An>Bn на 360
An > Bn в 1,5 раза
6
1200
600
An>Bn на 600
An > Bn в 2 раза
8
1350
450
An>Bn на 900
An > Bn в 3 раза
9
1400
400
An > Bn на 1000
An > Bn в 3,5 раза
10
1440
360
An>Bn на 1080
A n> Bn в 4 раза
12
1500
300
An>Bn на 1200
An > Bn в 5 раз
15
1560
240
An>Bn на 1320
A n> Bn в 6,5 раза
16
157,50
22,50
An>Bn на 1350
An > Bn в 7 раз
18
1600
200
An>Bn на 1400
A n> Bn в 8 раз
20
1620
180
An>Bn на 1440
A n> Bn в 9 раз
24
1650
150
An>Bn на 1500
A n> Bn в 11 раз
30
1680
120
An>Bn на 1560
A n> Bn в 14 раз
36
1700
100
An>Bn на 1600
An > Bn в 17 раз
Желаю успехов!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 267 013 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 11.03.2015
- 495
- 0
- 11.03.2015
- 2889
- 12
- 11.03.2015
- 628
- 0
- 11.03.2015
- 720
- 1
- 11.03.2015
- 1008
- 1
- 11.03.2015
- 2012
- 0
- 11.03.2015
- 960
- 0
-
Настоящий материал опубликован пользователем Маркова Галина Иннокентьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 2565
-
Всего материалов:
2
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
| Определение многоугольника |
| Диагонали n – угольника |
| Внешний угол многоугольника |
| Свойства углов треугольника |
| Свойства углов многоугольника |
| Свойства углов правильного n – угольника |
| Доказательства теорем о свойствах углов многоугольника |
Варианты определений[ | ]
Существуют три различных варианта определения многоугольника; последнее определение является наиболее распространённым[1].
- Плоская замкнутая ломаная — наиболее общий случай;
- Плоская замкнутая ломаная без самопересечений, любые два соседних звена которой не лежат на одной прямой;
- Часть плоскости, ограниченная замкнутой ломаной без самопересечений — плоский многоугольник
; в этом случае сама ломаная называется
контуром
многоугольника.
Существуют также несколько вариантов обобщения данного определения, допускающие бесконечное число звеньев ломаных, несколько несвязных граничных ломаных, ломаные в пространстве, произвольные отрезки непрерывных кривых вместо отрезков прямых и др.[1]
Свойства углов правильного n – угольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы правильного n – угольника | Все углы правильного n – угольника равны | |
| Внешние углы правильного n – угольника | Все внешние углы правильного n – угольника равны |
| Углы правильного n – угольника |
| Все углы правильного n – угольника равны |
| Внешние углы правильного n – угольника |
| Все внешние углы правильного n – угольника равны |
Связанные определения[ | ]
Основной источник: [2]
- Вершины многоугольника называются соседними
, если они являются концами одной из его сторон. - Стороны многоугольника называются смежными
, если они прилегают к одной вершине. - Общая длина всех сторон многоугольника называется его периметром
. - Диагоналями
называются отрезки, соединяющие несоседние вершины многоугольника. - Углом
(или
внутренним углом
) плоского многоугольника при данной вершине называется угол между двумя сторонами, сходящимися в этой вершине. Угол может превосходить 180 ∘ {displaystyle 180^{circ }} в том случае, если многоугольник невыпуклый. Число углов простого многоугольника совпадает с числом его сторон или вершин. - Внешним углом
выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В случае невыпуклого многоугольника
внешний угол
— разность между 180 ∘ {displaystyle 180^{circ }} и внутренним углом, он может принимать значения от − 180 ∘ {displaystyle -180^{circ }} до 180 ∘ {displaystyle 180^{circ }} . - Перпендикуляр, опущенный из центра вписанной окружности правильного многоугольника на одну из сторон, называется апофемой.
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство |
|
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
δ = α + β Посмотреть доказательство |
| Углы треугольника |
| Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство |
| Внешний угол треугольника |
| Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
δ = α + β Посмотреть доказательство |
Виды многоугольников и их свойства[ | ]
Основной источник: [2]
- Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и так далее. Многоугольник с n {displaystyle n} вершинами называется n {displaystyle n} -угольником
.
Многоугольник, вписанный в окружность Многоугольник, описанный около окружности
- Выпуклый многоугольник
— это многоугольник, который лежит по одну сторону от любой прямой, содержащей его сторону (то есть продолжения сторон многоугольника не пересекают других его сторон). Существуют и другие эквивалентные определения выпуклого многоугольника. Выпуклый многоугольник всегда простой, то есть не имеет точек самопересечения. - Выпуклый многоугольник называется правильным
, если у него равны все стороны и все углы, например равносторонний треугольник, квадрат и правильный пятиугольник. Символ Шлефли правильного n {displaystyle n} -угольника равен { n } {displaystyle {n}} . - Многоугольник, у которого равны все стороны и все углы, но который имеет самопересечения, называется правильным звёздчатым многоугольником
, например, пентаграмма и октаграмма. - Многоугольник называется вписанным
в окружность, если все его вершины лежат на одной окружности. Сама окружность при этом называется описанной, а её центр лежит на пересечении серединных перпендикуляров к сторонам многоугольника. Любой треугольник является вписанным в некоторую окружность. - Многоугольник называется описанным
около окружности, если все его стороны касаются некоторой окружности. Сама окружность при этом называется вписанной, а её центр лежит на пересечении биссектрис углов многоугольника.. Любой треугольник является описанным около некоторой окружности. - Выпуклый четырёхугольник называется внеописанным
около окружности, если продолжения всех его сторон (но не сами стороны) касаются некоторой окружности.[3] Окружность при этом называется вневписанной. Вневписанная окружность существует также и у произвольного треугольника.
Простейшие четырёхугольники
Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.
Наиболее часто приходится сталкиваться со следующими видами:
- прямоугольник — четырёхугольник, у которого все углы прямые, то есть равняются 900;
- ромб — фигура с четырьмя сторонами одинаковой длины;
- квадрат — многоугольник, удовлетворяющий одновременно условиям ромба и прямоугольника.
Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.
Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.
Из-за особенностей прямоугольника формулу для расчёта периметра можно переписать так: P = 2*(a + b). В то же время площадь такой фигуры находится путём простого перемножения примыкающих сторон: S = a*b. Параметры квадрата можно вычислить, зная длину только одной стороны. Всё дело в том, что длины отрезков, из которых он состоит, равны друг другу, поэтому для квадрата периметр находится как P = 4*a, а площадь: S = a*a = a2.
Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.
Общие свойства[ | ]
Теорема о сумме углов многоугольника[ | ]
Сумма внутренних углов простого плоского n {displaystyle n} -угольника равна[4] 180 ∘ ( n − 2 ) {displaystyle 180^{circ }(n-2)} . Сумма внешних углов не зависит от числа сторон и всегда равна 360 ∘ . {displaystyle 360^{circ }.}
Число диагоналей[ | ]
- Число диагоналей всякого n {displaystyle n} -угольника равно n ( n − 3 ) 2 {displaystyle {tfrac {n(n-3)}{2}}} .
Площадь[ | ]
Пусть { ( X i , Y i ) } , i = 1 , 2 , . . . , n {displaystyle {(X_{i},Y_{i})},i=1,2,…,n} — последовательность координат соседних друг другу вершин n {displaystyle n} -угольника без самопересечений . Тогда его площадь вычисляется по формуле Гаусса:
S = 1 2 | ∑ i = 1 n ( X i + X i + 1 ) ( Y i − Y i + 1 ) | {displaystyle S={frac {1}{2}}left|sum limits _{i=1}^{n}(X_{i}+X_{i+1})(Y_{i}-Y_{i+1})right|} , где ( X n + 1 , Y n + 1 ) = ( X 1 , Y 1 ) {displaystyle (X_{n+1},Y_{n+1})=(X_{1},Y_{1})} .
Если даны длины сторон многоугольника и азимутальные углы сторон, то площадь многоугольника может быть найдена по формуле Саррона [5].
Площадь правильного n {displaystyle n} -угольника вычисляется по одной из формул[6]:
- половина произведения периметра n {displaystyle n} -угольника на апофему:
- S = n 4 a 2 ctg π n {displaystyle S={frac {n}{4}} a^{2}mathop {mathrm {} } ,operatorname {ctg} {frac {pi }{n}}} .
- S = 1 2 n R 2 sin 360 ∘ n ; {displaystyle S={frac {1}{2}}nR^{2}sin {frac {360^{circ }}{n}};}
- S = n r 2 t g π n {displaystyle S=nr^{2}mathop {mathrm {tg} } ,{frac {pi }{n}}}
где a {displaystyle a} — длина стороны многоугольника, R {displaystyle R} — радиус описанной окружности, r {displaystyle r} — радиус вписанной окружности.
Квадрируемость фигур[ | ]
С помощью множества многоугольников определяется квадрируемость и площадь произвольной фигуры на плоскости. Фигура F {displaystyle F} называется квадрируемой
, если для любого ε > 0 {displaystyle varepsilon >0} существует пара многоугольников P {displaystyle P} и Q {displaystyle Q} , таких, что P ⊂ F ⊂ Q {displaystyle Psubset Fsubset Q} и S ( Q ) − S ( P ) < ε {displaystyle S(Q)-S(P)<varepsilon } , где S ( P ) {displaystyle S(P)} обозначает площадь P {displaystyle P} .
Теорема об углах
Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.
Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.
В каждом треугольнике сумма углов равняется 180 градусов. Отсюда следует, что искомая сумма будет равняться 1800 * (n — 2). Например, для восьмиугольного она равняется 180 * (8 — 2) = 10800. Для многоугольника можно вести понятие внешнего угла.
К любой вершине можно построить 2 таких смежных угла. Если взять каждый из них, то их сумма будет равняться: a1 + a2 +…+ an = 3600. Доказать это можно так. Угол a1 равняется (180 — ∠A1), a2 = (180 — ∠A2) и так далее. Таких слагаемых будет n штук. Тогда можно записать, 180 * n — 180 * (n — 2) = 180 * 2 = 360. Таким образом, сумма всех внешних углов равняется 3600.
Лучше всего понять сказанное можно, рассмотрев пример, рассчитанный на учащихся средней школы. Пусть есть правильный шестиугольник. Нужно определить его угол. У такой фигуры все стороны, а значит и углы равны. Для начала следует определить их сумму. Она будет равняться 180 * (4−2) = 1800 * 4 = 7200. Но так как это шестиугольник, результат необходимо поделить на 6. Таким образом, искомый угол правильной фигуры будет равняться 120 градусам.
Примечания[ | ]
- ↑ 123
Многоугольник // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. — С. 749—752. - ↑ 123
Элементарная математика, 1976, с. 383—384. - Картаслов.ру
- Элементарная математика, 1976, с. 499.
- Хренов Л. С.
Вычисление площадей многоугольников по способу Саррона // Математическое просвещение. 1936. Выпуск 6. С. 12—15 - Элементарная математика, 1976, с. 503—504.
Свойства углов многоугольника
| Углы n – угольника |
| Сумма углов многоугольника равна Посмотреть доказательство |
| Внешние углы n – угольника |
| Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°
Посмотреть доказательство |
Построение
Отличительная особенность правильного 65537-угольника — это тот факт, что его возможно построить, используя только циркуль и линейку.
Первый шаг в построении 65537-угольника
Число 65 537 — это самое большое известное простое число Ферма:
65537 = 2 2 4 + 1 {displaystyle 65537=2^{2^{4}}+1} .
Гауссом в 1796 году было доказано, что правильный n
-угольник можно построить циркулем и линейкой, если нечётные простые делители
n
являются различными числами Ферма. В 1836 году П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует. Ныне это утверждение известно как теорема Гаусса — Ванцеля.
В 1894 году Иоганн Густав Гермес после более чем десятилетних исследований нашёл способ построения правильного 65537-угольника и описал его в рукописи размером более 200 страниц[2] (оригинал рукописи хранится в библиотеке Гёттингенского университета).
Один слишком навязчивый аспирант довёл своего руководителя до того, что тот сказал ему: «Идите и разработайте построение правильного многоугольника с 65537 сторонами». Аспирант удалился, чтобы вернуться через 20 лет с соответствующим построением[3].
Дж. Литлвуд
Примечания
- «В сложных словах, начинающихся составным числительным свыше 1000, название первого числа в составе сложного слова остаётся неизменным, а все остальные названия чисел ставятся в род. п. в соответствии с правилами согласования: пятьтысячдевятисотдолларовый чек
,
четыретысячидевятисотдолларовый
,
дветысячивосьмисотдолларовый
и т. д.» (
Граудина Л. К., Ицкович В. А., Катлинская Л. П.
Грамматическая правильность русской речи. Опыт частотно-стилистического словаря вариантов / Под ред. С. Г. Бархударова, И. Ф. Протченко, Л. И. Скворцова. — М.: Наука, 1976. — С. 269. — 456 с.). - Johann Gustav Hermes (1894). «Über die Teilung des Kreises in 65537 gleiche Teile». Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse3
: 170–186. (нем.) - Дж. Литлвуд.
Математическая смесь. — М.: Наука, 1990. — С. 43. — ISBN 5-02-014332-4.
( 1 оценка, среднее 4 из 5 )