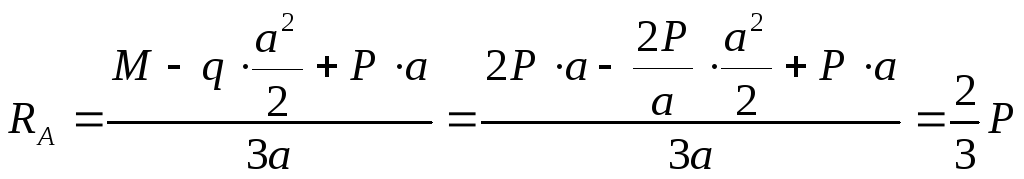Как найти внешний изгибающий момент - Исправление недочетов и поиск решений вместе с Examum.ru

В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.

В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.

Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.

Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.

Поперечные силы и изгибающие моменты

При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (M_изг).

Поперечные силы и изгибающие моменты в произвольном сечении балки

Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.

Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.

Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!

Обозначения поперечных сил и изгибающих моментов

Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.

Например, если выбрать следующие обозначения для координатных осей:

Обозначения поперечных сил и изгибающих моментов с привязкой к координатным осям

То, поперечная сила, будет обозначаться, как Q_y (параллельна оси y), а изгибающий момент, как M_x (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Q_y, M_z или Q_z, M_x. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – M_изг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.

Расчётная схема балки

Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

Простая схема балки, свободная от нагрузок

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.

К примеру, балка может иметь прямоугольное поперечное сечение:

Балки имеющая прямоугольную форму поперечного сечения

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.

Правила знаков для поперечных сил и изгибающих моментов

В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).

Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и М_изг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).

Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.

Правило знаков для поперечных сил

Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

Правило – положительное значение поперечной силы

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Правило – отрицательное значение поперечной силы

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:

Правило знаков для изгибающих моментов

Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.

Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Схема показывающая верхние и нижние волокна консольной балки

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

Схема деформированной балки с указанием растянутых и сжатых волокон

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.

На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

Правило – отрицательное значение изгибающего момента

• нижние волокна, то нужно учесть его с «плюсом».

Правило – положительное значение изгибающего момента

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.

Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:

Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:

Отрицательное значение изгибающего момента – правило

Положительное значение изгибающего момента – правило

Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:

Как построить эпюры поперечных сил и изгибающих моментов ?

В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.

Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉

Построение эпюр для консольной балки

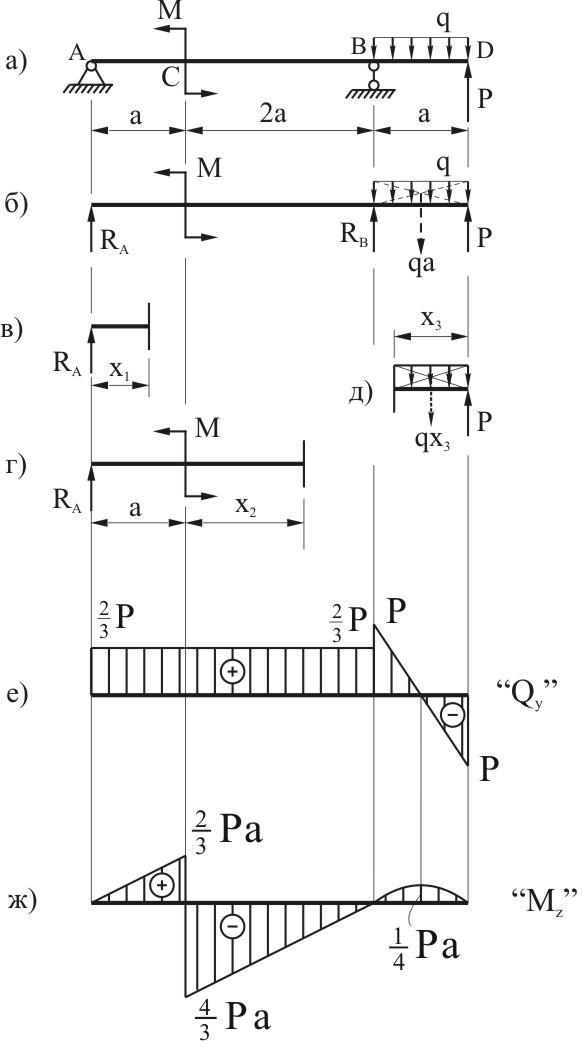
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Расчётная схема — консольной балки, загруженной силами и моментом

Будем рассчитывать балку справа налево.

Рассмотрим первый участок

Обозначим некоторое сечение 1-1 на расстоянии x₁, от свободного торца балки, при этом x₁ будет находиться в диапазоне: 0 ≤ x₁≤ 4м.

Указание расчётного сечения на первом участке

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.

Поперечные силы на первом участке

Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:

Как видишь, поперечная сила будет постоянна на первом участке:

Уже можем отразить это на эпюре поперечных сил:

Построение эпюры поперечных сил на первом участке

Изгибающие моменты на первом участке

Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:

Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Построение эпюры изгибающих моментов на первом участке

Расчёт второго участка

Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x₂ от начала участка (0 ≤ x₂≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке

Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:

Теперь можем показать окончательную эпюру поперечных сил:

Построение окончательной эпюры поперечных сил

Изгибающие моменты на втором участке

Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:

Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Построение окончательной эпюры изгибающих моментов

Проверка построенных эпюр

Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.

Определение реакций в жёсткой заделке

Первым делом, нам потребуется определить реакции в заделке:

Обозначение реакций в жёсткой заделке на расчётной схеме

Расчёт эпюр поперечных сил и изгибающих моментов

Рассчитываем все участки теперь слева направо:

Обозначение расчётных сечений для участков балки

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Построение эпюр изгибающих моментов для расчёта балки слева направо

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Схема демонстрирующая, что расчёт балки можно выполнять с двух сторон

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.

Эпюра моментов со стороны растянутых или сжатых волокон

По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.

Причем сама эпюра была построенна со стороны растянутых волокон:

Эпюра изгибающих моментов построенная со стороны растянутых волокон

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Эпюра изгибающих моментов построенная со стороны сжатых волокон

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.

Учёт распределённой нагрузки

Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.

Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Расчётная схема консольной балки, загруженной распределённой нагрузкой

Определение поперечной силы и изгибающего момента в сечении A

Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.

После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Сворачивание распределённой нагрузки до сосредоточенной силы

Тогда поперечная сила Q_A будет равна:

Изгибающий момент M_{изг, A} будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов

Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Обозначение расчётного сечения для написания уравнений

Уравнение для поперечных сил будет следующее:

Рассчитаем значения на эпюре поперечных сил:

Построение эпюры поперечных сил для консольной балки от распределённой нагрузки

Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:

Откладывание ординат для построения эпюры изгибающих моментов

На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.

Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Построение эпюры изгибающих моментов со стороны растянутых волокон для консольной балки от распределённой нагрузки

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюры изгибающих моментов со стороны сжатых волокон для консольной балки от распределённой нагрузки

Построение эпюр для двухопорной балки

А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Расчётная схема двухопорной балки с обозначением реакций в опорах

Рассчитываем первый участок:

Строим эпюры на первом участке:

Построение эпюр сил и моментов на первом участке

Определение экстремума на эпюре моментов

Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.

Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:

Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Указание экстремума на эпюре изгибающих моментов

Расчет эпюр на остальных участках

Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:

Определение экстремума:

Построение эпюр поперечных сил и изгибающих моментов для двухопорной балки

Оценка правильности построенных эпюр поперечных сил и изгибающих моментов

И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.

Вот несколько признаков, правильно построенных эпюр:

На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.

Источник

From Wikipedia, the free encyclopedia

In solid mechanics, a bending moment is the reaction induced in a structural element when an external force or moment is applied to the element, causing the element to bend.^[1]^[2] The most common or simplest structural element subjected to bending moments is the beam. The diagram shows a beam which is simply supported (free to rotate and therefore lacking bending moments) at both ends; the ends can only react to the shear loads. Other beams can have both ends fixed (known as encastre beam); therefore each end support has both bending moments and shear reaction loads. Beams can also have one end fixed and one end simply supported. The simplest type of beam is the cantilever, which is fixed at one end and is free at the other end (neither simple or fixed). In reality, beam supports are usually neither absolutely fixed nor absolutely rotating freely.

The internal reaction loads in a cross-section of the structural element can be resolved into a resultant force and a resultant couple.^[3] For equilibrium, the moment created by external forces/moments must be balanced by the couple induced by the internal loads. The resultant internal couple is called the bending moment while the resultant internal force is called the shear force (if it is transverse to the plane of element) or the normal force (if it is along the plane of the element). Normal force is also termed as axial force.

The bending moment at a section through a structural element may be defined as the sum of the moments about that section of all external forces acting to one side of that section. The forces and moments on either side of the section must be equal in order to counteract each other and maintain a state of equilibrium so the same bending moment will result from summing the moments, regardless of which side of the section is selected. If clockwise bending moments are taken as negative, then a negative bending moment within an element will cause «hogging», and a positive moment will cause «sagging». It is therefore clear that a point of zero bending moment within a beam is a point of contraflexure—that is, the point of transition from hogging to sagging or vice versa.

Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres (N·m), or pound-foot (lb·ft). The concept of bending moment is very important in engineering (particularly in civil and mechanical engineering) and physics.

Background[edit]

Tensile and compressive stresses increase proportionally with bending moment, but are also dependent on the second moment of area of the cross-section of a beam (that is, the shape of the cross-section, such as a circle, square or I-beam being common structural shapes). Failure in bending will occur when the bending moment is sufficient to induce tensile/compressive stresses greater than the yield stress of the material throughout the entire cross-section. In structural analysis, this bending failure is called a plastic hinge, since the full load carrying ability of the structural element is not reached until the full cross-section is past the yield stress. It is possible that failure of a structural element in shear may occur before failure in bending, however the mechanics of failure in shear and in bending are different.

Moments are calculated by multiplying the external vector forces (loads or reactions) by the vector distance at which they are applied. When analysing an entire element, it is sensible to calculate moments at both ends of the element, at the beginning, centre and end of any uniformly distributed loads, and directly underneath any point loads. Of course any «pin-joints» within a structure allow free rotation, and so zero moment occurs at these points as there is no way of transmitting turning forces from one side to the other.

It is more common to use the convention that a clockwise bending moment to the left of the point under consideration is taken as positive. This then corresponds to the second derivative of a function which, when positive, indicates a curvature that is ‘lower at the centre’ i.e. sagging. When defining moments and curvatures in this way calculus can be more readily used to find slopes and deflections.

Critical values within the beam are most commonly annotated using a bending moment diagram, where negative moments are plotted to scale above a horizontal line and positive below. Bending moment varies linearly over unloaded sections, and parabolically over uniformly loaded sections.

Engineering descriptions of the computation of bending moments can be confusing because of unexplained sign conventions and implicit assumptions. The descriptions below use vector mechanics to compute moments of force and bending moments in an attempt to explain, from first principles, why particular sign conventions are chosen.

Computing the moment of force[edit]

Computing the moment of force in a beam.

An important part of determining bending moments in practical problems is the computation of moments of force.
Let be a force vector acting at a point A in a body. The moment of this force about a reference point (O) is defined as^[2]

where is the moment vector and is the position vector from the reference point (O) to the point of application of the force (A). The times symbol indicates the vector cross product. For many problems, it is more convenient to compute the moment of force about an axis that passes through the reference point O. If the unit vector along the axis is , the moment of force about the axis is defined as

M=mathbf {e} cdot mathbf {M} =mathbf {e} cdot (mathbf {r} times mathbf {F} )

where cdot indicates the vector dot product.

Example[edit]

The adjacent figure shows a beam that is acted upon by a force . If the coordinate system is defined by the three unit vectors $mathbf {e} _{x},mathbf {e} _{y},mathbf {e} _{z}$ , we have the following

$mathbf{F} = 0,mathbf{e}_x - F,mathbf{e}_y + 0,mathbf{e}_z quad text{and} quad mathbf{r} = x,mathbf{e}_x + 0,mathbf{e}_y + 0,mathbf{e}_z ,.$

Therefore,

$mathbf{M} = mathbf{r}timesmathbf{F} = left|begin{matrix}mathbf{e}_x & mathbf{e}_y & mathbf{e}_z \ x & 0 & 0 \ 0 & -F & 0 end{matrix}right| = -Fx,mathbf{e}_z ,.$

The moment about the axis $mathbf{e}_z$ is then

$M_z = mathbf{e}_zcdotmathbf{M} = -Fx ,.$

Sign conventions[edit]

The negative value suggests that a moment that tends to rotate a body clockwise around an axis should have a negative sign. However, the actual sign depends on the choice of the three axes $mathbf {e} _{x},mathbf {e} _{y},mathbf {e} _{z}$ . For instance, if we choose another right handed coordinate system with $mathbf{E}_x = mathbf{e}_x, mathbf{E}_y = -mathbf{e}_z, mathbf{E}_z = mathbf{e}_y$ , we have

$mathbf{F} = 0,mathbf{E}_x + 0,mathbf{E}_y -F,mathbf{E}_z quad text{and} quad mathbf{r} = x,mathbf{E}_x + 0,mathbf{E}_y + 0,mathbf{E}_z ,.$

Then,

$mathbf{M} = mathbf{r}timesmathbf{F} = left|begin{matrix}mathbf{E}_x & mathbf{E}_y & mathbf{E}_z \ x & 0 & 0 \ 0 & 0 & -F end{matrix}right| = Fx,mathbf{E}_y quad text{and} quad M_y = mathbf{E}_ycdotmathbf{M} = Fx ,.$

For this new choice of axes, a positive moment tends to rotate body clockwise around an axis.

Computing the bending moment[edit]

In a rigid body or in an unconstrained deformable body, the application of a moment of force causes a pure rotation. But if a deformable body is constrained, it develops internal forces in response to the external force so that equilibrium is maintained. An example is shown in the figure below. These internal forces will cause local deformations in the body.

For equilibrium, the sum of the internal force vectors is equal to the negative of the sum of the applied external forces, and the sum of the moment vectors created by the internal forces is equal to the negative of the moment of the external force. The internal force and moment vectors are oriented in such a way that the total force (internal + external) and moment (external + internal) of the system is zero. The internal moment vector is called the bending moment.^[1]

Though bending moments have been used to determine the stress states in arbitrary shaped structures, the physical interpretation of the computed stresses is problematic. However, physical interpretations of bending moments in beams and plates have a straightforward interpretation as the stress resultants in a cross-section of the structural element. For example, in a beam in the figure, the bending moment vector due to stresses in the cross-section A perpendicular to the x-axis is given by

$mathbf{M}_x = int_A mathbf{r} times (sigma_{xx} mathbf{e}_x + sigma_{xy} mathbf{e}_y + sigma_{xz} mathbf{e}_z), dA quad text{where} quad mathbf{r} = y,mathbf{e}_y + z,mathbf{e}_z ,.$

Expanding this expression we have,

$mathbf{M}_x = int_A left(-ysigma_{xx}mathbf{e}_z + ysigma_{xz}mathbf{e}_x + zsigma_{xx}mathbf{e}_y - zsigma_{xy}mathbf{e}_xright)dA =: M_{xx},mathbf{e}_x + M_{xy},mathbf{e}_y + M_{xz},mathbf{e}_z,.$

We define the bending moment components as

$begin{bmatrix} M_{xx} \ M_{xy} \M_{xz} end{bmatrix} := int_A begin{bmatrix} ysigma_{xz} - zsigma_{xy} \ zsigma_{xx} \ -ysigma_{xx} end{bmatrix},dA ,.$

The internal moments are computed about an origin that is at the neutral axis of the beam or plate and the integration is through the thickness ()

Example[edit]

Computing the bending moment in a beam.

In the beam shown in the adjacent figure, the external forces are the applied force at point A ( $-Fmathbf{e}_y$ ) and the reactions at the two support points O and B ( $mathbf{R}_O = R_Omathbf{e}_y$ and $mathbf{R}_B = R_Bmathbf{e}_y$ ).
For this situation, the only non-zero component of the bending moment is

${displaystyle mathbf {M} _{xz}=-left[int _{z}left[int _{0}^{h}y,sigma _{xx},dyright],dzright]mathbf {e} _{z},.}$

where is the height in the direction of the beam. The minus sign is included to satisfy the sign convention.

In order to calculate ${displaystyle mathbf {M} _{xz}}$ , we begin by balancing the forces, which gives one equation with the two unknown reactions,

${displaystyle R_{O}+R_{B}-F=0,.}$

To obtain each reaction a second equation is required. Balancing the moments about any arbitrary point X would give us a second equation we can use to solve for $R_{0}$ and $R_{B}$ in terms of . Balancing about the point O is simplest but let’s balance about point A just to illustrate the point, i.e.

${displaystyle -mathbf {r} _{A}times mathbf {R} _{O}+(mathbf {r} _{B}-mathbf {r} _{A})times mathbf {R} _{B}=mathbf {0} ,.}$

If is the length of the beam, we have

${displaystyle mathbf {r} _{A}=x_{A}mathbf {e} _{x}quad {text{and}}quad mathbf {r} _{B}=Lmathbf {e} _{x},.}$

Evaluating the cross-products:

${displaystyle left|{begin{matrix}mathbf {e} _{x}&mathbf {e} _{y}&mathbf {e} _{z}\-x_{A}&0&0\0&R_{0}&0end{matrix}}right|+left|{begin{matrix}mathbf {e} _{x}&mathbf {e} _{y}&mathbf {e} _{z}\L-x_{A}&0&0\0&R_{B}&0end{matrix}}right|=-x_{A}R_{0},mathbf {e} _{z}+(L-x_{A})R_{B},mathbf {e} _{z}=0,.}$

If we solve for the reactions we have

$R_O = left(1 - frac{x_A}{L}right) F quad text{and} quad R_B = frac{x_A}{L},F ,.$

Now to obtain the internal bending moment at X we sum all the moments about the point X due to all the external forces to the right of X (on the positive side), and there is only one contribution in this case,

${displaystyle mathbf {M} _{xz}=(mathbf {r} _{B}-mathbf {r} _{X})times mathbf {R} _{B}=left|{begin{matrix}mathbf {e} _{x}&mathbf {e} _{y}&mathbf {e} _{z}\L-x&0&0\0&R_{B}&0end{matrix}}right|={frac {Fx_{A}}{L}}(L-x),mathbf {e} _{z},.}$

We can check this answer by looking at the free body diagram and the part of the beam to the left of point X, and the total moment due to these external forces is

${displaystyle mathbf {M} =(mathbf {r} _{A}-mathbf {r} _{X})times mathbf {F} +(-mathbf {r} _{X})times mathbf {R} _{O}=left[(x_{A}-x)mathbf {e} _{x}right]times left(-Fmathbf {e} _{y}right)+left(-xmathbf {e} _{x}right)times left(R_{O}mathbf {e} _{y}right),.}$

If we compute the cross products, we have

${displaystyle mathbf {M} =left|{begin{matrix}mathbf {e} _{x}&mathbf {e} _{y}&mathbf {e} _{z}\x_{A}-x&0&0\0&-F&0end{matrix}}right|+left|{begin{matrix}mathbf {e} _{x}&mathbf {e} _{y}&mathbf {e} _{z}\-x&0&0\0&R_{0}&0end{matrix}}right|=F(x-x_{A}),mathbf {e} _{z}-R_{0}x,mathbf {e} _{z}=-{frac {Fx_{A}}{L}}(L-x),mathbf {e} _{z},.}$

Thanks to the equilibrium, the internal bending moment due to external forces to the left of X must be exactly balanced by the internal turning force obtained by considering the part of the beam to the right of X

${displaystyle mathbf {M} +mathbf {M} _{xz}=mathbf {0} ,.}$

which is clearly the case.

Sign convention[edit]

In the above discussion, it is implicitly assumed that the bending moment is positive when the top of the beam is compressed. That can be seen if we consider a linear distribution of stress in the beam and find the resulting bending moment. Let the top of the beam be in compression with a stress and let the bottom of the beam have a stress $sigma _{0}$ . Then the stress distribution in the beam is $sigma_{xx}(y) = -ysigma_0$ . The bending moment due to these stresses is

$M_{xz} = -left[int_zint_{-h/2}^{h/2} y,(-ysigma_0),dy,dzright] = sigma_0,I$

where is the area moment of inertia of the cross-section of the beam. Therefore, the bending moment is positive when the top of the beam is in compression.

Many authors follow a different convention in which the stress resultant $M_{xz}$ is defined as

$mathbf{M}_{xz} = left[int_zint_{-h/2}^{h/2} y,sigma_{xx},dy,dzright]mathbf{e}_z ,.$

In that case, positive bending moments imply that the top of the beam is in tension. Of course, the definition of top depends on the coordinate system being used. In the examples above, the top is the location with the largest -coordinate.

References[edit]

^ ^a ^b Gere, J.M.; Timoshenko, S.P. (1996), Mechanics of Materials:Forth edition, Nelson Engineering, ISBN 0534934293
^ ^a ^b Beer, F.; Johnston, E.R. (1984), Vector mechanics for engineers: statics, McGraw Hill, pp. 62–76
^ Baker, Daniel W.; Haynes, William. Statics: Internal Loads.

External links[edit]

Stress resultants for beams

Free online Calculation tools for bending moment

Источник

Определение поперечных сил и изгибающих моментов.

Как уже было сказано, при плоском
поперечном изгибе в поперечном сечении
балки возникают два внутренних силовых
фактора
и.

Перед определением
иопределяют реакции опор балки (рис. 6.3,
а), составляя уравнения равновесия
статики.

Для определения
иприменим метод сечений. В интересующем
нас месте сделаем мысленный разрез
балки, например, на расстоянииот левой опоры. Отбросим одну из частей
балки, например правую, и рассмотрим
равновесие левой части (рис. 6.3, б).
Взаимодействие частей балки заменим
внутренними усилиямии.

Установим следующие правила знаков для
и:

Поперечная сила
в сечении положительна, если ее векторы
стремятся вращать рассматриваемое
сечение по часовой стрелке;
Изгибающий момент
в сечении положителен, если он вызывает
сжатие верхних волокон.

Рис. 6.3

Для определения данных усилий используем
два уравнения равновесия:

1.
;;.

2.
;

;

Таким образом,

а) поперечная сила
в поперечном сечении балки численно
равна алгебраической сумме проекций
на поперечную ось сечениявсех внешних сил, действующих по одну
сторону от сечения;

б) изгибающий момент в поперечном сечении
балки численно равен алгебраической
сумме моментов (вычисленных относительно
центра тяжести сечения) внешних сил,
действующих по одну сторону от данного
сечения.

При практическом вычислении руководствуются
обычно следующим:

Если внешняя нагрузка стремится
повернуть балку относительно
рассматриваемого сечения по часовой
стрелке, (рис. 6.4, б) то в выражении для
она дает положительное слагаемое.
Если внешняя нагрузка создает относительно
рассматриваемого сечения момент,
вызывающий сжатие верхних волокон
балки (рис. 6.4, а), то в выражении для
в этом сечении она дает положительное
слагаемое.

Рис. 6.4

Построение эпюр ив балках.

Рассмотрим двухопорную балку
(рис. 6.5, а). На балку действует в точкесосредоточенный момент,
в точке— сосредоточенная силаи на участке— равномерно распределенная нагрузка
интенсивностью.

Определим опорные реакции
и(рис. 6.5, б).
Равнодействующая распределенной
нагрузки равна,
а линия действия ее проходит через центр
участка.
Составим уравнения моментов относительно
точеки.

Определим поперечную силу и изгибающий
момент в произвольном сечений,
расположенном на участке
на расстоянииот точки А(рис. 6.5, в).
Расстояниеможет изменяться в пределах ().

Значение поперечной силы не зависит
от координаты сечения
,
следовательно, во всех сечениях участкапоперечные силы одинаковы и эпюраимеет вид прямоугольника.

Изгибающий момент изменяется по
линейному закону

Для построения эпюры вычисляем ординаты
на границах участка.

При
:

При

Рис. 6.5

Определим поперечную силу и изгибающий
момент в произвольном сечений,
расположенном на участке
на расстоянииот точки(рис. 6.5, г).Расстояниеможет изменяться в пределах ().

Значение поперечной силы не зависит от
координаты сечения
,
следовательно, во всех сечениях участкапоперечные силы одинаковы и эпюраимеет вид прямоугольника. Изгибающий
момент

Изгибающий момент изменяется по линейному
закону. Определим ординаты эпюры для
границ участка.

Определим поперечную силу и изгибающий
момент в произвольном сечений,
расположенном на участке
на расстоянииот точки(рис. 6.5, д).Расстояниеможет изменяться в пределах ().

Поперечная сила изменяется по линейному
закону. Определим для границ участка.

Изгибающий момент

Эпюра изгибающих моментов на этом
участке будет параболической.

Чтобы определить экстремальное значение
изгибающего момента, приравниваем к
нулю производную от изгибающего момента
по абсциссе сечения
:

Отсюда

Для сечения с координатой
значение изгибающего момента будет
составлять

В результате получаем эпюры поперечных
сил (рис. 6.5, е) и изгибающих
моментов(рис. 6.5, ж).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Лекция 8. ИЗГИБ

Плоский поперечный изгиб прямых стержней (брусьев, балок).
Определение внутренних сил (поперечных сил и изгибающих моментов)
в произвольном поперечном сечении стержня и построение их эпюр.
Дифференциальные зависимости между нагрузкой, поперечными силами,
изгибающими моментами, их использование при построении диаграмм
и контроля правильности построения.

Плоский изгиб. Под плоским поперечным изгибом понимают такой вид
деформации, при которой происходит искривление оси прямого бруса,
и в поперечном сечении бруса действует два силовых фактора: изгибающий
момент М и поперечная сила Q. Осью бруса называется геометрическое место
точек центров тяжестей поперечных сечений бруса. Изгиб – плоский, если
ось балки после деформации остается плоской линией. В противном случае
имеет место косой изгиб. Если поперечная сила не возникает, изгиб
называется чистым изгибом.

Рассмотрим, например, балку, нагруженную вертикальной
сосредоточенной силой P. Для определения внутренних усилий при прямом
изгибе, возникающих в поперечном сечении, расположенном на расстоянии z
от места приложения нагрузки, воспользуемся методом сечений.

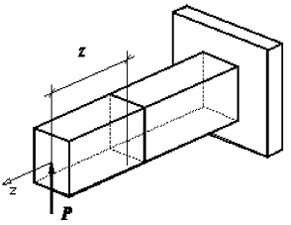
а б

Рис. 22. Плоский изгиб:
а – балка под нагрузкой Р; б – внутренние силы при изгибе

Разрежем мысленно балку в интересующем месте на две части.Отбросим
левую часть балки, нагруженную силой P. Заменим действие отброшенной
левой части балки на оставленную правую часть внутренними силами.

Внутренние усилия возникают во всех точках поперечного сечения
балки и распределены по неизвестному закону. Не имея возможности
определить эти внутренние усилия для каждой точки сечения, заменяем их
статически эквивалентными внутренними силовыми факторами, приложенными
в центре тяжести поперечного сечения.

Внутренние силовые факторы определяются из условия равновесия
рассматриваемой части балки. Однако можем внутренние силовые факторы
найти и непосредственно, как действие отброшенной левой части на правую
часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть
рассматриваемую нами правую часть выпуклостью вниз, а также пытается
произвести срез. Следовательно, в сечении должны возникнуть поперечная
сила и изгибающий момент.

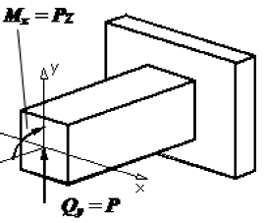
Осуществим параллельный перенос силы P в центр тяжести поперечного
сечения балки. По правилам теоретической механики добавляется момент,
равный Pz.

Таким образом, в поперечном сечении балки возникают два внутренних силовых фактора:

– изгибающий момент, численно равный алгебраической сумме моментов
всех сил, приложенных к отбрасываемой части балки, относительно главной
центральной оси, проходящей через центр тяжести рассматриваемого
сечения (в данном примере М = Рz);

– поперечная сила, численно равная алгебраической сумме всех
внешних сил (активных и реактивных), действующих на отбрасываемую часть
балки (в нашем примере Q = P).

Построение эпюр поперечных сил и изгибающих моментов. При расчете
балок на прочность необходимо знать характер изменения изгибающего
момента и поперечной силы вдоль оси балки и знать положение опасного
сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов.

Если внешняя сила стремится повернуть отсеченную часть по часовой
стрелке относительно рассматриваемого сечения, то поперечная сила
положительна.

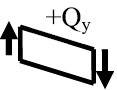
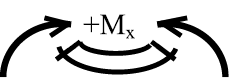
а б

Рис. 23. Правило знаков для внутренних усилий:
а – для поперечной силы; б – для изгибающего момента

Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз.

Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере.

Пусть на балку действует внешний изгибающий момент m = 6 кН•м
и внешняя сила F = 12 кН, l = 1 м. Определим реакции в опорах A и B.
Составим уравнения равновесия моментов всех внешних сил относительно
опор A и B

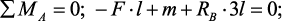
откуда

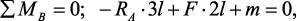
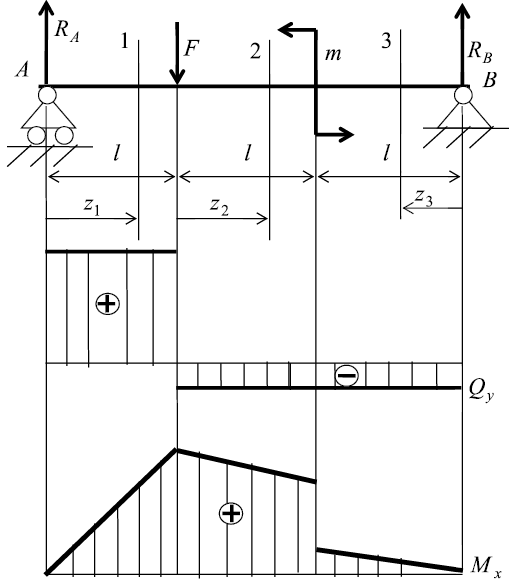
Рис. 24. Эпюры Q_y, Mx

Проведем сечения на каждом характерном участке и определим значения поперечной силы Qy и изгибающего момента M_x.

В сечении 1

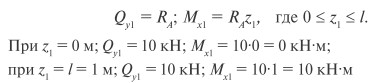
В сечении 2

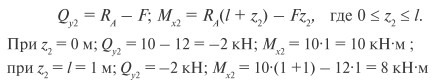
В сечении 3

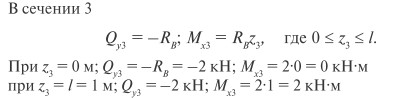
По полученным значениям строим эпюры поперечных сил и изгибающих моментов (рис. 24).

Дифференциальные зависимости при изгибе.

Выделим на участке балки с произвольной нагрузкой в месте, где нет
сосредоточенных сил и моментов, малый элемент dz. Так как вся балка
находится в равновесии, то и элемент dz будет находиться в равновесии
под действием приложенных к нему поперечных сил, изгибающих моментов
и внешней нагрузки. Поскольку Qy и Mx в общем случае меняются вдоль оси
балки, то в сечениях элемента dz будут возникать поперечные силы Qy
и Qy + dQy, а также изгибающие моменты M_x и M_x + dM_x.

Из условия равновесия выделенного элемента получим:

следовательно

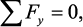
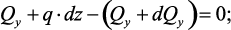
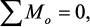
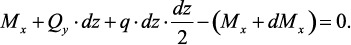
Первое из двух записанных уравнений дает условие

(10)

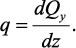
Из второго уравнения, пренебрегая слагаемым 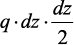как бесконечно малой величиной второго порядка, найдем

(11)

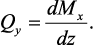
Рассматривая полученные выражения, совместно можем получить

(12)

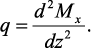
Полученные соотношения называют дифференциальными зависимостями Д.И. Журавского при изгибе.

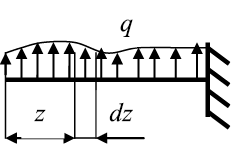
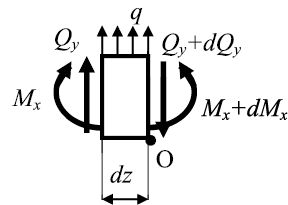
Рис. 25. Внутренние усилия в балке при изгибе

Анализ дифференциальных зависимостей при изгибе позволяет
установить некоторые правила построения эпюр изгибающих моментов
и поперечных сил:

– на участках, где нет распределенной нагрузки q, эпюры Q
ограничены прямыми, параллельными базе, а эпюры М – наклонными прямыми;

– на участках, где к балке приложена распределенная нагрузка q,
эпюры Q ограничены наклонными прямыми, а эпюры М – квадратичными
параболами;

– в сечениях, где к балке прикладывается сосредоточенная сила, на
эпюре Q будут скачки на величину и в направлении данной силы, а на эпюре
М – перегибы, острием направленные в направлении действия этой силы;

– в сечениях, где к балке прикладывается сосредоточенный момент,
на эпюре Q изменений не будет, а на эпюре М – скачок на величину
момента;

– в сечении, где приложена сосредоточенная внешняя сила эпюра
изгибающих моментов делает резкое изменение угла наклона смежных
участков эпюры (излом эпюры). Излом эпюры направлен навстречу вектору
силы;

– сосредоточенная (или распределенная) пара сил влияния на закон
изменения поперечных сил на участке не оказывает, и на эпюре Q это ни
как не отражается;

– в сечении, где приложена пара сил, эпюра изгибающих моментов делает скачок на величину этой пары и с ее знаком;

– на участке, где приложена равномерно распределенная нагрузка q,
эпюра поперечных сил имеет вид прямой наклонной линии с угловым
коэффициентом q;

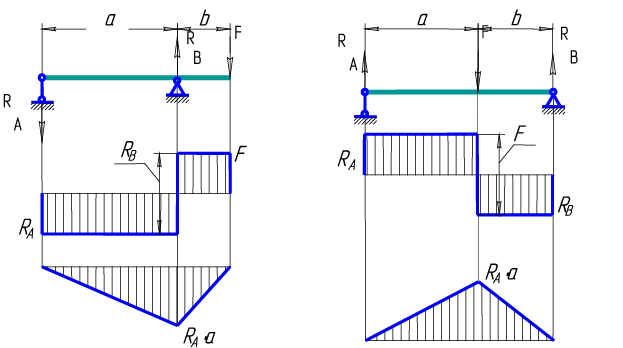
Рис. 26. В сечении, в котором к балке приложена сосредоточенная
внешняя сила, перпендикулярная к оси балки, эпюра поперечных сил Q
делает скачок
на величину этой силы и с ее знаком

– на участке, где приложена равномерно распределенная нагрузка, эпюра изгибающих моментов ограничена параболической кривой;

– в сечении, где приложена сосредоточенная сила, эпюра изгибающих
моментов делает резкое изменение угла наклона смежных участков эпюры
(излом эпюры). Излом эпюры направлен навстречу вектору силы;

– на участке, где поперечная сила равна нулю, наблюдается
деформация чистого плоского изгиба, при котором изгибающий момент
является постоянной величиной.

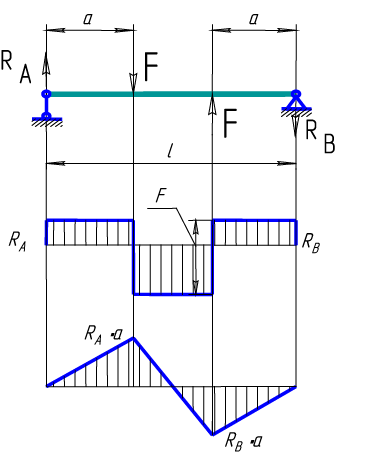
Рис. 27. Пример действия пары сил

Источник

Поперечные силы и изгибающие моменты

Обозначения поперечных сил и изгибающих моментов

Расчётная схема балки

Правила знаков для поперечных сил и изгибающих моментов

Расчётная схема

Правило знаков для поперечных сил

Правило знаков для изгибающих моментов

Как построить эпюры поперечных сил и изгибающих моментов ?

Построение эпюр для консольной балки

Рассмотрим первый участок

Поперечные силы на первом участке

Изгибающие моменты на первом участке

Расчёт второго участка

Поперечные силы на втором участке

Изгибающие моменты на втором участке

Проверка построенных эпюр

Определение реакций в жёсткой заделке

Расчёт эпюр поперечных сил и изгибающих моментов

Эпюра моментов со стороны растянутых или сжатых волокон

Учёт распределённой нагрузки

Определение поперечной силы и изгибающего момента в сечении A

Расчёт эпюр поперечных сил и изгибающих моментов

Построение эпюр для двухопорной балки

Определение экстремума на эпюре моментов

Расчет эпюр на остальных участках

Оценка правильности построенных эпюр поперечных сил и изгибающих моментов

Background[edit]

Computing the moment of force[edit]

Example[edit]

Sign conventions[edit]

Computing the bending moment[edit]

Example[edit]

Sign convention[edit]

See also[edit]

References[edit]

External links[edit]

Определение поперечных сил и изгибающих моментов.

Построение эпюр ив балках.

Лекция 8. ИЗГИБ