Углы правильного многоугольника делятся на :
- центральный угол;
- внутренний угол;
- внешний угол.
Сумма внутреннего и внешнего угла равна (180°).
Сумма внутренних углов правильного многоугольника с (n) сторонами равна:
((n — 2)180°)
Для нахождения внутреннего угла используют формулу:
(alpha = frac{{{{180}^o}(n — 2)}}{n})
(n)— число сторон
Для нахождения внешнего угла используют формулу:
(varphi = frac{{{{360}^o}}}{n})
(n)— число сторон
Для нахождения центрального угла используют формулу:
(beta = frac{{{{360}^o}}}{n})
(n)— число сторон
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Инфоурок
›
Математика
›Другие методич. материалы›Таблица значений сторон, внешних и внутренних углов правильного многоугольника
Таблица значений сторон, внешних и внутренних углов правильного многоугольника
Скачать материал
Скачать материал


- Сейчас обучается 22 человека из 17 регионов


- Сейчас обучается 27 человек из 13 регионов


- Сейчас обучается 353 человека из 69 регионов


Краткое описание документа:
С помощью таблицы учитель составляет задачи нахождения сторон, внешних и внутренних углов правильного многоугольника.
Уважаемые коллеги
Предлагаю вам таблицу, которая поможет вам легко составить задачи на
нахождение сторон, внутренних и внешних углов правильного многоугольника.
Для решения задач нужны формулы:
формула нахождения внутреннего угла правильного многоугольника
формула нахождения внешнего угла правильного многоугольника
An и Bn cмежные углы, поэтому An+ Bn= 1800
Количество сторон правильного многоуголь- ника
n
Внутренний угол правильного многоуголь- ника
An
Внешний угол правиль-
ного многоуголь
ника Bn
Зависимость внешнего и внутреннего угла правильного многоугольника
An и Bn
Зависимость внешнего и внутреннего угла правильного многоугольника
An и Bn
3
600
1200
An< Bn на 600
An < Bn в 2 раза
4
900
900
Bn = An
An = Bn
5
1080
720
An>Bn на 360
An > Bn в 1,5 раза
6
1200
600
An>Bn на 600
An > Bn в 2 раза
8
1350
450
An>Bn на 900
An > Bn в 3 раза
9
1400
400
An > Bn на 1000
An > Bn в 3,5 раза
10
1440
360
An>Bn на 1080
A n> Bn в 4 раза
12
1500
300
An>Bn на 1200
An > Bn в 5 раз
15
1560
240
An>Bn на 1320
A n> Bn в 6,5 раза
16
157,50
22,50
An>Bn на 1350
An > Bn в 7 раз
18
1600
200
An>Bn на 1400
A n> Bn в 8 раз
20
1620
180
An>Bn на 1440
A n> Bn в 9 раз
24
1650
150
An>Bn на 1500
A n> Bn в 11 раз
30
1680
120
An>Bn на 1560
A n> Bn в 14 раз
36
1700
100
An>Bn на 1600
An > Bn в 17 раз
Желаю успехов!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 268 729 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 11.03.2015
- 496
- 0
- 11.03.2015
- 2893
- 12
- 11.03.2015
- 628
- 0
- 11.03.2015
- 720
- 1
- 11.03.2015
- 1008
- 1
- 11.03.2015
- 2012
- 0
- 11.03.2015
- 961
- 0
-
Настоящий материал опубликован пользователем Маркова Галина Иннокентьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 2 месяца
- Подписчики: 0
- Всего просмотров: 2568
-
Всего материалов:
2
Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
a1 = a2 = a3 = … = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
2. Формула площади n-угольника через радиус вписанной окружности:
3. Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
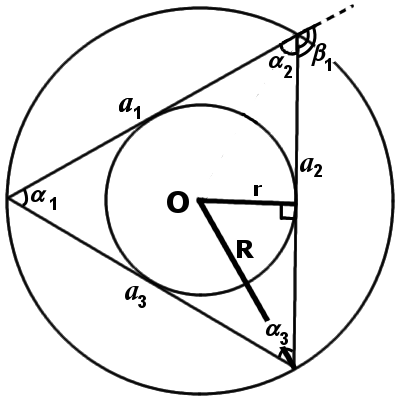 |
| Рис.3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника:
α = 60°
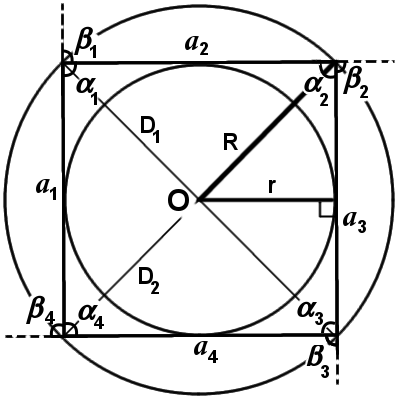 |
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
α = 135°
Внешний угол правильного многоугольника Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | Правильный многоугольник ↺ | |
| Правильный многоугольник | 2D геометрия ↺ | |
| 2D геометрия | Углы правильного многоугольника ↺ |
|
✖Количество сторон правильного многоугольника обозначает общее количество сторон многоугольника. Количество сторон используется для классификации типов многоугольников.ⓘ Количество сторон правильного многоугольника [NS] |
+10% -10% |
|
✖Внешний угол правильного многоугольника — это угол между одной стороной многоугольника и линией, идущей от следующей стороны многоугольника.ⓘ Внешний угол правильного многоугольника [∠Exterior] |
⎘ копия |
Внешний угол правильного многоугольника Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Количество сторон правильного многоугольника: 8 —> Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.785398163397448 Радиан —>45.0000000000085 степень (Проверьте преобразование здесь)
4 Углы правильного многоугольника Калькуляторы
Внешний угол правильного многоугольника формула
Внешний угол правильного многоугольника = (2*pi)/Количество сторон правильного многоугольника
∠Exterior = (2*pi)/NS
Что такое правильный многоугольник?
Правильный многоугольник имеет стороны одинаковой длины и равные углы между сторонами. Правильный n-сторонний многоугольник имеет вращательную симметрию порядка n и также известен как вписанный многоугольник. Все вершины правильного многоугольника лежат на описанной окружности.
Что такое внешний угол?
Внешний угол — это угол, образованный за пределами ограждения многоугольника одной из его сторон и продолжением примыкающей к нему стороны. Сумма внешних углов многоугольника равна 360 градусов.
Углы многоугольника
- Сумма внутренних углов
- Сумма внешних углов
Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.
Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.
Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
s = 2d(n — 2),
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
s = 2d(n — 2) = 180 · 4 = 720°.
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
s = 4d,
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
Следовательно, если многоугольник имеет n сторон (и n вершин), то сумма внешних и внутренних углов при всех n вершинах будет равна 2dn. Чтобы из этой суммы 2dn получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть 2d(n — 2):
s = 2dn — 2d(n — 2) = 2dn — 2dn + 4d = 4d.




