Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Определение.
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
На рисунке:
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
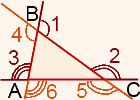
∠1=∠4, ∠2=∠5, ∠3=∠6.
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано: ∆АВС, ∠1 — внешний угол при вершине С.
Доказать: ∠1=∠А+∠В.
Доказательство:
Так как сумма углов треугольника равна 180º, ∠А+∠В+∠С=180º.
Следовательно, ∠С=180º-(∠А+∠В).
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Что и требовалось доказать.
Внешний угол треугольника
Определение. Внешним углом треугольника называется угол, смежный к любому углу этого треугольника.
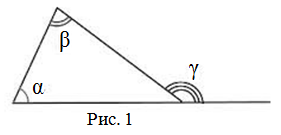
На Рис.1 угол 4 внешний так как углы 2 и 4 смежные.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Доказательство. Докажем, что ( small angle 4=angle 1+ angle 3. ) Поскольку сумма углов треугольника равна 180°, то имеем:
 . . |
(1) |
Так как углы 2 и 4 смежные, то:
 . . |
(2) |
Вычитая (1) из (2) получим:
 , , |
 , , |
 . . |
- Главная
- Справочник
- Теорема о внешнем угле треугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Теорема о внешнем угле треугольника
Содержание:
- Формулировка теоремы о внешнем угле треугольника
- Примеры решения задач
Формулировка теоремы о внешнем угле треугольника
Теорема
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним:
$$angle gamma=angle alpha+angle beta$$
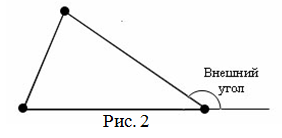
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине
(внутренним углом) (рис. 2).
Следствие
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Примеры решения задач
Пример
Задание. В треугольнике
$ABC$ угол
$A$ равен
$30^{circ}$, угол
$B — 80^{circ}$. Найти
градусную меру угла, смежного с
третьим углом треугольника.
Решение. Согласно теореме о внешнем угле треугольника, искомый угол равен сумме углов не смежных с ним, то есть:
$$alpha=30^{circ}+80^{circ}=110^{circ}$$
Ответ. $alpha=110^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В треугольнике $ABC$ угол
$A$ равен
$30^{circ}$, а внешний угол при вершине
$C$ равен
$45^{circ}$. Найти остальные углы треугольника
$ABC$ .
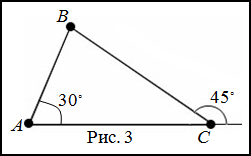
Решение. Сделаем чертеж к задаче (рис. 3).
Согласно теореме о внешнем угле треугольника, получаем равенство для нахождения градусной меры угла
$B$:
$$45^{circ}=30^{circ}+angle B Rightarrow angle B=15^{circ}$$
Угол $C$, как смежный угол, равен
$$angle C=180^{circ}-45^{circ}=135^{circ}$$
Ответ. $angle B=15^{circ}, angle C=135^{circ}$
Статьи по теме
- Теоремы по математике и геометрии
- Теорема Пифагора
- Теорема о среднем
- Теорема о сумме углов треугольника
- Теорема о трех перпендикулярах
- Все темы раздела «Теоремы по математике и геометрии»

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Теорема о внешнем угле треугольника: формулировка и задачи
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .
-
сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .
Исходя из теоремы: β = γ – α = 115° – 28° = 87° .
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине .
Зная , найдем по формуле
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные определения
Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:
- угла и треугольника;
- смежных углов;
- параллельных прямых.
Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.
Определение 1
Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.
На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.
Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ
Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.
Теорема о сумме углов треугольника
Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:
Сумма углов треугольника равна $180^{circ}$.
«Внешний угол треугольника: определение и свойство» 👇
Приведём её доказательство.
Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.
Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.
Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Видим, что углы 1 и 5 — накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.
Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.
Внешний угол треугольника
В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:
Определение 2
Внешний угол треугольника — это угол, являющийся смежным с каким-нибудь углом данного треугольника.
Имеем теорему:
Теорема 2
Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.
Докажем эту теорему.
Рассмотрим следующий рисунок:
Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ
Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:
$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.
Рассмотрим пример задачи на данную тему.
Пример 1
Задача. $triangle ABC$ — равнобедренный. $AC$ — основание этого треугольника. $AC$=37 см, внешний угол при $B$ равняется $60^{circ}$. Нужно найти расстояние от точки $C$ до прямой $AB$.
Решение. Сделаем рисунок:
Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ
На рисунке прямая, обозначающая расстояние от точки $C$ до прямой $AB$ обозначена как $CD$. В математике такое расстояние называют высотой. По определению высоты треугольника, прямая высоты перпендикулярна той стороне, на которую опущена. То есть $angle ADC = 90^{circ}$.
По теореме о внешнем угле треугольника находим $angle B$: $angle B=180-60=120^{circ}$. По теореме о сумме углов треугольника получается, что $angle A + angle C = 180-120=60$. Так как треугольник равнобедренный, углы у основания равны по $30^{circ}$.
Рассмотрим $triangle ADC$. Из вышеуказанного следует, что он прямоугольный. Из свойства прямоугольных треугольников известно, что катет такого треугольника, который лежит против угла $30^{circ}$, равен половине гипотенузы. В нашем случае, $СD$ является катетом против угла $30^{circ}$, а $AC$ — гипотенуза. Поэтому справедливо утверждать, что $CD=37/2=18,5$ см.
Ответ: 18,5 см.
Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме