Как найти внешний угол в арке - Исправление недочетов и поиск решений вместе с Examum.ru

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы в окружности

Рассмотрим углы в окружности и углы, связанные с окружностью.

Угол с вершиной в центре окружности.
Угол с вершиной на окружности (его стороны пересекают окружность).
Угол с вершиной внутри окружности (не в центре).
Угол с вершиной вне окружности, стороны которого пересекают окружность.

I. Угол с вершиной в центре окружности называется центральным углом.

Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.

Например, центральному углу AOC соответствует дуга AC (или дуга AFC. Обычно дугу называют двумя буквами. Но, поскольку любую из двух, на которые точки A и C делят окружность, можно назвать AC, то третью, дополнительную букву, иногда используют для уточнения выбранной дуги).

Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:

II. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.

Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).

Вписанный угол равен половине дуги, на которую он опирается:

Есть другой вариант формулировки свойства вписанного угла.

Вписанный угол равен половине соответствующего ему центрального угла:

Вписанный угол, опирающийся на полуокружность — прямой.

И наоборот: любой прямой вписанный угол опирается на полуокружность.

Другая формулировка этого утверждения:

(обратно: Если вписанный угол прямой, то он опирается на диаметр).

III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.

Угол между пересекающимися хордами равен полусумме дуг, заключённых между его сторонами и сторонами вертикального ему угла.

IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN — ⋃MN = 180° — 70° = 110°

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Задание. Чему равен ∠AВС на рисунке?

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

источники:

Углы в окружности

http://100urokov.ru/predmety/urok-10-ugly-v-okruzhnosti

Источник

При выполнении отделки арки самой сложной задачей является выравнивание углов. Но даже если ремонт будет сделан идеально, то края арочного проема все равно остаются самой уязвимой его частью. Чтобы облегчить себе задачу и продлить срок службы выполненной отделки, рекомендуется использовать специальные детали – арочные гибкие уголки.

Арка – элемент, который красиво смотрится практически в любом интерьере. Но она сможет украсить помещение только в том случае, если будет выполнена красивая отделка. А для выполнения качественной отделки арок специалисты рекомендуют использовать специальные уголки. Рассмотрим, что это за детали, какие функции они выполняют и как их нужно правильно клеить.

Гибкий арочный уголок в отделке проема

В наши дни часто вместо традиционных дверных проемов прямоугольной формы устраивают арки, посредством которых обеспечивается соединение смежных помещений. Наряду с ними в стенах возводят ниши округленной формы и перегородки с уникальным дизайном. Они позволяют создать в помещении оригинальное оформление.
При проведении таких работ без использования угловых элементов с жесткой конструкцией просто не обойтись. Их установка позволяет обеспечить защиту кроя. Поэтому важно найти материал, который обеспечит не только защитные свойства, но и подойдет для отделки конструкций. Хорошо известно, что именно отделка дверных проемов изнашивается быстрее — обои обрываются, а краска стирается.

В практике ведения работ наиболее распространено использование уголка из пластика. Основная функция этого изделия — декоративная. Наряду с ней он обеспечивает защиту конструкции. Так же, как и наличник, этот элемент защищает обои и краску от истирания.

Одна из его полок имеет цельную конструкцию с перфорацией. Что касается другой, то она состоит из сегментов трапециевидной формы, которые тоже имеют перфорацию. Использование такой конструкции обеспечивает возможность для легкого сгибания материала до нужного радиуса. Применяя их во время работ, появляется возможность формировать различные изгибы.

Одним из достоинств этого материала является его пластичность. Его можно использовать для отделки проемов ниш и окон самого разного размера. Наряду с этим его можно применять для отделки конструкции криволинейной формы. Сегменты, имеющие трапециевидную форму, позволяют с одной стороны уголка перейти к внешнему радиусу внутреннего. Применяют эти изделия главным образом для создания формы, а также для обеспечения защиты поверхностей изогнутых форм архитектурных элементов.

С помощью гибких уголков можно создать плавный силуэт. По причине того, что длина этих элементов может доходить до 3 метров, имеется возможность выполнить крепёж без образования традиционного шва. Это положительно отражается на эстетичности вида создаваемой конструкции. Одним из достоинств арочных пластиковых уголков является то, что процедура их монтажа простая и на ее выполнение уходит немного времени.

Если во время работы у вас возникла потребность в использовании гибких уголков, то вы без проблем сможете купить его в специализированном магазине или на строительном рынке.

Гибкие материалы: Медная лента М1 0,3 х 60 м: купить, цены

В настоящий момент есть несколько вариантов отделки проемов округлой формы. Способ отделки с использованием арочного пластикового уголка отличается своей простотой и практичностью. Цвет материала, применяемого во время работы может быть любым, что позволяет сочетать его с элементами отделки помещения.

Для проведения работ потребуется:

арочный уголок;
монтажный клей, предназначенный для пластика или пробкового материала;
декор;
металлические гвозди без шляпок;
герметическая обработка;
клей или жидкие гвозди;
резиновый молоточек.

Важная функция арочных уголков

Арочные декоративные уголки

Отделочный уголок уже много лет используется для упрощения ремонтных работ. Он позволяет сформировать углы, а также защитить дверной проем. Главным преимуществом арочных уголков является возможность продления срока службы отделки, так как с ними и обои не будут обрываться на углах, и краска не сотрется.

А если в процессе установки межкомнатной арки потребуется штукатурка угла из ДСП или гипсокартона, то алюминиевый уголок позволит вывести 90 градусов. Любой домашний угол подвергается внешнему влиянию, особенно это касается арочных проемов – перестановка мебели или обычная субботняя уборка может его повредить. Решение есть – приклеить декоративный уголок.

Благодаря перфорации уголком можно обрамлять не только четкие линии, его можно загибать и выводить различные формы. Мягкий изогнутый элемент предоставляет возможность оформить не только квадратные или закругленные арки в классическом стиле, но и выводить полуарки, а также проемы с нестандартными изгибами. Уголки для арки отличаются такими преимуществами:

Доступная цена.
Практичен – допускается использование в большинстве интерьерных решений.
Финишный – производится в широкой цветовой гамме.
Установить декоративные элементы не составит труда.

Перфорированный арочный профиль

Гибкий угловой профиль под штукатурку может быть изготовлен из металла, пластика или пробки. Свое название перфорированный арочный уголок получил из-за отверстий, которые расположены по всей его поверхности. С одной стороны, изделие оснащается надрезами, которые напоминают лепестки и придают ему Г-образную форму. Перфорированная поверхность позволяет в процессе штукатурных работ получить ровную красивую грань на самых неровных и криволинейных участках арочного проема.

Необходимый инструмент

Жидкие гвозди
Пластиковый уголок для межкомнатной арки нужно правильно закрепить. Для этого заранее подготавливается перечень таких инструментов:

Пластмассовый элемент под стиль помещения.
Монтажный клей.
Прикрепить элемент помогут жидкие гвозди.
Резиновый молоточек.

Приделать согнутый уголок лучше всего с помощью монтажного клея или жидких гвоздей, так как монтаж при помощи металлических гвоздиков или саморезов смотрится нелепо, а также увеличивает шансы на появление трещин и сколов.

Гипсокартон относится к самым распространенным материалам для создания межкомнатных порталов. Он легкий, крепится на каркас и дает возможность выводить внутренний и наружный радиусный угол. Так как материал требует последующей облицовки, для простоты оформления используют уголки. Клей для укладки – шпатлевка.

Гибкие материалы: Купить Ленту ППЭ, Уплотнительную Самоклеющуюся, Межвенцовый Уплотнитель для Пластиковых Окон (ПВХ), Сэндвич-панелей, Вентиляции в Москве || Гибкий самоклеющаяся лента

Монтаж декоративных уголков

Любая квартира будет смотреться намного эффектнее, если в ней окантовка существующих арок будет оформлена с помощью пластиковых уголков. Поэтому давайте рассмотрим, как приклеить пластиковый уголок на межкомнатную арку и сделать обрамление долговечным и надежным.

Бывают две необходимости использовать пвх деталь: наклеить и вывести прямой угол или же оклеить дугу. Условие для оформления прямых углов:

Обработка поверхности проникающим раствором грунтовки.
При помощи угольника провести разметку, поставить отметку и отрезать нужный размер болгаркой.
Нанести клеевую смесь на две внутренние плоскости элемента.
Приложить полосу, мягко прижимая его по всей длине.

Сперва следует выровнять поверхность проема
Гибкий уголок для дугообразной арки фиксируется немного иным способом. Фото и видео помогут новичкам разобраться в различиях и особенностях монтажа. Самостоятельно сделать укладку такого элемента будет не тяжелее предыдущего варианта, но обратите внимание на такие нюансы:

Ширина сторон уголка при отделке дуги разнится. Укладка широкой стороны происходит на торцовый угол арки, а узкая сторона прижимается к стене.
Силиконовый герметик или клеевой раствор наносится на элемент, как и в первом случае.
Крепить нужно при помощи нескольких гвоздей – необходимая мера, так как горячий раствор должен полностью схватиться.
Вместо гвоздей разрешено использовать малярную ленту – ею фиксируется край пластикового уголка.

Поклейка декоративного уголка
Уголки для межкомнатных арок на обои клеить просто. Отделочный материал быстро схватывается с клеем и позволяет уже на следующий день испытывать себя на прочность. А вот если вам захотелось обклеить арку уголком из МДФ, то воспользуйтесь такими советами:

Эта разновидность не требует дополнительной фиксации, но нанеся клей на уголок и прижав его к поверхности следует выдержать пару секунд, а затем снова отклеить элемент.
Дождавшись, когда клей загустеет можно смело возвращать его на место. Обычно хватает 1-2 минут.

Деревянный уголок лучше использовать для арочных проемов из такого-же материала. Согнуть его трудно, поэтому поклеить можно на прямые плоскости. Идеальное использование – прямоугольные порталы, где круглый элемент отсутствует.

Приклеить пластиковый уголок к арке
Обшить арку также допускается при помощи обычных пластиковых уголков, но в этом случае эластичный порог будет намного меньше. Чтоб без повреждений изделия выгнуть его до нужного размера, следует нагреть материал строительным феном.

Гибкие материалы: Гибкая подводка для воды. Выбор и монтаж гибкой подводки

Для декоративного оформления арок и стен используется полиуретан и пенополиуретан – в этом случае все поверхности должны быть ровными. Если имеются небольшие перепады, то склеивать элементы нужно аккуратно прижимая и увеличивая количество клея в данных местах.

Порядок приклеивания арочного уголка из пластика на клей

Подготовка поверхности. Важно отметить, что нельзя клеить накладки из пластика на обои. Если рабочая поверхность обклеена обоями, их нужно обязательно удалить. Лишние обои удаляют с помощью острого канцелярского ножа.
После того как удалена вся грязь, пыль и старые обои, производится грунтовка поверхности. Процесс приклеивания должен производиться не ранее, чем через 30-40 минут.
Клей наносят на изделие, равномерно его распределяют по поверхности тонким слоем.
Профиль прикладывают к месту, где он должен находиться согласно замыслам дизайнера.
Для лучшего схватывания с поверхностью уголок нужно слегка подвигать, чтобы нанесенный клей равномерно распределился по его поверхности.
Затем уголок нужно убрать и подождать пять минут, а потом снова приложить и уже окончательно приклеить и зафиксировать малярным скотчем.
После того, как клей полностью высох, липкую фиксирующую ленту можно снять.

Крепление отделочного уголка на гипсокартон и другие поверхности

Первое, что следует сделать — очистить от грязи и пыли арку. Перед самым началом установки отделки следует обезжирить место крепления специальными составами. Эти работы необходимы для того, чтобы монтаж получился надежным.

Если проем просто покрыть слоем штукатурки, то необходимо следить за тем, чтобы во время работ он не осыпался. Трещины на нем должны отсутствовать, а сама штукатурка должна быть гладкой. Если имеются какие-либо дефекты — сколы и трещины, то в этом случае необходимо удалить нарушенный слой, а потом наложить новый.

Для крепления отделки используют специальный клеевой состав. Или же могут применяться жидкие гвозди. Материал наносится на внутреннюю часть уголка. Так как он будет выступать еще и украшением интерьера, то подбирать его цвет нужно на тон светлее или темнее преобладающего в помещении отделки. В этом случае будет создаваться определенный контраст. Оформленный таким образом проем, приобретет оригинальный вид.

Теперь стоит отдельно поговорить об установке отделочных материалов из пластика и пробки для имеющихся в помещении декоративных объемных конструкций.

Особенности монтажа: как и чем клеить арочный уголок

При покупке арочных уголков, лучше взять больше материала, чтобы не возникло погрешностей в работе. Для этого нужно измерить общую длину арки и добавить еще 10% для запаса. Если вес конструкции небольшой, то чтобы приклеить пластиковые арочные уголки, можно воспользоваться жидкими гвоздями. Если же предполагается более громоздкая и тяжелая отделка арочного проема, то лучше использовать специальный клей.

Клей для арочного уголка выбирается в зависимости от его цвета: белые элементы лучше клеить на белый клей, а для цветных использовать бесцветный. Перфорированные уголки крепятся при помощи скоб, саморезов, гвоздиков без шляпок или их можно приклеить на шпаклевку. Если планируется клеить пробковые уголки, то нужно использовать специальный клей для пробки. Клеить уголки в проем – несложный процесс и не требует особых навыков.

( 2 оценки, среднее 4.5 из 5 )

Источник

Арка — архитектурный элемент, криволинейное перекрытие сквозного или глухого проёма в стене или пролёта между двумя опорами (колоннами, устоями моста). Как и любая сводчатая конструкция, создаёт боковой распор. Как правило, арки симметричны относительно вертикальной оси.

Арки впервые появились во II тысячелетии до н. э. в архитектуре Древнего Востока, в частности в Древней Месопотамии, где строительство кирпичных сооружений достигло высокого уровня. Широкое распространение также получили арки в архитектуре Древнего Рима.

В настоящее время арки применяются в павильонах, крытых рынках, ангарах, спортивных залах и т.п. большепролетных сооружениях. По затрате металла арки оказываются значительно выгоднее, чем балочные и рамные системы. Кроме того арки просты в изготовлении и монтаже.

Механика

Арка — это криволинейный брус плавного обриса, несущая строительная конструкция. В отличие от балки которая испытывает нормальное механическое напряжение, арка испытывает касательное механическое напряжение, из-за чего возникает горизонтальная опорная реакция (распор). От свода арка отличается лишь значительно меньшей шириной. Под вертикальной нагрузкой арка работает в большей степени на сжатие и в меньшей степени на изгиб.

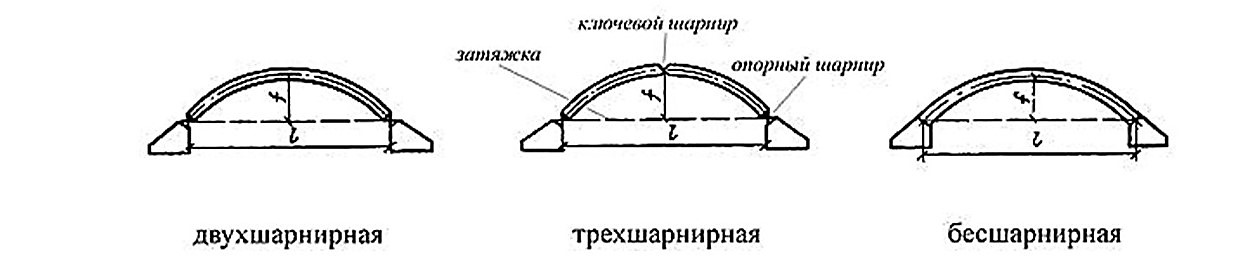
Арки бывают бесшарнирные, двухшарнирные и трёхшарнирные; если опорные концы арки соединить стержнем (затяжкой, которая воспринимает горизонтальную реакцию), то получается арка с затяжкой.

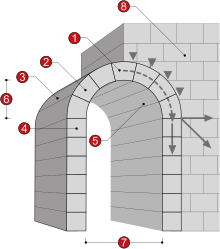
Арка из каменной кладки: 1. Замковый камень 2. Клинчатый камень 3. Внешняя поверхность свода (экстрадос) 4. Пятовый камень (импост) 5. Внутренний свод (интрадос) 6. Стрела подъёма 7. Пролёт 8. Опорная стена

Названия частей арки

Замковый камень — поперечное сечение около вершины
Клинчатый камень
Внешняя поверхность свода (экстрадос)
Пятовый камень (импост) — поперечное сечение около опоры, пята арки
Внутренний свод (интрадос)
Стрела подъёма — расстояние центра замкового камня арки от линии, которая соединяет центры двух пятовых камней арки
Пролёт
Опорная стена

Расстояние между центрами пят называется расчётной проймой. При увеличении стрелы подъёма уменьшается распор арки. Ось арки подбирают так, чтобы сжатие на изгиб было минимальным; тогда арка будет наиболее крепкой и стойкой.

Крепость арки зависит от её формы. Простейшие арки имеют форму полукруга, однако теоретически наиболее крепкими являются арки с формой параболы или цепной линии. Параболические арки впервые использовал испанский архитектор Антонио Гауди. Такие арки передают весь распор на опорную стену и не требуют дополнительных элементов.

Арки, перекрывающие несквозной проем, называются слепыми. Одной из целей этого является увеличение прочности стены при экономии материала. В древности известен приём, когда арка делалась для облегчения, например, когда перекрытие проёма в стене было выполнено в виде плоской арки, для разгрузки которой над нею делалась слепая арка.

Кирпичная кладка стен во дворце Августов. Древний Рим. Использованы разгрузочные арки.

Типы арок


Треугольная	Плоская сжатая арка	Трёхлопастная арка

Подковообразная	Трёхцентровая арка	Эллиптическая арка

Вогнутая арка	Килевидная арка	Опрокинутая килевидная арка

Круглая или полуциркульная	Круглая пологая арка или сегментная	Ползучая или косая арка

Стрельчатая	Четырёхцентровая арка — «Тюдор»	Параболическая арка

По форме различают арки:

аравийская — имеет повышенный центр построения, была распространена в зодчестве народов востока, в испано-мавританской архитектуре.
аркбутан — арка с пятами на разных уровнях, наклонно передающая распор свода на внешнюю опору.
вогнутая — перекрытая двумя дугами, обращёнными выпуклыми сторонами в пролёт.
двулопастная — сложенная из двух малых арок одинаковых размеров, импосты и соединения которых расположены на одном уровне.
двуцентровая — дуга, образованная из двух дуг одного и того же радиуса, пересекающихся в замке под тупым углом.
диагональная — расположена в крестовом своде по диагонали квадрата или прямоугольника, то есть Нервюра, которую называют «ожива».
эллиптичная — образована в пересечении частью эллипса.
заплечная — устроенная над углублением в стене, тип круглой арки.
обратная — с обращенной вниз выпуклостью дуги.
зубчатая — с равномерным расположением по внутренней поверхности остроконечных выступов.
килеподобная (килевидная или «ослиный хребет») — имеет вид поперечного разреза опрокинутого килевого судна, нашла применение в русском зодчестве.
клинчатая — выложенная их клинчатых камней или из прямоугольных камней с клинчатыми швами.
косая — см. ползучая.
коробовая или эллиптическая — дуга, описанная из трёх, пяти, семи центров. Разновидностью её является седловидная арка.
круговая (стиснутая) — описана полукругом из центра, расположенного ниже пят.
угловая — то же самое, что и митровая.
ланцетоподобная (копьеподобная) — образована двумя дугами, которые соединяются под углом и имеет формы стрельчатой равносторонней, стрельчатой стиснутой, стрельчатой плоской.
ломаная — см. стрельчатая.
лучковая (круговая) — с дугой менее полуокружности (одноцентровая).
мавританская — то же самое, что и аравийская
митровая — с двумя симметричными спадами в завершении.
многолопастная — вид арки, составленной из трёх или большего числа кривых, пересекающихся под острым углом.
овальная — образует в своде часть овала.
выпукло-вогнутая — выгибы у пят обращены выпуклыми сторонами в середину пролёта и плавно переходят в одноцентровой или многоцентровой подъём по вертикальной оси.
параболическая — образует в своде часть параболы.
опрокинутая — такая, в которой замок находится ниже пят. Выполняет функции разгрузочной и устраивается в нижней части стены.
перспективная — концентрическая, уходящая внутрь стены уступами уменьшающихся радиусов, находит применение при оформлении порталов.
полуциркульная или полукруглая — её дуга описана полуокружностью; наиболее распространённый вид арки.
подвесная — состоит из двух дуг, точка пересечения которых расположена ниже вершины арки.
подковообразная — то же самое, что аравийская.
сводная — то же самое, что ланцетоподобная.
стрельчатая — состоит из двух дуг, пересекающихся в замке под острым углом. Получила широкое применение в готической архитектуре. Различают стрельчатую арку, сжатую и ланцетовидную.
плоская — со стрелой подъёма в несколько раз меньше пролёта.
ползучая или «кобылья голова» — арка, имеющая опоры (пяты) на различных уровнях, например, под маршами лестниц.
подпружная — вспомогательная арка, укрепляющая или поддерживающая различные конструкции сводов.
портьерная — образована двумя или четырьмя дугами с центрами за пределами пролёта.
притупленная — пологая стрельчатая с округлениями в пятах.
пятилистная — навершие окна в виде пятилистника.
разгрузочная — арка, заделанная в стене и распределяющая нагрузку от верхних частей здания на опоры, или наоборот, от отдельных опор на стенку фундамента.
сжатая (лежачая) — завершенная горизонтальной перемычкой.
скамеечка — беседка в виде триумфальной арки со сквозными решетчатыми стенками, к которым примыкают сиденья.
ступенчатая — система арок в виде нескольких ярусов закомар.
трёхлопастная — образована тремя полуокружностями, причём приподнятое среднее опирается на концы боковых, которые зеркально повторяют друг друга.
трёхцентровая — полуовальная в разрезе, состоит из дуг трёх окружностей, из которых наибольшее среднее построенное радиусом из центра на оси пролёта. Две другие дуги прокладываются радиусами из точек, что находятся значительно выше.
«тюдор» — пологая с заострённым верхом.
воображаемая или фальшивая — арка, не дающая горизонтального распора, так как выложена путём горизонтального напуска камней.
царская — расположенная в Царских вратах иконостаса христианского храма.
щековая — подпружная крестового свода, расположена по бокам прямоугольника его плана. Окружает свод перпендикулярно к его образующей.
упорная — см. аркбутан.

Арки возводятся также в виде отдельных сооружений:

мемориальная — сооруженная в память о важном событии или исторической личности.
триумфальная — подробнее см. триумфальная арка.

Полуциркульная (полукруглая) арка — арка, имеющая форму полуокружности, центр которой расположен на уровне пят арки.

Простейший и наиболее распространённый тип арки. Присутствует в зодчестве разных эпох, стран и стилей. Наиболее характерна для классической архитектуры, где она чаще всего бывает обрамлена архивольтом (от лат. arcus volutus — «обрамляющая дуга») или выделена рядом клинчатых камней с замковым камнем посередине. Обычно опирается на пилоны.

Лучковая арка — арка, имеющая форму дуги примерно в четверть окружности. В Древнем Риме арки такой формы служили перемычкой оконных проемов в жилых зданиях. Типичным примером применения лучковой арки является сегментный арочный мост.


Римский мост с полуциркульными арками. Алькантара, Испания	Нюрнберг. Замок на воде Обербюрг. Ворота в виде двух лучковых арок	Собор Парижской Богоматери

Мясной мост в Нюрнберге	Большой Москворецкий мост в Москве

На Востоке полукруглая арка претерпела наиболее сильную трансформацию, превратившись в так называемую стрельчатую, или ломаную арку, дуги которой пересекаются под углом.

По форме различают несколько видов стрельчатых арок:

равносторонние арки, центры дуг которых находятся в пятах арок;
сжатые арки, центры дуг которых находятся на горизонтальной линии, проходящей через пяты арок;
плоские арки, центры дуг которых находятся ниже пят арок.

Природная арка. Формы в виде арки являются весьма частыми в природе, являясь лишь малой частью криволинейных объектов и поверхностей, что свойственны природным объектам. Они могут быть из камня, изо льда, из дерева. Арочные формы в природе повлияли, скорее всего, на применение их человеком в строительных конструкциях. Являясь зачастую проходом из одного места в другое, они стали нести и сакральный смысл, символизируя своеобразный портал в то место, где возможно ожидать чего-то нового и ранее неизведанного. Являясь продуктом эрозии, арочные каменные конструкции играют незначительную роль в горообразовании, изучение их позволяет получить дополнительную информацию о происходивших на земле процессах.

Иногда природные арочные образования служат в качестве реальных конструкций, так как по ним могут быть проложены действующие дороги. Примеры подобных арок можно найти в природных парках Carter Caves State Resort Park и Natural Bridge State Resort Park в Кентукки.

Согласно классификации национального парка Арчес (штат Юта, США), каменный проём должен иметь ширину не менее 3 футов (0,914 метра) и располагаться в достаточно большой стене, чтобы считаться аркой. При этом арки через естественные водотоки, а также через пересохшие русла, называются природными мостами. Отверстия в скалах, расположенные достаточно далеко от краёв и не влияющие на форму скалы, арками не считаются.

Расчёт арок

В основе расчёта арочных конструкций лежит расчёт кривого стержня, элемента отличного от прямой балки, у него ось представляет собой тот или иной тип кривой линии (ось — линия, проходящая через центры тяжести поперечных сечений элемента). С допустимым приближением касательные напряжения от поперечной силы для кривых стержней можно определять по той же формуле Журавского, что и для прямых балок:

${displaystyle tau ={frac {QS(z)}{J_{x}b}}}$

где

Соответственно, условие прочности по касательным напряжениям для кривых стержней будет представляться следующим образом:

${displaystyle tau _{max}={frac {Q_{max}S_{max}}{Jb}}leq |tau |}$

Напряжения в кривом стержне, вызываемые нормальной силой, нормальны к сечению и равномерно распределены по его площади, то есть:

${displaystyle sigma ={frac {N}{F}}}$

где

Гиперболический закон распределения нормальных напряжений в криволинейном стержне от действия момента

Изгибающий момент, как и в прямой балке, вызывает в кривом стержне только нормальные напряжения. Распределение их по высоте сечения определяется следующей формулой:

${displaystyle sigma ={frac {z}{rho }}{frac {delta dvarphi }{dvarphi }}E}$

где

Получается, что в отличие от прямой балки, где напряжения распределяются по линейному закону, в криволинейном стержне нормальные напряжения от момента распределяются по гиперболическомузакону. Из этого следует несколько важных выводов, а именно: при изгибе кривого стержня нейтральная ось не проходит через центр тяжести сечения; напряжения в наружных волокнах элемента меньше, чем при таком же изгибе прямой балки, а во внутренних волокнах — больше; рост напряжений по высоте сечения происходит с разной скоростью. Наибольшей величины напряжения достигают с внутренней стороны. Однако они достаточно быстро убывают по глубине. Если конструкция работает в статическом режиме и сделана из пластичных материалов, не подверженных хрупкому разрушению, то перенапряжения на самом краю сечения с внутренней стороны могут не представлять опасности.

Формула нормальных напряжений от момента будет иметь вид:

${displaystyle sigma ={frac {M}{S}}cdot {frac {z}{rho }}}$

а формула полных нормальных напряжений в кривом стержне:

${displaystyle sigma ={frac {N}{F}}+{frac {M}{S}}cdot {frac {z}{rho }}}$

Радиус кривизны нейтрального слоя определяется из уравнения:

${displaystyle r={frac {F}{int limits _{F}{frac {dF}{rho }}}}}$

Из формул следует, что чем меньше отношение радиуса кривизны стержня к высоте его сечения, тем больше работа кривого стержня отличается от работы прямой балки. Когда же радиус оси намного превосходит размеры сечения, работа кривого стержня похожа на работу прямой балки и нормальные напряжения в этих случаях будут почти равны. Чаще всего арки в строительных конструкциях относятся ко второй категории кривых стержней. К первой же можно отнести разнообразные криволинейные детали: крюки, звенья цепей, колец и пр^[1].

Деформации, возникающие в кривых стержнях, в общем случае определяются следующими выражениями:

${displaystyle {begin{matrix}f=int limits _{S}{frac {MdS}{EJ}}cdot {frac {delta M}{delta P}}+int limits _{S}{frac {NdS}{EF}}cdot {frac {delta N}{delta P}}\theta =int limits _{S}{frac {MdS}{EJ}}cdot {frac {delta M}{delta M_{0}}}+int limits _{S}{frac {NdS}{EF}}cdot {frac {delta N}{delta M_{0}}}end{matrix}}{Bigg }}}$

где

В большинстве случаев, однако, влиянием кривизны для определения деформаций можно пренебречь.

Очертание оси арки может быть самым разнообразным, но чаще встречаются следующие виды:

Очертания осей арок


Циркульная (круговая)	Параболическая	Коробовая

Треугольная	«Ползучая»

Наиболее распространёнными являются следующие типы расчётных схем арок:

Типы арок по статической работе

Трёхшарнирная арка	Двухшарнирная арка	Бесшарнирная арка

Каждый из типов имеет свои преимущества и недостатки, и выбор той или иной конструкции определяется инженером-проектировщиком исходя как из прочностных требований, так и из необходимости применения тех или иных материалов для арки, архитектурных задач, стоимости и местных условий строительства. Так, например, трёхшарнирная арка является статически определимой системой, в силу чего подобная конструкция не так чувствительна к температурным воздействиям и осадкам опор. Также трёхшарнирные арочные конструкции удобны с точки зрения монтажных работ и транспортировки, так как состоят из двух отдельных частей.

Однако наличие дополнительного шарнира приводит к большой разнице моментов по длине обоих частей, что, соответственно, требует дополнительного расхода материала. Противоположна ей в этом плане бесшарнирная арка, которая благодаря защемлению пят арок в опорах имеет наиболее благоприятное распределение моментов по длине и может быть изготовлена с минимальными сечениями. Но защемление в опорах, в свою очередь, приводит к необходимости устройства более мощных фундаментов, арка чувствительная как к перемещениям опор, так и к температурным напряжениям. Наибольшее распространение получила двухшарнирная арка. Являясь единожды статически неопределимой системой, она также имеет хорошее распределение моментов по длине и избавлена от необходимости устройства массивных опор.

Очертание арок выбирается близким к линии давления. При симметричной, равномерно распределенной по хорде арки нагрузке (в пологих арках ) наиболее выгодным является очертание арки по квадратной параболе. Параболу часто заменяют дугой окружности, что в пологих арках не приводит к существенному изменению усилий, но значительно упрощается проектирование и изготовление арок, поскольку при постоянной кривизне дуги достигается наибольшая стандартизация конструктивных элементов и узлов арки.

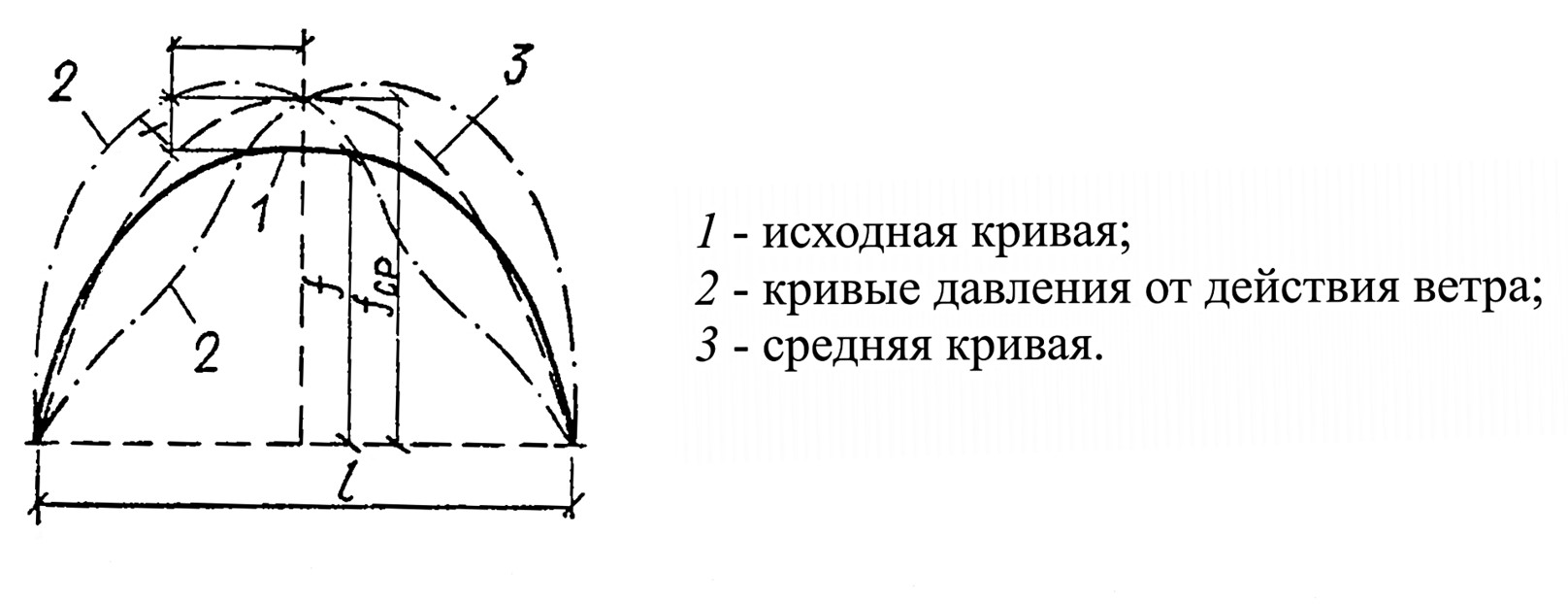
Для высоких арок с большим собственным весом целесообразно принимать очертание по цепной линии (катеноиду), Однако в высоких арках большие усилия вызывает ветровая нагрузка, которая может действовать с обеих сторон и давать две резко расходящиеся линии давления. В этом случае очертание арки целесообразно принимать по середине между двумя крайними линиями давления.

В многопролетных арках распоры смежных пролетов в значительной мере уравновешиваются, и средние опоры работают на изгиб только от односторонней временной вертикальной и ветровой нагрузок.

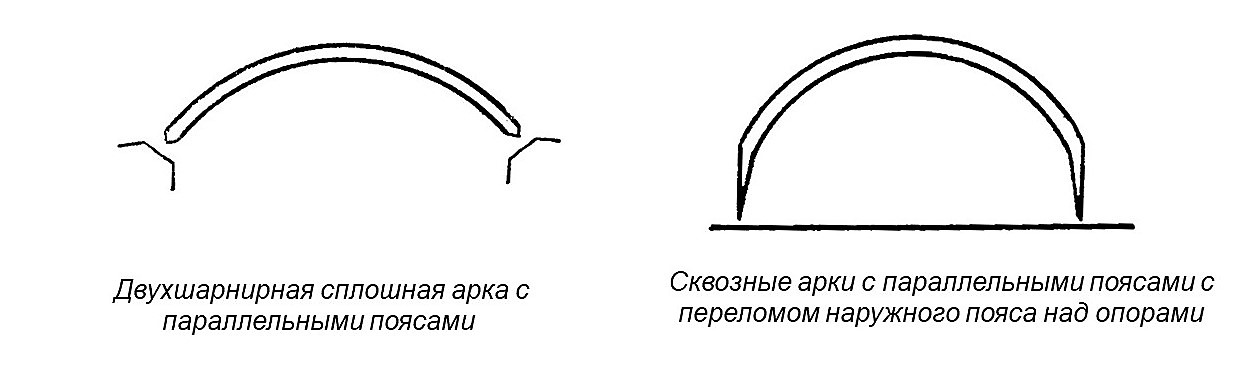
Двухшарнирные сплошные арки проектируют чаще всего с параллельными поясами.

Сквозные арки делают или с параллельными поясами или, при большой высоте арки, с переломом наружного пояса, который над опорами имеет вертикальные участки. Около опор пояса арок сближаются и заканчиваются опорным устройством – шарниром.

Высоту сечения сплошных арок назначают в пределах (1/50÷1/80) пролета, сквозных – в пределах (1/30÷1/60) пролета. Возможность применения в арках небольшой высоты сечения объясняется малой величиной изгибающих моментов.

Сплошные арки проектируются сварными с сечением в виде широкополочного двутавра (как и в сплошных рамах), в пологих арках продольные силы велики, поэтому стенку поперечного сечения арки можно назначать большей толщины, чем в раме.

Сквозные арки проектируются аналогично легким фермам. Пояса их компонуются из двух уголков или из двух легких швеллеров.

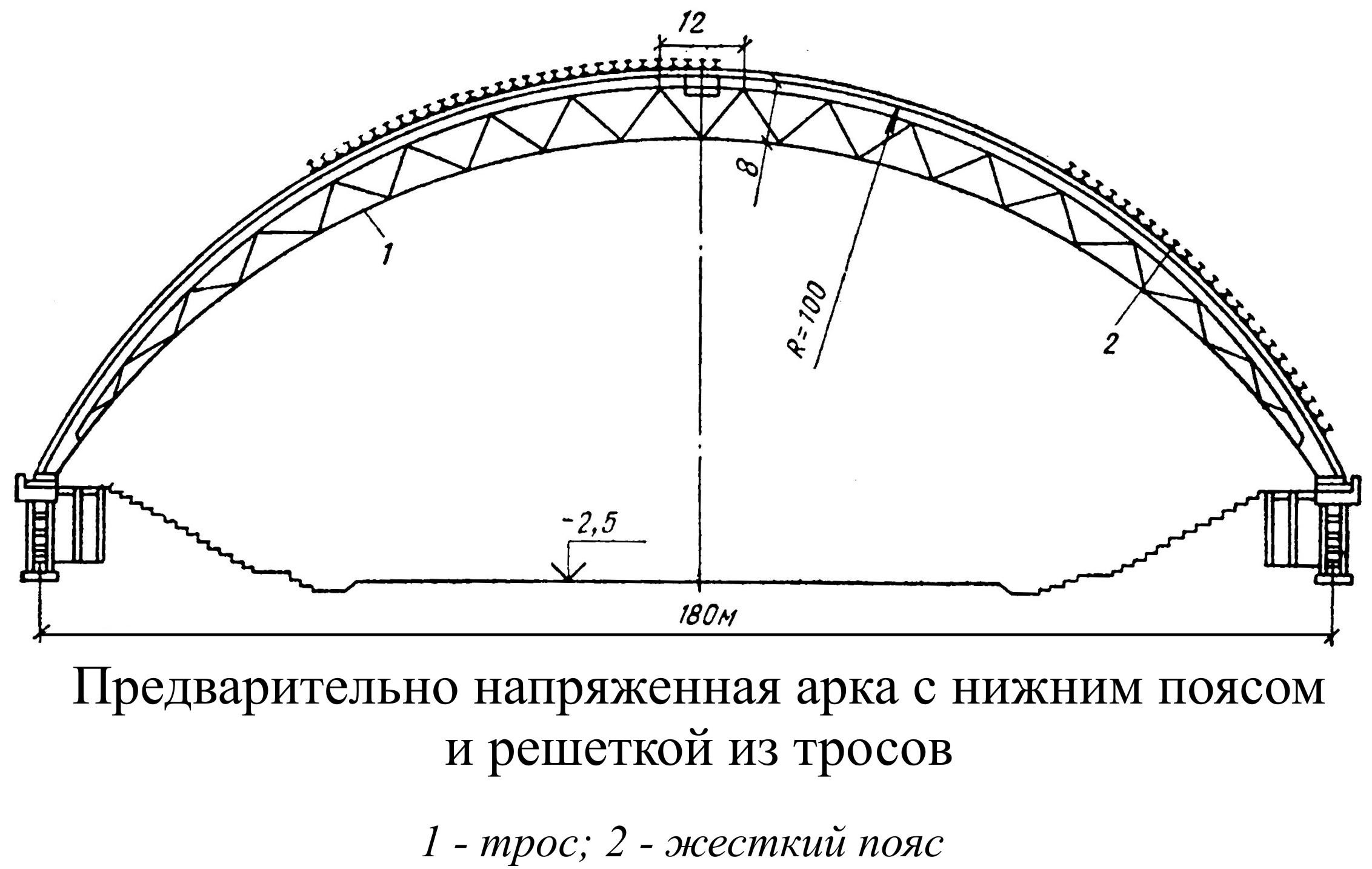
При больших усилиях применяются двухстенчатые сечения. Если кривая давления не выходит за пределы высоты сечения, то оба пояса оказываются сжатыми и тогда особое внимание необходимо обратить на обеспечение устойчивости. Сечения элементов, поскольку поперечная сила мала, подбирают по гибкости из уголков или из небольших швеллеров. Криволинейное очертание сплошных арок усложняет их изготовление.

Сквозные арки в целях упрощения изготовления могут иметь ломаное очертание. В арках применяется также предварительное напряжение или регулирование усилий.

Одним из приемов рационального распределения усилий является принудительное смещение опорных узлов наружу после установки арки на опоры. При этом в нижнем поясе и раскосах арки возникает растягивающие напряжения, которые могут быть достаточными для погашения сжимающих напряжений от внешней нагрузки. В этом случае нижний пояс и решетка арки могут быть выполнены из стальных канатов, а верхний пояс – жестким.

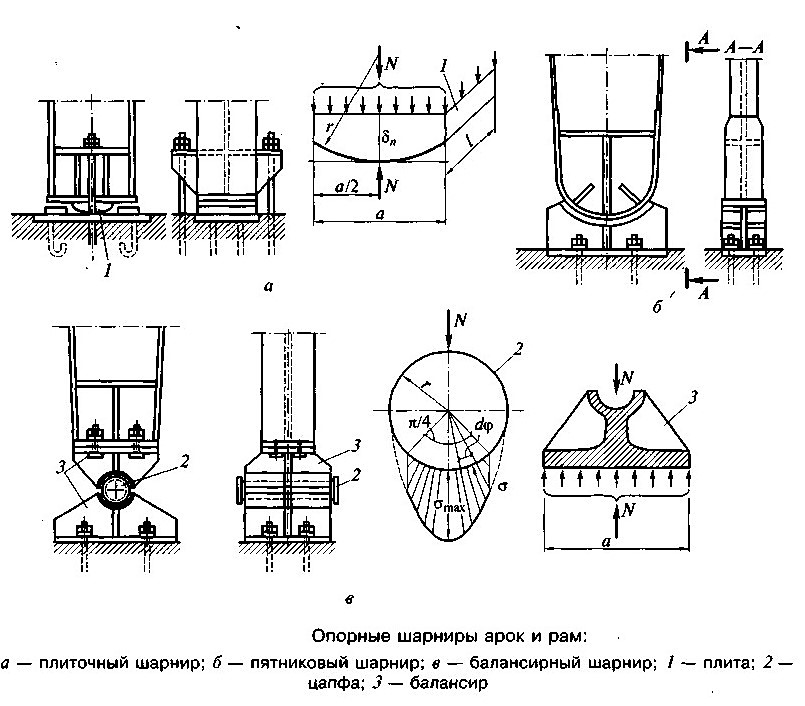
Наиболее сложными конструктивными узлами в арках, так же как и в рамах, являются опорные и ключевые шарниры.

Опорные шарниры могут быть трех типов: плиточные, пятниковые и балансирные.

Плиточные шарниры имеют наиболее простую конструкцию. Применяются они при сравнительно небольших опорных давлениях и преимущественно при вертикальном положении примыкающей к шарниру части арки.

Пятниковые шарниры имеют специальное опорное гнездо – пятник, в который вставляется закругленная опорная часть арки. Пятник делают литым или сварным из листовой стали.

Балансирные шарниры применяют в тяжелых арках. Конструкция шарнира состоит из верхнего и нижнего балансиров, в гнезда которых укладывают плотно пригнанную цилиндрическую цапфу. Арку крепят к верхнему балансиру через плиту, которую приваривают к контуру опорного сечения арки и притягивают болтами к балансиру. Торцы опорных сечений арки обычно фрезеруют.

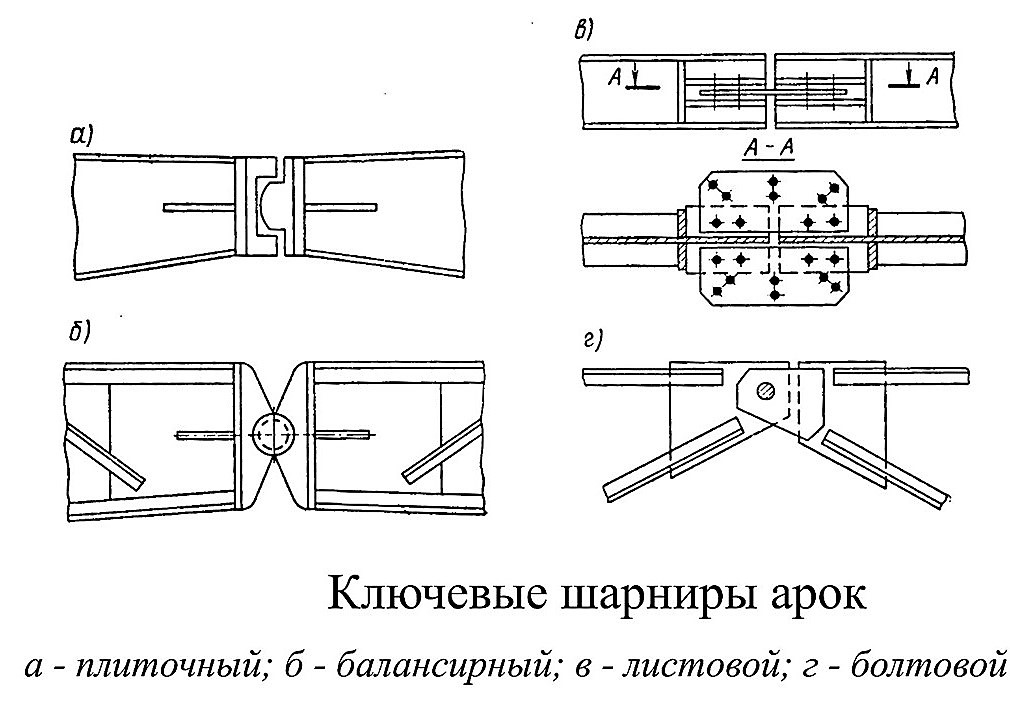
Для восприятия отрицательных реакций от действия ветра может появиться необходимость крепления легких и высоких арок к опорам анкерными болтами. Анкерные болты следует располагать по оси арки, чтобы они не мешали свободному повороту конструкции в опорных шарнирах, закрепляют анкеры в консолях, приваренных к стенке арки (см. плиточный шарнир).

В ключе арки также могут быть применены плиточные или балансирные шарниры, которые проектируются аналогично опорным. В ключе легких арок могут применяться листовые или болтовые шарниры.

Арочные конструкции рассчитывают на вертикальные (собственный вес, снег) и ветровые нагрузки. Температурные воздействия для арок обычно несущественны. Вертикальные нагрузки относят к основным сочетаниям нагрузок, ветровые и температурные воздействия – к дополнительным, величина которых при определении расчетного усилия принимается с коэффициентом сочетания n_c= 0,9.

Существенной нагрузкой для арочных конструкций является давление ветра. Ветровая нагрузка для арочных покрытий, не имеющих стен, принимается по упрощенной схеме.

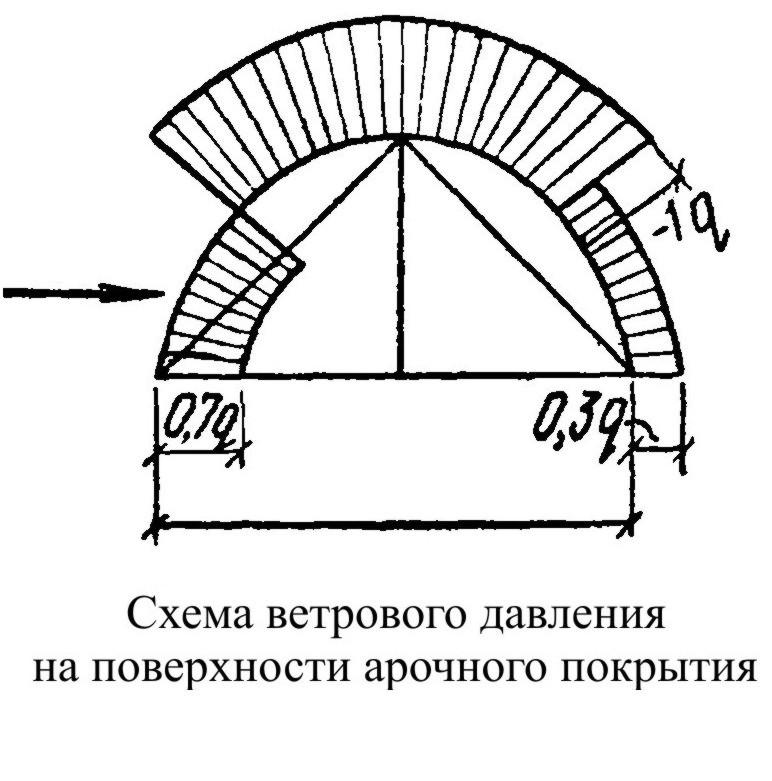
Расчетный коэффициент обтекания имеет положительное значение только в первой четверти дуги арки с наветренной стороны; в средней части дуги коэффициент обтекания имеет max по абсолютной величине отрицательное значение (отсос) и в последней четверти величина его резко падает, сохраняя отрицательное значение.

Ветровое давление считается приложенным нормально к поверхности арочного покрытия. Отрицательные ветровые усилия в высоких арках при малом собственном весе арки могут вызвать отрицательные опорные реакции.

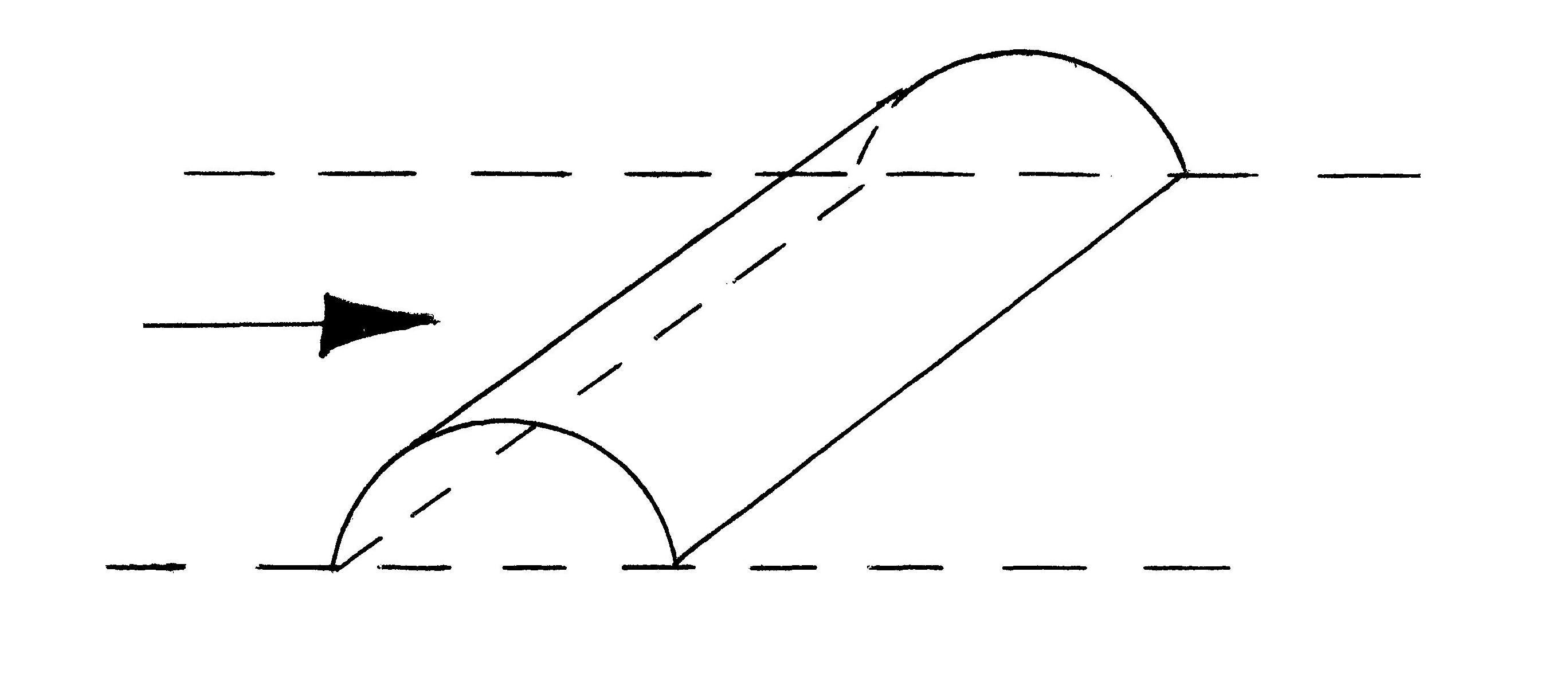
На величину ветрового давления существенное влияние оказывают открытые проемы. При открытых торцах арочных покрытий ветер направленный параллельно торцам, обтекает сооружение с двух сторон, и внутри образуется вакуум, увеличивающий положительное давление на арки и уменьшающий отсос.

Для покрытий, торцы которых могут быть открытыми (навесы, вокзальные перекрытия и т.п.) необходимо учитывать возможные комбинации трех видов ветровых нагрузок:

бокового или торцового давления ветра на сооружение;
вакуума, создаваемого вследствие отсоса воздуха из-под арочного покрытия;
действия ветра внутри сооружения, который попадает под покрытие через широкие проемы и создает отрицательное давление.

Последние два вида нагрузок не нормированы и устанавливаются специальными техническими условиями для данного сооружения или на основе аэродинамических испытаний на моделях.

Конструкции арочных покрытий при расчете расчленяют на отдельные элементы (арки, прогоны и т.п.) и рассчитывают методами строительной механики (определяют M, Q, N).

Сечения стержней сквозных арок подбирают так же, как сечения стержней ферм. Арка как криволинейный сжатый брус требует проверки устойчивости.

Схема определения усилий в арке

При использовании арок в качестве перекрытий, они рассчитываются в общем случае на равномерно распределённую нагрузку (нагрузка от вышележащих конструкций перекрытий, снеговая нагрузка, нагрузка от собственного веса арки). В ходе расчета строятся эпюры усилий, возникающих в сечениях арки, по которым определяются наиболее опасные сечения. Формулы для определения усилий в каком-либо сечении арки следующие:

1. Изгибающий момент

${displaystyle M_{x}=M_{x}=M_{o}p+{M_{x}}^{b}-F_{h}y}$

где

Распор определяется из выражения:

${displaystyle F_{h}=k{M_{c}}^{b}/f}$

где

2. Продольная сила

${displaystyle N_{x}=-{Q_{x}}^{b}sin varphi -F_{h}cos varphi }$

где

3. Поперечная сила

${displaystyle Q_{x}={Q_{x}}^{b}cos varphi -F_{h}sin varphi }$

Литература

Арка // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
АРКА — Термины на А, — терминология и типы арок.
Арка — статья в Большой советской энциклопедии.
Ю.М.Даниловский. МУ по расчету трехшарнирных арок – Хабаровск: Изд-во Хабар. гос. техн. ун-та, 2004. — 21 с.
Деревянные конструкции. Круговая и стрельчатая клееные арки. Конструирование и расчет: / Г.Н.Шмелёв.– Казань: Изд-тво Казанск. гос. архитект.-строит. ун-та, 2016. – 124 с.
Манжосов, В. К. Расчет трехшарнирных арок : методические указания. – Ульяновск : УлГТУ, 2010. – 36 с.
Арочные конструкции
2-х шарнирная рама с ригелем в виде клеефанерной балки
Расчёт трёхшарнирной арки на статическую нагрузку

Источник

Внешний угол треугольника

Сумма внешних углов

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

∠1 + ∠4 = 180°.

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

∠2 + ∠3 + ∠4 = 180°.

Из этого следует, что

∠1 + ∠4 = ∠2 + ∠3 + ∠4.

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

∠1 = ∠2 + ∠3.

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.

Источник

Оклеенные обоями и зашпаклеванные наружные углы нуждаются в защите. Обои от частого контакта затираются, шпаклевка разрушается. Решить проблему можно при помощи декоративных уголков. Уголки для защиты углов стен могут быть из разных материалов.

Содержание статьи

1 Уголки для защиты углов стен: варианты подбора
2 Виды защитных уголков: из каких материалов
3 Формы и размеры
4 На что крепить
5 Отделка арки
6 Чем резать отделочные уголки

Уголки для защиты углов стен: варианты подбора

Этот прием оформления углов стен — защитные уголки — нравятся не все, но особых альтернатив нет. Во всяком случае на стенах оклеенных обоями, уголок все-таки лучше торчащих и порванных полотен.

Доступно только одно решение целостности обоев без использования декоративных уголков — сделать не острый угол откоса, а округлый. В таком случае не будет проблемы с его отделкой. Можно будет просто завернуть полотно обоев, не обрезая его. Но вывести угол надо идеально, иначе снова придется резать, а, значит, опять встанет вопрос о защите стыка обоев на углу.

Важно правильно подобрать декоративный уголок, чтобы он не смотрелся чужеродным. Для этого есть специальные приемы.

Интерьер в соответствующем стиле выглядит неплохо

Подобрать уголки для защиты углов стен надо исходя из общего оформления помещения. Есть несколько стандартных решений:

В тон с отделкой стен. Желательно полное совпадение цвета, а еще лучше, если и фактура будет похожей.

Либо в тон с отделкой стен, либо в тон с дверьми
В тон с дверьми. Материал лучше выбрать тот же — дерево, МДФ. И окраску подобрать один в один. Этот прием часто используют в прихожих и коридорах, куда выходит много дверей. В комнатах более уместно подбирать в тон стен.
В том с плинтусами.

Один из вариантов, вполне логичный
Использовать один из дополнительных цветов (про сочетание цветов в интерьере читайте тут), которые будут не только на углах, но и в обрамлении картин или в обивке панелей, декоративных медальонах и т.д.
Одного цвета и фактуры с напольным покрытием.

В общем, подбирать уголки для защиты углов стен надо привязываясь к оформлению комнаты. Сделать это можно уже после того, как будет расставлена мебель и развешен текстиль. В таком случае проще представить конечный результат. Потому что картинка у нас в голове может сильно отличаться от действительности.

Один из прозрачных защитных уголков

Если вам ну никак не удается подобрать приемлемый цвет, а углы в квартире защитить надо, обратите внимание на прозрачные пластиковые уголки. Они есть разных видов — жесткие, гибкие, с разной толщиной стенки.

Виды защитных уголков: из каких материалов

По области применения уголки бывают для внешнего (на улице) и внутреннего использования. Пока поговорим о том, как защитить углы в квартире и доме — в помещениях. Начнем с материалов. Уголки для защиты углов стен могут быть:

Из пластика (ПВХ). Разные цвета, фактуры, есть даже прозрачные.
Из металла. Латунные, алюминиевые (полированные и нет), из нержавеющей стали, с окраской и без.
Деревянные. Из разных сортов древесины, гладкие, с рельефом.

Угол на арке оклеен гибким пластиковым уголком
МДФ. С имитацией различных сортов древесины, гладкоокрашенные, с различными рисунками.
Из пробки. Может быть интересным ходом, если добавить отделку из пробки не только на углах.

Пробковые уголки для защиты углов
Резиновые. Обычно применяются в больницах или детских садах. Отлично защитят углы в гараже.
Вспененный каучук. То же что и резиновые, но более мягкие. Подойдет для защиты от травм слишком активных детей.
Декоративные — с резьбой, стразами, узорами и т.д.

Наиболее ходовые — пластиковые уголки для защиты углов стен. Не стоит думать, что смотрится такая защита убого. В любом случае не хуже, чем обтрепанные углы. Просто пластик есть по виду разный — полированный, с металлизированным эффектом, с сатинированной (матовой) поверхностью, с различным рельефом. Понятное дело, что для того, чтобы найти что-то определенное или особенное, придется побегать по строительным магазинам и рынкам. Но видов оформления немало. Если уголки для защиты углов стен подобраны правильно, они органично вписываются в оформление, абсолютно не привлекая внимание. При этом защищают и декорируют стыки очень надежно.

Формы и размеры

Готовые уголки имеют, как правило, угол в 90°. Сам угол не всегда острый, есть варианты со скругленным. По виду уголки для защиты углов стен разделяются на:

жесткие
- внешние;
- внутренние;
гибкие (пластиковые, резиновые)
универсальные.

Универсальный уголок из МДФ

Вопросы могут быть лишь по универсальным. Это две полосы пластика или МДФ, соединенные тонкой полоской гибкого материала того же цвета. Благодаря такому соединению, можно оформить тупой или острый угол, внутренний или внешний — без особой разницы. Но по надежности защиты он уступает жестким — все-таки гибкая часть довольно тонкая.

Также стоит знать, что уголки могут быть с полочками одинаковой и разной ширины. Чаще встречаются с одинаковыми, но вполне можно найти и такие, у которых одна шире, другая уже.

Виды, формы, размеры

Ширина полочки у разных производителей отличается. Пластиковые, например, могут иметь полочки от 10 мм до 50 мм. Уголки МДФ минимально делают с шириной полочки 20 мм, металлические — от 10 мм, но максимальная длинна полочки — 90 мм (алюминиевые). Так что выбрать есть из чего.

На что крепить

Выбор способа крепления уголков для защиты углов стен, зависит от материала уголка, от того, на какую поверхность их будут крепить. Чаще всего применяют клей. Причем в лидерах «жидкие гвозди». Это универсальный состав, но перед покупкой проверьте, чтобы конкретная марка могла склеивать нужные вам материалы.

На клей можно посадить уголок, если он ровный, без больших огрехов. Если же есть ямы/впадины, вряд ли его приклеишь. В этом случае можно использовать силикон. Если клеите белые уголки, силикон можно взять белый. Под цветные лучше брать прозрачный. Не везде желательно использовать кислотный. Хоть он и дешевле, но может повредить металлам или краске.

В обоих случаях стена и уголок должны быть чистыми, сухими. На уголок наносится состав, он прижимается к углу, фиксируется полосками малярного скотча. Прихватываем через 40-60 см. Если все ровно, можно и через 60 см, если надо повторять форму, через 40 см или даже чаще.

Как и чем приклеить ПВХ уголок к обоям

Оставляют в таком состоянии пока не высохнет клей или не затвердеет силикон. Точное время смотрите на упаковке. Затем малярную ленту можно снимать. Она отличается от обычного скотча тем, что даже с бумажных обоев отклеивается без повреждения поверхности. Но чтобы быть уверенными, попробуйте приклеить и отклеить в незаметном месте.

Уголок из вспененного каучука — Г-образный и универсальный на самоклеящейся основе

Есть еще один вариант того, как можно приклеить уголки на стену с обоями, покраской. Можно использовать двусторонний скотч. Его приклеить сначала к уголку, затем, сняв защитное покрытие, прижать к углу. Есть уголки, к которым скотч уже приклеен. Некоторые виды вспененной резины или из пластика (обычно гибкие или универсальные).

Отделка арки

Оформление арки часто становится проблемой. Вообще, в квартире не так много наружных углов, но на арке они есть обязательно. И в проходе они очень часто задеваются. То мебелью, то другим грузом или просто не вписавшимся в проем жителем. И есть с прямой частью вопросов не возникает, то округлая часть может быть проблемой.

И не только в дверном проходе может быть арочный свод

Вообще, для арки можно использовать универсальные уголки. Они гибкие, что очень удобно. Есть гибкие не универсальные — пластиковые, из специального полимера повышенной эластичности.

Но вообще, для оформления арок применяют уголки с разной шириной полочек. Их даже называют арочными. У них одна полочка 10 мм (наружная) вторая — внутренняя — 30 мм и больше. Гнутся они легко. В бублик не скрутите, но любой кривизны дугу получить несложно. Надо будет только использовать надежную фиксацию на время высыхания клея.

Это арочный пластиковый уголок

Если гнуть хотите обычный уголок, это можно сделать прогрев пластик. Для этой работы нужен строительный фен. Обычный — для волос — не подойдет, так как температура у него слишком низкая. Еще нужен шаблон, по которому будем сгибать пластиковый уголок. Возьмите кусок ДВП, закрутите саморезы или вбейте гвозди, сформировав тот профиль, который вам требуется.

Так можно оформить углы арки защитными уголками

Гнуть начинают с середины. Прогреваете участок, постоянно надавливая на середину, а феном двигаясь от центра к краям. Так надо довести уголок до нужной кривизны и оставить в таком положении остывать. Чтобы он не выпрямился, параллельно с рядом саморезов делают отверстия под второй ряд. Расстояние между рядами равно ширине полочки уголка. После того как пластик согнулся, вставляем и слегка закручиваем саморезы. После остывания пластика их снимаем.

Чем резать отделочные уголки

Практически всегда уголки для защиты углов стен приходится резать. Продаются они планками длиной от 2 до 3 метров. Инструмент для нарезки подбирают в зависимости от типа материала. Для дерева и металла, толстого пластика потребуется ножовка, вот только полотно разное — по дереву, и с мелким зубом по металлу или толстостенному пластику.

Тонкий пластик можно резать строительным или канцелярским ножом, острыми ножницами. Если отрезать надо перпендикулярно, проще использовать ножницы. Ими дорезаем до угла с двух сторон, сгибаем уголок, оставшиеся миллиметры дорезаем канцелярским ножом. Если есть огрехи, их легко поправить тем же ножом или наждачной бумагой с очень мелким зерном (полировочная).

Как резать защитный пластиковый уголок (ПВХ)

Если пластиковый уголок надо разрезать вдоль сгиба, надрезаем его по внутреннему углу при помощи канцелярского ножа. Прорезать на всю толщину не имеет смысла. Надо только заметную полосу оставить. Затем отгибаем кусок, который надо удалить. Он отрывается по месту реза. Неровности убираем ножом или наждачкой.

Источник