Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС
Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Далее
Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»
где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
[quads id=1]
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Что такое внутреннее сопротивление источника питания
Содержание
- 1 Что такое внутреннее сопротивление
- 2 Как измеряется внутреннее сопротивление
- 3 Зачем нужно знать внутреннее сопротивление
- 4 Видео по теме
Любой источник тока, будь то генератор или гальванический элемент, обладает внутренним сопротивлением. Его величина характеризирует количество энергетических потерь, появляющихся при протекании тока через источник питания. Для генератора внутреннее сопротивление определяется сопротивлением обмоток статора, для аккумулятора — электродов и электролита. Для него используется та же единица измерения, что и для общего сопротивления цепи — Ом.
Что такое внутреннее сопротивление
В электрической цепи обязательно присутствует источник питания. Обычно, оценивая его параметры, указывают, какую разность потенциалов между клеммами он обеспечивает. Если говорить об идеальной модели источника питания, то можно предположить, что он способен обеспечить в электрической цепи любую мощность с учётом имеющейся разности потенциалов.
Реальные устройства в этом аспекте сильно отличаются друг от друга. Чтобы определить работоспособность аккумулятора важно знать, что такое внутреннее сопротивление. Обычно с течением времени и вследствие износа оно постепенно возрастает. Анализируя уровень и скорость того, как изменяется внутреннее сопротивление источника тока, можно принять решение о продолжении использования батареи или о необходимости её замены.
Сказанное следует пояснить на примере. Для запуска мотора автомобиля используется аккумулятор на 12 Вольт. Известно, что при этом сила тока может достигать 250 Ампер. Однако, если взять другой элемент питания с такой же разницей потенциалов, то вполне возможна ситуация, когда от него запуск мотора осуществить не получится.
В качестве примера такого источника можно рассмотреть несколько гальванических элементов, соединённых последовательно. Разница в двух рассматриваемых ситуациях определяется наличием различного внутреннего сопротивления.
Этот параметр для аккумулятора представляет собой сумму нескольких слагаемых: сопротивление каждого вывода, корпуса и используемого электролита. В некоторых источниках тока при этом могут учитываться дополнительные элементы, включённые в данную цепь.
Важно учитывать, что понятие омического сопротивления в этой ситуации неприменимо, поскольку требуется наличие в цепи только пассивных элементов. Когда создана замкнутая цепь, ток протекает не только по ней, но и внутри источника тока. Внутреннее сопротивление определяет величину потерь энергии в нём.
Его наличие в цепи можно проиллюстрировать ещё одним примером. Если на клеммах аккумулятора имеется 12 вольт, то на первый взгляд можно легко предсказать, какая сила тока будет при нагрузке 1 Ом. Очевидно, что нужно ожидать, что по цепи пройдёт ток, равный 12 Ампер.
На самом деле это утверждение не соответствует действительности: ток будет немного меньше — примерно 11.2 Ампера. Здесь нет никакого несоответствия физике. Ведь при расчёте дополнительно требуется учитывать сопротивление источника тока, из-за которого происходит расход энергии. Оно называется внутренним. Его можно мысленно представить как резистор, соединённый последовательно с источником тока.
Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.
Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.
Зачем нужно знать внутреннее сопротивление
На первый взгляд может показаться, что наличие внутреннего сопротивления интересно только с теоретической точки зрения. На самом деле в некоторых ситуациях знать чему оно равно бывает жизненно важным.
Одна из таких ситуаций — определение работоспособности автомобильного аккумулятора. Его внутреннее сопротивление не является постоянным. Оно изменяется под воздействием различных факторов и влияет на напряжение на клеммах. Чтобы быть уверенным в работоспособности оборудования, нужно не только уметь найти его внутреннее сопротивление, но и знать, какая его величина соответствует норме.
На внутреннее сопротивление источника питания могут оказывать влияние такие факторы:
- Температурные условия. Чем холоднее, тем с меньшей скоростью в аккумуляторе протекают химические процессы. Это приводит к увеличению внутреннего сопротивления и постепенному уменьшению напряжения на клеммах.
- Срок службы аккумулятора. У новых устройств внутреннее сопротивление имеет минимальную величину. Постепенно оно начинает расти. Это связано с тем, что в аккумуляторе происходит необратимый химический процесс. В некоторых случаях он относительно медленный, а в других может быть довольно заметным. Последнее, например, относится к свинцово-кислотным аккумуляторам.
- Емкость аккумулятора.
- Иногда на устройство может оказываться механическое воздействие, из-за которого появляются внутренние обрывы.
- Количество используемого электролита.
- Ток, который создаётся батареей, зависит от нагрузки цепи. В зависимости от него меняется сопротивление.
Влияние большого количества факторов приводит к тому, что в качестве нормального можно рассматривать различные значения внутреннего сопротивления. Однако его стандартным увеличением за год принято считать 5%. Если эта норма превышена, значит, на исправность аккумулятора нужно обратить особое внимание.
При анализе стоит принимать во внимание не только те значения, которые указаны в технической документации. Необходимо учитывать и то, насколько интенсивно происходят изменения сопротивления со временем. Это даст более точную информацию об исправности батареи и поможет понять, чего нужно добиваться, чтобы обеспечить работоспособность оборудования.
Один из наиболее простых способов измерения внутреннего сопротивления можно продемонстрировать на следующем примере. Его применение возможно при условии, что ЭДС аккумулятора известна.
ЭДС (ℰ, единица измерения — вольты, В) — это электродвижущая сила источника питания, равная отношению работы сторонних сил по перемещению заряда от отрицательного полюса источника к положительному к величине этого заряда: ℰ=A/q. Если к источнику питания не подключена нагрузка, то ЭДС по своему значению равно напряжению на его клеммах.
Будет рассмотрена ситуация, когда ЭДС равна 1.5 В. Составляется электрическая цепь, в которой выходы аккумулятора присоединяются к электрической лампочке. Измеряется падение напряжения на ней и ток, проходящий через цепь. Они, соответственно, равны 1.2 В и 0.3 А.
Цифры, которые здесь приводятся, являются условными. При измерении мастер может выбрать другой тип электрической нагрузки, если сочтёт это необходимым.
По закону Ома можно определить сопротивление лампочки:
R = U / I = 1.2 / 0.3 = 4 Ом.
В этой формуле буквой R обозначается полное сопротивление цепи. Его можно выразить, как сумму r + R, где r — внутреннее и R — обычное сопротивление.
Тогда: R + r = ℰ / I
Из этой формулы определяется r = ℰ / I − R = 1.5 / 0.3 − 4 = 1 Ом.
Важным условием нахождения значения r является знание величины электродвижущей силы. Эта характеристика имеет максимальное значение у новых и хорошо заряженных батарей. Те, что уже долго были в использовании, могут иметь значительно меньшую ЭДС вследствие разряда, износа, который часто связан с необратимыми химическими процессами в аккумуляторе.
Для определения ℰ необходимо отключить любую нагрузку от клемм источника питания и подключить вольтметр или мультиметр в режиме измерения напряжения. Прибор покажет значение ЭДС. Почему — это легко понять. По закону Ома для полной цепи:
I = ℰ / (R + r),
так как вольтметр имеет сопротивление R→∞, то ток I≈0. Следовательно напряжение на клеммах равно ЭДС:
U = I·R = ℰ – I·r = ℰ.
Также следует упомянуть, что нулевым внутренним сопротивлением «r» обладает только идеальный генератор напряжения. Также существуют элементы с большим внутренним сопротивлением — это разные датчики, источники сигналов, а r=∞ обладает только идеальный источник тока. Помимо этого, существуют двухполюсники с отрицательным значением r, его можно получить в схемах с обратной связью и в элементах с отрицательным дифференциальным сопротивлением. Расчеты применимы не только для аккумулятора, но и для любого другого источника тока, например, гальванической батареи, двухполюсника, петли фаза-нуль. Использовать эти знания можно для согласования источника и нагрузки, понижения высоких напряжений и минимизации шума.
Видео по теме
Что означает внутреннее сопротивление?
Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет. В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r.
Внутреннее сопротивление источника тока .
Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Ток в замкнутой цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r.
В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.
Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до сотни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:


Цепляем лампочку


Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.


На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Далее


Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»


где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.
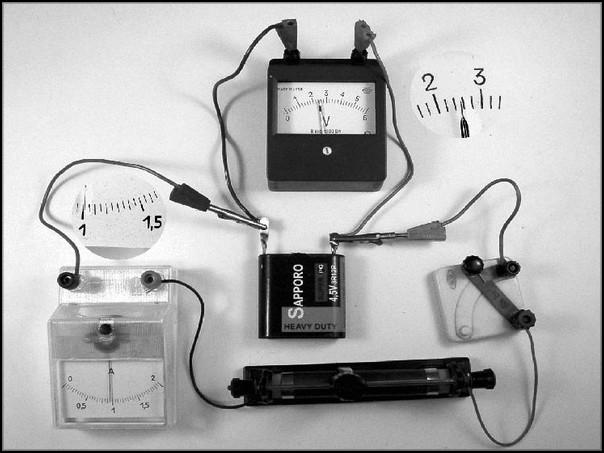
Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.
Зачем нужно знать внутреннее сопротивление
На первый взгляд может показаться, что наличие внутреннего сопротивления интересно только с теоретической точки зрения. На самом деле в некоторых ситуациях знать чему оно равно бывает жизненно важным.
Одна из таких ситуаций — определение работоспособности автомобильного аккумулятора. Его внутреннее сопротивление не является постоянным. Оно изменяется под воздействием различных факторов и влияет на напряжение на клеммах. Чтобы быть уверенным в работоспособности оборудования, нужно не только уметь найти его внутреннее сопротивление, но и знать, какая его величина соответствует норме.

На внутреннее сопротивление источника питания могут оказывать влияние такие факторы:
- Температурные условия. Чем холоднее, тем с меньшей скоростью в аккумуляторе протекают химические процессы. Это приводит к увеличению внутреннего сопротивления и постепенному уменьшению напряжения на клеммах.
- Срок службы аккумулятора. У новых устройств внутреннее сопротивление имеет минимальную величину. Постепенно оно начинает расти. Это связано с тем, что в аккумуляторе происходит необратимый химический процесс. В некоторых случаях он относительно медленный, а в других может быть довольно заметным. Последнее, например, относится к свинцово-кислотным аккумуляторам.
- Емкость аккумулятора.
- Иногда на устройство может оказываться механическое воздействие, из-за которого появляются внутренние обрывы.
- Количество используемого электролита.
- Ток, который создаётся батареей, зависит от нагрузки цепи. В зависимости от него меняется сопротивление.
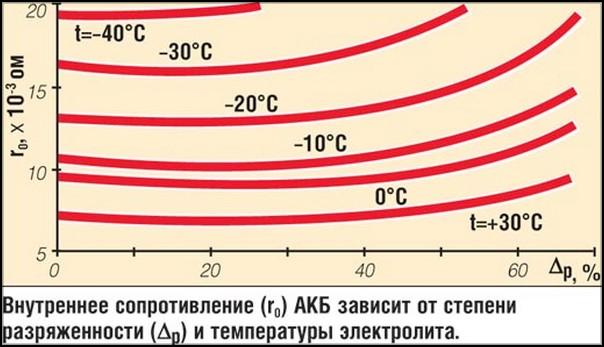
Влияние большого количества факторов приводит к тому, что в качестве нормального можно рассматривать различные значения внутреннего сопротивления. Однако его стандартным увеличением за год принято считать 5%. Если эта норма превышена, значит, на исправность аккумулятора нужно обратить особое внимание.
При анализе стоит принимать во внимание не только те значения, которые указаны в технической документации. Необходимо учитывать и то, насколько интенсивно происходят изменения сопротивления со временем. Это даст более точную информацию об исправности батареи и поможет понять, чего нужно добиваться, чтобы обеспечить работоспособность оборудования.
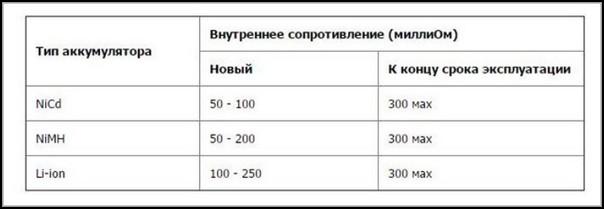
Один из наиболее простых способов измерения внутреннего сопротивления можно продемонстрировать на следующем примере. Его применение возможно при условии, что ЭДС аккумулятора известна.
ЭДС (ℰ, единица измерения — вольты, В) — это электродвижущая сила источника питания, равная отношению работы сторонних сил по перемещению заряда от отрицательного полюса источника к положительному к величине этого заряда: ℰ=A/q. Если к источнику питания не подключена нагрузка, то ЭДС по своему значению равно напряжению на его клеммах.
Будет рассмотрена ситуация, когда ЭДС равна 1.5 В. Составляется электрическая цепь, в которой выходы аккумулятора присоединяются к электрической лампочке. Измеряется падение напряжения на ней и ток, проходящий через цепь. Они, соответственно, равны 1.2 В и 0.3 А.
Цифры, которые здесь приводятся, являются условными. При измерении мастер может выбрать другой тип электрической нагрузки, если сочтёт это необходимым.
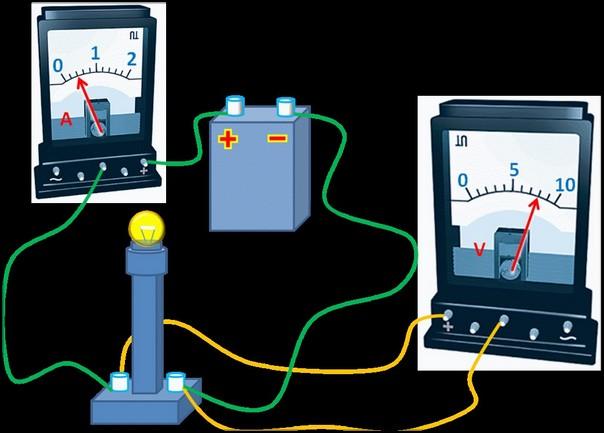
По закону Ома можно определить сопротивление лампочки:
R = U / I = 1.2 / 0.3 = 4 Ом.
В этой формуле буквой R обозначается полное сопротивление цепи. Его можно выразить, как сумму r + R, где r — внутреннее и R — обычное сопротивление.
Тогда: R + r = ℰ / I
Из этой формулы определяется r = ℰ / I − R = 1.5 / 0.3 − 4 = 1 Ом.
Важным условием нахождения значения r является знание величины электродвижущей силы. Эта характеристика имеет максимальное значение у новых и хорошо заряженных батарей. Те, что уже долго были в использовании, могут иметь значительно меньшую ЭДС вследствие разряда, износа, который часто связан с необратимыми химическими процессами в аккумуляторе.
Для определения ℰ необходимо отключить любую нагрузку от клемм источника питания и подключить вольтметр или мультиметр в режиме измерения напряжения. Прибор покажет значение ЭДС. Почему — это легко понять. По закону Ома для полной цепи:
I = ℰ / (R + r),
так как вольтметр имеет сопротивление R→∞, то ток I≈0. Следовательно напряжение на клеммах равно ЭДС:
U = I·R = ℰ – I·r = ℰ.
Также следует упомянуть, что нулевым внутренним сопротивлением «r» обладает только идеальный генератор напряжения. Также существуют элементы с большим внутренним сопротивлением — это разные датчики, источники сигналов, а r=∞ обладает только идеальный источник тока. Помимо этого, существуют двухполюсники с отрицательным значением r, его можно получить в схемах с обратной связью и в элементах с отрицательным дифференциальным сопротивлением. Расчеты применимы не только для аккумулятора, но и для любого другого источника тока, например, гальванической батареи, двухполюсника, петли фаза-нуль. Использовать эти знания можно для согласования источника и нагрузки, понижения высоких напряжений и минимизации шума.
Расчет внутреннего сопротивления источника напряжения
Реальные источники напряжения обладают собственным электрическим сопротивлением, которое называется «внутреннее сопротивление». Присоединенная на выводы источника нагрузка обозначается под названием «внешнее сопротивление» – R.
Батарея аккумуляторов генерирует ЭДС:
ε = E/Q, где:
- Е – энергия (Дж);
- Q – заряд (Кл).
Суммарная ЭДС аккумуляторного элемента является напряжением его разомкнутой цепи при отсутствии нагрузки. Его можно проконтролировать с хорошей точностью цифровым мультиметром. Разность потенциалов, измеренная на выходных контактах батареи, когда она включена на нагрузочный резистор, составит меньшую величину, чем ее напряжение при незамкнутой цепи, по причине протекания тока через нагрузочное внешнее и через внутреннее сопротивление источника, это приводит к рассеиванию энергии в нем как теплового излучения.
Внутреннее сопротивление аккумулятора с химическим принципом действия находится между долей ома и несколькими омами и в основном связано с сопротивлением электролитических материалов, используемых при изготовлении батареи.
Если резистор сопротивлением R подсоединить к батарее, ток в цепи I = ε/(R + r).
Внутреннее сопротивление – не постоянная величина. На него влияет род батареи (щелочная, свинцово-кислотная и т. д.), оно изменяется в зависимости от нагрузочного значения, температуры и срока использования аккумулятора. К примеру, у разовых батареек внутреннее сопротивление возрастает во время использования, а напряжение в связи с этим падает до прихода в состояние, непригодное для дальнейшей эксплуатации.
Если ЭДС источника – заранее данная величина, внутреннее сопротивление источника определяется, измеряя ток, протекающий через нагрузочное сопротивление.
- Так как внутреннее и внешнее сопротивление в приближённой схеме включены последовательно, можно использовать законы Ома и Кирхгофа для применения формулы:
- Из этого выражения r = ε/I — R.
Пример.
Аккумулятор с известной ЭДС ε = 1.5 В и соединен последовательно с лампочкой. Падение напряжения на лампочке составляет 1,2 В. Следовательно, внутреннее сопротивление элемента создает падение напряжения: 1,5 — 1,2 = 0,3 В. Сопротивление проводов в цепи считается пренебрежимо малым, сопротивление лампы не известно. Измеренный ток, проходящий через цепь: I = 0,3 А. Нужно определить внутреннее сопротивление аккумулятора.
- По закону Ома сопротивление лампочки R = U/I = 1,2/0,3 = 4 Ом;
- Теперь по формуле для расчета внутреннего сопротивления r = ε/I — R = 1,5/0,3 — 4 = 1 Ом.
В случае короткого замыкания внешнее сопротивление падает почти до нуля. Ток может ограничивать свое значение только маленьким сопротивлением источника. Сила тока, возникающая в такой ситуации, настолько велика, что источник напряжения может быть поврежден тепловым воздействием тока, существует опасность возгорания. Риск пожара предотвращается установкой предохранителей, например, в цепях автомобильных аккумуляторов.
Внутреннее сопротивление источника напряжения – важный фактор, когда решается вопрос, как передать наиболее эффективную мощность подсоединенному электроприбору.
Важно!
Максимальная передача мощности происходит, когда внутреннее сопротивление источника равно сопротивлению нагрузки.
Однако при этом условии, помня формулу Р = I² x R, идентичное количество энергии отдается нагрузке и рассеивается в самом источнике, а его КПД составляет всего 50%.
Требования нагрузки должны быть тщательно рассмотрены для принятия решения о наилучшем использовании источника. Например, свинцово-кислотная автомобильная батарея должна обеспечивать высокие токи при сравнительно низком напряжении 12 В. Ее низкое внутреннее сопротивление позволяет ей это делать.
В некоторых случаях источники питания высокого напряжения должны иметь чрезвычайно большое внутреннее сопротивление, чтобы ограничить ток к. з.
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.
Таблица удельных сопротивлений различных материалов
| Удельное сопротивление
ρ, Ом*мм2/м |
Удельное сопротивление
ρ, Ом*мм2/м |
| Алюминий | 0,028 |
| Бронза | 0,095 – 0,1 |
| Висмут | 1,2 |
| Вольфрам | 0,05 |
| Железо | 0,1 |
| Золото | 0,023 |
| Иридий | 0,0474 |
| Константан ( сплав Ni-Cu + Mn) | 0,5 |
| Латунь | 0,025 – 0,108 |
| Магний | 0,045 |
| Манганин (сплав меди марганца и никеля – приборный) | 0,43 – 0,51 |
| Медь | 0,0175 |
| Молибден | 0,059 |
| Нейзильбер (сплав меди цинка и никеля) | 0,2 |
| Натрий | 0,047 |
| Никелин ( сплав меди и никеля) | 0,42 |
| Никель | 0,087 |
| Нихром ( сплав никеля хрома железы и марганца) | 1,05 – 1,4 |
| Олово | 0,12 |
| Платина | 0.107 |
| Ртуть | 0,94 |
| Свинец | 0,22 |
| Серебро | 0,015 |
| Сталь | 0,103 – 0,137 |
| Титан | 0,6 |
| Хромаль | 1,3 – 1,5 |
| Цинк | 0,054 |
| Чугун | 0,5-1,0 |
Ответ: нить накаливания сделана из константана.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
I = U/R
I — сила тока [A]
U — напряжение [В]
R — сопротивление [Ом]
Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Измерение внутреннего сопротивления.
Существует несколько методик измерения внутреннего сопротивления. Две из них прописаны в ГОСТ Р МЭК 61960-2007. Перед замером любым из приведенных ниже методов аккумулятор должен быть полностью заряжен. Испытания проводятся при температуре 20±5ºC.
Измерение внутреннего сопротивления методом переменного тока (а.с.)
С помощью этого метода измеряется импеданс, который на частоте 1000 Гц приблизительно равен сопротивлению.
Электрический импеданс (комплексное электрическое сопротивление) (англ. impedance от лат. impedio «препятствовать») — комплексное сопротивление между двумя узлами цепи или двухполюсника для гармонического сигнала.
Описание методики из ГОСТ
В течение одной – пяти секунд измеряем среднеквадратичное значение переменного напряжения Urms, возникающего при прохождении через аккумулятор переменного тока со среднеквадратичным значением Irms , следующего с частотой 1000 Гц. Внутреннее сопротивление Ra.c., Ом рассчитываем по формуле Ra.c.= Urms / Irms .
Irms (rms – Root Mean Square – среднеквадратичное значение).
Переменный ток должен иметь такое значение, чтобы пиковое напряжение не превышало 20 мВ.
Этот метод сложно воплотить в домашних условиях без специального оборудования. Популярный прибор YR1035 отлично справляется с измерениями с точностью 0,01 мОм. Зарядные устройства SKYRC MC3000 ,Opus BT-C3100V2.2, Liitokala Lii-500 также измеряют методом АС, но весьма с посредственной точностью.
Измерение внутреннего сопротивления методом постоянного тока (d.c.)
Этот метод возможно выполнить в домашних условиях с помощью обычных вольтметра и амперметра и пары подходящих нагрузочных сопротивлений. В качестве сопротивлений вполне можно использовать несколько автомобильных ламп накаливания или импровизированный резистор из нихромовой проволоки.
Описание метода из ГОСТ
- Разряжаем аккумулятор постоянным током I1= 0,2 Iн. На десятой секунде измеряем значение напряжения U1 на клеммах аккумулятора.
- Увеличиваем разрядный ток до значения I2=Iн. На следующей секунде измеряем значение напряжения U2 на клеммах аккумулятора.
Внутреннее сопротивление Rd.c., Ом рассчитываем по формуле Rd.c. = (U1-U2)/(I2-I1)
- Iн – номинальный ток разряда аккумулятора.
Схема для измерения внутреннего сопротивления по методике постоянного тока (d.c.)
Сопротивление R1 и R2 подбирается таким образом, чтобы протекали токи I1 и I2 нужной величины. Ориентироваться нужно на номинальный разрядный ток аккумулятора.
Вольтметр необходимо подключать непосредственно на полюса источника, чтобы исключить влияние от падения напряжения на проводах .
Идеальный источник тока
Идеальный источник тока представляет собой активный элемент, ток которого не зависит от напряжения на его зажимах. Предполагается, что внутреннее сопротивление идеального источника тока бесконечно велико , и поэтому параметры внешней электрической цепи, от которых зависит напряжение на зажимах источника, не влияют на ток источника. Условные обозначения идеального источника тока приведены на рис. 1
Стрелка в источнике тока или знаки «+» и «—» указывают положительное направление тока i(t)
или полярность источника, т. е. направление перемещения положительных зарядов.
Сейчас принято обозначать источники тока буквой J, и чаще всего применяется нижнее условно графическое изображение.
Идеальный источник тока
По мере неограниченного увеличения сопротивления внешней электрической цепи, присоединенной к идеальном
у источнику тока, напряжение на его зажимах и соответственно мощность, развиваемая им, неограниченно возрастают.Поэтому идеальный источник тока, так же как и идеальный источник напряжения, рассматривается как источник бесконечной мощности.
Источник тока конечной мощности изображается в виде идеального источника тока с параллельно подключенным к его зажимам пассивным элементом который характеризует внутренние параметры источника и
Представляя собой теоретическое понятие, источник тока применяется в ряде случаев для расчета электрических цепей.
Некоторым подобием источника тока может служить устройство, состоящее из аккумулятора, соединенного последовательно с дополнительным большим сопротивлением Другим примером источника тока может являться пяти электродная усилительная электронная лампа (пентод). Имея внутреннее сопротивление несоизмеримо большее, чем сопротивление внешней электрической цепи, эти устройства отдают ток, почти не зависящий от изменения внешней нагрузки в широких пределах, и именно в этом отношении они аналогичны источнику тока.
Чему равно внутреннее сопротивление источника тока?
Внутреннее сопротивление источника тока r будет определяться формулой: r = ЭДС / I — R. Подставим данные из условия задачи: r = 10 В / 2 А — 4 Ом = 1 Ом. Ответ: источник тока имеет внутреннее сопротивление r = 1 Ом.
Как правильно пользоваться мультиметром: инструкция для чайников
Рассмотрим, как измерить несколько электрических характеристик.
Потенциал
Алгоритм для определения напряжения:
- Установить режим в позицию ACV или DCV в предполагаемом интервале.
- Черный провод подключить к коннектору СОМ, красный — к разъему VΩmA.
- Наконечники щупов соединить с контактами цепи. Например, ввести в отверстия розетки или на полюса батарейки.
- Провести измерение.
Высветившееся на дисплее число — величина напряжения в вольтах. Знак «минус» говорит о том, что полярность была нарушена. Если мультиметр поддерживает функцию удержания, значение можно зафиксировать кнопкой HOLD. Это удобно для большой цепочки измерений.
Сила тока
Эта характеристика измеряется только при последовательном подключении тестера в цепь и включенном питании. Большинство приборов дают возможность определить силу тока до 10 А, поскольку в быту большие значения используются редко.
Для проведения измерений в цепи устраивается разрыв. Дальнейшие действия по следующей схеме:
- Черный щуп — в гнездо СОМ.
- Красный — в разъем до 200 мА или 10А.
- Наконечниками осторожно прикоснуться к контактам.
- Считать с дисплея значение напряжения.
При работе с оголенными проводами необходимо соблюдать технику безопасности, чтобы не допустить удара током.
Сопротивление
Эту характеристику можно измерить без подачи питания. Исследуемый элемент просто замыкается между двумя щупами. Если проводимости нет, на экране высвечивается единица.
Последовательность действий:
- Установить режим Ω, выбрав максимальный диапазон.
- Щупы вставить в соответствующие коннекторы.
- Проверить состояние — замкнуть щупы друг на друга. Должен появиться 0 или небольшое число, которое нужно учитывать при измерении сопротивления цепи.
- Концы проводников набросить на контакты исследуемого объекта.
- На экране появится сопротивление элемента или участка цепи.
Для точных измерений рекомендуется провести 2-3 попытки.
Измерение транзисторов
Для проверки исправности pn-переходов и определения коэффициента усиления:
- Установить режим
- Вставить ножки транзистора в разъем в соответствии с цоколевкой, соблюдая зоны PNP и NPN.
- Отображением на дисплее будет значение усиления сигнала.
Диоды и простейшие транзисторы также измеряются при установленном режиме «диод». К базе подключается красный щуп (плюс), на эмиттер или коллектор черный (минус). При правильной полярности на экране высветится коэффициент передачи.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
ЭДС. Закон Ома для полной цепи
-
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
-
Сторонняя сила
-
Закон Ома для полной цепи
-
КПД электрической цепи
-
Закон Ома для неоднородного участка
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила
, направленная против движения заряда (т.е. против направления тока).
к оглавлению ▴
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы
называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом,
— это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду
. Поэтому отношение
уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается
:
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
к оглавлению ▴
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением
подключён к резистору
(который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение
на резисторе
.
За время по цепи проходит заряд
. Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и
. Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и
(рис. 2). Потенциал точки
равен потенциалу положительной клеммы источника; потенциал точки
равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь
умножается на дробь, меньшую единицы. Но есть два случая, когда
.
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт
.
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина
неотличима от
, и формула (5) снова даёт нам
.
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
к оглавлению ▴
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время
, обозначим
.
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
к оглавлению ▴
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна
, его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно
, можно просто заменить резистор
на резистор
).
Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки
к точке
. Этот ток не обязательно вызван одним лишь источником
. Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток
является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и
равны соответственно
и
. Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время
через участок проходит заряд
, при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло:
.
Подставляем сюда выражения для ,
и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд
от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки
к точке
.
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем
— закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене
на
:
Теперь замкнём наш участок, соединив точки и
. Получим рассмотренную выше полную цепь. При этом окажется, что
и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от
к
, направлен против действия сторонних сил источника.
Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке
. Если направление тока совпадает с направлением сторонних сил, то перед
ставится «плюс»; если же эти направления противоположны, то ставится «минус».
Повторим основные понятия и определения по теме «Закон Ома».
Напомним, что напряжение измеряется в вольтах.
Сила тока измеряется в амперах.
Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.
Основные определения, которые мы используем в решении задач:
Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.
Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.
Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.
Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.
По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).
Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.
Сопротивление измеряют в омах (Ом).
Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).
Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:
- Сопротивление проводника тем больше, чем больше его длина.
- Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.
Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм2/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:
Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.
Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм2 от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм2/м.
Решение:
Из закона Ома для проводника или участка цепи без источника следует:
По графику: при
Из формулы сопротивления выражаем и находим длину проводника:
Ответ: 10.
Задача 2. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике? Ответ дайте в амперах.
Решение:
По определению силы тока:
Заряд всех электронов: где е — модуль заряда электрона,
Кл.
Тогда
Ответ: 2.
Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)
Решение:
По закону Ома для полной цепи:
Тогда
Ответ: 0,07.
Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.
Решение:
Сила тока короткого замыкания определяется следующим образом:
Отсюда выражаем и находим внутреннее сопротивление источника:
При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:
Отсюда выражаем сопротивление резистора и находим его:
Ответ: 1,9.
Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.
Решение:
Выражаем время в секундах: t = 10 минут = 600 с.
Определяем силу тока по закону Ома для полной цепи:
Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.
По определению силы тока:
Отсюда Кл.
Ответ: 1500.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Электродвижущая сила и внутреннее сопротивление ведут нескончаемую битву внутри наших источников напряжения. Что стоит за этими концепциями? Каковы их отношения и каковы последствия их существования?
Электродвижущая сила
Электродвижущая сила звучит как термин из учебника по физике, и мало кто даже из радиолюбителей точно знает, для чего она нужна и что это значит. В Википедии описание выглядит так:
Электродвижущая сила (ЭДС) – фактор, вызывающий протекание тока в электрической цепи, равный электрической энергии, полученной единичным зарядом, перемещаемым в устройстве (источнике) электрического тока в направлении, противоположном силе электрического поля, действующего на это обвинение.
Понять это с первого раза может далеко не каждый. Единственное, что стоит помнить из этого описания, – это тот факт, что электродвижущую силу часто сокращают как ЭДС – это просто короче и проще. В английском языке аббревиатура EMF, которая означает Electromotive Force.
Начнем с того, что электродвижущую силу очень часто путают с напряжением, наверное потому, что оба эти значения выражаются в вольтах. Но если посмотрим на определение напряжения, то можно увидеть что оно полностью отличается от описания ЭДС и намного короче:
Электрическое напряжение – разница электрических потенциалов между двумя точками электрической цепи или электрического поля.
Так является ли ЭДС чем-то совершенно другим, чем напряжение? Не совсем. Фактически, ЭДС и напряжение – это одно и то же физическое понятие. Они оба вызывают протекание тока и оба говорят об энергии, которую несет электрический заряд. Что же делает их особенными?
Говоря проще – ЭДС это то что хотим, а напряжение – это то что получаем. Рассмотрим тему на примере водяной установки. В этом случае можно назвать электродвижущую силу номинальным давлением насоса, который достаем из коробки. Номинальный означает то, что насос теоретически способен производить. Другими словами, ЭДС описывает сколько «толкающей силы» источник может дать. Но действительно ли получим эту силу на практике?
Теперь переходим к напряжению, эквивалентом которого в водяной системе является фактическое давление воды, которое получаем после подключения нашего насоса. Конечно любые засоры в трубах или повреждение установки снижают это давление, так же как резистор вызывает падение напряжения в цепи. Но на интересует может ли насос протолкнуть воду с мощностью, обещанной производителем, и обычно это не так. Точно так же, если у нас есть аккумулятор с ЭДС 9 В, то после его подключения и измерения напряжения на клеммах может оказаться, что там всего 8,5 В. Почему? У каждого источника напряжения есть свои недостатки, которые нельзя преодолеть физически.
Таким образом, ЭДС – это виртуальная величина. Можем определить это как напряжение, которого достигли бы, если бы аккумулятор не имел дефектов и его эффективность составляла 100%. Электроника даже изобрела концепцию идеального источника напряжения, заключающуюся в том, что в определенных ситуациях человек закрывает глаза на недостатки источника и принимает рабочее напряжение, равное ЭДС (U = ЭДС). Но в действительности идеальных батарей, аккумуляторов и генераторов не существует, поэтому вырабатываемое во время работы напряжение всегда ниже значения ЭДС.
Эта потеря велика или нет? Чтобы проверить можно взять обычную батарею AA. На этикетке указано 1,5 В. Это значение производители называют номинальным напряжением. Так это имеется ввиду ЭДС или рабочее напряжение? Чтобы измерить ЭДС батареи, понадобится вольтметр. Важно чтобы измеряемая батарея была новой – надо видеть полный заряд, которым ее снабдил производитель, а не какое-либо остаточное напряжение в использованной батарее.
Можете измерить несколько батарей от разных производителей, и каждая из них даст разный результат. Один раз 1,60 В, в другой 1,65 В или 1,57 В. Почему же на каждой из этих батарей есть метка 1,5 В, хотя их ЭДС выше? Установите на них небольшой резистор, и результат колеблется между 1,55 В и 1,62 В, что все равно больше, чем предсказывал производитель. Что же тут происходит?
Если посмотрим в книги по электротехнике, те, которые касаются аккумуляторов, то там найдем определение до 10 различных типов напряжения! Вот несколько примеров:
- Теоретическое напряжение (theoretical voltage) – величина энергии, возникающая от батарей в зависимости от материалов. Например использование цинка и меди в качестве электродов даст напряжение 1,1 В, в то время как самые современные литиевые батареи могут достигать даже 3,5 В.
- Напряжение холостого хода (open-circuit voltage) – можем описать их как «напряжение батареи из коробки» или просто ЭДС. Это значение часто немного ниже теоретического напряжения, потому что конструкция батареи влечет за собой определенные ограничения.
- Рабочее напряжение (closed-circuit voltage) – батареи под нагрузкой теряют часть ЭДС. Насколько велико падение зависит от нескольких вещей, о которых расскажем далее.
- Номинальное напряжение – (nominal voltage) – ЭДС каждой батареи (угольной, щелочной или литиевой) может быть разным – иногда это 1,55 В, в другой раз, например, 1,62 В. Почему же тогда на каждой из них написано 1,5 В? Причина – стандартизация. Чтобы избежать путаницы и не заставлять потребителя задаваться вопросом, какое именно напряжение будет наилучшим в данном случае, было введено несколько стандартных напряжений, таких как 1,5 В, 3 В и 9 В, которым назначены ячейки. Во всех случаях ЭДС немного выше номинального напряжения, так что это «обман» в нашу пользу.
- Напряжение отключения (cut-off voltage) – при разрядке источник теряет энергию и, таким образом, снижает значение его ЭДС и рабочего напряжения. Через некоторое время наступит момент, когда напряжение станет слишком низким для продолжения питания устройства и он будет считаться разряженным. Но эта граница довольно плавная и зависит от нагрузки. Разряженный аккумулятор может не питать фонарик, но если поместим его в электронные часы, он сможет запитывать его еще несколько дней.
Откуда же это несоответствие? Ответ на вопрос требует изучения внутреннего сопротивления.
Внутреннее сопротивление
Сопротивление – это явление, которое можно рассматривать как положительное и отрицательное (плохое). Оно препятствует прохождению тока, забирает энергию у электронов и вызывает падение напряжения. Когда эти явления хороши? Когда хотим преобразовать электричество в тепло или свет. Без него не работали бы такие устройства, как бойлер, тостер, сушилка или лампочка.
Отрицательной стороной сопротивления будет то, что все кабели, которые подают энергию в дом и питают устройства, также обременены им. Следовательно, они также потребляют, точнее тратят впустую некоторую энергию. К счастью, сопротивление медных проводов очень низкое, и почти не почувствуются эти потери в домашних условиях.
Но есть еще один момент отрицательного сопротивления. Оно называется внутренним сопротивлением и возникает там, где меньше всего этого ожидаем – внутри источников напряжения.
Внутреннее сопротивление можно назвать узким местом источников напряжения. Это причина того, что рабочее напряжение ниже электродвижущей силы. Другими словами, оно тратит энергию еще до того, как оставит батареи или генераторы на электростанции. В нормальных условиях невозможно избежать внутреннего сопротивления. Это естественный недостаток всех источников электроэнергии – батарей, аккумуляторов, солнечных панелей, ветряных турбин или любых трехфазных генераторов, которые снабжают энергией наши дома. Откуда же оно взялось?
Внутреннее сопротивление генераторов
Начнем с генераторов переменного напряжения, потому что в их случае дело обстоит проще. Генераторы переменного тока – это просто большие электродвигатели. Они используют принцип электромагнитной индукции, то есть магнит, движущийся рядом с проводом, генерирует в нем ток.
Проще говоря, если возьмете неодимовый магнит и начнете его раскачивать возле какого-то провода, то создадите в нем электричество. Правда этого тока недостаточно для питания даже самого маленького светодиода. Во-первых, для генерации сильного тока требуется магнит гораздо большего размера, а во-вторых, гораздо больше проводов. Вращающийся магнит генерирует ток в десятках метров витой проволоки, которая его окружает. Так можно вкратце описать основы работы генераторов, типов конечно много, но здесь не будем останавливаться на них. Важно то, что это огромное количество спиральной проволоки (иногда заменяемой стержнями или листами) является важным элементом любого генератора, обеспечивая нужное количество движущихся электронов, реагирующих на вращение магнита. Примерно так работает любой генератор переменного тока.
У каждого, даже самого лучшего проводника, есть сопротивление. Обмотки, без которых было бы невозможно производить электричество, в то же время являются слабым звеном каждого генератора. С одной стороны они позволяют току течь, с другой – нагреваются через существующее сопротивление, посылая часть энергии в воздух в виде тепла.
Как с этим справляется электроэнергетика? Во-первых, турбогенераторы вырабатывают очень высокое напряжение. Благодаря этому можно добиться такой же мощности при довольно низкой силе тока, и чем меньше ток – тем меньше потери из-за сопротивления. Также надо помнить, что электричество должно пройти сотни километров, прежде чем достигнет домов, поэтому стоит поддерживать высокое напряжение как можно дольше. На практике оно снижается до 220 В только на трансформаторных подстанциях, разбросанных в городах. Трансформатор – это тоже устройство, сделанное из большого количества проволоки, и на нем тоже происходит падение напряжения. Его величина зависит от нагрузки, поэтому чем больше подключено к сети оборудование, тем ниже измеряемое напряжение в розетке.
Внутреннее сопротивление батареи
Батарея или аккумулятор – это устройства, внутри которых нет проводов, но это не значит, что на них не распространяется внутреннее сопротивление. Ячейки по существу состоят из двух электродных материалов (положительного и отрицательного), которые погружены в электролит. Один из электродов, например, из цинка, отдает электроны, другой, например, из меди – принимает электроны. Соединение обоих электродов проводом позволяет возникнуть потоку электронов между ними. Поддержание обмена возможно благодаря электролиту, специальному раствору, обеспечивающему необходимые элементы химической реакции. Примерно так работают аккумуляторы.
Рассмотрим где в аккумуляторе скрывается внутреннее сопротивление. Ответ непрост, потому что в ячейке происходит множество процессов, каждый из которых добавляет свой вклад к сопротивлению. Основные из них:
- Дефекты электродов – каждый материал имеет дефекты в виде поврежденной структуры или примесей. Это, в свою очередь, влияет на способность электродов отдавать и принимать электроны.
- Ограниченная проводимость электролита – электролит заполнен ионами (положительно и отрицательно заряженными атомами), которые перемещаются между электродами, чтобы обеспечить баланс заряда и предотвратить его накопление (поляризацию). К сожалению, ионы являются частицами намного тяжелее и медленнее электронов, поэтому их поток характеризуется определенным естественным сопротивлением.
- Коррозия электродов – продукты химических реакций, происходящих между электролитом и электродами, должны куда-то уходить. Иногда они создают газ, который выходит из батарей с помощью специальных микроскопических клапанов, иногда это твердое вещество, которое невозможно удалить наружу. К сожалению, в случае некоторых типов аккумуляторов эти отходы могут оседать на электродах, создавая на них своего рода покрытие, которое значительно мешает правильной работе аккумулятора.
- Износ электродов – обмен электронами связан с изменением структуры электродов. Отрицательный электрод (например, цинк), отдавая электроны, буквально растворяется в электролите. Его уменьшающаяся поверхность означает, что он не может выпускать электроны с той же скоростью, что значительно снижает рабочие параметры батареи, особенно в более старом типе.
Приведенные выше примеры показывают, что сопротивление батареи намного более проблематично, чем сопротивление генератора, по крайней мере, по нескольким причинам:
- Чтобы производить батареи с низким внутренним сопротивлением, многие факторы должны быть идеально согласованы друг с другом, что непросто.
- Батареи работают на основе химических реакций, и они, естественно, чувствительны к температуре – слишком низкая или слишком высокая температура немедленно истощит элемент.
- Внутреннее сопротивление батареи переменное. Из-за разрушения электролита и электродов сопротивление батареи увеличивается по мере ее разряда. Только новейшие литий-ионные конструкции способны минимизировать эту проблему.
Как насчет того, чтобы попытаться устранить проблему внутреннего сопротивления, увеличивая напряжение ячеек? Здесь мы сталкиваемся с рядом ограничений. Во-первых, не выйдет получать более 3,5 В от химических реакций (по крайней мере в настоящее время). Вот почему батареи с напряжением 9 В строятся путем соединения обычно 6 ячеек по 1,5 В каждая. А аккумуляторы питающие электромобили Тесла, вырабатывают напряжение 400 В, весят более 500 кг и состоят из 8256 небольших литий-ионных элементов. Аккумуляторы Tesla занимают всю поверхность пола автомобиля.
Как рассчитать внутреннее сопротивление
Раз уж внутреннее сопротивление невозможно победить, стоит хотя бы выяснить, как его можно измерить и каких значений оно может достичь. Чтобы узнать это нужно будет сделать 3 измерения.
Каждый мультиметр имеет возможность измерять сопротивление. Но нельзя пытаться измерить внутреннее сопротивление любого источника напряжения Омметром. Попытка измерить внутреннее сопротивление трансформатора, вставив щупы измерителя в розетку, – одна из худших идей, которые можно придумать. Никогда не пытайтесь это сделать!
Как тогда правильно измерить внутреннее сопротивление АКБ? Есть два метода, и вот более простой. Сначала измерьте ЭДС аккумулятора. Установите мультиметр на измерение постоянного напряжения и приложите щупы к обоим полюсам батареи.
Затем нужно измерить рабочее напряжение АКБ. Лучше всего взять резистор с известным значением, приложить его концы к обоим полюсам и снова измерить напряжение, как это делали только что.
Как видите, разница между ЭДС и напряжением новой батареи очень мала – всего 0,013 В. Следовательно, чем лучше у вас прибор, тем больше вероятность, что вы сможете измерить его. Но и не забудьте еще измерить сопротивление резистора, который используете. Тот факт, что он 47 Ом, не означает, что у него такое сопротивление. В данном случае это 46,1 Ом.
Имея все измерения (ЭДС, рабочее напряжение, сопротивление резистора), достаточно запомнить Закон Ома, потому что именно по нему сделаем необходимые вычисления:
Теперь выполним 3 простых шага:
- Шаг 1 – Рассчитайте разницу между ЭДС и рабочим напряжением. Это значение, поглощаемое внутренним сопротивлением, или падение напряжения на внутреннем сопротивлении. В этом случае 1,595 В – 1,583 В = 0,013 В.
- Шаг 2 – Рассчитайте ток, протекающий в цепи во время работы. Для этого делим рабочее напряжение на сопротивление резистора. Получаем 1,583 В / 46,1 Ом = 0,034 А.
- Шаг 3 – Вычисляем внутреннее сопротивление батареи, разделив падение напряжения, вызванное протекающим через нее током. Для этого эксперимента это будет 0,013 В / 0,034 А = 0,382 Ом.
Это много или мало? Зависит от того, какие батареи хотим использовать. Для сравнения, внутреннее сопротивление типичных батареек АА в лет 30 назад составляло от 1 Ом до 3 Ом, что в несколько раз больше, чем сегодня. Конечно, в 1980-х щелочные батареи только выходили на рынок, и литиевые приходилось ждать до 1995 года. Это показывает насколько сильно изменилась технология производства аккумуляторов за последние годы. Снижение внутреннего сопротивления аккумулятора позволяет снизить потери энергии, а значит повысить его КПД. Сегодняшние батареи способны питать гораздо больше энергоемких устройств, чем раньше, без сильного нагрева и поддержания постоянного напряжения в течение гораздо более длительного времени. Вот в принципе и вся теория, надеемся с практикой теперь у вас проблемы не возникнут. А если что осталось неясным – добро пожаловать на форум!