Как найти внутренний односторонний угол - Исправление недочетов и поиск решений вместе с Examum.ru

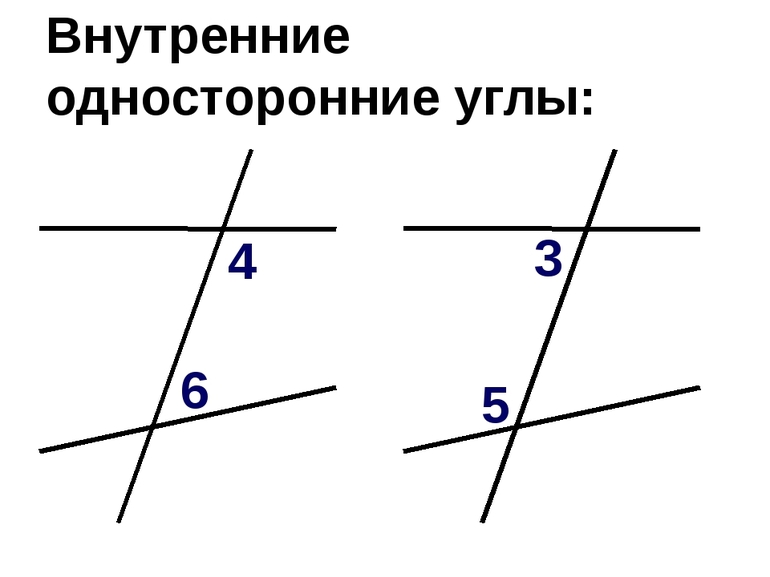
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.

Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).

При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

∠1 и∠2

∠3 и∠4

— внутренние односторонние углы при прямых a и b и секущей c.

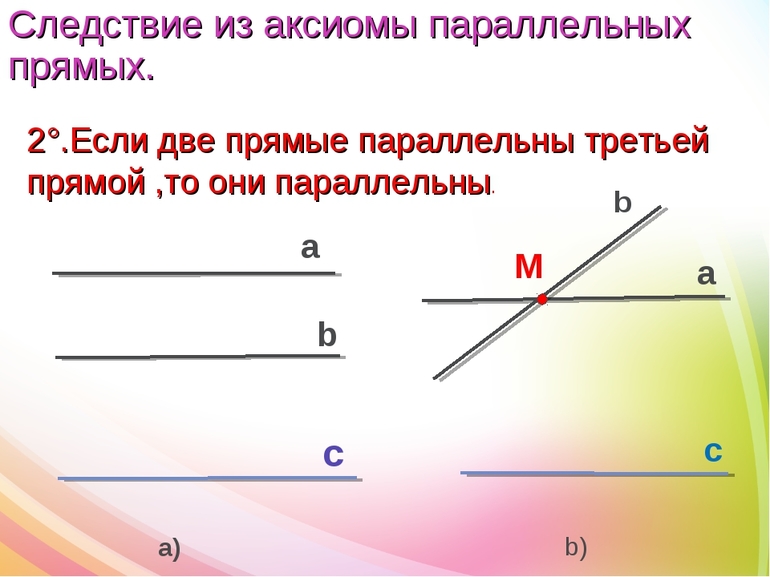
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.

Свойство параллельных прямых

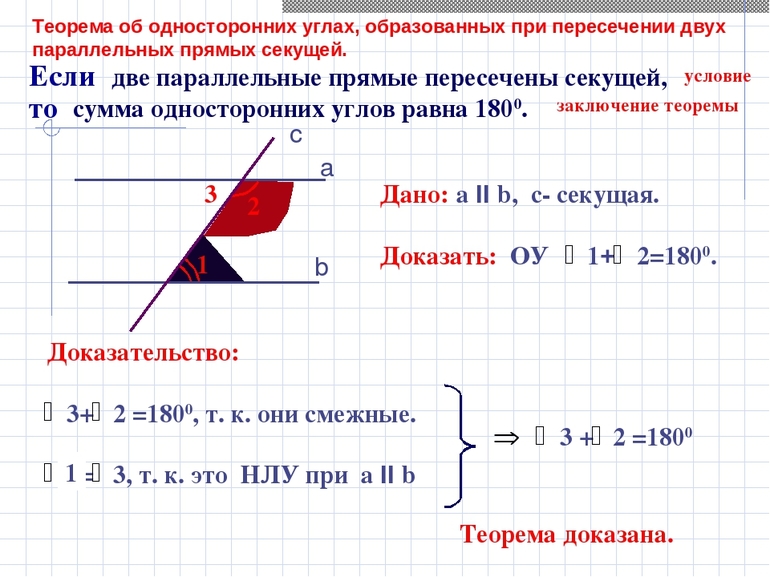
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

Если a ∥ b, то

∠1 +∠2 =180º

(как внутренние односторонние при a ∥ b и секущей c).

Признак параллельных прямых

Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

∠3+∠4 =180º

А так как эти углы — внутренние односторонние при a и b и секущей c,

то a ∥ b (по признаку параллельных прямых).

Могут ли быть внутренние односторонние углы равны?

Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1 и ∠2 — внутренние односторонние углы при прямых a и b и секущей c

∠1 =∠2

тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.

Источник

Внутренние односторонние углы — теория, правило и свойства

Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.

Углы по определению

Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.

Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.

Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.

Доказательство теоремы

Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.

Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.

Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.

Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.

Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.

Следствие из свойства прямых

На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.

Далее можно провести через С1 линию с, перпендикулярную а.

Затем через точку А нужно начертить АС2, которая параллельна с.

После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.

Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.

Построение параллелограмма

Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.

Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.

Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:

По построению AB=BD=AD.

Следовательно, AB=CD.

Точки C и D равноудалены от A и B.

Отрезки AB и CD параллельны.

Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.

Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.

Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.

Углы при пересечении двух прямых

Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.

При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.

На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).

Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:

Углы при пересечении параллельных прямых

Если секущая пересекает две параллельные прямые линии, то:

внутренние накрест лежащие углы равны;
сумма внутренних односторонних углов равна 180°;
соответственные углы равны;
внешние накрест лежащие углы равны;
сумма внешних односторонних углов равна 180°.

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

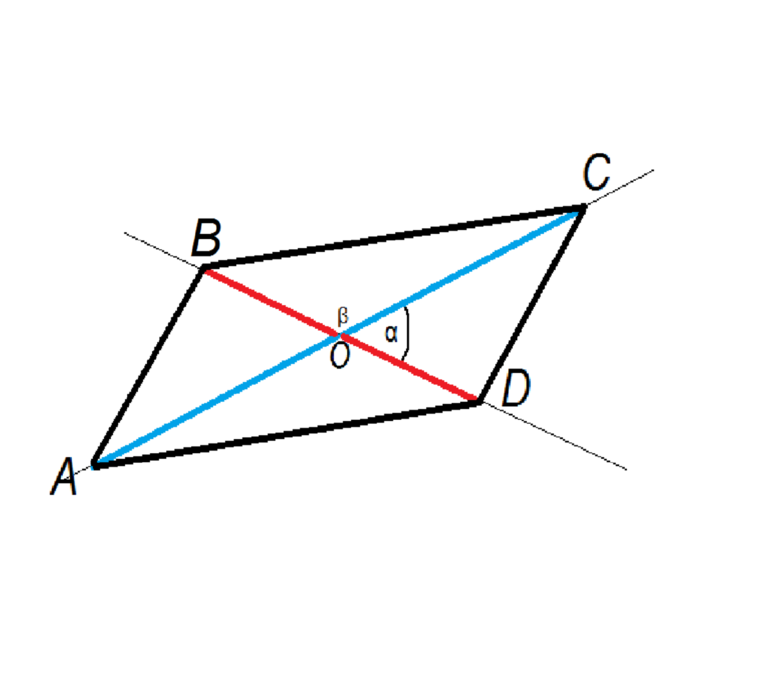
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

источники:

http://izamorfix.ru/matematika/planimetriya/ugly_dvuh_pryam.html

http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/

Источник

Углы по определению

Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.

Доказательство теоремы

Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.

Следствие из свойства прямых

Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.
Далее можно провести через С1 линию с, перпендикулярную а.
Затем через точку А нужно начертить АС2, которая параллельна с.
После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.
Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.

Построение параллелограмма

По построению AB=BD=AD.
Следовательно, AB=CD.
Точки C и D равноудалены от A и B.
Отрезки AB и CD параллельны.
Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.

Источник

На этой странице вы узнаете:

Какими бывают углы?
По каким признакам можно сказать, что треугольники равны?
Что такое коэффициент подобия?
Какие бывают многоугольники?
Какими формулами пользоваться, чтобы найти площадь фигуры?
Что такое окружность и из чего она состоит?
Когда можно вписать окружность в многоугольник, а когда около него можно её описать?

Прямая, отрезок, луч, углы

Квадрат, круг, треугольник. Несомненно, вы знаете о таких геометрических фигурах, эти фигуры относятся к разделу геометрии, который называется планиметрия. Планиметрия – это наука о изучении геометрических фигур на плоскости. Точки, прямые, отрезки, лучи и углы являются основой этого раздела геометрии. Давайте их и рассмотрим.

Прямая – это линия, не имеющая ни начала, ни конца, такая линия может быть бесконечной.

Отрезок – это часть прямой, ограниченная с обеих сторон.

Луч – это отрезок, ограниченный только с одной стороны.

Угол – это фигура, образованная двумя лучами, исходящими из одной точки, измеряется в градусах.

Рассмотрим части угла:

Углы бывают четырёх видов:

Смежные и вертикальные углы

Смежные углы – это углы, имеющие одну общую сторону, а две другие стороны этих углов лежат на одной прямой.

Смежные углы в сумме дают 180°.

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого угла.

Рассмотрим углы при параллельных прямых

Накрест лежащие углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по разные стороны от секущей между параллельным прямыми. Такие углы всегда равны.

Внутренние односторонние углы – это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей между параллельным прямыми. Сумма этих углов 1800.

Соответственные углы — это углы, образованные при пересечении двух параллельных прямых секущей и лежащие по одну сторону от секущей так, что один угол находится между двумя прямыми относительно одной прямой, а другой угол прилегает к другой прямой с внешней стороны. Эти углы равны.

Пусть a || b, а с – секущая

Тогда 3 и 6, 4 и 5 накрест лежащие; 3 и 5, 4 и 6 внутренние односторонние; 1 и 5, 2 и 6, 3 и 7, 4 и 8 соответственные

Треугольники, их виды и признаки их равенства

Сумма углов любого треугольника равна 180°

Для треугольников также верно следующее утверждение: каждая сторона треугольника меньше суммы двух других его сторон

Элементы треугольника:

Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Также медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины (в треугольнике медиана показана как BM)

Биссектриса – это отрезок, делящий угол на два равных угла. Также центром вписанной в треугольник окружности является точка пересечения биссектрис углов треугольника (в треугольнике биссектриса показана как BD)

Высота – это перпендикуляр, опущенный из вершины на одну из сторон треугольника. Также высоты или их продолжения пересекаются в одной точке, которая называется ортоцентром (в треугольнике высота показана как ВН)

Средняя линия – это отрезок, соединяющий середины сторон. Средняя линия треугольника параллельна основанию, и по длине она равна половине основания. Средняя линия трапеции равна половине суммы оснований и параллельна основаниям.

Виды треугольников:

У равностороннего треугольника все стороны равны и углы по 600.

У равнобедренного треугольника равны только две стороны и углы при основании. Медиана, проведенная в нём к основанию, также является биссектрисой и высотой.

У прямоугольного треугольника один угол равен 900 и сумма двух других углов тоже равна 900. Сторона, лежащая напротив прямого угла в таком треугольнике, называется гипотенузой, а две другие — катетами. Катет, лежащий напротив угла 300, равен половине гипотенузы. Медиана, проведённая в прямоугольном треугольнике из вершины прямого угла, равна половине гипотенузы

Признаки равенства треугольников:

Треугольники равны по двум сторонам и углу между ними

АВ = А₁В₁

АС = А₁С₁

Угол ВАС = угол В₁А₁С₁

Треугольники равны по стороне и двум прилежащим к ней углам

АВ = А₁В₁

Угол ВАС = угол В₁А₁С₁

Угол АВС = угол А₁В₁С₁

Треугольники равны по трём сторонам

АВ = А₁В₁

АС = А₁С₁

ВС = В₁С₁

Давайте теперь разберёмся, что значит подобие:

Если треугольники похожие, но отличаются только размером, тогда поможет подобие треугольников

Коэффициент подобия – это число, в которое отличаются стороны треугольников

Если АВС подобен А1В1С1, тогда верно равенство, где к – коэффициент подобия

Если треугольники подобны, тогда отношение их площадей равно квадрату коэффициента подобия

Признаки подобия треугольников:

По двум сторонам и углу между ними

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами, равны, то такие треугольники подобны

По двум углам

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны

По трём сторонам

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны

Площадь треугольника

Площадь треугольника, если известна высота и основание, к которому она проведена

Площадь треугольника с двумя известными сторонами и углом между ними

Площадь прямоугольного треугольника с известными катетами

Площадь правильного треугольника, если известна только сторона

Формула Герона позволяет вычислить площадь треугольника, если известны его стороны

Площадь треугольника, когда известен полупериметр и радиус вписанной окружности

Площадь треугольника, когда известны стороны и радиус описанной окружности

Многоугольник

Многоугольник – это часть плоскости, ограниченная замкнутой ломаной линией

Многоугольники бывают выпуклые и невыпуклые

Многоугольник является выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону

Для нахождения площади любого выпуклого четырёхугольника существует формула:

Виды многоугольников:

Параллелограмм – это четырёхугольник, у которого стороны попарно параллельны

Свойства параллелограмма:

Противоположные стороны равны
Противоположные углы равны
Диагонали делятся точкой пересечения пополам

Формулы площади

Прямоугольник – это четырехугольник, у которого все углы прямые

Свойства прямоугольника:

Диагонали равны
Противоположные стороны параллельны и равны
Угол между сторонами прямой
Сумма углов 360 градусов

Формула площади

Квадрат – это частный случай прямоугольника

Свойства квадрата:

Диагонали взаимно перпендикулярны и равны
Диагонали делят углы квадрата пополам
Все стороны равны
Угол между сторонами прямой
Сумма углов 360 градусов

Формулы площади

Трапеция – это четырёхугольник с двумя параллельными сторонами (основаниями), а две другие стороны у него не параллельны

Трапеция может быть произвольной, равнобедренной или прямоугольной.

Общие свойства трапеции:

Сумма углов, прилежащих к боковой стороне, равна 180 градусов
Средняя линия равна полусумме оснований
Отрезок, соединяющий середины диагоналей, равен полуразности её оснований

Свойства равнобедренной трапеции:

Углы при основании равны
Диагонали равны

Формулы площади

Ромб – это параллелограмм, у которого все стороны равны

Свойства ромба:

Противоположные углы равны
Все стороны равны
Диагонали делятся точкой пересечения пополам
Диагонали перпендикулярны друг другу
Диагонали являются биссектрисами углов

Формулы площади

Окружность

Окружность – это замкнутая прямая на плоскости, все точки которой равноудалены от центра (например, обруч)

Дуга – это часть окружности, заключённая между двумя точками, лежащими на этой окружности

В окружности можно провести радиус, диаметр и хорду

Радиус – расстояние от центра до окружности

Диаметр – прямая, соединяющая две точки на окружности и проходящая через центр окружности

Хорда – прямая, соединяющая две любых точки окружности

Также в окружности есть два вида углов

Вписанный угол – угол, у которого вершина лежит на окружности, а стороны угла пересекают её. Такой угол равен половине дуги, на которую опирается

Центральный угол – угол, у которого вершина находится в центре окружности, а стороны угла пересекают её. Данный угол равен дуге, на которую опирается

Окружность, вписанная в четырёхугольник

Чтобы вписать окружность в четырёхугольник, суммы длин противоположных сторон четырёхугольника должны быть равны

a + c = b + d

Окружность, вписанная в прямоугольный треугольник

У вписанной в прямоугольный треугольник окружности радиус вычисляется по формуле r

Окружность, описанная около четырёхугольника

Чтобы описать окружность около четырёхугольника, необходимо и достаточно выполнения одного из условий:

Сумма противоположных углов треугольника равна 180 градусов
Вписанные углы, опирающиеся на одну хорду, равны

Окружность, описанная около прямоугольного треугольника

Диаметр окружности равен гипотенузе вписанного треугольника
Радиус описанной окружности равен половине гипотенузы

R=c/2, где c-диаметр

Теорема синусов:

Отношения длин сторон треугольника к синусам противолежащих углов равны между собой, а также равны двум радиусам описанной окружности

Фактчек

Равенство треугольников можно определить по одному из трёх признаков равенства треугольников (по двум сторонам и углу между ними, по стороне и прилежащим к ней углам, по трем сторонам).

Признаки подобия немного отличаются от признаков равенства треугольников (по двум сторонам и углу между ними, по двум углам, по трём сторонам), по ним определяется отношение соответственных сторон одного треугольника к сторонам другого.

Для нахождения площади выпуклого четырёхугольника есть универсальная формула
S = ½* d1* d2 *sin α , где d 1, d 2 — длины диагоналей четырехугольника, α — угол между диагоналями четырехугольника.

Окружность можно вписать в четырёхугольник, если суммы его противоположных сторон равны, а описать окружность около четырёхугольника можно, если пара противоположных углов в сумме даёт 180 градусов.

Так же стоит помнить, что в теореме синусов равны не только отношения противолежащих сторон к синусам углов, но и каждое такое отношение равно двум радиусам описанной окружности.

Проверь себя

Задание 1.
Чему равен отрезок соединяющий середины диагоналей в трапеции с основаниями а и b?

1. (a + b) / 2
2. (a — b) / 2
3. a-b
4. a+b

Задание 2.
В прямоугольном треугольнике один из катетов равен половине гипотенузы, чему равен угол напротив этого катета?

1. 90°
2. 60°
3. 30°
4. 20°

Задание 3.
Чему равен вписанный угол, опирающийся на хорду равную 84 градусам?

1. 42°
2. 21°
3. 84°
4. 90°

Задание 4.
Чему равен радиус описанного прямоугольного треугольника с катетами 3 и 4?

1. 5
2. 1,5
3. 2,5
4. 2

Задание 5.
Из каких длин сторон треугольника нельзя получить треугольник?

1. 4 16 12
2. 5 6 9
3. 3. 41 18 24
4. 17 14 28

Ответы: 1. — 2; 2. — 2; 3. — 1; 4. — 3; 5. — 1.

Источник

Внутренние углы с одинаковой стороны — это два угла, которые находятся на одной стороне от поперечной линии и между двумя пересекающимися параллельными линиями. Поперечная линия — это прямая линия, пересекающая одну или несколько линий.

Теорема об односторонних внутренних углах утверждает, что если трансверсаль разрезает две параллельные прямые, то внутренние углы на той же стороне трансверсали являются дополнительными. Дополнительные углы — это углы, которые в сумме составляют 180 °.

Доказательство теоремы об односторонних внутренних углах

Пусть L ₁ и L ₂ — параллельные прямые, разрезанные трансверсалью T, так что ∠2 и ∠3 на рисунке ниже являются внутренними углами на одной стороне T. Покажем, что ∠2 и ∠3 являются дополнительными.

Поскольку ∠1 и ∠2 образуют линейную пару, они дополняют друг друга. То есть ∠1 + ∠2 = 180 °. По теореме об альтернативном внутреннем угле ∠1 = ∠3. Таким образом, 3 + ∠2 = 180 °. Следовательно, 2 и ∠3 дополнительные.

Теорема об односторонних внутренних углах

Джон Рэй Куэвас

Обращение теоремы о односторонних внутренних углах

Если трансверсаль разрезает две линии и пара внутренних углов на одной стороне трансверсали является дополнительной, то линии параллельны.

Доказательство теоремы обратного одностороннего внутреннего угла

Пусть L ₁ и L ₂ — две прямые, разрезанные трансверсалью T, такие, что ∠2 и ∠4 являются дополнительными, как показано на рисунке. Докажем, что L ₁ и L ₂ параллельны.

Поскольку ∠2 и ∠4 дополнительные, то ∠2 + ∠4 = 180 °. По определению линейной пары ∠1 и ∠4 образуют линейную пару. Таким образом, ∠1 + ∠4 = 180 °. Используя свойство транзитивности, имеем ∠2 + ∠4 = ∠1 + ∠4. По свойству сложения 2 = ∠1

Следовательно, L ₁ параллельна L ₂.

Обращение теоремы о односторонних внутренних углах

Джон Рэй Куэвас

Пример 1: Нахождение угловых мер с помощью теоремы о внутренних углах одной стороны

На прилагаемом рисунке отрезок AB и отрезок CD, ∠D = 104 °, и луч AK делят пополам ∠DAB . Найдите меру ∠DAB, ∠DAK и ∠KAB.

Пример 1: Нахождение угловых мер с помощью теоремы о внутренних углах одной стороны

Джон Рэй Куэвас

Решение

Так как сторона АВ и параллельны, то внутренние углы, ∠D и ∠DAB , являются дополнительными. Таким образом, ∠DAB = 180 ° — 104 ° = 76 °. Кроме того, поскольку луч AK делит пополам ∠DAB, то ∠DAK ≡ ∠KAB.

Окончательный ответ

Следовательно, ∠DAK = ∠KAB = (½) (76) = 38.

Пример 2: Определение параллельности двух линий, разрезанных поперечно

Определите, параллельны ли линии A и B с учетом внутренних углов с одной стороны, как показано на рисунке ниже.

Пример 2: Определение параллельности двух линий, разрезанных поперечно

Джон Рэй Куэвас

Решение

Примените теорему об односторонних внутренних углах, чтобы выяснить, параллельна ли прямая A прямой B. Теорема утверждает, что внутренние углы на одной стороне должны быть дополнительными, если прямые, пересекаемые поперечной линией, параллельны. Если два угла в сумме составляют 180 °, тогда прямая A параллельна прямой B.

127 ° + 75 ° = 202 °

Окончательный ответ

Поскольку сумма двух внутренних углов составляет 202 °, линии не параллельны.

Пример 3: Нахождение значения X двух внутренних углов с одинаковой стороны

Найдите значение x, при котором L ₁ и L _{2 будут} параллельны.

Пример 3: Нахождение значения X двух внутренних углов с одинаковой стороны

Джон Рэй Куэвас

Решение

Приведенные уравнения являются внутренними углами одной стороны. Поскольку прямые считаются параллельными, сумма углов должна составлять 180 °. Составьте выражение, складывающее два уравнения до 180 °.

(3x + 45) + (2x + 40) = 180

5х + 85 = 180

5x = 180 — 85

5x = 95

х = 19

Окончательный ответ

Конечное значение x, которое удовлетворяет уравнению, равно 19.

Пример 4: Нахождение значения X с учетом уравнений односторонних внутренних углов

Найдите значение x при m∠4 = (3x + 6) ° и m∠6 = (5x + 12) °.

Пример 4: Нахождение значения X с учетом уравнений односторонних внутренних углов

Джон Рэй Куэвас

Решение

m∠4 + m∠4 = 180

3х + 6 + 5х + 12 = 180

8x + 20 = 180

8x = 180 — 20

8x = 160

х = 20

Окончательный ответ

Окончательное значение x, которое удовлетворяет уравнению, равно 20.

Пример 5: Нахождение значения переменной Y с помощью теоремы о внутренних углах одной стороны

Решением для значения y с учетом его угловой меры является внутренний угол той же стороны с углом 105 °.

Пример 5: Нахождение значения переменной Y с помощью теоремы о внутренних углах одной стороны

Джон Рэй Куэвас

Решение

Проследите, чтобы y и тупой угол 105 ° были внутренними углами одной стороны. Это просто означает, что эти два должны равняться 180 °, чтобы удовлетворять теореме об односторонних внутренних углах.

у + 105 = 180

у = 180 — 105

у = 75

Окончательный ответ

Конечное значение x, которое удовлетворяет теореме, равно 75.

Пример 6: Определение угловой меры для всех внутренних углов с одинаковой стороны

Линии L ₁ и L ₂ на схеме, показанной ниже, параллельны. Найдите угловые размеры m∠3, m∠4 и m∠5.

Пример 6: Определение угловой меры для всех внутренних углов с одинаковой стороны

Джон Рэй Куэвас

Решение

Прямые L ₁ и L ₂ параллельны, и согласно теореме об односторонних внутренних углах углы на одной стороне должны быть дополнительными. Обратите внимание, что m∠5 является дополнением к данной угловой мере 62 °, и

m∠5 + 62 = 180

m∠5 = 180 — 62

m∠5 = 118

Поскольку m∠5 и m∠3 являются дополнительными. Составьте выражение, сложив полученную угловую меру m∠5 с m∠3 до 180.

m∠5 + m∠3 = 180

118 + m∠3 = 180

m∠3 = 180 — 118

m∠3 = 62

То же самое относится к измерению угла mÀ4 и данному углу 62 °. Приравняйте сумму двух к 180.

62 + m∠4 = 180

m∠4 = 180 — 62

m∠4 = 118

Это также показывает, что m∠5 и m∠4 — углы с одинаковой угловой мерой.

Окончательный ответ

m∠5 = 118 °, m∠3 = 62 °, m∠4 = 118 °

Пример 7: Доказательство того, что две прямые не параллельны

Линии L ₁ и L ₂, как показано на рисунке ниже, не параллельны. Опишите угловую меру z?

Пример 7: Доказательство того, что две прямые не параллельны

Джон Рэй Куэвас

Решение

Учитывая, что L ₁ и L ₂ не параллельны, нельзя предполагать, что углы z и 58 ° являются дополнительными. Значение z не может быть 180 ° — 58 ° = 122 °, но это может быть любая другая мера большей или меньшей меры. Кроме того, из показанной схемы очевидно, что L ₁ и L ₂ не параллельны. Отсюда легко сделать умное предположение.

Окончательный ответ

Угловая мера z = 122 °, что означает, что L ₁ и L ₂ не параллельны.

Пример 8: Решение угловых величин внутренних углов на одной стороне

Найдите угловые меры ∠b, ∠c, ∠f и ∠g, используя теорему о внутреннем угле с той же стороны, учитывая, что прямые L ₁, L ₂ и L ₃ параллельны.

Пример 8: Решение угловых величин внутренних углов на одной стороне

Джон Рэй Куэвас

Решение

Учитывая, что L ₁ и L ₂ параллельны, m∠b и 53 ° являются дополнительными. Составьте алгебраическое уравнение, показывающее, что сумма m∠b и 53 ° равна 180 °.

m∠b + 53 = 180

m∠b = 180 — 53

m∠b = 127

Так как поперечная линия разрезает L ₂, поэтому m∠b и м ∠c являются дополнительными. Составьте алгебраическое выражение, показывающее, что сумма ∠b и ∠c равна 180 °. Подставим полученное ранее значение m∠b.

m∠b + m∠c = 180

127 + m∠c = 180

m∠c = 180–127

m∠c = 53

Поскольку прямые L ₁, L ₂ и L ₃ параллельны, и прямая поперечная линия разрезает их, все внутренние углы с одной стороны между прямыми L ₁ и L ₂ одинаковы с внутренней стороной L ₂ с той же стороны. и L ₃.

m∠f = m∠b

m∠f = 127

m∠g = m∠c

m∠g = 53

Окончательный ответ

m∠b = 127 °, m∠c = 53 °, m∠f = 127 °, m∠g = 53 °

Пример 9: Определение внутренних углов одинаковой стороны на диаграмме

Приведите сложный рисунок ниже; определить три внутренних угла с одинаковой стороны.

Пример 9: Определение внутренних углов одинаковой стороны на диаграмме

Джон Рэй Куэвас

Решение

На рисунке присутствует множество внутренних углов с одной стороны. Путем внимательного наблюдения можно с уверенностью сделать вывод, что три из многих внутренних углов одной стороны равны 6 и ∠10, ∠7 и ∠11, а также ∠5 и ∠9.

Пример 10: Определение параллельных линий с учетом условия

Учитывая, что ∠AFD и ∠BDF являются дополнительными, определите, какие линии на рисунке параллельны.

Пример 10: Определение параллельных линий с учетом условия

Джон Рэй Куэвас

Решение

При внимательном наблюдении, при условии, что ∠AFD и ∠BDF являются дополнительными, параллельными линиями являются линия AFJM и линия BDI.

Изучите другие статьи по математике

Как найти общий термин последовательностей
Это полное руководство по поиску общего термина последовательностей. Приведены примеры, демонстрирующие пошаговую процедуру нахождения общего члена последовательности.
Задачи о возрасте и смеси и решения в алгебре Задачи о
возрасте и смеси — сложные вопросы в алгебре. Это требует глубоких навыков аналитического мышления и больших знаний в области создания математических уравнений. Практикуйте эти возрастные и смешанные задачи с решениями по алгебре.
Метод AC: разложение квадратичных трехчленов на множители с помощью метода AC
Узнайте, как использовать метод AC для определения факторизации трехчлена. После того, как доказана факторизация, перейдите к нахождению факторов трехчлена, используя сетку 2 x 2.
Как вычислить
момент инерции сложных или сложных форм Это полное руководство по вычислению момента инерции сложных или неправильных форм. Знать основные необходимые шаги и формулы и владеть решающим моментом инерции.
Методы калькуляции четырехугольников в плоской геометрии
Узнайте, как решать задачи, связанные с четырехугольниками в плоской геометрии. Он содержит формулы, методы калькулятора, описания и свойства, необходимые для интерпретации и решения задач Четырехугольника.
Как построить график эллипса с учетом уравнения
Узнайте, как построить график эллипса с учетом общей формы и стандартной формы. Знать различные элементы, свойства и формулы, необходимые для решения задач, связанных с эллипсом.
Как рассчитать приблизительную площадь фигур неправильной формы с помощью правила Симпсона 1/3
Узнайте, как приблизить площадь фигур неправильной формы с помощью правила 1/3. В этой статье рассматриваются концепции, проблемы и решения о том, как использовать правило Симпсона 1/3 для аппроксимации площади.
Определение площади поверхности и объема усиков пирамиды и конуса
Узнайте, как рассчитать площадь поверхности и объем усеченных поверхностей правого кругового конуса и пирамиды. В этой статье рассказывается о концепциях и формулах, необходимых для определения площади поверхности и объема усеченных твердых тел.
Определение
площади поверхности и объема усеченных цилиндров и призм Узнайте, как вычислять площадь поверхности и объем усеченных твердых тел. В этой статье рассматриваются концепции, формулы, проблемы и решения, касающиеся усеченных цилиндров и призм.
Как использовать правило знаков Декарта (с примерами)
Научитесь использовать правило знаков Декарта для определения количества положительных и отрицательных нулей в полиномиальном уравнении. Эта статья представляет собой полное руководство, которое определяет Правило знаков Декарта, процедуру его использования, а также подробные примеры и решения.
Решение проблем связанных ставок в исчислении
Научитесь решать различные виды задач связанных ставок в исчислении. Эта статья представляет собой полное руководство, которое показывает пошаговую процедуру решения проблем, связанных со связанными / связанными ставками.

Источник