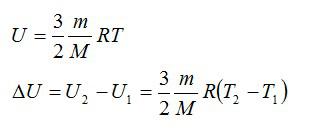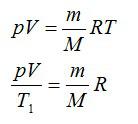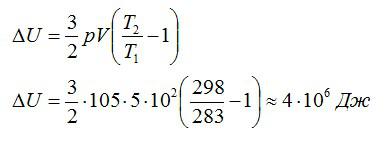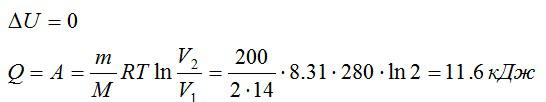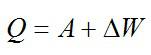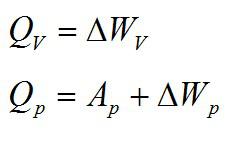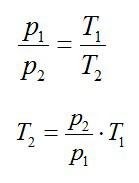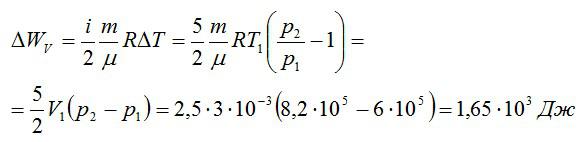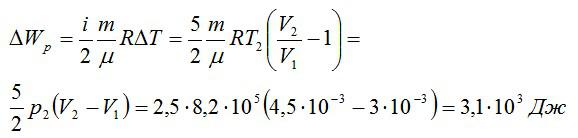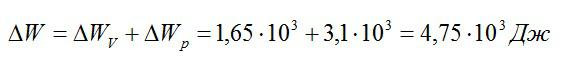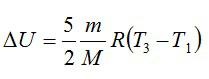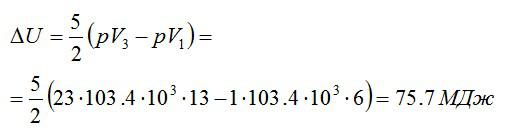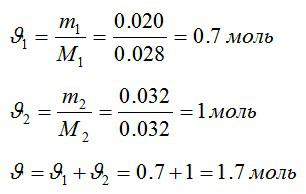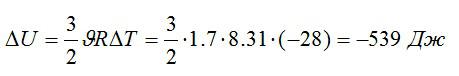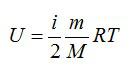ТЕРМОДИНАМИКА
Внутренней энергией тела в молекулярно-кинетической теории называется суммарная кинетическая энергия хаотического движения всех молекул тела плюс суммарная потенциальная энергия взаимодействия этих молекул друг с другом (но не с другими телами).
Внутренняя энергия одноатомного идеального газа
В одноатомном идеальном газе молекулы не взаимодействуют друг с другом, по этому его внутренняя энергия такого газа будет определяться как кинетическая энергия беспорядочного движения молекул.
Тогда внутренняя энергия будет определяться как произведение средней кинетической энергии и количества молекул из которых состоит наш газ:
Вспоминаем что средняя кинетическая энергия поступательного движения молекул определяется как:
А количество молекул в газе можно найти следующим образом:
Делаем небольшие алгебраические преобразования.
Так как произведение числа Авогадро и постоянную Больцмана
называют универсальной газовой постоянной
, получаем:
Из полученного уравнения видно что внутренняя энергия одноатомного идеального газа напрямую зависит от его температуры. В таком случае изменение внутренней энергии можно определить как:
Работа газа при изобарном процессе
Работа газа при произвольном процессе равна площади под гафиком процесса в координатах (P,V). При линейной зависимости давления от объема равна:
Первый закон термодинамики количество теплоты сообщаемое газу идет на изменение внутренней энергии этого газа (), а так же на совершение работы этим газом (
).
Применение первого закона термодинамики к изопроцессам.
Изобарный
Изохорный
Изотермический
Адиабатный
Адиабатный процесс — процесс протекающий без внешнего теплообмена с окружающей средой.
Еще одна интерпретация первого закона термодинамики звучит следующим образом: «Изменение внутренней энергии () тела происходит в результате теплообмена (теплопередачи) либо совершения работы (
) над этим телом».
Количество теплоты () — энергия которую приобретает или теряет тело в результате теплообмена.
Теплопередача — это процесс передачи тепла от более нагретого тела жидкости или газа к менее нагретому. Можно выделить три вида теплопередачи: 1. Теплопроводность — передача тепла между различными частями одного тела, либо между телами при их непосредственном контакте; 2. Конвекция — вид теплообмена, при котором тепло передается струями и потоками жидкости или газа; 3. Излучение — передача тепла с помощью инфракрасного спектра электромагнитных волн.
Количество теплоты при нагревании или охлаждении
Удельная теплоемкость () — количество теплоты необходимое чтоб нагреть 1 килограмм данного вещества на 1 градус.
Количество теплоты при плавлении (кристаллизации) При плавлении тело получает тепло, по этому количество теплоты берется со знаком плюс, а при кристаллизации, жидкость напротив отдает свою энергию, по этому количество теплоты имеет отрицательное значение.
Удельная теплота плавления и кристаллизации () — количество теплоты необходимое для того, чтоб расславить 1 килограмм данного вещества.
Количество теплоты при парообразовании (конденсации) При кипении жидкость получает тепло, по этому количество теплоты берется со знаком плюс, а при конденсации, пар напротив теряет энергию, по этому количество теплоты имеет отрицательное значение.
Удельная теплота парообразования и конденсации () — количество теплоты необходимое для того, чтоб превратить в пар 1 килограмм жидкости.
Количество теплоты выделяемое при сгорании топлива
Удельная теплота сгорания () — количество теплоты выделяемое при сгорании одного килограмма топлива.
Уравнение теплового баланса В изолированной системе в результате теплообмена устанавливается тепловое равновесие, а католичества теплоты получаемые или отдаваемые телами этой системы в сумме будут равны нулю.
Тепловая машина
Тепловая машина — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник).
В циклическом процессе изменение внутренней энергии за цикл равно нулю, а работа выполняемая машиной за цикл будет равна разности теплоты полученной от нагревателя
и теплоты отданной холодильнику
.
КПД циклического процесса
КПД идеальной тепловой машины работающей по циклу Карно
— соответственно температуры нагревателя и холодильника.
Термодинамика
в отличие от молекулярно-кинетической
теории, изучает физические свойства
макроскопических тел (термодинамических
систем), не вникая в их молекулярное
строение. Термодинамический метод
базируется на законе сохранения и
превращении энергии.
Физические
величины, характеризующие термодинамическую
систему, называются термодинамическими
параметрами. К ним относятся: объем,
давление, температура, концентрация и
др. Любое изменение в термодинамической
системе, связанное с изменением ее
параметров, называетсятермодинамическим
процессом, а уравнение, связывающее
между собой параметры системы, называетсяуравнением состояния. Примером
такого уравнения является уравнение
Менделеева — Клапейрона (6.1)
Внутренняя энергия идеального газа
Важнейшей
характеристикой термодинамической
системы является ее внутренняяэнергияU, складывающая
из потенциальной энергии взаимодействия
частиц системы и кинетической энергии
их теплового движения.
Внутренняя
энергия является функцией состояния
системы, т.е. в каждом состоянии система
обладает вполне определенным значением
внутренней энергии, не зависящим от
того, каким путем система перешла в это
состояние.
Так как в
идеальном газе потенциальная энергия
молекул равна нулю (считается, что
молекулы между собой не взаимодействуют),
то внутренняя энергия идеального газа
равна полной кинетической энергии всех
его молекул. Обозначив внутреннюю
энергию одного моля газа через Uμ,
а среднюю кинетическую энергию молекулы
через,
можем записать для одного моля газа:
Uμ
= NA(6.18)
где NA– число Авогадро.
Подставляя
значение
из формулы (6.12), получим внутреннюю
энергию для одного моля газа:
(6.19)
Если число молей
,
то для любого количества вещества
(6.20)
Следовательно,
внутренняя энергия газа пропорциональна
его массе, числу степеней свободы
молекулы и абсолютной температуре газа.
Первый закон термодинамики
Внутреннюю
энергию термодинамической системы
можно изменить за счет работы, которую
либо внешние тела совершают над ней,
либо сама система совершает над внешними
телами. Например, приложив внешнюю силу,
мы сжимаем газ, в результате чего его
температура повышается, а, следовательно,
увеличивается и внутренняя энергия.
Внутреннюю энергию можно изменить
также, передавая системе (или отнимая
у нее) некоторое количество теплоты.
Согласно закону
сохранения энергии, изменение внутренней
энергии системы должно равняться сумме
полученной ею теплоты и совершенной
над ней работы. Эта формулировка
закона сохранения энергии применительно
к термодинамическим системам носит
названиепервого закона термодинамики:
ΔU = Q – A
или
Q = ΔU
+ A (6.21)
Условимся
считать, что теплота положительна Q>0
тогда, когда она сообщается системе, а
работа положительна, когда система
совершает ее над внешними телами.
В дифференциальной
форме первый закон термодинамики имеет
вид:
dQ=dU+dA
Необходимо
подчеркнуть, что в отличие от внутренней
энергии, являющейся функцией состояния,
работа и количество теплоты зависят не
только от начального и конечного
состояний системы, но и от пути, по
которому происходило изменение ее
состояния. Следовательно, величины dQиdА не являются полными
дифференциалами, по которым может
производиться интегрирование. Для того,
чтобы подчеркнуть это обстоятельство
для бесконечно малых приращений тепла
и работы применяют более корректное
обозначение
Qи
Aи тогда первый закон примет вид:
Q=dU+
A(6.22)
Найдем в общем
виде работу, совершаемую газом, (рис.6.6,
а). Если газ, расширяясь, перемещает
поршень на расстояние dx,
то он производит работу (см. формулу
2.19):
Рис.6.6
A
= F · dx = P · S · dx = PdV,
(6.22)
где S– площадь
поршня;Sdx=dV– изменение объема газа в цилиндре.
Полная работа, совершаемая
газом при изменении его объема от V1доV2, равна:


Графически
процесс изменения состояния газа при
его расширении изображается участком
кривой 1-2 в координатах Р – V(рис.6.6, б). Точки 1 и 2 соответствуют
начальному и конечному состояниям газа.
Элементарная работаPdVизображается заштрихованной площадью.
Полная работа, определяемая формулой
6.23, изображается площадьюV1– 1 – 2 -V2под кривой
1 – 2.
Теплоемкость
идеальных газов.
Количество
тепла, которое надо сообщить телу, чтобы
изменить его температуру на 1 К, называется
теплоемкостьютела С.
Согласно этому
определению
,
[С] = Дж/К
(6.24)
Теплоемкость
единицы массы вещества называется
удельной теплоемкостью Суд
(6.25)
Теплоемкость
одного моля называется молярной
теплоемкостьюСм.
,
[См] = Дж/моль · К
(6.26)
где ν = m/μ– число молей.
Как следует из
формул (6.25) и (6.26), удельная теплоемкость
связана с молярной соотношением:
См= Суд· μ
(6.27)
Теплоемкость
газа зависит от того, при каких условиях
она определяется: при постоянном объеме
или постоянном давлении. Покажем это,
для чего запишем первый закон термодинамики
с учетом формулы (6.22):
δQ = dU + PdV
(6.28)
Если газ
нагревается при постоянном объеме
(изохорный процесс), то dV=0
и работа РdV= 0. В этом
случае δQ=dU,
т.е. передаваемое газу тепло идет только
на изменение его внутренней энергии.
Теплоемкость газа при постоянном объеме:
С учетом формулы
(6.20)
(6.29)
и тогда изохорная теплоемкость
(6.30)
Для одного моля
(m/µ = 1) молярная теплоемкость
при постоянном объеме
(6.31)
Теперь, с учетом
равенства (6.28), найдем теплоемкость при
постоянном давлении (изобарный процесс):
(6.32)
(при этом учли,
что dU/dT=CV).
Из (6.32) следует, что СP>CV.
Это объясняется тем, что при нагревании
приP=constсообщенное газу тепло идет не только
на увеличение его внутренней энергии,
но и на совершение работы.
Для одного
моляидеального газа уравнение
Менделеева – Клапейрона имеет видPV=RTи потокуPdV=RdT.
Учитывая это, получимуравнение Майера,
выражающее связь междумолярнымитеплоемкостями при постоянном давлении
и постоянном объеме:
Смр= Сmv+R(6.33)
Учитывая
выражение (6.31) можно записать в виде
(6.34)
При рассмотрении
термодинамических процессов важно
знать характерное для каждого газа
отношение СPк СV:
(6.35)
Величина γ
называется коэффициентом Пуассона,i– число степеней
свободы молекул (см. рис.6.2).
Повышение
температуры приводит, как отмечалось
выше, к появлению колебательных степеней
свободы, в результате чего теплоемкость
возрастает. Наоборот, при низких
температурах число степеней свободы
уменьшается, так как «вымораживаются»
вращательные степени свободы и
теплоемкость газа уменьшается.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статьи
Линия УМК А. В. Грачева. Физика (7-9)
Линия УМК А. В. Грачева. Физика (10-11) (БУ)
Линия УМК Г. Я. Мякишева, М.А. Петровой. Физика (10-11) (Б)
Линия УМК А. Е. Гуревича. Физика (7-9)
Физика
Первый закон термодинамики. Как рассказать просто о сложном?
Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях.
05 июля 2019
1. Определение первого закона термодинамики
Термодинамика — раздел физики, в котором изучаются процессы изменения и превращения внутренней энергии тел, а также способы использования внутренней энергии тел в двигателях. Собственно, именно с анализа принципов первых тепловых машин, паровых двигателей и их эффективности и зародилась термодинамика. Можно сказать, что этот раздел физики начинается с небольшой, но очень важно работы молодого французского физика Николя Сади Карно.
Самым важным законом, лежащим в основе термодинамики является первый закон или первое начало термодинамики. Чтобы понять суть этого закона, для начала, вспомним что называется внутренней энергией. ВНУТРЕННЯЯ ЭНЕРГИЯ тела — это энергия движения и взаимодействия частиц, из которых оно состоит. Нам хорошо известно, что внутреннюю энергию тела можно изменить, изменив температуру тела. А изменять температуру тела можно двумя способами:
- совершая работу (либо само тело совершает работу, либо над телом совершают работу внешние силы);
- осуществляя теплообмен — передачу внутренней энергии от одного тела к другому без совершения работы.
Нам, также известно, что работа, совершаемая газом, обозначается Аг, а количество переданной или полученной внутренней энергии при теплообмене называется количеством теплоты и обозначается Q. Внутреннюю энергию газа или любого тела принято обозначать буквой U, а её изменение, как и изменение любой физической величины, обозначается с дополнительным знаком Δ, то есть ΔU.

Физика. 10 класс. Базовый уровень. Учебник
Большое количество красочных иллюстраций, графиков и схем, разнообразные вопросы и задания, а также дополнительные сведения и любопытные факты способствуют эффективному усвоению учебного материала.
Купить
Сформулируем ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ для газа. Но, прежде всего, отметим, что когда газ получает некоторое количество теплоты от какого-либо тела, то его внутренняя энергия увеличивается, а когда газ совершает некоторую работу, то его внутренняя энергия уменьшается. Именно поэтому первый закон термодинамики имеет вид:
ΔU = Q — Aг
Так как работа газа и работа внешних сил над газом равны по модулю и противоположны по знаку, то первый закон термодинамики можно записать в виде:
ΔU = Q + Aвнеш.
Понять суть этого закона довольно просто, ведь изменить внутреннюю энергию газа можно двумя способами: либо заставить его совершить работу или совершить над ним работу, либо передать ему некоторое количество теплоты или отвести от него некоторое количество теплоты.
2. Первый закон термодинамики в процессах
Применительно к изопроцессам первый закон термодинамики может быть записан несколько иначе, учитывая особенности этих процессов. Рассмотрим три основных изопроцесса и покажем, как будет выглядеть формула первого закона термодинамики в каждом из них.
- Изотермический процесс — это процесс, происходящий при постоянной температуре. С учётом того, что количество газа также неизменно, становится ясно, что так как внутренняя энергия зависит от температуры и количества газа, то в этом процессе она не изменяется, то есть U = const, а значит ΔU = 0, тогда первый закон термодинамики будет иметь вид: Q = Aг.
- Изохорный процесс — это процесс, происходящий при постоянном объёме. То есть в этом процессе газ не расширяется и не сжимается, а значит не совершается работа ни газом, ни над газом, тогда Аг = 0 и первый закон термодинамики приобретает вид: ΔU = Q.
- Изобарный процесс — это процесс, при котором давление газа неизменно, но и температура, и объём изменяются, поэтому первый закон термодинамики имеет самый общий вид: ΔU = Q — Аг.
- Адиабатный процесс — это процесс, при котором теплообмен газа с окружающей средой отсутствует (либо газ находится в теплоизолированном сосуде, либо процесс его расширения или сжатия происходит очень быстро). То есть в таком процессе газ не получает и не отдаёт количества теплоты и Q = 0. Тогда первый закон термодинамики будет иметь вид: ΔU = —Аг.
3. Применение
Первое начало термодинамики (первый закон) имеет огромное значение в этой науке. Вообще понятие внутренней энергии вывело теоретическую физику 19 века на принципиально новый уровень. Появились такие понятия как термодинамическая система, термодинамическое равновесие, энтропия, энтальпия. Кроме того, появилась возможность количественного определения внутренней энергии и её изменения, что в итоге привело учёных к пониманию самой природы теплоты, как формы энергии.
Ну, а если говорить о применении первого закона термодинамики в каких-либо задачах, то для этого необходимо знать два важных факта. Во-первых, внутренняя энергия идеального одноатомного газа равна: 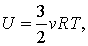
4. Методические советы учителям
-
Обязательно обратить внимание учащихся на знаки работы газа, количества теплоты и изменения внутренней энергии и научить их по графику процесса в координатах р—V определять эти знаки, для чего удобно использовать подобную таблицу:
Процесс
р
V
T
U
ΔU
Aг
Q
- Лучше всего, рассмотреть не только сам вид первого закона термодинамики в различных процессах, но и способы расчёта всех входящих в него величин.
- Обязательно на конкретных примерах, как числовых, так и графических, показать применение первого закона термодинамики.
- Уделить особое внимание процессу, в котором давление линейно зависит от объёма — с графиками и примерами применения к этому процессу первого закона термодинамики.
- Показать примеры на расчёт коэффициента полезного действия по графику циклического процесса с применением первого закона термодинамики и формул работы газа и изменения его внутренней энергии.
#ADVERTISING_INSERT#
Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
Массу гелия выразим из уравнения Клапейрона-Менделеева:
Тогда можно записать:
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
В изохорном и изобарном процессе соответственно:
Изохорное нагревание:
Изменение внутренней энергии при изохорном процессе:
Изменение внутренней энергии при изобарном процессе:
Общее изменение внутренней энергии:
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
Изменение внутренней энергии:
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
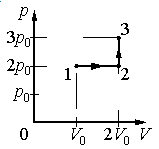
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.2k