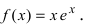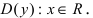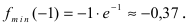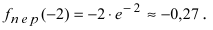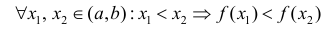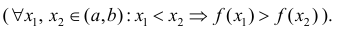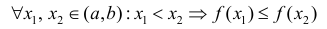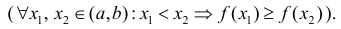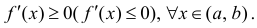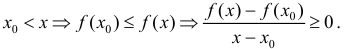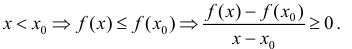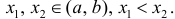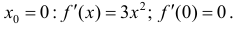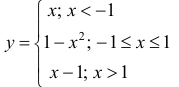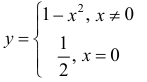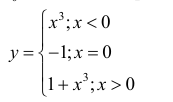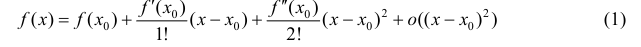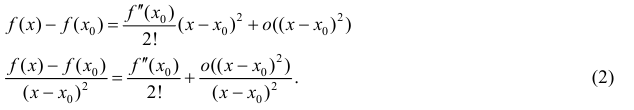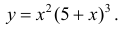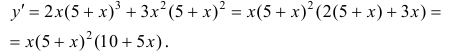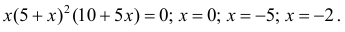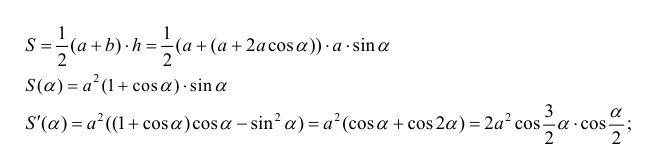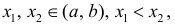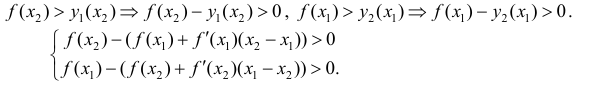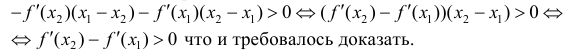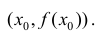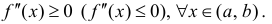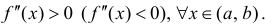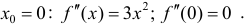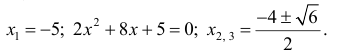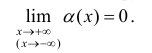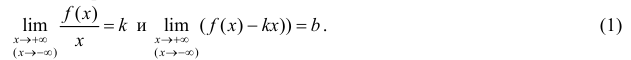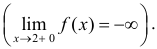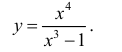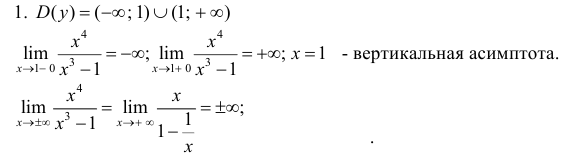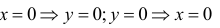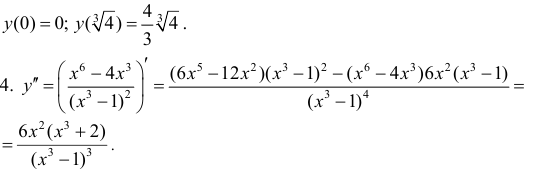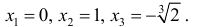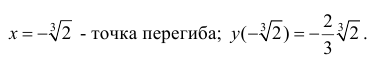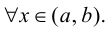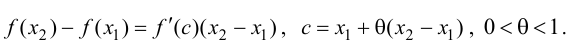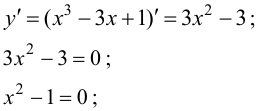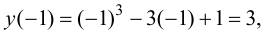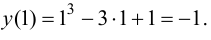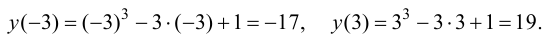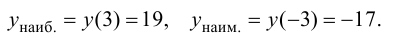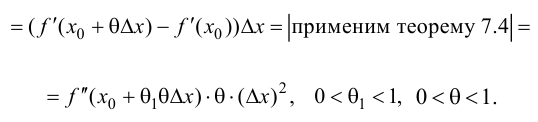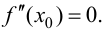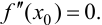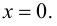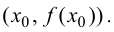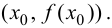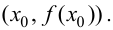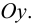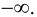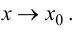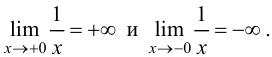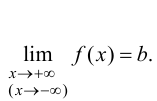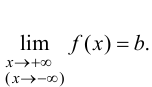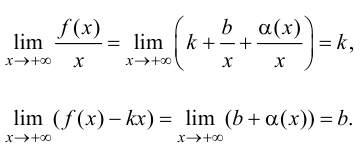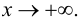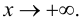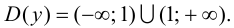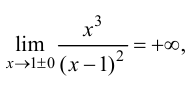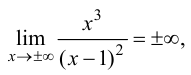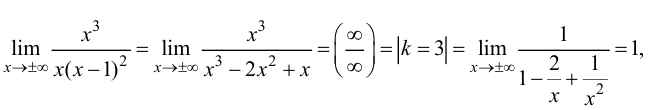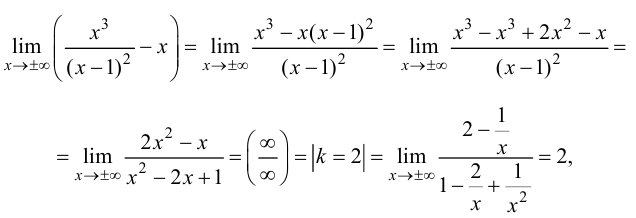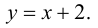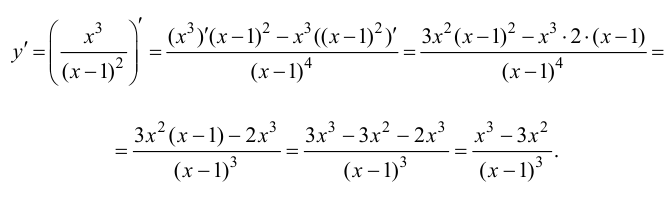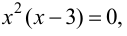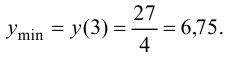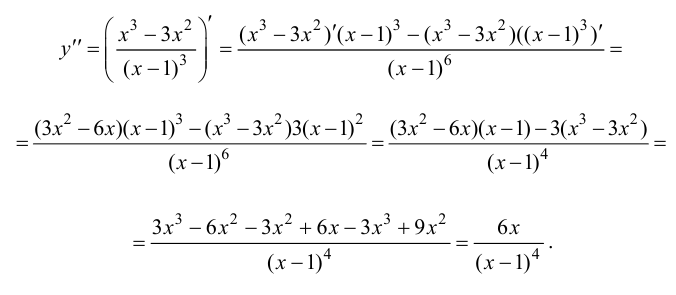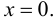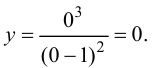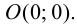Выпуклость, вогнутость кривой. Точки перегиба.
Исследование
функции на экстремум и определение его
типа (максимум или минимум) во многих
случаях проще выполняется не путем
анализа перемены знака производной при
ее прохождении через критическую
точку, а с помощью второй производной.
Определение
1.
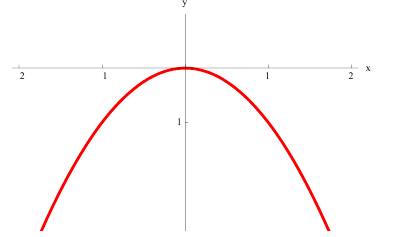
Непрерывная линия называется
выпуклой или обращенной выпуклостью
вверх на отрезке [а, b],
если все точки этой линии лежат выше
(не ниже) хорды, соединяющей любые две
ее точки (рис. 4. а).
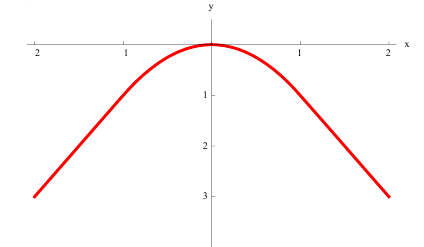
Аналогично,
вогнутой (обращенной
выпуклостью вниз)
называется линия, проходящая ниже
(не выше) своих хорд (рис.
4, б).
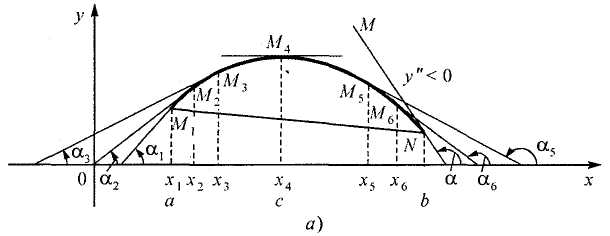

Рис.
4.
Замечание.
В некоторых руководствах
выпуклость и вогнутость иногда
определяются противоположным образом.
Определение
2. Точки,
отделяющие выпуклые участки линии от
вогнутых (и наоборот), называются точками
перегиба.
Теорема.
Если вторая производная функции
у = f(х) в
данном промежутке значений х
положительна, то кривая вогнута в этом
промежутке, а если отрицательна —
выпукла.
Точками
перегиба являются те точки, при переходе
через которые вторая производная меняет
знак.
Линия
называется выпуклой (или
вогнутой) в точке, если
значение ее второй производной в
данной точке меньше (или больше) нуля.
Пример
1. Выяснить, выпуклая или вогнутая
линия у = 3x3
+ 8 в точке с абсциссой х = 3.
Решение.
Находим производные у’ = 6х2
и у» = 12х. В точке х
= 3 имеем:
у»(3) = 12 • 6
= 36 > 0. Значит, в точке х = 3 данная
линия вогнута.
Нахождение точки перегиба
Чтобы
исследовать функцию на вогнутость,
необходимо определить знак второй
производной. Если на данном промежутке
f «(х) < 0 для
всех х, то линия вогнута, если f
«(х) > 0 для всех х, то линия
выпукла. Выпуклую часть кривой от
вогнутой отделяет точка перегиба.
Правило
нахождения точек перегиба
Чтобы
найти точку перегиба линии у
= f(х),
нужно:
1. Найти
вторую производную функции у =
f(х).
2.
Приравняв ее к нулю, решить полученное
уравнение.
3.
Расположив корни второй производной
х1, х2, х3,
… в порядке их возрастания, подставить
в выражение для второй производной
сначала любое число, меньшее х1
затем — любое число
х
(х1, х2); если в обоих
случаях получатся разные знаки, то
при х = х1 имеется точка перегиба;
если же одинаковые, то точки перегиба
нет; аналогично определяется знак второй
производной и далее аналогично поступить
с числами х2, х3 и т.
д.
4. Найти
ординаты точек перегиба, т. е. найти
значения функции в соответствующих
точках.
Пример
1. Найти точки перегиба линии
f(х) = х3.
Решение.
Находим: f ‘(х) =
Зх2; f «(х)
= 6х; 6х = 0 => х = 0;
f(0) = 0.
Следовательно,
A (0;0) – точка
перегиба.
Пример
2. Найти точки перегиба линии
у = х 4 — 2х2 —
3.
Решение.
1) у’ = 4х3 — 4х;
у» = 12х2 — 4.
2)
у» = 0 => 12х2 = 4; х
= ±
.
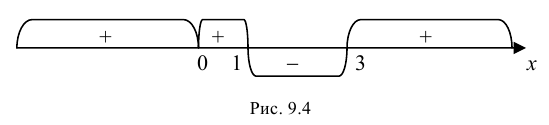
3)
При |х| >
имеем у» > 0 — линия вогнута; при
|х| <
имеем у» < 0 — линия выпукла.
Точки ±
являются точками перегиба (рис. 7).
Асимптоты
графика функции.
Определение
1. Асимптотой
графика функции y
= f (x)
называется прямая, обладающая тем
свойством, что расстояние от точки
M(x,
f(x))
до этой прямой стремится к нулю при
неограниченном удалении точки графика
от начала координат.
Определение
2. Прямая
x = xo
называется вертикальной асимптотой
графика функции
y
= f(x),
если хотя бы один из односторонних
пределов f(xо–
0) =
(предел слева) или f(xо
+ 0) =
(предел
справа) равен +
или —
(см. рис. 8).
Определение
3. Прямая
у = kx + b
называется наклонной асимптотой
графика функции y
= f(x)
при x
+
если
функцию y = f(x)
можно представить в виде
f(x)
= kx + b + a(x),
где
a(x)
при x

При x
наклонная асимптота называется правой,
а при x
— левой. При k
= 0
асимптота
называется горизонтальной.
Теорема.
Для того чтобы график функции у =
f(x)
имел при
наклонную асимптоту y
= kx + b,
необходимо и достаточно, чтобы существовали
пределы
и
.
Пример
2. Рассмотрим функцию y
=

Так
как y = f(x)
= x + 2 +
,
где a (x)
=
при x
,
то прямая у = x +
2 является левой и правой наклонной
асимптотой графика функции.
Замечание.
Для рациональной функции (отношение
двух многочленов) левая и правая асимптоты
совпадают.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Теоремы о выпуклости функции и точках перегиба
- Схема исследования функции на выпуклость, вогнутость
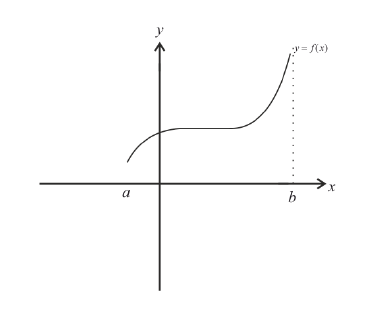
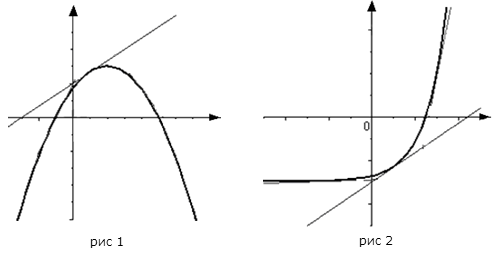
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале выпуклым, если график
этой функции в пределах интервала $(a ; b)$ лежит не выше любой
своей касательной (рис. 1).
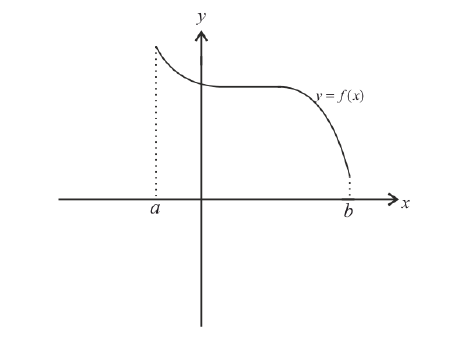
График функции $y=f(x)$, дифференцируемой на интервале
$(a ; b)$, является на этом интервале вогнутым, если график
этой функции в пределах интервала $(a ; b)$ лежит не ниже любой
своей касательной (рис. 2).
Теоремы о выпуклости функции и точках перегиба
Теорема
(Об условиях выпуклости или вогнутости графика функции)
Пусть функция $y=f(x)$ определена на интервале
$(a ; b)$ и имеет непрерывную, не равную нулю в точке
$x_{0} in(a ; b)$ вторую производную. Тогда, если
$f^{prime prime}(x)>0$ всюду на интервале
$(a ; b)$, то функция имеет вогнутость на этом интервале,
если $f^{prime prime}(x) lt 0$, то функция имеет выпуклость.
Определение
Точкой перегиба графика функции $y=f(x)$
называется точка $Mleft(x_{1} ; fleft(x_{1}right)right)$, разделяющая промежутки выпуклости и вогнутости.
Теорема
(О необходимом условии существования точки перегиба)
Если функция $y=f(x)$ имеет перегиб в точке
$Mleft(x_{1} ; fleft(x_{1}right)right)$, то
$f^{prime prime}left(x_{1}right)=0$ или не существует.
Теорема
(О достаточном условии существования точки перегиба)
Если:
- первая производная $f^{prime}(x)$
непрерывна в окрестности точки $x_{1}$; - вторая производная $f^{prime prime}(x)=0$ или не существует в точке $x_{1}$;
- $f^{prime prime}(x)$ при переходе через точку $x_{1}$ меняет свой знак,
тогда в точке $Mleft(x_{1} ; fleft(x_{1}right)right)$ функция $y=f(x)$ имеет перегиб.
Схема исследования функции на выпуклость, вогнутость
- Найти вторую производную функции.
- Найти точки, в которых вторая производная равна нулю или не существует.
- Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.
Пример
Задание. Найти интервалы выпуклости/вогнутости функции
$y=frac{x^{3}}{6}-x^{2}+3 x+1$
Решение. Найдем вторую производную заданной функции:
$y^{prime prime}=left(frac{x^{3}}{6}-x^{2}+3 x+1right)^{prime prime}=left(frac{x^{2}}{2}-2 x+3right)^{prime}=x-2$
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
$y^{prime prime}(x)=0$:
$y^{prime prime}(x)=x-2=0 Rightarrow x=2$
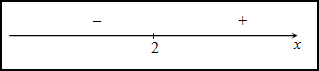
Исследуем знак второй производной слева и справа от полученной точки:
Так как на промежутке $(-infty ; 2)$ вторая производная
$y^{prime prime}(x) lt 0$, то на этом промежутке функция
$y(x)$ выпукла; в силу того, что на промежутке
$(2 ;+infty)$ вторая производная
$y^{prime prime}(x)>0$ — функция вогнута. Так как при переходе через
точку $x=2$ вторая производная сменила знак, то
эта точка является точкой перегиба графика функции.
Ответ. Точка $x=2$ — точка перегиба графика функции.
На промежутке $(-infty ; 2)$ функция выпукла, на промежутке
$(2 ;+infty)$ функция вогнута.
Читать дальше: асимптоты графика функции.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Исследование функций с помощью производных
Необходимое условие возрастания и убывания функции
Из определений возрастающей и убывающей функций следует необходимое условие возрастания и убывания функции.
Теорема: Если дифференцируемая функция
Доказательство: Пусть дифференцируемая функция 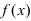
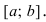
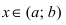
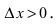
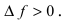
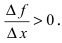
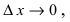
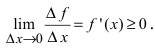
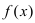
Замечание: С геометрической точки зрения возрастающая на сегменте 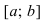
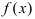
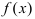
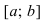
Пример:
Найти интервалы возрастания и убывания функции
Решение:
Из графика этой функции видно, что 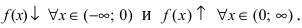
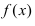
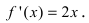
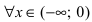
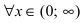
Достаточное условие возрастания и убывания функции
Теорема: Пусть функция 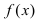
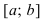
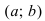
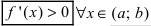
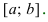
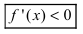
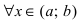
Доказательство: Пусть первая производная функции 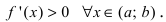
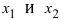
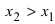
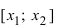
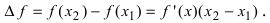
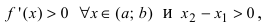
Таким образом, функция 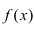
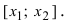
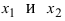
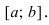
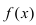
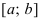
Условия постоянства функции на сегменте (a; b)
Условия постоянства функции на сегменте 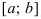
ТЗ. Пусть функция 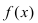
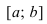
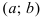
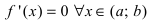
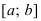
Доказательство: Пусть первая производная функции 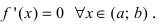
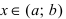
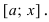
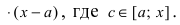
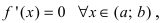
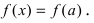
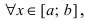
Минимум и максимум (экстремумы) функции
Пусть функция 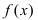
Определение: Функция 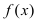
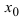
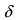
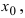
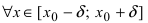
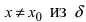

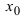
Обозначение
Определение: Функция 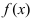
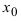
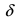
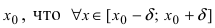
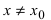
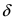
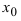
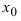
Обозначение
Пример:
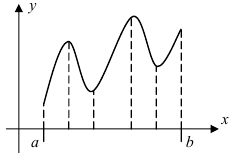
Найти на заданном графике точки максимума и минимума (Рис. 77).
Рис. 77. Максимумы и минимумы заданной функции.
Решение:
Определение: Точки минимума и максимума объединяются под общим названием точки экстремума.
Замечание: Точки экстремума всегда являются внутренними точками области определения функции.
Замечание: Не следует путать минимальное значение функции 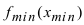
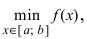
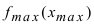
Замечание: Из определения экстремума следует, что в точке минимума выполняется неравенство 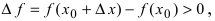
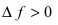
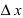
Необходимое условие существования экстремума функции
Теорема: Если дифференцируемая функция 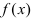
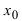
Доказательство: Пусть в точке 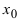
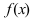
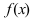
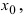
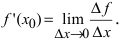
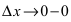
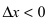
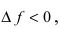
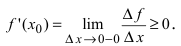
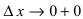
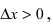
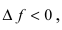
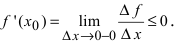
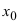
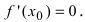
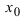
Замечание: Обращение в нуль первой производной функции в точке х0 я взлетел необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке х0 даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
Пример:
Доказать, что функция 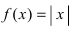
Решение:
Из Рис. 72 видно, что в точке 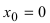
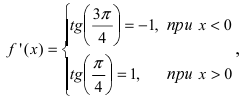
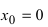
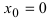
Определение: Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).
Замечание: Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.
Пример:
Доказать, что функция 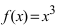
Решение:
В точке 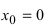
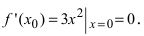
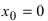
Исследование функций с помощью производных
Первый и второй достаточные признаки существования экстремума
Первый достаточный признак существования экстремума:
Теорема: Если функция 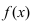
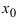
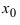
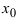
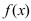
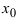
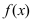
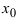
Второй достаточный признак существования экстремума:
Теорема: Если в точке 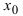
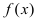
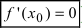
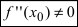
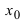
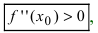
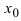
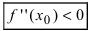
Пример:
Найти и определить тип экстремумов функции
Решение:
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 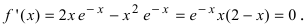
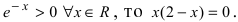
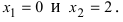
При переходе слева направо через точку 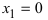
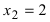
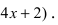
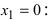
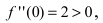
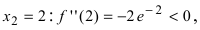
Наименьшее и наибольшее значения функции на сегменте (a; b)
Наименьшее и наибольшее значения функции на сегменте
Пусть функция 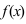
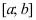
- Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
- Находят критические точки, для чего решают уравнение
и точки, в которых первая производная функции не существует.
- Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
- Из полученных чисел выбирают наименьшее
и наибольшее
.
Пример:
Найти наименьшее и наибольшее значения функции 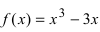
Решение:
Действуя согласно вышеприведенной схеме, находим:
1. 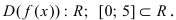
2. Вычислим первую производную 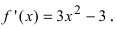
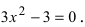
3. Вычислим значение функции в критических точках и на концах заданного сегмента:
4. Из полученных чисел выбираем наименьшее 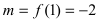
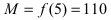
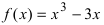
Выпуклость и вогнутость графика функции. Точки перегиба
Определение: График функции 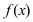
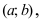
Рис. 78. Выпуклый график функции
Определение: График функции 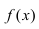
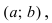
Рис. 79. Вогнутый график функции
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
ТЗ. Если вторая производная функции 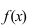
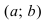
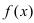
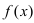
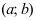
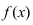
Пример:
Определить интервалы вогнутости и выпуклости графика функции
Решение:
Найдем вторую производную от заданной функции 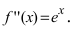
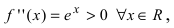
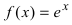
Пример:
Определить интервалы вогнутости и выпуклости графика функции
Решение:
Найдем вторую производную от заданной функции 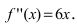
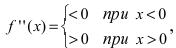
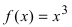
Определение: Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.
Необходимое и достаточное условия существования точки перегиба
Рассмотрим необходимое условие существования точки перегиба.
Теорема: Если функция 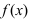
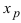
Замечание: Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Пример:
Доказать, что точка 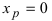
Решение:
Если вычислить вторую производную от заданной функции, то она будет равна 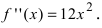
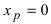
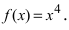
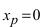
Теорема: Пусть функция 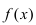
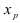
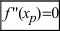
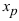
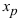
Пример:
Найти точки перегиба и интервалы выпуклости и вогнутости графика функции
Решение:
Найдем вторую производную заданной функции 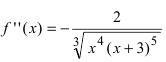
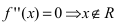
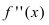

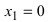
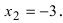
Из рисунка видно, что точка 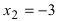
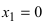
Асимптоты графика функции f (x)
Асимптоты графика функции
В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.
Определение: Прямая (l): 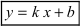
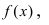
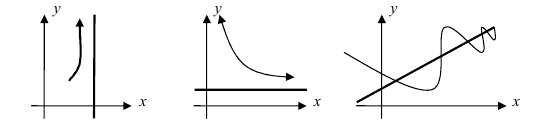
Замечание: График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 80).
Рис. 80. Различные случаи приближения графика функции к асимптотам.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Определение: Вертикальная прямая 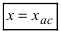
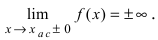
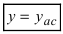
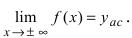
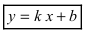
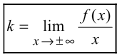
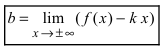
Горизонтальная асимптота является частным случаем наклонной асимптоты: если 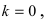
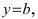
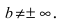
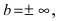
Полная схема исследования функции с помощью производных
Из изложенного в Лекциях № 20 и №21 материала следует следующая схема исследования функции с помощью производных:
- Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.
- Находят точки пересечения с координатными осями.
- Определяют четная, нечетная или общего вида заданная функция.
- Определяют периодическая или непериодическая заданная функция.
- Находят критические точки, решая уравнение
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
) и убывания(
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
- Находят точки подозрительные на перегиб, решая уравнение
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
) и выпуклости (
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
- Находят асимптоты графика функции.
- Результаты исследования заносят в сводную таблицу
- Поданным таблицы строят схематичный график функции.
Замечание: При нахождении области определения функции надо помнить о действиях, запрещенных в области действительного переменного:
- нельзя делить на нуль, поэтому выражение, стоящее в знаменателе дроби, не должно равняться нулю;
- нельзя извлекать корень четной степени из отрицательного числа, поэтому выражение, стоящее под корнем четной степени, должно быть неотрицательным (
);
- основание логарифмической функции должно быть строго положительным и не равным единице;
- выражение, стоящее под логарифмом, должно быть строго положительным;
- выражение, стоящее под знаком arcsin или arccos, по модулю не должно превышать единицу (
).
Пример:
Исследовать и построить схематичный график функции
Решение:
Используя схему исследования графика функции с помощью производных, найдем:
1.
2. Найдем точки пересечения графика функции с координатными осями
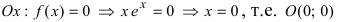
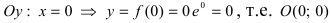
3. Вычислим 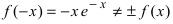
4. Функция непериодическая (периодическими среди элементарных функций являются функции: sinx, cosx, tgx и ctgx).
5. Найдем первую производную функции 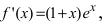
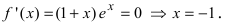

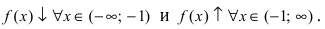
6. Найдем вторую производную функции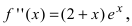
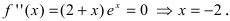

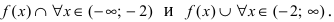
7. Найдем асимптоты графика функции, для чего вычислим угловой коэффициент прямой 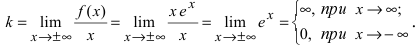
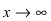
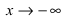
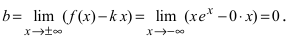
8. Построим сводную таблицу
О(0; 0) — точка пересечения с координатными осями.
у = 0 — горизонтальная асимптота.
9. Построим схематичный график функции, выбрав по координатным осям разные масштабы измерения:
———
Исследование функций с помощью производных
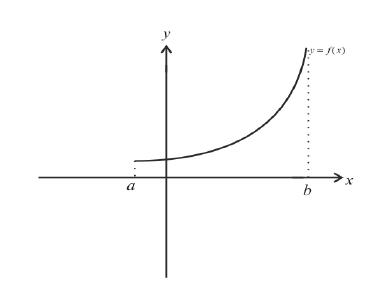
Определение 1. Функция y=f(x) называется возрастающей (убывающей) на интервале ( a,b ), если
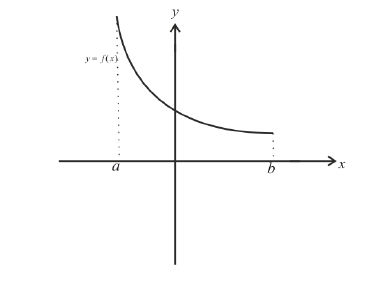
Функция y=f(x) называется неубывающей (невозрастающей) на
интервале ( a,b ), если
Возрастает:
Убывает:
Неубывает:
Невозрастает:
Функции из определения 1 называются монотонными.
Теорема 1. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) не убывала (не возрастала) на этом интервале необходимо и достаточно,
чтобы
Доказательство. Необходимость. Рассмотрим случай, когда f(x) не
убывает и докажем, что производная 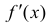
Пусть
Пусть
Таким образом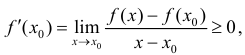
Достаточность. Рассмотрим случай, когда 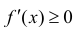
Тогда по теореме Лагранжа (теорема 4 § 12) ∃ точка 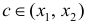
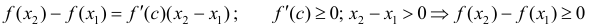
Теорема 2. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) возрастала (убывала) на этом интервале достаточно, чтобы
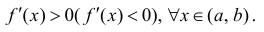
Доказательство теоремы аналогично доказательству достаточности в теореме 1. Нужно заметить, что условие 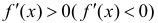
Пример 1.
Рассмотрим функцию 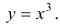
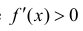
Теорема 3. (необходимое условие экстремума).
Пусть функция y=f(x) определена в некоторой окрестности точки 
Доказательство.
Если производная 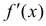

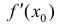
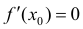
Определение 2. Пусть функция y=f(x) непрерывна в точке 

Замечание. Для непрерывной функции любая точка локального экстремума
будет критической. Наоборот – не верно.
Пример 2.
Для функции 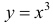
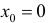
Для функции
(см. пример 9 §5) 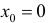

Для функции
точка 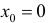



Для функции
точка 


Теорема 4. (достаточное условие экстремума функции). Пусть функция y=f(x)
дифференцируема в некоторой окрестности 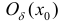


а) Пусть при переходе через точку 
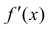
на «+» :
Тогда 
Пусть при переходе через точку 
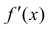
Тогда 
б) Пусть при переходе через точку 
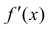
Тогда 
Доказательство следует из теоремы 2. При этом важно, чтобы функция y=f(x) была непрерывна в точке 

Теорема 5. (второе достаточное условие экстремума функции).
Пусть 
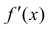
Пусть 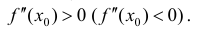

максимума).
Доказательство. Запишем формулу Тейлора 2-ого порядка для функции y=f(x) в окрестности точки 
(см. теорему 1 §14).
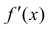
Из (2) следует, что ∃ окрестность точки 
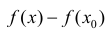
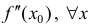
Теорема 6. Пусть функция y=f(x) имеет в точке 
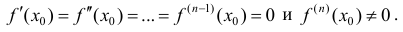
1) если n – четное и 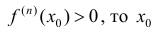
2) если n – четное и 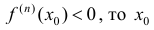
3) если n – нечетное, то в точке 
Доказательство аналогично доказательству теоремы 5.
Пример 3.
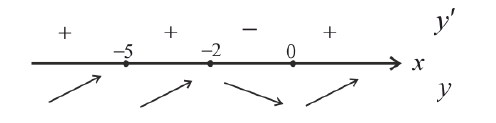
Исследовать на экстремум функцию
Решение. Функция непрерывна ∀x∈R .
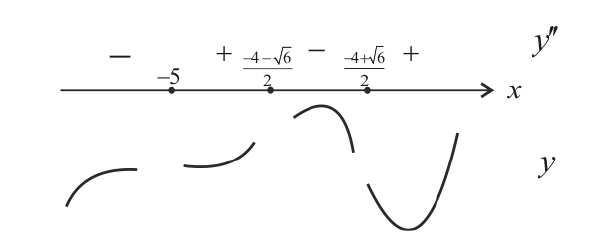
Найдем критические точки:
x=-2 — точка локального максимума: y(-2) = 108 y;
x = 0 — точка локального минимума; y(0) = 0.
x = −5 — не является точкой экстремума.
При исследовании функции на экстремум точки разрыва(если они есть)
также наносят на числовую прямую. При переходе через эти точки может
изменятся направление возрастания (убывания) функции.
Замечание. При решении ряда технических и экономических задач приходится находить не локальные, а глобальные экстремумы (наибольшие и наименьшие значения функций на некотором множестве). Из теоремы Вейерштрасса (см. теорему 1 §11) следует, что для непрерывной функции y=f(x) заданной на отрезке [ a,b] глобальные min и max существуют. При этом точки с 1 и с 2 – глобального min и max лежат либо на концах отрезка [ a,b], либо являются критическими для функции f(x).
Пример 4.
Найти наибольшее и наименьшее значение функции 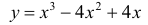
Решение. Функция непрерывна ∀x∈R. Найдем критические точки:
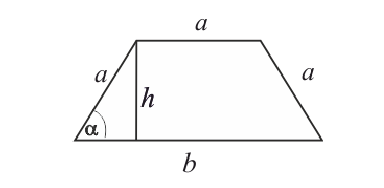
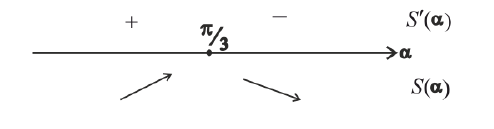
Пример 5.
Боковые стороны и меньшее основание трапеции = а . Найти
длину большего основания, при котором площадь трапеции – наибольшая.
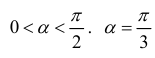
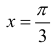
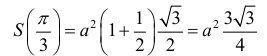
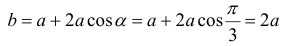
——-
Исследование функций с помощью производных(часть вторая)
Определение 1. Пусть функция y=f(x) дифференцируема на интервале ( a,b) . И пусть 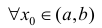
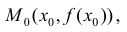
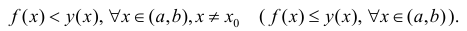
Пусть 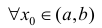
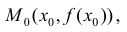
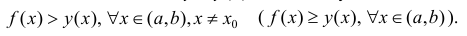
Пример 1.
а) 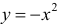
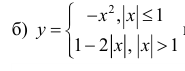
в) 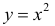
г) 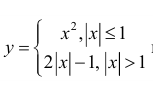
Теорема 1. Для того, чтобы дифференцируемая функция y=f(x) была вогнутой (выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы ее производная 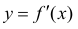
Докажем для случая, когда y=f(x) — вогнута.
Необходимость. Пусть
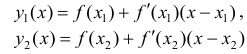
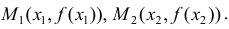
Сложим эти неравенства:
Достаточность. Пусть 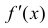
Пусть 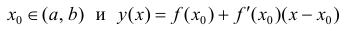
Пусть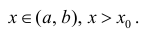
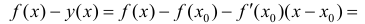
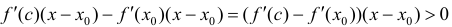
Теорема 2. Для того, чтобы дифференцируемая функция y=f(x) была нестрого вогнутой (нестрого выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы производная 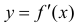
Доказательство аналогично доказательству теоремы 1.
Теорема 3. Для того, чтобы дважды дифференцируемая на интервале (a,b) функция y=f(x) была не строго вогнутой (не строго выпуклой) необходимо и
достаточно, чтобы
Доказательство следует из теоремы 2 и теоремы 1 §15.
Теорема 4. Для того, чтобы дважды дифференцируемая на интервале (a,b)
функция y=f(x) была вогнутой (выпуклой) на этом интервале достаточно, чтобы
Доказательство следует из теоремы 1 и теоремы 2 §15. Нужно заметить, что
условие 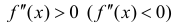
Пример 2.
Рассмотрим функцию 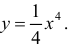
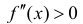
Теорема 6 (достаточное условие перегиба функции). Рассмотрим функцию
y=f(x) дважды дифференцируемую в некоторой окрестности 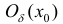
возможного перегиба 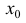
Предположим также, что вторая производная 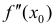
через точку 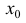
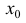
Доказательство следует из теоремы 4.
Пример 3.
Найдем точки перегиба и интервалы выпуклости-вогнутости функции
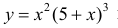
Решение.
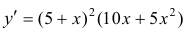
Найдем точки возможного перегиба(точки, где y′′ равна 0 или не существует).
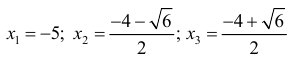
При нахождении интервалов выпуклости-вогнутости точки, где функции
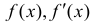
через эти точки может меняться направление выпуклости-вогнутости.
Определение 4. Прямая y= kx +b называется наклонной асимптотой функции y=f(x) при x →+∞ (x→−∞), если 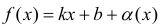
Теорема 7. Для того, чтобы прямая y =kx +b была наклонной асимптотой для функции y=f(x) при x →+∞ (x→−∞) необходимо и достаточно, чтобы существовали пределы
Доказательство. Рассмотрим, например, случай x → +∞ .
Необходимость. Пусть 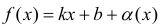
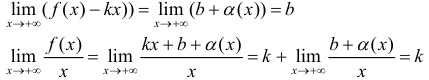
Достаточность. Пусть выполняется (1). Докажем, что y =kx +b — асимптота для y=f(x).
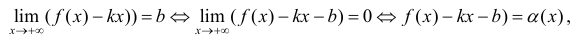
Замечание. Наличие наклонной асимптоты значит, что при x →+∞ (x→−∞) график функции очень близок к прямой линии y =kx +b.
Пример 4.
Для функции 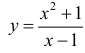
Для функции 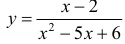
Для функции 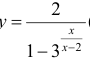
Для функции , 1(0 1) 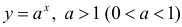
асимптота при x →+∞ (x→−∞).
Определение 5. Прямая 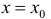
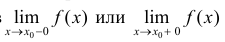
Пример 5.
Для функции 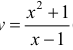
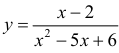
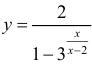
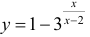
При построении графиков функции используют результаты §15, 16. Это можно проводить по следующей схеме:
1. Найти область определения D(f) функции и исследовать поведение функции в граничных точках D(f) . Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность.
2. Найти наклонные асимптоты.
3. Найти интервалы монотонности, точки локального экстремума.
4. Найти интервалы выпуклости, вогнутости, точки перегиба.
5. Построить график.
Пример 6.
Провести полное исследование и построить график функции
Нули функции
Таким образом график пересекает оси координат в точке О(0; 0). Функция
ни четная, ни нечетная, не периодическая.
2. Наклонные асимптоты. По формулам (1);
x = 0 — точка локального максимума; 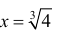
Точки где y′′ равна 0 или не существует:
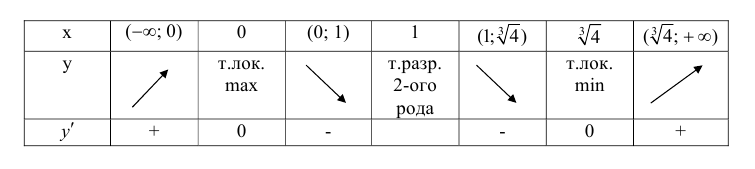
5. График функции.
———
Исследование функции с помощью производных
Монотонность функции
Теорема 9.1. Пусть функция 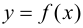
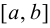
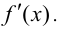
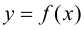
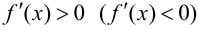
Доказательство.
Возьмем отрезок 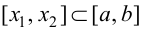
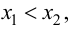
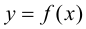
Тогда, если 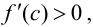
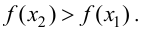
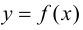
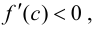
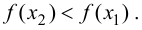
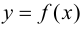
Замечание 9.1. Утверждение теоремы сохраняет силу и в том случае, если 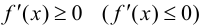
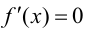
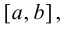
Пример 9.1. Рассмотрим функцию 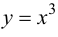
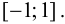
- Заказать решение задач по высшей математике
Достаточные условия экстремума
Теорема 9.2 (первое достаточное условие экстремума). Пусть функция 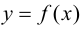
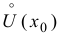
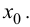
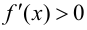
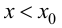
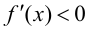
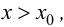
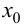
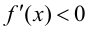
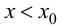
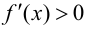
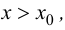
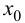
Доказательство следует из теоремы 9.1.
Теорема 9.3 (второе достаточное условие экстремума). Если в критической точке 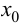
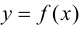
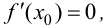
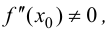
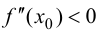
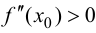
Доказательство.
Если в точке 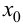
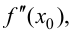
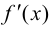
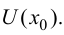
Пусть 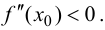
При 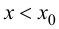
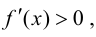
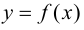
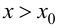
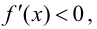
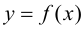
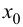
Случай 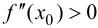
Замечание 9.2. Так как теорема формулирует только достаточное условие, то при 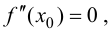
Пример 9.2. Функция 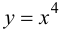
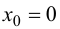
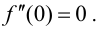
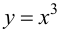
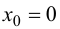
Наибольшее и наименьшее значения функции на отрезке
Пусть функция 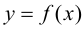
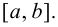
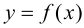
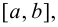
Таким образом, непрерывная функция 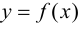
Исходя из вышесказанного, можно предложить следующий алгоритм поиска наибольшего и наименьшего значений непрерывной функции 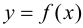
1. Найти все критические точки. Если критическая точка 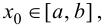
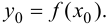
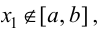
2. Вычислить значения функции на концах отрезка, т. е. найти 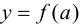
3. Из всех полученных выше значений функции выбрать наибольшее и наименьшее, они и будут представлять собой наибольшее и наименьшее значения функции 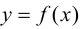
Пример 9.3. Найти наибольшее и наименьшее значения функции 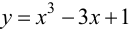
Решение.
Так как функция 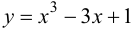
1. Найдем критические точки функции.
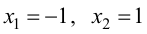
Так как 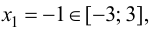
так как 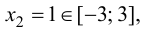
2. Определим значения функции на концах отрезка:
3. Сравним вычисленные значения функции и выберем наибольшее и наименьшее:
Ответ:
Выпуклость и вогнутость графика функции, точки перегиба
Пусть функция 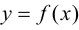
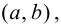
Определение 9.1. График функции 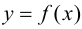
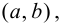
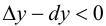
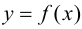
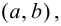
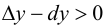
Определение 9.2. Точки графика функции, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
Теорема 9.4. Пусть функция 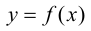
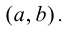
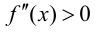
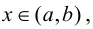
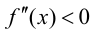
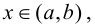
Доказательство.
Рассмотрим разность 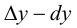
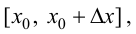
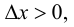
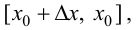
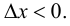
Поэтому
Тогда, при 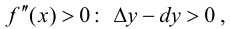
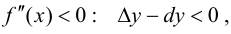
Теорема 9.5 (необходимое условие точки перегиба). Пусть график функции 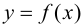
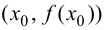
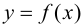
Доказательство.
Пусть 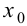
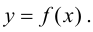
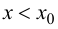
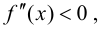
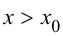
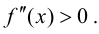

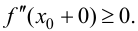
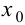
Определение 9.3. Точка 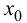
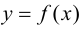
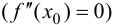
Замечание 9.3. Не всякая точка 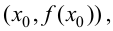
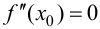
Пример 9.4. График функции 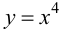
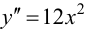
Теорема 9.6 (достаточное условие точки перегиба). Пусть функция 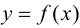
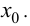
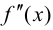
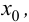
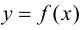
Доказательство.
Из того, что 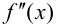
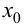
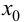
Замечание 9.4. Теорема остается верной, если функция 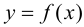
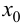
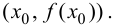
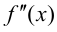
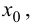
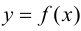
Пример 9.5. Точка (0; 0) является точкой перегиба графика функции 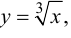
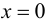
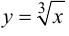
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 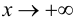
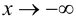
Определение 9.4. Прямая 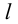
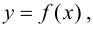
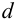
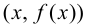
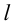
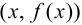
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 9.5. Прямая 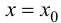
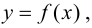
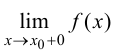
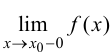
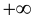
В этом случае расстояние от точки графика функции 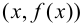
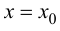
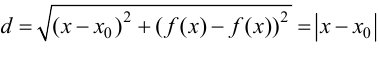
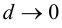
Пример 9.6. График функции 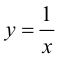
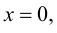
Определение 9.6. Прямая 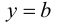
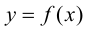
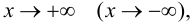
В этом случае расстояние от точки графика функции 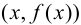
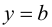
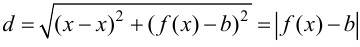
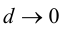
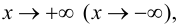
Пример 9.6 (продолжение). График функции 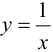
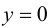
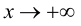
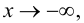
Определение 9.7. Прямая 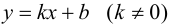
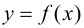
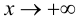
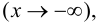
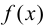
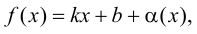
где 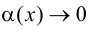
Теорема 9.7. Для того чтобы прямая 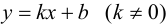
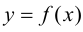
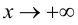
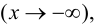
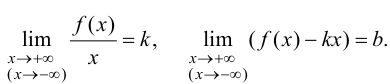
Доказательство. Рассмотрим случай
Необходимость.
Если 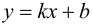
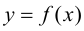
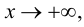
Достаточность.
Пусть существуют пределы (9.2). Тогда из второго равенства следует, что
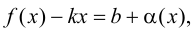
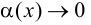
Полученное равенство легко преобразовать к виду (9.1), т. е. прямая 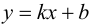

Схема исследования функции и построения ее графика
Рассмотрим примерный план, по которому целесообразно исследовать поведение функции и строить ее график:
1. Найти область определения функции.
2. Проверить выполнение свойств четности или нечетности, периодичности.
3. Указать промежутки непрерывности, точки разрыва и их тип, проверить наличие асимптот.
4. Найти промежутки монотонности и точки экстремума.
5. Найти промежутки выпуклости и вогнутости, точки перегиба.
6. Найти точки пересечения графика функции с осями координат.
7. Построить график функции.
Замечание 9.5. Если исследуемая функция 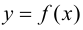
Замечание 9.6. Если исследуемая функция 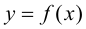
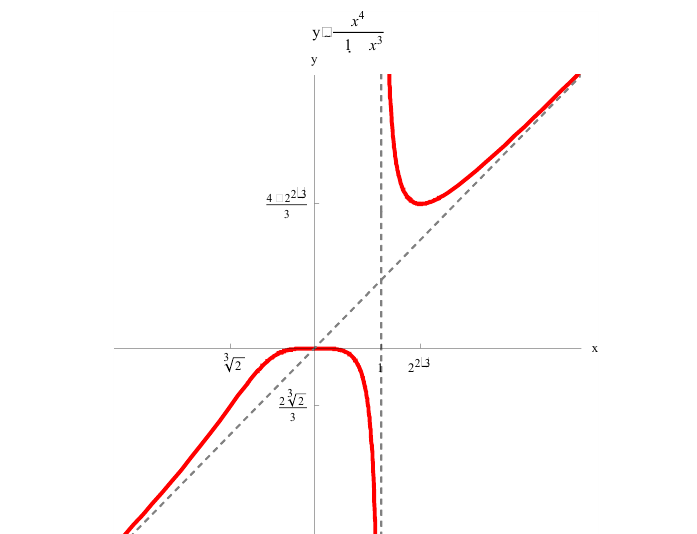
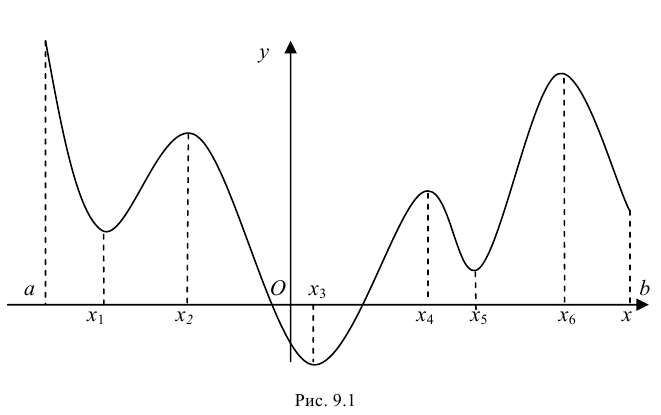
Пример 9.7. Исследовать функцию 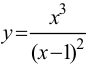
Решение.
1.
2. Так как область определения функции несимметрична относительно начала координат, то эта функция общего вида, т. е. функция ни четная, ни нечетная, непериодическая.
3. Функция непрерывна на области определения как элементарная. Точкой разрыва является 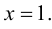
то 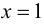
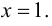
Проверим наличие горизонтальных асимптот. Так как
то данная функция не имеет горизонтальных асимптот. Проверим наличие наклонных асимптот. Так как
то график функции имеет наклонную асимптоту с угловым коэффициентом 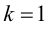
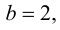
4. Определим промежутки возрастания и убывания функции, точки экстремума. Для этого найдем критические точки первого рода:
Решим уравнение 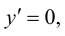
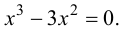
откуда 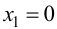
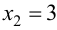
Так как 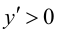
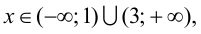
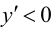
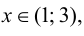
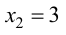
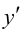
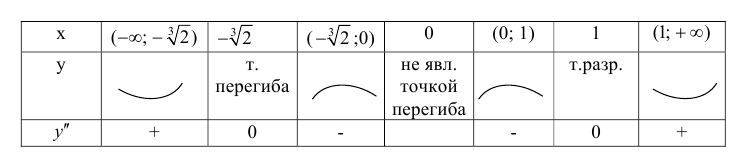
5. Определим промежутки выпуклости и вогнутости графика функции, точки перегиба. Для этого найдем критические точки второго рода:
Решим уравнение 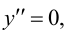
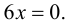
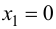
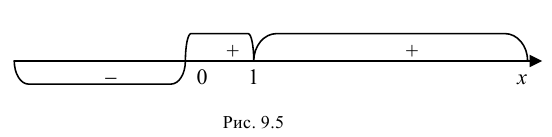
Так как 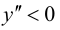
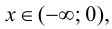
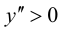
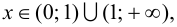
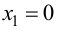
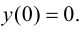
6. Найдем точки пересечения графика функции с осями координат.
Для точек оси 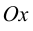
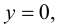
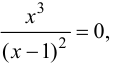
Для точек оси 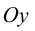
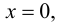
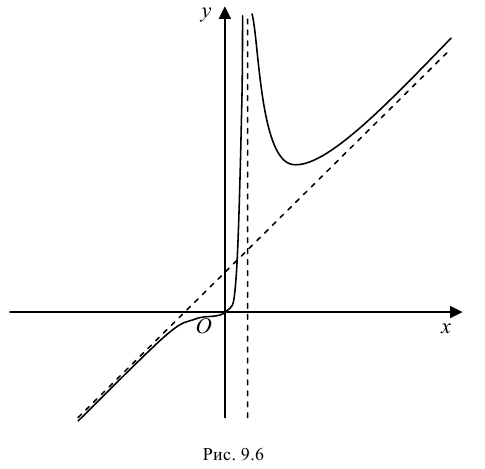
Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат
7. Построим график функции на рис. 9.6.
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
1. Исследование выпуклости графика функции
График функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функции на ((a,b)).
Если функция (f(x)) имеет на интервале ((a,b)) вторую производную и
f′′(x)≥0
(
f′′(x)≤0
) во всех точках ((a,b)), то график функции (f(x)) имеет на ((a,b)) выпуклость, направленную вниз (вверх).
Пример:
определить выпуклости функции
f(x)=x3+x
.
Вторая производная этой функции — это
f′′(x)=6x
. Она отрицательна, если (x<0), положительна, если (x>0).
Значит, график (f(x)) в интервале
−∞;0
имеет выпуклость, направленную вверх, и в интервале
0;+∞
имеет выпуклость, направленную вниз.
2. Нахождение точек перегиба функции
Чтобы определить точки перегиба функции (f(x)), нужно найти точки, в которых вторая производная этой функции является нулём или не существует (и которые принадлежат области определения функции). Тогда можно определить знак второй производной функции в соответствующих интервалах — вычислив значения второй производной в какой-либо точке интервала.
Если вторая производная функции в точке меняет знак, эта точка является точкой перегиба, если не меняет, не является точкой перегиба.
Пример:
рассмотрим функцию
f(x)=x3+x
.
Вторая производная этой функции — это
f′′(x)=6x
. Она отрицательна, если (x<0), и положительна, если (x>0). Значит, в точке (x=0) вторая производная меняет знак, и эта точка — точка перегиба функции.
Download Article
Learn how to take the derivative of a function to get its inflection points
Download Article
- Understanding Concavity and Inflection
- Finding the Derivatives of a Function
- Checking the Candidate Inflection Points
- Troubleshooting
- Using a Scientific Calculator
- Video
- Q&A
- Tips
|
|
|
|
|
|
|
You just learned about inflection points in calculus and now you’ve got a bunch of math problems asking you to find them. You’ve got a function and a graph, so where do you go from there? With our help and a bit of derivative magic, finding a function’s inflection points is actually pretty easy! In this article, we’ll provide you with all the steps you need to find and check points of inflection. As a bonus, we’ll show you how to use your scientific calculator to calculate points of inflection for you. If you’re ready to solve your math problems, read on!
Things You Should Know
- An inflection point is where a function changes concavity and where the second derivative of the function changes signs.
- Take the first and second derivative of the function using the power rule.
- Set the second derivative equal to 0 to find the candidate, or possible, inflection points.
- Plug in a value greater than and less than the candidate point to see if the second derivative changes signs at the point.
-
1
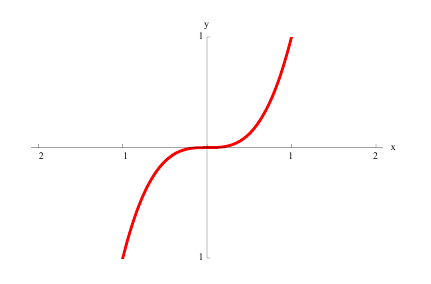
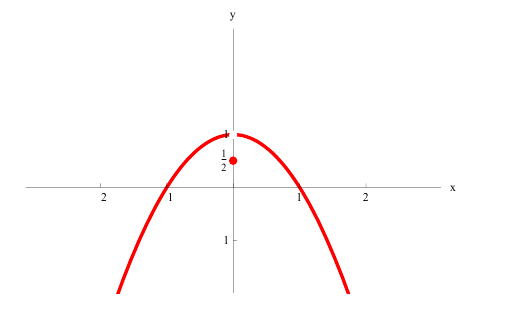
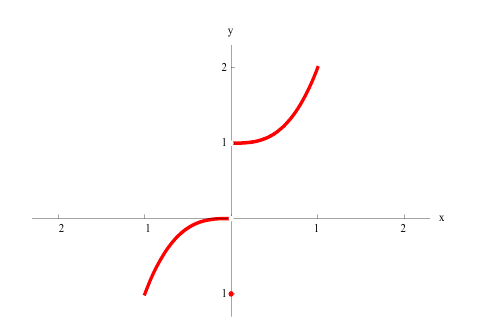
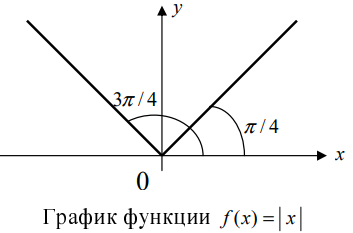
Learn the difference between concave up and concave down. To understand inflection points, you need to understand when a function is concave up or down on a graph. Many functions have both concave up and concave down intervals, with an inflection point existing where a function changes concavity. Luckily, concave up and down are easy to distinguish based on their names and what they look like.[1]
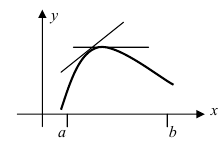
- A concave down function is shaped like a hill or an upside-down U. It’s a function where the slope is decreasing. When it’s graphed, no line segment that joins 2 points on its graph ever goes above the curve.
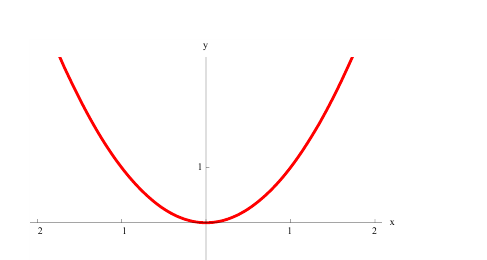
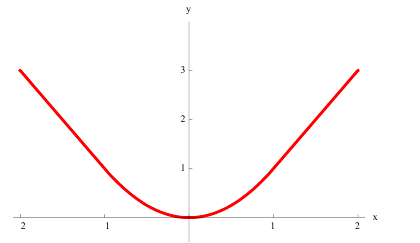
- A concave up function, on the other hand, is shaped like a U. It’s a function where the slope is increasing. No line segment that joins 2 points on its graph ever goes below the curve.
- In the graph above, the red curve is concave up, while the green curve is concave down.
-
2
Identify the roots of a function. A root of a function is the point where the function equals zero, or where the function intersects the x-axis. In the graph above, the roots of the green parabola are at
and
[2]
- A function can also have more than 1 root.
Advertisement
-
3
Find an inflection point where a function changes concavity. Remember how there’s a difference between concave up and concave down? An inflection point is a point on a function where its concavity changes, either from upwards to downwards or downwards to upwards. It is also the point where the second derivative of the function changes signs from positive to negative or negative to positive. For the point to be a point of inflection, it has to both switch concavity and change signs on the second derivative.[3]
- To find the inflection point on a graph, look for the point where the function switches concavity. On the graph above, it’s the middle point where the function changes from concave down to concave up.
Advertisement
-
1
Take the first derivative of the given function. You’ll need your function’s second derivative to find your inflection points. Before you get the second derivative, you have to find the first derivative of the function. First derivatives are denoted as
or
. To solve your function’s first derivative, use the power rule. Multiply x by its exponent and then reduce the exponent by 1.[4]
- For example, find the inflection point of the function below.
- The derivatives of basic functions are usually found in most calculus textbooks; you need to learn how to find basic derivatives before moving on to more complex functions.
-
2
Differentiate the function again to get the second derivative. The second derivative is the derivative of the first derivative. It is denoted as
or
Simply use the power rule again to get the second derivative.
-
3
Set f’’(x) equal to 0 to find the candidate inflection points. Solving f’’(x) = 0 only gives you the candidate inflection points. These are the x-values of the possible inflection points for the function. You still need to test the points on the second derivative to make sure it changes concavity, or switches its sign from positive to negative or negative to positive.[5]
Advertisement
-
1
Plug a value higher and lower than the inflection point into f’’(x). To check if the second derivative changes signs, select 1 value that is greater than the candidate point and 1 value that is less than it. Then, plug each value into the second derivative. If the sign of the second derivative is different for both values, the candidate inflection point is an inflection point. If the sign doesn’t change, the candidate point is not an inflection point.[6]
-
2
Substitute the inflection point into the original function to get its y-value. While you now know the x-value of the inflection point, you don’t know where it is on the y-axis. Simply go back to the original function and plug in the inflection point to get its y-value.[7]
-
3
Evaluate the function to find the inflection point’s coordinates. The coordinate of the inflection point is denoted as
In our example, the coordinates of the inflection point are
[8]
Advertisement
-
1
Check the concavity of every candidate inflection point. Oftentimes, people assume there’s no inflection point when the candidate point is
. However, this isn’t true. Remember, 0 can be graphed, so if you get 0 as your candidate point, it might be an inflection point.[9]
-
2
Include candidate points where the derivative is undefined. When you find possible inflection points, you have to look for instances where the second derivative equals 0 and where the second derivative is undefined. If you only look for points where the second derivative is 0, you might miss inflection points where the function is undefined.[10]
-
3
Analyze the second derivative, not the first one. When you’re finding inflection points, you only consider the second derivative. If you set the first derivative equal to 0, your answer will give you extremum points instead.[11]
Advertisement
-
1
Head to your “Plots” function on your calculator. It’s easy to use a scientific calculator to find inflection points. On most scientific calculators, just press the “diamond” or the “second” button, then click F1. This takes you to your Y plots where you can enter up to 7 functions.[12]
- This is true on both the TI-84 and the TI-89, but it may not be the exact same on older models.
-
2
Enter the function into y1. Clear out any remaining functions you had in your y plots. Then, type in the function after the equal sign. Remember to keep any parentheses involved in the function so your answer is correct.[13]
- For example, the function might be
- For example, the function might be
-
3
Click “graph.” On most calculators, you press the “diamond” or “second” button then click F3. If you have to adjust your window on the calculator, hit “diamond” or “second” and press F2. Then, select “standard zoom.”[14]
- Don’t worry if your screen doesn’t show the whole graph just yet—you will adjust the zoom later.
-
4
Adjust the window until you see the whole graph. When you open up the graphing window, you might not see the entire curve of your graph. If that’s the case, click the “diamond” or “second” button, then open up F2 for zoom again. Simply increase or decrease your minimum and maximum axis to get the graph to fit inside the window.[15]
- It might take a little adjustment and back-and-forth to find your graph.
-
5
Click “Math,” then “Inflection.” Hit the “diamond” or “second” button, then select F5 to open up “Math.” In the dropdown menu, select the option that says “Inflection.”[16]
- This is—you guessed it—how to tell your calculator to calculate inflection points.
-
6
Place the cursor on the lower and upper bound of the inflection. Your calculator will give you a message saying “Lower?” Move the arrows on your calculator until the cursor is to the left of the inflection point. Then, your calculator will ask “Upper?” Move your cursor so it’s to the right of the inflection point. To get your inflection point, hit “Enter.”[17]
- This is how you get your calculator to guess where the inflection point is. Now you have your answer!
Advertisement
Add New Question
-
Question
What if the second derivative intersects with the x-axis, but does not dip below it?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
The second derivative has to cross the x-axis for there to be an inflection point. If the second derivative only touches the x-axis but doesn’t cross it, there’s no inflection point.
-
Question
What if the second derivative is a constant? How do I find the inflection point?
Inflection points are where the second derivative changes sign. If it is constant, it never changes sign, so there exists no inflection point for the function.
-
Question
Can the first derivative become zero at an inflection point?
Orangejews
Community Answer
Yes, for example x^3. It changes concavity at x=0, and the first derivative is 0 there.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Alternatively, take the third derivative of a function to find the inflection points. If the third derivative does not equal 0, there is an inflection point. If the third derivative is positive, the inflection point is increasing; if it’s negative, the point is decreasing.[18]
However, taking such derivatives with more complicated expressions is often not desirable. -
All linear functions have no inflection points. This is because linear functions do not change slope (the entire graph has the same slope), so there is no point at which the slope changes.
-
When you’re testing the candidate points, you are only looking for a sign change. You are not actually evaluating the value.
Show More Tips
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find inflection points, start by differentiating your function to find the derivatives. Then, find the second derivative, or the derivative of the derivative, by differentiating again. To locate a possible inflection point, set the second derivative equal to zero, and solve the equation. Finally, find the inflection point by checking if the second derivative changes sign at the candidate point, and substitute back into the original function. For more tips on finding inflection points, like understanding concave up and down functions, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 337,574 times.
Reader Success Stories
-
«Here is what helped me: If the sign of the second derivative changes as you pass through the candidate inflection…» more






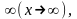









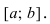
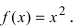
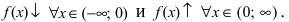
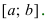
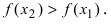
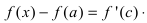
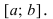
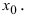
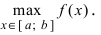
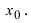
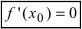
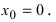
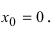
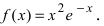

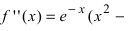
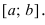
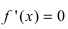 и точки, в которых первая производная функции не существует.
и точки, в которых первая производная функции не существует.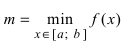 и наибольшее
и наибольшее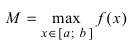 .
.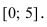
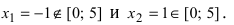
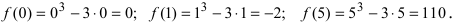
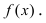
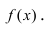
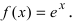
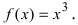
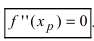
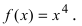
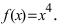
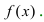
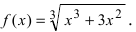

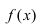
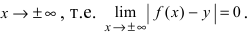
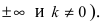
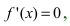 и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (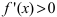 ) и убывания(
) и убывания( 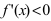 ) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.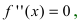 и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (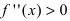 ) и выпуклости (
) и выпуклости (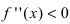 ) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.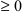 );
);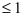 ).
).