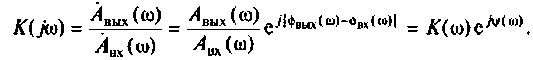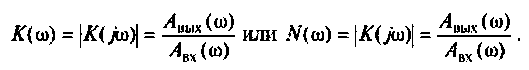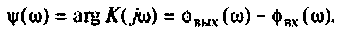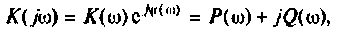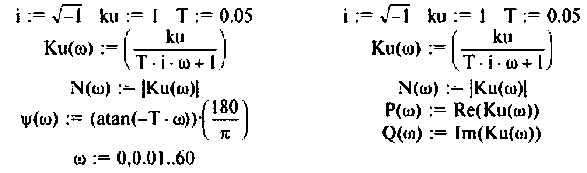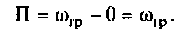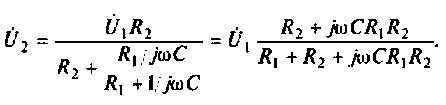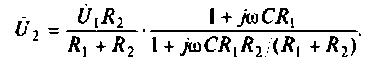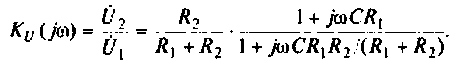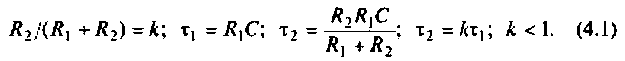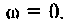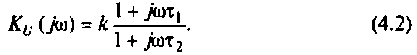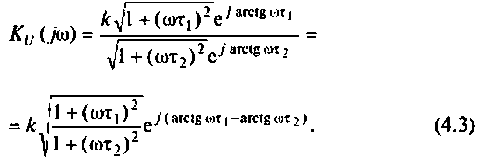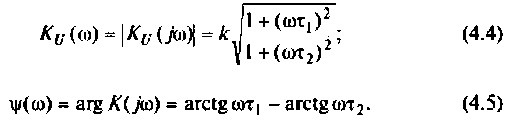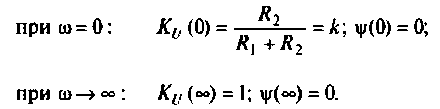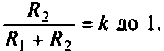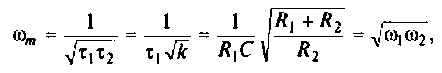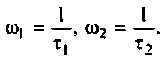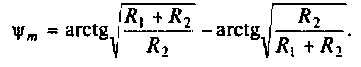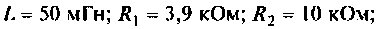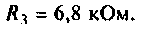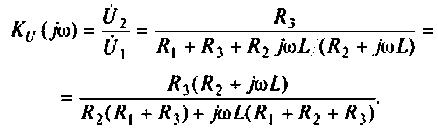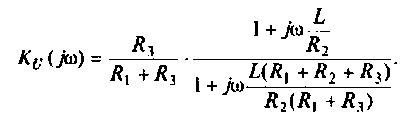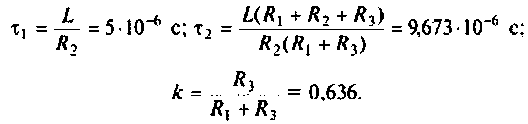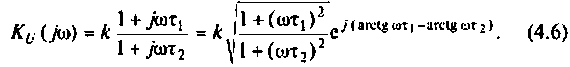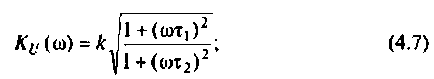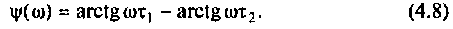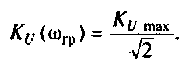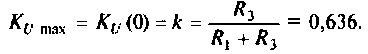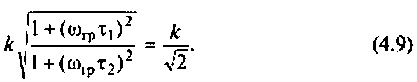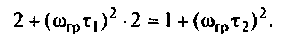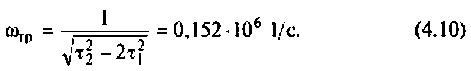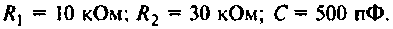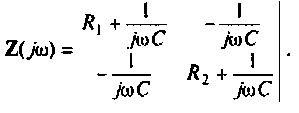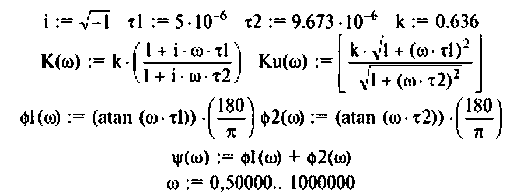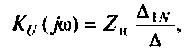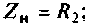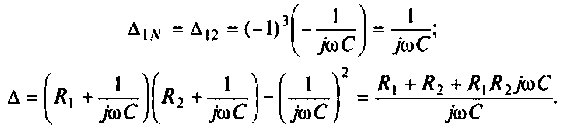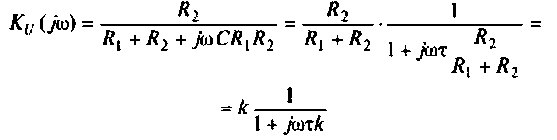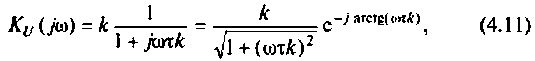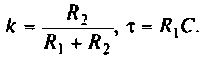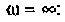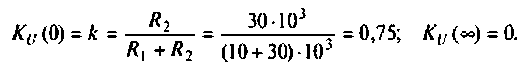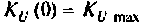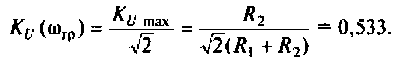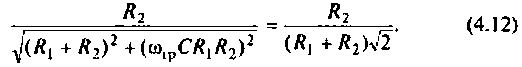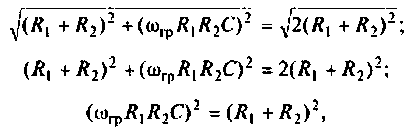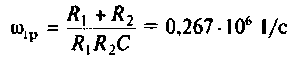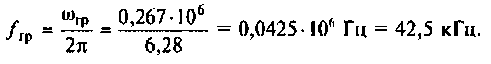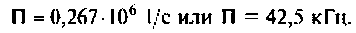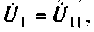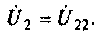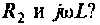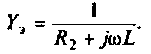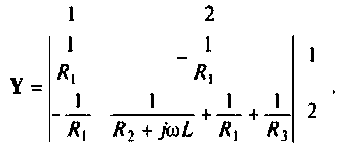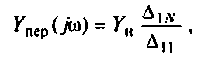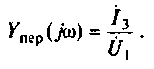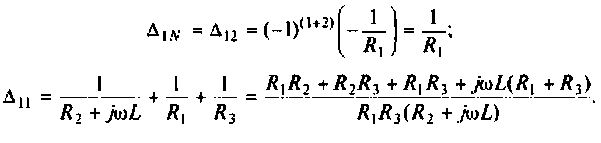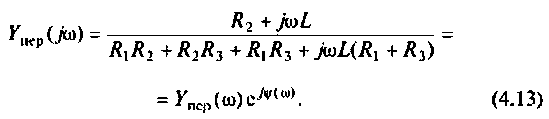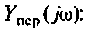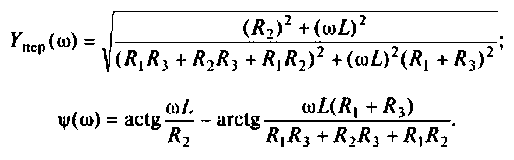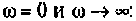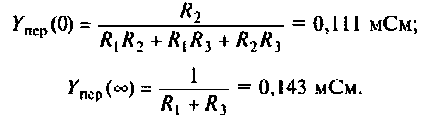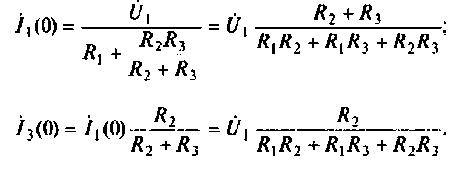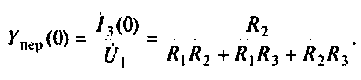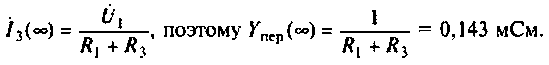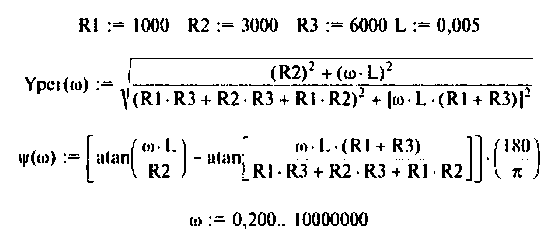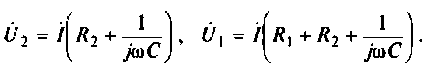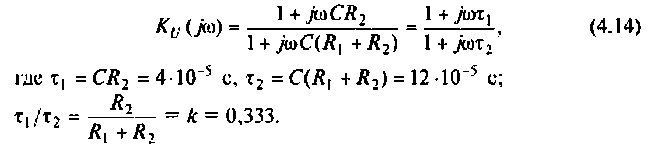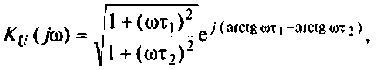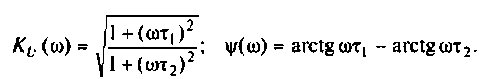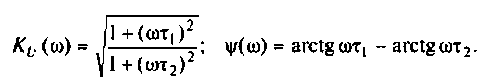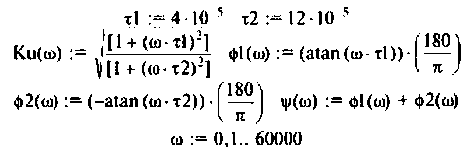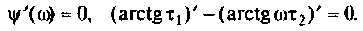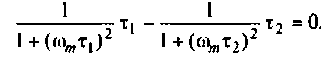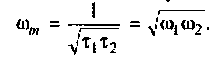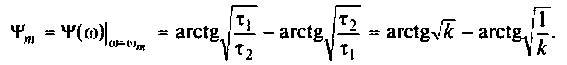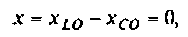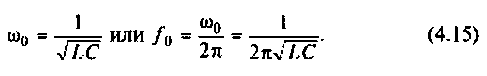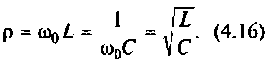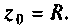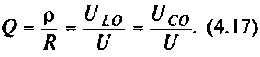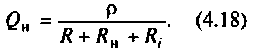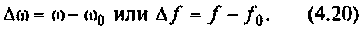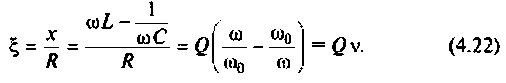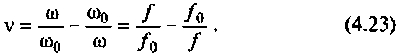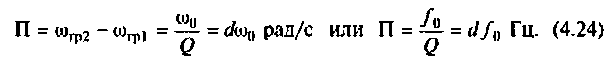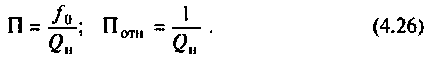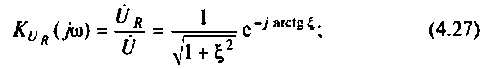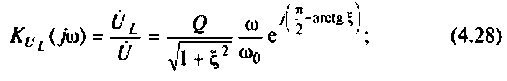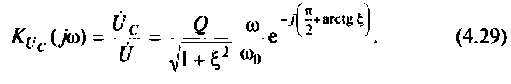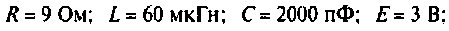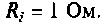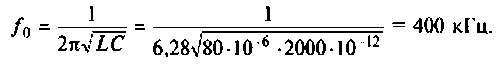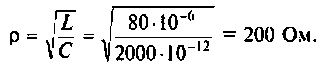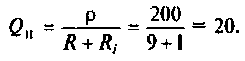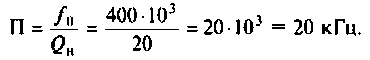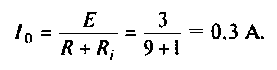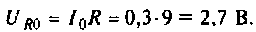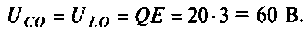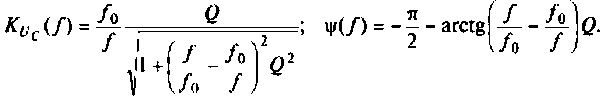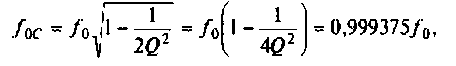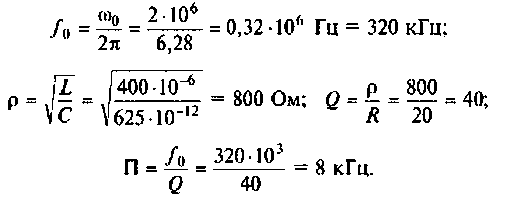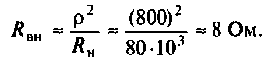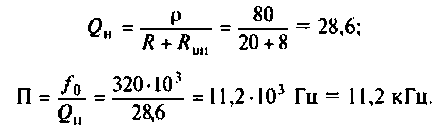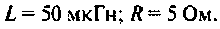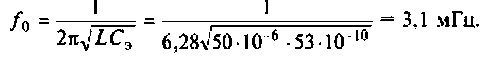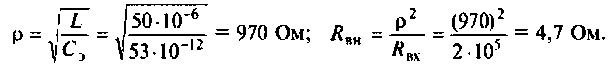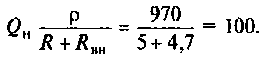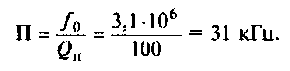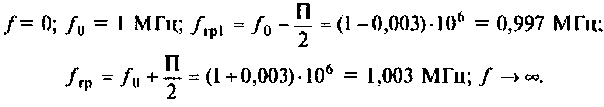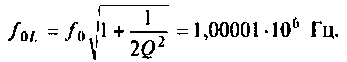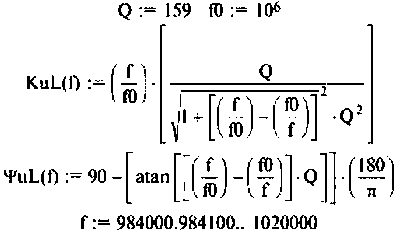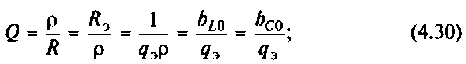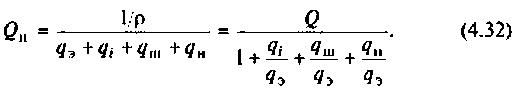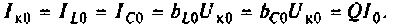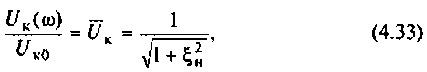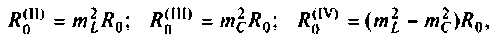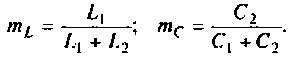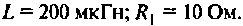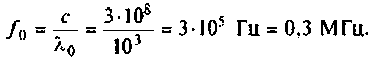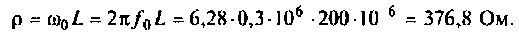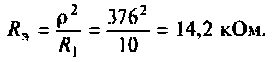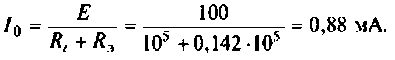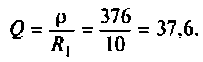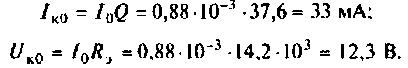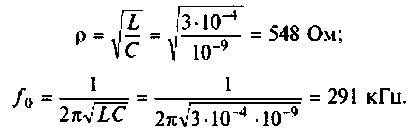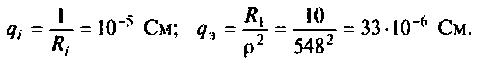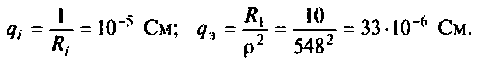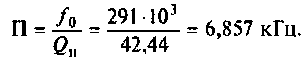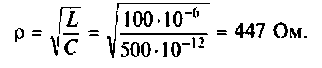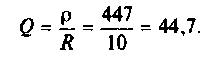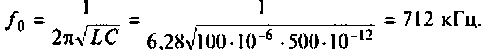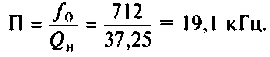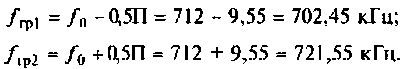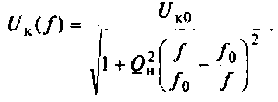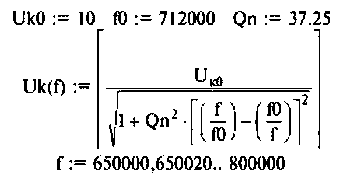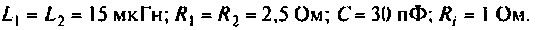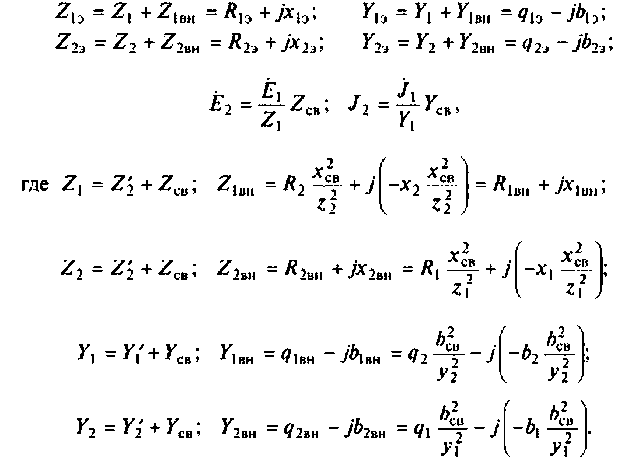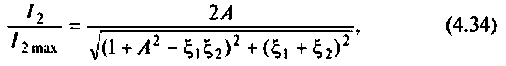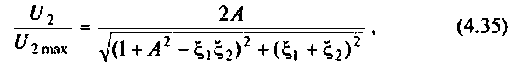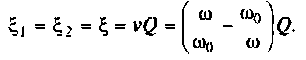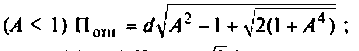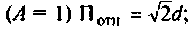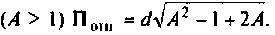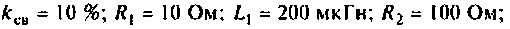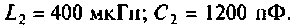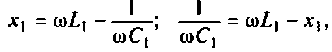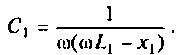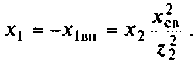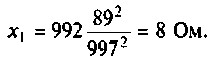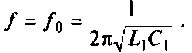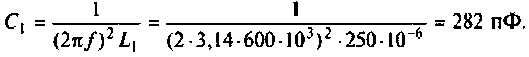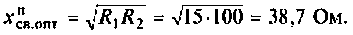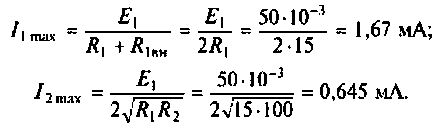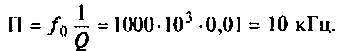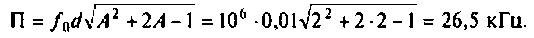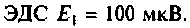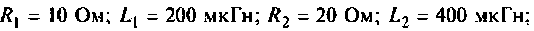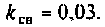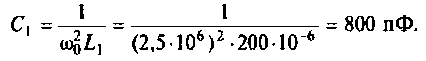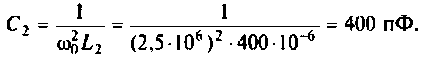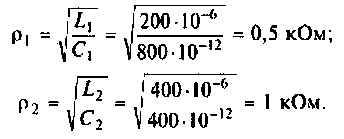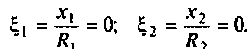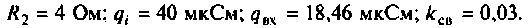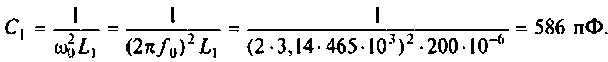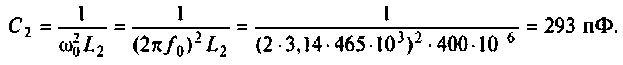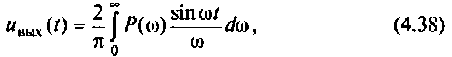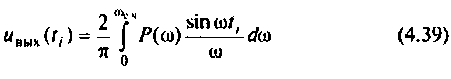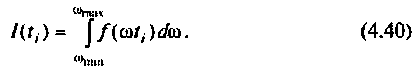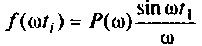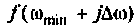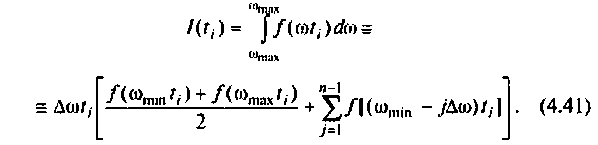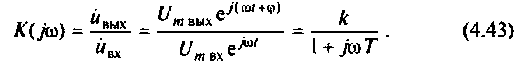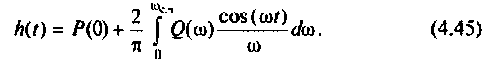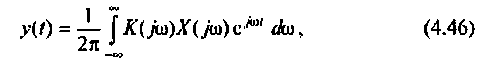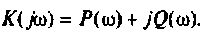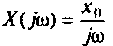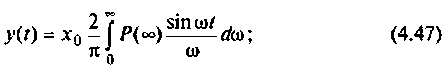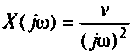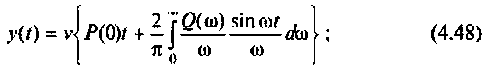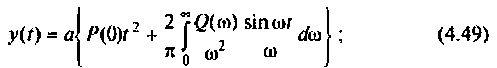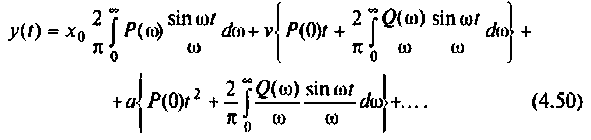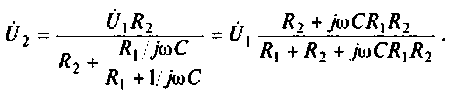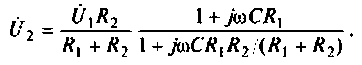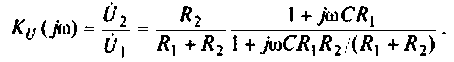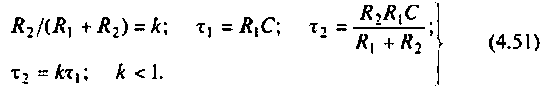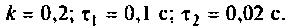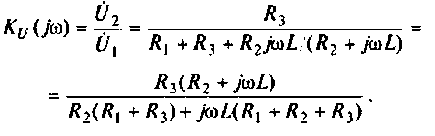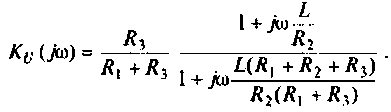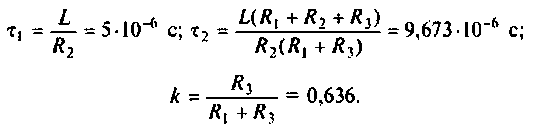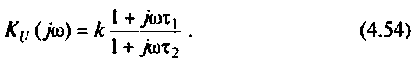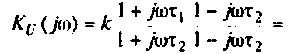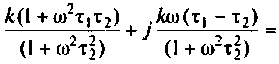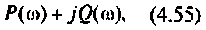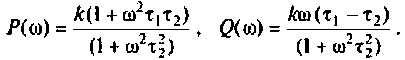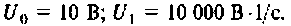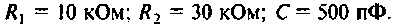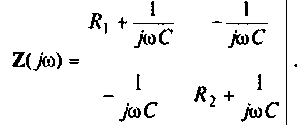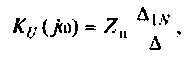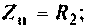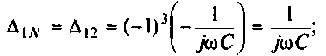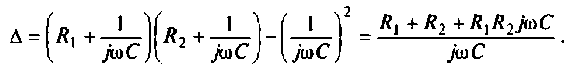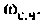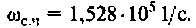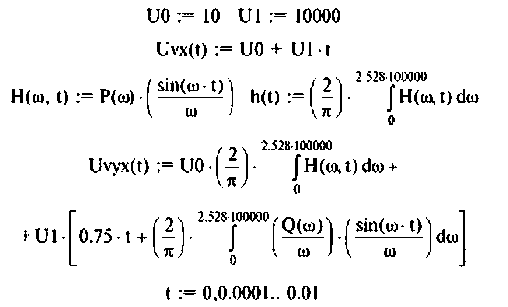Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
Амплитудно-частотная характеристика (АЧХ)
Фазочастотная характеристика (ФЧХ)
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
где 
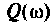
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
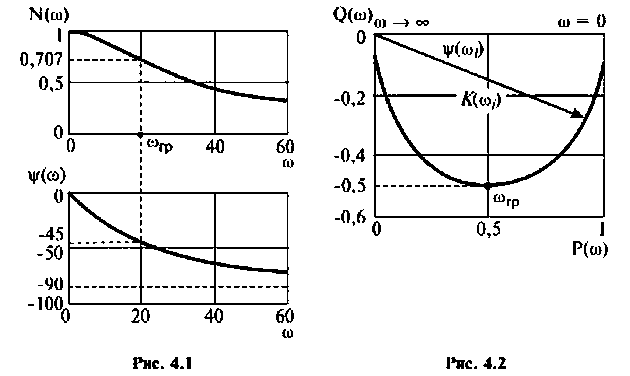
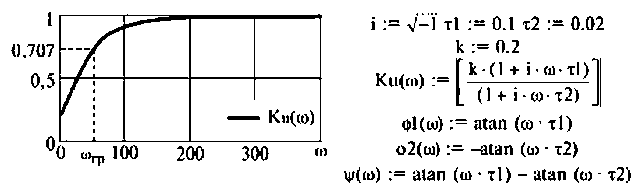
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 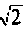
Полоса пропускания может измеряться в радианах в секунду 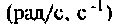
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
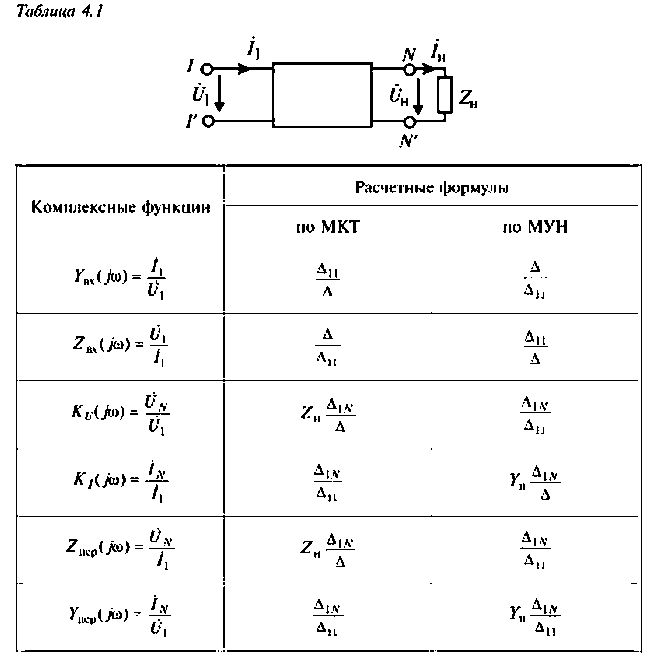
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
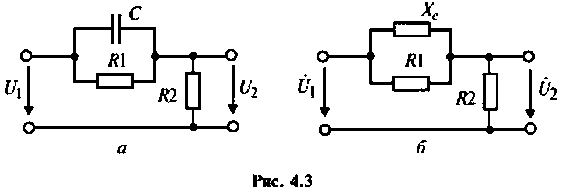
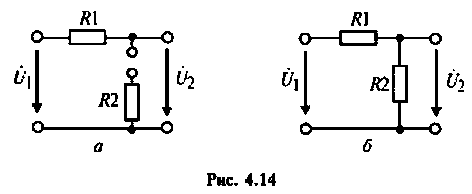
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 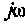
Следовательно.
Введем обозначения:
Величина 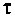
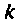
С учетом принятых обозначений
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 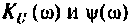
График АЧХ 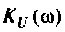
График функции ФЧХ 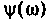
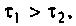
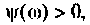
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
где
Подставляя 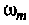
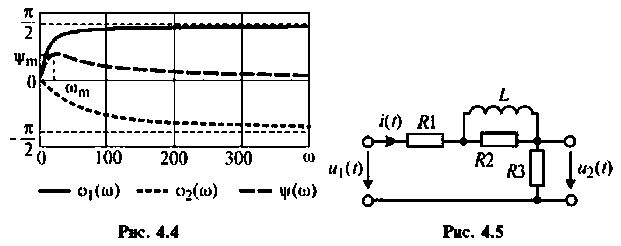
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 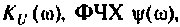
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Отсюда: АЧХ
ФЧХ
2. Рассчитаем граничную частоту. По определению
Из (4.7) найдем
Следовательно,
Из уравнения (4.9) получаем, что
Отсюда
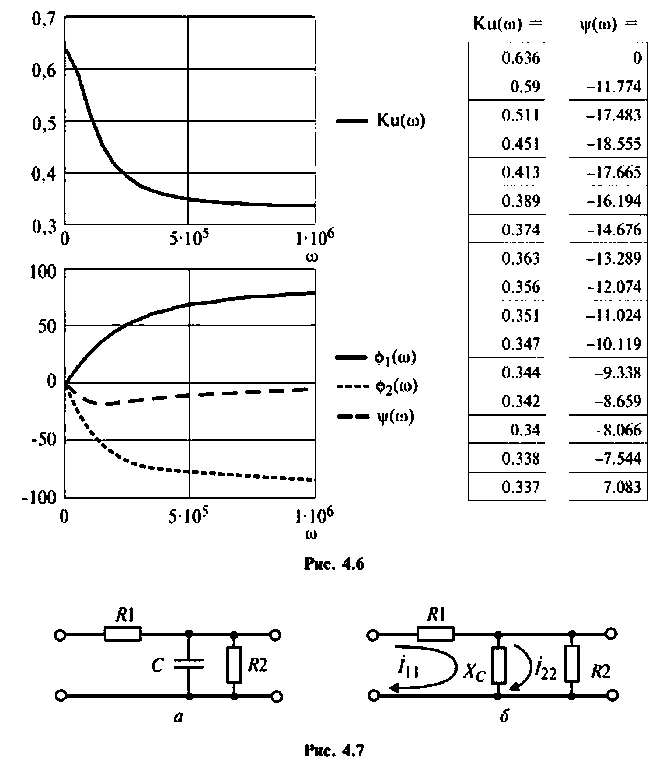
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи:
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 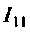
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки равно
Подставляя найденные выражения, получаем
или
где
4. Рассчитаем 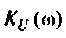
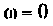
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 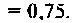
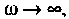
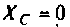
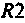
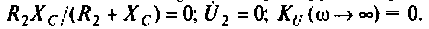
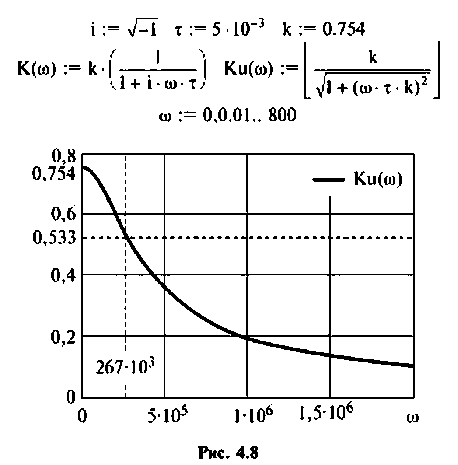
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
Поэтому из (4.11) имеем
После преобразований уравнения (4.12) получаем
откуда
или
Следовательно, цепь имеет полосу пропускания
На рис. 4.8 указана граничная частота
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 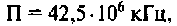

Пример 4.2.4.
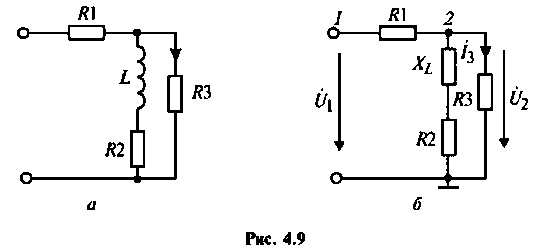
Найти комплексную передаточную проводимость 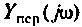
Параметры цепи: 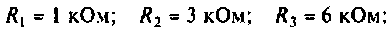
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 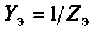
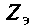
В начале рассчитывают комплексное сопротивление этой ветви, 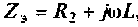
Составим матрицу проводимостей цепи 1 2
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 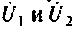
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
где 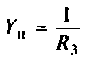
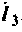
Найдем алгебраические дополнения:
После подстановки найденных значений получим
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента
4. Рассчитаем значения 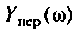
Примечание. Эти значения можно найти без вывода аналитического выражения для 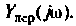
Учитывая, что 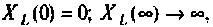
Для первой схемы:
Следовательно,
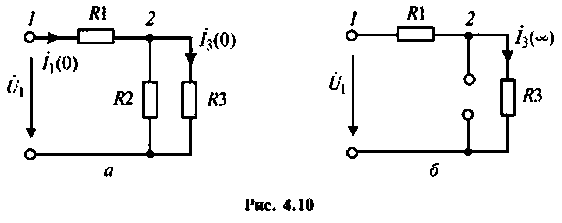
Аналогично для второй схемы получим
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
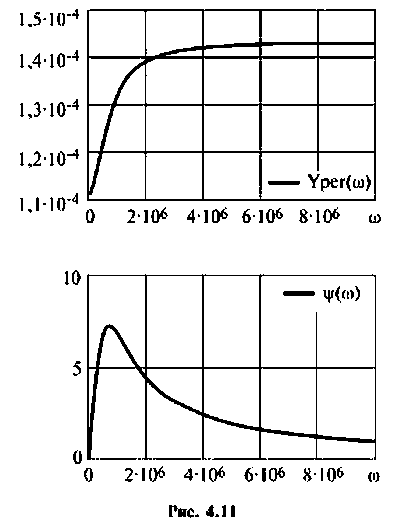
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
Пример 4.2.5.
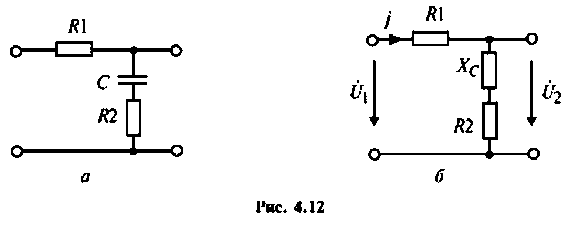
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 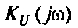
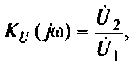
Следовательно.
3. Для нахождения АЧХ и ФЧХ комплексную функцию 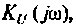
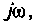
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 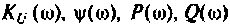
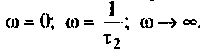
Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
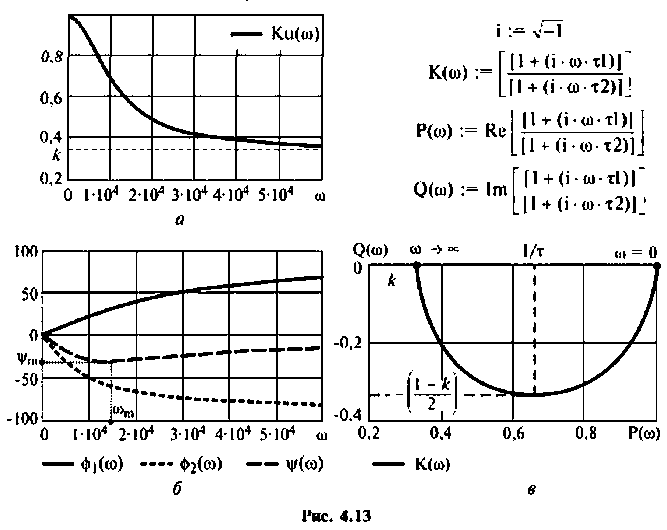
Графики характеристик приведены на рис. 4.13.
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте 
Взяв производную, получим
Решая полученное уравнение относительно 
Подставляя 
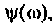
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 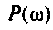
Радиус окружности нетрудно определить из соотношения:
МЧХ:
Отрицательное значение 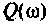
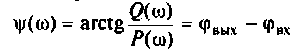
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 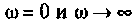
На частоте 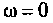
При 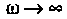
Подставляя эти значения частот в аналитическое выражение (4.14) для 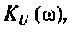
Следовательно, расчет АЧХ выполнен верно.
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
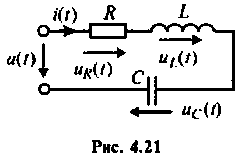
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
т. е. 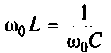
Резонансная частота
Волновое сопротивление контура
Сопротивление контура при резонансе
Собственная добротность контура
Добротность нагруженного контура
Затухание контура
Абсолютная расстройка
Относительная расстройка
Обобщенная расстройка
Фактор расстройки:
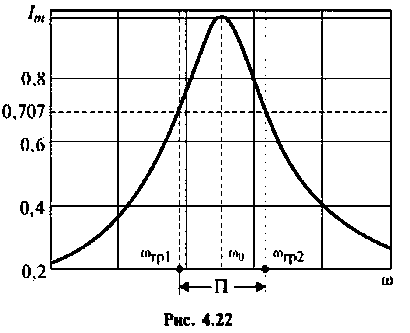
Абсолютная полоса пропускания (рис. 4.22)
Относительная полоса пропускания
Для нагруженного контура:
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
на индуктивности
на емкости
Примеры решения типовых задач:
Пример 4.3.1.
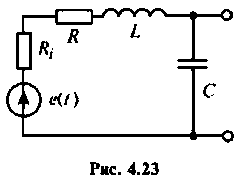
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи:
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
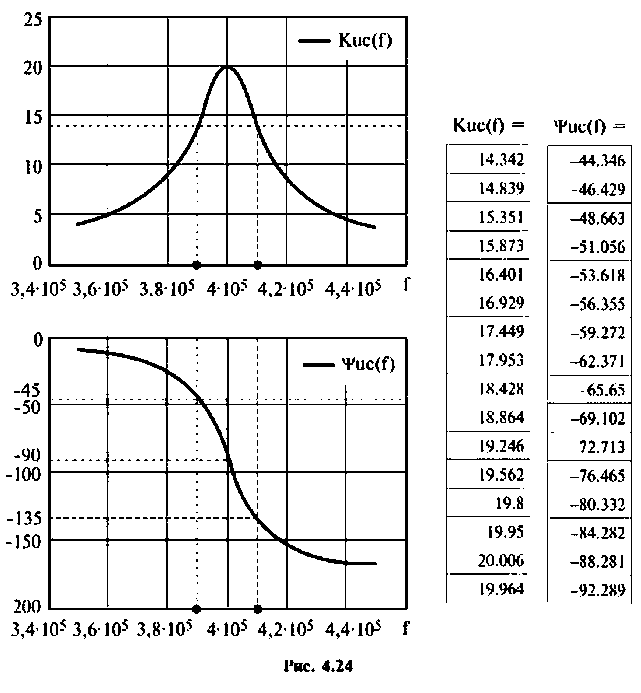
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
1. Определяем резонансную частоту контура
2. Находим волновое сопротивление контура
3. Вычисляем добротность нагруженного контура
4. Определяем полосу пропускания
5. Рассчитываем ток и напряжения на элементах контура при резонансе
Напряжение на R равно
Напряжения на реактивных элементах
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
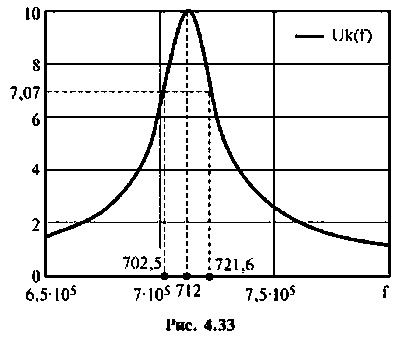
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
т.е. при 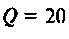
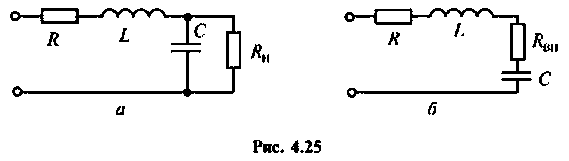
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 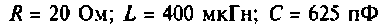
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 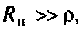
Для определения добротности рассчитаем сопротивление 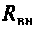
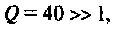
Следовательно,
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
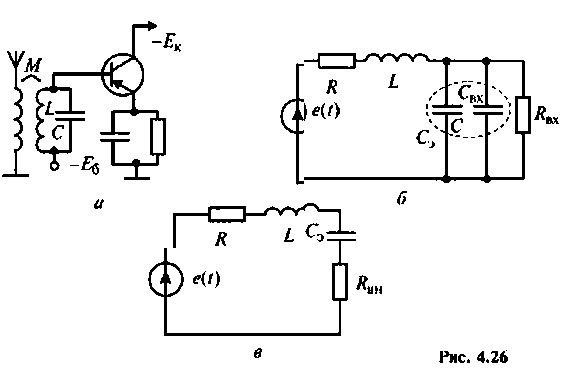
Пример 4.3.3.
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ: 
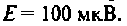
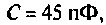
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
2. Рассчитываем резонансную частоту контура
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
4. Определяем добротность нагруженного контура
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
6. Находим ток в контуре
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 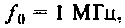
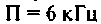
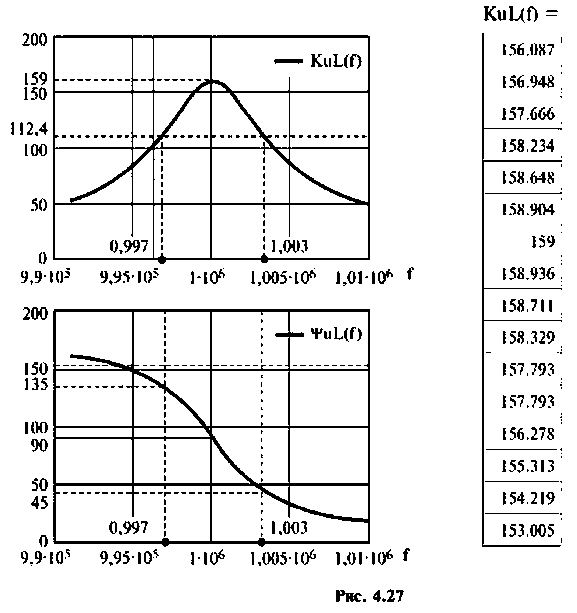
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
2. Рассчитаем емкость конденсатора. Из формулы 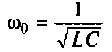
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
Вычислим значения функций на частотах:
Определим частоту, при которой АЧХ имеет максимум
Смещением частоты 
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
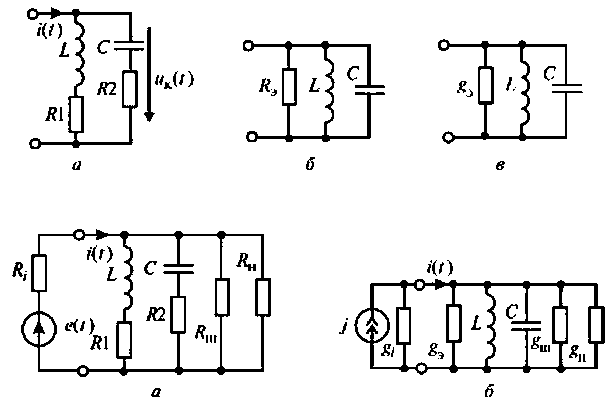
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений
где резонансная частота колебаний
Для реального контура 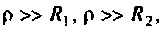
При резонансе сопротивление контура является активным, поэтому ток 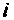
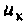
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
где
Добротность 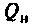
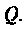
или через их проводимости
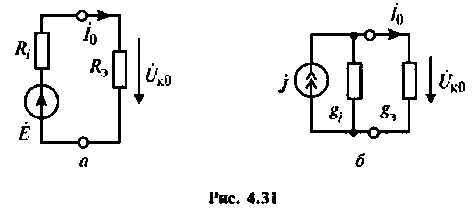
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
При этом напряжение на контуре максимально и равно
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
где 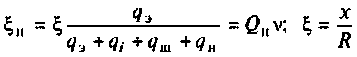
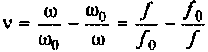
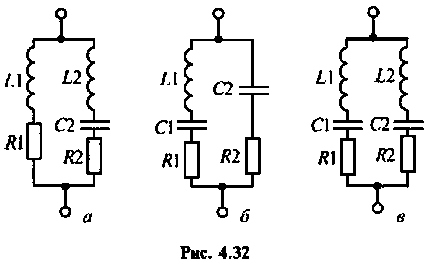
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
где 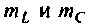
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 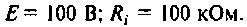
Параметры катушки индуктивности:
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
2. Рассчитаем волновое сопротивление
3. Определим сопротивление контура при резонансе
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
5. Определим соответственную добротность контура
6. Найдем ток в контуре и напряжение на нем:
7. Определим добротность нагруженного контура
8. Рассчитаем абсолютную и относительную полосы пропускания:
9. Определяем добавочное cопротивление 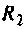
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано:
Определить сопротивление 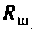
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
Тогда
3. Определим полосу пропускания
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
Тогда из (4.32) получаем
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 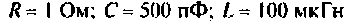
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
2. Рассчитаем собственную добротность контура
3. Найдем сопротивление контура при резонансе
4. Определим добротность нагруженного контура по формуле (4.31)
5. Рассчитаем резонансную частоту
6. Найдем полосу пропускания
7. Определим граничные частоты полосы пропускания:
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот: 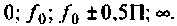
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано:
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
Сопротивление контура при резонансе
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
3. Найдем добротность нагруженного контура II вида
Сравним значения 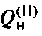
Вывод. За счет неполного включения индуктивности 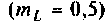
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
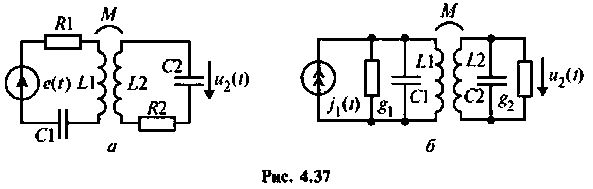
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
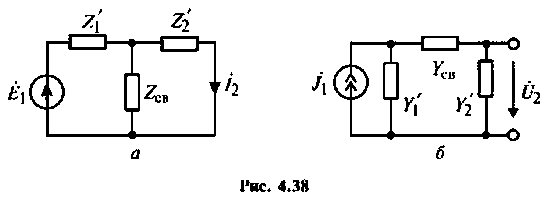
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 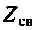
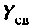
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;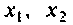
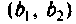
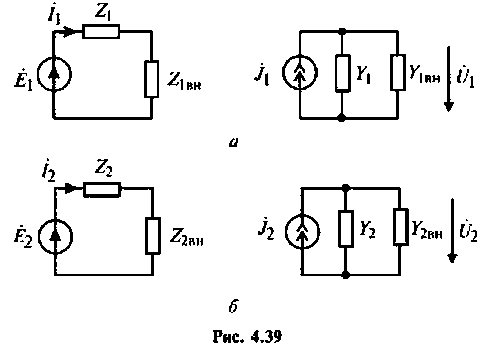
Для этого используют понятия вносимого сопротивления 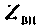
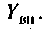
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.
Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
где
параллельного питания:
где 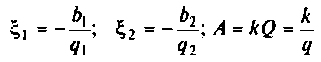
Если контуры идентичны, то обобщенная расстройка
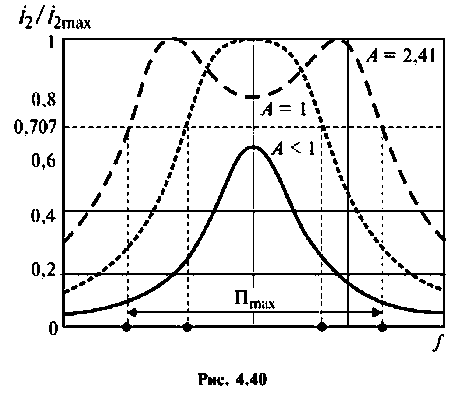
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая
б) связь критическая
в) связь сильная
При 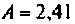
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
Определить емкость 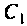
Решение
Емкость конденсатора 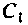
отсюда
Определим реактивное сопротивление 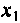
Peaктивное сопротивление второго контура
Рассчитаем полное сопротивление второго контура
Определим сопротивление связи контуров
Следовательно
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано:
Решение
1. Определим емкость конденсатора 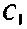
Отсюда
2. Сопротивление оптимальной связи при полном резонансе
3. Рассчитаем токи в первом и втором контурах при полном резонансе
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 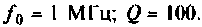
Решение
1. Определим полосу пропускания одиночного контура
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для
Таким образом при 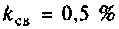
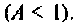
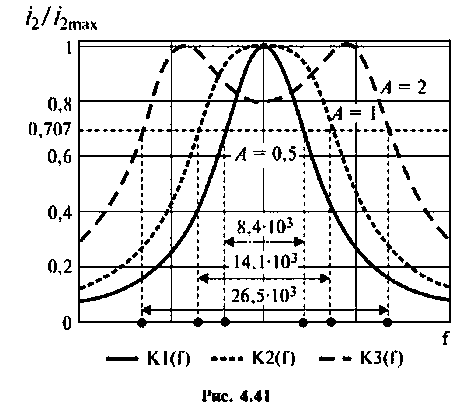
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
2) при 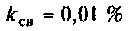
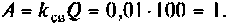
3) если 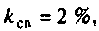
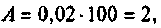
Рассчитаем полосу пропускания для этого случая.
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 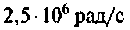
Дано:
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
Емкость конденсатора второго контура
2. Рассчитаем волновое сопротивление контуров:
3. Рассчитаем добротности контуров и параметр связи:
4. Определим взаимную индуктивность двух связанных контуров
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
С учетом этого рассчитаем ток во втором контуре
6. Найдем напряжение на конденсаторе вторичного контура
Пример 4.5.5.
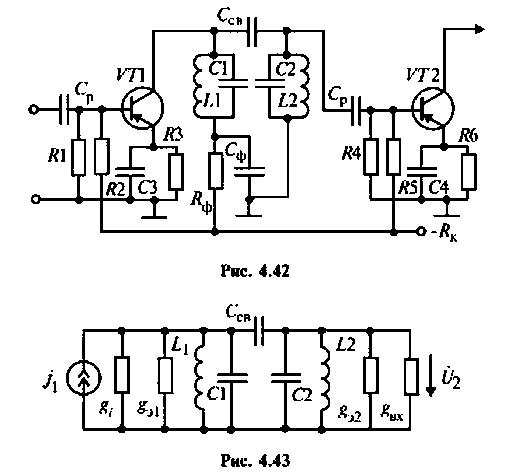
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 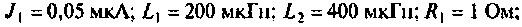
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 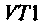
Емкость второго контура с учетом влияния входной емкости транзистора 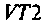
2. Определим емкость связи
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
где
где
4. Рассчитаем параметр связи
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс 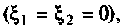
Найдем проводимость контуров
Тогда
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 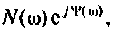
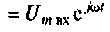
где 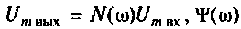
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 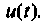
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида
Каждому из этих колебаний соответствует выходное колебание 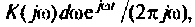
Представляя 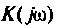
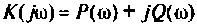
где 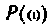
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 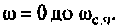

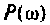
В результате интегрирования получают совокупность значений 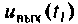
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
Вид подынтегральной функции, соответствующей выражению
при фиксированном времени 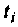
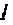
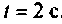
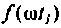
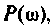
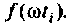
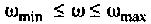
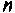
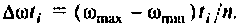
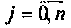

Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 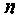
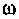
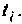
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
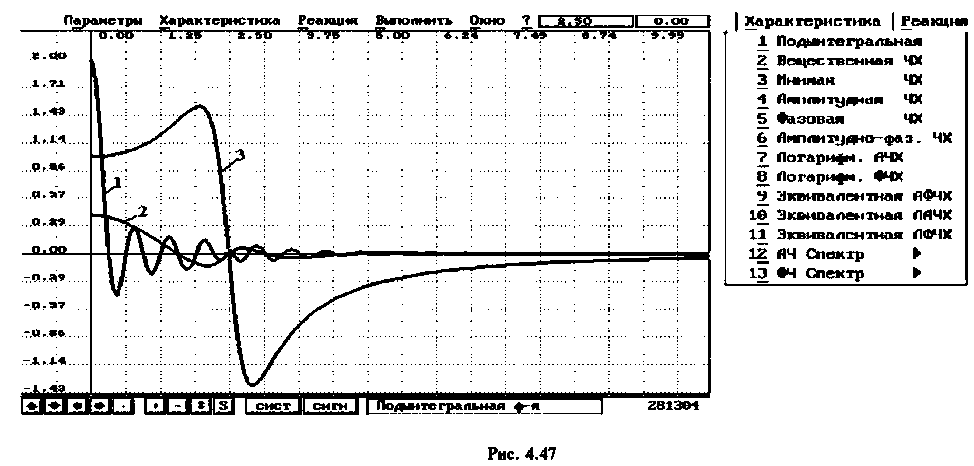
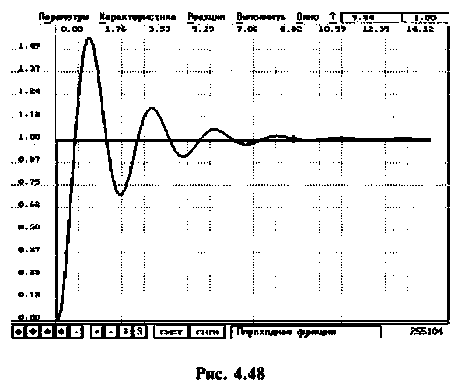
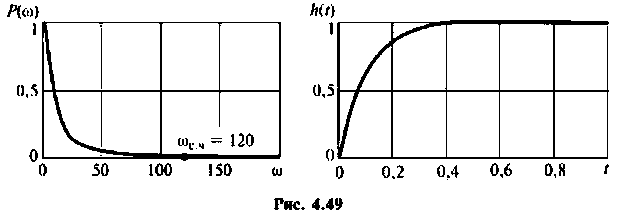
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 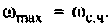
Алгебраическая форма КФ
где 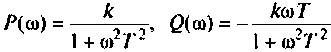
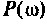
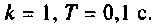
Из графика ВЧХ видно, что при 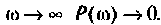
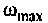
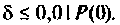
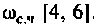
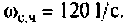
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 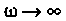
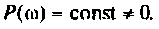
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
где
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 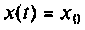
2) для линейной входной функции 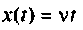
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 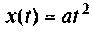
4) для полиномиального воздействия вида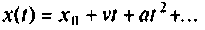
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
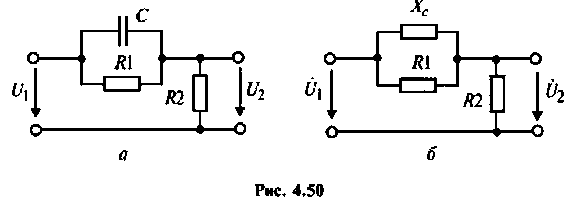
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 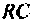
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 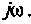
Следовательно
Введем обозначения:
Величина 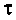
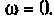
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Примем:
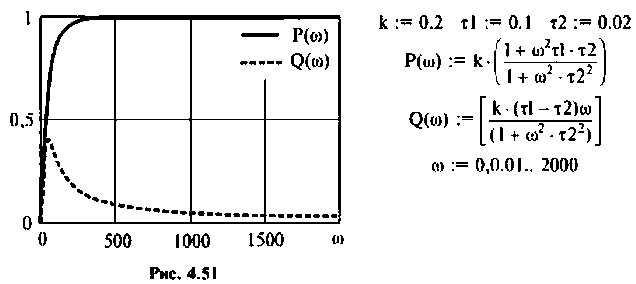
Для определения частоты 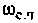
Из частотных характеристик КПФ принимаем 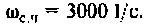
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
Пример 4.6.2.
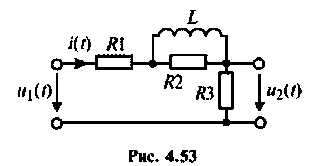
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 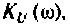
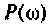
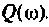
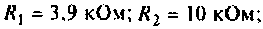
Решение
1. Найдем комплексную функцию 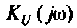
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Для определения частоты 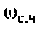
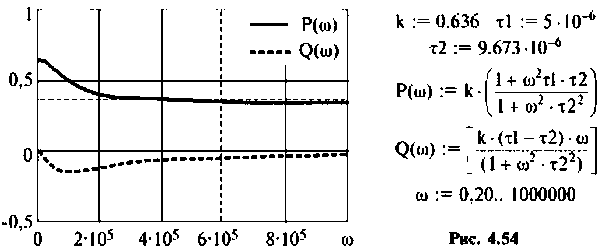
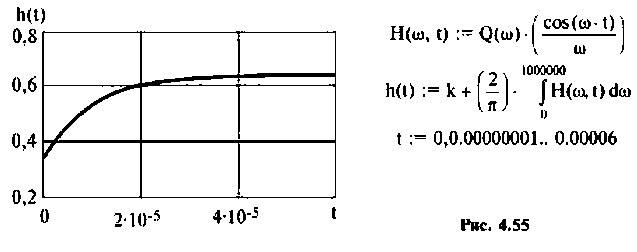
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 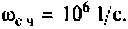
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
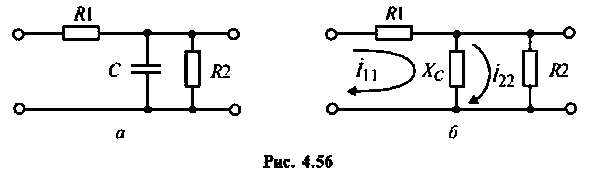
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 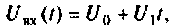
Параметры цепи:
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 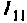
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки
Подставляя найденные выражения, получаем
т.е.
где
4. Рассчитаем 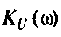
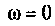
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 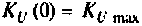
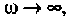
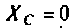
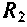
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
где 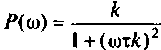
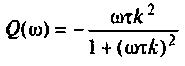
Амплитудно-частотную характеристику запишем в виде
6. В среде Mathcad построим частотные характеристики и определим
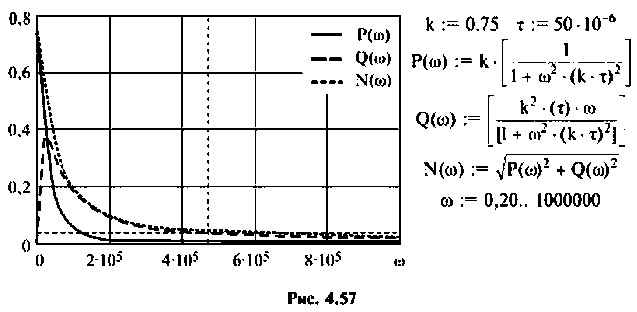
По ВЧХ на рис. 4.57 определяем, что существенная частота
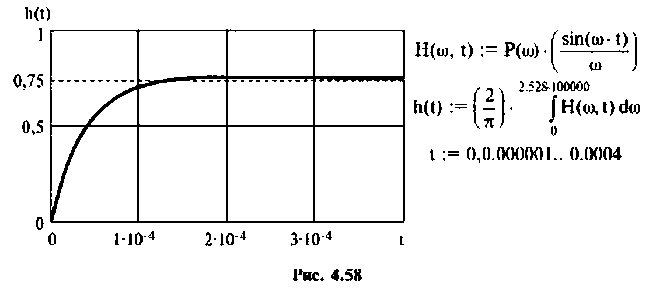
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
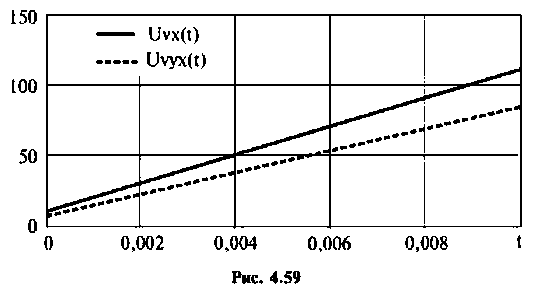
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
Чтобы взаимодействовать
с электромагнитными излучениями,
вещественная форма сама должна быть
колебательной системой. И потому
все внутренние процессы являются
электромагнитными по характеру своему.
И потому Жизнь носит черты электромагнитного происхождения.
§1. Собственные незатухающие колебания в электрическом колебательном контуре
Все существующие формы вещества являются живыми электромагнитными автоколебательными системами, все они живут внутри электромагнитных автоколебательных полей, и потому вещество, и поле имеют одну общую природу – электромагнитную. Общая задача всех колебательных систем поддерживать и сохранять неизменным ритм своих незатухающих колебаний (свою жизнь) за счёт взаимодействия с ритмами электромагнитного поля. Поскольку все формы вещества и вся Вселенная полностью являются колебательными системами, а явления внутри них носят электромагнитный характер, поскольку в них ритмично протекает процесс превращения магнитной энергии в электрическую, и обратно, то Живой процесс имеет электромагнитную основу происхождения.
В природе космоса реально фиксируются два вида материи – вещественная или атомарная, и полевая или фотонная, она же светоносная материя, материя, которая переносит электромагнитные волны. Возбуждение волн в фотонной среде осуществляется активными излучателями, генераторами волн, которыми в реальных условиях природы являются генетические центры или центры памяти. Такой центр памяти (ядро) существует и у Вселенной, и у каждого атома. Все звёзды являются локальными генетическими центрами.
В Солнечной системе таким центром является Солнце. Сливаясь в систему по линии своих центров памяти, индивидуальные элементы, обладая своим сознанием и ощущением своего бытия, не размазываются с потерей индивидуальности и не растворяются, наоборот, обобщая свои системы ощущения в единую чувствительную систему, а свои информационные знания в единую структуру памяти, они расширяют область своих знаний, будучи единой сущностью. Система тел способна работать с длиной волны, большей, чем одиночный элемент системы. Поэтому при объединении в систему происходит распределение функциональных обязанностей между элементами системы.
Надо хорошо представлять, что вся жизнь биосферы планеты, жизнь самой планеты и всей Солнечной системы происходит внутри электромагнитных полей той или иной интенсивности. Надо так же помнить, что все формы вещества и само вещество имеет одно и тоже электромагнитное происхождение, что и все виды излучений. Поэтому все формы вещества являют собою колебательные системы, внутри которых происходят электромагнитные физические превращения.
Чтобы стал понятным живой процесс человека и всех форм жизни в условиях электромагнитных полей на Земле и в космосе, необходимо хорошо представлять взаимодействие вещества с излучениями. Все формы вещества имеют электрически заряженную внешнюю оболочку, исполненную в форме последовательного колебательного контура, и структуру памяти в форме параллельного колебательного контура. Все формы вещества состоят из этих двух частей, и все они являются колебательными системами – колебательными контурами. Чувствительные элементы электрически заряжены и эквивалентны электрическому конденсатору. А структура памяти обладает индуктивными свойствами, она эквивалентна катушке индуктивности (спиральной формы) в колебательном контуре, обладает магнитной энергией.
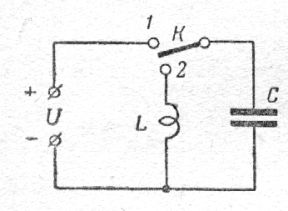
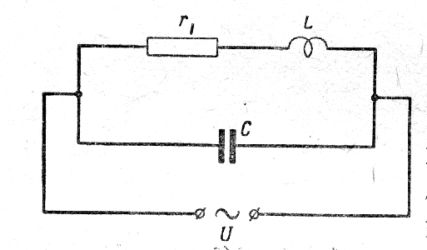
Колебательный контур является универсальной структурой, в которой бесконечно долго можно сохранять колебания, которые не зависят от информационного содержания колебаний электромагнитных волн. И потому всё разнообразие живых форм вещества, владея разным информационным содержанием, являются колебательными системами.Контур колебаний состоит всего из двух элементов – конденсатора (накопителя электрической энергии) и индуктивности, регулирующей ток колебаний. Разберём процесс колебаний на примере радиотехнического колебательного контура (Рис.1).
Рис.1. Схема колебательного контура. Переключатель К показан в нейтральном положении.
Источник питания постоянного, а не переменного тока выбран только для того, чтобы рассмотреть один период колебания заряда и разряда конденсатора.
Создадим электрическую цепь, в которой можно будет зарядить конденсатор C от источника электрической энергии с постоянным напряжением U через катушку индуктивности L в положении 1 переключателя К , а затем разрядить этот же конденсатор через ту же катушку индуктивности в положении 2 переключателя К.
Конденсатор обладает ёмкостью С, в него можно закачивать электрическую энергию. А катушка обладает свойством индуктивности[1]. Величина ёмкости С конденсатора зависит от площади обкладок конденсатора, от расстояния между обкладками и от диэлектрической проницаемости диэлектрика между пластинами. С = ε S / d, где ε — диэлектрическая проницаемость диэлектрика между пластинами конденсатора, S – площадь пластин, d– расстояние между пластинами (обкладками).
Поставим переключатель К в положение 1, подключив тем самым конденсатор к источнику электрического напряжения U, а катушка индуктивности L будет отключена от электрической цепи. И конденсатор C начнёт заряжаться до тех пор, пока напряжение на его пластинах (обкладках) не сравняется с величиной напряжения источника питания. В результате заряда конденсатора в его электрическом поле между пластинами накопится потенциальная электрическая энергия, равная половине произведения величины ёмкости конденсатора на величину напряжения в квадрате. . Wэ. m = CU2m /2. Где W- энергия электрического поля конденсатора в джоулях, Um– максимальное напряжение на конденсаторе в вольтах. С – ёмкость конденсатора в фарадах.
В момент полного заряда конденсатора отключим его от источника напряжения электрической энергии подсоединим его к катушке индуктивности L, поставив переключатель К в положение 2 (рис.1). Конденсатор начнёт разряжаться через катушку индуктивности. Изобразим ход разряда конденсатора С через индуктивность L графически (Рис.2).
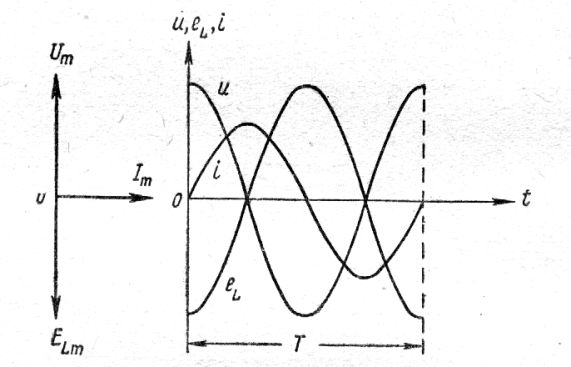
Рис. 2. Векторная и развёрнутая во времени диаграмма напряжений и тока колебательного разряда конденсатора.
В момент t= 0 конденсатор имеет максимальное значение U, а ток I, равный нулю. Далее ток разряда начнёт увеличиваться, создавая в катушке магнитное поле, которое будет нарастать по мере того, как ток разряда будет увеличиваться. Изменяющееся во времени магнитное поле индуктирует в проводнике катушки электродвижущую силу самоиндукции, направленную навстречу току разряда конденсатора (рис. 3), и (согласно правилу Ленца) будет препятствовать, но не прекращать нарастание тока. Практически э.д.с. самоиндукции автоматически управляет поведением тока разряда конденсатора, он изменяется не мгновенно, без скачков, а плавно.
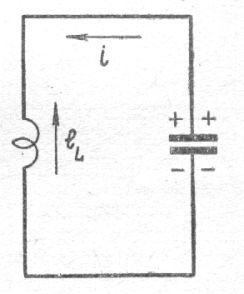
Рис. 3. Схема разряда конденсатора через индуктивность. Возникшая в катушке Э.Д.С. (электродвижущая сила) самоиндукции
eL направлена навстречу току разряда i.
Силы электрического поля конденсатора ещё велики и они,преодолевая силу сопротивления сил индукционного электрического поля катушки, совершают работу, в результате которой потенциальная энергия электрического поля конденсатора плавно переходит в магнитное поле катушки индуктивности. И в момент времени полного разряда конденсатора его напряжение станет равным нулю, энергия его электрического поля полностью перейдёт в энергию магнитного поля индуктивности, достигнув максимального значения. На рис.2 этот момент показан при U= 0.
Ток разряда в этот момент достигает максимальной величины, проходя через катушку. И магнитное поле индуктивности станет максимальным по величине, запасая в себе максимальную магнитную энергию, равную половине произведения величины индуктивности на квадрат максимальной величины тока.
Wм. m = LI2m/2., где ток в амперах, индуктивность в генри, энергия в джоулях.
Поскольку энергия электрического поля конденсатора не расходовалась ни на какие другие преобразования (не нагревала провода катушки и пр.), то она полностью перешла в магнитную энергию поля индуктивности.
CU2m /2 = LI2m/2.
Итак, в результате полного разряда конденсатора потенциальная энергия его электрического поля неподвижных зарядов преобразовалась в кинетическую энергию магнитного поля тока движущихся электрических зарядов. Тем самым становится понятным, что магнитное поле существует до тех пор, пока есть движение электрических зарядов. Тем самым понятно, что в элементах памяти, обладающих магнитным полем, текут динамические процессы перемещения зарядов. Память исчезнет, если не будет внутреннего потока зарядов в замкнутом элементе памяти. Поэтому магнитный элемент памяти всегда нуждается в притоке электрических зарядов.
Мы остановились в своих рассуждениях о колебательном процессе в момент, когда электрическое напряжение конденсатора стало равным нулю, исчезло вместе с исчезновением зарядов на обкладках конденсатора. Исчезло и электрическое поле конденсатора, все электрические заряды перешли в электрическую цепь с катушкой индуктивности. Исчезла и сила, создающая течение тока, все заряды в пути своего движения. Магнитное поле при этом максимально большое.
Поскольку исчезло электрическое напряжение и электрическое поле конденсатора (инициатора всего процесса превращения энергии электрической в магнитную энергию индуктивности), то тот час же начнёт уменьшаться величина живительного электрического тока, начнёт уменьшаться и величина магнитного поля индуктивности. Здесь прямая зависимость магнитного поля от величины тока.
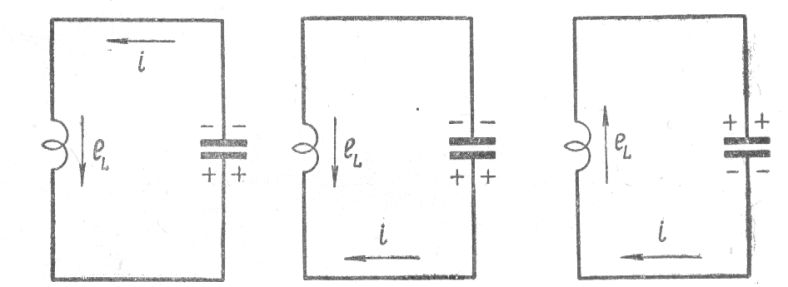
Поскольку ток начнёт уменьшаться, то магнитное поле отреагирует созданием электродвижущей силы самоиндукции, которая создаст ток того же направления, что и исходный ток разряда конденсатора. Так э.д.с. самоиндукции станет препятствовать убыванию тока, ибо от его наличия зависит состояние магнитного поля, а оно – хранитель памяти предыдущего нарастания тока. И теперь источником зарядки конденсатора, но в противоположной полярности, станет сама индуктивность. С убыванием изначального тока разряда начинается процесс перезарядки конденсатора (рис.4, левый контур).
Рис. 4.Схема разряда конденсатора и его перезарядки с учётом возникшей электродвижущей силы eLв катушке индуктивности.
Силы индукции в момент перезарядки конденсатора поддерживаю изначальный ток (предыдущего разряда конденсатора), способствуя перемещению электрических зарядов на обкладки (пластины) конденсатора. Магнитная энергия индуктивности полностью переходит в электрическую энергию конденсатора в момент его полной перезарядки. Общий ток, постепенно убывая, становится равным нулю. В момент, когда исходный ток станет равным нулю, исчезнет и магнитное поле индуктивности. Произойдёт полная перезарядка обкладок конденсатора. Та, которая была положительно заряженной (рис.3), будет иметь отрицательный заряд, а та, которая была отрицательной, станет положительно заряженной (рис.4).
Итак, в момент времени, равный половине периода колебания, когда ток в общей цепи станет равным нулю (см. рис.2), энергия магнитного поля полностью перешла в энергию электрического поля конденсатора, изменив его полярность на противоположную. Запомним, ритм магнитного поля изменил полярность электрически заряженных чувствительных органов.
Как только общий ток в цепи контура стал равным нулю, а сам конденсатор зарядился с изменением своей полярности, то теперь ничто не мешает ему начать снова разряжаться по той же цепи контура, но уже ток потечёт в обратном направлении. Время колебания изменило своё направление на обратное движение тех же самых электрических зарядов (рис. 4, . средний контур). Такой процесс заметит внешний наблюдатель процесса колебания, находясь за пределами контура.Для человека этот процесс физических превращений является невидимым, но, создав электроизмерительные приборы и осциллограф, человек увидел весь процесс колебаний внутри электрического колебательного контура.
Итак, начался второй полупериод колебательного процесса. Конденсатор, совершив перезарядку, станет снова разряжаться, снова будет нарастать величина электрического тока, появится магнитное поле, которое создаст э.д.с. самоиндукции, препятствующей нарастанию тока, потом ток достигнет максимальной величины. Снова исчезнет электрическое поле конденсатора, и начнётся новая перезарядка конденсатора, которая вернёт его в исходное состояние, время t = 0, в начало нового периода колебания.
Как показывает опыт, перезарядка конденсатора может происходить сколь угодно долго (если нет необратимых потерь) с равными промежутками времени – периодами колебаний. В реальных условиях индуктивность излучает электромагнитные волны, которые несут информацию об этом колебательном процессе, унося на себе часть энергии магнитного поля. И тогда, чтобы колебания не затухали, надо периодически подключать конденсатор к внешнему источнику электрической энергии, чтобы компенсировать потери на излучения.
И параллельный колебательный контур (как элемент памяти) снабжается последовательным колебательным контуром, как чувствительным элементом для взаимодействия с внешними электромагнитными полями и излучениями.
Как показывает математический анализ, незатухающий колебательный разряд конденсатора является электромагнитным процессом, изменяющимся во времени по синусоидальному – периодическому закону.
§2.Частота собственных незатухающих колебаний
Определим частоту собственных незатухающих колебаний в колебательном контуре, исходя из условия равенства электрической энергии конденсатора и магнитной энергии индуктивности. CU2m /2 = LI2m/2.
Исходя из формулы закона Ома, определим величину тока в цепи с конденсатором.
I= U/ 1/ωС.Величина 1/ωС – это емкостное сопротивление цепи тока,ω – угловая частота колебаний. Так в контуре будет равен: I = ω2LC. Отсюда определим угловую частоту, исходя из параметров элементов контура – индуктивности и ёмкости,ω = 1/ √LC.
Угловая частота колебаний в контуре равна единице, делённой на корень квадратный из произведения величины индуктивности на величину ёмкости. Отсюда находим частоту собственных незатухающих колебаний f = ω/2π = 1/ 2π√LC
Отсюда определяем период собственных незатухающих колебаний
T = 1/f = 2π√LC Индуктивность в генри, ёмкость в фарадах, период в секундах, частота в герцах.
Для определения частоты колебаний при известной длине волны обычно используют формулу λ = 300/f– читается: -длина волны колебаний в МЕТРАХ равна делению числа 300 на частоту в мегагерцах.
В колебательном контуре распространяется волновое колебание, и потому важно знать волновое сопротивление контура. Сопротивление, равное порознь индуктивному и емкостному сопротивлениям колебательного контура при наличии в нём собственных незатухающих колебаний, называется волновым сопротивлением контура: ρ = √L/C – читается так: волновое сопротивление (в Омах) колебательного контура равно корню квадратного от деления индуктивности на величину ёмкости.
Из полученных экспериментальных данных видно, что мгновенные значения энергий электрического поля конденсатора и магнитного поля индуктивности несинусоидальные, так как зависят от квадрата косинуса и синуса угла ωt.
Сумма мгновенных значений энергии электрического поля конденсатора и магнитного поля катушки (спирали) индуктивности в колебательном контуре при наличии в нём собственных незатухающих колебаний является величиной постоянной, не зависящей от времени, и равной порознь величинам максимальной энергии электрического поля и магнитного поля. Эти поля полностью обеспечивают себя энергией и не нуждаются в получении её от внешнего источника энергии. Это в идеальном случае, когда нет потерь на излучение и тепловых потерь.
В реальности, чтобы в электрической цепи, состоящей из индуктивности и ёмкости с активным сопротивлением, происходили незатухающие синусоидальные колебания, необходимо эту цепь питать электрической энергией от источника с переменным синусоидальным напряжением. При этом, если, например, максимальная энергия, запасаемая в магнитном поле катушки индуктивности (элемент памяти), больше максимальной энергии, запасаемой в электрическом поле конденсатора, LI2m/2 › CU2m /2, то магнитное поле индуктивности, исчезая в процессе колебания, передаст не всю свою энергию электрическому полю конденсатора, а только часть, равную максимальной величине этого поля. Оставшуюся часть магнитное поле возвратит в тот источник, который возбудил колебания в контуре.
И наоборот, когда электрического поля конденсатора недостаточно для получения максимальной магнитной энергии, индуктивность получает её от источника возбуждения колебаний, например, из внешнего электромагнитного поля.
Когда индуктивное и емкостное сопротивления близки по величине друг к другу, но при этом значительно превосходят величину активного сопротивления в цепи контура, возникающие напряжения на ёмкости и индуктивности могут значительно превышать даже само напряжение источника электрической энергии. При этом возникает представление, что энергия возникает как бы из ниоткуда.
Например, рассмотрим электрическую цепь переменного тока, состоящую из последовательно соединённых активного сопротивления 20Ом, катушки с индуктивностью 0,3 гн, и ёмкости 4 мкф. К цепи приложено напряжение 120вольт с угловой частотой 1 000сек-1.
При этом на конденсаторе образуется напряжение 557,5 в, напряжение на катушке 660в при общем токе 2 ампера.
§3. Электрический резонанс напряжения и резонанс токов
Резонанс напряжения.
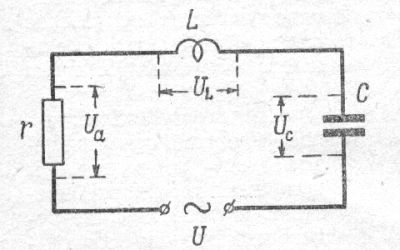
Как уже говорилось ранее, все чувствительные оболочки вещественных форм, начиная с атома водорода, являются электрически заряженными, и по своей структуре выглядят как последовательный колебательный контур. Если к электрической цепи, состоящей из последовательно соединённых активного сопротивления, индуктивности и ёмкости (рис.5), приложить переменное напряжение, изменяющееся по синусоидальному закону, u = Um Sinωt, то в этом контуре возникнут ВЫНУЖДЕННЫЕ электромагнитные колебания переменного тока, частота которого будет совпадать с частотой приложенного к цепи контура напряжения. Переменный ток, возникающий в этом контуре, будет так же изменяться по закону синуса,
i = Im Sin (ωt-φ). Величина угла сдвига фаз φзависит от величин сопротивления индуктивности, ёмкости и активного сопротивления. tgφ = (ωL – 1/ωC)/r. Изменяя величины L, C, угловую частоту ω, можно добиться такого режима, когда tgφ = 0. Значит, и сам угол сдвига фаз φ колебаний будет равен нулю. Это будет означать, что ток и напряжение в цепи контура будут совпадать по фазе колебаний.
Рис.5. Схема цепи с последовательным соединение индуктивности, ёмкости и активным сопротивлением.
Режим колебаний, когда в цепи с индуктивностью (элемент памяти) и ёмкостью (накопитель энергии, чувствительная оболочка) напряжение и ток совпадают по фазе колебаний, называется ЭЛЕКТРИЧЕСКИМ РЕЗОНАНСОМ. Различают два вида электрического резонанса – резонанс напряжений и резонанс токов.
Резонанс напряжений возникает в цепи последовательного колебательного контура, когда индуктивность и ёмкость включены последовательно с источником электрического питания (рис.5). Это условие в точности соответствует подключению чувствительных органов/рецепторов к внешним электромагнитным полям.
Резонанс токов возникает в цепи колебательного контура, где индуктивность и электрическая ёмкость подключены параллельно к источнику электрического тока (рис. 6).
Рис.6. Схема электрического колебательного контура, состоящего из параллельно соединённых индуктивности, ёмкости и активного сопротивления.
Важно понять, что при резонансе напряжений оперативная память и чувствительная система рецепторов соединены последовательно. В этом случае ток и напряжение будут совпадать по фазе колебаний с частотой и фазой внешнего переменного напряжения. В этом явлении информация внешней среды без искажения трансформируется в токи, напряжения, электрическое и магнитное поле чувствительного элемента живой формы вещества.
Это очень важное свойство имеют все живые системы: они безошибочно руководствуются сведениями внешнего энергоинформационного поля.
Поэтому можно сказать, что резонанс напряжений – это такое явление в цепях переменного тока живых колебательных систем, при котором наблюдается совпадение частоты вынужденных колебаний с частотой собственных незатухающих колебаний живой системы.
При резонансе напряжений в колебательном контуре местное напряжение на индуктивности находится в противофазе с местным напряжением на ёмкости (сдвинуты по фазе на 180°), их геометрическая сумма векторов равна нулю. Это и приводит к тому, что всё приложенное напряжение при резонансе напряжений расходуется только на преодоление активного сопротивления.
Важно! Если окажется, что при явлении резонанса напряжений индуктивное сопротивление будет равно емкостному сопротивлению, и при этом каждое из них будет значительно превышать активное сопротивление (мало активное сопротивление), то падение напряжения на индуктивности и ёмкости будут значительно превышать падение напряжения на активном сопротивлении.Следовательно, напряжения на рецепторах и на оперативной памяти будут значительно превышать приложенное из внешней среды напряжение. Тем самым в живых системах происходит значительное усиление электромагнитных сигналов внешней среды. Этим и объясняется слабое и сверхслабое взаимодействие в биологии и медицине и проблема КТ решается просто.
Перенапряжения, возникающие на индуктивности (оперативная память) и на ёмкости (рецепторы) при резонансе напряжений, обусловлены тем, что внутри цепи колебательного контура возникают относительно мощные местные колебания энергии между магнитным полем индуктивности и электрическим полем конденсатора. Это колебания между структурой оперативной памяти и рецепторами. Например, колебания между протоном и электронной оболочкой в атоме водорода. Такое явление резонанса напряжения свойственно всем атомам – между ядром и электронной оболочкой.
В любой момент времени при резонансе напряжений общее количество энергии, ЗАПАСАЕМОЕ в электрическом и магнитных полях резонансного контура, постоянно (внутренний гомеостаз живой системы). Оно равно максимальному количеству энергии, запасаемой магнитным полем индуктивности (оперативной памяти) ИЛИ электрическим полем конденсатора (рецепторной системой).
При резонансе напряжений колебательный контур живой системы (любое биологическое существо, любой атом и вещественная форма) по отношению к внешнему информационному полю является чисто активной системой. И в этом случае СЛАБОЕ внешнее электромагнитное поле посылает в электрическую цепь структуры организма только ту энергию, которая нужна для покрытия активных потерь.
Что же касается энергии, потребной для сохранения магнитного поля индуктивности (сохранение знаний структуры памяти), и энергии, потребной для создания электрического поля конденсатора (рецепторное электрическое поле), то внешнее электромагнитное поле разгружен от них. Это вызвано тем, что индуктивность и конденсатор (память и рецепторы) взаимно обмениваются энергией. Тем самым Жизнь данного элемента может длительно сохраняться при отсутствии внешнего электромагнитного поля нужного диапазона частот, что мы и наблюдаем на примере, например, атомов или вирусов.
Чем меньше активное сопротивление данного элемента живой и последовательной колебательной системы, те при прочих равных условиях будут мощнее электромагнитные колебания в цепи контура при резонансе напряжений. Тем большим количеством энергии обмениваются оперативная память (индуктивность) и рецепторы (конденсатор).
Индуктивное и емкостное сопротивления при резонансе напряжений порознь равны волновому сопротивлению электропроводной цепи контура. Тем самым находим объяснение избирательного взаимодействия формы вещества с внешними электромагнитными полями. Каждому виду живых существ нужна своя персональная гармоника электромагнитного поля, своя поляризация (угол наклона вектора электрического поля). Поэтому все формы вещества взаимодействуют под некоторым углом к внешнему полю.
Затухание полезного сигнала (невежество) в последовательном колебательном контуре численно равно отношению величины напряжения внешнего электромагнитного поля к величине падения напряжения на индуктивности (оперативная структура памяти) или на конденсаторе (рецепторе).
При исследовании резонансных явлений и определения добротности (жизнеспособности) живых колебательных систем важную роль играет зависимость действующего значения токов и напряжений в колебательном контуре от частоты внешней электромагнитной волны, от параметров индуктивности (структуры памяти) и ёмкости (рецепторная ёмкость) колебательной системы.
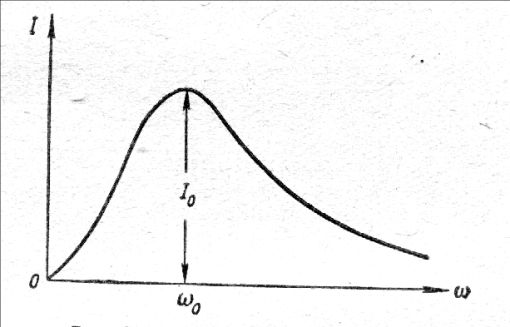
Рис.7. Резонансная кривая тока последовательного колебательного контура.
Посмотрим, как зависит величина действующего тока в последовательном колебательном контуре в зависимости от частоты сигнала внешних полей при неизменной величины их напряжения.
Величина тока I = U/ √ r2 + (ωL – 1/ωC)2
— ток равен отношению величины приложенного напряжения к корню квадратному из суммы активного сопротивления в квадрате и разности индуктивного и емкостного сопротивления в квадрате.
Не изменяя никаких других параметров (индуктивности, ёмкости, напряжения, активного сопротивления), будем изменять только частоту колебаний внешней электромагнитной волны т нуля до бесконечности.
Так при ω = 0 (смотри формулу) подкоренное выражение будет равно бесконечности. Следовательно ток будет равен нулю, тока не будет. В этом особенность всякой колебательной системы: нет внешней частоты, нет внешнего поля, не будет и живых колебательных систем.
Далее полагаем, что частота равна бесконечности. Подкоренное выражение равно бесконечности, и ток равен нулю. И опять, при бесконечно большой частоте и бесконечно малой длине волны не возможны колебательные процессы жизни.
Выберем такое состояние, когда индуктивное сопротивление структуры памяти равно емкостному сопротивлению рецепторов: ωL = 1/ωC
И тогда из формулы видно, что при равенстве сопротивлений индуктивности и ёмкости ток будет иметь максимальное значение. Смотри график Рис.7. Следовательно, сама частота
ω = ω0 = 1/√LC. И тогда собственная частота незатухающих колебаний будет равна
f = ω/2π = 1/ 2π√LC
Величина максимального тока в контуре будет равна отношению напряжения волны к величине активного сопротивления. Поэтому не надо сопротивляться закону природы, надо спокойно ему следовать, и тогда жизненные токи будут максимальными (рис. 8).
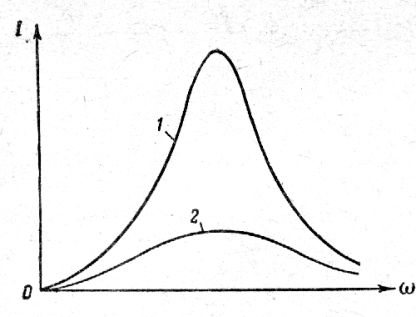
Рис. 8. Резонансная кривая тока: 1 – при малом затухании, малом активном сопротивлении. 2 – при большом активном сопротивлении, большое затухание тока жизни.
Резонанс токов
Резонансом токов называется такой режим в цепи переменного тока параллельного колебательного контура, когда индуктивность и ёмкость подсоединены параллельно к внешнему источнику синусоидального напряжения (рис.6), при котором ток в неразветвлённом участке электрической цепи и напряжение внешнего источника энергии, совпадают по фазе колебаний.
Параллельный колебательный контур является замкнутым контуром тока, он тождественен замкнутому элементу памяти. Вспомним, что последовательный колебательный контур является разомкнутым контуром по отношению к внешнему электромагнитному полю, которое является источником электрического напряжения для входных чувствительных систем.
Резонанс токов возникает в параллельном колебательном контуре тогда, когда реактивные составляющие проводимости параллельных ветвей с индуктивностью и ёмкостью численно равны друг другу. Тогда ток в неразветвлённом участке цепи при резонансе токов равен сумме активных составляющих токов в параллельных ветвях. Но в ветви с ёмкостью активная составляющая равна нулю, поскольку в ней активное сопротивление равно нулю. И тогда ток в неразветвлённой части будет равен активной составляющей тока в цепи с индуктивностью (в структуре памяти). Но активное сопротивление в цепи с индуктивностью значительно меньше реактивного индуктивного сопротивления. И ток в параллельных ветвях оказывается во много раз больше тока в неразветвлённом участке цепи контура.
Тем самым можно считать, что при резонансе токов в структуре памяти, а она тождественна параллельному контуру, резко увеличивается БЫСТРОТА МЫШЛЕНИЯ. Если при резонансе напряжения во входных устройствах организма (органы чувствования) происходит многократное усиление слабых электромагнитных сигналов, и мы решаем проблему КТ биологии, то при резонансе токов мы решаем проблему быстрого мышления.
Определим резонансную частоту, т.е. частоту, при которой при заданных параметрах индуктивности, ёмкости и активного сопротивления наступает резонанс токов. На практике чаще всего имеют дело с резонансными контурами, в которых активное сопротивление в параллельной цепи с ёмкостью отсутствует, а в цепи с индуктивностью активное сопротивление r1 значительно меньше индуктивного сопротивления ωL. В этом случае резонансная частота определяется по той же формуле, что и для резонанса напряжений: ω0 = 1/ √LC.Читается, как единица, делённая на корень квадратный из произведения индуктивности на величину ёмкости. При резонансе токов токи в параллельных ветвях равны между собой.
Рис.9. Схема резонансного контура без активного сопротивления в цепи с ёмкостью.
Важной особенностью резонанса токов в параллельном колебательном контуре является то, что реактивные составляющие токов параллельных ветвей компенсируют друг друга, а токи в этих ветвях обычно значительно превышают ток в неразветвлённой части (общая цепь сети), то этот электрический резонанс и назван резонансом токов.
Вывод. Токи в параллельных ветвях резонансного контура I1 и I2 (смотри рис.6) при резонансе токов порознь во столько раз больше тока I0 неразветвлённого участка контура, во сколько раз волновое сопротивление контура ρ = √L/C, больше его активного сопротивления r.
Добротность или качество контура Q = ρ/r1 (рис.9). И тогда добротность контура – это величина, показывающая, во сколько раз ток в резонаторе (резонансный контур) больше тока неразветвлённой части цепи при резонансе токов. I1/I = I2/I = Q (рис.6). Качество резонаторов достигает большой величины (1 000 и более), поэтому важно знать условие резонанса токов в параллельном контуре.
В этом одно из важнейших свойства структуры памяти – резонансное узнавание информации и быстрота мышления.
В отличие от резонанса напряжений (в чувствительных системах) при резонансе токов в структуре памяти сумма энергий электрического и магнитного полей контура памяти не является величиной постоянной. Это означает, что имеются такие моменты, когда электрическая или магнитная энергия полей контура расходуются частично или полностью в активном сопротивлении контура памяти.
Имеются и такие промежутки времени, когда источник энергии питания памяти -чувствительная система -пополняет запас энергии, израсходованный электрическим и магнитным полями контура. Однако обмена реактивной энергией между чувствительной системой и магнитной энергией структуры памяти в параллельном контуре не происходит. Последовательный колебательный контур чувствительной системы в общей сложности за один период колебаний доставляет в контур памяти такое количество энергии, которое было израсходовано в активном сопротивлении контура – на нагревание при мышлении и на излучение электромагнитных волн мыслей.
Удивительно то, что работа головного мозга человека, обеспечиваемая ретикулярной формацией продолговатого мозга как источником электрического поля, до деталей в точности тождественна работе технического параллельного колебательного контура при резонансе токов[2].
В реальности каждый человек ощущает это явление каждую ночь в режиме так называемого быстрого (или парадоксального) сна. Нейроны мозга в режиме отдыха тела (при отключении органов ощущения) питаются энергией ретикулярной формации. А в режиме бодрствования органы ощущения напрямую подзаряжают ретикулярную систему, и так повторяется всю жизнь. Мозг не может мыслить без энергии, ретикулярная формация не может сама вырабатывать электрическую энергию, ей нужна система чувствования, способная взаимодействовать с электромагнитной средой, преобразовывая излучения в токи той же частоты, свойственной данному виду живых существ. Поэтому в природе существует главный закон – закон сохранения и развития жизни, осуществляемый через процесс познания законов природы и сохранения этих знаний.
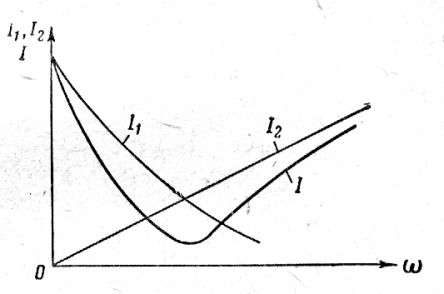
В заключении рассмотрим,как изменяются реактивные токи: I1 в параллельной ветви с индуктивностью; I2 в параллельной ветви с ёмкостью; и общий ток I в неразветвлённой цепи колебательного контура в зависимости от частоты вынужденных колебаний ω. Рассмотрим это для реального случая, когда активное сопротивление спиральной структуры памяти мало, а в цепи накопителя энергии оно вообще равно нулю (рис. 10).
I1 = U /ω0 L;
I2 = U / (1 / ω0 C) = U ω0 C.
Рис. 10. График изменения токов I1; I2 в параллельных ветвях колебательного контура и общего тока Iв зависимости от угловой частоты ω.
Ток в параллельной ветви с индуктивностьюI1 (а это ток элемента памяти) изменяется в зависимости от частоты вынужденных колебаний по гиперболическому закону. При ω = 0 ток в этом участке равен отношению напряжения к малой величине активного сопротивления в индуктивной цепи. А при ω → ∞ ток I1 стремится к нулю.
Это означает, что ток в структуре памяти I1 с ростом частоты вынужденных колебаний уменьшается до полного прекращения. Поэтому-то высокочастотные колебания, поступающие из внешней среды, вредны для структуры памяти – она прекращает мыслить. С ростом частоты внешних сигналов память перестаёт реагировать на них, она не различает их изменения, не развивается и полностью от них отключается.
У чувствительных систем с ёмкостными свойствами, наоборот, с ростом частоты вынужденных колебаний внешней среды растут токи I2 до бесконечности, что гибельно для самих элементов. При малой частоте колебаний внешней волны рецепторы не воспринимают эту волну, они теряют бдительность, не замечая изменений.
Это также говорит о том, что чувствительная система начинает своё развитие с высокочастотных сигналов, постепенно переходя к более низким частотам. Книга жизни читается с начала, а не с конца, путём логического считывания информации с нарастанием её смысла, т.е. с нарастанием длины волны.
Когда в поведении людей отмечается быстрота разговорной речи, следует видеть конец их эволюции.
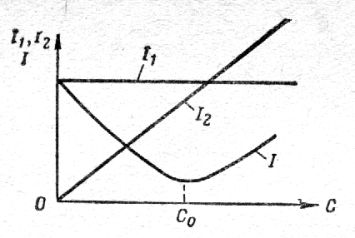
Как зависит течение токов в параллельном колебательном контуре, особенно в индуктивной его части, при неизменной частоте напряжения, идущего от чувствительной системы, но при этом изменяется величина электрической ёмкости? Другими словами, как реагирует структура памяти на величину электрической ёмкости её источника питания в условиях неизменной сигнальной информации среды? Ход изменения токов представлен на рис. 11.
Рис. 11. График изменения токов в структуре памяти (в виде параллельного колебательного контура) в зависимости от изменения электрической ёмкости от нуля до бесконечности.
Ток в индуктивном элементе памяти I1 = U /ω0L
не зависит от величины электрической ёмкости (от размеров источника питания) в параллельно ветви контура при постоянстве действующего напряжения вынужденных колебаний со стороны чувствительной системы.
Ток в ёмкостной цепи I2 растёт с ростом величины самой ёмкости: I2 = UωC. При этом структура самой памяти не берёт тока больше, чем это ей надо. Сама природа показывает, что элита от природы даже при нарастании всяческих благ, нарастании жизненной энергии (источников питания) не берёт для себя излишеств, довольствуясь номинальной потребностью. Общая потребительская корзина I (рис.11) сначала падает до оптимального уровня роста источника питания C0, а потом стремительно нарастает. А разум говорит, что ему не требуется больше того, что необходимо. Потребительский спрос растёт там, где мало ума, нет опыта жизни, чем больше имеют, тем больше хочется иметь.
Мыслит или не мыслит каждая форма вещества? Косвенным доказательством мышления у каждой формы вещества служит наличие частоты собственных незатухающих колебаний,наличие собственного источника энергии питания у каждой структуры памяти. Затраты энергии на мышление компенсируются энергией источника питания. Если есть источник питания, значит,форма вещества мыслит, какой бы малой она ни была!
Непрерывная мысль состоит из дискретных её единиц. Наименьшей формой вещества, обладающей наименьшей порцией мысли, является универсальная форма дейтерия – соединение последовательной колебательной структуры атома водорода и параллельной колеблющейся структуры нейтрона (универсальный элементарный квадруполь). Атомы химических элементов представляют собой отдельные «буквы общей Азбуки»жизни, из них слагаются слоги, слова, предложения, тексты, течёт мысль, воплощаясь в формы материи.
Вывод
Поскольку все формы вещества и излучений имеют одну и ту же электромагнитную природу происхождения, то все они являются колебательными системами. Все внутренние процессы в колебательной системе, состоящей из структуры памяти (индуктивности) и чувствительной оболочки (рецепторы с электрическими свойствами) являются электромагнитными. Поэтому делаем вывод: жизнь имеет электромагнитное происхождение.
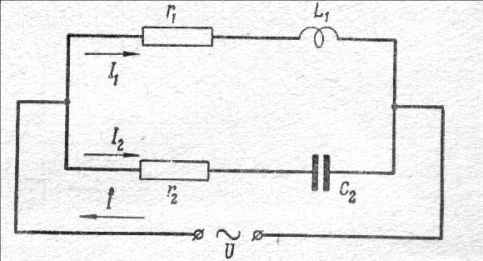
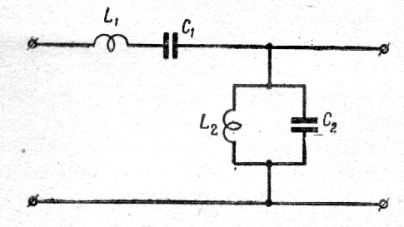
Рис. 12. Эквивалентная схема живой вещественной системы.
Последовательный колебательный контур L1 C1 — чувствительная система и параллельный колебательный контур L2 C2 – образуют единое целое, живую структурную форма вещества.
Два Начала, одно с магнитными свойствами индуктивности, а другое с электрическими свойствами,образуют целостную структуру, готовую к ритму колебательного процесса. Готовую, но ещё не колеблющуюся.
Данная система возбуждается, в полном смысле слова – оживает, с приходом в область её пребывания электромагнитной волны соответствующего диапазона частот. Порция энергии волны вдохнула жизнь в данную форму, и в ней возникает волнообразный процесс перекачки энергии от электрической ёмкости к индуктивной спиральной форме памяти и обратно от индуктивности к ёмкости без участия внешнего поля волны. Началась самостоятельная жизнь данной формы вещества, и этот колебательный процесс может длиться долго.
Но внешняя волна пришла снова, и своим напряжением возбудила чувствительные элементы последовательного колебательного контура, за счёт чего слабое напряжение волны усилилось в сотни тысяч раз. И усиленное напряжение без искажения смысла передаётся в параллельную структуру колебательного контура, где вызывает токи, текущие по замкнутому контуру в режиме незатухающих колебаний. Так напряжение внешней волны преобразовывается в токи структуры памяти, и хранится в неизменном виде незатухающих колебаний. Движение токов формирует магнитное поле той же формы, что и токоведущая система. Так формируется форма мысли за пределами контура токов.
Потери энергии за счёт мышления требуют компенсации от своего источника энергии, которому в свою очередь требуется подзарядка от чувствительной системы, а рецепторам нужно наличие внешнего электромагнитного поля, которое формируется генетическим центром следующего уровня иерархии форм. Так возбуждается жизнь, возникает рост и развитие под внешним управлением до уровня совершенствования, заданного геномом внешней среды.
Назначением каждой формы вещества является поддержание своих внутренних колебаний в заданном диапазоне параметров. Если в среде заметна убыль ЭМИ данного уровня, одиночные родственные элементы объединяются на том же принципе диполей, так формируются системы, способные воспринимать ЭМИ длинных волн и расщеплять их до нужного предела. Начался живой процесс. Так форма материи становится МЕРОЙ информационного содержания во внешнем электромагнитном поле
Контрольные вопросы к уроку №8
1.Почему Жизнь имеет электромагнитное происхождение?
2.В чём проявляется универсальность колебательной системы?
3.В чём разница параллельного и последовательного колебательного контура?
4.Расскажите процесс зарядки и разряда конденсатора.
5.Что такое индуктивность, самоиндукция, индукция?
6.Что препятствует быстрому заряду и разряду источника питания структуры памяти?
7.Как связано существование магнитного поля с динамикой электрических зарядов?
8.Что такое круговая частота и частота собственных незатухающих колебаний? Связь частоты и длины волны излучений через скорость света. Связь частоты колебаний со временем и пространством.
9.Что такое резонанс напряжений, где он возникает, и что он даёт?
10.Почему все чувствительные органы работают в напряжённом режиме?
11.Что служит причиной приёма и обработки электромагнитной информации без искажения во внутрь живой системы?
12.Чем объяснить индивидуальное существование взаимозависимых элементов в системе тел и систем между собой?
13.Что такое резонанс токов и кому он принадлежит?
14.Чем можно объяснить сверхслабые взаимодействия в биологии и медицине?
15.Расскажите суть БЫСТРОГО или парадоксального сна у всех млекопитающих? У кого он может ещё быть?
Нужен ли источник электрической энергии для структуры памяти? Роль белковых молекул для генома – ДНК.
[1] Индуктивность – иначе называется как коэффициент самоиндукции, количественная характеристика связи между силой электрического тока в замкнутом контуре с магнитным потоком через контур, созданным током в контуре.
Магнитная индукция – мера магнитного состояния магнитного поля, величина векторная.
[2] Цыган В.Н., Богославский М.М.,Князькин И.В., Апчел В.Я. Физиология и патология сна. СПб.: ВМА. Специальная литература. 2006. – 160с.
Урок №8. Презентация Microsoft PowerPoint.ppt
Другой разновидностью линейных цепей являются колебательные контуры. С их помощью решается одна из важнейших задач радиотехники – осуществление частотной селекции (избирательности). Из множества несущих частот различных радиостанций, поступающих в антенну радиоприемника, необходимо выбрать узкую полосу частот интересующей нас радиостанции. Для решения этой задачи нужны частотно–избирательные цепи в виде колебательных контуров. Колебательный контур – это линейная электрическая цепь, составленная из конденсатора и катушки индуктивности
3.4.1.Свободные колебания в идеальном контуре
Рассмотрим вначале колебательный контур, в котором отсутствуют потери электрической энергии, то есть контур из идеальной катушки индуктивности и идеального конденсатора. Зарядим однократно конденсатор от внешней батареи до напряжения . При этом электрическая энергия, запасенная конденсатором, будет равна

За счет разряда конденсатора через катушку индуктивности происходит преобразование электрической энергии в магнитную энергию. При этом магнитная энергия, запасенная катушкой индуктивности, становится равной

Затем происходит обратное преобразование магнитной энергии в электрическую энергию. В результате в контуре происходит колебательный процесс на некоторой частоте , Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:

Учитывая, что , подставим значение
В предыдущее выражение:

Отсюда резонансная частота колебаний
, (3.49)
А период колебаний

Из равенства энергий найдем волновое (характеристическое) сопротивление контура :

На резонансной частоте модуль реактивного сопротивления катушки индуктивности равен модулю реактивного сопротивления конденсатора:

Подставляя значение резонансной частоты в выражения для модулей реактивных сопротивлений, получим:

=
(3.54)
Таким образом, на резонансной частоте сопротивления реактивных элементов контура равны волновому сопротивлению. В идеальном контуре колебания будут незатухающими.
3.4.2.Свободные колебания в реальном контуре
Рассмотрим физические процессы в реальном контуре, состоящем из последовательно соединенных катушки индуктивности, конденсатора и некоторого активного сопротивления потерь . Сопротивление
эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.
Рис. 3.11. Последовательный колебательный контур
Если зарядить однократно от внешней батареи конденсатор, то в контуре возникнет колебательный процесс. На основе второго закона Кирхгофа можно записать:
. (3.55)
Или:
(3.56)
Продифференцируем все слагаемые уравнения (2.55) по времени и разделим на :

Обозначим , Где
— коэффициент затухания.
Учитывая, что , перепишем уравнение в следующем виде:

Ищем решение этого уравнения в виде: .
Подставим это решение в уравнение:

Или:

Где: .
— резонансная частота реального контура.
Решение последнего уравнения имеет вид:
(3.61)
Отсюда ток в контуре равен:
. (3.62)
Полагая начальную фазу j=0, ток в контуре будет равен:
(3.63)
Если a=0, то колебания не затухают. При этом:
(3.64)
(3.65)
В реальном контуре , поэтому колебания на частоте
Будут затухающими.
Рис. 3.12. Затухающие колебания в контуре с потерями
Период колебаний реального контура:

Если , то период колебаний
. При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.
Колебательный процесс возможен только, когда или
.
Отсюда: 
.
У радиотехнических контуров волновое сопротивление .
Поэтому с большой степенью точности можно считать, что период колебаний и резонансная частота в реальном контуре определяются следующими выражениями:
(3.67)
(3.68)
По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается добротностью:
(3.69)
Для радиотехнических контуров добротность
Добротность контура равна отношению напряжения на индуктивности или на емкости
к напряжению на активном сопротивлении при резонансе:

В этом выражении — Ток в контуре на резонансной частоте.
Умножим числитель и знаменатель на :

Добротность равна умноженному на 2 отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.
Величина обратная добротности называется затуханием контура:

3.4.3.Последовательный контур. Вынужденные колебания.
На рис. 3.13 представлен последовательный колебательный контур, к которому подключен генератор гармонических сигналов , внутреннее сопротивление которого равно нулю.
Рис3.13. Последовательный контур с внешним генератором
На основании второго закона Кирхгофа запишем:
. (3.73)
Ток в контуре будет равен:

Входное сопротивление
. (3.75)
Реактивная составляющая входного сопротивления
. (3.76)
В зависимости от расстройки контура относительно резонансной частоты возможны три случая:
— При этом реактивная составляющая входного сопротивления
носит индуктивный характер;
При этом реактивная составляющая входного сопротивления
носит емкостный характер;
при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.
На резонансной частоте входное сопротивление контура равно активному сопротивлению и ток в контуре равен значению .
Эквивалентная схема контура при резонансе приведена на рисунке.
Рис. 3.14. Эквивалентная схема последовательного контура на
Резонансной частоте.
Амплитуды напряжений на реактивных элементах на резонансной частоте равны по величине и противоположны по фазе.

Из этого выражения найдем резонансную частоту:
. (3.78)
Оценим величину отношения напряжений на реактивных элементах на резонансной частоте к напряжению внешнего генератора:


Таким образом, на резонансной частоте в последовательном контуре напряжения на реактивных элементах равны по абсолютной величине и в Q раз превышают напряжение внешнего генератора. Такой резонанс называется резонансом напряжений.
3.4.4.Амплитудно-частотная характеристика последовательного контура.
Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.
Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, представленного на рис. 2.14, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:


Реактивная составляющая входного сопротивления контура равна:

Здесь
(3.83)
— относительная расстройка контура.
Для небольших абсолютных расстроек контура (в пределах полосы пропускания)
(3.84)
С учетом этого амплитудно-частотная характеристика контура

Где: 
Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:

Фазовая характеристика контура
(3.87)
При настройке контура в резонанс , обобщенная расстройка
, реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно
. Характер зависимости
свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности
, который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров
. АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.
Рис.2.15 АЧХ последовательного контура
Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:

Отсюда полоса пропускания контура на уровне Будет равна:

Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:

Фазовая характеристика последовательного контура, построенная по выражению (2.98), приведена на рис. 3.16.

Рис.3.16. Фазовая характеристика последовательного контура
3.4.5. Параллельный колебательный контур.
Параллельный колебательный контур состоит из параллельно включенных катушки индуктивности и конденсатора, как показано на рис. 3.17. Активное сопротивление катушки индуктивности равно , а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению
. Контур питается идеальным генератором тока.
Рис. 3.17. Параллельный колебательный контур.
Входное сопротивление контура равно:

Для высокодобротных контуров в области резонансной частоты 


Где: ;
.
Таким образом, входное сопротивление зависит от частоты. Токи в ветвях контура также зависят от частоты. На резонансной частоте сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток

Входное сопротивление контура при резонансе становится активным и равно:
(3.95)
Следовательно, ток в контуре на резонансной частоте равен:

Таким образом, токи в ветвях контура при резонансе в раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.
Зависимость отношения амплитуды напряжения на контуре на текущей частоте к амплитуде напряжения на контуре на резонансной частоте
от частоты называют амплитудно-частотной характеристикой параллельного контура.
Запишем выражение для амплитудно-частотной характеристики параллельного контура:

Входное сопротивление контура равно:
(3.98) Умножим числитель и знаменатель этого выражения на (
):

Найдем модуль входного сопротивления:

Подставив модуль входного сопротивления в выражение (3.97), окончательно получим:

Таким образом, АЧХ параллельного и последовательного контуров описываются одним и тем же выражением.
Фазовая характеристика параллельного контура (рис. 2.18) построена на основании выражения
(3.102)
Рис. 3.18. Фазовая характеристика параллельного контура
3.4.6. Методы измерения добротности колебательных контуров
Существует несколько методов измерения добротности колебательных контуров.
Если подключить к контуру генератор гармонических сигналов и, изменяя частоту генератора, снять резонансную кривую контура, то добротность можно рассчитать по формуле:

Где: — резонансная частота;
— полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.
Добротность контура можно также измерить по затухающим колебаниям в контуре, если подключить к контуру генератор прямоугольных импульсов. При этом прямоугольные импульсы должны быть достаточно короткими и с большим периодом, чтобы к моменту прихода следующего импульса колебания в контуре уже успели закончится (рис. 3.19).
Рис. 3.19. Определение добротности по затухающим колебаниям
Если обозначить начальную амплитуду затухающих колебаний , то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в
раз, можно рассчитать добротность, исходя из следующих выражений:
, (3.104)

. (3.106)
Таким образом, добротность равна умноженному на числу периодов, в течение которых начальная амплитуда колебаний уменьшается в
Раз.
Кроме названных методов измерения добротности существуют специальные приборы — измерители добротности колебательных контуров.
3.4.7. Связанные контуры.
Недостатком одиночных колебательных контуров является их плохая избирательность. Количественно избирательность оценивается коэффициентом прямоугольности, который равен отношению ширины полосы пропускания на уровне 0,7 к ширине полосы пропускания на уровне 0,1 (иногда на уровне 0,01):

Чем ближе значение коэффициента прямоугольности к 1, тем лучше избирательность контура.
Коэффициент прямоугольности одиночного контура = 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.
Ценным свойством связанных контуров является возможность осуществить АЧХ по форме, близкую к прямоугольной. Связанные контуры взаимно влияют друг на друга. Степень влияния зависит от сопротивления связи. В качестве элементов связи используют конденсаторы и индуктивности. Чаще всего используют индуктивную (трансформаторную) связь. В этом случае степень связи определяется коэффициентом взаимной индукции . В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где
— коэффициент взаимной индукции,
– сопротивление связи.

Рис. 3.20. Связанные контуры и их эквивалентная схема
Коэффициент взаимной индукции равен:
, (3.108)
Где: — магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;
— магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.
Для неферромагнитной среды .
Эдс, индуцируемая во втором контуре, равна:
(3.109)
Сопротивление связи равно
. (3.110)
Степень связи между контурами оценивается коэффициентом связи , который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.
Коэффициент передачи напряжения из первого контура во второй равен:
(3.111)
Если включить генератор во второй контур, то получим коэффициент передачи напряжения из второго контура в первый:

Коэффициент связи между контурами равен среднему геометрическому из коэффициентов передачи:

Коэффициент связи выражает отношение общего магнитного потока, пронизывающего обе катушки индуктивности, к полному магнитному потоку. Величина () характеризует поток рассеяния.
Выясним характер и форму амплитудно-частотной характеристики системы из двух индуктивно связанных контуров, представленных на рис.2.20. Для упрощения предположим, что контуры состоят из одинаковых элементов и поэтому имеют одинаковую резонансную частоту
. АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте
. Две другие соответствуют максимуму коэффициента передачи и будут на частотах


Частоты зависят от коэффициента связи
и величины затухания контуров
и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи.
— быстрая частота связи, а
— медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.
Рис. 3.21. Зависимость частот связи от коэффициента связи
При критической связи и на резонансной кривой будет один максимум на частоте
.
При связи меньше критической формулы для частот связи
и
не имеют смысла и на АЧХ будет только один максимум на частоте
.
При связи больше критической () на АЧХ появляются два максимума на частотах
и
.
Рис. 3.22. АЧХ одиночного и двух связанных контуров ().
Полоса пропускания связанных контуров определяется, как ширина АЧХ на уровне 0,7 от максимальной ординаты при этом минимум АЧХ также должен быть на уровне 0,7. Можно показать, что при одинаковом затухании и Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности
= 0,6 , а для трёх – 0,65.
В серийно выпускаемой радиоаппаратуре в качестве элементов, обеспечивающих высокую избирательность используют пъезофильтры, созданные на основе пьезоэлектриков. Пьезоэлектрики – кристаллические вещества, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация (прямой пьезоэффект). Следствием прямого пьезоэффекта является обратный пьезоэффект – появление механической деформации под действием электрического поля. Пьезофильтр состоит из отдельных, объединенных в группы пьезоэлементов (стержней, пластинок) с нанесенными на определенные поверхности электродами, к которым подводится электрическое напряжение, для создания деформации в результате обратного пьезоэффекта. Пьезофильтр обеспечивает хорошую прямоугольность АЧХ. Добротность керамических пьезофильтров составляет несколько тысяч, а затухание вне полосы составляет -60дБ.
Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики — в механике это различного типа маятники и звуковые резонаторы (струны, мембраны, трубы, свистки, органы), в электродинамике — колебательные контуры, закрытые и открытые резонаторы с распределенными параметрами, в оптике — лазерные резонаторы, эталоны Фабри — Перо и т.д. Принципы описания всех колебательных систем настолько общи, что теория колебаний стала самостоятельным разделом физики. Поэтому изучение параметров, свойств и характеристик колебательного контура полезно рассматривать как общее введение в мир резонансных колебательных систем.
В теории колебаний выделяются два класса явлений — явления в линейных и нелинейных колебательных системах. Линейными называются такие системы, параметры которых не зависят от амплитуды колебаний. Например, для маятников это означает такие малые колебания, при которых упругость пружин и стержней не зависит от амплитуды колебания, а натяжение нити подвеса определяется только гравитационными силами. Для электрических колебательных контуров независимыми от амплитуды токов и напряжений должны оставаться такие величины, как индуктивность $L$, емкость $C$ и сопротивление $R$.
Резонансные системы имеют два важных свойства.
-
Свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы.
-
Свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника.
Колебательный контур характеризуется двумя основными параметрами: частотой собственных (резонансных) колебаний $omega _{0} $ и добротностью $Q$, характеризующей отношение мощности энергии собственного колебания к мощности потерь за период.

На рис. 18 приведены примеры «параллелей» электрических и механических колебательных систем. В электрических резонаторах происходит периодический переход электрической энергии, запасенной в конденсаторе $(W_Э =frac 12 CU^2),$ в магнитную энергию катушки индуктивности $(W_M =frac 12 LI^2)$ и обратно. В маятниках происходит аналогичный циклический переход энергии из потенциальной (поднятого груза или сжатой пружины) в кинетическую и обратно.
Свободные колебания происходят в замкнутой цепи без вынуждающей силы (рис. 19,а).
Согласно второму закону Кирхгофа для такой цепи можно написать:
$$
Rcdot I+U_{C} =-Lcdot frac{dI}{dt}.
$$
Выражая $U_{C} $ через заряд $q$, получим уравнение
$$
Rcdot I+Lcdot frac{dI}{dt} +frac{q}{C} =0 mbox{ (СИ). }
$$
Дифференцируя по времени и учитывая равенство $I=frac{dq}{dt} $, получаем
$$
Lfrac{d^{2} I}{dt^{2} } +Rfrac{dI}{dt} +frac{I}{C} =0 mbox{ (СИ). }
$$
Разделив на $L$ и вводя обозначения
$delta =frac{R}{2cdot L} $ и $omega _{0}^{2} =frac{1}{LC} $,
получим общее уравнение для свободных колебаний линейной резонансной системы:
$$
I»+2delta , I’+omega _{0}^{2} I=0,
$$
где параметр $delta $ называется затухание, а параметр $omega _{0} $ — собственная частота, или частота свободных колебаний. Оно решается подстановкой $I=Acdot e^{iomega , t} $, которая приводит к характеристическому уравнению
$$
-omega ^{2} +2iomega , delta +omega _{0}^{2} =0,
$$
с решением
$$
lambda , _{1,2} =i, delta pm sqrt{omega _{0}^{2} -delta ^{2} } .
$$
Общее решение имеет две составляющие
$$
I=Acdot e^{iomega _{1} , t} +Bcdot e^{iomega _{2} , t} .
$$
Константы $A$ и $B$ определяются начальными данными задачи, например, зарядом $q_{0} $ или напряжением на конденсаторе $U_{0} $. Характер начальных данных определяется конкретной физической системой.
Частный пример схемы для возбуждения свободных колебаний в колебательном контуре приведен на рис. 19,б. Конденсатор $C$ заряжается от батареи до напряжения $U_{0} $ (положение «а» переключателя), а затем переключается в точку «б». Свободные колебания будут представлять собой циклический переход энергии электрического поля (в конденсаторе) в энергию магнитного поля (в индуктивности) и обратно.
Подставив найденные значения $A$ и $B$, получим общее решение для свободных колебаний в контуре
$$
I=ifrac{U_{0} }{Lsqrt{omega _{0}^{2} -delta ^{2} } } e^{-delta , t} frac{e^{isqrt{omega _{0}^{2} -delta ^{2} } , t} -e^{-isqrt{omega _{0}^{2} -delta ^{2} } , t} }{2} .
$$
Если бы колебательный контур состоял только из идеальных (без потерь) реактивных элементов (индуктивности $L$ и емкости $C$), то переход энергии из электрической в магнитную и обратно совершался бы без потерь, а в контуре существовали бы незатухающие свободные колебания с собственной частотой $omega _{0} =2pi , f=sqrt{frac{1}{LC}}.$
Наличие в схеме активного элемента $R$ приводит к тому, что часть энергии за каждый период переходит в тепло и колебания затухают с некоторой постоянной времени $tau $. Роль частоты в уравнении теперь играет величина $omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } $, зависящая от отношения реактивной мощности к потерям на активном сопротивлении $R$. При этом вовсе не обязательно в схему должен быть включен отдельный резистор. В его качестве может выступать, например, омическое сопротивление провода, которым намотана катушка индуктивности, а также сопротивление утечки изоляторов конденсатора. Кроме того, часть энергии колебаний может излучаться контуром в окружающее пространство в виде электромагнитной волны. На этом основано действие так называемых связанных контуров: если вблизи данного колебательного контура расположен другой, то в нем «наводятся» (возникают) колебания за счет того, что часть энергии трансформируется из первого контура во второй. Передача энергии совершается переменным электромагнитным полем, возникающим вокруг первого контура.
Если затухание мало, т. е. $delta <omega _{0} $, то мы получаем уравнение слабо затухающих колебаний в виде
$$
I=-frac{U_{0} }{Lomega _{p} } e^{-delta , t} sin omega _{p} t=-I_{0} e^{-delta , t} sin omega _{p} t.
$$
При этом резонансная частота приближается к частоте собственных колебаний:
$$
omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } approx omega _{0} left(1-frac{1}{2} frac{delta ^{2} }{omega _{0}^{2} } right).
$$
Таким образом, при малом затухании резонансная частота практически совпадает с собственной, однако колебания при этом не являются гармоническими. Для гармонических колебаний должно соблюдаться условие $Ileft(tright)=Ileft(t+Tright)$, где $T$ — период колебания. В нашем случае $Ileft(tright)ne Ileft(t+Tright)$, и о периоде можно говорить лишь как о времени, через которое повторяются нули функции (рис. 20). Именно в этом смысле мы будем ниже использовать термин «период колебаний».

Введем понятия добротности $Q$ и логарифмического декремента затухания $gamma $ контура. Из отношение амплитуд $n$–того и $(n + k)$–го колебаний равно
$I_{n} I_{n+k}^{-1} = e^{kdelta T}$, где $T=2, pi omega ^{-1} $ — период колебания («повторения нулей»). Логарифмическим декрементом затухания $gamma $ называется величина
$$
gamma =delta , T=frac{1}{k} ln frac{I_{n} }{I_{n+k} } =ln frac{I_{n} }{I_{n+1} } .
$$
Из уравнения для тока видно, что величина $delta $ обратно пропорциональна времени, за которое амплитуда колебаний уменьшается в $e$ раз. Из последнего уравнения следует, что декремент затухания $gamma $ показывает уменьшение амплитуды за период колебания:
$$
gamma =delta , T=frac{2; pi , delta }{omega } .
$$
С логарифмическим коэффициентом затухания однозначно связан другой, более распространенный параметр, характеризующий колебательную систему, добротность $Q$.
Добротность контура $Q$ определяется соотношением
$$
Q=frac{omega _{0} L}{R} =frac{1}{omega _{0} CR} =frac{rho }{R},
$$
где $rho =sqrt{frac LC} $ (СИ).
Физический смысл добротности заключается в отношении запасенной в контуре энергии к энергии потерь за период колебания
$$
Q=omega cdot frac{W_0}{Delta W},
$$
откуда можно найти связь добротности с другими параметрами контура
$$
Q=frac{pi }{gamma } =frac{pi }{delta , T} =frac{omega }{2, delta } =omega frac{L}{R} mbox{ (СИ).}
$$
Экспериментально добротность определяется по резонансной кривой как отношение резонансной частоты $omega _{p} $ к полосе частот $2cdot Delta omega $, определяемой на уровне $U_{1,2} =pm frac{U_p}{sqrt{2}}$:
$$
Q=frac{omega _{з}}{2cdot Delta omega } =frac{f_{з}}{2cdot Delta f} ,
$$
где $U_{p} $ — амплитуда колебания на резонансной частоте контура. Величина $rho =sqrt{frac LC}$ называется характеристическим (волновым) сопротивлением контура.
При большом затухании, т.е. при $delta >omega _{0} $, величина $omega _{0}^{2} -delta ^{2} $ отрицательна, корень из нее мнимый. Такой случай называется апериодическим процессом. Общее решение, аналогичное, полученному ранее, будет иметь вид
$$
I=-frac{U_{0} }{Lsqrt{(delta ^{2} -omega _{0}^{2} )} } e^{-delta , , t} mbox{sh}sqrt{(delta ^{2} -omega _{0}^{2} )} , t.
$$
График этой функции приведен на рис. 21.
Критическим условием, при котором затухающие колебания переходят в апериодический процесс, является условие $delta =omega _{0} $. В этом случае решение общего уравнения имеет вид
$$
I=-frac{U_{0} }{omega L} (omega t)e^{-delta , t} , =-frac{U_{0} }{L} t, e^{-delta , t} .
$$
Остается добавить, что аналогичные параметры могут быть введены для любой резонансной колебательной системы независимо от ее физической природы (механические, термодинамические, электромагнитные, оптические, аэро– и гидродинамические системы).
Колебательный контур, рассмотренный в предыдущем разделе, представлял собой замкнутую электрическую цепь, в которой совершаются свободные колебания.
В случае вынужденных колебаний мы должны подводить к контуру электрическую энергию от внешнего источника (генератора). Есть много способов для подключения источника внешней энергии к контуру, которые сводятся к той или иной комбинации двух основных: в разрыв цепи контура (рис. 22, а) или параллельно емкостной и индуктивной ветвям контура (рис. 22,б).
В зависимости от способа включения различают соответственно последовательный (рис. 22,а) и параллельный (рис. 22,б) колебательные контуры. Они предъявляют разные требования к согласованию с генератором и нагрузкой. Поэтому нужно отличать собственные параметры контура от параметров нагруженного контура, получаемые с учетом влияния генератора и «нагрузки» (входного сопротивления той цепи, в которую включен контур). В параллельном контуре (рис. 22,б) возникает резонанс токов. Для его поддержания в качестве вынуждающей силы необходимо применение генератора стабильного тока. В последовательном контуре (рис. 22,а) имеет место резонанс напряжений, и для его поддержания должен применяться внешний генератор стабильного напряжения.
Закон Кирхгофа, позволяющий исследовать процессы в контуре (рис. 22,а) в зависимости от частоты, записывается в виде
$$
U=U_{R} +U_{L} +U_{C} =IR+iI(omega L-frac{1}{omega C} )=Icdot Z.
$$
Контур представляет для генератора некоторое комплексное сопротивление
$$
Z=R_L +icdot (omega L-frac{1}{omega C} ),
$$
$$
left|Zright| = sqrt{R_L^2 +(omega L-frac{1}{omega C})^2}, mbox{tg}varphi =frac{omega L-frac{1}{omega C} }{R_L}
$$
где $left|Zright|$ — модуль комплексного сопротивления; $R_{L}$ — омическое сопротивление катушки индуктивности; $varphi $ — сдвиг фазы между активным и реактивным сопротивлениями, равный сдвигу фазы между током $I$ в цепи и входным напряжением $U$.
Из последнего выражения видно, что сопротивление цепи будет минимально и равно активному сопротивлению $R_{L} $ на некоторой частоте $omega _{0} $, определяемой условием
$$
omega _0 L=frac{1}{omega _0 C} , mbox{ где } omega _{0} =frac{1}{sqrt{LC}} mbox{ (СИ).}
$$
Таким образом, на резонансной частоте сопротивление контура минимально, чисто активно, а ток в цепи совпадает по фазе с входным напряжением (напряжением генератора). Фактически это и есть определение резонанса в последовательном колебательном контуре.
Для практических целей представляет интерес исследовать поведение напряжений на реактивных элементах контура в зависимости от частоты генератора и определить его добротность $Q$.
Поскольку фазы $U_{L} $ и $U_{C} $ независимо от частоты всегда сдвинуты относительно тока $I$ на $+$ и $-90^{circ}$ соответственно, то достаточно исследовать зависимость от частоты их модулей. Это можно сделать исходя из уравнений
$$
U_{R} =IR, U_{L} =Iomega L, U_{C} =frac{I}{omega C}, I=frac{U}{Z} .
$$
Для примера раскроем уравнения для $I$ и $U_{L} $. Используя введенное для свободных колебаний понятие добротности $Q=left(omega _{0} RCright)^{-1}$, получим следующее выражение для тока в последовательном контуре:
$$
I=frac{U}{sqrt{R^{2} +(omega L-frac{1}{omega C} )^{2} } } =frac{U}{R} frac{1}{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Тогда напряжение на индуктивности будет равно
$$
U_{L} =omega LI=Ufrac{Qfrac{omega }{omega _{0} } }{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Аналогичное уравнение можно получить для напряжения на $C$. При $omega =omega _{0} $ напряжения на $L$ и $C$ будут равны $U_{L0} =U_{C0} =Qcdot U$, т.е. в $Q$ раз больше напряжения вынуждающей эдс.
На самом деле максимумы напряжения на элементах $L$ и $C$ несколько выше и смещены от резонансной частоты и выражаются следующими соотношениями:
$$
omega _{Lmax } =omega _{0} sqrt{frac{2}{2-frac{R^{2} C}{L} } } =omega _{0} sqrt{frac{2}{2-left(frac{1}{Q} right)^{2} } } , omega _{Cmax } =frac{omega _{0}^{2} }{omega _{L} } .
$$
При добротности контура $Q ge 10$ сдвиг частот максимумов $U_{L} $ и $U_{C} $ относительно резонансной частоты $omega _{0} $ не превышает 1% и экспериментально резонансную частоту и добротность можно определять по резонансной кривой любого из напряжений $U_{L} $ и $U_{C} $. Напряжение на реактивных элементах $U_{L} $ и $U_{C} $ при $omega =omega _{0} $ в $Q$ раз больше, чем входное напряжение $U$, поэтому резонанс в последовательном контуре называется резонансом напряжений.
Важно отметить, что для нашего анализа существенно, что само входное напряжение $U$ от частоты не зависит. В противном случае все параметры зависели бы не только от самого контура, но и от параметров источника сигнала. Как было показано в предыдущем параграфе, для этого выходное сопротивление генератора должно быть много меньше $R$.
Схема подключения параллельного контура представлена на рис. 21,б. Из–за комплексного характера нагрузки ток генератора является комплексной величиной. Поэтому модуль тока $I$ может оказаться меньше не только суммы модулей токов индуктивной и емкостной ветвей контура, но и каждого из них в отдельности. Именно это и происходит при резонансе в параллельном контуре: токи в индуктивной и емкостной ветвях контура в $Q$ раз больше, чем ток, потребляемый от генератора тока. Поэтому резонанс в параллельном контуре называется резонансом токов.
Комплексное сопротивление параллельного контура равно
$$
Z=frac{Z_{1} Z_{2} }{Z_{1} +Z_{2} } =
frac{(R_{L} +iomega L)(iomega C)^{-1}}{R_{L} +i(omega L-(omega C)^{-1} )} approx
frac{LC^{-1}}{R_{L} +i(omega L-(omega C)^{-1})} .
$$
Мы пренебрегли величиной $R_{L} $ в числителе, поскольку она в $Q$ раз меньше индуктивного сопротивления, но этого нельзя делать в знаменателе, поскольку при резонансе величина в скобках стремится к нулю.
Условие резонанса для параллельного контура то же, что и для последовательного — равенство реактивных сопротивлений ветвей с $L$ и $C$:
$$
omega _{0} L=frac{1}{omega _{0} C}, mbox{ где } omega _{0} =frac{1}{sqrt{LC} } mbox{ (СИ). }
$$
Таким образом, при резонансе сопротивление контура становится чисто активным и равным
$$
R_{э} =frac{L}{ C R_{L} } =frac{rho ^{2} }{R_{L} } ,
$$
где — $rho =sqrt{frac LC} $ волновое сопротивление контура.
Сопротивление $R_{э} $ отдельного физического эквивалента в контуре не имеет, а является комбинацией волнового сопротивления $rho $ и сопротивления потерь $R_{L} $. Поэтому оно не составляет отдельной ветви параллельного контура и не ответвляет в себя ток. Следовательно, «переносить» его куда–либо или к чему–нибудь «подсоединять» (например, к внутреннему сопротивлению источника тока) бессмысленно. На схеме это просто условное обозначение того факта, что на резонансной частоте параллельный колебательный контур представляет для внешнего генератора некоторое чисто активное сопротивление величиной $R_{э} $, а в формулах символическая запись определенной комбинации $rho $ и $R_{L} $, даваемой последней формулой.
Добротность параллельного контура
$$
Q=frac{omega _{0} L}{R_{L} } =frac{1}{R_{L} omega _{0} C} =frac{R_{э} }{rho } =R_{э} sqrt{frac{C}{L} } .
$$
Собственные параметры параллельного контура, т.е. резонансная частота $omega _{0} $ и добротность $Q$ будут такими же, как и в последовательном контуре при тех же $C$, $L$ и $R_{L}.$
Волновое сопротивление линии
Содержание
- 1 Природа волнового сопротивления
- 2 Виды сопротивлений в электрических цепях
- 2.1 Активное сопротивление
- 2.2 Реактивное сопротивление
- 2.3 Импеданс
- 2.4 Волновое сопротивление проводов
- 3 Формулы для расчёта
- 4 Практическое использование волнового сопротивления
- 5 Что делать, если не указано волновое сопротивление
- 6 Видео по теме
Волновое сопротивление — один из параметров электропроводящей линии, состоящей из металлических проводников. Оно показывает, какое сопротивление оказывает линия источнику энергии (генератору). Этот параметр необходимо учитывать при создании различных электрических схем, чтобы избежать значительных потерь энергии.
Природа волнового сопротивления
Волновое сопротивление линии передачи определяется отношением напряжения к току в электромагнитной волне, распространяющейся вдоль линии передачи. Оно является характеристикой среды распространения электромагнитной волны. Волновое сопротивление любого проводника не зависит от его длины, сопротивления нагрузки на линии и выходного сопротивления источника напряжения. Оно определяется лишь конструктивными параметрами сечения передающих проводников.
Для коаксиальных кабелей такими параметрами являются диаметры центрального и внутреннего проводников, а также значение диэлектрической постоянной материала заполнителя. Для линии, состоящей из двух проводов, — это расстояние между проводами, их диаметр и характеристики материала, используемого для заполнения пространства между ними.
Численно волновое сопротивление равно входному сопротивлению бесконечно длинной линии с конечной нагрузкой, равной ее собственному волновому сопротивлению. Измеряется оно в Омах и показывает, в каком соотношении находятся электрическая и магнитная составляющие электромагнитной волны.
Несмотря на то, что ток по проводнику распространяется практически мгновенно, любой электрический провод или кабель обладает волновым сопротивлением. Обычный электрический провод включает два проводника, изолированные друг от друга. Если проверить омическое сопротивление между ними, оно будет бесконечным. Если при помощи омметра проверить его, подключившись к разным концам одного проводника, то станет видно, что оно нулевое.
На маркировке кабеля указывается его импеданс (сопротивление). В большинстве обычных ситуаций он примерно равен 50 или 75 Ом. Если воспользоваться омметром, будет получен результат, о котором было рассказано выше. Важно понимать, что на самом деле речь идёт не об омическом, а о волновом сопротивлении.
Виды сопротивлений в электрических цепях
В электроцепях существует три вида сопротивлений, имеющих разную природу:
- активное;
- реактивное;
- полное или импеданс.
Активное сопротивление
Напряжение, приложенное к электрической цепи, создаёт ток, сила которого пропорциональна имеющейся разнице потенциалов. Коэффициент пропорциональности между ними является активным сопротивлением, которое также называют омическим. Когда в приведённом выше примере измерение проводилось омметром, то речь шла именно о таком сопротивлении. Величина активного сопротивления определяется из закона Ома.
Реактивное сопротивление
Если в цепи присутствует ёмкость, то возникает такой вид сопротивления, как емкостное. Оно равно нулю в том случае, когда ток постоянен. Ёмкостное сопротивление проявляется в цепи переменного тока, а также в тех случаях, когда между деталями нет прямого контакта.
Действие этого сопротивления основано на том, что расположенные рядом, но не имеющие непосредственного соединения проводники накапливают электрические заряды до определённой предельной величины, а затем постепенно разряжаются. При этом возникающий ток направлен противоположно его первоначальному изменению.
Это свойство используется в конденсаторах. Однако нужно учитывать, что ёмкость возникает практически в любых расположенных рядом проводниках, по которым течёт ток. В частности, это относится к двум жилам, из которых состоит электрический провод. В результате любое изменение силы тока в них обеспечит возникновение емкостного сопротивления.
Также существует индуктивное сопротивление. При изменениях напряжения создаётся переменное электромагнитное поле, которое индуцирует ток. Он всегда направлен противоположно первоначальному изменению. То есть, увеличивающееся индукционное сопротивление создает ток, который тормозит первоначальное изменение и наоборот.
Этим свойством обладают катушки индуктивности, но практически любые электрические детали имеют индуктивность, которая действует указанным образом. Это относится также к электрическим проводам. Они имеют определённую индуктивность, которую можно определить, поэтому оказывают сопротивление переменному току. Индуктивное сопротивление возникает также при включении или выключении нагрузки в цепи постоянного тока.
Разницу емкостного и индуктивного сопротивлений называют реактивным сопротивлением.
Импеданс
При определении импеданса или полного сопротивления учитываются все три физические разновидности сопротивления. С этой целью используют прямоугольный треугольник, у которого длина одного катета выражает значение активного сопротивления, а другого — разницу между величинами емкостного и индуктивного сопротивления.
Гипотенуза в этом случае является полным сопротивлением. Его можно определить, воспользовавшись теоремой Пифагора.
Практически в любой электрической цепи присутствуют все виды сопротивления. Однако некоторые из них могут быть пренебрежимо малы. При рассмотрении двух жил, составляющих электрический провод, учитывается лишь емкостное и индуктивное сопротивление. Следовательно, их полное сопротивление будет выражаться лишь реактивной составляющей. В этом случае можно сказать, что волновое сопротивление — это импеданс в кабеле. Он учитывает емкостную и индуктивную нагрузки.
Волновое сопротивление проводов
Если представить себе провод бесконечной длины, состоящий из двух жил и подключённый к источнику питания, то можно заметить, что не только переменный ток, но и постоянный в моменты включения и выключения создаёт волновое сопротивление.
В момент включения распространение тока по проводам будет иметь очень большую скорость, но, тем не менее, конечную. При этом в первые доли секунды ток можно рассматривать как переменный. Так как расположенные рядом провода условно являются пластинами конденсатора, начнётся процесс зарядки ёмкости, что обеспечит возникновение емкостного сопротивления.
Оба провода имеют индуктивность. Она пренебрежимо мала по сравнению с тем, какая у катушки, но она существует. Это в момент включения порождает индуктивное сопротивление. На самом деле получающийся импеданс можно измерить. Именно он представляет собой волновое сопротивление кабеля или провода.
Это относится к различным видам кабелей и справедливо как для многожильных, так и для коаксиальных кабелей. Предположение о значительной длине провода позволяет не рассматривать наложение на распространяющуюся волну отражённых волн. Расчет волнового сопротивления выполняется по специальным формулам.
Формулы для расчёта
Для двухпроводной электролинии без потерь значение внутреннего сопротивления рассчитывается по формуле:
Поскольку при определении волнового сопротивления используется понятие бесконечного проводника, имеющего идеальную форму, то для расчёта применяются формулы, учитывающие геометрические особенности и материал проводников. Далее приведены те, которые применяются в наиболее простых случаях.
Если рассматривается электропровод, состоящий из двух жил, то волновое сопротивление определяется по формуле:
При использовании коаксиальных кабелей формула будет выглядеть таким образом:
Практическое использование волнового сопротивления
Зная эту характеристику, можно предвидеть, какое будет полное сопротивление при пропускании тока высокой частоты через кабель. Чем волновое или полное сопротивление выше, тем меньше он приспособлен работать с высокой частотой. Поэтому в каждом случае использование определённого кабеля подразумевает определённые требования к волновому сопротивлению кабеля.
На практике наибольшее распространение получили коаксиальные кабели с сопротивлением 50 Ом. Это связано с тем, что они способны обеспечить передачу радиосигналов с наименьшими потерями по мощности. Применение коаксиальных кабелей 75 Ом в телевидении объясняется таким их достоинством, как наименьшее ослабление сигнала, что для телевизионного приемника является необходимым условием.
Волновое сопротивление очень важно при использовании сложных систем. Обычно его подбирают таким образом, чтобы оно соответствовало характеристикам платы, заземления и другим особенностям оборудования. Смысл волнового сопротивления подразумевает, что при использовании кабеля с неподходящей характеристикой поведение устройства может стать непредсказуемым.
Рассматриваемая характеристика измеряется для идеального провода. Он, в частности, должен не иметь изгибов, неровностей, скручиваний и аналогичных особенностей. Каждая из них нарушает идеальность распространения волны вдоль проводника, создаёт искажения и отражения. Эти изменения могут существенно влиять на электрические параметры кабеля, чего нельзя допускать. При использовании волнового сопротивления такие отклонения должны быть учтены.
Нужно также учитывать затухание сигнала, которое происходит при его реальном прохождении через проводник. Его величина будет зависеть от используемой частоты.
Когда используется электрическая энергия, важно, чтобы система обладала максимальным коэффициентом полезного действия. Одним из важных условий для этого является равенство трёх сопротивлений – передатчика, приёмника и линии передачи. Рассогласование между ними приводит к потере энергии и соответствующему снижению КПД.
Что делать, если не указано волновое сопротивление
При использовании кабеля важны все его характеристики. Однако нельзя исключить ситуацию, когда в руки попадает такой, волновое сопротивление которого остаётся неизвестным.
В этом случае нужно воспользоваться соответствующей формулой. Сказанное будет пояснено на примере. Выше была приведена формула расчёта для коаксиального кабеля. Мастер, взяв его в руки, понял, что были использованы следующие материалы:
- Центральный провод сделан из меди.
- Изолятор произведён из пористого полиэтилена.
- Оболочка представляет собой медный экран.
Расстояние от провода до оболочки равно 7.5 мм. Толщина провода составляет 2.7 мм. Используемый коэффициент выражает свойства используемого изолятора. Для пористого полиэтилена он составляет 1.5.
Если бы для изоляции применялся обычный полиэтилен, коэффициент был бы равен 2.5, а для ПВХ — 3.5.
Чтобы получить ответ, необходимо подставить имеющиеся значения в формулу. Таким образом, можно подсчитать:
138/√1.5 × (log(7.5мм/2.7мм) = 49.9 Ом.
В формуле расчета волнового сопротивления учитываются и погонное сопротивление проводов, и погонное сопротивление изоляции между ними. Но на высокой частоте эти факторы оказывают на волновое сопротивление настолько незначительное влияние, что ими вполне можно пренебречь.
Если же сопротивление нагрузки равняется волновому сопротивлению линии, то через кабель заданного диаметра можно передать максимальный уровень мощности с наименьшими потерями.