Как найти волновой вектор

волновой вектор

ВОЛНОВОЙ ВЕКТОР — вектор k, определяющий направление распространения и пространственный период плоской монохроматич. волны

где — постоянные амплитуда и фаза волны, — круговая частота, r — радиус-вектор. Модуль В. в. наз. волновым числом k=, где — пространственный период или длина волны. В направлении В. в. происходит наибыстрейшее изменение фазы волны , поэтому оно и принимается за направление распространения. Скорость перемещения фазы в этом направлении, или фазовая скорость , определяется через волновое число . При классич. описании волновых процессов с В. в. связана плотность импульса , где — плотность энергии. В квантовом пределе соответственно импульс . Направление переноса энергии волной, вообще говоря, может и не совпадать с направлением В. в., как это имеет место, напр., в анизотропных средах или даже в изотропных средах с аномальной дисперсией, где возможен перенос энергии в направлении, противоположном В. в.

Понятие о В. в. может быть обобщено на случай квазигармонич. волн вида , если ввести локальный В. в. и мгновенную частоту . Однако, однозначная интерпретация этих величин допустима только при выполнении неравенств:

где k; — декартовы составляющие В. в. (i, j=1, 2, 3). Эти условия устанавливают применимость лучевого описания волновых процессов (приближения геометрической оптики и геометрической акустики, квазиклассич. приближения).

Для эл—магн. гармонической волны (в вакууме) В. в. k и величина (с — скорость света) объединяются в единый волновой четырёхвектор, компоненты к-рого подчиняются при переходе от одной инерциальной системы отсчёта к другой (движущейся с относит. скоростью u) Лоренца преобразованием:

Первое из этих соотношений определяет Доплера аффект, второе — эффект аберрации углов прихода волн (или формируемых ими лучей).

M. А. Миллер, Г. В. Пермитин.

Волновой вектор как найти

Чтобы освободиться от использования системы координат запишем (см. Лекция 1, формула 15) с помощью векторных обозначений, полагая . Пусть вектор равен по модулю волновому числу и направлен параллельно оси в сторону положительных значений (рис. 1). Такой вектор называется волновым. Принимая во вниание, что , запишем для произвольной точки, характеризуемой радиусом-вектором , выражение

Рис. 1 Рис. 2

Эта формула не зависит от системы координат и характеризует плоскую волну, распространяющуюся в направлении вектора .

Аналогичное выражение для волны можно также написать с использованием синуса:

которое при подходящем выборе начала отсчета времени может быть сведено к предыдущему, поскольку .

Представление плоской волны в комплексной форме . Принимая во внимание формулу Эйлера

представим выражения (1) и (2) формулами

где и — вещественная и мнимая части комплексного числа. В расчетах удобно пользоваться комплексным представлением плоской волны в виде

обозначая комплексную величину тем же символом, что и действительную. Это упрощает написание формул и не приводит к путанице. В тех случаях, когда путаница все же возможна, будем в явном виде указывать, о каком представлении идет речь.

Величина в (6) может быть как действительной, так и комплексной или мнимой. Учитывая, что в общем случае

запишем выражение (6) в виде

где — амплитуда плоской волны. Поэтому и в (7) — амплитуда плоской волны, а — фаза.

Будем искать решение уравнений Максвелла (см. Лекция 1, формула 2) и (см. Лекция 1, формула 3) в виде

где и — постоянные векторы, не зависящие от координат и времени. Компоненты этих векторов могут быть комплексными.

Подставляя выражения (8) в уравнения (см. Лекция 1, формула 2) и (см. Лекция 1, формула 3) и учитывая, что

получаем следующие соотношения:

Из соотношений (11) следует, что векторы и плоской волны перпендикулярны вектору , т. е. направлению распространения. Это означает, что электромагнитная волна является поперечной. Соотношения (10) показывают, что векторы и взаимно перпендикулярны. Таким образом, , и составляют тройку взаимно перпендикулярных векторов.

Поперечность световых колебаний была открыта в 1817г. Т.Юнгом (1773 — 1829). С помощью этого представления он объяснил отсутствие интерференции лучей света, поляризованных во взаимно перпендикулярных плоскостях, обнаруженное в 1816г. экспериментально в совместной работе Д.Ф.Араго (1786 — 1853) и О.Ж.Френеля (1788 — 1827).

Взяв от обеих частей второго уравнения (10) модули и учитывая, что , , находим следующее соотношение между напряженностью электрического поля и магнитной индукцией плоской волны в вакууме:

Поскольку в (10) — вещественные величины, из (8) заключаем, что и в плоской волне изменяются в одинаковой фазе, т. е. одновременно достигают максимальных и нулевых значений (рис. 2).

ЭНЕРГИЯ ВОЛНЫ. ВЕКТОР УМОВА

ЛЕКЦИЯ №2

МЕХАНИЧЕСКИЕ ВОЛНЫ. АКУСТИКА

ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

В широком смысле, под волной понимают процесс распространения в пространстве колебаний или возмущений состояния вещества или поля с течением времени. Математически этот процесс выражается функцией, описывающей распространение в пространстве изменений какой-либо физической величины. Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные. Рассмотрим механические волны, т.е. процессы распространения механических возмущений в упругой среде.

Механические колебания, возбужденные в какой-либо точке пространства вследствие взаимодействия между упруго связанными частицами среды будут распространяться в ней с некоторой конечной скоростью. Частицы среды последовательно вовлекаются в колебательное движение около своих положений равновесия, но не перемещаются вместе с волной. Таким образом, в волновом процессе не происходит переноса массы. От частицы к частице передается только колебательное движение, а значит, и энергия.Перенос энергии без переноса вещества – это основное свойство всех волн, независимо от их природы.

Волны бывают продольные, если колебания частиц среды происходят вдоль направления распространения, и поперечные, если направление колебаний перпендикулярно вектору скорости волны. Очевидно, что в случае продольных волн в среде возникают деформации сжатия и разрежения, которые в свою очередь приводят к образованию локальных областей сгущения и разрежения вещества, т.е. области повышенного и пониженного давления. Такие волны могут возникать в любых средах: в газах, жидкостях и твердых телах. Поперечные механические волны обусловлены деформациями сдвига. Это означает, что они могут существовать только в твердых телах.

В общем случае, волны представляют собой пространственное образование. Геометрическое место точек (поверхность), до которых колебания дошли к некоторому моменту времени, называется фронтом волны. В зависимости от формы фронта волны бывают: плоские, сферические, цилиндрические и т.д.

Поверхность, точки которой имеют одно и то же значение фазы, называется волновой поверхностью. Волновых поверхностей

бесчисленное множество, а фронт волны всегда один.

УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. Тогда, очевидно, что колебания в некоторой точке М, удаленной от точки 0 на расстояние 0М = х, будут совершаться по тому же закону, но с некоторым отставанием по времени τ от колебаний в точке 0:

Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид:

s= A cos ω( t-τ ) = A cos ω( t — ). (2)

Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω( t — ) – фаза колебаний в точке с координатой х, u – скорость плоской волны.

Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1).

Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u/ν. Т.к. ω = 2πν, то (2) можно переписать в виде:

s = Acosω( t — ) = Acos2π(vt — ) = Acos(ωt — 2π ). (3)

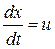
Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω( t – ) = С, т.е. const. Выразим х: х = ut — Cu/ω. Продифференцировав это выражение по t, получим: (С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.

Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой: . Для поперечных волн – . Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.

Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция.

ВОЛНОВОЕ УРАВНЕНИЕ

Аналогично тому, как уравнение колебаний является решением дифференциального уравнения, описывающего процесс колебаний, так и уравнение волны представляет собой решение дифференциального уравнения, описывающего процесс распространения волн в среде. Это дифференциальное уравнение второго порядка в частных производных называется волновым. Найдем его вид. Запишем первые и вторые производные уравнения волны (2) по переменным t и х:

; ;

; ; (4)

; . (5)

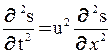
В трехмерном случае:

.

СТОЯЧИЕ ВОЛНЫ

Рассмотрим в качестве примера проявления волновых свойств механизм образования стоячих волн. Они возникают в результате наложения (интерференции) двух встречных плоских когерентных волн с одинаковой амплитудой. Например, волны падающей и этой же волны отраженной от границы раздела сред. Запишем уравнения двух плоских волн, движущихся навстречу друг другу в виде (3).

s 1= Acos(ωt – 2π ) = А(cosωt cos2π + sinωt sin2π ) . (6)

s2 = Acos(ωt + 2π ) = А(cosωt cos2π – sinωt sin2π ). (7)

Складывая эти равенства, получим уравнение результирующего процесса – уравнение стоячей волны:

(8)

Из (8) видно, что в каждой точке среды происходит колебание той же частоты ω, что и у интерферирующих волн. Однако амплитуда колебаний каждой частицы зависит от координаты точки среды, в которой она расположена: Ах = 2А cos2π . В точках, где аргумент 2π = ±nπ (при n = 0, 1, 2…) и |cos2π | = 1, амплитуда имеет максимальное значение –2А. Эти точки называются пучностями стоячей волны. В точках, где аргумент 2π = ±(n + )π, амплитуда минимальна и равна нулю, т.к. в этом случае cos2π = 0. Эти точки называются узлами стоячей волны.

На рис.2 показано как меняется расположение частиц среды в стоячей волне в течение периода.

ЭНЕРГИЯ ВОЛНЫ. ВЕКТОР УМОВА

Последовательное вовлечение в колебательное движение частиц среды означает, что волна передает от частицы к частице некоторую механическую энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Найдем выражение для энергии, переносимой плоской волной. Для этого рассмотрим некоторый объем V среды, все частицы которой вовлечены волной в колебательное движение (рис.3). В момент времени t каждая частица массой m0 имеет определенные значения смещения и скорости. Однако, как мы установили ранее, полная механическая энергия частицы от этого не зависит и равна Ем = , где m0 – масса одной частицы. Полагая, что все частицы среды одинаковы, а их число в объеме V равно N, получим для энергии этого объема:

, (9)

где m = m0·N масса вещества в объеме V. Разделив правую и левую часть этого равенства на V , получим количество энергии в единице объема волны. Эта величина называется объемной плотностью энергии:

, (10)

где ρ = m / V – плотность вещества среды, в которой распространяется волна. Объемная плотность энергии измеряется в Дж / м 3 .

Определим энергию, переносимую волной через площадку площадью S перпендикулярную 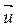(рис.3). За время t волна удалится от S на расстояние Δl = u·t и вовлечет в колебательное движение частицы в объеме V = S·u·t, перенеся при этом через площадку S энергию W = w∙V = w∙S∙ut.

Количество энергии, перенесенное через площадку S за единицу времени называется потоком энергии волны:

Ф = = w∙ S∙u. (11)

Поток энергии измеряется в Дж / с = Вт.

Количество энергии переносимое через единицу площади за единицу времени называется интенсивностью (или плотностью потока) энергии волны и измеряется в Вт / м 2 или Дж / (с·м 2 ):

. (12)

Т.к. скорость величина векторная, а w скалярная, то справа в этом равенстве стоит вектор. Это означает, что и левая величина дол-жна быть векторной, т.е. интенсивность энергии волны в направлении переноса – это некий вектор:

. (13)

Эта величина для упругих волн называется вектором Умова, который определяет количество энергии переносимое механической волной через единицу площади за единицу времени в направлении .

ЭФФЕКТ ДОПЛЕРА

Эффектом Доплера называют изменение частоты колебаний, воспринимаемых наблюдателем (приёмником волны) вследствие движения источника волны и наблюдателя относительно среды.

Рассмотрим простейший случай, когда источник волны и наблюдатель движутся вдоль соединяющей их прямой. Скорость распространения волны в рассматриваемой среде будем считать равной u, скорость источника – , скорость наблюдателя (приёмника) – , частота колебаний источника – ν0, период колебаний источника – Т = 1/ ν0. Все скорости определены относительно среды. Скорость источника будем считать положительной, если он движется по направлению к приёмнику, и отрицательной, если источник удаляется от приёмника. Аналогичное правило знаков скоростей примем и для приёмника.

В исходном состоянии источник находится в начале координат (точка 0), а приёмник в точке А. Скорость распространения колебаний зависит только от свойств среды, поэтому при неподвижном источнике за одну секунду волна пройдет в направлении к приемнику расстояние u. На этом расстоянии уложится ν0 колебаний. Соответственно, длина волны – λ0 = u / ν0 (рис.4а).

Пусть наблюдатель неподвижен и находится на расстоянии u от источника, а источник волны движется с постоянной скоростью по направлению к наблюдателю. Будем считать, что

источники:

http://moodle.yspu.org/pluginfile.php/2285/mod_scorm/content/14/node2.html

http://poisk-ru.ru/s22378t4.html

Источник

From Wikipedia, the free encyclopedia

In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation.

A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2π radians per cycle.[a]

It is common in several fields of physics to refer to the angular wave vector simply as the wave vector, in contrast to, for example, crystallography.[1][2] It is also common to use the symbol k for whichever is in use.

In the context of special relativity, wave vector can refer to a four-vector, in which the (angular) wave vector and (angular) frequency are combined.

Definition[edit]

Wavelength of a sine wave, λ, can be measured between any two consecutive points with the same phase, such as between adjacent crests, or troughs, or adjacent zero crossings with the same direction of transit, as shown.

The terms wave vector and angular wave vector have distinct meanings. Here, the wave vector is denoted by {displaystyle {tilde {boldsymbol {nu }}}} and the wavenumber by {displaystyle {tilde {nu }}=left|{tilde {boldsymbol {nu }}}right|}. The angular wave vector is denoted by k and the angular wavenumber by k = |k|. These are related by {displaystyle mathbf {k} =2pi {tilde {boldsymbol {nu }}}}.

A sinusoidal traveling wave follows the equation

{displaystyle psi (mathbf {r} ,t)=Acos(mathbf {k} cdot mathbf {r} -omega t+varphi ),}

where:

  • r is position,
  • t is time,
  • ψ is a function of r and t describing the disturbance describing the wave (for example, for an ocean wave, ψ would be the excess height of the water, or for a sound wave, ψ would be the excess air pressure).
  • A is the amplitude of the wave (the peak magnitude of the oscillation),
  • φ is a phase offset,
  • ω is the (temporal) angular frequency of the wave, describing how many oscillations it completes per unit of time, and related to the period t by the equation {displaystyle omega ={tfrac {2pi }{T}},}
  • k is the angular wave vector of the wave, describing how many oscillations it completes per unit of distance, and related to the wavelength by the equation {displaystyle |mathbf {k} |={tfrac {2pi }{lambda }}.}

The equivalent equation using the wave vector and frequency is[3]

{displaystyle psi left(mathbf {r} ,tright)=Acos left(2pi left({tilde {boldsymbol {nu }}}cdot {mathbf {r} }-ftright)+varphi right),}

where:

Direction of the wave vector[edit]

The direction in which the wave vector points must be distinguished from the «direction of wave propagation». The «direction of wave propagation» is the direction of a wave’s energy flow, and the direction that a small wave packet will move, i.e. the direction of the group velocity. For light waves in vacuum, this is also the direction of the Poynting vector. On the other hand, the wave vector points in the direction of phase velocity. In other words, the wave vector points in the normal direction to the surfaces of constant phase, also called wavefronts.

In a lossless isotropic medium such as air, any gas, any liquid, amorphous solids (such as glass), and cubic crystals, the direction of the wavevector is the same as the direction of wave propagation. If the medium is anisotropic, the wave vector in general points in directions other than that of the wave propagation. The wave vector is always perpendicular to surfaces of constant phase.

For example, when a wave travels through an anisotropic medium, such as light waves through an asymmetric crystal or sound waves through a sedimentary rock, the wave vector may not point exactly in the direction of wave propagation.[4][5]

In solid-state physics[edit]

In solid-state physics, the «wavevector» (also called k-vector) of an electron or hole in a crystal is the wavevector of its quantum-mechanical wavefunction. These electron waves are not ordinary sinusoidal waves, but they do have a kind of envelope function which is sinusoidal, and the wavevector is defined via that envelope wave, usually using the «physics definition». See Bloch’s theorem for further details.[6]

In special relativity[edit]

A moving wave surface in special relativity may be regarded as a hypersurface (a 3D subspace) in spacetime, formed by all the events passed by the wave surface. A wavetrain (denoted by some variable X) can be regarded as a one-parameter family of such hypersurfaces in spacetime. This variable X is a scalar function of position in spacetime. The derivative of this scalar is a vector that characterizes the wave, the four-wavevector.[7]

The four-wavevector is a wave four-vector that is defined, in Minkowski coordinates, as:

{displaystyle K^{mu }=left({frac {omega }{c}},{vec {k}}right)=left({frac {omega }{c}},{frac {omega }{v_{p}}}{hat {n}}right)=left({frac {2pi }{cT}},{frac {2pi {hat {n}}}{lambda }}right),}

where the angular frequency {displaystyle {tfrac {omega }{c}}} is the temporal component, and the wavenumber vector {vec {k}} is the spatial component.

Alternately, the wavenumber k can be written as the angular frequency ω divided by the phase-velocity vp, or in terms of inverse period T and inverse wavelength λ.

When written out explicitly its contravariant and covariant forms are:

{displaystyle {begin{aligned}K^{mu }&=left({frac {omega }{c}},k_{x},k_{y},k_{z}right),\[4pt]K_{mu }&=left({frac {omega }{c}},-k_{x},-k_{y},-k_{z}right)end{aligned}}}

In general, the Lorentz scalar magnitude of the wave four-vector is:

{displaystyle K^{mu }K_{mu }=left({frac {omega }{c}}right)^{2}-k_{x}^{2}-k_{y}^{2}-k_{z}^{2}=left({frac {omega _{o}}{c}}right)^{2}=left({frac {m_{o}c}{hbar }}right)^{2}}

The four-wavevector is null for massless (photonic) particles, where the rest mass m_o = 0

An example of a null four-wavevector would be a beam of coherent, monochromatic light, which has phase-velocity v_p = c

{displaystyle K^{mu }=left({frac {omega }{c}},{vec {k}}right)=left({frac {omega }{c}},{frac {omega }{c}}{hat {n}}right)={frac {omega }{c}}left(1,{hat {n}}right),} {for light-like/null}

which would have the following relation between the frequency and the magnitude of the spatial part of the four-wavevector:

{displaystyle K^{mu }K_{mu }=left({frac {omega }{c}}right)^{2}-k_{x}^{2}-k_{y}^{2}-k_{z}^{2}=0} {for light-like/null}

The four-wavevector is related to the four-momentum as follows:

P^{mu }=left({frac {E}{c}},{vec {p}}right)=hbar K^{mu }=hbar left({frac {omega }{c}},{vec {k}}right)

The four-wavevector is related to the four-frequency as follows:

{displaystyle K^{mu }=left({frac {omega }{c}},{vec {k}}right)=left({frac {2pi }{c}}right)N^{mu }=left({frac {2pi }{c}}right)left(nu ,nu {vec {n}}right)}

The four-wavevector is related to the four-velocity as follows:

{displaystyle K^{mu }=left({frac {omega }{c}},{vec {k}}right)=left({frac {omega _{o}}{c^{2}}}right)U^{mu }=left({frac {omega _{o}}{c^{2}}}right)gamma left(c,{vec {u}}right)}

Lorentz transformation[edit]

Taking the Lorentz transformation of the four-wavevector is one way to derive the relativistic Doppler effect. The Lorentz matrix is defined as

{displaystyle Lambda ={begin{pmatrix}gamma &-beta gamma & 0 & 0 \-beta gamma &gamma &0&0\0&0&1&0\0&0&0&1end{pmatrix}}}

In the situation where light is being emitted by a fast moving source and one would like to know the frequency of light detected in an earth (lab) frame, we would apply the Lorentz transformation as follows. Note that the source is in a frame Ss and earth is in the observing frame, Sobs.
Applying the Lorentz transformation to the wave vector

{displaystyle k_{s}^{mu }=Lambda _{nu }^{mu }k_{mathrm {obs} }^{nu }}

and choosing just to look at the mu =0 component results in

{displaystyle {begin{aligned}k_{s}^{0}&=Lambda _{0}^{0}k_{mathrm {obs} }^{0}+Lambda _{1}^{0}k_{mathrm {obs} }^{1}+Lambda _{2}^{0}k_{mathrm {obs} }^{2}+Lambda _{3}^{0}k_{mathrm {obs} }^{3}\[3pt]{frac {omega _{s}}{c}}&=gamma {frac {omega _{mathrm {obs} }}{c}}-beta gamma k_{mathrm {obs} }^{1}\&=gamma {frac {omega _{mathrm {obs} }}{c}}-beta gamma {frac {omega _{mathrm {obs} }}{c}}cos theta .end{aligned}}}

where cos theta is the direction cosine of k^{1} with respect to {displaystyle k^{0},k^{1}=k^{0}cos theta .}

So

{displaystyle {frac {omega _{mathrm {obs} }}{omega _{s}}}={frac {1}{gamma (1-beta cos theta )}}}

Source moving away (redshift)[edit]

As an example, to apply this to a situation where the source is moving directly away from the observer (theta =pi ), this becomes:

{displaystyle {frac {omega _{mathrm {obs} }}{omega _{s}}}={frac {1}{gamma (1+beta )}}={frac {sqrt {1-beta ^{2}}}{1+beta }}={frac {sqrt {(1+beta )(1-beta )}}{1+beta }}={frac {sqrt {1-beta }}{sqrt {1+beta }}}}

Source moving towards (blueshift)[edit]

To apply this to a situation where the source is moving straight towards the observer (θ = 0), this becomes:

{displaystyle {frac {omega _{mathrm {obs} }}{omega _{s}}}={frac {1}{gamma (1-beta )}}={frac {sqrt {1-beta ^{2}}}{1-beta }}={frac {sqrt {(1+beta )(1-beta )}}{1-beta }}={frac {sqrt {1+beta }}{sqrt {1-beta }}}}

Source moving tangentially (transverse Doppler effect)[edit]

To apply this to a situation where the source is moving transversely with respect to the observer (θ = π/2), this becomes:

{displaystyle {frac {omega _{mathrm {obs} }}{omega _{s}}}={frac {1}{gamma (1-0)}}={frac {1}{gamma }}}

See also[edit]

  • Plane wave expansion
  • Plane of incidence

References[edit]

  1. ^ In most contexts, both the radian and the cycle (or period) are treated as the dimensionless quantity 1, reducing this constant to 2π.
  1. ^ Physics example: Harris, Benenson, Stöcker (2002). Handbook of Physics. p. 288. ISBN 978-0-387-95269-7.{{cite book}}: CS1 maint: multiple names: authors list (link)
  2. ^ Crystallography example: Vaĭnshteĭn (1994). Modern Crystallography. p. 259. ISBN 978-3-540-56558-1.
  3. ^ Vaĭnshteĭn, Boris Konstantinovich (1994). Modern Crystallography. p. 259. ISBN 978-3-540-56558-1.
  4. ^ Fowles, Grant (1968). Introduction to modern optics. Holt, Rinehart, and Winston. p. 177.
  5. ^ «This effect has been explained by Musgrave (1959) who has shown that the energy of an elastic wave in an anisotropic medium will not, in general, travel along the same path as the normal to the plane wavefront …», Sound waves in solids by Pollard, 1977. link
  6. ^ Donald H. Menzel (1960). «§10.5 Bloch wave». Fundamental Formulas of Physics, Volume 2 (Reprint of Prentice-Hall 1955 2nd ed.). Courier-Dover. p. 624. ISBN 978-0486605968.
  7. ^ Wolfgang Rindler (1991). «§24 Wave motion». Introduction to Special Relativity (2nd ed.). Oxford Science Publications. pp. 60–65. ISBN 978-0-19-853952-0.

Further reading[edit]

  • Brau, Charles A. (2004). Modern Problems in Classical Electrodynamics. Oxford University Press. ISBN 978-0-19-514665-3.
Источник

Вы хотите знать, в чем разница между волновым числом и угловым волновым числом и как их рассчитать? Тогда эта статья как раз для вас. Мы подробно объясним эту тему и покажем на примере, как можно рассчитать эти величины.

Если вы рассматриваете электромагнитную волну с определенной длиной волны, то волновое число является обратным этой длине волны — оно ведет себя противоположным образом. Например, если длина волны увеличивается, волновое число уменьшается. Если, с другой стороны, длина волны уменьшается, то волновое число увеличивается.

Волновое число в спектроскопии

Волновое число k определяется в спектроскопии как обратная величина длины волны λ, то есть ξ = 1 / λ (называется еще пространственной частотой). Однако его также можно выразить через частоту f и скорость света в вакууме c, тогда ξ = f / c или также через число n длин волн, укладывающихся в определенную длину l, то есть ξ = n / l .

В целом, для волнового числа применимо следующее соотношение: ξ = 1 / λ = f / c = n / l .

Важно: Волновое число ξ не следует путать с частотой f. Частота имеет единицу измерения Гц = 1 / с = с-1 и определяется через обратную величину периода T: f = 1 / T . Она показывает, как часто электромагнитная волна колеблется в секунду.

Электромагнитная волна и волновое число

Единица измерения волнового числа

Обычно волновое число выражается в в следующих единицах измерения (в СИ): 1 / м = м-1 , что соответствует числу колебаний на метр. Однако единица может быть также преобразована, например, в единицы 1 / см = см-1 или 1 / мм = мм-1 .

Между этими единицами измерения существует следующая взаимосвязь: 1 м-1 = 0,01 см-1 = 0,001 мм-1 , соответственно 1 мм-1 = 100 см-1 = 1000 м-1 .

Разница между волновым числом и угловым волновым числом

Угловое волновое число часто ошибочно называют просто волновым числом. Однако, угловое волновое число k является величиной волнового вектора k и связано с волновым числом ξ следующим образом: k = | k | = 2*π*ξ = ω / c = 2*π / λ . В этой формуле где ω представляет собой так называемую угловую частоту. Волновой вектор — это вектор, перпендикулярный волновому фронту волны. Эта формула показывает, что волновое число ξ также может быть вычислено из углового волнового числа k: ξ = k / 2*π .

Важно: Угловую частоту и частоту также нельзя путать друг с другом. Угловая частота ω связана с частотой f следующим образом: ω = 2*π*f .

Физический смысл волнового числа.

Волновое число численно равно числу периодов волны, укладывающихся в отрезок 2π метров. Это пространственный аналог круговой частоты ω (рад·с-1). Характеристика периодического процесса в пространстве.

Пример расчета волнового числа

Если мы наблюдаем электромагнитную волну с длиной волны λ = 500 нм и хотим вычислить по ней волновое число ξ, то поступаем следующим образом. Чтобы получить размерность м-1 сначала переведите длину волны в метры. То есть 500 нм = 500 * 10-9 м = 5*10-7 м.

Используя представленную выше формулу, вы можете определить соответствующее волновое число: ξ = 1 / λ = 1 / 5*10-7 = 2*106 м-1 .

На одном метре волна колеблется 2 миллиона раз. Если преобразовать единицу измерения, то можно сказать, что волна колеблется 2000 раз на одном миллиметре: 2 * 106 м-1 = 0,001 * 2 * 106 мм-1 = 2000 мм-1 .

Пример расчета углового волнового числа

Если использовать ту же длину волны λ = 500 нм =5 *10-7 м, как в предыдущем примере, и подставьте это значение в формулу для расчета углового волнового числа, то это приведет к следующим результатам: k = 2 * π / λ = 2 * π / 5 *10-7 м = 1,2566 * 107 м-1 .

Легко видеть, что угловое волновое число k отличается от волнового числа ξ из предыдущего примера:

ξ = 2*106 м-1 ↔ k = 1,2566 * 107 м-1

Преобразование длины волны в волновой число

В следующей таблице показаны два направления преобразования из длины волны в волновое число и наоборот. Кроме того, в последней колонке перечислены некоторые области применения спектроскопии:

Волновое число в 1/мм Волновое число в 1/см Волновое число в 1/м Длина волны в нм Длина волны в мкм Длина волны в мм Применение
1 000 10 000 1 000 000 1 000 1 0,001 Инфракрасная спектроскопия
100 1 000 100 000 10 000 10 0,01 Инфракрасная спектроскопия/терагерцовая спектроскопия
10 100 10 000 100 000 100 0,1 Терагерцовая спектроскопия
1 10 1 000 1 000 000 1 000 1 Микроволновая спектроскопия
0,1 1 100 10 000 000 10 000 10 Микроволновая спектроскопия/электронный спиновый резонанс

Список использованной литературы

  1. Мартин Шапер, Mehrdimensionale Ortsfiltertechnik, Springer-Verlag 2014, ISBN 3-658-04944-8 
  2. Физическая энциклопедия. В 5 томах/ Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин. — М.: Советская энциклопедия + Большая российская энциклопедия. — 1998.
Источник

Волной
(волновым процессом) называется процесс
распространения колебаний в пространстве
с течением времени. Для волновых процессов
характерен перенос энергии без переноса
вещества.

Длиной
волны называется расстояние, на которое
распространяется волновой процесс за
время одного периода: 

Виды
волн:

1)На
поверхности жидкости

2)Упругие
(механические) – механические возмущения,
распространяющиеся в упругой среде.
Упругие волны бывают продольные и
поперечные.

Продольные
волны – частицы среды колеблются в
направлениях распространения волны.

Поперечные
волны – в плоскостях, в перпендикулярных
направлению распространения волны.

Упругая
волны называется гармонической, если
соответствующие ей колебания частиц
среды являются гармоническими.

3)Электромагнитные
– электромагнитные колебания,
распространяющиеся в пространстве с
конечной скоростью.

Волновой
вектор — вектор,
направление которого перпендикулярно фазовому
фронту бегущей волны, а абсолютное
значение равно волновому
числу.

Волновой
вектор обычно обозначается латинской
буквой 
 и
измеряется в обратных сантиметрах.

Волновое
число связано с длиной
волны λ соотношением:

.
Связь между волновым вектором
и частотой задаётся законом
дисперсии. Все возможные значения
волновых векторов образуют обратное
пространство или k-пространство.

Волновое
число —
это отношение 2π радиан
к длине волны, то есть это пространственный
аналог круговой частоты ω. Единица
измерения — рад·м−1.

Волновое
число численно
равно числу
периодов волны, укладывающихся в отрезок
2π метров.

Обозначение — k,
формула:

где:

 — λ —  длина
волны,

 — ν ( — частота,

 — vp =
vф — Фазовая
скорость волны,

 — ω — угловая
частота,

 — E — энергия,

 — ħ — постоянная
Планка

9. Уравнение плоской и сферической волны. Волновое уравнение.

Плоская
волна – волна, волновые поверхности
которой имеют вид плоскостей, параллельных
друг другу.

Сферическая
волна – волна, волновые поверхности
которой имеют вид концентрических сфер.

Волновое
уравнение:

10. Энергия упругой волны, вектор Умова.

В
среде распространяется плоская упругая
волна и переносит энергию, величина
которой в объеме
равна

Где


объемная
плотность среды. Если выбранный объем
записать как
где
S – площадь его поперечного сечения, а


—
его длина, то среднее количество энергии,
переносимое волной за единицу времени
через поперечное сечение S, называется
потоком

через
его поверхность

Количество
энергии, переносимое волной за единицу
времени через единицу площади поверхности,
расположенной перпендикулярно направлению
распространения волны, называется
плотностью потока энергии волны.

Эта
величина определяется соотношением:

где

-объемная
плотность энергии волны,

—
фазовая скорость волны. Так как фазовая
скорость волны

—
вектор, направление которого совпадает
с направлением распространения волны,
то можно величине плотности потока
энергии I придать смысл векторной
величины:

Величина

вектор плотности энергии волны, впервые
была введена Н.А. Умовым в 1984 году и
получила название вектора Умова. Подобная
величина для электромагнитных волн
называется вектором Умова — Пойнтинга.

Интенсивностью
волны называется модуль среднего
значения вектора Умова

Плотностью
потока энергии называется энергия,
переносимая волной в единицу времени
через единичную площадку, расположенную
перпендикулярно направлению распределения
волны.

Вектор
плотности потока энергии – это вектор,
численно равный плотности потока энергии
и совпадающий по направлению с направлением
распространения волны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #

    30.03.201535.87 Mб18Теория государства и права Хропанюк В.Н..pdf

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Вектор, описывающий волну; часто направление его распространения

В физике волновой вектор (также обозначаемый волновой вектор ) представляет собой вектор, который помогает описать волну. Как и любой вектор, он имеет величину и направление, оба из которых важны. Его величина — это либо волновое число, либо угловое волновое число волны (обратно пропорционально длине волны ), а его направление обычно является направлением волны . распространение (но не всегда, см. ниже).

В контексте специальной теории относительности волновой вектор также может быть определен как четырехвектор.

Содержание

  • 1 Определения
    • 1.1 Определение физики
    • 1.2 Кристаллографическое определение
  • 2 Направление волнового вектора
  • 3 В физике твердого тела
  • 4 В специальной теории относительности
    • 4.1 Преобразование Лоренца
      • 4.1.1 Уход источника (красное смещение)
      • 4.1.2 Источник движется навстречу (синее смещение)
      • 4.1.3 Источник движется по касательной (поперечный эффект Доплера)
  • 5 См. Также
  • 6 Ссылки
  • 7 Дополнительная литература

Определения

Длина волны синусоидальная волна, λ, может быть измерена между любыми двумя последовательными точками с одинаковой фазой, например, между соседними гребнями или впадинами, или соседними пересечениями нуля с в том же направлении прохождения, как показано.

Есть два общих определения волнового вектора, которые различаются по величине в 2π раз. Одно определение предпочтительнее в физике и связанных областях, тогда как другое определение предпочтительнее в кристаллографии и связанных областях. В этой статье они будут называться «физическим определением» и «определением кристаллографии» соответственно.

В обоих определениях ниже величина волнового вектора представлена ​​как k { displaystyle k}k ; направление волнового вектора обсуждается в следующем разделе.

Физическое определение

Идеальная одномерная бегущая волна следует уравнению:

ψ (x, t) = A cos ⁡ (kx — ω t + φ) { displaystyle psi (x, t) = A cos (kx- omega t + varphi)} psi (x, t) = A cos (kx- omega t + varphi)

где:

  • x — позиция,
  • t — время,
  • ψ { displaystyle psi} psi (функция x и t) — возмущение, описывающее волну (например, для океанской волны, ψ { displaystyle psi} psi будет избыточной высотой воды, или для звуковой волны, ψ { displaystyle psi} psi будет превышением атмосферное давление ).
  • A — это амплитуда волны (пиковая величина колебаний),
  • φ { displaystyle varphi} varphi — фазовый сдвиг, описывающий, как две волны могут быть не синхронизированы друг с другом,
  • ω { displaystyle omega} omega — временная угловая частота волны, описывающий, сколько колебаний он совершает за единицу времени, и относящийся к периоду T { displaystyle T}T по уравнению ω = 2 π / T { displaystyle omega = 2 pi / T} omega = 2 pi / T ,
  • k { displaystyle k}k — пространственная угловая частота (волновое число ) волны, описывающая, сколько колебаний она совершает на единицу пространства, и связанная с длиной волны уравнением k = 2 π / λ { displaystyle k = 2 pi / lambda}k = 2 pi / lambda .

k { displaystyle k}k — величина волнового вектора. В этом одномерном примере направление волнового вектора тривиально: эта волна движется в направлении + x со скоростью (точнее, фазовая скорость ) ω / k { displaystyle omega / k} omega / k . В многомерной системе скаляр kx { displaystyle kx}kx будет заменен векторным скалярным произведением k ⋅ r { displaystyle { mathbf {k }} cdot { mathbf {r}}}{ displaystyle { mathbf {k}} cdot { mathbf {r}}} , представляющие волновой вектор и вектор положения соответственно.

Определение кристаллографии

В кристаллографии одни и те же волны описываются с использованием немного разных уравнений. В одном и трех измерениях соответственно:

ψ (x, t) = A cos ⁡ (2 π (kx — ν t) + φ) { displaystyle psi (x, t) = A cos (2 pi (kx- nu t) + varphi)} psi (x, t) = A cos (2 pi (kx- nu t) + varphi)
ψ (r, t) = A соз ⁡ (2 π (k ⋅ r — ν t) + φ) { displaystyle psi left ({ mathbf {r}}, t right) = A cos left (2 pi ({ mathbf {k}} cdot { mathbf {r}} — nu t) + varphi right)} psi left ( {{ mathbf r}}, t right) = A cos left (2 pi ({{ mathbf k}} cdot {{ mathbf r}} - nu t) + varphi right)

Различия между двумя приведенными выше определениями заключаются в следующем:

Направление k обсуждается в следующем разделе.

Direction волнового вектора

Направление, в котором указывает волновой вектор, должно отличаться от «направления распространения волны ». «Направление распространения волны» — это направление потока энергии волны и направление, в котором будет двигаться небольшой волновой пакет , то есть направление групповой скорости . Для световых волн это также направление вектора Пойнтинга . С другой стороны, волновой вектор указывает в направлении фазовой скорости. Другими словами, волновой вектор указывает в нормальном направлении на поверхности постоянной фазы, также называемые волновыми фронтами.

В без потерь изотропная среда, такая как воздух, любой газ, любая жидкость, аморфные твердые вещества (например, стекло ) и кубические кристаллы, направление движения волновой вектор точно такой же, как направление распространения волны. Если среда анизотропна, волновой вектор в целом указывает в направлениях, отличных от направления распространения волны. Условие для того, чтобы волновой вектор указывал в том же направлении, в котором распространяется волна, заключается в том, что волна должна быть однородной, что не обязательно выполняется, когда среда является анизотропной. В однородной волне поверхности постоянной фазы также являются поверхностями постоянной амплитуды. В случае неоднородных волн эти два вида поверхностей различаются по ориентации. Волновой вектор всегда перпендикулярен поверхности постоянной фазы.

Например, когда волна проходит через анизотропную среду, например, световые волны через асимметричный кристалл или звуковые волны через осадочные породы, волновой вектор может не указывать точно в направлении распространения волны.

В физике твердого тела

В физике твердого тела «волновой вектор» ( также называемый k-вектор ) электрона или дырки в кристалле является волновым вектором его квантово-механического волновая функция. Эти электронные волны не являются обычными синусоидальными волнами, но у них есть своего рода функция огибающей, которая является синусоидальной, а волновой вектор определяется через эту огибающую волну, обычно с использованием «физического определения «. Подробнее см. волна Блоха.

В специальной теории относительности

Движущаяся волновая поверхность в специальной теории относительности может рассматриваться как гиперповерхность (трехмерное подпространство) в пространстве-времени, образованная по всем событиям, прошедшим по волновой поверхности. Цепь волн (обозначаемая некоторой переменной X) можно рассматривать как однопараметрическое семейство таких гиперповерхностей в пространстве-времени. Эта переменная X является скалярной функцией положения в пространстве-времени. Производная этого скаляра — это вектор, который характеризует волну, четырехволновой вектор.

Четырехволновой вектор — это волна четырехвектор, который определяется в координатах Минковского., как:

K μ = (ω c, k →) = (ω c, ω vpn ^) = (2 π c T, 2 π n ^ λ) { displaystyle K ^ { mu} = left ({ frac { omega} {c}}, { vec {k}} right) = left ({ frac { omega} {c}}, { frac { omega} { v_ {p}}} { hat {n}} right) = left ({ frac {2 pi} {cT}}, { frac {2 pi { hat {n}}}} { lambda}} right) ,}K ^ mu = left ( frac { omega} {c }, vec {k} right) = left ( frac { omega} {c}, frac { omega} {v_p} hat {n} right) = left ( frac {2 pi} {cT}, frac {2 pi hat {n}} { lambda} right) ,

где угловая частота ω c { displaystyle { frac { omega} {c}}}frac{omega}{c}— временная составляющая, а волновое число вектор k → { displaystyle { vec {k}}}{ vec {k}} — пространственный компонент.

В качестве альтернативы, волновое число k { displaystyle k}k можно записать как угловую частоту ω { displaystyle omega} omega , деленную на фазовая скорость vp { displaystyle v_ {p}}v_p , или в терминах обратного периода T { displaystyle T}T и обратная длина волны λ { displaystyle lambda} lambda .

При явном написании его контравариантной и ковариантной формы являются:

K μ = (ω c, kx, ky, kz) { displaystyle K ^ { mu} = left ({ frac { omega} {c}}, k_ {x}, k_ {y}, k_ {z} right) ,}K ^ mu = left ( frac { omega} {c}, k_x, k_y, k_z right) ,
К μ = (ω c, — kx, — ky, — kz) { displaystyle K _ { mu} = left ({ frac { omega} {c}}, — k_ {x}, — k_ {y}, — k_ {z} right) ,}K_ mu = left ( frac { omega} {c}, -k_x, -k_y, -k_z right) ,

В общем, скалярная величина Лоренца волнового четырехвектора равна:

K μ K μ = (ω c) 2 — kx 2 — ky 2 — kz 2 = (ω oc) 2 = (moc ℏ) 2 { displaystyle K ^ { mu} K _ { mu} = left ({ frac { omega} {c}} right) ^ {2} -k_ {x} ^ {2} -k_ {y} ^ {2} -k_ {z} ^ {2} = left ({ frac { omega _ {o}} {c} } right) ^ {2} = left ({ frac {m_ {o} c} { hbar}} right) ^ {2}}K ^ mu K_ mu = left ( frac { omega} {c} right) ^ 2 - k_x ^ 2 - k_y ^ 2 - k_z ^ 2 = left ( frac { omega_o} {c} right) ^ 2 = left ( frac {m_o c} { hbar} right) ^ 2

Четырехволновой вектор нулевой для безмассовых (фотонных) частиц, где масса покоя mo = 0 { displaystyle m_ {o} = 0}m_o = 0

Примером нулевого четырехволнового вектора может быть луч когерентного, монохроматического света, который имеет фазовую скорость vp = c { displaystyle v_ {p} = c}v_p = c

К μ = (ω c, k →) = (ω c, ω cn ^) = ω c (1, n ^) { displaystyle K ^ { mu } = left ({ frac { omega} {c}}, { vec {k}} right) = left ({ frac { omega} {c}}, { frac { omega} {c}} { hat {n}} right) = { frac { omega} {c}} left (1, { hat {n}} right) ,}K ^ mu = left ( frac { omega } {c}, vec {k} right) = left ( frac { omega} {c}, frac { omega} {c} hat {n} right) = frac { omega } {c} left (1, hat {n} right) , {для светоподобного / нулевого}

, у которого будет следующее соотношение между частотой и величиной пространственной части четырехволнового вектора:

K μ K μ = (ω c) 2 — kx 2 — ky 2 — kz 2 = 0 { displaystyle K ^ { mu} K _ { mu} = left ({ frac { omega} {c}} right) ^ {2} -k_ {x} ^ { 2} -k_ {y} ^ {2} -k_ {z} ^ {2} = 0}K ^ mu K_ mu = left ( frac { omega} {c} right) ^ 2 - k_x ^ 2 - k_y ^ 2 - k_z ^ 2 = 0 {for light-like / null}

Четырехволновой вектор связан с четырехимпульсный следующим образом:

п μ знак равно (E c, p →) знак равно ℏ K μ знак равно ℏ (ω c, k →) { displaystyle P ^ { mu} = left ({ frac {E} {c}}, { vec {p}} right) = hbar K ^ { mu} = hbar left ({ frac { omega} {c}}, { vec {k}} right)}P ^ { mu} = left ({ frac {E} {c}}, { vec {p}} right) = hbar K ^ { mu} = hbar left ({ frac { omega} {c}}, { vec {k}} right)

Четырехволновой вектор связан с четырехчастотным следующим образом:

K μ = (ω c, k →) = (2 π c) N μ = (2 π c) (ν, ν N →) { Displaystyle K ^ { mu} = left ({ frac { omega} {c}}, { vec {k}} right) = left ({ frac {2 pi} {c}} right) N ^ { mu} = left ({ frac {2 pi} {c}} right) ( nu, nu { vec {n}})}{ displaystyle K ^ { mu} = left ({ frac { omega} {c}}, { vec {k}} right) = left ({ frac {2 pi} {c}} right) N ^ { mu} = left ({ frac {2 pi} {c }} right) ( nu, nu { vec {n}})}

Четырехволновой вектор связан с четырехскоростной следующим образом:

K μ = (ω c, k →) = (ω oc 2) U μ = (ω oc 2) γ (с, и →) { Displaystyle К ^ { му} = влево ({ гидроразрыва { omega} {с}}, { vec {k}} справа) = влево ({ гидроразрыва { omega _ {o}} {c ^ {2}}} right) U ^ { mu} = left ({ frac { omega _ {o}} {c ^ {2}}} right) gamma (c, { vec {u}})}K ^ mu = left ( frac { omega} {c}, vec {k} right) = left ( frac { omega_o} {c ^ 2} right) U ^ mu = left ( frac { omega_o} {c ^ 2} right) gamma (c, vec { u})

преобразование Лоренца

Взятие преобразования Лоренца четырехволнового вектора — один из способов вывести релятивистский доплеровский эффект. Матрица Лоренца определяется как

Λ = (γ — β γ 0 0 — β γ γ 0 0 0 0 1 0 0 0 0 1) { displaystyle Lambda = { begin {pmatrix} gamma — beta gamma 0 0 \ — beta gamma gamma 0 0 \ 0 0 1 0 \ 0 0 0 1 end {pmatrix}}} Lambda = { begin {pmatrix} gamma - beta gamma 0 0 \ - beta gamma gamma 0 0 \ 0 0 1 0 \ 0 0 0 1 end {pmatrix}}

В ситуации, когда свет испускается быстро движущимся источником, и хотелось бы знать частоту света, обнаруженного в земном (лабораторном) кадре, мы применим преобразование Лоренца следующим образом. Обратите внимание, что источник находится в кадре S, а Земля в кадре наблюдения S. Применение преобразования Лоренца к волновому вектору

ks μ = Λ ν μ kobs ν { displaystyle k_ {s} ^ { mu} = Lambda _ { nu} ^ { mu} k _ { mathrm {obs}} ^ { nu} ,}k_ { s} ^ {{ mu}} = Lambda _ { nu} ^ { mu} k _ {{{ mathrm {obs}}}} ^ { nu} ,

и выбирая только для просмотра μ = 0 { displaystyle mu = 0} mu = 0 компонент дает

ks 0 = Λ 0 0 kobs 0 + Λ 1 0 kobs 1 + Λ 2 0 kobs 2 + Λ 3 0 kobs 3 { displaystyle k_ {s} ^ { 0} = Lambda _ {0} ^ {0} k _ { mathrm {obs}} ^ {0} + Lambda _ {1} ^ {0} k _ { mathrm {obs}} ^ {1} + Лямбда _ {2} ^ {0} k _ { mathrm {obs}} ^ {2} + Lambda _ {3} ^ {0} k _ { mathrm {obs}} ^ {3} ,}k_ {s} ^ {{0}} = Лямбда _ {0} ^ {0} k _ {{{ mathrm {obs}}}} ^ {0} + Lambda _ {1} ^ {0} k _ {{{ mathrm {obs}}}} ^ { 1} + Lambda _ {2} ^ {0} k _ {{{ mathrm {obs}}}} ^ {2} + Lambda _ {3} ^ {0} k _ {{{ mathrm {obs}} }} ^ {3} ,

Итак,

ω obs ω s = 1 γ (1 — β cos ⁡ θ) { displaystyle { frac { omega _ { mathrm {obs}}} { omega _ {s}}} = { frac {1} { gamma (1- beta cos theta)}} ,}{ frac { omega _ {{{ mathrm {obs}}}}} { omega _ {s}}} = { frac { 1} { gamma (1- beta cos theta)}} ,

Источник удаляется (красное смещение)

В качестве примера применим это к ситуации, когда источник движется прямо от наблюдателя (θ = π { displaystyle theta = pi } theta = pi ), это становится:

ω obs ω s = 1 γ (1 + β) = 1 — β 2 1 + β = (1 + β) (1 — β) 1 + β = 1 — β 1 + β { displaystyle { frac { omega _ { mathrm {obs}}} { omega _ {s}}} = { frac {1} { gamma (1+ beta)} } = { frac { sqrt {1- beta ^ {2}}} {1+ beta}} = { frac { sqrt {(1+ beta) (1- beta)}} {1 + beta}} = { frac { sqrt {1- beta}} { sqrt {1+ beta}}} ,}{ frac { omega _ {{{ mathrm {obs}}}}}} { omega _ {s}}} = { frac {1} { gamma (1+ beta)}} = { frac {{ sqrt {1- beta ^ {2}}}} {1+ beta}} = { frac {{ sqrt {(1+ beta) (1- beta)}}} {1+ beta}} = { fr ac {{ sqrt {1- beta}}} {{ sqrt {1+ beta}}}} ,

Источник движется в сторону (синее смещение)

Применить это в ситуации, когда источник движется прямо к наблюдателю (θ = 0 { displaystyle theta = 0} theta = 0 ), это становится:

ω obs ω s = 1 γ ( 1 — β) = 1 — β 2 1 — β = (1 + β) (1 — β) 1 — β = 1 + β 1 — β { displaystyle { frac { omega _ { mathrm {obs}}} { omega _ {s}}} = { frac {1} { gamma (1- beta)}} = { frac { sqrt {1- beta ^ {2}}} {1- beta}} = { frac { sqrt {(1+ beta) (1- beta)}} {1- beta}} = { frac { sqrt {1+ beta}} { sqrt {1- beta}}} ,} frac { omega _ { mathrm {obs}}} { omega_s} = frac {1} { gamma (1 - beta)} = frac { sqrt {1- beta ^ 2}} { 1- beta} = frac { sqrt {(1+ beta) (1- beta)}} {1- beta} = frac { sqrt {1+ beta}} { sqrt {1 - beta}} ,

Источник движется по касательной ( поперечный эффект Доплера)

Чтобы применить это к ситуации, когда источник движется поперек наблюдателя (θ = π / 2 { displaystyle theta = pi / 2} theta = pi / 2 ), это принимает следующий вид:

ω obs ω s = 1 γ (1-0) = 1 γ { displaystyle { frac { omega _ { mathrm {obs}}} { omega _ {s }}} = { frac {1} { gamma (1-0)}} = { frac {1} { gamma}} ,} frac { omega _ { mathrm {obs}}} { omega_s} = frac {1} { gamma (1–0)} = frac {1} { gamma} ,

См. также

Ссылки

Дополнительная литература

  • Brau, Charles A. (2004). Современные проблемы классической электродинамики. Издательство Оксфордского университета. ISBN 978-0-19-514665-3.
Источник

Понравилась статья? Поделить с друзьями:
  • Нули передаточной функции как найти
  • Как найти комплексную амплитуду тока
  • Шагомер на андроид встроенный как найти
  • Как найти наибольшую мощность
  • Как составить акт по тренировке по