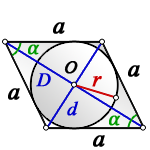
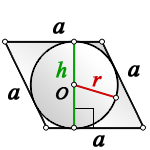
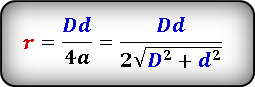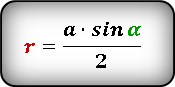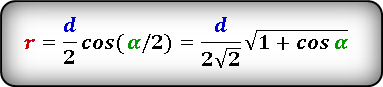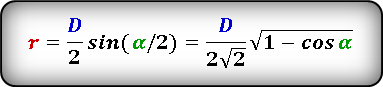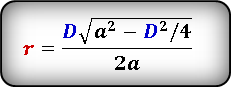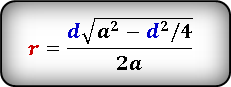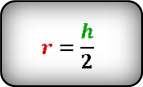Как найти вписанную окружность в равностороннем треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

2. Радиус вписанной окружности ромба, равен половине его высоты

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

Формула радиуса вписанной окружности в ромб ( r ) :

Источник

Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.

1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.

Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.

Например, в правильном треугольнике ABC AB=BC=AC=a

точка O — центр вписанной окружности.

AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.

2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:

$[OF = frac{1}{3}BF,]$

$[r = frac{1}{3} cdot frac{{asqrt 3 }}{2} = frac{{asqrt 3 }}{6}]$

Таким образом, формула для радиуса вписанной в правильный треугольник окружности

$[r = frac{{asqrt 3 }}{6}]$

Обратно, сторона равностороннего треугольника через радиус вписанной окружности:

$[a = frac{{6r}}{{sqrt 3 }} = frac{{6r cdot sqrt 3 }}{{sqrt {3 cdot } sqrt 3 }} = frac{{6r cdot sqrt 3 }}{3} = 2rsqrt 3 .]$

3) Так как формула для нахождения площади равностороннего треугольника через сторону

$[S = frac{{{a^2}sqrt 3 }}{4},]$

можем найти площадь через r:

$[S = frac{{{{(2rsqrt 3 )}^2} cdot sqrt 3 }}{4} = frac{{4{r^2} cdot 3 cdot sqrt 3 }}{4} = 3sqrt 3 {r^2}.]$

Таким образом, формула площади правильного треугольника через радиус вписанной окружности —

$[S = 3sqrt 3 {r^2}.]$

3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:

$[AD = BD = BK = CK = CF = AF = frac{a}{2}.]$

4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.

5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:

$[left. begin{array}{l} OF = r,BO = R\ OF = frac{1}{3}BF,BO = frac{2}{3}BF end{array} right} Rightarrow r = frac{1}{2}R.]$

Источник

Свойства равностороннего треугольника

Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})

Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})

Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).

Почему так? А посмотрим-ка на равносторонний треугольник.

Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.

ravnostoronnij treugolnik bissektrisy i mediany

Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!

В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!

Итак, ещё раз:

Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.

Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)

vpisannaya okruzhnost ravnobedrennyj treugolnik

Уже должно быть очевидно, отчего так.

Посмотри на рисунок: точка( O) – центр треугольника.

Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).

Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.

Поэтому (OB=2cdot OK), то есть (R=2cdot r).

Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.

Давай удостоверимся в этом.

Источник

В любой треугольник можно вписать окружность. Радиус такой окружности будет представлять собой квадратный корень из отношения разности полупериметра с каждой стороной к самому полупериметру.

Если упростить данную формулу для прямоугольного треугольника, воспользовавшись теоремой Пифагора, то мы получим следующее выражение:

Так как в равнобедренном треугольнике боковые стороны равны, то в формуле остаются только обозначения a и b, и ее вид упрощается из все того же первого радикала до следующей формы:

В случае с равносторонним треугольником все еще гораздо проще, и его формула может быть выведена не только из формулы для произвольного треугольника, но также и из свойств высоты-медианы-биссектрисы, которые совпадают и делят любую из сторон на две равные части:

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.

Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Примеры задач

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.

где a, b, c – стороны треугольника, S – его площадь.

Прямоугольный треугольник

Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.

где a и b – катеты, c – гипотенуза треугольника.

Равнобедренный треугольник

Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:

где a – боковые стороны, b – основание треугольника.

Равносторонний треугольник

Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:

где a – сторона треугольника.

Примеры задач

Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.

Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:

Остается только применить соответствующую формулу для вычисления радиуса круга:

Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.

Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:

Источник