Как найти вписанный угол в окружности огэ - Исправление недочетов и поиск решений вместе с Examum.ru

Окружность. Центральный и вписанный угол

Центральный угол — это угол, вершина которого находится в центре окружности.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.

Отрезок, соединяющий две точки окружности, называется хорда.

Самая большая хорда проходит через центр окружности и называется диаметр.

На рисунках — центральные и вписанные углы, а также их важнейшие свойства.

Угол, вершина которого лежит в центре окружности, называется центральным. Величина центрального угла равна угловой величине дуги, на которую он опирается. Угол beta тоже можно назвать центральным. Только он опирается на дугу, которая больше 180 ^circ .

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, — прямой.

Величина центрального угла равна угловой величине дуги, на которую он опирается. Значит, центральный угол величиной в градусов будет опираться на дугу, равную 90^circ , то есть $displaystyle frac{1}{4}$ круга. Центральный угол, равный 60^circ , опирается на дугу в 60 градусов, то есть на шестую часть круга.

Докажем, что величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу.

Пусть угол AOC — центральный и опирается на дугу АС, тогда ОА и ОС — радиусы окружности.

Пусть angle ABC — вписанный угол, опирающийся на дугу АС,

АВ и ВС — хорды окружности.

Первый случай: Точка O лежит на BC, то есть ВС — диаметр окружности.

Треугольник AOB — равнобедренный, АО = ОВ как радиусы. Значит,

— внешний угол а внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Получили, что

Второй случай: Центр окружности точка О не лежит на ВС. Построим диаметр BК:

Если точка О лежит внутри вписанного угла АВС, как на рисунке слева, то

Если О лежит вне вписанного угла АВС, как на рисунке справа, то

Мы получили, что в каждом из этих случаев величина центрального угла в два раза больше, чем величина вписанного угла, опирающегося на ту же дугу.

Теорема доказана.

При решении задач по геометрии также применяются следующие теоремы:

1. Равные центральные углы опираются на равные хорды.

2. Равные вписанные углы опираются на равные хорды.

3. Равные хорды стягивают равные дуги.

Докажем теорему 3.

Пусть хорды AB и CD равны. Докажем, что AMB дуги CND имеют одинаковую градусную меру, то есть равны.

Доказательство:

По условию, AB = CD. Соединим концы хорд с центром окружности. Получим: AO = BO = CO = DO = r.

по трем сторонам, отсюда следует, что центральные углы равны, т.е. Значит, и дуги, на которые они опираются, также равны, т.е. дуги AMB и CND имеют одинаковую градусную меру.

Теорема доказана.

Верна и обратная теорема:

Если две дуги окружности равны, то равны и хорды, их стягивающие.

Пусть дуги AMB и CND равны. Тогда как центральные углы, опирающиеся на эти дуги. Значит, треугольники и равны по двум сторонам и углу между ними, и тогда AB=CD, что и требовалось доказать.

Эти две теоремы можно объединить в одну, которая формулируется так:

Хорды окружности равны тогда и только тогда, когда равны дуги, которые они стягивают.

Разберем задачи ЕГЭ и ОГЭ по теме: Окружность, центральный угол, вписанный угол.

Задача 1, ЕГЭ. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.

Вписанный угол, опирающийся на диаметр, — прямой.

Ответ: 90.

Задача 2, ЕГЭ. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.

Решение:

Пусть центральный угол равен , а вписанный угол, опирающийся на ту же дугу, равен .

Мы знаем, что x=2y.

Отсюда

y=36.

Ответ: 36.

Задача 3, ЕГЭ. Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную Ответ дайте в градусах.

Решение:

Пусть хорда AB равна Тупой вписанный угол, опирающийся на эту хорду, обозначим alpha. В треугольнике AOB стороны AO и OB равны 1, сторона AB равна Нам уже встречались такие треугольники. Очевидно, что треугольник AOB — прямоугольный и равнобедренный, то есть угол AOB равен 90 ${}^circ .$ Тогда дуга ACB равна 90 ${}^circ ,$ а дуга AKB равна $360{}^circ - 90{}^circ = 270 {}^circ .$ Вписанный угол alpha опирается на дугу AKB и равен половине угловой величины этой дуги, то есть 135.

Ответ: 135.

Задача 4, ЕГЭ. Хорда AB делит окружность на две части, градусные величины которых относятся как 5 : 7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Решение:

Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки С?»

Представьте, что вы сидите в точке С и вам необходимо видеть всё, что происходит на хорде AB. Так, как будто хорда AB — это экран в кинотеатре
Очевидно, что найти нужно угол ACB.
Сумма двух дуг, на которые хорда AB делит окружность, равна то есть

Отсюда и тогда вписанный угол ACB опирается на дугу, равную Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол ACB равен

Ответ: 105.

Задача 5, ЕГЭ.

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32 ${}^circ .$

Решение:

Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

$angle BAC=displaystyle frac{1}{2}angle BOC.$

Значит, $angle BOC=2cdot angle BAC=2cdot 32{}^circ =64{}^circ.$

Ответ: 64.

Задача 6, ЕГЭ. Найдите центральный угол AOB, если он на $15{}^circ$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах.

Решение:

Пусть величина угла АОВ равна градусов. Величина вписанного угла АСВ равна половине центрального угла, опирающегося на ту же дугу, то есть $displaystyle frac{x}{2}$ градусов.

Получим уравнение: $displaystyle x-frac{1}{2} x = 15{}^circ,$ откуда $x ={30}^circ.$

Ответ: 30.

Задача 7, ЕГЭ. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Решение.

Рассмотрим треугольник AOB. Он равносторонний, так как AO = OB = AB = R.

Поэтому угол AOB = 60. Вписанный угол ACB равен половине дуги, на которую он опирается, то есть 30 ${}^circ.$

Ответ: 30.

Задача 8, ЕГЭ.

Дуга окружности AC, не содержащая точки B, составляет 200 ${}^circ.$ А дуга окружности BC, не содержащая точки A, составляет 80 ${}^circ.$ Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:

Вписанный угол равен половине угловой величины дуги, на которую он опирается. Дуга АВ равна $360{}^circ -200{}^circ -80{}^circ -80{}^circ .$ Тогда $angle ACB=40{}^circ.$

Ответ: 40.

Задачи ОГЭ по теме: Центральный и вписанный угол, градусная мера дуги.

Задача 9, ОГЭ. Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен ${60}^circ.$ Найдите радиус окружности.

Решение.

Рассмотрим треугольник AOB: он равнобедренный, его боковые стороны равны радиусу окружности.

Углы при основании равнобедренного треугольника равны. Пусть AOB равен , тогда $x + 60{}^circ + 60{}^circ = 180{}^circ,$ где $x = 60{}^circ.$ Треугольник, у которого все углы равны, — равносторонний треугольник; значит, радиус равен 6.

Ответ: 6.

Задача 10, ОГЭ. В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен ${30}^circ.$ Найдите величину угла OAB.

Решение.

Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны, угол $OAB ={30}^circ.$

Ответ: 30.

Задача 11, ОГЭ. Найдите градусную меру центрального angle MON, если известно, что NP — диаметр, а градусная мера angle MNP равна 18 ${}^circ.$

Решение:

Треугольник MON — равнобедренный. Тогда $angle MON = 180{}^circ$ − $2cdot 18{}^circ = 144{}^circ.$

Ответ: 144.

Задача 12, ОГЭ.

Найдите angle DEF, если градусные меры дуг DE и EF равны ${150}^circ$ и ${68}^circ$ соответственно.

Решение.

Дуга FD, не содержащая точку Е, равна ${360}^circ - {150}^circ - 68{}^circ = 142{}^circ.$ Вписанный угол DEF, опирающийся на эту дугу, равен половине ее угловой величины, $angle DEF = 71{}^circ.$

Ответ: 71.

Задача 13, ОГЭ. В окружности с центром O AC и BD — диаметры. Угол ACB равен ${26}^circ.$ Найдите угол AOD. Ответ дайте в градусах.

Решение.

Угол ACB — вписанный, он равен половине центрального угла, опирающегося на ту же дугу, то есть AОВ = 52 ${}^circ.$ Угол ВОD — развернутый, поэтому угол AOD равен ${180}^circ - 52{}^circ = 128{}^circ.$

Ответ: 128.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Окружность. Центральный и вписанный угол» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности.

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается. ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

M N – диаметр.

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

∪ A B = ∪ C D = α

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

l = 2 π R

Длина дуги окружности, на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Разбор заданий ОГЭ №16

Центральный и вписанный угол

Разобрать и законспектировать!

Задача 1

Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 52°. Ответ дайте в градусах.

Решение

Градусная мера центрального угла (вершина в центре окружности) равна градусной мере соответствующей дуги окружности:

Градусная мера вписанного угла (вершина лежит на окружности) измеряется половиной дуги, на которую он опирается:

Ответ: 26

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 2

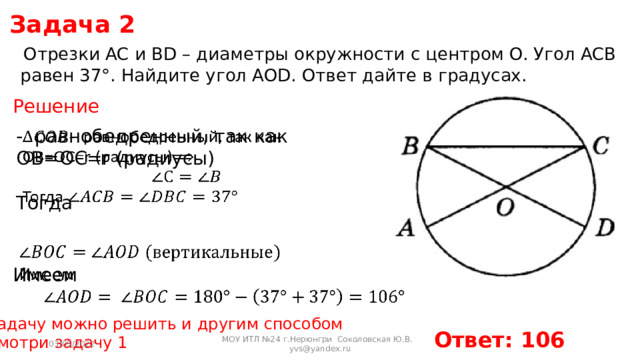
Отрезки AC и BD – диаметры окружности с центром O. Угол ACB равен 37°. Найдите угол AOD. Ответ дайте в градусах.

Решение

— равнобедренный, так как OB=OC=r (радиусы)

Тогда

Имеем

Задачу можно решить и другим способом

Смотри задачу 1

Ответ: 106

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 3

В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен 46°. Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение

Задачу можно решить и другим способом

Смотри задачу 2

Ответ: 67

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 4

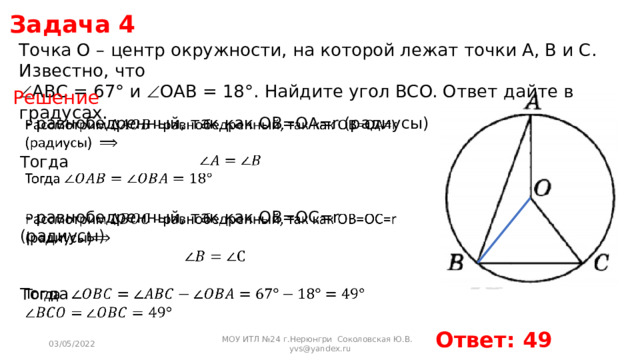
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что

 ABC = 67° и  OAB = 18°. Найдите угол BCO. Ответ дайте в градусах.

Решение

— равнобедренный, так как OB=OA=r (радиусы)

Тогда

— равнобедренный, так как OB=OC=r (радиусы)

Тогда

Ответ: 49

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 5

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что NBA = 40°. Найдите угол NMB. Ответ дайте в градусах.

Решение

вписанный угол (вершина лежит на окружности), а

градусная мера вписанного угла измеряется половиной дуги, на которую он опирается. Поэтому

Так как AB диаметр (по условию), то

Тогда

А так как

Ответ: 50

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 6

Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и  ABC = 84°. Найдите величину угла BOC. Ответ дайте в градусах.

Решение

Градусная мера вписанного угла измеряется половиной дуги, на которую он опирается:

Градусная мера центрального угла равна градусной мере соответствующей дуги окружности:

Рассмотрим  AOB и  BOC. Они равны по трём сторонам (AB = BC по условию, AO=OB=OC — радиусы)

Тогда

Ответ: 96

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 7

Четырёхугольник ABCD вписан в окружность. Угол ABC равен 105°, угол CAD равен 28°. Найдите угол ABD. Ответ дайте в градусах.

Решение

вписанный угол (вершина лежит на окружности), а

градусная мера вписанного угла измеряется половиной дуги, на которую он опирается. Поэтому

вписанный угол, аналогично

— вписанный угол, поэтому

Ответ: 77

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 8

Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол OAB и угол ABC. Ответ дайте в градусах.

Решение

Рассмотрим ромб OABC. По определению OA=AB=BC=OC и равны радиусу.

OB тоже радиус.

Тогда — равносторонний

(как односторонние)

Ответ: 60 и 120

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Задача 9

Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что  ABC = 111° и  OAB = 51°. Найдите угол BCO. Ответ дайте в градусах.

Решение

Проведём отрезок OB и рассмотрим  AOB. Он равнобедренный, так как OA=OB (радиусы)

Рассмотрим  BOС, он так же равнобедренный,

так как OB=OC (радиусы)

Ответ: 60

03/05/2022

МОУ ИТЛ №24 г.Нерюнгри Соколовская Ю.В. [email protected]

Источник

Сегодня говорим о типе задач на окружности, которые встретятся в КИМах ОГЭ по математике. Приготовьте тетрадки и ручки (ну или кнопки для скринов), ведь мы начинаем!

Типы задач на окружности

На самом деле, список этих задач немаленький. Взгляните сам:

Окружность №16. Центральные и вписанные углы;
Треугольники №15. Медиана, проведенная из прямого угла;
Окружность №18. Центральные и вписанные углы;
Окружность №16. Вписанные многоугольники;
Окружность №16. Описанные многоугольники;
Окружность №16. Квадрат и окружность;
Окружность №16. Свойства хорд, касательных, секущих.

Сегодня подробно говорим о первом пункте – центральных и вписанных углах, с которыми встречаемся в номере 16. Поехали!

Немного теории

Итак, начинать разговор про окружности нужно с объяснения базовых понятий.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны опираются на окружность.

Центральный угол – это угол, вершина которого лежит в центре окружности, а стороны опираются на окружность. Равен градусной мере дуги, на которую опирается.

Свойства вписанного угла

Вписанный угол равен половине центрального угла, если они оба опираются на одну дугу.

Задача №1

В окружность вписан равносторонний восьмиугольник. Найдите величину угла RAV.

Решение:

Как поступаем первым делом? Рисуем центральный угол, который опирается на те же самые точки. Именно так впоследствии мы придем к нужному нам вписанному углу.

Можем ли мы как-нибудь его посчитать? Ответ положительный! Перед нами восьмиугольник, своеобразная пицца, сумма углов которой дает 360 градусов. Соответственно “цена” одного кусочка =45 градусам.

Вписанный угол по правилам будет вдвое меньше. То есть наш RAV=22,5 градусам.

Вуаля, записываем ответ!

Задача №2

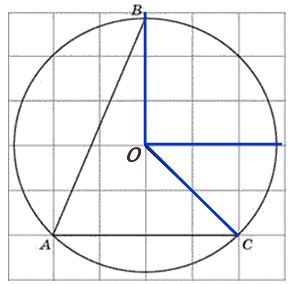
Найдите угол RAV (дан только рисунок)

Решение:

На первый взгляд выглядит нерешаемо. Но вы точно сможете это сделать))

На этом рисунке нам даны клетки. А в математике, как у Чехова, если ружье висит, то обязательно должно выстрелить.

Клетки, конечно, стрелять не будут, но вот найти центральный угол нам точно помогут. Благодаря ним мы можем разделить окружность ровно на 4 части, сделав это, мы видим, что точка V находится ровно посередине между двумя точками.

Снова делим пиццу на 8 частей. 360 делим на 8 и получаем 45, а 45 снова уменьшаем вдвоем и получаем 22,5.

Вот такой постоянный наш угол RAV, равный 22,5 градусам.

Задача №3

Найдите угол RAV (дан только рисунок)

Решение:

Рисуем центральный угол с точкой О. Потом снова действуем по рабочей системе пиццы. Делим на 8 частей, обнаруживаем, что центральный угол состоит сразу из трех кусочков нашей пиццы.

Выполняем махинации с числами: 360/8 и получаем 45. А 45 уже умножаем на 3. 135 градусов – наш центральный угол.

Вписанный по теореме вдвое меньше центрального, соответственно наш RAV=135/2=67,5.

Задача №4

Итак, приступаем к нашему боссу, как в старых компьютерных играх, помните? Хотя девятиклассники часто путаются и ошибаются в этом месте, вам повезло – сегодня вы раз и навсегда запомните, какой же чит надо использовать, чтобы пройти уровень.

Найдите угол RAV (дан только рисунок)

Решение:

Как мы можем заметить, здесь нам дан тупой угол. Мы снова делим нашу пиццу на 8 частей и ищем середину. Рисуем центральный угол, опирающийся на точки R и V.

Вот тут-то и сыплются ошибки, ведь многие забывают, что центральный и вписанный углы должны опираться на одну дугу! Вы по старинке считаете 145 градусов, не замечая, что сейчас нас интересует другая, бОльшая дуга.

Итак, центральный угол состоит из пяти кусочков, 45*5=225 градусов. Наш RAV, как мы помним, вдвое меньше, делим 225 на 2 и в ответе получаем 112,5.

Готово!

Секретная информация

Почему же мы делим центральный угол на 2? Секрет в том, что мы действуем аналогично поиску углов в равнобедренном треугольнике. Послушаем нашего Данира Баева, который сказал, что доказывать это очень и очень скучно даже фанатикам математики, и просто примем это к сведению.

Надеемся, что сегодняшние задачи если и попадутся вам в КИМах, то будут решены без ошибок. Мы разобрали первый тип заданий на окружность ОГЭ по математике. Впереди еще много интересного.

Стремитесь к заветным пятеркам и готовьтесь к экзаменам с удовольствием вместе с Умскул!

Источник

Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.

Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?

Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?

Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.

Чему равен этот угол?

Понятно, что 45 градусам.

А этот?

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).

А такой?

225 градусов (180 + 45 или 360 – 135).

Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.

Ещё раз напомню основное свойство вписанного угла.

«Вписанный угол равен половине центрального,

опирающегося на ту же дугу»

27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.

Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:

По клеткам видно, что угол ВОС равен 90⁰ + 45⁰= 135⁰ (ОС проходит по диагонали клеток).

Ответ: 135

27887. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение

27888. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение

27889. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение

27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.

Посмотреть решение

Небольшой итог!

Нужно знать свойство вписанного угла (обязательно).

Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.

На этом всё. Успеха Вам!

С уважением, Александр Крутицких

Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Вписанный угол, касательная. | ЕГЭ-№3Окружность КругУглы

Подготовка к ОГЭ по математике. Полный курс!

Полный Видеокурс по РУССКОМУ ЯЗЫКУ!

ПРЕМИУМ-КУРС по математике на 100 баллов!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

© 2007 — 2022 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель: Никитенко Евгений Игоревич

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

Фотографии предоставлены

Создайте Ваш сайт учителя

Курсы ПК и ППК
Видеоуроки

Олимпиады
Вебинары для учителей

Главная
Математика
Презентации
Задачи на клетчатой бумаге(для подготовки егэ и огэ)

Данные задачи разработанны для уроков математики девятого и одиннадцатого классов при подготовке к единому государственному экзамену и основной итоговой аттестации. В презентации используются задачи для нахождения тангенсов углов, а также построения углов. Далее представлены задачи из егэ B6. Имеются задачи нахождения площадей через формулу Пика, а также нахождения радиусов вписанной окружности.

Вы уже знаете о суперспособностях современного учителя?