Как найти время через силу кулона

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

$F=k{|q_1|·|q_2|}/{r^2}$

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).

Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:

$k=9·10^9H·м^2$/$Кл^2$

Часто его записывают в виде $k={1}/{4πε_0}$, где $ε_0=8.85×10^{-12}Кл^2$/$H·м^2$ — электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

$C={q}/{φ}$

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:

$C={q}/{U}={ε_{0}εS}/{d}$

где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_{0}$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.

Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.

Энергия поля конденсатора

Энергия заряженного конденсатора выражается формулами

$E_n={qU}/{2}={q^2}/{2C}={CU^2}/{2}$

которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.

Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:

$ω={εε_{0}E^2}/{2}$

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

$I={∆q}/{∆t}$

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

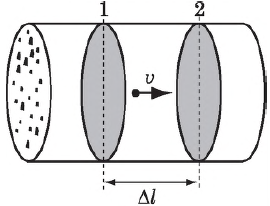
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t={∆l}/{υ}$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:

$I={∆q}/{∆t}={q_{0}nS∆l·υ}/{∆l}=q_{0}nυS$

В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).

Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.

Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:

$I={U}/{R}$

Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I={U}/{R}$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I={U}/{R}$ следует:

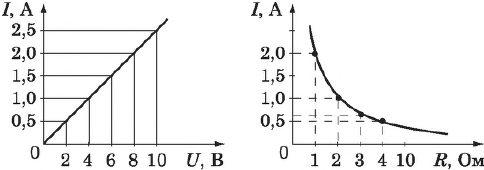
1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

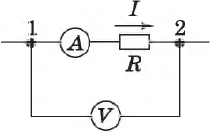
Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.

Удельное сопротивление

Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:

$R=ρ{l}/{S}$

где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы $R=ρ{l}/{S}$ следует, что

$ρ={RS}/{l}$

Величина, обратная $ρ$, называется удельной проводимостью $σ$:

$σ={1}/{ρ}$

Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^{-1}м^{-1}$.

На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^{-6}$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^{-2}$) Ом$·$м$м^2$/м, диэлектрики — в $10^{15}-10^{20}$ раз большим.

Зависимость сопротивления от температуры

С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.

Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:

$α={R_t-R_0}/{R_0t}$

Зависимость удельного сопротивления проводников от температуры выражается формулой:

$ρ=ρ_0(1+αt)$

В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=({1}/{273})K^{-1}$. Для растворов электролитов $α < 0$. Например, для $10%$-го раствора поваренной соли $α=-0.02K^{-1}$. Для константана (сплава меди с никелем) $α=10^{-5}K^{-1}$.

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Параллельное и последовательное соединение проводников

Для параллельного соединения проводников справедливы следующие соотношения:

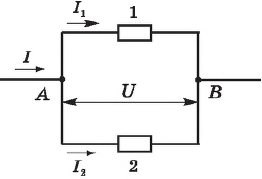
1) электрический ток, поступающий в точку $А$ разветвления проводников (она называется также узлом), равен сумме токов в каждом из элементов цепи:

$I=I_1+I_2;$

2) напряжение $U$ на концах проводников, соединенных параллельно, одно и то же:

$U=U_1=U_2;$

3) при параллельном соединении проводников складываются их обратные сопротивления:

${1}/{R}={1}/{R_1}+{1}/{R_2}, R={R_1·R_2}/{R_1+R_2};$

4) сила тока и сопротивление в проводниках связаны соотношением:

${I_1}/{I_2}={R_2}/{R_1}$

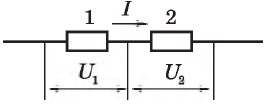
Для последовательного соединения проводников в цепи справедливы следующие соотношения:

1) для общего тока $I$:

$I=I_1=I_2,$

где $I_1$ и $I_2$ — ток в проводниках $1$ и $2$ соответственно; т. е. при последовательном соединении проводников сила тока на отдельных участках цепи одинакова;

2) общее напряжение $U$ на концах всего рассматриваемого участка равно сумме напряжений на отдельных его участках:

$U=U_1+U_2;$

3) полное сопротивление $R$ всего участка цепи равно сумме последовательно соединенных сопротивлений:

$R=R_1+R_2;$

4) также справедливо соотношение:

${U_1}/{U_2}={R_1}/{R_2}$

Работа электрического тока. Закон Джоуля-Ленца

Работа, совершаемая током, проходящим по некоторому участку цепи, согласно ($U=φ_1-φ_2={A}/{q}$) равна:

$A=qU$

где $А$ — работа тока; $q$ — электрический заряд, прошедший за данное время через рассматриваемый участок цепи. Подставляя в последнее равенство формулу $q=It$, получаем:

$A=IUt$

Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.

Закон Джоуля-Ленца

Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:

$Q=I^2Rt$

Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.

Из закона Джоуля — Ленца следует, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это используется в технике, например, для распыления металлов.

При параллельном соединении все проводники находятся под одинаковым напряжением, но токи в них разные. Из формулы ($Q=I^2Rt$) следует, что, так как, согласно закону Ома $I={U}/{R}$, то

$Q={U^2t}/{R}$

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.

Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.

Мощность электрического тока

Действие тока характеризуют не только работой $A$, но и мощностью $Р$. Мощность тока показывает, какую работу совершает ток за единицу времени. Если за время $t$ была совершена работа $А$, то мощность тока $P={A}/{t}$. Подставляя в это равенство выражение ($A=IUt$), получаем:

$P=IU$

Это выражение можно переписать в разных формах, воспользовавшись законом Ома для участка цепи:

$P=IU=I^{2R}={U^2}/{R}$

Из соотношения для ЭДС легко получить мощность источника тока:

$P_ε=εI$

В СИ работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время -в секундах (с). При этом

$1$Вт$=1$Дж/с, $1$Дж$=1$Вт$·$с.

Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать $I=10$А, то при напряжении $U=220$В соответствующая электрическая мощность оказывается равной:

$Р=10А·220В=2200Вт=2.2кВт.$

Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока, и потому недопустимо.

В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения прямо пропорциональна силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах ($кВт·ч$).

$1кВт·ч$ — это работа, совершаемая электрическим током мощностью $1кВт$ в течение $1ч$. Так как $1кВт=1000Вт$, а $1ч=3600с$, то $1кВт·ч=1000Вт·3600с=3600000 Дж$.

Закон Кулона. Калькулятор онлайн.

Онлайн калькулятор Закона Кулона с решением позволит вычислить силу взаимодействия двух зарядов, электрический заряд, а так же расстояние между зарядами, единицы измерения которых, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие и даст подробное решение.

Калькулятор вычислит:
Силу взаимодействия двух точечных зарядов.
Точечный электрический заряд.
Расстояние между зарядами.

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Определение силы тока .

Силой тока называют отношение(деление) величины заряда, прошедшего по проводнику к времени,
за которое этот заряд прошел через этот проводник.

(I= dfrac{q}{t} )

(I ) — сила тока, измеряется в Амперах [А]

(q) — заряд, измеряется в Кулонах [Кл]

(t ) — время, измеряется в секундах [с]

---

Задача 1.

Через поперечное сечение проводника проходит заряд ( q=1 Кл ) за время (t= 10 с . )

Найдите силу тока в этом проводнике.

Показать ответ
Показать решение
Видеорешение

---

Задача 2.

Через провод проходит заряд ( q=0,2 Кл ) за время (t= 40 с . )

Найти силу тока в этом проводе.

Дать ответ в миллиамперах.

Показать ответ
Показать решение
Видеорешение

---

Задача 3.

Через провод, идущий от плюсовой клеммы аккумулятора тепловоза проходит заряд ( q=9000 Кл ) за время (t= 8 с . )

Найти силу тока в этом проводе.

Дать ответ в килоамперах.

Показать ответ
Показать решение
Видеорешение

---

Задача 4.

Через поперечное сечение проводника за минуту проходит заряд (q=30 Кл . )

Найти силу тока в этом проводнике.

Показать ответ
Показать решение
Видеорешение

---

Задача 5.

Через спираль лампы накаливания за час

проходит заряд (q=900 Кл . )

Найти силу тока в этой лампе.

Показать ответ
Показать решение
Видеорешение

---

Задача 6.

Какой заряд пройдет через обмотку электродвигателя за две секунды, если сила тока в нем (I=3 А ? )

Показать ответ
Показать решение
Видеорешение

---

Закон Кулона. Силы и ускорения.

В статье рассмотрены задачи, сочетающие законы динамики и взаимодействие зарядов. Здесь встретится и сила упругости, и сила натяжения нити, и нормальное ускорение при движении по окружности. Задачи среднего уровня сложности.

Задача 1. Два одинаковых заряда , соединенных резиновыми шнурами со стенками так, как показано на рисунке, находятся на расстоянии друг от друга. Расстояние между стенками , длина каждого недеформированного шнура . Определить жесткость шнура, массой зарядов пренебречь.

Жесткость шнура равна  , где — сила натяжения шнура, — удлинение шнура.

Определим, насколько шнур стал длиннее.

Определим силу кулоновского взаимодействия зарядов:

Определим силу натяжения шнура, для этого приравняем проекции сил кулоновского взаимодействия и натяжения шнуров:

Найдем косинус угла из геометрических соображений:

Тогда можем подставить все в формулу для жесткости:

Ответ: .

Задача 2. Внутри гладкой сферы диаметром находится маленький заряженный шарик. Какой минимальной величины заряд нужно поместить в нижней точке сферы, для того чтобы шарик находился в ее верхней точке в устойчивом равновесии? Заряд шарика , его масса .

Минимальная сила, которая может нам понадобиться, это кулонова сила, равная силе тяжести. Тогда

Посмотрим, достаточно ли этого, чтобы равновесие было устойчивым: если шарик отклонится на небольшой угол от вертикали, то кулонова сила может быть разложена на две составляющие, причем раскладывать силу будем, направив ось по касательной к сфере, а ось — перпендикулярно касательной. Тогда проекция кулоновой силы на данное направление равна , а проекция силы тяжести на это же направление равна . Чтобы шарик возвращался назад в точку равновесия нужно, чтобы проекция кулоновой слы была бы больше проекции силы тяжести. Осталось установить, как соотносятся углы и . Посмотрим на рисунок: угол — центральный, а угол — вписанный. Поэтому .

Тогда:

В силу малости углов можно принять , . Тогда

Иными словами, устойчивым равновесие будет, если

Ответ:

Задача 3. Два заряженных шарика соединены нитью см. Отношение масс шариков , заряды по модулю одинаковы Кл, но противоположны по знаку. Какую минимальную внешнюю силу надо приложить к шарику массой , чтобы в процессе движения нить не провисала?

Шарики заряжены одноименно, то есть будут притягиваться. Нужно, чтобы левый шарик «убегал» от правого с определенным ускорением. Нарисуем чертеж:

Запишем второй закон Ньютона для левого шарика:

Здесь — внешняя сила, — кулонова сила, — сила натяжения нити.

Для правого шарика

Чтобы нить не провисала, достаточно чтобы натяжение нити было нулевым, :

Подставим второе в первое:

Подставим ускорение из записанного ранее равенства:

Ответ: 27 мН

Задача 4. Вокруг неподвижного положительного заряда Кл движется по окружности отрицательный заряд. Радиус окружности 1 см. Один оборот заряд совершает за время с.  Найти отношение заряда к массе для движущегося заряда.

При движении по окружности всегда присутствует нормальное ускорение, поворачивающее вектор скорости. Чтобы его найти, надо бы узнать скорость движения заряда. Мы знаем время прохождения одного оборота, длина же окружности радиуса равна , поэтому линейная скорость движения заряда равна .

Нормальное ускорение:

Кулонова сила равна центростремительной:

Запишем иначе:

Ответ: Кл/кг

Задача 5. Шарик массой и зарядом , подвешенный на непроводящей нити длиной  ,  вращается вокруг вертикальной оси так, что нить образует с вертикалью угол . Определить период  обращения шарика  и  силу натяжения нити, если неподвижный точечный заряд находится: а) в точке подвеса; б) в центре окружности, описываемой шариком; в) на оси вращения, на расстоянии от шарика  внизу.

Первый случай. Заряд – в месте прикрепления нити к потолку, сила кулоновского взаимодействия направлена вдоль нити вниз. Нарисуем картинку и запишем второй закон Ньютона.

В векторной форме:

Здесь — сила натяжения нити, — кулонова сила, — сила, обусловленная наличием нормального ускорения.

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

Определим отсюда силу натяжения нити:

Теперь займемся периодом. Для его определения нужно знать скорость шарика. Распишем второе уравнение, подставив силу натяжения нити и нормальное ускорение:

Так как , то

Второй случай – заряд в центре окружности.

Сила кулоновского взаимодействия направлена вдоль радиуса, наружу. Нарисуем картинку и запишем второй закон Ньютона.

В векторной форме:

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

Определим отсюда силу натяжения нити:

Тогда первое уравнение:

Определим период. Скорость знаем, длину окружности – тоже. Тогда:

Упростим немного выражение:

Наконец, рассмотрим третий случай, когда заряд находится на оси вращения внизу. Сила кулоновского взаимодействия направлена вдоль линии, проведенной через заряды, вверх и влево.

Нарисуем картинку и запишем второй закон Ньютона.

В векторной форме:

Разложим теперь вектора на проекции вдоль координатных осей. Ось абсцисс направим горизонтально вправо, ось ординат – вверх. Тогда:

Определим отсюда силу натяжения нити:

Зная скорость, определим период: