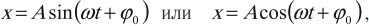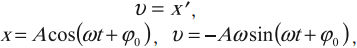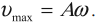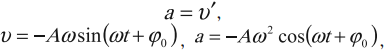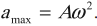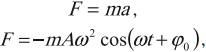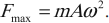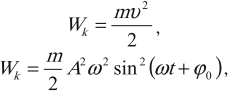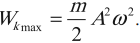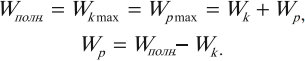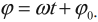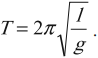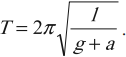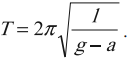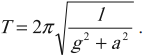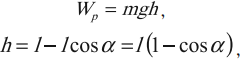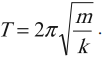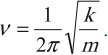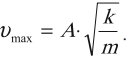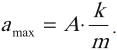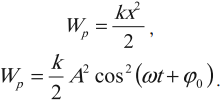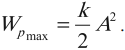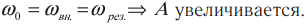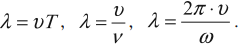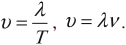Отдельные частицы любого тела — твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-то частица начинает колебаться, то благодаря взаимодействию между частицами это движение с некоторой скоростью начинает распространяться во все стороны.
Определение
Волна — колебания, распространяющиеся в пространстве с течение времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря силам упругости. Эти силы осуществляют связь между отдельными частями тела. В образовании волн на поверхности воды играют роль сила тяжести и сила поверхностного натяжения. Такие волны позволяют наиболее наглядно рассмотреть главные особенности волнового движения.
Волна на поверхности воды представляет собой бегущие вперед валы округлой формы. Расстояние между валами, которые также называют гребнями, примерно одинаковы. Волны распространяются в среде с определенной скоростью. Так, если чайка летит вперед, а по ней в любой момент времени оказывается один и тот же гребень, то скорость распространения волны можно принять равной скорости полета чайки. Волны на воде наблюдать удобно потому, что скорость их распространения невелика.
Если бросить в воду легкий предмет, он не будет увлекаться волной, а начнет совершать колебания вверх и вниз, оставаясь примерно на одном месте, как поплавок. Это говорит о том, что частицы воды остаются на месте в то время, как волна распространяется на большие расстояния.
Если же резко толкнуть горизонтальную пружину, можно будет наблюдать, как в одних местах она разрежается, в других — уплотняется. Это тоже волна. Видно, что энергия, полученная от толчка руки, переносится через пружину, хотя ее частицы остаются на месте.
Примеры с поплавком на воде и горизонтальной пружиной позволяют сделать вывод, что волна переносит энергию, но не переносит вещество среды.
Виды механических волн
По характеру колебаний частиц среды относительно положения равновесия различают два вида волн:
Определения
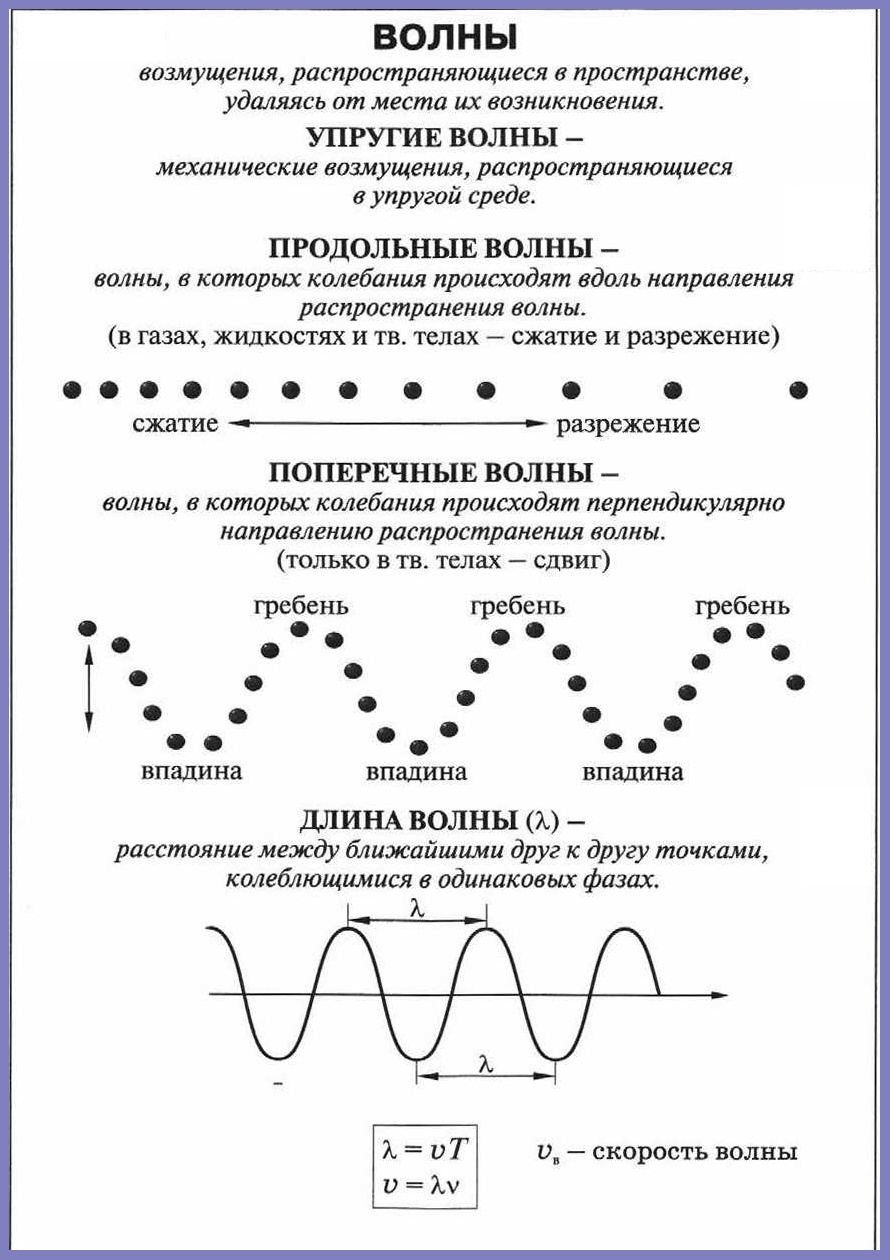
- Поперечная волна — волна, при которой частицы среды колеблются перпендикулярно направлению распространения этой волны.
- Продольная волна — волна, при которой частицы среды колеблются параллельно направлению распространения этой волны.
Волны, распространяющиеся вдоль резинового шнура, являются поперечными (см. рисунок ниже). Чтобы появилась волна, нужно взять конец шнура, прикрепленного к вертикальной опоре, и дернуть его. При этом волна побежит к вертикальной опоре, а сам шнур будет менять свою форму. Каждая частица шнура станет совершать колебания относительно своего неизмененного положения равновесия сверху вниз (перпендикулярно направлению распространения волны).
Рассмотрим поперечные волны подробнее. Каждый участок шнура обладает массой и упругостью. При деформации шнура в любом его сечении появляются силы упругости. Эти силы стремятся возвратить шнур в исходное положение. Благодаря инертности участок колеблющегося шнура не останавливается в положении равновесия, а проходит его, продолжая двигаться до тех пор, пока силы упругости не остановят этот участок в момент максимального отклонения от положения равновесия.
На рисунках а, б, в, г, д и е изображен процесс распространения поперечной волны. На них показаны положения частиц среды в последовательные моменты времени.
Теперь рассмотрим распространение в среде продольной волны. Такую волну можно наблюдать, собрав установку из цепочки массивных шариков, связанных пружинками. Шары подвешены так, чтобы они могли колебаться только вдоль цепочки (см. рисунок ниже).
Если первый шар привести в колебательное движение, то вдоль цепочки побежит продольная волна, состоящая из чередующихся уплотнений и разрежений шаров. Уплотнения и разрежения (см. рисунок ниже) появляются вследствие горизонтальных колебаний шаров у положения равновесия. Волна также распространяется горизонтально.
Физические характеристики волны
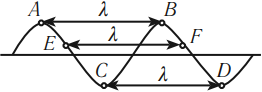
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Определение
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ2, колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
v=λT
Но мы знаем, что период равен величине, обратной частоте колебаний:
T=1ν
Тогда скорость распространения волны равна:
v=λν
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
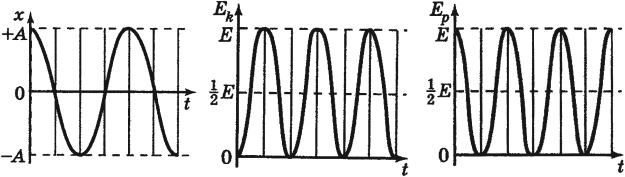
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
ν=nt
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v=λν=λnt=1·105=2 (мс)
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
s = s(x, t)
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = smaxsin ωt
smax — амплитуда колебаний (рис. а).
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
τ=xv
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s(x, t)=0,1sin(2πt−xπ2). Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s=smaxsin [ω(t−τ)]=smaxsin [ω(t−xv)]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω=2π (радс)
v=4 (мс)
Циклическую частоту также можно рассчитать по формуле:
ω=2πν
Тогда частота волны равна:
ν=ω2π=2π2π=1 (Гц)
Тогда длина волны равна:
λ=vν=41=4 (м)
Задание EF18242
Ответ:
а) π/3
б) π/2
в) π
г) 2π
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
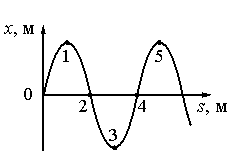
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу, которая связывает скорость волны с ее частотой и длиной.
3.Выполнить решение задачи в общем виде.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Частота звуковой волны: ν = 400 Гц.
Скорость звука — это отношение длины волны к ее периоду. Но период — это обратная величина частоте. Следовательно, скорость звука — есть произведение длины волны на частоту:
v=λν=4·400=1600 (мс)
Ответ: 1600
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18803
На расстоянии 510 м от наблюдателя рабочие вбивают сваи с помощью копра. Какое время пройдёт от момента, когда наблюдатель увидит удар копра, до момента, когда он услышит звук удара? Скорость звука в воздухе равна 340 м/с.
Алгоритм решения
1.Записать исходные данные.
2.Выполнить решение задачи в общем виде.
3.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Скорость распространения звука в воздухе: v = 340 м/с.
• Расстояние наблюдателя до источника звука: s = 510 м.
Звук от удара проделает путь, равный одинарному расстоянию от наблюдателя до источника звука. Следовательно, для нахождения времени, через которое наблюдатель услышит звук, нужно разделить этот путь на скорость звука в воздухе:
t=sv=510340=1,5 (с)
Ответ: 1,5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.1k
Расстояние, пройденное за единицу времени звуковой волковой, распространяющейся через упругую среду
| Измерения звука | |
|---|---|
| Характеристика | Символы |
| Звуковое давление | p, SPL, L PA |
| Скорость частиц | v, SVL |
| Смещение частиц | δ |
| Интенсивность звука | I, SIL |
| Звуковая мощность | P, SWL, L WA |
| Звуковая энергия | W |
| Плотность звуковой энергии | w |
| Звуковое воздействие | E, SEL |
| Акустическое сопротивление | Z |
| Звуковая частота | AF |
| Потери при передаче | TL |
|
|
|
|
скорость звука — это расстояние, которое проходит через единицу времени ковая волна, когда она распространяется через упругую среду. При 20 ° C (68 ° F) скорость звука в воздухе составляет около 343 метров в секунду (1235 км / ч; 1125 футов / с; 767 миль / ч; 667 узлов), или километр за 2,9 с или милю в 4.7 с. Это сильно зависит от температуры, а также от среды, которая распространяется звуковая волна.
Скорость звука в идеальном газе зависит только от его температуры и состава. Скорость имеет слабую зависимость от частоты и давления в обычном воздухе, немного отклоня от идеального поведения.
В разговорной речи скорость звука относится к скорости звуковых волн в воздухе. Однако скорость звука рассматривается от вещества к веществу: обычно звук распространяется медленнее всего в газах, быстрее в жидкостях и еще быстрее в твердых телах. Например, как указано выше, он распространяется по воздуху со скоростью 343 м / с, он распространяется со скоростью 1481 м / с в воде (почти в 4,3 раза быстрее) и со скоростью 5120 м / с в железе (почти в 15 раз быстрее). Быстрее). В исключительно жестком материале, таком как алмаз, звук распространяется со скоростью 12 000 метров в секунду (39 000 футов / с), что примерно в 35 превышает скорость в воздухе и является максимальной скоростью, которую он может распространять в нормальных условиях.
Звуковые волны в твердых телах состоят из волн (как в газах и жидкостях) и звуковой волны другого типа, называемой поперечной волной, которая возникает только в твердых телах. Как показано в сейсмологии, поперечные волны в твердых телах обычно происходят с разными скоростями. Скорость сжатия волн в твердых телах определяет сжимаемостью среды, модулем сдвига и плотностью. Скорость поперечного волн определяется только модулем сдвига и плотностью твердого материала.
В гидродинамике скорость звука в текучей среде (газе или жидкости) используется в качестве относительной меры для скорости объекта, движущегося через среду. Отношение скорости объекта к скорости звука в жидкости называется число Маха объекта. Объекты, движущиеся со скоростью, превышающая число Маха1, считаются движущимися со скоростью сверхзвуковой.
Содержание
- 1 История
- 2 Основные концепции
- 2.1 Сжатие и поперечные волны
- 3 Изменение
- 4 Зависимость от среды
- 5 Зависимость высоты и последствия для атмосферной акустики
- 6 Практическая формула для сухого воздуха
- 7 Подробная информация
- 7.1 Скорость звука в идеальных газах и воздухе
- 7.2 Воздействие сдвига ветра
- 7.3 Таблицы
- 8 Влияние частоты и состава газа
- 8.1 Общие физические соображения
- 8.2 Практическое применение в воздухе
- 9 Число Маха
- 10 Экспериментальные методы
- 10.1 Методы однократной синхронизации
- 10.2 Другие методы
- 10.3 Высокоточные измерения в воздухе
- 11 Негазообразные среды
- 11.1 Скорость звука в твердых телах
- 11.1.1 Трехмерные твердые тела
- 11.1.2 Одномерные твердые тела
- 11.2 Скорость звука в жидкостях
- 11.2.1 Вода
- 11.2.2 Морская вода
- 11.3 Скорость звука в плазме
- 11.1 Скорость звука в твердых телах
- 12 Градиенты
- 13 См. Также
- 14 Ссылки
- 15 Внешние ссылки
История
Сэр Исаак Ньютон 1687 Princi pia включает вычисление скорости звука в воздухе как 979 футов в секунду (298 м / с). Это слишком мало примерно на 15%. Несоответствие вызвано, прежде всего, пренебрежением (тогда неизвестным) эффектом быстро меняющейся температуры в звуковой волне (в современной терминах стрессе и расширении воздуха звуковой волной — это адиабатический процесс, а не изотермический процесс ). Эта ошибка была позже исправлена Лапласом.
В течение 17 века было несколько попыток точно измерить скорость звука, включая технологию Марина Мерсенна в 1630 году (1380 парижских футов в секунду), Пьер Гассенди в 1635 году (1473 парижских фута в секунду) и Роберт Бойль (1125 парижских футов в секунду). В 1709 году преподобный Уильям Дерхам, ректор Апминстера, опубликовал более точные данные о скорости звука: 1072 парижских футов в секунду. (Парижская стопа составляющая 325 мм. Этонее, чем стандартная «международная стопа», широко используемая сегодня, официально определена в 1959 году как 304,8 мм, что означает скорость звука при 20 ° C (68 ° F) 1055 парижских футов в секунду).
Дерхэм использовал телескоп с башни церкви Святого Лаврентия, Апминстер, чтобы наблюдать вспышку выстрела из дробовика, а измерил время, пока он не услышал выстрел из пистолета. полсекундный маятник. Были произведены замеры выстрелов из других источников, включая церковь Северный Окендон. Расстояние было с помощью триангуляции, и, таким образом, было рассчитано распространение звука.
Основные понятия
Передача звука может быть проиллюстрирована с помощью моделей состоящий из сферических объектов, связанных между собой пружинами.
В реальном материальном плане частицы молекулы материала, а пружины представляют собой связи между ними. Звук проходит через систему, сжимая и расширяя пружины, передавая акустическую соседним сферам. Это помогает энергоснабжению, в свою очередь, пружинам (связям) соседней сферы и так далее.
Скорость звука через модель зависит от жесткости / жесткости пружин и массы сфер. Пока расстояние между сферами остается постоянным, жесткие пружины / связи передают энергию быстрее, в то время как более крупные сферы передают медленнее.
В реальном материале жесткость пружин известна как «модуль упругости », а масса плотности материала. При прочих равных условиях (при прочих равных условиях ) звук будет распространяться медленнее в пористых материалах и быстрее в более жестких. Такие эффекты, как дисперсия и отражение, также можно понять с помощью этой модели.
. Например, звук в никеле распространяется в 1,59 раза быстрее, чем в бронзе, из-за большей жесткости никеля примерно при такой же плотности. Точно так же звук распространяется примерно в 1,41 раза быстрее в газе легкого водорода (протий ), чем в газе тяжелого водорода (дейтерий ), поскольку дейтерий имеет аналогичные свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых жидкостях, чем в газах, что твердые тела сложнее сжимать, чем жидкость, а жидкость, в свою очередь, труднее сжимать. чем газы.
В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это понятие проиллюстрировано представлением данных для трех материалов, таких как воздух, вода и сталь, каждый из которых имеет разную сжимаемость, что более чем компенсирует разницу в плотности. Наглядным примером этих двух эффектов является всего в 4,3 раза больше, чем в воздухе, несмотря на огромные различия в сжимаемости двух сред. Причина в том, что большая плотность воды, сокращает объем воды в воде по сравнению с воздухом, почти компенсирует разницу в сжимаемости двух сред.
Практический пример можно наблюдать в Эдинбурге, когда в восточной части Эдинбургского замка стреляют из «Пистолета на час». Стоя у подножия западной оконечности Касл-Рока, звук ружья можно услышать сквозь скалу, незадолго до того, как он прибудет по воздуху, частично задержанный немного более длинным маршрутом. Это особенно эффективно, если производится салют из нескольких пистолетов, например, «День рождения королевы».
волны сжатия и поперечные волны


в газе или жидкости звук из волн сжатия. В твердых телах волны распространяются двух разных типов. Продольная волна использует со сжатием и декомпрессией в направлении движения и представляет собой тот же процесс в газах и жидкостях, с аналогичной волной типа сжатия в твердых телах. В газах и жидкостях поддерживаются только волны сжатия. Дополнительный тип волны, поперечная волна, также называемая поперечной волной, возникает только в твердых телах, потому что только твердые тела упругие деформации. Это связано с упругой деформацией среды перпендикулярно вокруг волны; направление деформации сдвига называется «поляризацией » этого типа волны. В общем, поперечные волны создают как пара ортогональных поляризаций.
Эти разные волны (волны сжатия и разные поля поперечных волн) могут иметь разные скорости на одной и той же частоте. Следовательно, они прибывают к наблюдателю в разное время, крайним примером является землетрясение , когда сначала приходят резкие волны сжатия, а секунды спустя — колебательные поперечные волны.
Скорость волны сжатия в жидкости определяется сжимаемостью и плотностью среды. В твердых телах волны сжатия аналогичны волнам в жидкостях, в зависимости от сжимаемыми факторами модуля сдвига, который влияет на эффективность сжатия из-за внеосевой упругой энергии. при сжатии. Скорость сдвиговых волн, которые могут возникнуть только в твердых телах, определяется просто модулем сдвига и плотностью твердого материала.
Уравнения
Скорость звука в математической системе обозначения условно обозначается буквой c, от латинского celeritas, означающего «скорость».
Для жидкостей в целом скорость звука c определяется уравнением Ньютона — Лапласа:
- c = K s ρ, { displaystyle c = { sqrt { frac {K_ {s})} { rho} }},}
где
- Ks- коэффициент жесткости, изэнтропический модуль объемной упругости (или модуль объемной упругости для газов);
- ρ { displaystyle rho}
— это плотность.
Таким образом, скорость звука увеличивает жесткость (сопротивление упругого тела деформации под действием приложенной силы) материала. Для идеальных газов объемный модуль K — это просто давление газа, умноженное на безразмерный показатель адиабаты, который составляет около 1,4 для воздуха при нормальных условиях давления и температуры.
Для <общих состояний, если используется классическая механика, скорость звука c получена следующим образом:
Рассмотрим звук волны, распространяющаяся по трубе с площадью поперечного сечения A { displaystyle A}




- dvdt = — 1 ρ dpdz → dp = (- ρ dv) dzdt = (vd ρ) v → v 2 ≡ с 2 знак равно dpd ρ { displaystyle { begin {align} { frac {dv} {dt}} = — { frac {1} { rho}} { frac {dp} {dz}} \ rightarrow dp = (- rho dv) { frac {dz} {dt}} = (vd rho) v \ rightarrow v ^ {2} Equiv c ^ {2} = { frac {dp} {d rho}} end {align}}}
И поэтому:
- c = (∂ p ∂ ρ) s, { displaystyle c = { sqrt { left ({ frac { partial p} { partial rho}} right) _ {s}}},}
где
- p — давление;
- ρ { displaystyle rho}
— плотность, а производная берется изоэнтропически, то есть есть при энтропии s. Это звуковая волна распространяется так быстро, что ее распространение можно представить как адиабатический процесс.
Если релятивистские эффекты важны, скорость звука рассчитывается по релятивистским уравнениям Эйлера.
В недисперсионной среде скорость звука не зависит от частоты звука, поэтому скорости передачи и распространения звука одинаковы для всех частот. Воздух, смесь кислорода и азота, представляет собой недиспергирующую среду. Однако воздух действительно содержит небольшое количество CO 2, который является диспергирующей средой и вызывает дисперсию в воздухе на ультразвуковых частотах (>28 кГц ).
в диспергирующая среда, скорость звука представляет собой функцию частоты звука через дисперсионное соотношение. Каждая частотная компонента распространяется со своей собственной скоростью, называемой фазовой скоростью, в то время как энергия возмущения распространяется с групповой скоростью . То же явление происходит и со световыми волнами; см. Описание в оптической дисперсии.
Зависимость от среды
Скорость звука переменная и зависит от свойств В твердом телах скорость поперечного (или поперечного) волн зависит от деформации сдвига под действием сдвига (называется модулем сдвига ) и плотностью среды. х зависит от тех же двух факторов, что и добавление зависимости от сжимаемости.
жидкостей только сжимаемость и плотность среды являются важными факторами, поскольку жидкость не передают напряжение сдвига. В гетерогенных жидкостях, таких как жидкость, наполненная пузырьками газа, плотность жидкости и сжимаемость газа аддитивно влияние на скорость звука, как показано в эффекте горячего шоколада.
В газах, адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (индекс адиабаты), в то время как давление и обратно пропорциональны температуре и молекулярной массе, поэтому важны только полностью независимые свойства температуры и молекулярной структуры. (Коэффициент теплоемкости может определяться температурой и молекулярной структурой, но простой молекулярной массы недостаточно для его определения).
Звук распространяется быстрее в газах с низкой молекулярной массой, таких как гелий, чем в более тяжелых газах, таких как ксенон. Для одноатомных газов скорость звука составляет около 75% от средней скорости движения элементов в этом газе.
Для данного идеального газа молекулярный состав фиксирован, и таким образом скорость звука зависит только от его температуры. При постоянной температуре газа давление не влияет на скорость звука, плотность больше, так как давление и плотность (также пропорциональная давлению) равны, но противоположны влияют на скорость звука, и эти два вклада полностью компенсируются. Аналогичным образом, волна сжатия в твердой телах зависит как от сжимаемости, так и от плотности — как и в жидкостях, — но в газах плотность сжимаемости таким образом, что некоторая часть каждого атрибута учитывается, изменяет зависимость от температуры, молекулярная масса и коэффициент теплоемкости, которые могут быть независимо получены из температуры и молекулярного состава (см. выводы ниже). Таким образом, для одного данного газа (при условии, что молекулярная масса не изменяется) и в небольшом диапазоне температур (для которого теплоемкость относительно постоянна) скорость звука становится зависимой только от температуры газа.
В режиме поведения неидеального газа, для которого будет использоваться буква газа Ван-дер-Ваальса, пропорциональность не точной, и существует небольшая зависимость скорости звука от давления газа.
Влажность оказывает небольшое, но измеримое влияние на скорость звука (вызывая ее увеличение примерно на 0,1–0,6%), потому что молекулы кислорода и азот воздух заменяется более легкими молекулами воды. Это простой эффект смешивания.
Изменение высоты и последствия для атмосферной акустики

В атмосфере Земли главным фактором, влияющим на скорость звука, является температура. Для данного идеального газа с постоянной теплоемкостью и составом скорость звука зависит исключительно от температуры; см. Подробности ниже. В таком идеальном случае эффекты пониженной плотности и пониженного давления на высоте компенсируют друг друга, за исключением остаточного эффекта температуры.
Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до 11 км, звук преломляется вверх, вдали от слушателей на земле, создавая акустическую тень на некотором расстоянии от источника. Уменьшение скорости звука с высотой упоминается как отрицательный градиент скорости звука.
. Однако есть вариации в этой тенденции выше 11 км. В частности, в стратосфере выше примерно 20 км скорость звука увеличивается с высотой из-за увеличения температуры в результате нагрева внутри озонового слоя. Это дает положительный градиент скорости звука в этой области. Еще одна область положительного градиента наблюдается на очень больших высотах, в хорошо названной термосфере выше 90 км.
Практическая формула для сухого воздуха
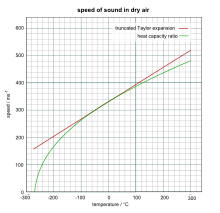
Приблизительную скорость звука в сухом (влажность 0%) воздухе в метрах в секунду при температуре около 0 ° C можно рассчитать по формуле
- cair = (331,3 + 0,606 ⋅ ϑ) м / с, { displaystyle c _ { mathrm {air}} = (331,3 + 0,606 cdot vartheta) ~~~ mathrm {m / s},}
где ϑ { displaystyle vartheta }
Это уравнение получено из первых двух членов разложения Тейлора следующее более точное уравнение:
- cair = 331,3 1 + ϑ 273,15 м / с. { displaystyle c _ { mathrm {air}} = 331.3 ~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~~ mathrm {m / s}.}
Деление первая часть и умножение второй части в правой части на √273,15дает точно эквивалентную форму
- cair = 20,05 ϑ + 273,15 м / с. { displaystyle c _ { mathrm {air}} = 20.05 ~ { sqrt { vartheta +273.15}} ~~~~ mathrm {m / s}.}
, который также можно записать как
- cair = 20,05 T м / с { displaystyle c _ { mathrm {air}} = 20,05 ~ { sqrt {T}} ~~~~ mathrm {m / s}}
где T обозначает термодинамический показатель.
Значение 331,3 м / с, которое представляет скорость при 0 ° C (или 273,15 K), основано на теоретических (и некоторых измеренных) значениях коэффициент теплоемкости, γ, а также тот факт, что при 1 атм реальный воздух очень хорошо описывается приближением идеального газа. Обычно найденные значения скорости звука при 0 ° C могут обсуждаться от 331,2 до 331,6 из-за допущений, сделанных при ее расчетах. Если принять γ идеального газа равным 7/5 = 1,4, то скорость при 0 ° C вычисляется (см. Раздел ниже) и составляет 331,3 м / с, коэффициент, использованный выше.
Это уравнение верно для более широкого диапазона температур, но все же зависит от приближения отношений теплоемкости, не зависящего от температуры, и по этой причине не будет работать особенно при более высоких температурах. Он дает хорошие прогнозы в относительно сухих, холодных условиях низкого давления, таких как стратосфера Земли. Уравнение не работает при низких давлениях и коротких длинах волн из-за предположения, что длина волны звука в газе намного больше, чем средняя длина свободного пробега между столкновениями молекул газа. Вывод этих условий будет дан в следующем разделе.
График, на котором сравниваются результаты двух соотношений справа, с немного другим размером 331,5 м / с для скорости звука при 0 ° C.
Подробности
Скорость звука в идеальных газах и воздухе
Для идеального газа K (модуль объемной упругости в уравнениях выше, эквивалентный C, коэффициент жесткости в твердых телах) определяется как
- K = γ ⋅ p, { displaystyle K = gamma cdot p,}
таким образом, из уравнения Ньютона — Лапласа, приведенного выше, скорость звука в идеальном газе определяется как
- c = γ ⋅ p ρ, { displaystyle c = { sqrt { gamma cdot {p over rho}}},}
, где
- γ — индекс адиабаты, также известный как коэффициент изоэнтропического расширения. Это отношение удельной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме (C p / C v { displaystyle C_ {p} / C_ {v}}
) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;
- p равно давление ;
- ρ — это плотность.
. Используя закон идеального газа для замены p на nRT / V, и заменяя ρ на nM / V, уравнение для идеального газа становится
- cideal = γ ⋅ p ρ = γ ⋅ R ⋅ TM = γ ⋅ K ⋅ T м, { displaystyle c _ { mathrm {ideal}} = { sqrt { gamma cdot {p over rho}}} = { sqrt { gamma cdot R cdot T over M }} = { sqrt { gamma cdot k cdot T over m}},}
где
- cидеально — скорость звука в идеальном газе ;
- R (приблизительно 8, 314463 Дж · К · моль) — молярная газовая постоянная (универсальная газовая постоянная);
- k — постоянная Больцмана ;
- γ (гамма) — индекс адиабаты. При комнатной температуре, когда тепловая энергия полностью распределяется на вращение (полностью возбуждаются), но квантовые эффекты предотвращают возбуждение колебательных мод, согласно кинетической теории составляет 7/5 = 1.400 для двухатомных молекул. Гамма фактически измеряется экспериментально в диапазоне от 1,3991 до 1,403 при 0 ° C для воздуха. Гамма составляет точно 5/3 = 1,6667 для одноатомных газов, таких как благородные газы, и приблизительно 1,3 для газов с трехатомными молекулами;
- T — абсолютная температура;
- M — молярная масса газа. Средняя молярная масса для сухого воздуха составляет около 0,028 964,5 кг / моль;
- n — число молей;
- m — масса отдельной молекулы.
Некоторые другие условия, отмеченные как указано ниже, представлены некоторые другие условия, определенные ниже. Было обнаружено, что расчетные значения для c воздуха незначительно отличаются от экспериментально значения.
Ньютон, как известно, считал скорость звука до большей части разработки термодинамики и т. Д. неправильно использовались изотермические вычисления вместо адиабатических. В его отсутствовал коэффициент γ, но в остальном он был правильным.
Численная замена приведенных выше значений дает идеальное газовое приближение скорости звука для газов, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне Земли на уровне моря). Кроме того, для двухатомных газов использование γ = 1,4000 требует, чтобы газ существовал в достаточно высоком температурном диапазоне, чтобы вращательная теплоемкость была полностью возбуждена (т.е. вращение молекул полностью использовалось в качестве «перегородки» или резервуара тепловой энергии); Но в то же время должна быть достаточно низкая, чтобы колебательные моды не вносили свой вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, так как все колебательные квантовые моды выше моды минимальной энергии имеют слишком высокую энергию, заселить значительное количество молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температуре значительно ниже комнатной (см. Таблицы ниже). См. Раздел о газах в удельной теплоемкости для более полного обсуждения этого явления.
Для воздуха вводим сокращение
- R ∗ = R / M a i r. { displaystyle R _ {*} = R / M _ { mathrm {air}}.}
Кроме того, мы переключаемся на температуру по Цельсию ϑ { displaystyle vartheta}
- cair = γ ⋅ R ∗ ⋅ T = γ ⋅ R ∗ ⋅ (ϑ + 273.15), { displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R_ { *} cdot T}} = { sqrt { gamma cdot R _ {*} cdot ( vartheta +273.15)}},}
- cair = γ ⋅ R ∗ ⋅ 273,15 ⋅ 1 + ϑ 273,15, { displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R _ {*} cdot 273.15}} cdot { sqrt {1 + { frac { vartheta} {273.15}}}},}
где ϑ { displaystyle vartheta}
Подстановка числовых значений
- R = 8,314 463 Дж / (моль ⋅ K) { displaystyle R = 8.314 , 463 ~ mathrm {J / (mol cdot K)}}
для молярная газовая постоянная в Дж / моль / Кельвин и
- M воздух = 0,028 964 5 кг / моль { displaystyle M _ { mathrm {air}} = 0,028 , 964 , 5 ~ mathrm {кг / моль}}
для средней молярной массы воздуха в кг; и используя идеальное значение двухатомного газа γ = 1,4000, мы имеем
- c a i r = 331,3 1 + 273,15 м / с. { displaystyle c _ { mathrm {air}} = 331.3 ~~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~ mathrm {m / s}.}
Наконец, Разложение Тейлора оставшегося квадратного корня в ϑ { displaystyle vartheta}
- cair = 331,3 (1 + ϑ 2 ⋅ 273,15) м / с, { displaystyle c _ { mathrm {air}} = 331,3 ~ (1 + { frac { vartheta} {2 cdot 273.15}}) ~~~ mathrm {m / s},}
- cair = ( 331,3 + 0,606 ⋅ ϑ) РС. { displaystyle c _ { mathrm {air}} = (331.3 + 0.606 cdot vartheta) ~~~ mathrm {m / s}.}
Приведенный выше вывод включает первые два уравнения, приведенные в «Практической формуле для сухого воздуха »выше.
Эффекты сдвига ветра
Скорость звука зависит от температуры. Временная температура и скорость звука обычно снижаются от высоты, звук преломляется вверх, вдали Сдвиг ветра 4 м / (с · км) может вызвать рефракцию, равную типичную температуру градиент 7,5 ° C / км, слушателей на земле, создаваемая акустическая тень. Более высокие значения градиента ветра преломлять звук вниз к поверхности в подветренном направлении, устраняя акустическую тень на подветренной стороне.>
Для распространения звука экспоненциальное изменение скор ости ветра с высотой можно определить следующим образом:
- U (h) = U (0) h ζ, { Displaystyle U (час) = U (0) час ^ { zeta},}
- d U d H (час) = ζ U (час) час, { displaystyle { frac { mathrm {d} U} { mathrm {d} H}} (h) = zeta { frac {U (h)} {h}},}
где
- U (h) — скорость ветра при высоте h;
- ζ — экспоненциальный коэффициент, основанный на шероховатости поверхности земли, обычно от 0,08 до 0,52;
- dU / dH (h) — ожидаемый градиент ветра на высоте h.
В 1862 г. Гражданской войны в США Битва при Юке акустическая тень, усиленная северо-восточным ветром, удерживала две дивизии солдат Союза вне боя, потому что они могли не слышно звуков боя только в 10 км по ветру.
Таблицы
В стандартной атмосфере :
- T0составляет 273,15 K (= 0 ° C = 32 ° F), что дает теоретическое значение 331,3 м / с (= 1086,9 фут / с = 1193 км / ч = 741,1 миль / ч = 644,0 узлов ). Однако значения в диапазоне от 331,3 до 331,6 м / с можно найти в справочной литературе;
- T20равно 293,15 K (= 20 ° C = 68 ° F), что дает значение 343,2 м / с (= 1126,0 фут / с = 1236 км / ч = 767,8 миль / ч = 667, 2 kn );
- T25равно 298,15 K (= 25 ° C = 77 ° F), что дает значение 346,1 м / с (= 1135,6 фут / с = 1246 км / ч = 774,3 миль / ч = 672,8 kn ).
Фактически, предполагаемая идеальный газ, скорость звука зависит только от температуры, не от давления или плотности (они изменяются в шаг Воздух — почти идеальный газ. Температура воздуха меняется с высотой, что дает следующие изменения скорости звука при стандартных стандартах — фактические условия могут отличаться.
| Температура. T (°C ) | Скорость звука. c (m /s ) | Плотность воздуха. ρ (kg /m ) | Характеристическое удельное акустическое сопротивление. z0(Pa ·s /m ) |
|---|---|---|---|
| 35 | 351,88 | 1.1455 | ) 403,2 |
| 30 | 349.02 | 1.1644 | 406,5 |
| 25 | 346,13 | 1,1839 | 409,4 |
| 20 | 343,21 | 1,2041 | 413,3 |
| 15 | 340,27 | 1,2250 | 416,9 |
| 10 | 337,31 | 1,2466 | 420,5 |
| 5 | 334,32 | 1,2690 | 424,3 |
| 0 | 331,30 | 1,2922 | 428,0 |
| −5 | 328,25 | 1.3163 | 432,1 |
| −10 | 325.18 | 1.3413 | 436,1 |
| -15 | 322,07 | 1,3673 | 440,3 |
| −20 | 318.94 | 1,3943 | 444,6 |
| −25 | 315,77 | 1,4224 | 449,1 |
При нормальных атмосферных условиях, температуре и, следовательно, скорости звука, зависит от высоты:
| Высота | Температура | м / с | км / ч | миль / ч | kn |
| Уровень моря | 15 ° C (59 ° F) | 340 | 1,225 | 761 | 661 |
| 11000 м − 20 000 м. (крейсерская высота коммерческих самолетов,. и первый сверхзвуковой полет ) | -57 ° C (-70 ° F) | 295 | 1062 | 660 | 573 |
| 29000 м ( Полет X-43A ) | -48 ° C (-53 ° F) | 30 1 | 1,083 | 673 | 585 |
Влияние частоты и состава газа
Общие физические соображения
Среда, в которой звук распространяющаяся волна не всегда реагирует адиабатически, и в результате скорость звука может изменяться с частотой.
Ограничения концепции скорости звука из-за чрезмерного затухания также вызывают озабоченность. Затухание, которое существует на уровне моря для высоких частот, применяется к последовательно более низким частотам по мере уменьшения атмосферного давления или увеличения средней длины свободного пробега. По этой причине концепция скорости звука (за исключением частот, приближающихся к нулю) постепенно теряет свой диапазон применимости на больших высотах. Стандартные уравнения для скорости звука применимы с разумной точностью только к ситуациям, в которых длина звуковой волны значительно больше, чем длина свободного пробега молекул в газе.
Молекулярный состав газа влияет как на массу (M) молекул, так и на их теплоемкость, и поэтому оба фактора влияют на скорость звука. В общем, при той же молекулярной массе одноатомные газы имеют немного более высокую скорость звука (более чем на 9%), потому что у них более высокая γ (5/3 = 1,66…), чем у диатомовых (7/5 = 1,4). Таким образом, при той же молекулярной массе скорость звука одноатомного газа возрастает в
- раз, одноатомный газ, двухатомный = 5/3 7/5 = 25 21 = 1,091… { displaystyle {c _ { mathrm {газ, одноатомный}} over c _ { mathrm {газ, двухатомный}}} = { sqrt {{5/3} over {7/5}}} = { sqrt {25 over 21}} = 1.091 ldots}
Это дает разницу в 9% и будет типичным соотношением скоростей звука при комнатной температуре в гелии vs. дейтерий, каждый с молекулярной массой 4. Звук в гелии распространяется быстрее, чем в дейтерии, потому что адиабатическое сжатие нагревает гелий больше, поскольку молекулы гелия могут накапливать тепловую энергию от сжатия только при поступательном движении, но не при вращении. Таким образом, молекулы гелия (одноатомные молекулы) быстрее перемещаются в звуковой волне и быстрее передают звук. (Звук распространяется со скоростью примерно 70% от средней молекулярной скорости в газах; этот показатель составляет 75% в одноатомных газах и 68% в двухатомных газах).
Обратите внимание, что в этом примере мы предположили, что температура достаточно низкая, чтобы на теплоемкость не влияла молекулярная вибрация (см. теплоемкость ). Однако вибрационные режимы просто вызывают гаммы, которые уменьшаются до 1, поскольку колебания в многоатомном газе дают дополнительные возможности хранения тепла, которые не влияют на скорость молекулы и скорость звука. Таким образом, влияние более высоких температур и колебательной теплоемкости увеличивает разницу между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.
Практическое применение к воздуху
Безусловно, важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню из абсолютной температуры, что дает увеличение примерно на 0,6 м / с на градус Цельсия. По этой причине высота звука музыкального духового инструмента создается с помощью его температуры.
Скорость звука увеличивается из-за газа, но уменьшается из-за углекислого газа. Разница между влажностью 0% и 100% составляет около 1,5 м / с при стандартном давлении и температуре, но величина эффекта зависит от температуры. Содержание углекислого газа в воздухе не фиксировано как из-за загрязнения углерода, так и из-за человеческого дыхания (например, в воздухе, продуваемом духовыми инструментами).
В практических приложениях зависимости от частоты и давления обычно незначительна. В сухом воздухе скорость звука увеличивается примерно на 0,1 м / с при повышении частоты с 10 до 100 Гц. Для слышимых частот выше 100 Гц он относительно постоянен. Стандартные значения скорости звука указаны в пределе низких частот, где длина волны больше по сравнению со средней длиной свободного пробега.
Как показано выше, приблизительное значение 1000/3 = 333,33… м / с точно ниже 5 ° C и приблизительное для всех «обычных» наружных температур (по крайней мере, в умеренном климате)), отсюда обычное практическое правило для определения того, как далеко ударила молния: отсчитывайте секунды от начала вспышки молнии до начала применения раскатки грома и раздела на 3: результат — расстояние в километрах до ближайшей точки удара молнии.
Число Маха

Число Маха, полезная величина в аэродинамике, это отношение воздуха 342>скорость до качества Однако летательные аппараты летательных аппаратов перепад давления для вычислений числа Маха, а не Температура, следовательно, стандартная температура, благодаря чему давление за усилием, воспринимаемое трубкой Пито, также зависит от высоты как скорость.
Экспериментальные методы
Существуют
Самая ранняя достаточно точная оценка скорости звука в воздухе была сделана Уильямом Д ерхемом и подтвержден Исааком Ньютоном. У Дерхама был телескоп на вершине башни церкви Святого Лаврентия в Апминстере, Англия. анные карманные часы по помощнику, который стрелял из дробовика заранее определенное время с заметной точки за несколько миль от дома, через сельскую местность. Это может быть подтверждено телескопом. Затем он измерил интервал между появлением дыма и появлением звука с помощью полусекундного маятника. Расстояние от места выстрела определялось путем триангуляции, а простое деление (расстояние / время) давало скорость. Наконец, проведя множество наблюдений с использованием различных измерений, можно усреднить неточность полусекундного маятника, давшую окончательную оценку скорости звука. Современные секундомеры позволяют использовать этот метод сегодня на коротких расстояниях от 200 до 400 метров, и при этом не требуется что-то более громкое, чем дробовик.
Методы однократной синхронизации
Самая простая концепция — это измерение, выполняемое с использованием двух микрофонов и устройства быстрой записи, такого как цифровой объем памяти.. В этом методе используется следующая идея.
Если источник звука и два микрофона расположены по прямой линии звука на одном конце, то можно измерить следующее:
- Расстояние между микрофонами (x), называемое основанием микрофона.
- Время прихода между сигналами (задержка), достигающими разных микрофонов (t).
Тогда v = x / t.
Другие методы
В этом методе измерения времени было заменено измерением, обратным времени (частота ).
Трубка Кундта — пример эксперимента, который можно использовать для измерения скорости звука в небольшом объеме. Его преимущество состоит в том, что он может измерять скорость звука в любом газе. В этом методе используется порошок, чтобы сделать узлы и пучности видимыми для человеческих глаз. Это пример компактной экспериментальной установки.
A камертон можно удерживать возле горловины длинной трубы, которая погружается в бочку с водой. В этой системе труба может быть приведена в резонанс, если длина столба воздуха в трубе равна (1 + 2n) λ / 4, где n — целое число. точка антиузла для труб на открытом воздухе находится немного за пределами устья трубы, а затем измерить половину длины волны между ними.
Здесь v = fλ.
Высокоточные измерения в воздухе
Влияние примесей может быть значительным при проведении высокоточных измерений. Химические осушители можно использовать для осушения воздуха, но они, в свою очередь, загрязняют образец. Воздух можно осушить криогенным способом, но это также приведет к удалению углекислого газа; поэтому многие высокоточные измерения выполняются с воздухом, свободным от углекислого газа, а не с естественным воздухом. Обзор 2002 года показал, что измерение Смита и Харлоу в 1963 году с использованием цилиндрического резонатора дало «наиболее вероятное значение стандартной скорости звука на сегодняшний день». Эксперимент проводился с воздухом, из которого был удален углекислый газ, но результат был скорректирован с учетом этого эффекта, чтобы его можно было применить к реальному воздуху. Эксперименты проводились при 30 ° C, но с поправкой на температуру, чтобы сообщить о них при 0 ° C. Результат составил 331,45 ± 0,01 м / с для сухого воздуха в STP для частот от 93 Гц до 1500 Гц.
Негазообразные среды
Скорость звука в твердых телах
Трехмерные твердые тела
В твердом теле имеется ненулевая жесткость как для объемных деформации и деформации сдвига. Следовательно, можно генерировать звуковые волны с разными скоростями в зависимости от режима деформации. Звуковые волны, вызывающие объемные деформации (сжатие) и сдвиговые деформации (сдвиг), называются волнами давления (продольными волнами) и поперечными волнами (поперечными волнами) соответственно. В землетрясениях соответствующие сейсмические волны называются P-волнами (первичными волнами) и S-волнами (вторичными волнами) соответственно. Скорости звука этих двух типов волн, распространяющихся в однородном трехмерном твердом теле, соответственно задаются как
- csolid, p = K + 4 3 G ρ = E (1 — ν) ρ (1 + ν) (1-2 ν), { displaystyle c _ { mathrm {solid, p}} = { sqrt { frac {K + { frac {4} {3}} G} { rho}}} = { sqrt { гидроразрыв { E (1- nu)} { rho (1+ nu) (1-2 nu)}}},}
- csolid, s = G ρ, { displaystyle c _ { mathrm {solid, s}} = { sqrt { frac {G} { rho}}},}
где
- K — модуль объемной упругости упругих материалов;
- G — модуль сдвига упругих материалов;
- E — модуль Юнга; ;
- ρ — плотность;
- ν — Коэффициент Пуассона.
Последняя величина не является независимой, так как E = 3K (1 — 2ν). Обратите внимание, что скорость волн давления зависит как от давления, так и от свойств сопротивления сдвигу материала, в то время как скорость волн зависит от свойств сдвига.
Обычно волны давления распространяются в материалах быстрее, чем поперечные волны, и при землетрясениях это причина того, что начало землетрясения часто предшествует быстрый толчок, направленный вверх-вниз, до прихода волн, которые производят из стороны в сторону. Например, для типичного стального сплава K = 170 ГПа, G = 80 ГПа и ρ = 7700 кг / м, что дает скорость сжатия c твердого тела, p 6000 м / с. Это разумно согласуется с c solid, p, измеренным экспериментально при 5930 м / с для (возможно другого) типа стали. Скорость сдвига c solid, s оценивается в 3200 м / с с использованием тех же чисел.
Одномерные твердые тела
Скорость звука для волн давления в жестких материалах, таких как металлы, иногда указывается для длинных стержней рассматриваемого материала, в скорость легче мера. Величина давления меньше длины волны, скорость чистого давления может быть упрощена и выражена следующим образом:
- csolid = E ρ, { displaystyle c _ { mathrm {solid}} = { sqrt { frac {E } { rho}}},}
где E — модуль Юнга. Это похоже на выражение для поперечных волн, за исключением того, что модуль Юнга заменяет модуль сдвига. Эта скорость звука для волн давления в длинных стержнях всегда будет меньше той же скорости в однородных трехмерных телах, а соотношение скоростей в двух разных типах объектов зависит от коэффициента Пуассона для материала.
Скорость звука в жидкостях
В жидкости единственная ненулевая жесткость Секретари с объемной деформацией (жидкость не выдерживают поперечные силы).
Следовательно, скорость звука в жидкости определяется выражением
- cfluid = K ρ, { displaystyle c _ { mathrm {fluid}} = { sqrt { frac {K} { rho}}},}
где K — модуль объемной упругости жидкости.
Вода
В пресной воде звук распространяется со скоростью около 1481 м / с при 20 ° C (онлайн-калькуляторы см. В разделе «Внешние ссылки» ниже). Применение подводного звука можно найти в гидролокаторе, акустической связи и акустической океанографии.
морской водой

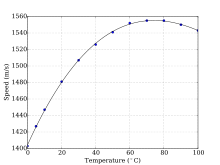
В соленой воде, не содержит пузырьков воздуха или взвешенных отложений, звук распространяется со скоростью около 1500 м / с (1500,235 м / с при 1000 килопаскалей, 10 ° C и 3% солености одним методом). Скорость звука в морской воде зависит от давления (следовательно, глубины), температуры (изменение на 1 ° C ~ 4 м / с) и солености (изменение на 1 ‰ ~ 1 м / с) с), и получены эмпирические уравнения для точного расчета скорости звука на основе этих чисел. Другие факторы, влияющие на скорость звука, незначительны. В качестве отрицательной температуры указывается, что отрицательная температура уменьшается, профиль скорости звука с глубиной уменьшается до минимума на несколько сотен метров. Ниже минимума скорость звука снова увеличивается, поскольку эффект увеличения давления преодолевает эффект снижения температуры (справа). Для получения дополнительной информации см. Dushaw et al.
Маккензи предоставил эмпирическое уравнение для скорости звука в морской воде:
- c (T, S, z) = a 1 + a 2 T + a 3 T 2 + a 4 T 3 + a 5 (S — 35) + a 6 z + a 7 z 2 + a 8 T (S — 35) + a 9 T z 3, { displaystyle c (T, S, z) = a_ {1} + a_ {2} T + a_ {3} T ^ {2} + a_ {4} T ^ {3} + a_ {5} (S-35) + a_ {6} z + a_ {7} z ^ {2} + a_ {8 } T (S-35) + a_ {9} Tz ^ {3},}
где
- T — температура в градусах Цельсия;
- S — соленость в частях на тысячу;
- z — глубина в метрах.
Константы a 1, a 2,…, A 9 равны
- a 1 = 1, 448,96, a 2 = 4,591, a 3 = — 5,304 × 10 — 2, a 4 = 2,374 × 10 — 4, a 5 = 1,340, a 6 = 1,630 × 10–2, a 7 = 1,675 × 10–7, a 8 = — 1,025 × 10–2, a 9 = — 7,139 × 10–13, { displaystyle { begin {align} a_ {1} = 1448.96, a_ {2} = 4.591, a_ {3} = — 5.304 times 10 ^ {- 2}, \ a_ {4} = 2.374 times 10 ^ {- 4}, a_ {5} = 1.340, a_ {6} = 1.630 times 10 ^ {- 2 }, \ a_ {7} = 1,675 times 10 ^ {- 7}, a_ {8} = — 1.025 times 10 ^ {- 2}, a_ {9} = — 7,139 times 10 ^ {- 13}, end {align}}}
с контрольным значением 1550,744 м / с для T = 25 ° C, S = 35 частей на тысячу, z = 1000 м. Это уравнение имеет стандартную ошибку 0,070 м / с для солености от 25 до 40 ppt. См. Технические руководства. Скорость звука в морской воде для онлайн-калькулятора.
(Примечание. График зависимости скорости звука от Deep не коррелирует напрямую с формулой МакКензи. Это связано с тем, что температура и соленость различаются на разных глубинах. Когда T и S остаются постоянными, Сама формула всегда увеличивается с глубиной.)
Другие уравнения скорости звука в морской воде точны в широком диапазоне условий, но гораздо сложнее, например, уравнение В.А. Дель Гроссо и Чена. -Уравнение Миллеро-Ли.
Скорость звука в плазме
Скорость звука в плазме для общего случая, когда электроны горячее, чем ионы (но не намного горячее) определяет формулой (см. здесь )
- cs = (γ Z K T e / mi) 1/2 = 90,85 (γ ZT e / μ) 1/2 м / с, { Displaystyle c_ {s} = ( gamma ZkT _ { mathrm {e}} / m _ { mathrm {i}}) ^ {1/2} = 90,85 ( gamma ZT_ {e} / mu) ^ {1/2} ~ mathrm {м / с},}
где
- mi- масса иона ;
- μ — отношение массы иона к протону масса μ = m i/mp;
- Teравна t he температура электрона;
- Z — состояние заряда;
- k — постоянная Больцмана ;
- γ — индекс адиабаты.
В отличие от Они связаны через колеблющееся электрическое поле.
Градиенты
Когда звук равномерно во всех направлениях в трех измерениях, его интенсивность падает пропорционально. обратному квадрату рату расстояния. В океане есть слой, называемый «глубокий канал» или канал SOFAR, который может ограничивать звуковые волны на определенной глубине.
В канале ГНФАР скорость звука ниже, чем в слоях выше и ниже. Подобно тому, как световые волны будут преломляться в направлении области с более высоким показателем , звуковые волны будут преломляться в направлении области, где их скорость уменьшается. В результате звук ограничивается слоем, так же как свет может быть ограничен листом стекла или оптическим волокном. Таким образом, звук по существу ограничен двумя измерениями. В двух измерениях интенсивность падает только обратной величине расстояния. Это позволяет волнам распространяться намного дальше, чем они становятся незаметно слабыми.
Подобный эффект происходит в атмосфере. Проект Могул успешно использовал этот эффект для обнаружения ядерного взрыва на значительном расстоянии.
См. Также
Ссылки
Внешние ссылки
Здравствуйте! Наш завершает тему «Механические колебания и волны», поэтому он будет посвящен контрольной работе. Наша контрольная работа так и называется «Механические колебания и волны. Звук». Мы рассмотрим различные задачи, посвященные этой теме. Первая задача, которую будем рассматривать, посвящена колебаниям обыкновенного нитяного маятника, звучит она следующим образом.
Задача 1
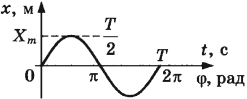
По представленному графику определите амплитуду и период колебаний нитяного маятника.
|
|
Решение: Ответ: А = 10-2 м, Т = 1 с. |
Мне бы хотелось отметить, что такого рода задачи часто встречаются в контрольных работах. Именно по графику определить характеристики колебаний. Давайте обратимся к записи, посмотрим на график и ответим на поставленный вопрос.
Итак, в данном случае график представлен на рисунке и выглядит он следующим образом. Сначала мы должны отметить точку равновесия. В данной точке тело когда находилось, оно находилось в положении равновесия. Дальше начинается движение маятника. С течением времени у нас смещение произошло сначала в одну сторону, затем в другую. Таким образом, мы представляем себе движение маятника в сочетании с осью времени. Мы знаем, что амплитудой является максимальное смещение от положения равновесия. Посмотрите, в данном случае смещение произошло на 1, на 1 в одну сторону относительно положения равновесия. И относительно положения равновесия в другую сторону тоже на 1. Если вы посмотрите, то смещение, обозначенное буквой х, измеряется в сантиметрах. По всему представленному графику смещение в данном случае максимальное постоянно, равно 1, т.е. 1 см. Это и есть амплитуда колебаний. Обратите внимание: необходимо сразу записать, что А = 1 см, или в системе интернациональной А = 1 см = 10-2 м.
Чтобы определить период колебаний, нам надо рассмотреть все колебания, представленные на этом графике. Что такое одно полное колебание? Это когда тело сходило в противоположную точку и вернулось обратно. Этот промежуток времени будет соответствовать периоду колебаний маятника. Таких движений за указанное время маятник совершил 2, таким образом, мы должны отметить, что число колебаний равно 2, а время этих колебаний составляет 2 с. Воспользуемся уравнением для определения периода колебаний: .
Обязательно необходимо записать ответ этой задачи. Ответ: А = 10-2 м, Т = 1 с.
Следующая задача, которую мы будем разбирать, – задача, посвященная колебаниям пружинного маятника. Звучит текст этой задачи следующим образом.
Задача 2
Пружинный маятник совершил за 4 с 16 полных колебаний. Необходимо определить период и частоту колебаний этого маятника.
Давайте посмотрим на краткую запись этой задачи и рассмотрим ее решение. Посмотрите, краткое условие следующее.
| Дано: | Решение: |
| N =16 |
Ответ: Т = 0,25 с, ν = 4 Гц. |
| t = 4 c | |
|
Найти: n — ? T — ? |
Решение этой задачи тоже достаточно простое. Мы воспользуемся уравнением, которое дает возможность определить период, тем более, что мы рассматривали его уже в предыдущей задаче – .
.
Что касается частоты, то в данном случае мы можем воспользоваться не одной, а двумя формулами. По выбору, кому какая формула больше нравится, как удобней вычислять эту величину. Можно воспользоваться уравнением, которое связывает у нас частоту и период. Посмотрите, мы записали это уравнение: . А мы определим частоту, используя те данные, которые у нас есть, т.е. формулу используем определения частоты
.
Обязательно надо сказать об ответе. Ответ: Т = 0,25 с, ν = 4 Гц.
Здесь мне бы хотелось обратить внимание на одну особенность, соответствующую механическим колебаниям. В данном случае получается довольно любопытная ситуация, что если мы частоту умножим на период, то получим 1. Обратите внимание на то, что для механических колебаний это довольно характерная особенность.
Следующая задача, которую мы рассмотрим, будет посвящена волнам. В данном случае условие задачи звучит следующим образом.
Задача 3
Длина океанической волны составляет 270 м, период составляет 13,5 с. Определите скорость распространения волн.
Такая задача, связанная с механическими волнами, в частности, с волнами океаническими. Давайте посмотрим на запись и на ее решение. Она тоже не будет представлять собой какой-либо сложности. Конечно, при условии, что мы помним уравнение для вычисления указанных величин. Итак, посмотрите.
| Дано: | Решение: |
| l = 270 м |
Ответ:
|
| Т = 13,5 с | |
|
Найти: V = ? |
Если мы помним, что надо определить скорость распространения волн, то в решении мы должны записать следующее уравнение: V = l * ν. Рассматривая вот это уравнение, мы можем записать следующее: скорость распространения волны может быть определена как . Если вместо частоты мы подставим выражение
, то получим уравнение, которое здесь записано:
. Подставляя теперь цифры, мы получим
. Обратите внимание на запись ответа. Ответ:
. Тоже хотелось бы обратить ваше внимание на то, какова скорость распространения океанических волн. Ведь
= 72 км/ч. Так что обратите внимание, какая величина этой скорости.
Следующая задача, которую мы рассмотрим, относится к звуковым волнам. Текст задачи звучит следующим образом.
Задача 4
Определите, во сколько раз будет отличаться длина звуковой волны при переходе из воздуха в воду. Считать, что скорость распространения звука в воздухе 340 м/с, в воде 1450 м/с.
Давайте посмотрим на краткую запись и на решение задачи. Посмотрите, в данном случае условие небольшое.
| Дано: | Решение: |
|
ν1 = ν2 Т1 = Т2
Ответ: n ≈ 4,3 раза. |
|
|
Найти: |
Определить нам надо, во сколько раз изменилась длина волны при переходе. Надо разделить длину волны в воде к длине волны в воздухе. Итак, что предпримем? Обращаю внимание, что здесь после слова «решение» написано достаточно важное выражение ν1 = ν2. Когда мы обсуждали это явление, мы говорили, что волна переходит из одной среды в другую, но при этом сохраняется частота колебаний. Меняется, скорость меняется, длина волны меняется, а частота колебания частиц остается прежней. Посмотрите, в данном случае мы записываем, что частота колебаний частиц волны в воздухе ν1 = ν2 частоте колебаний частиц, которые составляют волну в воде. Обратите внимание: если частоты равны, то будут равны и периоды колебаний этих частиц ν1 = ν2 Þ Т1 = Т2. Дальше, мы используем уравнение, которое нам встречалось в предыдущей задаче
l= V * Т. Записываем длину волны для воздуха l1 = V1 * Т и для воды l2 = V2 * Т. Почему в данном случае мы обозначили период Т и Т, т.е. без индексов? Разговор идет о том, что периоды у нас одинаковые, поэтому мы их обозначили одной величиной, одной буквой. Теперь разделим .
В этом случае период колебаний сократится, и мы получаем значение отношения длин волн .
Мы обозначили это отношение буквой n и в ответе записываем следующее, что n≈4,3 раза. Во столько будет отличаться длина волны.
Следующая задача, которую мы рассмотрим, будет посвящена также звуку, и мы должны обязательно рассмотреть вопрос, связанный с эхом. Итак, условия задачи следующие.
Задача 5
В результате выстрела было услышано эхо через 20 с после произведенного выстрела. Определите расстояние до преграды, если скорость звука составляла . В данной задаче мы должны учесть, что эхо – это отраженная волна, значит, звук дошел до преграды и вернулся обратно к наблюдателю, т.е. как раз в то место, где и был произведен выстрел. Итак, давайте посмотрим на решение задачи. Посмотрите, пожалуйста, мы запишем, что время от момента выстрела до того момента, когда было услышано эхо, 20 с. Скорость звука
составляло. Определить надо расстояние S до преграды.
| Дано: | Решение: |
| t = 20 c |
S1 = V * t; Ответ: S=3400 м = 3,4 км. |
|
Найти: S — ? |
Давайте определимся с тем, что именно за это время, за 20 с, волна прошла определенное расстояние. Это расстояние мы определим простым способом: как расстояние, пройденное телом за определенное время с постоянной скоростью. В данном случае у нас волна, поэтому мы определяем S1 = V * t, полное расстояние, прошедшее волной. Теперь мы должны отметить то, что это расстояние мы должны разделить обязательно пополам, . Почему? Дело в том, что эхо – это отраженная волна. Значит, волна звуковая дошла до преграды и вернулась обратно, следовательно,
. Теперь подставив сюда значение для вычисления
, мы получаем расстояние до преграды
.
Ответ, который мы здесь запишем: S=3400 м = 3,4 км. Расстояние достаточно большое, но выстрел – это достаточно громкий звук, и интенсивности его хватит, чтобы дойти до преграды и вернуться обратно.
В заключение контрольной работы мы рассмотрим задачу из ЕГЭ. Условие будет таким. Указан маятник, который совершает колебания между точками 1 и 3, как показано на рисунке. Надо определить, в каких точках кинетическая энергия маятника является минимальной. Обращаю ваше внимание, что эта задача связана с превращением энергии при колебательных процессах. Такая задача и выбирается в ЕГЭ. Давайте посмотрим на это условие и решим эту задачу.
Задача 6
В каких точках кинетическая энергия маятника является минимальной?
Рисунок
1. В точках 1 и 2.
2. В точках 1 и 3.
3. В точках 2 и 3.
4. Во всех точках одинаково.
Ответ: пункт 2.
Во-первых, нам надо рассмотреть сам рисунок. Представленный рисунок указывает цифру 2 – это положение равновесия нитяного маятника. И две крайних точки, точка 1 и 3. В условии задачи сказано, что именно между точками 1 и 3 совершаются колебания маятника. Дальше представлены 4 ответа. В каждом – определенный вид ответа, нам надо выбрать правильный. Давайте обсудим это решение. Кинетическая энергия – это энергия движения. Стало быть, это энергия тела в тот момент, когда тело обладает скоростью. В данном случае тело в точке 1 и в точке 3 на некоторую долю секунды замирает и обладает только потенциальной энергией относительно выбранной системы отсчета. Так что в точке 1 и 3 кинетическая энергия будет минимальна, т.е. она будет равна 0. Мы должны выбрать ответ из указанных, там, где именно эти цифры. Посмотрите, в первом ответе говорится точка 1 и 2, вторая точка в данном случае не подходит. Второй ответ: в точках 1 и 3. Соответствует правильному ответу. Ответ так и надо записать: пункт 2. Если мы посмотрим в пункт 3, там указывается точка 2 и 3, и в последнем, четвертом, говорится, что везде энергия одинакова. Конечно, эти ответы являются в данном случае неправильными.
Итак, мы рассмотрели контрольную работу, вариант контрольной работы, и следующий урок будет посвящен новой теме – электромагнитным явлениям. Тема закончена. До свидания.
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?
Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?
Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?
Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.
Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.
Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.
Краткая теория для решения Задачи на Механические волны.
Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Механические колебания и волны
Механические колебания – периодически повторяющееся перемещение материальной точки, при котором она движется по какой-либо траектории поочередно в двух противоположных направлениях относительно положения устойчивого равновесия.
Отличительными признаками колебательного движения являются:
- повторяемость движения;
- возвратность движения.
Для существования механических колебаний необходимо:
- наличие возвращающей силы – силы, стремящейся вернуть тело в положение равновесия (при малых смещениях от положения равновесия);
- наличие малого трения в системе.
Механические волны – это процесс распространения колебаний в упругой среде.
Содержание
- Виды волн
- Гармонические колебания
- Амплитуда и фаза колебаний
- Период колебаний
- Частота колебаний
- Свободные колебания (математический и пружинный маятники)
- Вынужденные колебания
- Резонанс
- Длина волны
- Звук
- Основные формулы по теме «Механические колебания и волны»
Виды волн
- Поперечная – это волна, в которой колебание частиц среды происходит перпендикулярно направлению распространения волны.
Поперечная волна представляет собой чередование горбов и впадин.
Поперечные волны возникают вследствие сдвига слоев среды относительно друг друга, поэтому они распространяются в твердых телах.
- Продольная – это волна, в которой колебание частиц среды происходит в направлении распространения волны.
Продольная волна представляет собой чередование областей уплотнения и разряжения.
Продольные волны возникают из-за сжатия и разряжения среды, поэтому они могут возникать в жидких, твердых и газообразных средах.
Важно!
Механические волны не переносят вещество среды. Они переносят энергию, которая складывается из кинетической энергии движения частиц среды и потенциальной энергии ее упругой деформации.
Гармонические колебания
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:
где ( x ) – координата тела – смещение тела от положения равновесия в данный момент времени; ( A ) – амплитуда колебаний; ( omega t+varphi_0 ) – фаза колебаний; ( omega ) – циклическая частота; ( varphi_0 ) – начальная фаза.
Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.
Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.
Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:
где ( v ) – мгновенное значение скорости, т. е. скорость в данный момент времени.
Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:
Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:
где ( a ) – мгновенное значение ускорения, т. е. ускорение в данный момент времени.
Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:
Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:
где ( F ) – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.
Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:
Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:
где ( W_k ) – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.
Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:
При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:
- потенциальная энергия равна нулю;
- кинетическая энергия максимальна.
При максимальном отклонении от положения равновесия:
- кинетическая энергия равна нулю;
- потенциальная энергия максимальна.
Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:
Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы.
Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.
Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).
Амплитуда и фаза колебаний
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия.
Обозначение – ( A, (X_{max}) ), единицы измерения – м.
Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени.
Обозначение – ( varphi ), единицы измерения – рад (радиан).
Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний.
Фаза гармонических колебаний в процессе колебаний изменяется.
( varphi_0 ) – начальная фаза колебаний.
Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.
Важно!
Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.
Период колебаний
Период колебаний – это время одного полного колебания.
Обозначение – ( T ), единицы измерения – с.
Период гармонических колебаний – постоянная величина.
Частота колебаний
Частота колебаний – это число полных колебаний в единицу времени.
Обозначение – ( nu ), единицы времени – с-1 или Гц (Герц).
1 Гц – это частота такого колебательного движения, при котором за каждую секунду совершается одно полное колебание:
Период и частота колебаний – взаимно обратные величины:
Циклическая частота – это число колебаний за 2π секунд.
Обозначение – ( omega ), единицы измерения – рад/с.
Свободные колебания (математический и пружинный маятники)
Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.
Условия возникновения свободных колебаний:
- при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
- силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.
При наличии сил трения свободные колебания будут затухающими.
Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.
Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.
Период колебаний математического маятника:
Частота колебаний математического маятника:
Циклическая частота колебаний математического маятника:
Максимальное значение скорости колебаний математического маятника:
Максимальное значение ускорения колебаний математического маятника:
Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:
Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:
Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:
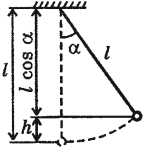
Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту ( h ), определяется по формуле:
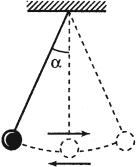
где ( l ) – длина нити, ( alpha ) – угол отклонения от вертикали.
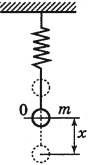
Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.
Период колебаний пружинного маятника:
Частота колебаний пружинного маятника:
Циклическая частота колебаний пружинного маятника:
Максимальное значение скорости колебаний пружинного маятника:
Максимальное значение ускорения колебаний пружинного маятника:
Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:
Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:
Важно!
Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий.
Вынужденные колебания
Вынужденные колебания – это колебания, происходящие под действием внешней периодически изменяющейся силы.
Вынужденные колебания, происходящие под действием гармонически изменяющейся внешней силы, тоже являются гармоническими и незатухающими. Их частота равна частоте внешней силы и называется частотой вынужденных колебаний.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
( v_0 ) – собственная частота колебаний маятника.
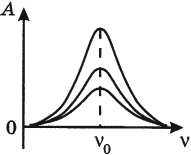
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях.
Также резонанс используется в акустике, радиотехнике и т. д.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах.
Обозначение – ( lambda ), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (( nu ) < 16 Гц);
- звуковой диапазон (16 Гц < ( nu ) < 20 000 Гц);
- ультразвук (( nu ) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.
Шум – хаотическая смесь тонов.
Основные формулы по теме «Механические колебания и волны»
Механические колебания и волны
3 (59.17%) 145 votes


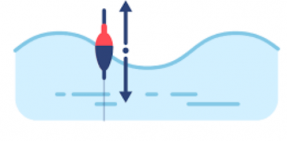

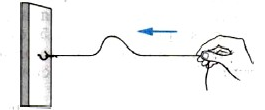
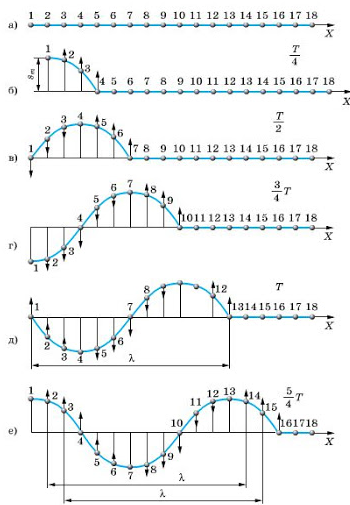
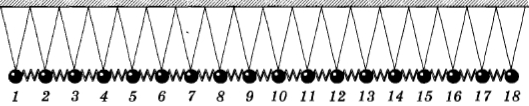
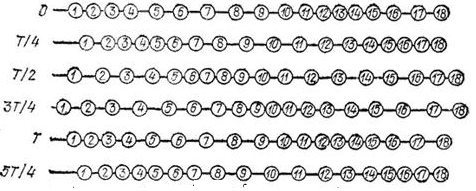
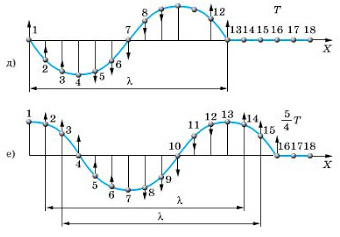
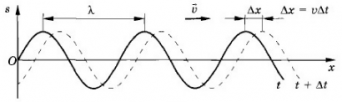
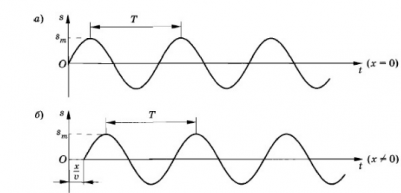

 — это плотность.
— это плотность.







 ) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;
) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, вызвать давление, вызванное этим сжатием;