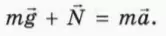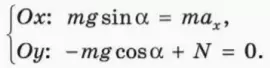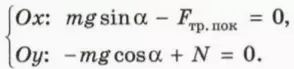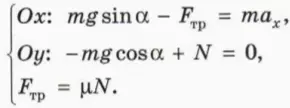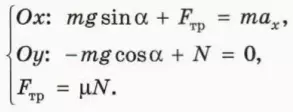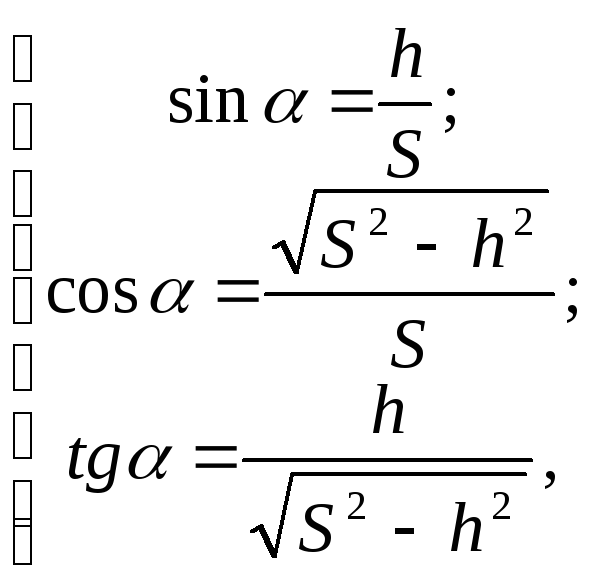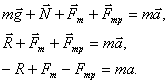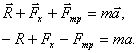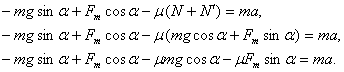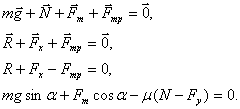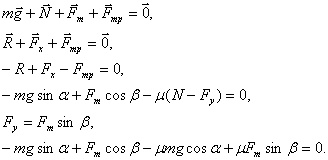Как найти время движения по наклонной плоскости

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

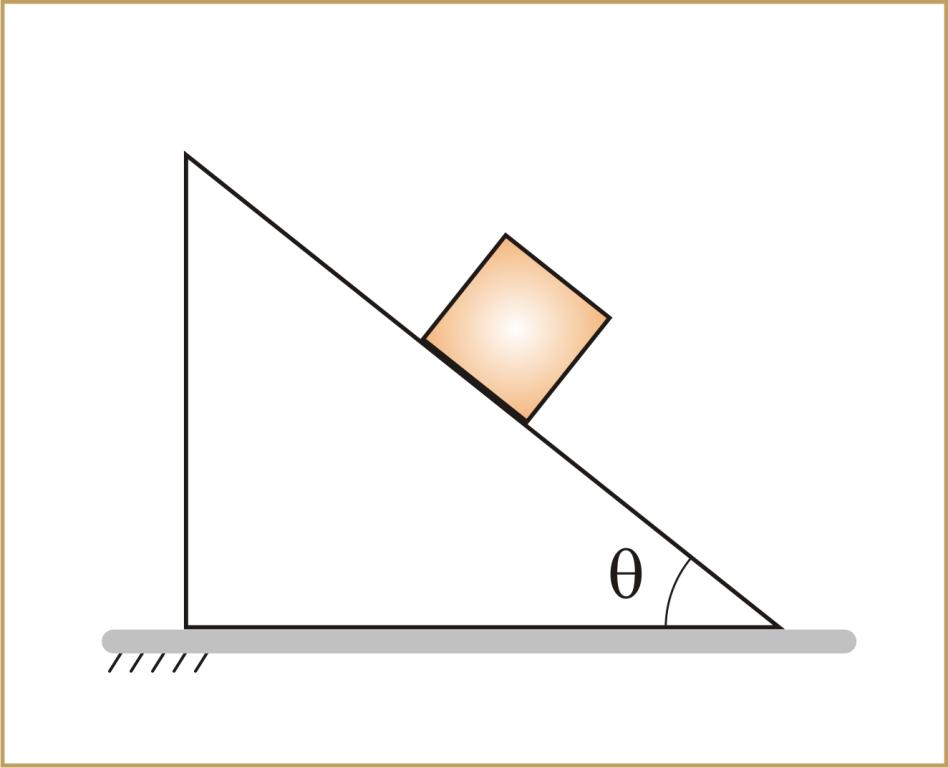
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) — F_r = m*a

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) — µ*cos(φ)) = m*a =>

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

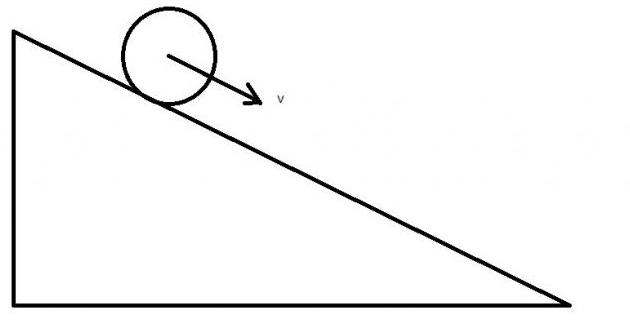
Задача со скатывающимся по плоскости цилиндром

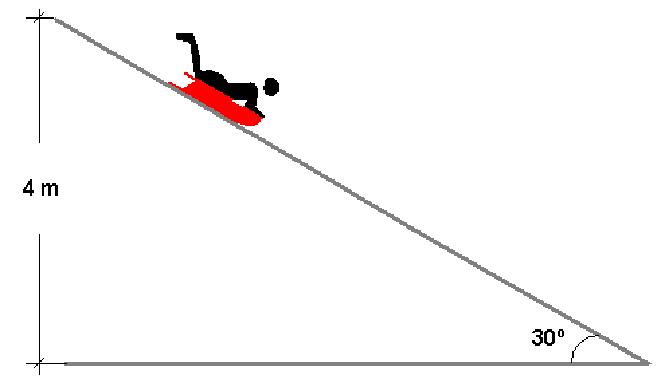
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) — F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) — 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Решение.
Для решения задачи используем закон сохранения энергии. Потенциальная энергия переходит в кинетическую энергию. Кинетическая энергия состоит из энергии поступательного движения и энергии вращательного движения.

[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{Jcdot {{omega }^{2}}}{2} (1). ]

m – масса тела которое скатывается, h – высота с которой скатывается тело (см. рис.), υ – линейная скорость тела, J – момент инерции тела, ω – угловая скорость вращения тела.
Запишем формулу нахождения высоты наклонной плоскости с которой скатывается тело

h = l∙sinα    (2).

Длину наклонной плоскости определим по формуле

[ l=frac{upsilon +{{upsilon }_{0}}}{2}cdot t,{{upsilon }_{0}}=0, l=frac{upsilon }{2}cdot t (3). ]

(3) подставим в (2) выразим скорость которую будет иметь шарик при достижении основания наклонной плоскости

[ h=frac{upsilon }{2}cdot tcdot sin alpha ,upsilon =frac{2cdot h}{tcdot sin alpha } (4). ]

Угловая скорость связана с линейной скоростью

[ omega =frac{upsilon }{R} (5). ]

Момент инерции шарика определяется по формуле

[ J=frac{2cdot mcdot {{R}^{2}}}{5} (6). ]

Подставим (6) и (5) и (4) в (1):

[ begin{align}
  & mcdot gcdot h=frac{m}{2}cdot {{(frac{2cdot h}{tcdot sin alpha })}^{2}}+frac{2cdot mcdot {{R}^{2}}cdot {{upsilon }^{2}}}{5cdot 2cdot {{R}^{2}}},mcdot gcdot h=frac{m}{2}cdot {{(frac{2cdot h}{tcdot sin alpha })}^{2}}+frac{2cdot mcdot {{R}^{2}}}{5cdot 2cdot {{R}^{2}}}cdot {{(frac{2cdot h}{tcdot sin alpha })}^{2}}, \
 & gcdot h=frac{1}{2}cdot {{(frac{2cdot h}{tcdot sin alpha })}^{2}}+frac{1}{5}cdot {{(frac{2cdot h}{tcdot sin alpha })}^{2}},g=frac{h}{2}cdot {{(frac{2}{tcdot sin alpha })}^{2}}+frac{h}{5}cdot {{(frac{2}{tcdot sin alpha })}^{2}},g={{(frac{2}{tcdot sin alpha })}^{2}}cdot (frac{h}{2}+frac{h}{5}), \
 & {{t}^{2}}=frac{1}{g}cdot {{(frac{2}{sin alpha })}^{2}}cdot frac{7cdot h}{10},t=sqrt{frac{1}{g}cdot {{(frac{2}{sin alpha })}^{2}}cdot frac{7cdot h}{10}}(7). \
 & t=sqrt{frac{1}{10}cdot {{(frac{2}{0,5})}^{2}}cdot frac{7cdot 0,3}{10}}=0,58. \
end{align} ]

Ответ: 0,58 с.

1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

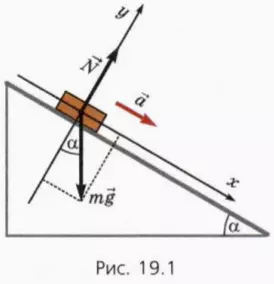
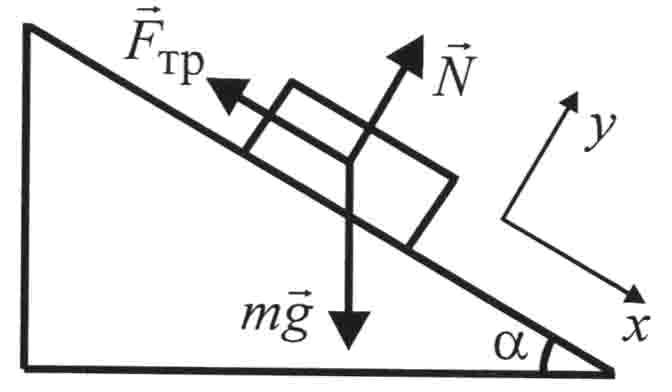
На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:

? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v₀.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя _тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

F_{тр.пок x} = –F_тр.пок

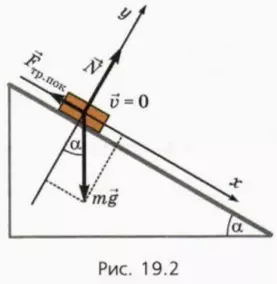
? 8. Объясните, почему справедливы следующие уравнения:

? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству F_тр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:
а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

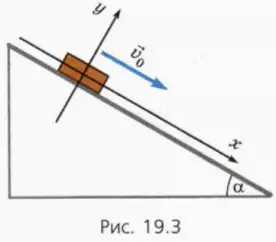
Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

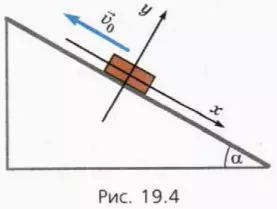
Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v₀. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?
б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

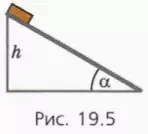
24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

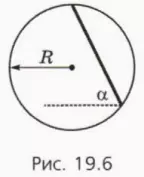
25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см. Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

ЛАБОРАТОРНАЯ
РАБОТА №
1.1

«ИЗУЧЕНИЕ ДВИЖЕНИЯ
ТЕЛ ПО НАКЛОННОЙ ПЛОСКОСТИ»

I.
Цель работы:
изучение влияния силы трения и момента
инерции на движение тел по наклонной
плоскости.

II.
Описание
установки

В комплект установки
входят: наклонная плоскость с регулируемой
высотой, миллисекундомер, набор тел
(брусок, шарик, сплошной и полый цилиндры).

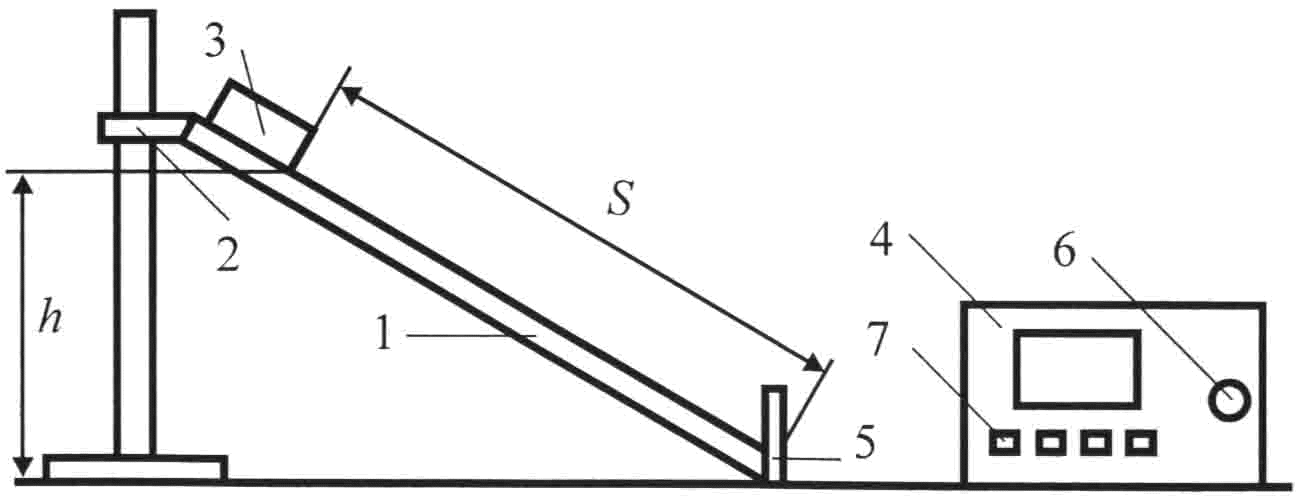
Общий вид установки
представлен на рисунке. Наклонная
плоскость представляет собой доску 1,
угол наклона которой можно варьировать,
изменяя высоту плоскости с помощью
кронштейна 2. На вершине плоскости
укреплен электромагнит 3, удерживающий
тело. Измерение времени скольжения или
скатывания проводится с помощью
миллисекундомера 4. Включение секундомера
с помощью переключателя 6 размыкает
цепь электромагнита, и тело начинает
двигаться вниз по наклонной плоскости.
При ударе скатывающегося тела о
специальную пластинку 5, расположенную
вертикально у основания наклонной
плоскости, происходит выключение
секундомера. Сняв отсчет времени по
шкале секундомера, необходимо привести
переключатель контакта 6 в исходное
положение. Клавиши секундомера 7,
отмеченные красной наклейкой, должны
быть нажаты, остальные — отжаты.

III.
Методика измерений и расчетные формулы

1. Рассмотрим тело
(брусок) массой m,
находящееся на наклонной плоскости
(см. рисунок). Угол наклона плоскости 
можно найти из следующих соотношений:

(1)

где S
— длина
наклонной плоскости; h
— ее высота, которая является переменной
величиной.

Тело будет находиться
в покое, если геометрическая сумма
действующих на него сил равна нулю:

В проекциях на оси
координат:

Если учесть, что
максимальное значение силы трения покоя
равно

то коэффициент трения покоя

можно найти из соотношения

(2)

где
—
максимальный угол, при котором тело еще
остается в покое.

Если
,
то
,
и тело будет двигаться ускоренно.
Согласно второму закону Ньютона

Если учесть, что
,
где

— коэффициент трения скольжения, то

.

Отсюда следует,
что

Величину ускорения
можно определить, если известны длина
пути S₁
и время движения t:

Путь S₁
пройденный бруском, находится из
соотношения

,

где l
— длина бруска (размер бруска вдоль
наклонной плоскости). Поэтому окончательно
коэффициент трения скольжения находим
из следующего расчетного соотношения:

(3)

Для определения
времени движения бруска по наклонной
плоскости расчетным путем можно
воспользоваться законом изменения
полной механической энергии:

где

— высота, на которую опускается центр
тяжести бруска. Поэтому учитывая, что
конечная скорость бруска при равноускоренном
движении равна

,
(4)
окончательно получаем:

(5)

2. При рассмотрении
движения скатывающихся тел (цилиндр,
шар) можно считать, что коэффициент
трения качения достаточно мал и поэтому
.
Поэтому можно воспользоваться законом
сохранения механической энергии:

(6)
где

— высота, на которую опускается центр
тяжести скатывающегося тела; r
и J —
радиус и момент инерции скатывающегося
тела. Поэтому, с учетом (6) и выражения
для конечной скорости скатывающегося
тела

(7)
получаем, что
время скатывания тел равно:

а) для сплошного
цилиндра
,
следовательно

(8)

б) для шарика ()

(9)

в) для отрезка
трубы ()

(10)

IV.
Порядок выполнения работы

Задание 1.
Определение коэффициента трения покоя

для металлической и деревянной
поверхностей бруска.

1. Положить брусок
деревянной поверхностью на наклонную
плоскость при малом угле наклона.

2. Медленно
увеличивать угол наклона плоскости до
тех пор, пока не начнется соскальзывание
бруска.

3. Измерить в этом
положении линейкой высоту h₀
наклонной плоскости.

4. Повторить п.п.
1-3 для металлической поверхности бруска.

Задание 2.
Определение коэффициента трения
скольжения

для обеих поверхностей.

1. Установить такой
угол наклона плоскости, чтобы брусок
мог двигаться равноускоренно ().

2. Измерить в этом
положении линейкой высоту h
наклонной плоскости.

3. Проверить
правильность установки клавиш секундомера
(см. раздел II).
Включить секундомер, нажав клавишу
«Питание».

4. Установить брусок
деревянной поверхностью на наклонной
плоскости так, чтобы он удерживался
электромагнитом.

5. Нажав клавишу
«Пуск», определить по секундомеру
время скольжения бруска t_on.
Опыт повторить 3-5 раз (не забывая приводить
секундомер в исходное состояние).

6. Повторить п.п.
1-5 для металлической поверхности бруска.

Задание 3.
Определение времени движения скатывающихся
тел.

1. Установить высоту
наклонной плоскости меньше, чем в
предыдущем задании.

2. Измерить в новом
положении линейкой высоту h
наклонной плоскости.

3. Проверить
правильность установки клавиш секундомера
(см. раздел II).
Включить секундомер, нажав клавишу
«Питание».

4. Установить шар
на наклонной плоскости так, чтобы он
удерживался электромагнитом.

5. Нажав клавишу
«Пуск», определить по секундомеру
время скатывания шара t_on.
Опыт повторить 3-5 раз (не забывая приводить
секундомер в исходное состояние).

6. Повторить п.п.
4-5 для сплошного и полого цилиндров.

V.
Таблицы измерений

1. Данные установки:

Длина наклонной
плоскости S
= (500±0,5) мм

Длина бруска l
= (60±0,5) мм

Радиус шара r
= (11,5±0,5) мм

Радиус сплошного
цилиндра r
=(10±0,5) мм

Радиус полого
цилиндра r
=(10±0,5) мм

2. Определение
коэффициента трения покоя. Высота
наклонной плоскости:

Деревянная
поверхность h₀
=

Металлическая
поверхность h₀
=

3. Определение
коэффициента трения скольжения.

Высота наклонной
плоскости h
=

Результаты измерений
внести в таблицу:

№ опыта	Деревянная поверхность	Металлическая поверхность
t, c	t, c
Средние значения

4. Определение
времени движения скатывающихся тел.

Высота наклонной
плоскости h
=

Результаты измерений
внести в таблицу:

№ опыта	Шар	Сплошной цилиндр	Полный цилиндр
t, c	t, c	t, c
Средние значения

VI.
Обработка результатов измерений

1. Вычислить
коэффициент трения покоя µ₀
для деревянной и металлической
поверхностей по формуле (2), учитывая
соотношения (1).

2. Рассчитать
коэффициент трения скольжения µ, для
деревянной и металлической поверхностей
по формуле (3) с учетом (1).

3. Рассчитать время
скольжения бруска t_pac
для деревянной и металлической
поверхностей по формуле (5) с учетом (1).

4. Вычислить время
скатывания t_pac
для шара, сплошного и полого цилиндров
по формулам (8), (9), (10), учитывая соотношения
(1).

5. Сравнить опытные
и расчетные данные времени движения
тел и определить процент отклонения по
формуле

Сделать вывод о
качестве экспериментов.

6. Результаты свести
в таблицу.

Исследуемое тело	µ0	µ	ton, c	tpac, c	ε, %
Брусок	Деревянная поверхность
Металлическая поверхность
Шар	—	—
Цилиндр	сплошной	—	—
полный	—	—

Контрольные
вопросы

1. Запишите второй
закон Ньютона для тела, соскальзывающего
с наклонной плоскости равномерно,
равноускоренно.

2. Как определить
скорость поступательного движения
соскальзывающего тела, скатывающегося
тела? Какова связь между угловой и
линейной скоростями?

3. Каковы причины
возникновения сил трения?

4. От чего зависит
коэффициент трения?

5. Чему равна работа
переменной силы?

6. Что такое энергия?
Чему равна кинетическая энергия
поступательного движения, вращательного?

7. Сформулируйте
закон сохранения механической энергии.
Запишите закон сохранения энергии
применительно к движению тела по
наклонной плоскости.

8. Влияет ли момент
инерции тела на линейную скорость тела
у основания наклонной плоскости (при
прочих равных условиях)? Как это можно
объяснить?

5

Итак, постараюсь подробно описать ход моих
рассуждений по этому вопросу. На первом уроке
ставлю перед учащимися вопрос: как может тело
двигаться по наклонной плоскости? Вместе
отвечаем: скатываться равномерно, с ускорением;
покоиться на наклонной плоскости; удерживаться
на ней; съезжать под действием силы тяги
равномерно, с ускорением; заезжать под действием
силы тяги равномерно, с ускорением. На рисунках
на двух-трех примерах показываем, какие при этом
на тело действуют силы. Попутно ввожу понятие
скатывающей равнодействующей. Записываем
уравнение движения в векторной форме, затем в нем
заменяем сумму  скатывающей
равнодействующей  (обозначайте,
как вам нравится). Это делаем по двум причинам:
во-первых, нет необходимости проецировать
векторы сил на ось  и решать два уравнения; во-вторых,
правильно будет показано соотношение сил, исходя
из условия задачи.

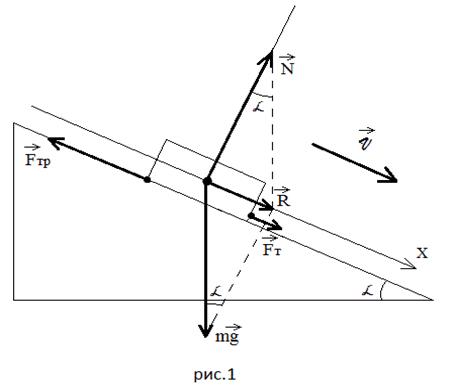
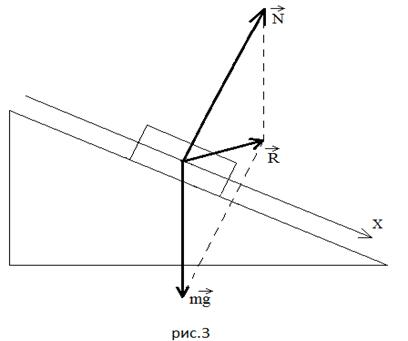
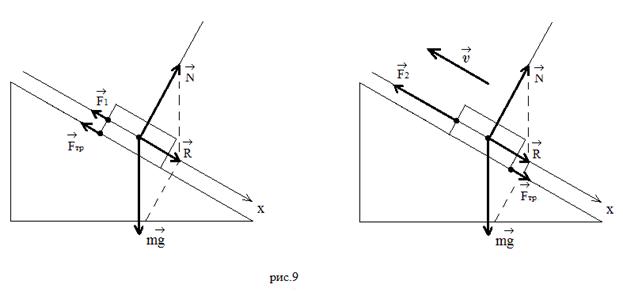
Покажу на конкретных примерах. Пример 1: тело
под действием силы тяги съезжает равномерно
(Рисунок 1).

Ученики первым делом должны усвоить алгоритм
построения рисунка. Изображаем наклонную
плоскость, посередине нее – тело в виде
прямоугольника, через середину тела параллельно
наклонной плоскости проводим ось . Направление оси не
существенно, но в случае равноускоренного
движения лучше показать в сторону вектора , чтобы в
алгебраической форме в уравнении движения в
правой части перед  был знак «плюс». Далее строим силы.
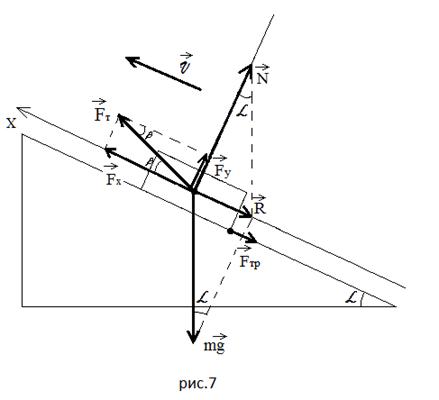
Силу тяжести  проводим
вертикально вниз произвольной длины (требую
рисунки делать крупными, чтобы всем было все
понятно). Затем из точки приложения силы тяжести
– перпендикуляр к оси , вдоль которого пойдет сила реакции
опоры .
Параллельно этому перпендикуляру из конца
вектора   проводим
пунктирную линию до пересечения с осью . Из этой точки –
пунктирную линию, параллельную  до пересечения с
перпендикуляром – получаем вектор  правильной длины.
Таким образом, мы построили параллелограмм на
векторах  и , автоматически
указав правильную величину силы реакции опоры и
построив по всем правилам векторной геометрии
равнодействующую этих сил , которую я называю скатывающей
равнодействующей (диагональ, совпадающая с осью ). В этом месте,
воспользовавшись методом из учебника, на
отдельном рисунке показываю силу реакции опоры
произвольной длины: сначала короче, чем нужно, а
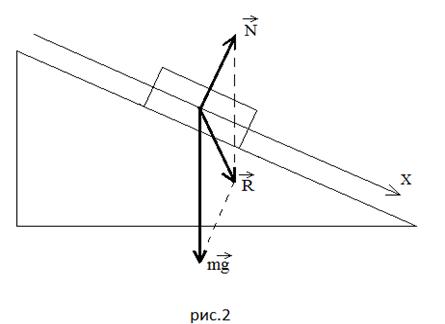
потом длиннее, чем нужно. Показываю
равнодействующую силы тяжести и силы реакции
опоры: в первом случае она направлена вниз под
углом к наклонной плоскости (Рисунок 2), во втором
случае – вверх под углом к наклонной плоскости
(Рисунок 3).

Делаем очень важный вывод: соотношение между
силой тяжести и силой реакции опоры должно быть
таким, чтобы тело под их действием (или под
действием скатывающей равнодействующей) в
отсутствие других сил двигалось вниз вдоль
наклонной плоскости. Далее я спрашиваю:
какие еще силы действуют на тело? Ребята
отвечают: сила тяги и сила трения. Я задаю
следующий вопрос: какую силу покажем сначала, а
какую потом? Добиваюсь правильного и
обоснованного ответа: сначала в этом случае надо
показать силу тяги, а затем силу трения, модуль
которой будет равен сумме модулей силы тяги и
скатывающей равнодействующей:  , т.к. по условию задачи тело
движется равномерно, следовательно,
равнодействующая всех сил, действующих на тело,
должна равняться нулю согласно первому закону
Ньютона. Для контроля задаю провокационный
вопрос: так сколько сил действует на тело? Ребята
должны ответить – четыре (не пять!): сила тяжести,
сила реакции опоры, сила тяги и сила трения.
Теперь записываем уравнение движения в
векторной форме согласно первому закону Ньютона:

. 

Заменяем сумму векторов  скатывающей равнодействующей :

.

Получаем уравнение, в котором все векторы
параллельны оси .
Теперь запишем это уравнение через проекции
векторов на ось :

.

Эту запись в дальнейшем можно пропускать.
Заменим в уравнении проекции векторов на их
модули с учетом направлений:

.

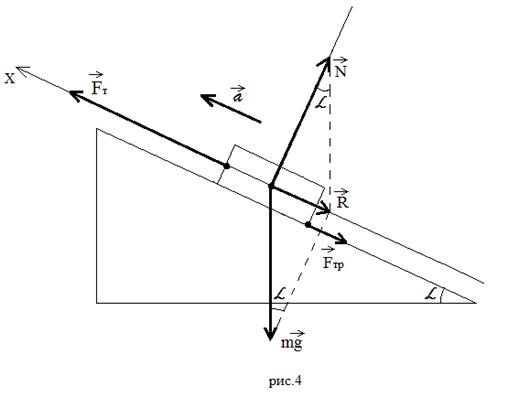
Пример 2:  тело под действием силы тяги
заезжает на наклонную плоскость с ускорением
(Рисунок 4).

В этом примере ученики должны сказать, что
после построения силы тяжести, силы реакции
опоры и скатывающей равнодействующей следующей
надо показать силу трения, последним –  вектор
силы тяги, который должен быть больше суммы
векторов , т.к.
равнодействующая всех сил должна быть
направлена так же, как вектор ускорения  согласно второму
закону Ньютона. Уравнение движения тела должны
записать согласно второму закону Ньютона:

 

Если есть возможность на уроке рассмотреть
другие случаи, то не пренебрегаем этой
возможностью. Если нет, то даю это задание домой.
Кто-то может рассмотреть все оставшиеся случаи,
кто-то некоторые – право выбора учеников. На
следующем уроке проверяем, исправляем ошибки и
переходим к решению конкретных задач,
предварительно выразив из векторных
треугольников  и
:

,
.

Равенство (2) желательно проанализировать для
различных углов .
При  имеем: , как при движении
горизонтально под действием горизонтальной силы
тяги. С ростом угла  его косинус уменьшается,
следовательно, уменьшается и сила реакции опоры
и становится все меньше и меньше силы тяжести. 
При угле  она
равна нулю, т.е. тело не действует на опору и
опора, соответственно, «не реагирует».

Предвижу вопрос оппонентов: как применить эту
методику для случаев, когда сила тяги
горизонтальна или направлена под углом к
наклонной плоскости? Отвечу на конкретных
примерах.

а) Тело с ускорением затаскивают на наклонную
плоскость, прикладывая силу тяги горизонтально
(Рисунок 5).

Горизонтальную силу тяги  раскладываем на две
составляющие: вдоль оси  –  и
перпендикулярную оси  –  (операция,
обратная построению равнодействующей
перпендикулярных сил). Записываем уравнение
движения:

.

Заменяем  скатывающей
равнодействующей, а вместо  пишем :

Из векторных треугольников выражаем :  и : .

Под действием горизонтальной силы  тело не только
поднимается вверх по наклонной плоскости, но еще
и дополнительно прижимается к ней. Поэтому
возникает дополнительная сила давления, равная
модулю вектора  и,
согласно третьему закону Ньютона,
дополнительная сила реакции опоры : . Тогда сила трения будет: .

Уравнение движения примет вид:

 

Вот мы полностью расшифровали уравнение
движения. Теперь осталось выразить из него
искомую величину. Попробуйте решить эту задачу
традиционным способом и вы получите такое же
уравнение, только решение будет громоздче.

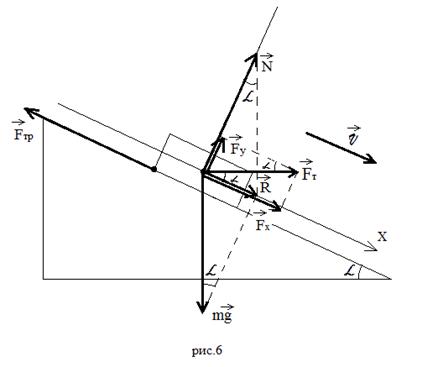
б) Тело стаскивают равномерно с наклонной
плоскости, прикладывая силу тяги горизонтально
(Рисунок 6).

В этом случае сила тяги кроме стаскивания тела
вниз вдоль наклонной плоскости еще и отрывает
его от наклонной плоскости. Итак, окончательное
уравнение имеет вид:

.

в) Тело затаскивают равномерно на наклонную
плоскость, прикладывая силу тяги под углом  к наклонной
плоскости (Рисунок 7).

Предлагаю рассмотреть конкретные задачи, дабы
еще убедительнее прорекламировать мой
методический подход к решению таких задач. Но
прежде обращаю внимание на алгоритм решения (я
думаю, все учителя физики на него обращают
внимание учеников, и все мое повествование было
подчинено этому алгоритму):

1) внимательно прочитав задачу, выяснить, как
движется тело;
2) сделать рисунок с правильным, исходя из условия
задачи, изображением сил;
3) записать уравнение движения в векторной форме
согласно первому или второму закону Ньютона;
4) записать это уравнение через проекции векторов
сил на ось x (этот шаг в дальнейшем, когда умение
решать задачи по динамике будет доведено до
автоматизма, можно опустить);
5) выразить проекции векторов через их модули с
учетом направлений и записать уравнение в
алгебраической форме;
6) выразить модули сил по формулам (если есть
необходимость);
7) выразить искомую величину.

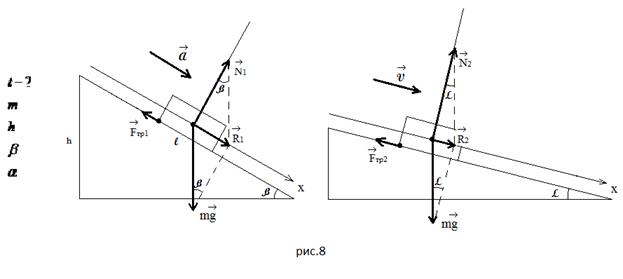
Задача 1. За какое время  тело массой  соскальзывает с наклонной
плоскости высотой  и углом наклона , если по наклонной плоскости с
углом наклона  оно
движется равномерно?

 

                                  
                                            
                                        
                                   
                                     

Каково было бы решать эту задачу привычным
способом!

Задача 2. Что легче: удержать тело на
наклонной плоскости или двигать его по ней
равномерно вверх?

Здесь при объяснении без скатывающей
равнодействующей, на мой взгляд, не обойтись.

Как видно из рисунков, в первом случае сила
трения помогает удерживать тело (направлена в ту
же сторону, что и удерживающая сила), во втором
случае она вместе со скатывающей
равнодействующей направлена против движения. В
первом случае ,
во втором случае .