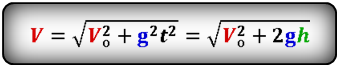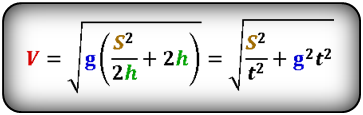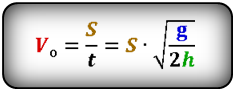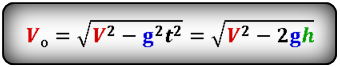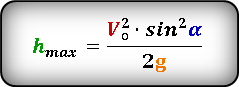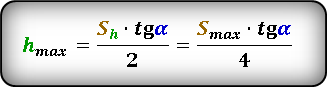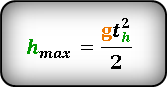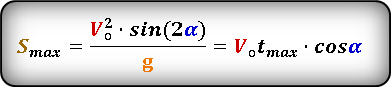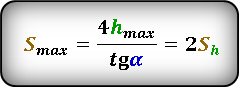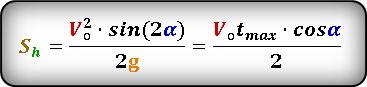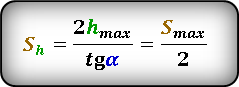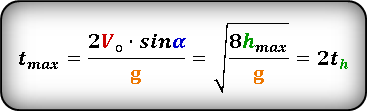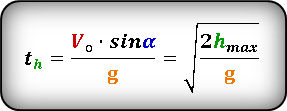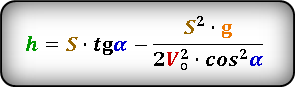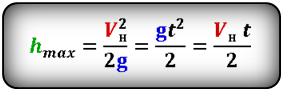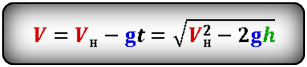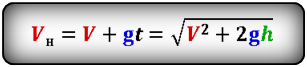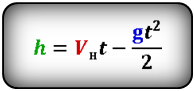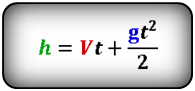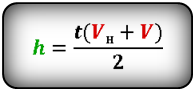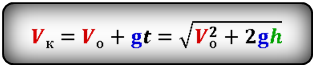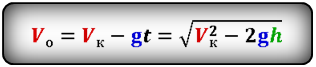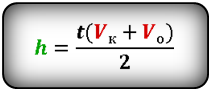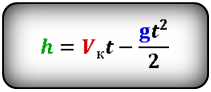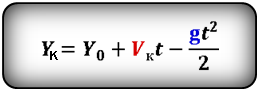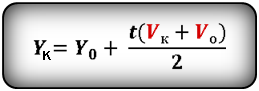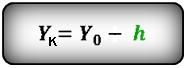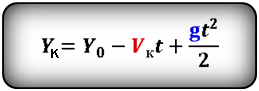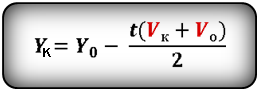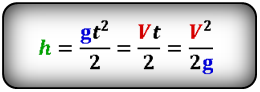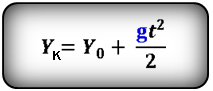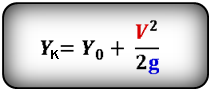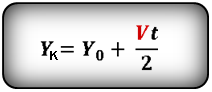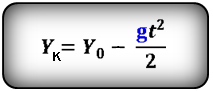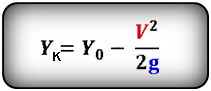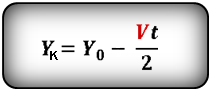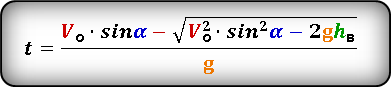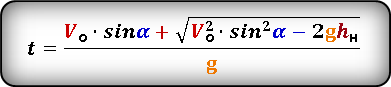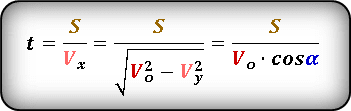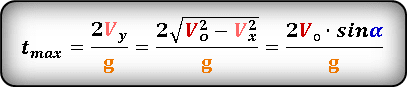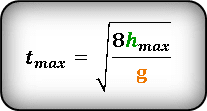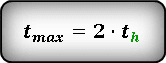Как найти время если известна площадь - Исправление недочетов и поиск решений вместе с Examum.ru

Скорость, время и расстояние

Расчеты

Скорость является физической величиной, определяющей путь, который преодолеет объект за единицу времени. Следовательно, формулу для определения скорости (при равномерном движении) можно представить как:

V = S / T

V — величина скорости;
S — величина пройденного пути;
Т — время в пути.

Показатели скорости чаще всего выражаются в м/сек; км/час; единицы расстояния — в метрах (м), километрах (км); единицами времени могут быть секунды, минуты, часы.

Исходя из вышеприведенной формулы скорости можно вывести формулу пути:

S = V * T

Т.е величину пройденного пути находим как произведение скорости на время в пути.
Если известно расстояние и скорость, определить время можно по формуле:

T = S / V

т.е. для нахождения времени делим расстояние на скорость.

Быстро и без ошибок вычислить время, скорость, расстояние в разных единицах измерения вам поможет онлайн калькулятор.

Расчет скорости, времени и расстояния

Источник

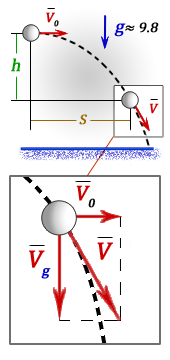
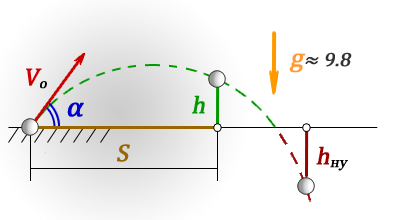
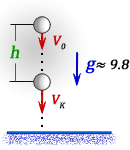
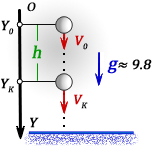
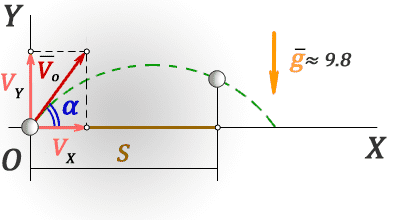
h — высота на которую опустилось тело за время t

S — расстояние по горизонтали, пройденное телом за время t

V — скорость тела, направленная по касательной к траектории движения, через время t

V_o — начальная скорость тела, которая является составляющей скорости V и направленна по горизонтали (не меняется со временем)

V_g — составляющая скорости V, направленная по вертикали вниз, возникает под воздействием силы тяжести и в начале броска равна нулю

t — время падения тела на высоту h

g ≈ 9,8 м/с² — ускорение свободного падения

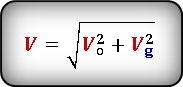
Используя теорему Пифагора, по формуле, находим численное значение скорости V, а по правилу сложения векторов, можем определить направление , которое всегда будет по касательной к траектории движения :

Формула скорости тела в момент времени t (V):

Формула начальной скорости тела (V_o):

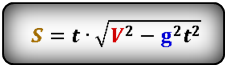
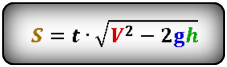
Формула расстояния по горизонтали, которое пролетело тело при падении (S):

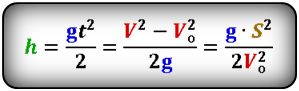
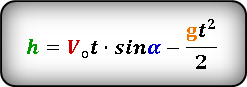
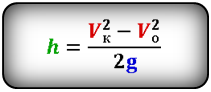
Формула высоты, на которую опустилось тело при падении (h):

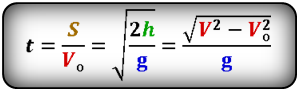
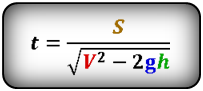
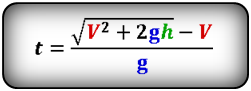
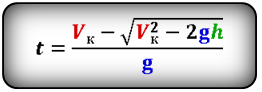
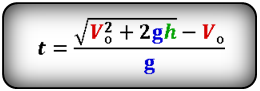
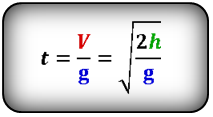
Формула времени падения тела (t):

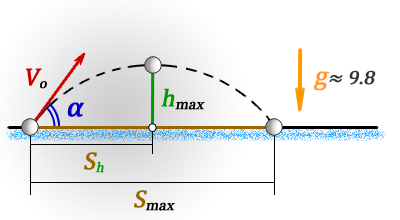
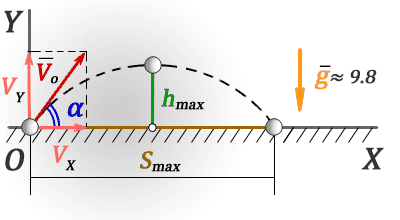
h_max — максимальная высота

S_max — максимальная дальность полета, если бросок и падение на одном уровне

S_h — расстояние пройденное по горизонтали до момента максимального подъема

t_max — время всего полета

t_h — время за которое тело поднялось на максимальную высоту

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость V_oи угол α под которым брошено тело. :

Формула для вычисления максимальной высоты, если известны, максимальное расстояние S _maxили расстояние по горизонтали при максимальной высоте S_hи угол α под которым брошено тело. :

По этой формуле, можно определить максимальную высоту, если известно время t_h за которое тело поднялось на эту высоту. :

Формула для расчета максимальной дальности полета, если даны, начальная скорость броска V_oи угол α под которым брошено тело. :

или известны максимальная высота h_maxи угол α под которым брошено тело. :

Формула для нахождения расстояния по горизонтали при максимальной высоте, если даны, начальная скорость броска V_oи угол α под которым брошено тело. :

или известны максимальная высота h_maxи угол α под которым брошено тело. :

* т. к. траектория движения симметрична относительно линии максимальной высоты, то расстояние S_hровно в два раза, меньше максимальной дальности броска S_max

Формула для определения времени затраченного на весь полет, если даны, начальная скорость V_oи угол α под которым брошено тело или если известна только максимальная высота h_max :

* т. к. траектория движения симметрична относительно линии максимальной высоты, то время максимального подъема t_hровно в два раза, меньше максимального времени t_max

Формула для определения времени за которое тело поднялось на максимальную высоту, если даны, начальная скорость V_oи угол α под которым брошено тело или если известна только максимальная высота h_max :

1. Определить, на какой высоте находится тело, в любой точке траектории движения

h — высота тела в момент времени t

h_ну — высота ниже уровня броска (принимает отрицательное значение)

S — дальность полета по горизонтали

t — время полета

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения высоты тела в момент времени t

Формула для определения значения высоты тела через расстояние S по горизонтали

h_ну — высота ниже уровня броска, принимает отрицательное значение

2. Найти максимальную высоту, на которую поднялось тело

h_max — максимальная высота

S_max — максимальная дальность полета, если бросок и падение на одном уровне

S_h — расстояние пройденное по горизонтали до момента максимального подъема

t_max — время всего полета

t_h — время за которое тело поднялось на максимальную высоту

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

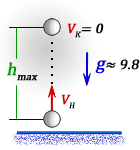
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту

h_max
— максимальная высота достигнутая телом за время t

V_к — конечная скорость тела на пике, равная нулю

V_н — начальная скорость тела

t — время подъема тела на максимальную высоту h

g ≈ 9,8 м/с² — ускорение свободного падения

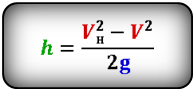
Формула максимальной высоты (h_max):

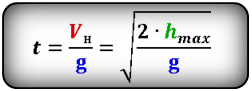
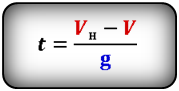
Формула времени за которое тело достигло максимальную высоту (t):

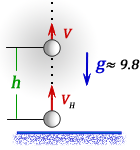
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести

h — расстояние пройденное телом за время t

V_н — начальная скорость тела

V — скорость тела в момент времени t

t — время подъема за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Формула скорости тела в момент времени t (V):

Формула начальной скорости тела (V_н):

Формулы высоты тела в момент времени t (h):

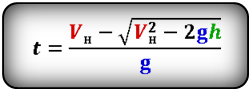
Формулы времени, за которое тело достигло высоту h (t):

1. Формулы скорости, высоты, времени

h — раcстояние пройденное телом за время t

V_o — начальная скорость тела

V_k — конечная скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Формула конечной скорости тела (V):

Формула начальной скорости тела (V_o):

Формула расстояния, которое пролетело тело при падении (h):

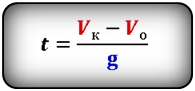
Формула времени падения тела (t):

2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости V

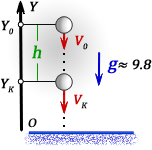
h — раcстояние пройденное телом за время t

V_o — начальная скорость тела

V_k — конечная скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Y_o , Y_к — начальная и конечная координаты тела на оси OY

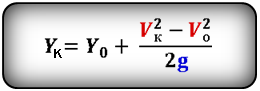
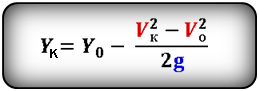
Формулы конечной координаты тела (Y_к ):

3. Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V

h — раcстояние пройденное телом за время t

V_o — начальная скорость тела

V_k — конечная скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Y_o , Y_к — начальная и конечная координаты тела на оси OY

Формулы конечной координаты тела (Y_к):

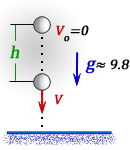
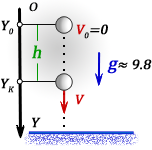
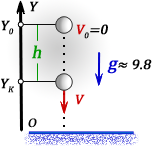
1. Формулы скорости, высоты, времени в условиях свободного падения при начальной скорости равной нулю

h — раcстояние пройденное телом за время t

V — скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние или опустилось на высоту h

g ≈ 9,8 м/с² — ускорение свободного падения

Формула скорости тела в определенный момент времени или на определенной высоте (V):

Формула высоты, на которую опустилось тело или расстояния, которое пролетело тело при падении (h):

Формула времени свободного падения тела вертикально вниз (t):

2. Формулы координаты тела, если направление оси OY совпадает с направлением скорости падующего тела V

h — раcстояние пройденное телом за время t

V — скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Y_o , Y_к — начальная и конечная координаты тела на оси OY

Формулы конечной координаты тела (Y_к):

3. Формулы координаты тела, если направление оси OY не совпадает с направлением скорости V

h — раcстояние пройденное телом за время t

V — скорость тела в момент времени t

t — время падения за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Y_o , Y_к — начальная и конечная координаты тела на оси OY

Формулы конечной координаты тела (Y_к):

1. Найти время полета тела на определенной высоте

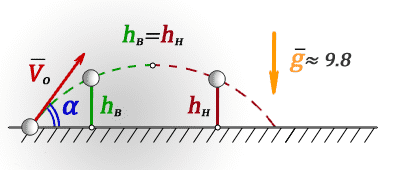
h_в — высота на восходящем участке траектории

h_н — высота на нисходящем участке траектории

t — время в момент которого тело находится на высоте h_в или h_н

V_o — начальная скорость тела

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, за которое тело поднялось на определенную высоту, на восходящем участке траектории

Формула для определения значения времени, за которое тело поднялось на определенную высоту, на нисходящем участке траектории

Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.

2. Найти время полета тела пролетевшее определенное расстояние

S — расстояние пройденное по горизонтали

t — время за которое тело прошло расстояние S

V_o — начальная скорость тела

V_x — проекция начальной скорости на ось OX

V_y — проекция начальной скорости на ось OY

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, за которое пройдено определенное расстояние

3. Значение времени при максимальных значениях высоты и дальности

S_max — максимальная дальность по горизонтали

h_max — максимальная высота

t_max — время всего полета

t_h — время за которое тело поднялось на максимальную высоту

V_o — начальная скорость тела

V_x — проекция начальной скорости на ось OX

V_y — проекция начальной скорости на ось OY

α — угол под которым брошено тело

g ≈ 9,8 м/с² — ускорение свободного падения

Формула для определения значения времени, затраченное на весь полет, если известна начальная скорость или ее проекции

Формула для определения значения времени, на максимальной высоте

Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту

Источник

Математика

5 класс

Урок № 35

Задачи на движение

Перечень вопросов, рассматриваемых в теме:

Понятия скорости, времени, расстояния.
Формулы нахождения скорости, времени, расстояния.
Понятия скорости сближения, скорости удаления.

Глоссарий по теме

Расстояние – это длина от одного пункта до другого.

Большие расстояния, в основном, измеряются в метрах и километрах.

Расстояние обозначается латинской буквой S.

Чтобы найти расстояние, надо скорость умножить на время движения:

S = v ∙ t

Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Скорость обозначается латинской буквой v.

Чтобы найти скорость, нужно расстояние разделить на время движения:

v = S : t

Время – это продолжительность каких-то действий, событий.

Время движения обозначается маленькой латинской буквой t.

Чтобы найти время, нужно расстояние разделить на скорость движения:

t = S : v

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

Основная литература

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010

Дополнительная литература

1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014

2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.

3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010

Теоретический материал для самостоятельного изучения

Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.

Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.

Рассмотрим задачу:

Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?

Решение:

Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.

Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:

200 м : 50 с = 4

Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:

200 м : 50 с = 4 (м/с)

Скорость движения первого школьника составляет 4 метра в секунду.

Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:

200 м : 100 c = 2 (м/с)

Скорость движения первого школьника – 4 (м/с).

Скорость движения второго школьника – 2 (м/с).

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.

Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.

Рассмотрим задачу:

От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?

Решение:

Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:

1200 : 600 = 2 (мин)

Ответ: мы доедем до спортивной секции за 2 минуты.

Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

S = v ∙ t

Рассмотрим задачу:

Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?

Решение:

Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:

v = 60 (м/мин)

t = 15 (минут)

S = v ∙ t = 60 ∙ 15 = 900 (метров)

Ответ: мы прошли 900 метров.

Если известно время и расстояние, то можно найти скорость:

v = S : t

Рассмотрим задачу:

Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?

Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:

S = 800 метров

t = 8 минут

v = S : t = 800 : 8 = 100 (м/мин)

Ответ: скорость школьника была 100 м/мин.

Если известна скорость и расстояние, то можно найти время:

t = S : v

Рассмотрим задачу:

От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?

Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?

Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:

S = 600 метров

v = 120 (м/мин)

t = S : v = 600 : 120 = 5 (минут).

Ответ: мы дойдём до спортивной секции за 5 минут.

Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:

Теперь рассмотрим типы задач на движение.

Задачи на сближение.

Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Задача.

Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.

Решение:

Найдём скорость сближения велосипедистов:

13 км/ч + 15 км/ч = 28 км/ч

Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:

28 ∙ 3 = 84 км

Ответ: расстояние между населёнными пунктами 84 км.

Задачи на скорость удаления.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Рассмотрим задачу:

С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?

Решение:

Определим скорость удаления. Для этого сложим их скорости:

60 + 130 = 190 км/ч.

Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.

Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:

190 ∙ 2 = 380 км.

Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.

Задачи на движение объектов в одном направлении.

В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.

Рассмотрим задачу:

Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?

Решение:

Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:

130 км/ч − 90 км/ч = 40 км/ч

Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:

40 ∙ 3 = 120 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.

Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.

Задача.

Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Решение:

Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:

90 ∙ 3 = 270 метров

Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:

85 ∙ 3 = 255 метров

Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):

900 + 255 = 1155 м

1155 – 270 = 885 м

Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):

900 – 270 = 630 м

630 + 255 = 885 м

Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.

Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?

В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:

90 ∙ 1 = 90 м

85 ∙ 1 = 85 м

900 + 85 – 90 = 985 – 90 = 895 м

Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:

90 ∙ 3 = 270 м

85 ∙ 3 = 255 м

900 + 255 – 270 = 1155 – 270 = 885 м

Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.

А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:

900 : 5 = 180 минут.

Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Заполните таблицу:

	S	v	t
1.	135 км	9 км/ч	____ ч
2.	____ м	12 м/с	4 с
3.	132 м	____ м/мин	11 мин

Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:

Надо найти время: t = S : v

135 : 9 = 15 часов.

Надо найти расстояние: S = v ∙ t

12 ∙ 4 = 48 м.

Надо найти скорость: v = S : t

132 : 11 = 12 м/мин.

Верный ответ:

	S	v	t
1.	135 км	9 км/ч	15 часов
2.	48 м	12 м/с	4 с
3.	132 м	12 м/мин	11 мин

№2. Тип задания: единичный / множественный выбор

Выберите верный ответ к задаче:

Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?

Варианты ответов:

Эта задача относится к типу задач на сближение, т.е. нам надо:

сложить скорости мотоциклиста и автомобилиста:

60 + 30 = 90 км/ч – скорость сближения;

узнать, сколько километров они пройдут за 3 часа вместе. Для этого:

90 ∙ 3 = 270 км;

из общего расстояния нам осталось вычесть пройденное:

300 – 270 = 30 км

Верный ответ: 2. 30 км.

Источник

Если известна скорость и расстояние, то можно найти время: t = s : v.

Как найти время в задачах на движение формула?

Задачи на движение

движение
скорость v=s/t.
время t=s/v.
расстояние s=v∗t.

Как найти время по формуле?

Время обозначается как t. Единица измерения времени – с (секунды). Самая простая формула при равномерном прямолинейном движении. Время, необходимое для прохождения пути равняется частному от деления пути на скорость равномерного прямолинейного движения: t = S / v.

Как найти время?

Чтобы найти время, надо расстояние разделить на скорость.

Как найти расстояние?

Чтобы узнать расстояние, нужно скорость умножить на время. Чтобы найти время, нужно расстояние разделить на скорость. Основная и дополнительная литература по теме урока: 1.

Как найти расстояние по формуле?

В большинстве случаев расстояние может быть вычислено по следующим формулам: d = s × t, где d — расстояние, s – скорость, t – время; d = √((x2 — x1)2 + (y2 — y1)2, где (x1, y1) и (x2, y2) – координаты двух точек.

Как найти когда встретятся автомобили?

60 — 40 = 20 (км/ч) — это скорость сближения автомобилей. Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч).

Как находится скорость?

Чтобы найти скорость, нужно расстояние разделить на время движения. Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

Как решать скорость время расстояние?

Скорость — это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
скорость = расстояние : время
время = расстояние : скорость
расстояние = скорость · время

Как найти формулу массы?

Вес можно рассчитать по формуле: m=V*p, где р – плотность, V – объем материала. Например, 10 м3 речного песка весят 13 тонн. Если известна масса материала, то объем можно узнать по формуле: V = m/ p.

Как найти время если есть расстояние и скорость?

Если известна скорость и расстояние, то можно найти время: t = s : v.

Как найти время формула 4 класс?

В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.

Как найти V в математике?

V=S/t = 180/2=90 км/ч. Аналогично предыдущему примеру узнаем время, за которое автомобиль преодалел то же расстояние, двигаясь со скоростью 120км/ч: t=S/V = 180/120=1,5ч. И, напоследок, решим задачу посложнее, в которой применяется формула скорости.

Источник

Онлайн калькулятор поможет вам рассчитать скорость, время или расстояние. Вычисление производится в любой из возможных единицах измерения скорости или расстояния. Он может пригодится как учащимся школ так и студентам.

Поделиться расчетом:

Расчет времени в зависимости от расстояния и скорости

Введите расстояние:

Введите скорость:

Часы =

Минуты =

Секунды =

Рассчитать

Расстояние в зависимости от скорости и времени

Введите скорость:

Часы:

Минуты:

Секунды:

Расстояние =

Рассчитать

Скорость в зависимости от расстояния и времени

Введите расстояние:

Часы:

Минуты:

Секунды:

Скорость:

Рассчитать

Источник