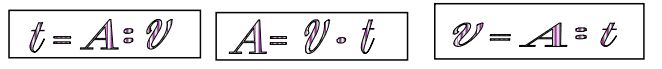Скачать материал

Скачать материал


- Сейчас обучается 26 человек из 13 регионов


- Сейчас обучается 104 человека из 36 регионов


- Сейчас обучается 140 человек из 43 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Тема урока:
«Решение задач»
28.05.18. -
2 слайд
«Токарь-фрезеровщик усовершенствовал способ обработки деталей на станке, и его производительность увеличилась
в 1,5 раза»
Что означает слово «производительность»?
Подумаем! -
3 слайд
Производительность – это сколько сделано за единицу времени
(за 1 час, за 1 минуту, за 1 сутки)
Производительность – это объем работы, выполненный за единицу времени
или: производительность садовода –
4 ведра картошки за 1 час
Например: 15 деталей в час
Запомним!
или: производительность
трактора – 0,5 га за 1 час -
4 слайд
А – работа , t – время,
v – производительность
(скорость работы)
A = v· t — работа
Запомним!
Тогда t = A : v — время работы -
5 слайд
Задача 1. Через первую трубу бассейн можно наполнить за 3 ч, через вторую — за 6 ч. Какую часть бассейна наполнит каждая труба за 1ч?
Какова производительность каждой трубы?
Ответ: 𝟏 𝟑 и 𝟏 𝟔 часть за 1 час
Решим вместе! -
6 слайд
Задача 2. За 1 ч первая труба наполняет 𝟏 𝟑 бассейна, а вторая — 𝟏 𝟔 бассейна.
Какую часть бассейна наполняют обе трубы за 1 ч совместной работы?
(Какова общая производительность?)За сколько часов наполнится бассейн через обе трубы?
Решим вместе!
Ответ:
𝟏 𝟐 бассейна;за 𝟐 часа -
7 слайд
Задача . Через первую трубу можно наполнить бак за 10 мин, через вторую — за 15 мин. За сколько минут можно наполнить бак через обе трубы?
Ответ: за 6 минут
На доске!
Самопроверка:
За 1 минуту трубы наполнят 𝟏 𝟏𝟎 + 𝟏 𝟏𝟓 = 𝟑+𝟐 𝟑𝟎 = 𝟓 𝟑𝟎 = 𝟏 𝟔 (часть) –общая производительность
Примем всю работу за 1.
Тогда 1: 𝟏 𝟔 =𝟔 (мин) – время работы -
8 слайд
1) Найти производительность v(сколько сделано за единицу времени)
Обобщаем!
Найти время работы t – для этого общую работу A разделить на производительность v
Алгоритм решения задачи:
t = A : v
Если объем работы неизвестен, а известны только ее части, то A = 1 -
9 слайд
Работа в парах.
Решите одну из задач (1 уровень):
Один ученик может убрать класс за 20 мин, а второй — за 30 мин. За сколько минут они могут убрать класс, работая вместе?2) Грузовая машина может проехать расстояние между двумя городами за 30 ч, а легковая — за 20 ч. Машины одновременно выехали из этих городов навстречу друг другу. Через сколько часов они встретятся?
3) Путешественник идет из одного города
в другой 10 дней, а другой путешественник тот же путь проходит за 15 дней. Через сколько дней встретятся путешественники, если выйдут одновременно навстречу друг другу из этих городов? -
10 слайд
Решите одну из задач (2 уровень):
1) Из «Арифметики» Ф.Магницкого.
Один путник идет от города в дом, а ходу его будет 17 дней, а другой путешественник
от дома до города тот же путь может пройти в 20 дней. Оба эти человека
пошли в один и тот же час от мест своих, и спрашивается, в сколько дней сойдутся.2) Из двух пунктов навстречу друг другу одновременно выехали мотоциклист и велосипедист. Велосипедист может проехать все расстояние за 3,5 ч, а мотоциклист — за 1,4 ч. Через сколько часов
после начала движения они встретятся?
Работа в парах -
11 слайд
Работа в парах
Решите задачу (3 уровень):
Старинная задача. Путешественник идет из одного города в другой 10 дней, а другой путешественник тот же путь проходит за 15 дней. Через сколько дней встретятся путешественники, если выйдут одновременно навстречу друг другу из этих городов? -
12 слайд
Проверь себя!
Ответы:1 уровень – 1) за 12 минут;
2) через 12 часов;
3) через 6 дней.2 уровень – 1) через 9 𝟕 𝟏𝟏 дней
2) через 1 час
3 уровень – за 8 дней
-
13 слайд
Домашнее задание:
Придумать и решить задачу с производительностью.
Творчество -
14 слайд
Итоги урока:
Чему мы научились?Что было интересным?
Что показалось трудным?
Возьмите цветной карандаш и изобразите свое впечатление от урока.
Краткое описание документа:
Цель урока — научиться находить общее время работы через понятие производительности. Разработан для учебника Э.Г.Гельфман, М.А.Холодной (6 класс) с использованием задач из сборника А.В.Шевкин. Текстовые задачи по математике 5-6.- (раздел «Задачи на бассейны и другие»). Опираясь на знания о производительности, полученные в начальной школе, вводим формулу работы, и используем ее для нахождения времени работы. Предполагает работу в парах или группах, активно развивает самостоятельное мышление, предлагая задачи разных уровней сложности. Задачи желательно распечатать на листочках для каждой пары (группы), можно оценить в баллах (1 уровень — по 2 балла, 2-й — по 3 балла, 3-й — 5 баллов — и набирать сумму).
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 264 193 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 07.06.2018
- 195
- 0
- 07.06.2018
- 889
- 0


- 07.06.2018
- 268
- 1



Рейтинг:
4 из 5
- 07.06.2018
- 7016
- 612

Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Урок 15. Формула работы
Гипермаркет знаний>>Математика>>Математика 3 класс>> Урок 15. Формула работы
Содержание
- 1 Что такое формула работы?
- 2 Практические задания
- 3 Подведение итогов
- 4 Вопросы на закрепление изученного материала
- 5 Домашнее задание
Что такое формула работы?

Решение:
Валя сделала меньше флажков, но она и работала меньше. Чтобы сравнить, кто из них работал быстрее, а кто медленнее, надо вычислить, сколько флажков сделала каждая из девочек за 1 час:
40: 2 = 20 (фл.) 45 : 3 = 15 (фл.)
Теперь видно, что Валя работала быстрее, так как она делала в час 20 флажков, а Галя только 15.
Скорость работы называют иначе производительностью. В нашем примере производительность Вали — 20 флажков в час, а производительность Гали — 15 флажков в час.
Итак, производительность — это работа, выполненная за единицу времени. Если обозначить всю выполненную работу буквой А, производительность — буквой V, а время работы — буквой I, то можно записать равенство:
Это равенство называется формулой работы. Оно означает, что работа равна производительности, умноженной на время работы.
Из формулы работы по правилу нахождения неизвестного множителя легко найти величины и t:
— Производительность равна работе, делённой на время работы.
— Время равно работе, делённой на производительность.
Практические задания
1. Объясни смысл предложений:
а) Вася ест мороженое с производительностью 3 мороженых в час.
б) Оля лепит пельмени с производительностью 2 штуки в минуту.
в) Денис делает табуретки с производительностью 4 табуретки в день.
г) Лёня читает книги с производительностью 5 книг в год.
д) Гена копает картошку с производительностью 3 ведра в час.
е) Ира печатает на машинке с производительностью 120 знаков в минуту.
2. Мастер вытачивает 8 деталей в час. Сколько деталей он сделает за 2 ч, 4 ч, 6 ч, 7 ч, 9 ч, t ч? Заполни таблицу и запиши формулу зависимости работы А, выполненной мастером, от времени работы t.
3. Тане надо вымыть 36 тарелок. Сколько времени она затратит на эту работу, если будет мыть в минуту 2 тарелки, 3 тарелки, 4 тарелки, 6 тарелок, 9 тарелок, тарелок? Заполни таблицу и запиши формулу зависимости времени работы t от производительности
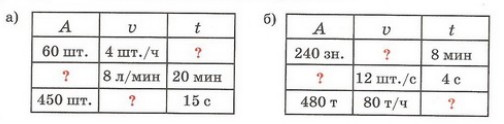
4. По данным таблицы составь задачи и реши их:
5. Завод выпускает 208 автомобилей в день. Сколько автомобилей выпустит завод в год? (Считать, что в году 365 дней.)
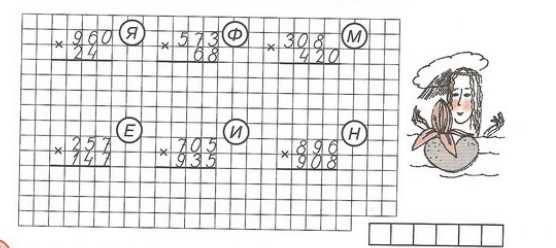
6. Расшифруй название цветка, расположив ответы примеров в порядке убывания. Почему цветок так называется?
7. Выполни действия:
152 • 387 492 • 604 999 • 555 333 • 707
8. Сравни:
7 дм 5 мм … 75 мм 6 т 8 ц … 6 800 кг
9 м 2 дм … 920 дм 6 кг 8 г … 6 800 г
2 км 32 м … 203 200 см 6 ч 8 мин … 68 мин
9. Реши уравнения с комментированием и сделай проверку:
а) (700 : х + 20): 4 — 40; б) 2 • (500-у :3) = 820.
10. Составь программу действий и вычисли:
а) 234 240 : 6 • 9 — (20 030 — 7358): 4;
б) 834 024 + 7900 ¦ 25 — (483 • 504): 8 • 10.
11. Запиши множество делителей и множество кратных числа 26.
12*. у Пусть А — множество чисел, меньших 5, а В — множество чисел, больших, чем 2, но меньших 7. Запиши множества А и В с помощью фигурных скобок. Найди их объединение и пересечение и нарисуй диаграмму Венна.
Подведение итогов
Каждый из вас, наверное, понимает, что люди трудятся для того, чтобы создавать разные полезные вещи, услуги, продукты и так далее. И важным в труде каждого человека является его производительность. А теперь давайте попробуем ответить, зачем необходимо увеличивать производительность труда? Оказывается, это делается по одной простой причине, ведь чем выше производительность труда, тем меньше затрат и времени уходит на производство какого-то одного товара.
А теперь давайте попробуем подвести итог нашего урока и выяснить, все ли нам понятно в этой теме? На этом уроке мы с вами ставили такие цели, как найти формулу работы, научиться ее пользоваться и попробовать решать задачи с помощью формулы работы. Как мне кажется, с этими задачами мы с вами справились.
На сегодняшнем уроке вы узнали, что такое формула работы и выглядит она вот так:
Также вы уже знаете, что обозначает каждая из букв в этой формуле:
Также, на сегодняшнем уроке вы при решении задач пробовали установить взаимосвязь между величинами, которые имеются в формуле работы:
Вопросы на закрепление изученного материала
1. А теперь давайте вспоминать, как нужно пользоваться формулой работы?
2. А теперь внимательно подумайте и вспомните, каким другим словом можно заменить скорость, с которой была выполнена работа?
3. Что нам необходимо сделать, что узнать производительность работы?
4. Какой буквой в формуле работы принято обозначать время?
5. Какой буквой принято в формуле работы обозначать выполненную работу?
6. Как мы можем найти время работы, если нам известна производительность и выполненная работа?
Домашнее задание
1. Решите задачи и узнайте, чему равна производительность, если:
а) Наталья съедает за 1 час 3 яблока.
б) Женя помогает маме готовить обед. Она за 2 минуты лепит 4 вареника.
в) За 1 год Таня прочитывает 8 книг.
г) Строитель кладет 60 кирпичей за 20 минут.
д) Миша моет 5 тарелок за 10 минут.
2. С помощью формулы работы составьте задачи, решите их и недостающие значения запишите в таблицу:
3. Подумайте, какую работу вы выполняете ежедневно дома, и составьте задачи, рассчитывающие вашу производительность в течение дня. Например, домашнее задание по математике вы делаете 30 минут, по природоведению – 10 минут, а по чтению – 20 минут, значит на выполнение домашних заданий по 3м предметам, вы тратите 60 минут. Так какая же ваша производительность при выполнении работы «домашнее задание»? Сравните свои результаты со своими одноклассниками.
Петерсон Людмила Георгиевна. Математика. 3 класс. Часть 3. — М.: Издательство «Ювента», 2005, — 64 с.: ил.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
гречиху фасуют два дозатора. В один дозатор засыпают (200) кг гречихи, и он расфасовывает крупу в пакеты за (20) мин. В другой засыпают (330) кг, и он расфасовывает крупу за (30) мин. Какой из дозаторов работает быстрее?
Сначала найдём, скорость каждого дозатора.
Эту задачу можно представить в виде таблицы:
— килограммов гречихи расфасовывает первый дозатор за (1) мин.
— килограммов гречихи расфасовывает второй дозатор за (1) мин.
Значит, работает быстрее второй дозатор.
Текстовые задачи на производительность
Задачи на производительность включают в себя задачи, в которых фигурирует какой-либо рабочий процесс и его характеристики: работа, время и производительность. Эти параметры связаны через формулу совместной работы:
(A = Pt,)
где (A) – работа, (t) – время, (P) – производительность.
Через эту формулу можно выразить производительность и время:
(P = frac{A}{t})
(t = frac{A}{P})
С помощью этих формул можно выражать одни характеристики работы через другие. Рассмотрим пример.
Пример №1:
За 5 дней работы рабочие на заводе произвели 35 деталей для автомобилей. Сколько деталей в день изготавливалось на заводе?
-
Для того, чтобы найти производительность, зная работу и время, нужно поделить работу на время:
(P = frac{A}{t} = frac{35}{5} = 7 деталей/день)
Ответ: 7.
ЗАДАЧИ НА ОБЩУЮ РАБОТУ
Часто в задачах на производительность можно увидеть вопрос на общую работу, когда нам известно время работы отдельных заводов или людей, а нужно найти совместное время, производительность или работу. В таком случае мы не сможем сложить время, т. к. при совместной работе время не увеличивается. А наоборот уменьшается за счет увеличения производительности. Рассмотрим на примере, как находить общее время работы.
Пример №2:
Для производства инструментов нужно сделать 600 деталей. Первый завод сделает эту работу за 10 дней, а второй завод за 15. За сколько дней будут готовы все детали, если их будут делать сразу два завода?
-
Мы знаем работу и время производства деталей в первом заводе. Найдем их производительность:
(P_{1} = frac{600}{10} = 60 )
(деталей в день делает первый завод)
-
Также найдем производительность для второго завода:
(P_{2} = frac{600}{15} = 40 )
(деталей в день делает второй завод)
-
Тогда за один день два завода вместе сделают:
(P_{общ} = 60 + 40 = 100 деталей в день)
Это производительность является общей для заводов.
-
С такой производительностью они сделают 600 деталей за:
(t_{общ} = frac{600}{100} = 6 дней)
Мы узнали, за какое время заводы сделаю 600 деталей, если каждый день будут работать вместе. Запишем ответ.
Ответ: 6.
ЗАДАЧИ С ДОПОЛНИТЕЛЬНЫМ УСЛОВИЕМ
Это такие задачи, где мы знаем, разницу между одной характеристикой нескольких рабочих или заводов. Тогда дополнительное условие позволяется связать нам данные и составить уравнение. Рассмотрим на примере.
Пример №3:
Заказ на 110 деталей второй рабочий выполняет на 1 час быстрее, чем первый. Сколько деталей за час изготавливает первый рабочий, если известно, что второй за час изготавливает на 1 деталь больше.
-
Составим таблицу. Вместо искомого поставим переменную 𝑥. В данном случае это производительность первого рабочего, т. к. спрашивают, сколько деталей он делает за час. Тогда производительность второго рабочего на единицу больше:
-
При этом рабочие выполняют одинаковую работу – по 110 деталей, тогда заполним колонку работы:
-
Тогда, зная производительность и работу каждого, выразим время для обоих рабочих:
(t_{1} = frac{110}{x})
(t_{2} = frac{110}{x + 1})
-
Теперь, когда мы знаем все характеристики работы рабочих, можем использовать дополнительное условие, которое заключается в том, что второй выполняет этот объем работы на час быстрее, значит, составим уравнение, которое объединяет время работы обоих рабочих:
(frac{110}{x + 1} + 1 = frac{110}{x})
-
Теперь работаем только с уравнением. Приведем обе части уравнения к одному знаменателю, в данном случае к знаменателю ((x + 1)x). Преобразуем получившееся уравнение, перенесем все в одну сторону и раскроем скобки:
(frac{110x}{(x + 1)x} + frac{(x + 1)x}{(x + 1)x} = frac{110(x + 1)}{x(x + 1)})
(frac{110x}{(x + 1)x} + frac{(x + 1)x}{(x + 1)x} – frac{110(x + 1)}{x(x + 1)} = 0)
(frac{110x + x^{2} + x – 110x – 110}{(x + 1)x} = 0)
-
Дробь будет равна нулю, если числитель равен нулю, а знаменатель его НЕ равен, т. е. (x neq –1) и (x neq 0):
(110x + x^{2} + x – 110x – 110 = 0)
(x^{2} + x – 110 = 0)
-
По т. Виета:
({x_{1} + x_{1} = –1 }{x_{1}x_{1} = –110})
Тогда:
(leftlbrack frac{x_{1} = 10}{x_{2} = –11} right. )
-
Проверим корни на адекватность. Оба решения являются корнями уравнения, но вернемся к тому, что мы искали. Мы приняли за x производительность первого рабочего, а такая реальная характеристика, как выполненная за час работа не может быть отрицательной. Таким образом ответом данной задачи будет являться первый корень уравнения. Запишем ответ.
Ответ: 10.
Производительность. Время. Работа
Производительность – это работа, которая выполняется за единицу времени. Другими словами, производительность – это скорость выполнения работы.
Чтобы найти производительность, надо весь объем работы разделить на время выполнения данной работы.
Чтобы найти время выполнения работы, надо весь объем работы разделить на производительность.
Чтобы найти объем работы, надо производительность умножить на время выполнения данной работы.