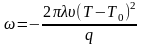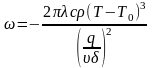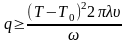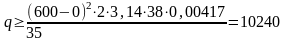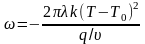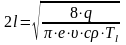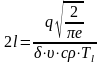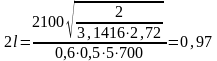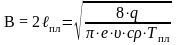Пусть мощность печей — Р.
Масса каждого металла — m.
Пусть медь плавилась время t1, олово плавилось время t2.
Теплота, выделившаяся при плавлении меди Q1.
Олова-Q2.
Q=mc( в общем случае)
Удельная теплота плавления меди с1=213 кДж/кг
Олова с2=59 кДж/кг
(лямбда не могу набрать, поэтому «с»)..
Р*t1=m*c1
P*t2=m*c2.
Разделим равенство на равенство :
t1/t2=c1/c2
=213/59=3,6101..~~3,6 раз
Ответ:
Отношение времен плавления равно с точностью до десятых 3,6.
Главная >> Применение >> Типовые примеры >>
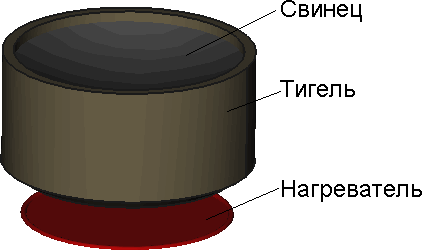
Плавление свинца
моделирование нагрева металла, температура плавления свинца
В тигле находится свинец. Определить время плавления свинца и нагрева расплава до требуемой температуры, 350 градусов.
Тип задачи
Теплопередача нестационарная.
Геометрия
Нагрев осуществляется со дна тигля. Охлаждение происходит со всех свободных поверхностей.
Дано
Теплопроводность жидкого свинца 35.3 Вт/K·м
Удельная теплоемкость жидкого свинца 150 Дж/кг·К
Плотность жидкого свинца 9810 кг/м³
Теплопроводность твердого свинца 35.3 Вт/K·м
Удельная теплоемкость твердого свинца 130 Дж/кг·К
Плотность твердого свинца 11340 кг/м³
Удельная теплота плавления свинца 25000 Дж/кг
Теплопроводность тигля 47 Вт/K·м
Удельная теплоемкость тигля 460 Дж/кг·К
Плотность тигля 7800 кг/м³
Начальная температура 0 градусов
Конечная температура 350 градусов.
Тепловой поток нагревателя 223000 Вт/м²
Коэффициент конвекции с поверхности тигля и свинца 30 Вт/K·м²
Решение
Сначала происходит нагрев твердого металла, затем его плавление, и позже нагрев жидкого металла. Каждый процесс смоделирован отдельно.
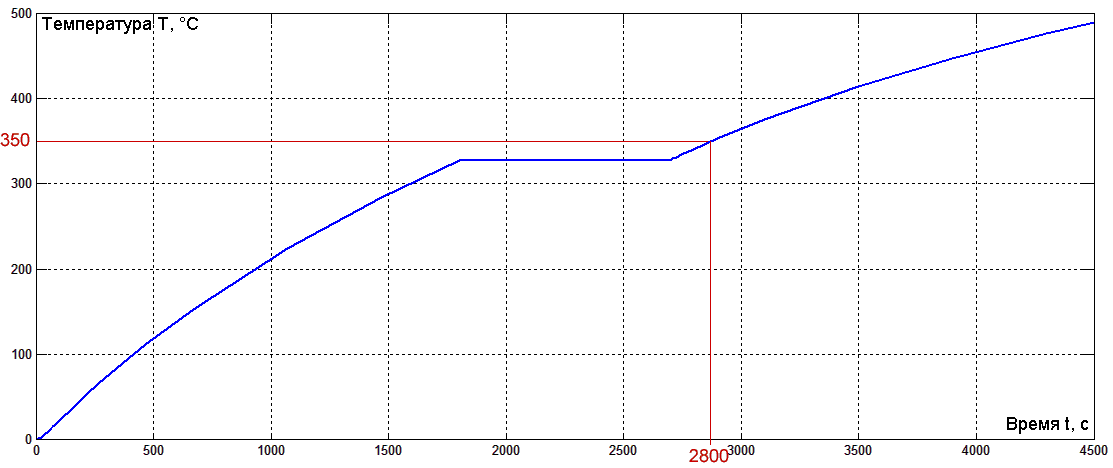
- Процесс нагрева твердого свинца смоделирован в первой части. Свинец достигает температуры плавления после 1800 секунд нагрева.
- При достижении температуры плавления температура свинца не меняется. Идет процесс расплавления. Время плавления определяется вручную:
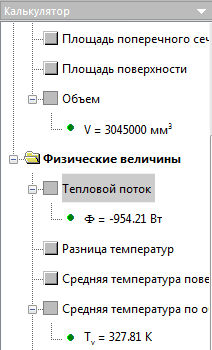
Объем свинца V = 3045 см³
Масса свинца m = V * ρ = 3045 * 11.34 = 34530.3 гр (34.5кг)
Теплота плавления Q = m * λ = 34.5 * 25000 = 8625000 Дж
Входящий тепловой поток F = 954.21 Вт
Время плавления t = Q / F = 8625000 / 954.21 = 903.8 сек. - Процесс дальнейшего нагрева идет от температуры, полученной в первой задаче (за время плавления температура не менялась). Для передачи температуры из одной задачи в другую используется связь задач.
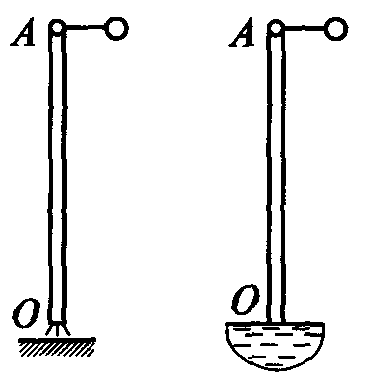
Результат
Требуемая температура свинца 350 градусов получается после нагрева в течении 2800 с (47 минут).
- Скачать файлы задачи
На заводе при обработке цветных металлов в двух тигельных печах плавились одинаковые массы меди и серебра. Используя таблицу, найдите отношение времени плавления меди ко времени плавления серебра, если мощности печей одинаковы. Ответ округлите до десятых долей.
Масса меди и масса серебра одинаковы, обозначим их буквой m. ma=mc=m
Мощность печи находится по формуле Р=Q/t, отсюда t=Q/Р, где t — время плавления металла, Р — мощность печи (мощности обеих печей по условию одинаковы), Q — количество теплоты, которое необходимо для плавления металла, его находим по формуле Q=λm.
Найдём отношение времени плавления меди ко времени плавления серебра:
tм/tс=Qм/Р/(Qс/Р)=(Qм/Р)*(Р/Qс)=Qм*/Qс
Подставим сюда формулу для нахождения количества теплоты Q=λm:
tм/tс=(λм*m)/(λс*m)=λм/λс
Подставим значения из таблицы: λм=213 кДж/кг и λс=87 кДж/кг
tм/tс=213/87=2,4
Ответ: 2,4.
Вполне очевидно, что время плавления данной массы металла обратно пропорционально его удельной теплоте плавления. То есть если оные удельные параметры относятся как 87:213, то значения времени плавления при равной мощности и равной массе относятся как 213:87.
На заводе при обработке цветных металлов в двух тигельных печах плавились одинаковые массы меди и олова. Используя таблицу, найдите отношение времени плавления меди к времени плавления олова, если мощности печей одинаковы. Ответ округлите до десятых долей.
| Металл | |
|---|---|
| Железо | 270 |
| Золото | 67 |
| Магний | 370 |
| Медь | 213 |
| Натрий | 113 |
| Олово | 59 |
| Свинец | 24,3 |
| Серебро | 87 |
| Сталь | 84 |
| Тантал | 174 |
| Цинк | 112,2 |
| Чугун (разные марки) | 96–140 |
Спрятать решение
Решение.
Мощность печи определяется формулой где теплота, необходимая на плавление
Отсюда находим соотношение
Ответ: 3,6.
В
инженерной практике часто возникает
необходимость расчетного определения
температурно-временных параметров
сварочных термических циклов в различных
зонах изделия, размеров зон нагрева,
скоростей нагрева и охлаждения и т. п.
Решение таких задач на основе упрощенных
аналитических подходов, изложенных
выше,
позволяет
получать численные оценки с приемлемой
для практических целей точностью.
3.1.
Термический
цикл при однопроходной сварке
В
результате действия сварочного источника
теплоты температуры точек тела непрерывно
изменяются: сначала повышаются, достигая
максимального значения, затем снижаются.
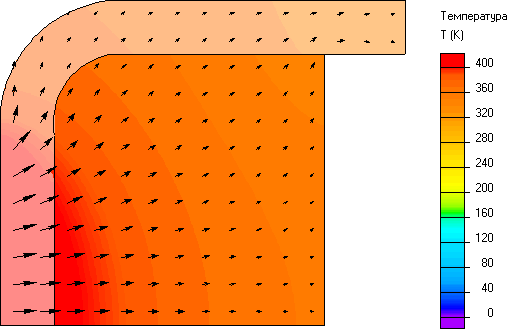
Сварочным термическим циклом (рис. 28)
называется
зависимость
T(t)
температуры
от времени в некоторой фиксированной
точке тела
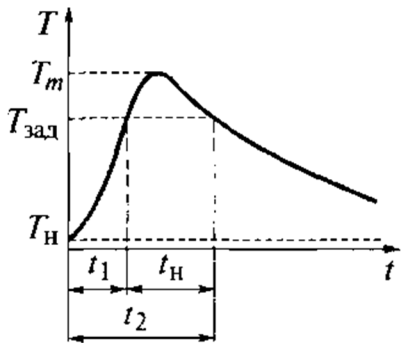
Рис.
28.
Сварочный
термический цикл
Он
во многом определяет свойстве различных
зон сварного соединение поэтому расчет
его основных параметров (максимальной
температуры Тm
скоростей нагрева и охлаждения
ω
при
заданных
температурах, времени tн
пребывания материала при температуре
выше заданной) представляет значительный
практический интерес. Так, например, в
сталях при температурах выше 1000
°С
происходит интенсивный рост аустенитного
зерна, что приводит
к охрупчиванию металла. Степень роста
зерна определяется максимальной
температурой термического цикла и
временем пребывания стали при
температурах выше 1000
°С.
Структурное состояние стали (степень
закалки) определяется скоростью
охлаждения в интервале температур
минимальной устойчивости аустенита.
Расчет
максимальных температур.
Если известна математическая зависимость
температуры от времени —
функция
T(t),
то
условием достижения максимальной
температуры является равенство нулю
ее первой производной: ∂Т/∂t=0.
Чтобы
получить выражение для расчета
максимальной температуры термического
цикла, необходимо выполнить следующие
действия:
1. Продифференцировать функцию t(t), и получить выражение для ее первой производной по времени ∂т/∂t;
2.
Приравнять производную нулю и решить
уравнение
∂Т/∂t=0,
т.
е. получить выражение для времени
достижения максимальной температуры
tm;
3.
Подставить полученное выражение для
tm
в
исходную зависимость
T(t)
и
получить математическое выражение для
максимальной температуры термического
цикла:
Tm
= T(tm).
Наиболее
простые выражения для максимальных
температур термических циклов получаются
при использовании моделей быстродвижущихся
источников. Так, для быстродвижущегося
точечного источника на поверхности
полубесконечного тела можно получить
следующее
выражение для максимальной температуры
термического цикла:
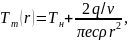
где
Tн
— начальная температура изделия или
температура подогрева;
r2=у2+z2
— расстояние от рассматриваемой точки
до оси шва. Таким образом, максимальное
приращение температуры в точках
массивного тела пропорционально погонной
энергии сварки
q/υ
и обратно пропорционально квадрату
расстояния до оси шва. Отсутствие
коэффициента теплопроводности λ
в выражении означает, что это свойство
материала, не влияет на максимальные
температуры термических циклов.
Для
вычисления максимальной температуры
при действии быстродвижущегося линейного
источника теплоты в бесконечной пластине
с теплоотдачей
используют выражение
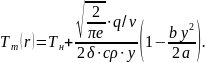
Из
этого выражения следует, что в пластине
без теплоотдачи с поверхности (b=0)
распределение
максимальных приращений температуры
имеет гиперболический характер.
Пример.
Определить
максимальную температуру нагрева на
расстоянии
у=4
см
от оси шва при механизированной
аргонодуговой сварке с полным проплавлением
листов алюминиевого сплава АМг6 толщиной
6
мм.
Режим сварки: ток
I
=
400 А,
напряжение дуги
U
= 16 В,
скорость сварки
υ=18
м/ч=0,5
см/с,
эффективный КПД дуги η=0,5.
Теплофизические
коэффициенты: λ=2,7
Вт/(см·К),
сρ=2,7
Дж/(см3·К).
Используем
схему быстродвижущегося линейного
источника теплоты в пластине без
теплоотдачи (b=0).
Начальную
температуру листов принимаем равной
комнатной температуре
(Тн
=
293 К).
Определяем эффективную мощность
источника и погонную энергию сварки:
q
= ηUI=0,5·16·400
= 3200 Вт;
q/υ
= 3200/0,5 = 6400 Дж/см.
Для
расчета максимальной температуры
используем соответствующее схеме
выражение при
b=0:
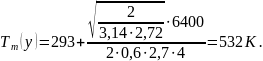
Расчет
мгновенных скоростей охлаждения.
Определение скорости охлаждения может
представлять интерес, когда изменение
скорости охлаждения в интервале
температур распада аустенита может
вызвать существенное изменение
механических свойств металла. Например,
при сварке закаливающихся материалов
путем изменения режима сварки и
термического цикла можно заметно
уменьшить степень закалки отдельных
зон и тем самым снизить вредные
последствия, вызванные термическим
циклом сварки.
Мгновенная скорость
охлаждения
является первой производной температуры
по времени
=T/t.
Ее определение, в
общем случае, производят следующим
образом. По формулам для расчета тепловых
полей в пластине или полубесконечном
теле находят координаты точки,
расположенной в интересующей зоне и
имеющей температуру, при которой
требуется определить скорость охлаждения.
Затем значения этих координат подставляют
в формулу скорости охлаждения .
Так как в большинстве
случаев оказывается достаточным
приближенное определение скорости
охлаждения, то используют теорию мощных
быстродвижущихся источников теплоты
без учета теплоотдачи. Скорости охлаждения
определяют только для оси шва, ввиду их
незначительного отличия от скоростей
охлаждения околошовных зон, нагревавшихся
до Т=800…900° С и выше.
Скорости охлаждения
точек оси шва при наплавке валика на
массивное тело при однопроходной сварке
пластин встык с учетом начальной
температуры находим из формул для
быстродвижущихся источников при r=0
и y=0.
массивное тело
;
пластина
.
где T0
— начальная температура изделия или
температура сопутствующего подогрева.
Знак минус в
уравнениях показывает, что происходит
остывание металла. Скорость охлаждения
зависит от формы изделия (массивное
тело, пластина), эффективной погонной
энергии и температуры подогрева.
Температура
подогрева T0
практически позволяет в большей степени
регулировать скорость охлаждения, чем
эффективная погонная энергия, но при
сварке крупных деталей ее значения
приходится ограничивать для соблюдения
температурного режима работы персонала.
Влияние подогрева
и погонной энергии сварки на скорость
охлаждения резче сказывается в пластинах,
чем в массивных телах. Это следует из
показателей степеней в формулах.
Пример. Для
случая наплавки углеродистой стали
определить рекомендуемую погонную
энергию, позволяющую избежать закалочные
структуры без подогрева, если известно,
что при 600 °С критическая скорость
охлаждения υохл = 35 °С/с (принять
= 38 Вт/(м
град). Какие параметры режима можно
рекомендовать при υ=15 м/ч ?
Используем формулу
для определения скорости охлаждения
при наплавке на массивное тело.
Т = 600 0С
– температура, при которой определяется
мгновенная скорость охлаждения, Т0
= 0 0С – наплавка без подогрева.
Скорость источника
υ = 15 м/ч = 0,00417 м/с.
,
Вт.
Пример. Для
случая наплавки массивного тела на
режиме: I=700 A, U=35
В, υ=20 м/ч рассчитать температуру
предварительного подогрева (То),
позволяющую избежать появления закалочных
структур, если известно, что допускаемая
критическая скорость охлаждения при Т
= 500 °С составляет 5 °С/с (принять
= 45 Вт/(м град)).
Мощность источника
теплоты (принимаем КПД η=0,8)
q
= U·I·η
= 700 · 35 · 0,8 = 19600 Вт.
Скорость источника
υ = 20 м/ч = 0,00556 м/с.
Используем формулу
для определения скорости охлаждения
при наплавке на массивное тело, откуда
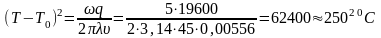
Т — Т0
= 250,
Т0
= Т – 250 = 250 0С.
В
случае расчетной схемы точечного
источника на поверхности плоского слоя
для расчета скорости охлаждения
используют выражение
,
где k
– поправочный коэффициент, определяемый
по номограмме (рис. 29) в зависимости от
значения критерия ζ, значения
которого вычисляют по формуле:
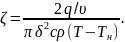
Следует
отметить, что при значениях критерия
ζ>2,5
скорости
охлаждения точек плоского слоя,
расположенных на оси шва почти совпадают
со скоростью охлаждения точек пластины,
а при ζ<0,4
— со скоростями охлаждения точек
полубесконечного тела.
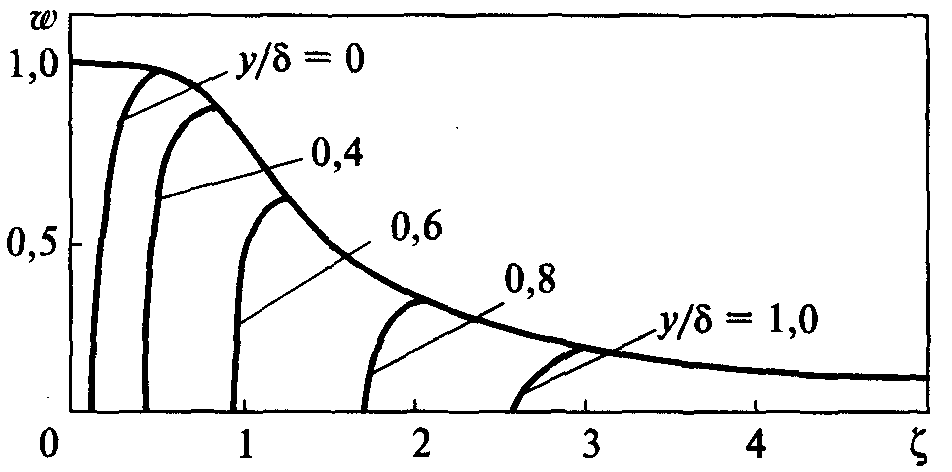
Рис.
29.
Номограмма для определения поправочного
коэффициента при расчетах мгновенных
скоростей охлаждения в плоском слое
Пример.
На стальной лист толщиной δ=24
мм наплавляют валик погонной энергии
q/υ=32
кДж/см. Теплофизические коэффициенты
равны: λ=0,38
Вт/(см·К), сρ=5,2
Дж/(см3·К).
Определить влияние начальной температуры,
изменяющейся в диапазоне от -30 до +20
(243…293 К), на мгновенную скорость охлаждения
металла на оси при температуре Т=
700 °С (973 К).
Решение.
Выбираем расчетную схему плоского слоя.
Определяем значение безразмерного
критерия ζ,
для начальной температуры
Тн
=
293 К:
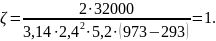
По
номограмме (рис. 6.2) находим соответствующее
значение поправочного коэффициента:
к=0,79.
Определяем скорость охлаждения при
Т=
973 К:
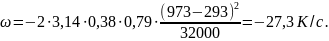
Повторяем
расчеты для начальной температуры
Тн=243
К
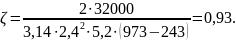
По
номограмме находим соответствующее
значение поправочного коэффициента:
к=0,87.
Определяем скорость охлаждения при
Т
= 973 К:
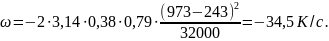
Таким
образом, при изменении начальной
температуры мгновенная скорость
охлаждения 700
на оси шва изменяется в пределах от 34,5
К/с (при
Тн=243
К) до 27,3 К/с (при
Тн
=293 К).
Расчет
длительности пребывания при температуре
выше заданной. Длительность
пребывания металла при температуре
выше заданной Тзад
выражается отрезком tн
= t2
— t1
на рис. 28. Для определения tн
необходимо, используя математическое
выражение термического цикла
T(t),
вычислить корни t2
и
t1
уравнения
T(t)
—
Тзад
=0.
Рассмотрим
два сварочных процесса: 1) наплавку на
массивное тело и 2) однопроходную сварку
листов встык, которые соответствуют
расчетным схемам точечного источника
на поверхности массивного тела и
плоского источника в бесконечной
пластине. Используя модели быстродвижущихся
источников теплоты для расчета термических
циклов без учета теплоотдачи с поверхности
(b=0)
и приведенные выше выражения для расчета
максимальных температур, возможно
получить уравнения
кривых связывающих безразмерную
температуру θ=(Т—Тн)/(Тm—Тн)
с безразмерными параметрами времени
τ2
и τ3:
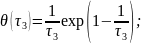

где
τ3=4at/r2
;
τ2=4at/y2.
Таким
образом, все многообразие термических
циклов для любых точек массивного тела
или пластины при различных параметрах
режима и разных теплофизических свойствах
материалов выражается одной обобщающей
кривой: θ(τ3)
—
для
массивного тела; θ(τ2)
— для
пластины (рис. 30).
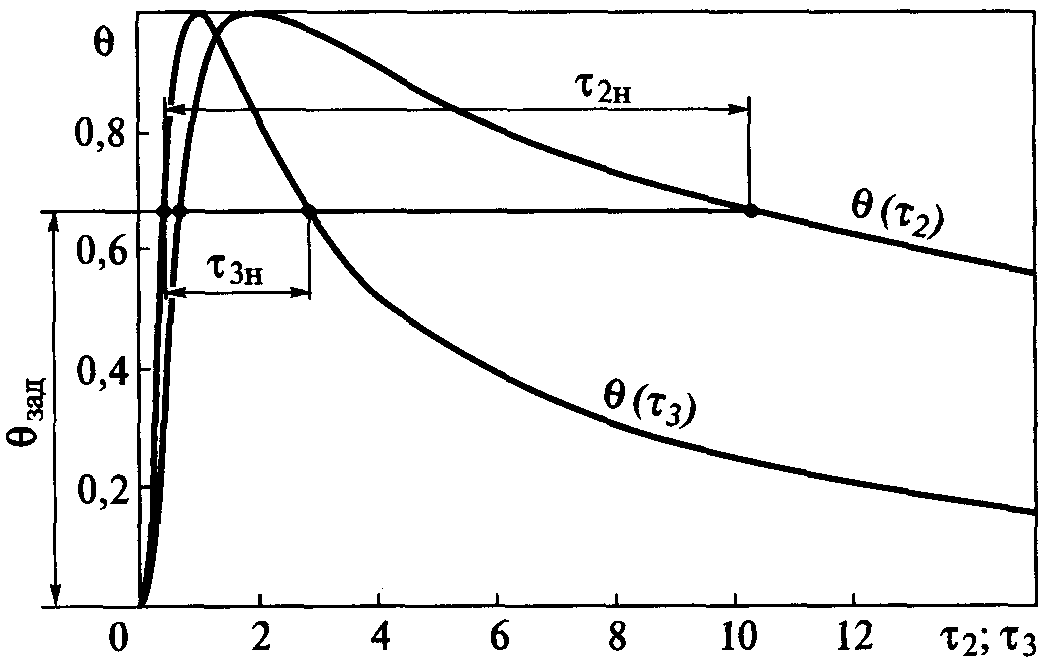
Рис.
30. Термические
циклы в безразмерных переменных для
схем нагрева массивного тела
быстродвижущимся точечным источником
θ(τ3)
и пластины
быстродвижущимся линейным источником
θ(τ2)
Сложная
зависимость между многими переменными
процесса распространения теплоты
значительно упрощается и сводится к
простой зависимости между двумя
рационально выбранными безразмерными
величинами, каждая из которых представляет
собой простое сочетание нескольких
переменных процесса. Из зависимостей,
представленных на рис. 6.3,
следует,
что заданной безразмерной температуре
θзад
соответствуют безразмерные длительности
пребывания материала при температуре
выше нее τ3н
для массивного тела и τ2н
для пластины.
Зависимости
размерной длительности нагрева найдем,
используя ее связь с безразмерными
параметрами времени τ3н
и τ2н:
t3н
= τ3н
r2/4a;
t2н
= τ2н
y2/4a;
Расстояния
r
и
у
в получим
из формул для определения максимальных
температур термического цикла:
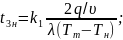
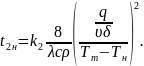
Коэффициенты
k1
и k2
определяем по номограмме (рис. 31)
в зависимости
от безразмерной температуры
θ=(Тзад—Тн)/(Тm—Тн),
где Тm
– максимальная температура термического
цикла в заданной точке изделия; Тзад
– температура, длительность пребывания
выше которой подлежит определению; Тн
— начальная
температура изделия.
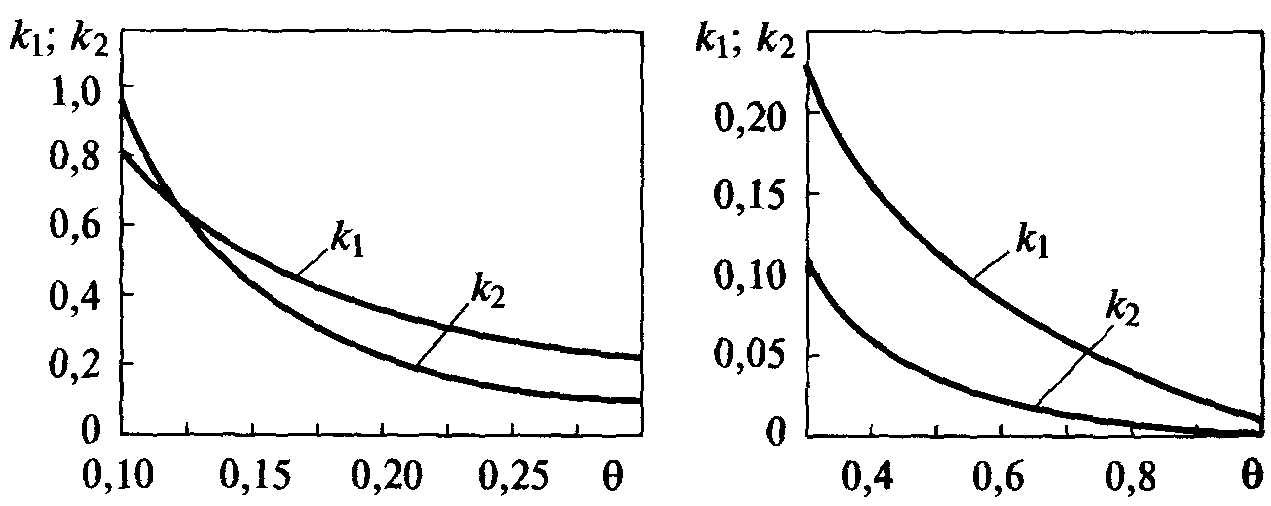
а
б
Рис.
31. Номограмма
для определения коэффициентов
k1
и
k2
в
зависимости от значений θ:
0,1… 0,3 (а) и
0,3.. .1 (б)
Пример.
Определить
длительность пребывания при температурах
выше 1000 °С
точек околошовной зоны, лежащих вблизи
зоны сплавления и испытавших нагрев
до подсолидусных температур
Тт=1350
°С при
электрошлаковой сварке стальных плит
толщиной δ=800
мм. Эффективная
мощность источника теплоты
q
=
130 кВт; скорость
сварки υ=0,3
м/ч =
0,0083 см/с;
начальная температура изделия
Тн=20
°С.
Теплофизические коэффициенты:
λ=
0,40 Вт/(см·К);
сρ=5
Дж/(см3·К).
Поскольку
при электрошлаковой сварке источник
теплоты (шлаковую ванну) нельзя считать
быстродвижущимся, то возможна лишь
ориентировочная оценка. Применим схему
линейного источника теплоты в пластине.
Определяем безразмерную температуру:
θ=(1000-20)/(1350-20)=0,73
По
номограмме (рис. 6.4)
определяем
значение коэффициента k2
для θ=0,73:
k2=0,012.
Определяем
длительность пребывания металла при
температурах выше заданной:

3.2.
Расчет ширины зоны
нагрева
Для
оценки термического влияния на свариваемый
металл бывает необходимо определить
размеры зоны 2l,
нагревавшейся выше
заданной температуры Тl
(рис. 32). В общем
случае ширина зоны
нагрева выше температуры Ти
определяемая величиной
2l,
будет найдена, если
определить координату у
точки А.
Точка А,
во-первых, находится
на изотерме и, следовательно, имеет
температуру Тl
во-вторых, в точке А
достигается
максимальная температура
на расстоянии y=l,
т. е. T/x=0.
Таким образом, для определения ширины
зоны необходимо решить систему двух
уравнений.
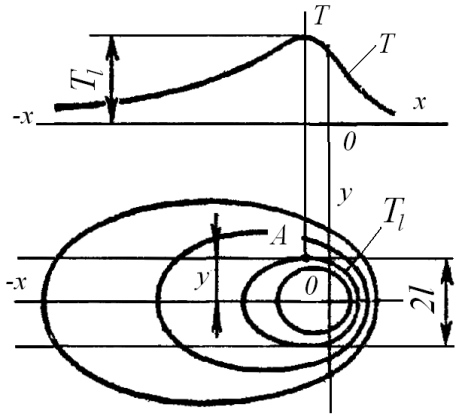
Рис. 32. Ширина зоны
2l,
нагревавшейся
выше температуры Тl
Для
мощного быстродвижущегося точечного
источника теплоты на поверхности
полубесконечного тела ширину зоны
термического влияния можно определить
из уравнения:
.
Ширина
зоны нагрева при сварке пластины
определяется аналогично полубесконечному
телу. Для мощного быстродвижущегося
линейного источника теплоты в пластине
при b=0
ширину зоны нагрева 2l
определяют по формуле:
.
Пример.
На поверхность массивного
тела наплавляется валик. Определить
ширину зоны, нагревшейся выше 600С,
при которой углеродистая сталь в
значительной мере теряет упругие
свойства. Режим: I
= 400 A,
U
= 25 В, υ = 9 м/ч (=0,6).
Теплофизические свойства: а=0,08
см2/с;
с=4,9
Дж/(см3град).
Мощность источника
теплоты
q
= U·I·η
= 400 · 25 · 0,6 = 6000 Вт
Скорость источника
υ = 9 м/ч = 0,25 см/с.
см.
Пример.
Как влияет величина
погонной энергии на размеры зоны
термического влияния? В каком из 3-х
случаев размер ЗТВ будет наименьшим и
наибольшим для режимов дуговой сварки
при прочих равных параметрах:
1
– I1
= 200 A; U1
= 28 В;
υ
1 = 7
м/ч.
2
– I2
= 400 A; U2
= 30 В;
υ
2 =
20 м/ч.
3 – I3
= 450 A;
U3
= 31 В; υ
3
=
25 м/ч.
Погонная энергия
– отношение эффективной энергии
источника теплоты (q)
к скорости его движения (υ).
Зависимость ширины
ЗТВ от отношения q/
υ описывается выражениями: для
точечного источника на поверхности
полубесконечного тела (1.16); для
линейного источника в пластине (1.17).
Вариант 1: q/
υ = UI/ υ = 200·28/ 7
= 800
Вариант 2: q/
υ = UI/ υ = 400·30/20
= 600
Вариант 3: q/
υ = UI/ υ = 450·31/25
= 560
Ширина ЗТВ наибольшая
в первом случае, наименьшая в третьем.
Пример. Тонкая
пластина из низколегированной стали
(
= 6 мм) проплавляется
дугой на режиме: I
= 350 A,
U
= 10 В, υ = 18 м/ч.
Определить ширину зоны, нагревшейся
выше 700°С (принять
= 0,6; с
= 5 Дж/(см3град)).
Мощность источника
теплоты
q
= U·I·η
= 350 · 10 · 0,6 = 2100 Вт
Скорость источника
υ = 18 м/ч = 0,5 см/с.
см.
3.3.
Плавление
основного металла
Плавление
основного металла при сварке осуществляется
с целью соединения между собой
свариваемых деталей. Идеальным в
отношении затрат теплоты представляется
такое тепловыделение в источнике, при
котором обеспечивается минимальная
глубина проплавления сопрягаемых
поверхностей, а присадочный металл не
используется вовсе или входит в соединение
в минимальном объеме. Если не рассматривать
диффузионную сварку и пайку, при которых
детали нагреваются полностью, и сварку
трением, при которой полного плавления
металла не достигается, наиболее точно
этому Идеальному представлению
соответствуют высокочастотная сварка
и некоторые виды контактной сварки
(точечная, шовная, рельефная). В
перечисленных способах сварки существенная
роль в образовании соединения принадлежит
давлению, что позволяет плавить основной
металл незначительно. Ограничимся
рассмотрением случаев плавления
основного металла в способах сварки
без применения давления.
Формы
сварочной ванны при различных способах
сварки.
При
электронно-лучевой сварке стыковых
соединений деталей толщиной до сотен
миллиметров удается получить минимальную
ширину зоны проплавления основного
металла. Сварочная ванна поперечном
сечении имеет форму, близкую к продольному
сечению конуса, а в плоскостях,
перпендикулярных лучу —
близкую
эллипсу.
При
электрошлаковой сварке также можно
получить минимальное проплавление
основного металла, но для ведения
шлакового процесса с целью получения
достаточного выделения тепло необходим
зазор, который затем должен быть заполнен
присадочным металлом. Сварочная ванна
может быть мелкой или глубокой зависимости
от скорости сварки и мощности источника.
Форма ванны при электрошлаковой сварке
зависит от соотношения мел количествами
теплоты, поступающими в основной металл
непосредственно от шлака и от опускающегося
в металлическую ванну перегретого
электродного металла.
При
использовании дуговых, плазменных и
газопламенных источников теплоты при
сварке встык листов металла небольшой
толщины форма ванны близка к форме
изотермы, которая соответствует
температуре плавления, рассчитанной
для схемы движущегося линейного источника
в пластине. С ростом толщины лист металла
разница в размерах ванны на верхней и
нижней поверхностях листа становится
все более значительной, а при некоторой
толщине полное проплавление уже не
достигается, как показано на рис. 33.
Для
увеличения проплавляющей способности
указанных источников используют
разделку кромок. Проплавляющую способность
различных источников теплоты обычно
оценивают экспериментальным путем,
расплавляя поверхность массивного тела
или толстой пластины.
Геометрические
размеры сварочной ванны и валика шва
характеризуются следующими параметрами
(рис. 33):
L
— длина
ванны, В
—
ширина
ванны, H
— глубина проплавления,
Нк
—
глубина
кратера, А
—
высота
выпуклости шва, Fnp
— площадь
проплавления, Fн
— площадь
наплавки. Форму зоны проплавления
оценивают; относительной глубиной
проплавления
H/В
или коэффициентом формы провара ψпр=B/H,
а
также коэффициентом полноты проплавления
μпр=Fnp/(HB),
значение
которого обычно составляет 0,6…0,8.
Для
дуговых видов сварки относительная
глубина проплавления
Н/В
достигает максимального значения,
приблизительно равного 3 (сварка под
флюсом). Очертания зоны наплавки
характеризуются коэффициентом формы
валика ψв=В/А
и коэффициентом полноты валика μв
= Fн
/(АВ).
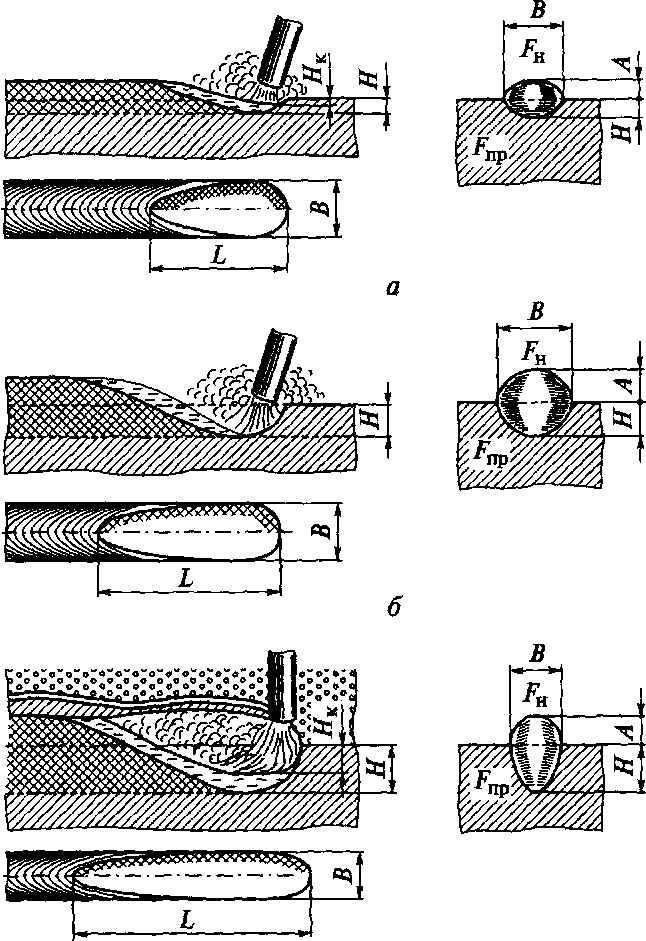
Рис.
33.
Формы
сварочной ванны при дуговой
сварке: а
—
поверхностная
дуга;
б
—
погруженная
дуга;
в —
дуга
под флюсом
Расчет
размеров зоны проплавления. Теоретически
очертание ванны расплавленного металла
соответствует очертанию изотермической
поверхности, соответствующей температуре
плавления Тпл.
Однако в известных расчетных схемах не
учитываются распределенный характер
источника теплоты, наличие зазора и
разделки кромок, давление дуги, движение
металла в сварочной ванне, скрытая
теплота плавления, переменны значения
теплофизических свойств и др. Вследствие
этого расчеты позволяет оценить размеры
ванны весьма приближенно.
Длина
ванны
L
при
наплавке валика на массивное тело может
быть рассчитана по формуле:
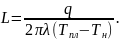
Ширина
ванны в предположении, что источник
теплоты быстродвижущийся, может быть
оценена с помощью выражения для вычисления
ширины зоны нагрева при Т=Тпл:
.
Площадь
проплавления основного металла при
наплавке валика на массивное тело
можно определить как площадь, ограниченную
в поперечном сечении линией максимальных
температур, равных температуре плавления
Тпл.
Принимая, что в поперечном сечении
изотермы представляют собой полуокружности,
получим следующее выражение для площади
проплавления:

Для
однопроходной сварки листов с полным
проплавлением, используя расчетную
схему быстродвижущегося линейного
источника в пластине без теплоотдачи,
получены следующие
выражения:

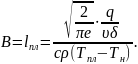
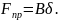
Форма
и размеры ванны при прочих равных
условиях (мощности источника теплоты
и скорости сварки) существенно зависят
от характера подачи и температуры
присадочного металла. При подаче в ванну
холодной непрерывной или рубленной на
мелкие части проволоки ванна становится
короче. Поэтому оценка
L,B
и
Fnp
по
приведенным выше формулам справедлива
лишь для идеализированных условий.
Поправочные коэффициенты для более
точного определения размеров ванны
могут быть получены экспериментально.
Температура
сварочной ванны. Температуры
жидкого металла в разных точках сварочной
ванны могут сильно различаться между
собой. У границы с твердым металлом
температура жидкого металла близка к
температуре плавления. Она может быть
как несколько ниже Тпл
вследствие кристаллизационного
переохлаждения, так и выше —
при
больших скоростях движения жидкого
металла вдоль твердой границы. Как
следует из рис. 33,
расплавляющийся
на передней кромке ванны жидкий металл
поступает в ее хвостовую часть, проходя
вдоль боковых поверхностей и дна ванны.
При этом скорости движения металла
могут превышать скорость сварки в
несколько раз. Максимальная температура
жидкого металла существенно зависит
от источника теплоты. При лучевых
способах сварки, особенно при значительной
концентрации энергии в пятне нагрева,
температура металла может достигать
температуры кипения.
Дуговые
и плазменные источники теплоты также
способны создавать на поверхности
металла довольно высокие температуры,
например у сталей —
до
2300
К.
При электрошлаковом процессе температура
жидкого присадочного металла, проходящего
через активную зону шлаковой ванны (где
выделяется теплота), достигает температуры
шлака, которая в средней по высоте части
шлаковой ванны составляет 2100…2200
К,
а на поверхности шлака около 2000
К.
При
способах сварки плавлением, особенно
с использованием дуги, происходит
интенсивное перемешивание жидкого
металла
как
вследствие его движения из головной
части ванны в хвостовую, так в результате
воздействия источника теплоты на жидкий
металл. Происходит интенсивный теплообмен
между отдельными порциями различно
нагретого жидкого металла, а также отвод
теплоты в твердый металл. Поэтому
состояние ванны целесообразно
характеризовать не только возможными
максимальными и минимальными температурами,
но и средней температурой жидкого
металла. Она зависит от режима сварки
(сварочного тока, напряжения дуги,
скорости сварки), характера подачи
присадочного металла, устойчивости
дуги и положения ее активного пятна.
Например, средняя температура ванны
при аргонодуговой сварке алюминиевого
сплава АМг6 может изменяться от 650
до
780
оС
(при
возрастании тока от 300
до
450
А)
при Uд=14
В
и от 800
до 930 °С
при Uд=8
В,
в то время как температура плавления
сплава АМг6 составляет 610
°С.
Тепловая
эффективность процесса проплавления.
Тепловую
эффективность процесса проплавления
оценив термическим (ηt)
или
полным тепловым (ηпр)
КПД процесса плавления основного
металла. На нагрев проплавляемой зоны
температуры плавления и перевод ее в
жидкое состояние расходуется только
часть
q‘
эффективной
тепловой мощности источника. Остальная
теплота
(q
— q‘)
затрачивается
на перегрев сварочной ванны выше и
нагрев основного металла, окружающего
сварочную ванну. Эти бесполезные (с
точки зрения образования сварного
соединения) потери теплоты практически
неизбежны при сварке вследствие
сосредоточенного характера источника
теплоты и значительной теплопроводности
основного металла.
Термический
КПД представляет собой отношение
полезной мощности
q‘
к
эффективной мощности источника теплоты
q:
ηt
= q‘/q
=υ·Fпр·ρ·ΔHпл
/q,
где
ΔHпл
—
приращение
энтальпии расплавленного металла при
нагреве до температуры плавления,
включающее скрытую теплоту плавления.
При
расплавлении металла массивного тела
точечным источником теплоты термический
КПД ηt
выше у мощных дуг, перемещающихся с
большой скоростью, и может достигать
предельного значения 0,368.
Это
значение можно получить из выражения
для
площади проплавления основного металла,
если
учесть, что в рамках классической теории
распространения теплоты при сварке
приращение энтальпии ΔНпл
=
с(Тпл—Тн):
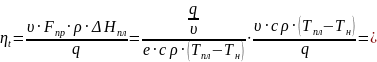
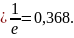
Для
схемы мощного быстродвижущегося
линейного источника
теплоты
в пластине предельное значение ηt
составляет
=0,484.
При
сварке швов, образуемых преимущественно
наплавленным металлом, тепловую
эффективность процесса наплавки
характеризуют полным тепловым КПД
процесса наплавки:
ηн
=υ·Fн·ρ·ΔHпл
/
(UI),
где
Fн
– площадь
сечения наплавленного металла;
UI
—
полная
тепловая мощность сварочного источника.
3.4.
Нагрев
и плавление присадочного металла
Термические
циклы в присадочном металле не имеют
самостоятельного значения, так как
в конечном итоге присадочный металл
подвергается переплавке. Изучение
нагрева присадочного металла и
распределения температур позволяет
оценить условия, в которых происходит
его плавление. Исследование процесса
нагрева электродов, имеющих покрытия,
имеет важное значение для определения
возможной потери свойств и разрушения
покрытия вследствие его перегрева.
Все
случаи нагрева присадочного металла
(электрода) можно разделить в основном
на две схемы:
—
присадочный стержень (электрод) имеет
конечную длину, при этом место токоподвода
относительно электрода не перемещается;
—
присадочный стержень (электрод)
бесконечен, при этом электрод перемещается
относительно места токоподвода (если
таковое имеется).
Первая
схема применяется при ручной дуговой
сварке штучными электродами, электрошлаковой
сварке пластинами, электрошлаковом
переплаве, электрошлаковой сварке
плавящим мундштуком (по отношению к
мундштуку), газовой или дуговой сварке
с присадкой, сварке неплавящимся
электродом (по отношению к вольфрамовому
или угольному электроду).
Вторая
схема нагрева характерна для
механизированной сварки плавящимся
электродом, электрошлаковой сварки
проволоками, сварки неплавящимся
электродом с механизированной подачей
присадочной проволоки в зону горения
дуги (по отношению
к присадочной
проволоке).
Первая
схема нагрева.
При
первой схеме нагрева в общем случае
(рис. 34)
электрод
конечной длины имеет в точке
А
токоподвод. По электроду протекает ток,
который его подогревает; в точке
О
электрод дополнительно нагревается
источником теплоты —
дугой
(рис. 34,
а)
или шлаком (рис. 34,
б)
и плавится.
Рассмотрим
отдельно процесс нагрева; электрода
протекающим током. Уравнение теплового
баланса элементарного участка
dx
стержня
площадью сечения
F
имеет
вид
dQ
= dQj
— dQα.
Левая
часть уравнения
представляем
собой накопление теплоты в элементе
стержня:
dQ
= cρ·F·dx·dT.
|
|
Рис. |
а
б
Первый
член правой части уравнения выражает
количество теплоты
dQj,
выделяемой
в элементе стержня от прохождения тока
I
в течение времени dt.
Согласно закону Джоуля — Ленца
dQj=I2dRdt,
где
dR
—
сопротивление участка проводника длиной
dx,
которое можно выразить через его площадь
сечения
F
и удельное сопротивление материала
r:
dR=r·dx/F.
Второй
член правой части уравнения выражает
потери теплоты
dQα
в окружающую среду с поверхности стержня
с периметром сечения
р:
dQα=α(Т-Tc)p·dx·dt.
Подставляя
полученные выражения в уравнение
теплового баланса и сокращая обе части
на
cρFdxdt,
получаем дифференциальное уравнение
процесса нагрева проводника проходящим
током:

где
j
— плотность тока;
b
— коэффициент температуроотдачи стержня.
Следует
отметить, что входящие в уравнение
удельное сопротивление r,
объемная теплоемкость cρ
и коэффициент поверхностной теплоотдачи
α
зависят от температуры, поэтому достаточно
хорошее приближение к точному решению
уравнения можно получить только методами
компьютерного моделирования.
Влияние
нагрева электрода теплотой дуги
сказывается только в непосредственной
близости от расплавляемого торца
электрода (рис. 35).
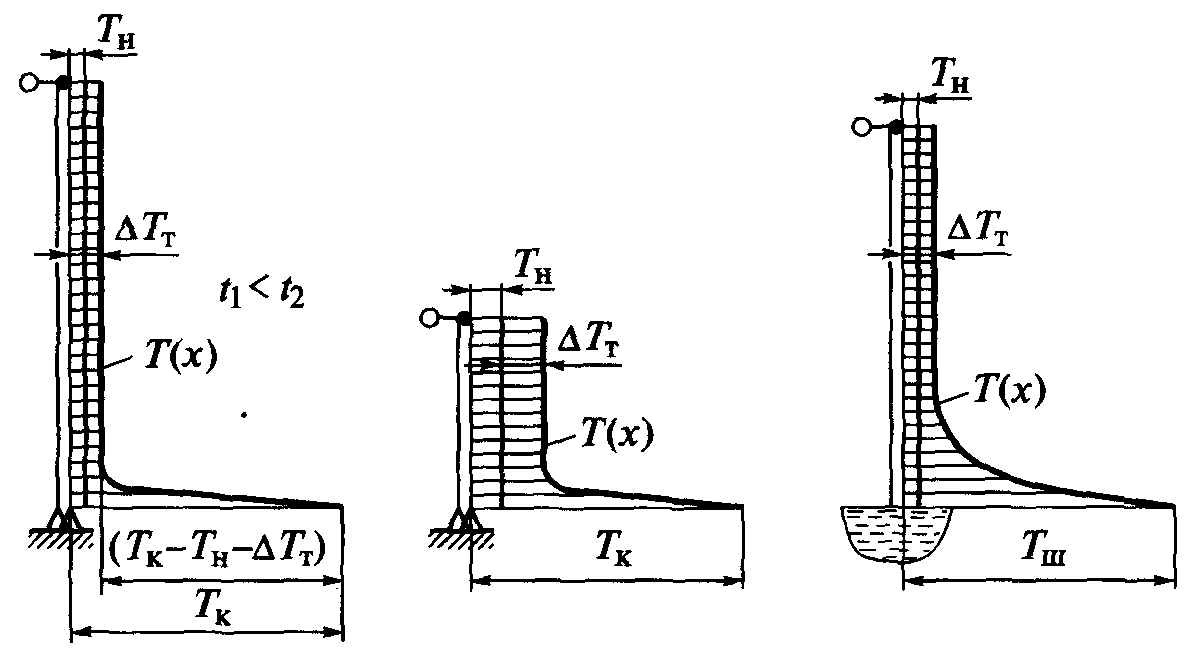
а
б в
Рис.
35.
Распределение
температуры вдоль оси электрода при
первой схеме
нагрева: а
— при
ручной сварке и малом времени нагрева
t1;
б-
при ручной сварке и значительном времени
нагрева
t2;
в
— при
электрошлаковой сварке пластинами
Быстрый
спад температуры впереди дуги обусловлен
значительной скоростью ее перемещения.
Распределение температуры
T(х)
в электроде вблизи дуги описывается
уравнением предельного состояния
процесса распространения теплоты от
подвижного плоского источника в стержне.
Учитывая, что температура на
торце электрода равна температуре
капель расплавленного металла
Тк,
уравнение для области впереди источника,
т. е. при х>0,
можно
записать в виде:
Т(х)
= TH
+ ΔTТ
+
(TK
—
TH
—
ΔTТ)ехр(-υx/a)
где
ΔTТ
—
приращение
температуры от подогрева электрода
протекающим током;
υ
—
скорость
плавления электрода.
Таким
образом, при первой схеме нагрева
распределение температур вдоль большей
части длины электрода является равномерным
и определяется тепловыделением,
обусловленным протеканием тока, (рис.
35).
Чтобы
избежать чрезмерного нагрева электродов,
приводящего к разрушению или потере
свойств их защитного покрытия, ограничивают
сварочный ток. Допустимый ток в основном
зависит от состава покрытия электрода.
Для электродов с органическим покрытием
допустимый ток значительно меньше, чем
для электродов с минеральным покрытием.
Вторая
схема нагрева
При
дуговой или электрошлаковой сварке с
механизированной подачей электродной
проволоки (рис. 36)
ее
нагрев также осуществляется двумя
источниками теплоты —
проходящим
током
(qT)
и
дугой
(q,
рис.
36,
б)
или шлаковой ванной рис. 36,
г).
Длина нагреваемой части при этом остается
постоянной и равной вылету электрода
l.
Ввиду
высокой скорости подачи проволоки
влияние нагрева теплотой дуги или
шлаковой ванны сказывается только в
непосредственной близости от расплавляемого
торца электрода.
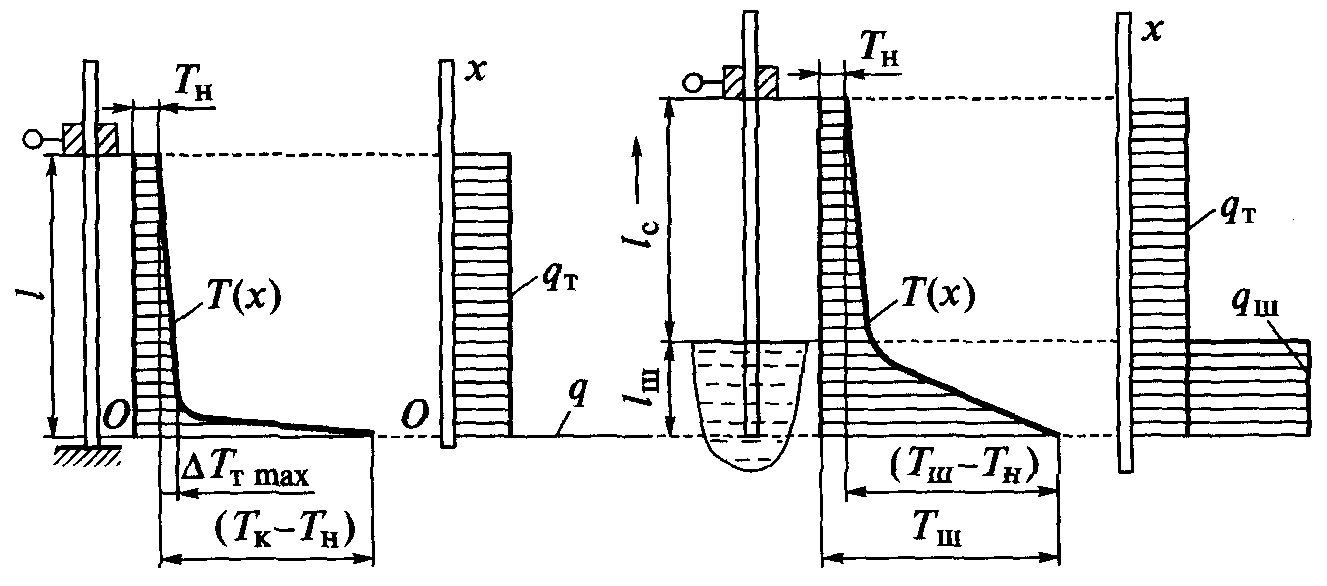
а
б в
г
Рис.
36.
Нагрев
электродной проволоки при механизированной
подаче: а
— распределение температур при дуговой
сварке; б —
схема
действия источников теплоты в проволоке
при дуговой сварке;
в
—
распределение
температур при электрошлаковой
сварке проволоками;
г
—
схема
действия источников теплоты в проволоке
при электрошлаковой сварке
В
отличие от первой схемы нагрева
распределение температур при нагреве
проходящим током в вылете движущегося
со скоростью подачи υпп
электрода не является равномерным. Это
обстоятельство связано с тем, что
время нагрева произвольного сечения
зависит от его положения (координаты
х).
Так, непосредственно у токоподвода (х
= l)
электрод имеет начальную температуру
Тн,
а на расстоянии х’
=
l
—
х
от токоподвода сечение испытывало
нагрев проходящим током в течение
времени
t‘
= x‘/υnn.
Используя
дифференциальное
уравнение процесса нагрева проводника
проходящим током
и
пренебрегая теплоотдачей с поверхности
(b=0),
а
также тепловым потоком в направлении
оси электрода, получаем линейное
распределение приращений температуры
по длине электрода:
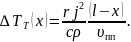
Таким
образом, в результате подогрева в вылете
электрод протекающим током при приближении
к расплавляемому тепле той дуги торцу
электрода металл уже подогрет до
температуры

С
учетом полученных выражений распределение
температур в электроде при второй схеме
нагрева может быть описано выражением
Т(х)
= TH
+ ΔTТ
(x)
+
(TK
—
TH
—
ΔTТ(l))ехр(-υnnx/a)
Производительность
расплавления электрода.
Плавление
электродов при дуговых способах сварки
осуществляется в результате нагрева
металла дугой от температуры подогрева
Тп=Тн+ΔТт
до температуры капель
Тк.
Приращение энтальпии материала электрода
при этом составляет
ΔН=ΔНК
–ΔНП.
Приравнивая количество теплоты
qΔt,
вводимое дугой в электрод, к количеству
теплоты, необходимому для расплавления
массы
υFρΔt
металла, получаем уравнение процесса
плавления электрода:
ηэUI
= υFρ
(ΔНК
– ΔНП),
где
ηэ
— эффективный КПД нагрева электрода
дугой;
υ
—
скорость плавления электрода.
Мгновенная
массовая скорость расплавления электрода
gp
= υFρ
при постоянных значениях ηэ
и
U
зависит от энтальпии ΔНП
подогретого
током металла и силы сварочного тока:
gp=
ηэUI/(ΔНК
– ΔНП).
Если
нагрев электрода током незначителен,
то производительность его расплавления
примерно пропорциональна силе сварочного
тока. В сварочной технике производительность
расплавления электрода обычно
характеризуют коэффициентом расплавления
αр,
г/(А∙ч), который определяется как
отношение массы расплавившейся части
электрода Δm
к произведению силы сварочного тока I
и времени горения дуги
Δt:
αр=Δm/(IΔt).
При
ручной дуговой сварке штучными стальными
электродами αр=8…15
г/(А·ч), причем производительность
расплавления возрастает к концу
расплавления электрода вследствие
нагрева его током. Неравномерность
расплавления электрода при правильно
выбранном режиме сварки обычно не
превышает 20…30 %.
При
механизированной подаче проволоки с
постоянным вылетом скорость расплавления
проволоки, равная скорости ее подачи
υпп,
определяется силой тока и вылетом
электрода. С увеличением вылета
производительность расплавления при
прочих равных условиях возрастает, так
как повышается ΔНП.
Значения αр
при механизированных способах дуговой
сварки сталей обычно находятся в
диапазоне 13.. .25 г/(А·ч).
Производительность
наплавки gн
зависит от производительности
расплавления электродной проволоки
gp:
gн
= gp(1
—
Кп),
где
Кп
— коэффициент потерь металла на угар и
разбрызгивание (при сварке открытой
дугой
Кп
=
0,05…0,2; при сварке под флюсом Кп
=
0,01.. .0,02).
Пример.
Определить температуру огарка электрода
диаметром
d=4
мм из низкоуглеродистой стали при
сварочном токе I=120
А. Длина рабочей части электрода Δl=400
мм, коэффициент расплавления αр=10
г/(А·ч). Удельное сопротивление
низкоуглеродистой стали ρ=14·10-6
Ом·см, объемная теплоемкость сρ
= 5 Дж/(см3·К).
Сначала
находим массу рабочей части стержня
электрода:
Δm=
ρ·F·Δl
= ρ·(πd2/4)·Δl
= 7,8·(3,14·0,42/4)·40
= 39,2 г.
Определяем
время протекания тока
Δt,
используя формулу αр=
Δm/(I·Δt):
Δt=Δm/(I·αр)=39,2/(10·120)=0,0327
ч = 117,6 c.
Время
расплавления рабочей части электрода
составляет приблизительно 2
мин.
В течение этого времени огарок электрода
нагревался
проходящим
током. Без учета теплоотдачи с поверхности
и нагрева дугой приращение температуры
огарка согласно равно
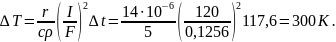
Таким
образом, с учетом начальной температуры
стержня 293
К
температура огарка составит 593
К
(320
°С).
Пример.
Для
электрода из предыдущего примера оценить
допустимый сварочный ток, если покрытие
начинает терять свои защитные свойства
температуре 773
К
(500
°С).
При
допустимом сварочном токе Iдоп
температура огарка
достигнет
своего предельного значения
Тдоп=773
К
за время
Δt,
которое
можно найти из формулы αр=
Δm/(I·Δt).
Используя
дифференциальное
уравнение нагрева стержня и
пренебрегая теплоотдачей с поверхности,
получаем выражение для приращения
температуры
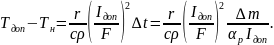
Отсюда
выражаем допустимый сварочный ток и,
подставляя исходные числовые значения,
получаем
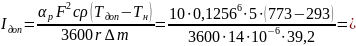
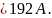
Следовательно,
для электрода диаметром
d=4
мм
из низкоуглеродистой стали допустимый
сварочный ток составляет 192
А.
Пример.
Определить
изменение температуры низкоуглеродистой
сварочной проволоки диаметром
d=4
мм
на расстоянии 30
мм
от токоподвода при механизированной
сварке током I=800
А.
Коэффициент расплавления принять равным
αp=20
г/(А·ч).
Удельное
сопротивление низкоуглеродистой
стали ρ=14·10-6
Ом·см, объемная теплоемкость сρ=5
Дж/(см3·К).
Решение.
Сначала определяем массу участка
проволоки длиной 30
мм
и время его расплавления:
Δm=
ρ·F·Δl
= ρ·(πd2/4)·Δl
= 7,8·(3,14·0,42/4)·3,0
= 2,94 г.
Δt=Δm/(I·αр)=2,94/(20·800)=0,000184
ч = 0,66 c.
В
течение этого промежутка времени
рассматриваемое сечение электрода
нагревалось проходящим током. Без учета
теплоотдачи с поверхности и нагрева
дугой приращение температуры в
рассматриваемом сечении составит
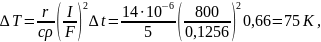
т.е.
на расстоянии 30 мм изменение температуры
проволоки равно 75
К.
3.5.
Термический
цикл при многослойной сварке
При
многослойной сварке сечение шва заполняют
за несколько сварочных проходов, поэтому
металл испытывает многократное тепловое
воздействие (рис. 37). Сложный термический
цикл складывается из термических циклов
отдельных сварочных проходов, которые
могут отличаться друг от друга параметрами
режима сварки и положением источника
теплоты в сечении шва. Наличие разделки
кромок, форма которой изменяется в
процессе ее заполнения, значительно
усложняет выбор расчетной схемы.
Вследствие сложности описания
процесса распространения теплоты при
многослойной сварке анализ термических
циклов целесообразно выполнять с
применением современных методов
компьютерного моделирования.
Аналитические
зависимости в рамках классической
теории распространения теплоты при
сварке позволяют дать лишь качественное
описание процесса. Количественные
оценки, получаемые для простейших схем
многослойной сварки, имеют ориентировочный
характер и служат для приближенного
определения параметров процесса.
При инженерных расчетах используют
значения параметров, которые
представлены в справочной литературе
и основаны преимущественно на
экспериментальных данных.
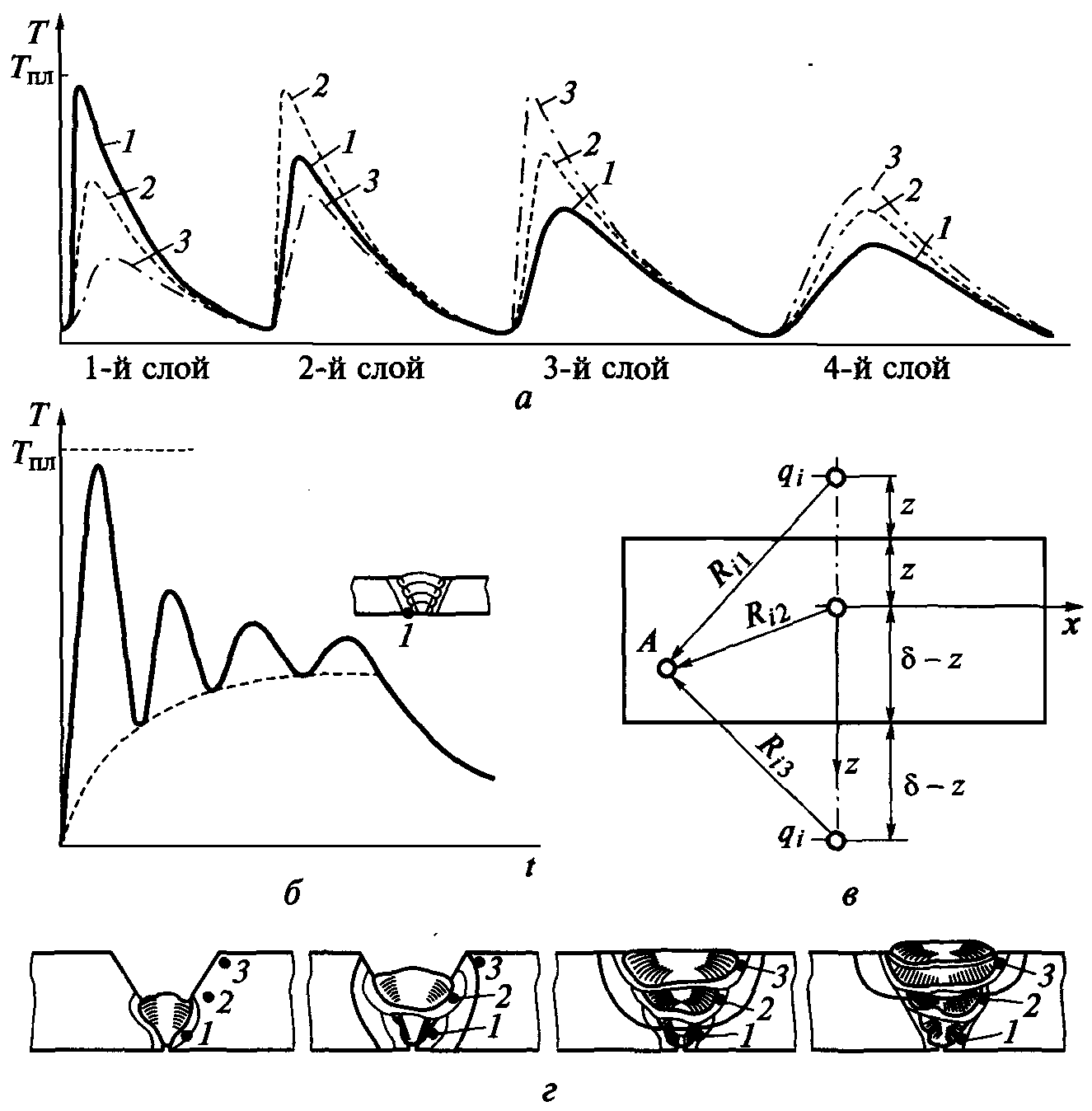
Рис.
37.
Термические
циклы при многослойной сварке: а
—
при
сварке длинными участками; б —
при
сварке короткими участками;
в —
расчетная
схема;
г
—
поперечное
сечение многослойного сварного соединения
Для
описания тепловых процессов при
многослойной сварке обычно применяют
расчетную схему бесконечного тела с
двумя адиабатическими границами (рис.
37,
в).
Учитывая значительную длительность
процесса многослойной сварки, рассматривают
температурные поля предельного
состояния от каждого прохода источника
теплоты. Суперпозиция таких температурных
полей в одном поперечном сечении
отражает характерную для всего изделия
тепловую обстановку. Особенности,
связанные с началом и прекращением
действия источника теплоты, не учитываются.
Основной
моделью источника теплоты при многослойной
сварке является подвижный точечный
источник постоянной мощности, действующий
внутри массивного тела. Выбор указанной
модели обусловлен необходимостью в
массивном объекте, каким обычно является
сварное соединение, выполняемое
многослойной сваркой, учитывать объемный
характер распространения теплоты
Адиабатические
границы учитывают введением в расчетную
схему двух фиктивных источников теплоты.
Таким
образом, приращение температур точек
изделия от каждого прохода источника
может быть вычислено как
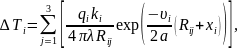
где
ki
—
поправочный коэффициент для учета
разделки кромок и положения источника
в сечении шва; Rij
— длины радиус-векторов, соединяющих
исследуемую точку с каждым источником
(включая фиктивные источники, введенные
для учета отражения от границ плоского
слоя); хi
— текущая координата рассматриваемого
поперечного сечения в подвижной системе
координат, связанной с источником;
i
— номер сварочного прохода.
Длины
радиус-векторов
Rij,
входящих в выражение, применительно к
точке с координатами (у,
z)
в поперечном сечении детали определяются
для каждого источника (включая фиктивные)
с координатами (уij,
zij)
по формуле
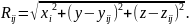
В
каждый момент времени температурное
поле при многослойной сварке является
суперпозицией полей приращений температур
от каждого прохода сварочного источника,
наложенной на однородное температурное
поле подогрева изделия:
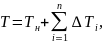
где
n
— число проходов при многослойной сварке.
Рассчитывают
приращения температур ΔTi
от прохода каждого источника рассчитывают,
при этом удаление xi
каждого источника qi,
от рассматриваемого поперечного сечения
рассчитывают с учетом скорости его
движения
υi
длины сварного шва lk
и времени перерывов Δtk
между укладкой отдельных валиков:
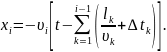
Тепловое
воздействие на металл при многослойной
сварке зависит от того, как осуществляют
сварку — длинными или короткими участками.
Сварка
длинными участками.
Под
сваркой длинными участками обычно
понимают укладку валика на всю длину
свариваемого соединения, составляющую
обычно более 0,5…
1 м.
При сварке склонных к закалке сталей
скорость охлаждения в интервале
температур наименьшей устойчивости
аустенита —
один
из параметров, определяющих возможность
появления закалочных структур. Наибольшая
скорость охлаждения
обычно бывает у первого слоя, так как
последующие слои, как правило, остывают
медленнее вследствие автоподогрева.
Однако,
если промежуток времени между укладкой
слоев достаточно велик (вследствие
длительных перерывов сварке или большой
протяженности сварного шва), массивное
изделие полностью остынет и скорость
охлаждения очередного слоя может
оказаться выше, чем первого слоя.
Для
оценки скорости охлаждения первого
слоя в стыковых (рис. 38,
б),
нахлесточных (рис. 38,
в),
тавровых (рис. 38,
г) крестовых
(рис. 38,
е)
соединениях используют расчетную схему
наплавки валика на плоский слой (рис.
38,
а)
с поправочными коэффициентами для
определения расчетной погонной энергии
(q/υ)расч
и расчетной толщины плоского слоя δрасч,
значения которых для разного вида
соединений приведены ниже:
Схема
(рис. 38) а б в г
д
δрасч
δ
1,5δ
δ δ δ
(q/υ)расч
q/υ
1,5q/υ
0,67q/υ
0,67q/υ
0,5q/υ
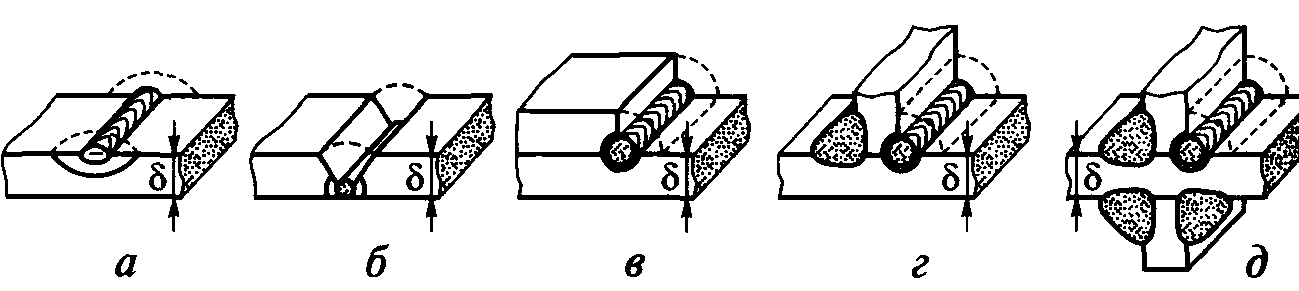
Рис.
38. Виды соединений,
выполняемых многослойной сваркой: а —
наплавка валика на поверхность; б —
стыковое соединение с разделкой кромок;
в — нахлесточное соединение; г — тавровое
соединение, д – крестовое соединение
Поправочный
коэффициент к погонной энергии вводят
для учета условий распространения
теплоты в области, непосредственно
прилегающей к месту введения теплоты,
а поправочный коэффициент к толщине в
стыковом сварном соединении с односторонней
V-образной
разделкой (рис. 38,
б)
—
для
учета условий распространения теплоты
вдали от шва (приведенное выше числовое
значение соответствует углу раскрытия
кромок 60
о).
Методика
расчета скоростей охлаждения в плоском
слое изложена выше.
Вместо
q/υ
и
δ
в
соответствующие формулы при расчете
подставляют указанные значения
(q/υ)расч
и δрасч.
Скорость
охлаждения первого слоя уменьшается с
увеличением его сечения, т. е. с увеличением
погонной энергии, с увеличением
температуры подогрева Тн
и с уменьшением толщины свариваемых
деталей δ.
Наиболее
сильно на скорость охлаждения влияет
температура подогрева
Тн.
Сварка
короткими участками.
К
многослойной сварке короткими участками
прибегают в тех случаях, когда стремятся
продлить пребывание металла выше
определенной температуры и не допустить
его охлаждения ниже этой температуры.
Выполнение коротких участков шва
способами «каскад» и «горка» практикуется
обычно при ручной дуговой сварке штучными
электродами. Режим многослойной сварки
включает помимо прочих три независимых
параметра —
погонную
энергию
q/υ,
которая
определяет сечение слоя, длину
завариваемого участка l,
температуру
подогрева Тн,
поэтому он более гибок, чем режим
однопроходной сварки.
Условия
сварки короткими участками выбирают
такими, чтобы температура охлаждения
каждого слоя к моменту наложения
следующего слоя не падала ниже определенной
температуры
Тв,
в качестве которой, например, часто
принимают температуру начала мартенситного
превращения свариваемой стали.
Температура
Тв,
до которой охлаждается первый слой,
зависит, в частности, от длины завариваемого
участка l,
погонной
энергии сварки
q/υ
и
температуры подогрева
Тн.
Время сварки
tc
участка
шва длиной l
складывается из времени чистого горения
дуги tг=
l/υ
и
перерывов tп:
tc
=
tг
+
tп.
Используя
схему быстродвижущегося линейного
источника пластине без теплоотдачи с
поверхности (рис. 39),
запишем
без вывода формулу для определения
длины завариваемого участка за время
сварки которого температура в его начале
не окажется ниже
Тв

где
—
k3
поправочный
коэффициент, найденный экспериментально
в зависимости от типа соединения;
kг
—
коэффициент
времени чистого горения дуги, принимаемый
при ручной сварке штучными электродами
равным 0,6
… 0,8.
Для
соединений встык k3=1,5;
для
соединений внахлестку и втавр k3=0,9;
для
крестового соединения k3=0,8.
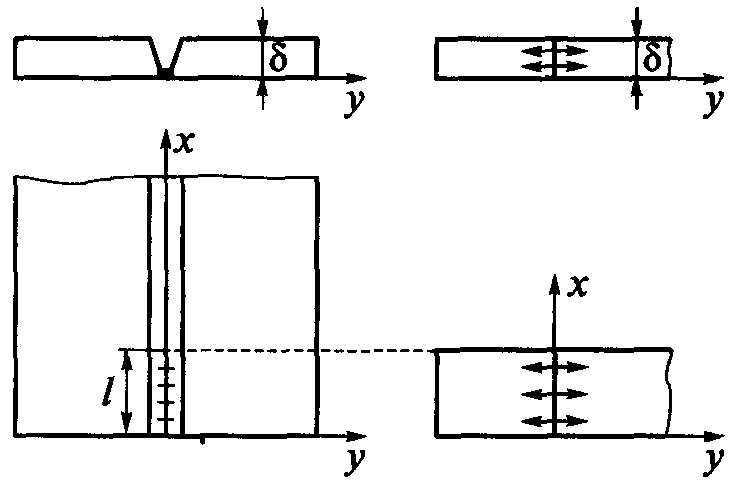
Рис.
39.
Расчетная
схема
определения
температуры остывания первого слоя
сварке короткими участками (стрелками
показаны тепловые потоки)
Следует
отметить, что в выбранной схеме (рис.
39),
строго
говоря, не учтен ряд особенностей
распространения теплоты
при
многослойной сварке. Однако она может
быть принята для расчета, если к моменту
достижения расчетной температуры Тв
(которая
обычно для сталей не превышает 650
К)
неравномерность
распределения
температур по толщине свариваемых
деталей невелика. Для практически
применяемых режимов многослойной сварки
разность температур к моменту охлаждения
первого слоя до
Тв=650
К,
как показывают экспериментальные
данные, не превышает 50…80
К.