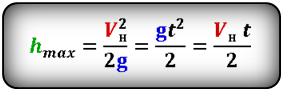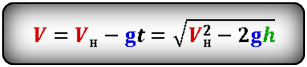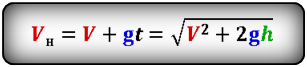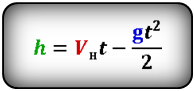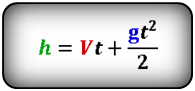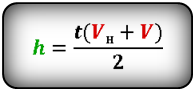Как найти время подъема на максимальную высоту - Исправление недочетов и поиск решений вместе с Examum.ru

Время подъема на максимальную высоту, тела, брошенного под углом к горизонту, формула

Время подъема на максимальную высоту определяется из условия, что вертикальная составляющая мгновенной скорости равна нулю

[ u_y = u_0 sin(α) — g t_{hmax} = 0 ]

из этого уравнения получаем:

[ t_{hmax} = frac{ u_0 sin(α) }{g} ]

Здесь:
u₀ — начальная скорость тела (м/с),
α — угол, под которым брошено тело к горизонту (°),
g — ускорение свободного падения 9.81 (м/c²),
t_hmax — время подъема на максимальную высоту (c)

Вычислить, найти время подъема на максимальную высоту тела, брошенного под углом к горизонту по формуле (2).

Время подъема на максимальную высоту тела, брошенного под углом к горизонту	стр. 418

Источник

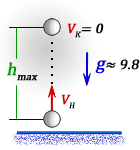
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту

h_max
— максимальная высота достигнутая телом за время t

V_к — конечная скорость тела на пике, равная нулю

V_н — начальная скорость тела

t — время подъема тела на максимальную высоту h

g ≈ 9,8 м/с² — ускорение свободного падения

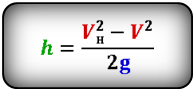
Формула максимальной высоты (h_max):

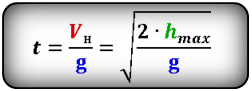
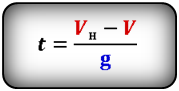
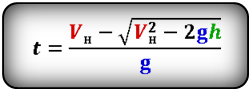
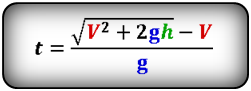
Формула времени за которое тело достигло максимальную высоту (t):

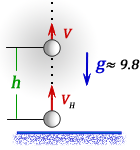
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести

h — расстояние пройденное телом за время t

V_н — начальная скорость тела

V — скорость тела в момент времени t

t — время подъема за которое тело пролетело расстояние h

g ≈ 9,8 м/с² — ускорение свободного падения

Формула скорости тела в момент времени t (V):

Формула начальной скорости тела (V_н):

Формулы высоты тела в момент времени t (h):

Формулы времени, за которое тело достигло высоту h (t):

Подробности

Опубликовано: 04 августа 2015

Обновлено: 13 августа 2021

Источник

В статье подробно, начиная с основ и базовых определений, рассказано о движении тела брошенного под углом к горизонту. Здесь вы найдете формулы параметров движения: общее время, дальность полета, максимальная высота. Также в конце приложены примеры задач с решениями.

Определение. Баллистическое движение — это движение некоторого тела в поле тяжести Земли при условии, что тело имеет вертикальную и горизонтальную проекции скорости.

Вначале вспомним основные формулы для равноускоренного движения.

Изменение скорости с течением времени задаётся соотношением

vₓ = v₀ₓ + aₓt,

где vₓ — конечная проекция скорости, v₀ₓ — начальная проекция скорости, aₓ — проекция ускорения тела.

Изменение координаты x во времени можно найти, используя следующее соотношение:

x = x₀ + v₀ₓt + aₓt² / 2,

где x — конечная координата тела, x₀ — начальная координата, v₀ₓ — начальная проекция скорости тела вдоль оси OX, aₓ — проекция ускорения тела.

Рис. 1

Замечание 1. Перемещением тела за время t называется величина Sₓ = x – x₀.

Замечание 2. Так как эти выражения справедливы для проекций, то их можно записать и в векторном виде.

Баллистическое движение — это случай равноускоренного движения (с постоянным ускорением свободного падения g). Любое тело, брошенное под углом α к горизонту, имеет некоторую вертикальную и горизонтальную проекции скорости (рис. 1).

Далее движение необходимо разбить на два участка:

Горизонтальное
Вертикальное

По горизонтали тело движется с одинаковой скоростью (обычно пренебрегаем силами различного трения):

v₁ = v₀cos(α)

А по вертикали это обычное движение тела, брошенного вертикально вверх с начальной скоростью:

v₂ = v₀sin(α)

Общее время движения

Разобьём траекторию на два участка. Первый — участок, на котором тело продолжает подниматься, а второй — участок, где тело спускается. Обозначим t₁ время подъёма тела (от нуля до максимальной высоты подъема), t₂ — время спуска тела.

Из уравнения движения:

v₀sin(α) – gt₁ = 0

(так как конечная проекция скорости в верхней точке траектории равна нулю),

t₁ = v₀sin(α) / g.

Найдём время спуска:

–gt₂ = –v₀sin(α),

(т. к. конечная скорость тела будет такая же, как и начальная),

t₂ = v₀sin(α) / g.

Общее время движения:

t = t₁ + t₂ = 2v₀sin(α) / g.

Замечание.Время спуска и время подъёма тела одинаковые. Это связано с тем, что движение симметрично.

Дальность полета

Так как по горизонтали (вдоль оси ОХ) движение тела равномерное, то, зная общее время движения, найдём дальность полета L:

L = tv₁ = (2v₀sin(α) / g) · v₀cos(α) = 2v₀²sin(α)cos(α) / g.

Замечание. Используя формулу из тригонометрии

2sin(α)cos(α) = sin(2α),

получим:

L = 2v₀²sin(2α) / g.

Следовательно, максимальная дальность полета тела будет при броске под углом 45° к горизонту (так как sin(90°) = 1).

Максимальная высота подъёма тела

Рассмотрим движение тела в проекции на ось OY:

H = v₀sin(α)t₁ – gt₁² / 2.

После подставления времени подъёма получим

H = v₀²sin²(α) / (2g).

Давайте теперь решим некоторые задачи.

Задачи

Задача 1. Пуля, летящая горизонтально со скоростью v = 500 м/с, пробивает первый листок бумаги. Найти, на каком расстоянии S находится второй листок бумаги, если известно, что его пуля пробила на h = 20 см ниже, чем первый.

Решение. Найдём, за какое время пуля прошла расстояние между листами. Нам известно, что за это же время она опустилась на высоту h = 20 см. Тогда:

h = gt² / 2,

t = √(2h/g).

Теперь, зная время движения пули между листами, найдём расстояние, которое прошла пуля за это время:

S = tv = v · √(2h/g) = 100 м.

Ответ: S = 100 м.

Задача 2. Школьник может бросить мяч в спортивном зале с максимальной скоростью v = 25 м/с. Пренебрегая силами сопротивления воздуха, найти максимальную дальность полета мяча в спортивном зале, если высота зала равна h = 4 м. Считать, что мяч не ударяется о потолок.

Решение. Пусть мальчик бросил мяч под некоторым углом α к горизонту. Тогда дальность полета мяча равна:

L = 2v₀²sin(α)cos(α) / g.

Как обсуждалось выше, тело имеет максимальную дальность полета, если его бросить под углом α = 45° к горизонту. Но в данной задаче возможно, что при таком угле мяч ударится о потолок. Проверим, какова максимальная высота подъёма мяча при условии, что угол равен α = 45°.

H = v₀²sin²(α) / (2g) = 16 м.

Следовательно, угол, под которым мальчик бросит мяч, будет значительно меньше. Найдём максимальный угол, при котором мяч не столкнется с потолком. Этот угол будет соответствовать предельному случаю, когда мяч побывает на высоте h = 4 м.

h = v₀²sin²(α) / (2g) => sin²(α) = 2gh / v₀².

Из основного тригонометрического тождества

sin²(α) + cos²(α) = 1

найдём cos²(α):

cos²(α) = 1 – 2gh / v₀².

Подставив все выражения в дальность полета L, получим:

L = 2√(2gh(v₀² – 2gh)) / g = 42 м.

Ответ: L = 42 м.

Замечание. Если в задаче не приведены числовые значения (задача в общем виде), то необходимо записать 2 ответа. Первый ответ при условии высокого потолка, при h > H —

L = 2v₀²sin(α)cos(α) / g, α = 45°.

И при h < H получаем ответ

L = 2√(2gh(v₀² – 2gh)) / g.

Список литературы

Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.

Автор: Роман Федоренко

Источник

Время подъема на максимальную высоту, тела, брошенного под углом к горизонту

Время подъема на максимальную высоту, тела, брошенного под углом к горизонту — определяется из условия, что проекция мгновенной скорости на ось y в точке максимального подъема равна нулю

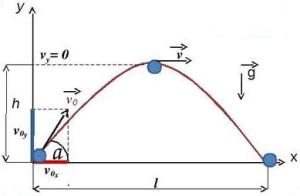
Движение тела, брошенного под углом к горизонту:

Обозначения:

v₀ — начальная скорость тела, брошенного под углом к горизонту

v_0х — проекция начальной скорости на ось x

v_0y — проекция начальной скорости на ось y

a — угол под которым было брошено тело

t — время тела в полете

g — ускорение свободного падения

Источник

Движение тела, брошенного под углом к горизонту, — движение тела в двумерной системе координат (по двум осям) при изначальном направлении начальной скорости под углом к горизонту. Данное движение является сложным видом механического движения с криволинейной траекторией. Такие типы движений принято рассматривать в проекции на оси выбранной системы координат. В нашем конкретном случае возьмём декартову систему координат и запустим тело под углом displaystyle alpha к оси ОХ (рис. 1).

Рис. 1. Тело бросили под углом к горизонту

Классическая постановка задач на подобную тематику: тело бросили под углом $displaystyle {{upsilon }_{0}}$ к горизонту с начальной скоростью $displaystyle {{upsilon }_{0}}$ , найти различные параметры движения.

Первое, что мы сделаем, это попробуем данное сложное движение представить как сумму простых (рис. 2).

Рис. 2. Тело бросили под углом к горизонту (максимальная высота подъёма, путь по горизонтали, движение)

Рассмотрим само движение. После броска траектория движущегося тела представляет собой параболу (докажем позже). Выберем произвольную точку на параболе и укажем ускорение, с которым движется тело в данный момент (ускорение свободного падения). Направление данного ускорения — вертикально вниз. Проекции данного ускорения на ось ОХ ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{g}_{y}}=-10$ ), а на ось OY ( $displaystyle {{c}^{2}}$ (м/ $displaystyle {{c}^{2}}$ ).

Тогда, вдоль оси ОХ, тело движется равномерно (т.к. ускорение вдоль этой оси равно 0). Более сложным является движение тела вдоль оси OY: между точками A и B тело движется замедляясь, при этом движение равнозамедленное. Между точками B и C движение равноускоренное (рис.2, подписи). Исходя из установленного вида движения, можем решать задачу.

Рис. 3. Тело бросили под углом к горизонту (проекции скоростей)

Для рассмотрения движения тела вдоль осей, введём начальные скорости движения тела вдоль выбранных нами осей (рис. 3). На рисунке представлена часть траектории в самом начале движения. Начальные скорости движения вдоль осей обозначим $displaystyle {{upsilon }_{0y}}$ и $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ . Исходя из треугольника, катетами которого являются наши проекции (можно построить параллельным переносом), а гипотенузой — модуль вектора начальной скорости ( $displaystyle left| {{{vec{upsilon }}}_{0}} right|$ ), можем найти значения необходимых нам проекций:

Вернёмся к рисунку 2. Попробуем найти полное время полёта ( $displaystyle {{t}_{max }}$ ). Для этого воспользуемся тем, что вдоль оси OY тело движется равнозамедленно, а в точке B движение вдоль этой оси и вовсе останавливается. Таким образом, конечная скорость в этой точке вдоль оси OY равна 0. Тогда, исходя из движения:

$displaystyle 0={{upsilon }_{0y}}-gfrac{{{t}_{max }}}{2}$ (3)

$displaystyle frac{{{t}_{max }}}{2}$ — т.к. время движения от точки А до B, и от B до C одинаково. Тогда:

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0y}}}{g}$ (4)

И, учитывая (2):

$displaystyle {{t}_{max }}=frac{2{{upsilon }_{0}}sin alpha }{g}$ (5)

Перейдём к вопросу о максимальной дальности броска в горизонтальном направлении ( $displaystyle {{S}_{max }}$ ).

Вдоль горизонта тело движется равномерно (рис. 2). Тогда путь, проделанный телом за время $displaystyle {{t}_{max }}$ :

$displaystyle {{S}_{max }}={{upsilon }_{0x}}{{t}_{max }}$ (6)

А с учётом (1) и (5):

$displaystyle frac{2upsilon _{0}^{2}sin alpha cos alpha }{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ = $displaystyle frac{upsilon _{0}^{2}sin (2alpha )}{g}$ (7)

Перейдём к максимальной высоте полёта ( $displaystyle {{H}_{max }}$ ). Данный параметр связан с движением тела вдоль оси OY, которое, как мы выяснили, является равноускоренным/равнозамедленным. Рассмотрим участок BC: для него вдоль соответствующей оси тело без начальной скорости движется с ускорением ( $displaystyle frac{{{t}_{max }}}{2}$ ) в течение времени $displaystyle frac{{{t}_{max }}}{2}$ , формируем уравнение:

$displaystyle {{H}_{max }}=frac{g{{left( {}^{{{t}_{max }}}!!diagup!!{}_{2}; right)}^{2}}}{2}=frac{g{{left( {{t}_{max }} right)}^{2}}}{8}$ (8)

С учётом (5):

$displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ = $displaystyle frac{upsilon _{0}^{2}{{sin }^{2}}alpha }{2g}$ (9)

Таким образом, ряд параметров движения при броске под углом к горизонту можно вычислить, зная лишь начальные параметры броска.

Рис. 4. Тело бросили под углом к горизонту (конечная скорость)

Далее попробуем найти конечную скорость движения (при таких движениях, конечная скорость — скорость при подлёте к Земле). Рассмотрим конечную точку движения С (рис. 4). Скорость тела направлена под неким углом displaystyle beta . Построим проекции данного вектора на оси OX и OY. На основании построенного треугольника реализуем теорему Пифагора для поиска модуля полной конечной скорости:

$displaystyle left| {vec{upsilon }} right|=sqrt{upsilon _{x}^{2}+upsilon _{y}^{2}}$ (10)

Найдём компоненты вектора displaystyle left| {vec{upsilon }} right| . Т.к. движение вдоль оси OX равномерное, значит, $displaystyle {{upsilon }_{x}}={{upsilon }_{0x}}$ , используя (1):

$displaystyle {{upsilon }_{x}}={{upsilon }_{0}}cos alpha$ (11)

Движение вдоль оси OY от точки B в точку C равноускоренное, причём, без начальной скорости за время $displaystyle frac{{{t}_{max }}}{2}$ , тогда:

$displaystyle {{upsilon }_{y}}=gfrac{{{t}_{max }}}{2}$ (12)

Используя (5), получим:

$displaystyle {{upsilon }_{y}}=gfrac{2{{upsilon }_{0}}sin alpha }{2g}={{upsilon }_{0}}sin alpha$ (13)

Подставим (12) и (13) в (10):

$displaystyle {{upsilon }_{0}}sqrt{{{(cos alpha )}^{2}}+{{(sin alpha )}^{2}}}$ = $displaystyle {{upsilon }_{0}}$ = $displaystyle {{upsilon }_{0}}$ (14)

Для избавления от тригонометрических функций мы воспользовались основным тригонометрическим тождеством. Таким образом, доказано, что конечная скорость такого движения равна начальной, кроме того, из треугольника видно, что тело подлетело к земле под углом displaystyle beta =alpha .

Вывод:

для движения тела, брошенного под углом к горизонту, выведены добавочные формулы: (5), (7), (9), которые могут существенно упростить решение задачи.
представлен один из общих способов нахождения скорости при криволинейном движении (через теорему Пифагора и поиск компонент вектора).

Источник

Время подъема на максимальную высоту, тела, брошенного под углом к горизонту, формула

Вычислить, найти время подъема на максимальную высоту тела, брошенного под углом к горизонту по формуле (2).

Время подъема на максимальную высоту тела, брошенного под углом к горизонту

Общее время движения

Дальность полета

Максимальная высота подъёма тела

Задачи

Список литературы

Время подъема на максимальную высоту, тела, брошенного под углом к горизонту