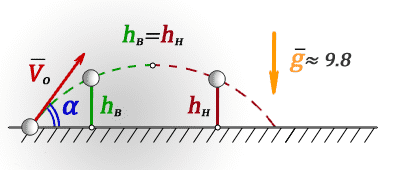
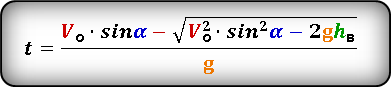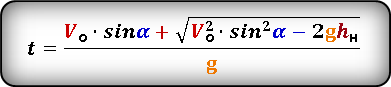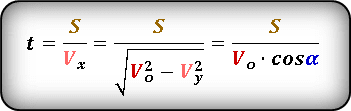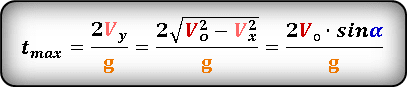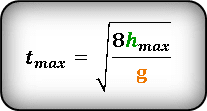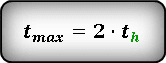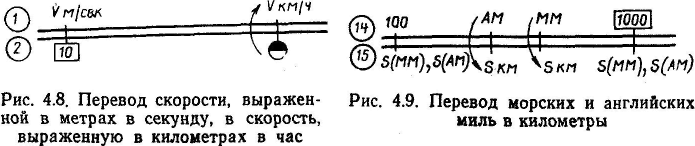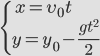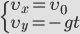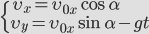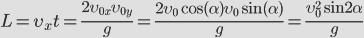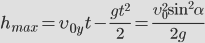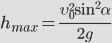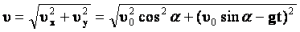1. Найти время полета тела на определенной высоте
hв — высота на восходящем участке траектории
hн — высота на нисходящем участке траектории
t — время в момент которого тело находится на высоте hв или hн
Vo — начальная скорость тела
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на восходящем участке траектории
Формула для определения значения времени, за которое тело поднялось на определенную высоту, на нисходящем участке траектории
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
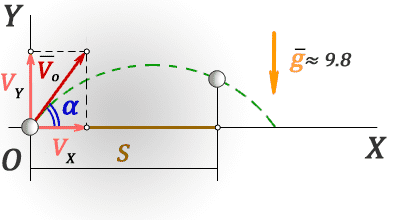
2. Найти время полета тела пролетевшее определенное расстояние
S — расстояние пройденное по горизонтали
t — время за которое тело прошло расстояние S
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, за которое пройдено определенное расстояние
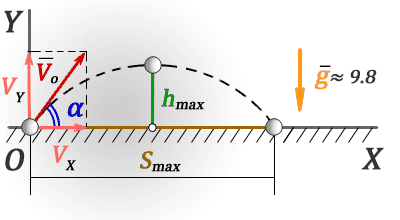
3. Значение времени при максимальных значениях высоты и дальности
Smax — максимальная дальность по горизонтали
hmax — максимальная высота
tmax — время всего полета
th — время за которое тело поднялось на максимальную высоту
Vo — начальная скорость тела
Vx — проекция начальной скорости на ось OX
Vy — проекция начальной скорости на ось OY
α — угол под которым брошено тело
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула для определения значения времени, затраченное на весь полет, если известна начальная скорость или ее проекции
Формула для определения значения времени, на максимальной высоте
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно — время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
- Подробности
-
Опубликовано: 20 июля 2015
-
Обновлено: 13 августа 2021
Пройденное расстояние
определяется по формуле
S
= Wt,
где
S—пройденное
расстояние, км
(м); W
—
путевая скорость, км/ч;
t
—
время полета, ч
и
мин
(мин и
сек).
Для
определения пройденного расстояния на
НЛ-10М необходимо установить треугольный
индекс шкалы 2
на
значение путевой скорости по шкале 1
и против деления шкалы 2,
соответствующего
времени полета, отсчитать на шкале 1
искомое расстояние в километрах (рис.
4.6).
Рис. 4.6. Определение
пройденного расстояния
Пример.
W=420
км/ч;
t=9
мин. Определить
пройденное расстояние S.
Решение. S=63
км.
Если
время полета выражено в секундах, то
пройденное расстояние определяется в
таком порядке: установить круглый индекс
шкалы 2
на
значение путевой скорости по шкале 1
и против деления шкалы 2,
соответствующего
времени полета, отсчитать на шкале 1
искомое расстояние в метрах или километрах
(см. рис. 4.6).
Пример.
W=300
км/ч;
t=45
сек.
Определить
пройденное расстояние S.
Решение. S=3750
м.
Время полета
определяется по формуле
t=
Чтобы
определить время полета на НЛ-10М,
необходимо треугольный индекс шкалы 2
установить
на значение путевой скорости по шкале
1
и против деления шкалы 1,
соответствующего данному расстоянию,
отсчитать по шкале 2
искомое
время полета.
Пример.
W=510
км/ч;
S
= 187 км.
Определить
время полета t.
Решение.
t=22
мин.
Если
данное расстояние выражено в метрах,
то время полета определяется в таком
порядке: установить круглый индекс
шкалы 2
на
значение путевой скорости по шкале и
против деления шкалы 1,
соответствующего
данному расстоянию, отсчитать искомое
время полета.
Пример.
W=270
км/ч;
S
= 4900 м.
Определить
время полета.
Решение.
t=65
сек.
Путевая скорость
определяется по формуле
W
=.
Для
определения путевой скорости на НЛ-10М
необходимо установить риску визирки
против деления шкалы 1,
соответствующего пройденному
расстоянию, и подвести под риску деление
шкалы 2,
соответствующее
времени полета, затем против треугольного
индекса шкалы 2
отсчитать
на шкале 1
искомое
значение путевой скорости в километрах
в час (рис. 4.7).
Пример.
S
= 72 км;
t=10
мин. Определить
путевую скорость.
Решение.
W=432
км/ч.
Если
пройденное расстояние небольшое и время
полета выражено в секундах, то путевая
скорость отсчитывается против круглого
индекса. Для этого необходимо установить
риску визирки на деление шкалы 1,
соответствующее пройденному расстоянию,
и подвести под риску деление шкалы 2,
соответствующее
времени полета в секундах, затем против
круглого индекса шкалы 2
отсчитать
Рис. 4.7. Определение
путевой скорости
на
шкале 1
искомую путевую скорость в километрах
в час (см. рис. 4.7 ).
Пример.
S
= 3000 м;
t
= 20 сек.
Определить
путевую скорость.
Решение.
W
=540 км/ч.
8. Перевод скорости, выраженной в метрах в секунду, в скорость, выраженную в километрах в час, и обратно
Такая операция
осуществляется по формулам:
V
км/ч =
V
м/сек ·3,6; V
м/сек =
V
км/ч:3,6.
Для
вычислений по этим формулам на НЛ-10М
используются шкалы 1
и
2.
Чтобы
перевести скорость, выраженную в метрах
в секунду, в скорость, выраженную в
километрах в час, необходимо прямоугольный
индекс 10 шкалы 2
установить
на деление шкалы 1,
соответствующее
скорости в метрах в секунду, и против
круглого индекса шкалы 2
отсчитать
на шкале 1
искомое значение скорости в километрах
в час (рис. 4.8).
Пример.
V
=12 м/сек. Перевести
в километры в час.
Решение.
V=43
км/ч.
Для
перевода скорости, выраженной в километрах
в час, в скорость, выраженную в метрах
в секунду, необходимо круглый индекс
шкалы 2
установить
на деление шкалы 1,
соответствующее
заданной скорости в километрах в час,
и против прямоугольного индекса 10
отсчитать
по шкале 1
искомое значение скорости в метрах в
секунду.
Пример.
V=480
км/ч.
Перевести
в метры в секунду
Решение.
V=
133 м/сек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
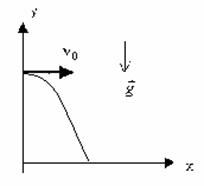
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
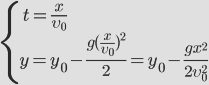
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
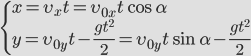
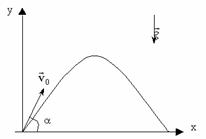
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:


Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
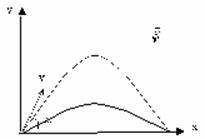
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 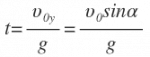
Время подъема:
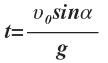
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
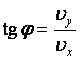
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t — frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 — gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 — 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
Цель работы: изучение движения тела, брошенного под углом к горизонту; определение времени, дальности и высоты полета.
Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения 

Проекции скорости тела, следовательно, изменяются со временем следующим образом:
где 
Координаты тела, следовательно, изменяются так:
При нашем выборе начала координат начальные координаты 
 |
(1) |
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т.к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:
 . . |
(2) |
Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т.е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т.е. в момент времени, равный t. Подставляя значение (2) в первую формулу (1), получаем:
 . . |
(3) |
Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т.к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем
 . . |
(4) |
Из уравнений (1) можно получить уравнение траектории тела, т.е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
и подставить его во второе уравнение. Тогда получим:
Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т.е. постоянные числа.
1. Найти время полета тела на определенной высоте
h в – высота на восходящем участке траектории
h н – высота на нисходящем участке траектории
t – время в момент которого тело находится на высоте h в или h н
V o – начальная скорость тела
α – угол под которым брошено тело
g ≈ 9,8 м/с 2 – ускорение свободного падения
Формула для определения значения времени , за которое тело поднялось на определенную высоту, на восходящем участке траектории
Формула для определения значения времени , за которое тело поднялось на определенную высоту, на нисходящем участке траектории
Таким образом, одному значению высоты будет соответствовать два значения времени, одно при подъеме, второе при падении.
2. Найти время полета тела пролетевшее определенное расстояние
S – расстояние пройденное по горизонтали
t – время за которое тело прошло расстояние S
V o – начальная скорость тела
V x – проекция начальной скорости на ось OX
V y – проекция начальной скорости на ось OY
α – угол под которым брошено тело
g ≈ 9,8 м/с 2 – ускорение свободного падения
Формула для определения значения времени , за которое пройдено определенное расстояние
3. Значение времени при максимальных значениях высоты и дальности
S max – максимальная дальность по горизонтали
h max – максимальная высота
t max – время всего полета
t h – время за которое тело поднялось на максимальную высоту
V o – начальная скорость тела
V x – проекция начальной скорости на ось OX
V y – проекция начальной скорости на ось OY
α – угол под которым брошено тело
g ≈ 9,8 м/с 2 – ускорение свободного падения
Формула для определения значения времени , затраченное на весь полет, если известна начальная скорость или ее проекции
Формула для определения значения времени , на максимальной высоте
Т. к. траектория движения тела симметрична относительно линии максимальной высоты, следовательно – время всего полета, в два раза больше времени затраченного при подъеме на максимальную высоту
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
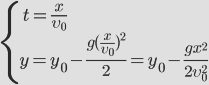
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
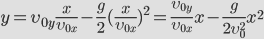
Мы получили квадратичную зависимость между координатами. Значит траектория – парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0. Следовательно, для решения этой задачи необходимо решить уравнение 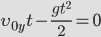
Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
– максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ;
– на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно: 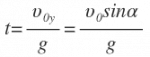
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
| Движение тела, брошенного горизонтально или под углом к горизонту. |
|
 |
 |
 |