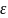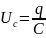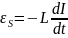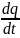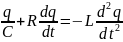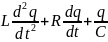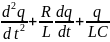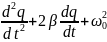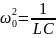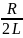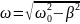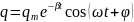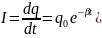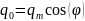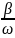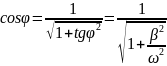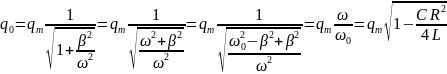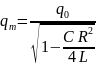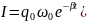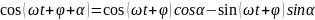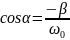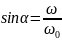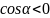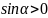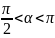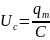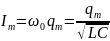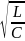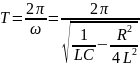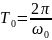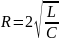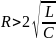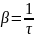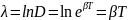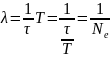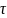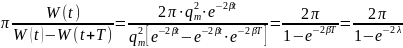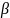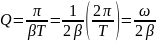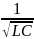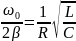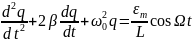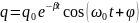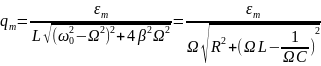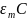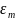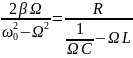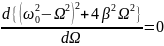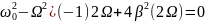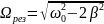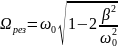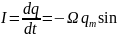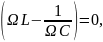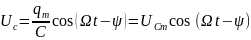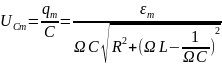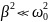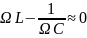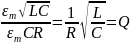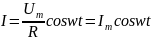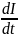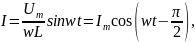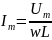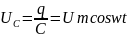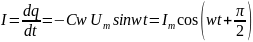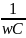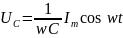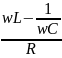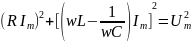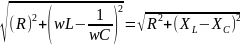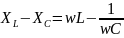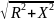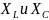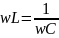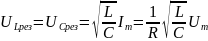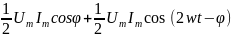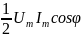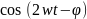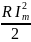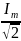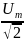1. Почему постоянный ток не может протекать через конденсатор?
Потому что цепь оказывается разомкнутой.
2. Что характеризует время релаксации R—С-цепи? Чему оно равно?
Время релаксации R-C цепи определяет по порядку величины время разрядки конденсатора емкостью С через сопротивление R.
3. Как, зная зависимость напряжения на конденсаторе от времени при разрядке через сопротивление R, можно графически найти время релаксации?
Производная U’C характеризуется тангенсом угла наклона касательной к кривой UC(t).
Когда t = 0, эта касательная пересекает ось t в точке τС = RC.
4. Какое физическое явление называют магнитоэлектрической индукцией?
Магнитоэлектрическая индукция — это явление возникновения в переменном электрическом поле магнитного поля.
5. Как соотносятся фазы силы тока, протекающего через конденсатор, и напряжения на его обкладках? Чему равно емкостное сопротивление конденсатора?
В цепи конденсатора колебания силы тока по фазе опережают колебания напряжения на его обкладках на л/2. Емкостное сопротивление:
ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными
РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи
IR=U,
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что 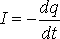
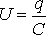
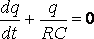
В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем
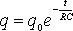
где q0 — начальный заряд конденсатора, е — основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t . Продифференцировав выражение (2) по времени, найдём закон изменения тока:
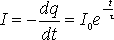
где I0 — сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.
Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:

ЗАРЯДКА КОНДЕСАТОРА.
Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:
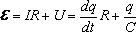
После разделения переменных уравнение примет вид:
Проинтегрировав это уравнение с учётом начального условия
q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим
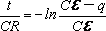
q = 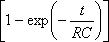
Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С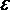
Подставляя в формулу (4) функцию I(t) = dq/dt, получим
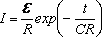
Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:
dAист= dQ + dW,
где dAист =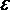
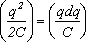
Аист(t)=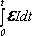
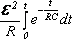
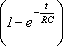
Q(t)=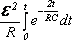
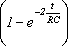
W(t) =
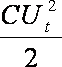
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В реальных электрических цепях постоянного тока, содержащих конденсаторы, переходные процессы разрядки и зарядки конденсаторов проходят за время порядка 10–6 – 10-3 с. Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
ЭКСПЕРИМЕНТ 1
Определение ёмкости конденсатора методом разрядки


Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка 





2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.
3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.
4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.
5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.
6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.
7. Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.
8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.
9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.
10. Проделайте опыты п.п.8, 9 ещё 4 раза.
Таблица 1. Суммарное значение э.д.с. источников тока
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Э.д.с.,В |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
Таблица 2. Определение сопротивления лампы.
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
I0, А |
||||||
|
It, А |
||||||
|
t, с |
||||||
|
C, Ф |
Таблица 3. Результаты измерений и расчётов.
ОБРАБОТКА РЕЗУЛЬТАТОВ:
1. По закону Ома для участка цепи Л1-Л4:
2. По формуле 
3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.
ЭКСПЕРИМЕНТ 2
Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора
- Выполняя действия, аналогичные описанным в эксперименте 1, зарядите конденсатор до напряжения, соответствующего суммарному значению э.д.с. для вашего варианта.
- Нажмите кнопку «Стоп» и отключите ключ К.
- Проведите 5-ти секундный процесс частичного разряда конденсатора через подключённые лампы. Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
- Запишите показания амперметра в таблицу 4 и вновь зарядите конденсатор до первоначального напряжения.
- Последовательно увеличивая длительность процесса разрядки конденсатора на 5 с, проделайте эти опыты до времени разрядки, соответствующему полному исчезновению заряда на конденсаторе. (Напряжение на конденсаторе и ток разрядки через лампы должен быть близким к нулю). Результаты измерений тока разрядки запишите в соответствующие ячейки таблицы 4.
Таблица 4. Результаты измерений и расчетов
|
Время разрядки t, с |
5 |
10 |
15 |
20 |
… |
5n |
|
Ток разряда I через t с, А |
||||||
|
Кол-во тепла Q за t с, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- Для каждого времени разрядки вычислите по формуле (4) количество тепла, выделившегося на шести лампах и запишите эти значения в соответствующие ячейки третьей строки табл.4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
- Постройте график зависимости количества выделившегося тепла Q к данному моменту времени от длительности процесса разрядки конденсатора t.
- Сравните рассчитанное количество тепла, выделившееся к моменту полного разряда конденсатора с его теоретическим значением, равным
.
- Сделайте выводы по графику и ответу и проведите расчёт погрешностей измерений.
ЭКСПЕРИМЕНТ 3
Проверка закона сохранения энергии в процессе зарядки конденсатора через сопротивление

- Соберите в рабочей части экрана опыта схему, показанную на рис.3. Вольтметр, включённый параллельно 5-ти лампам, будет показывать напряжение на внешнем сопротивлении, а амперметр – силу тока через нагрузку и источники тока. Напряжение на конденсаторе определяется программой автоматически и указывается в вольтах на экране монитора над конденсатором.
- Установите суммарную э.д.с. источников тока, соответствующую значению, приведённому в табл.1 для вашего варианта.
- При разомкнутом ключе К нажмите кнопку «Старт».
- Нажатием кнопки мыши замкните ключ К и начните процесс зарядки конденсаторов. Одновременно с замыканием ключа включите секундомер.
- Через время релаксации t = RС нажатием кнопки «Стоп» остановите процесс и запишите показания электроизмерительных приборов в таблицу 5.
- Нажмите кнопку «Выбор» и обнулите показания напряжений на всех конденсаторах и на электроизмерительных приборах.
- Повторите эти измерения ещё 4 раза и заполните две верхних строки таблицы 5.
Таблица 5. Результаты измерений и расчетов
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее |
|
I, A |
||||||
|
Uc, B |
||||||
|
UR, B |
||||||
|
Аист, Дж |
||||||
|
DW, Дж |
||||||
|
Q, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- По формулам 6, 7, 8 и измеренным значениям напряжения на конденсаторе Uc рассчитайте величины работу источника тока Аист, изменение энергии конденсатора DW и выделившегося на нагрузке количества тепла Q через время заряда, равного времени релаксации.
- Проверьте выполнение закона сохранения энергии в процессе зарядки конденсатора по формуле: Аист =DW + Q.
- Сделайте выводы по итогам работы.
Вопросы и задания для самоконтроля
Вопросы и задания для самоконтроля
- Что представляет собой конденсатор и от чего зависит его ёмкость?
- Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.
- Как изменяется разность потенциалов на обкладках конденсатора при его зарядке и разрядке?
- Какой ток называется квазистационарным?
- Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов
- Что такое время релаксации?
- Объясните принцип работы экспериментальной установки.
- Нарисуйте графики зависимости силы тока и напряжения от времени при зарядке и разрядке конденсатора.
- Соберите на мониторе такую цепь, состоящую из источника тока, двух ламп, выключателя и соединительных проводов, чтобы с выключением лампы в одной цепи загоралась лампа в другой.
Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.
- Конденсатор ёмкости С = 300 пФ подключается через сопротивление R =500 Ом к источнику постоянного напряжения U0. Определите: а) время, по истечению которого напряжение на конденсаторе составит 0,99 U0; в) количество тепла, которое выделится на этом сопротивлении при разрядке конденсатора за это же время.
- Имеется ключ, соединительные провода и две электрические лампочки. Составьте на мониторе электрическую схему включения в сеть этих лампочек, которая должна удовлетворять следующему условию: при замкнутом ключе горит только первая лампочка, при размыкании ключа первая гаснет, а вторая загорается.
- Конденсатору ёмкостью С сообщают заряд q, после чего обкладки конденсатора замыкают через сопротивление R. Определите: а) закон изменения силы тока, текущего через сопротивление; б) заряд, прошедший через сопротивление за время t; в) количество тепла, выделившееся в сопротивлении за это время.
- Определите количество тепла, выделившегося в цепи (рис. 4-6) при переключении ключа К из положения 1 в положение 2. Параметры цепи обозначены на рисунках.
Затухающие
колебания.
В
рассмотренном примере электромагнитных
гармонических колебаний не учитывались
потери энергии, связанные с выделением
теплоты на активном сопротивлении,
всегда присутствующем в реальной
электрической цепи. Поэтому рассмотренные
колебания можно назвать свободными
идеальными незатухающими колебаниями.
При потере системой энергии в процессе
колебаний амплитуда колебаний
уменьшается.
Затухающими
называются колебания, амплитуда которых
уменьшается с течением времени.
Рассмотрим
свободные затухающие колебания. В
реальном колебательном контуре кроме
катушки
индуктивности L,
конденсатора емкости С и ключа К имеется
активное сопротивление R
(рис. 1).
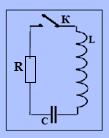
Рис.
1.
Запишем
для контура уравнение по второму правилу
Кирхгофа с учетом
активного
сопротивления цепи R:
Uc
+ IR=
S
, то есть напряжение на обкладках
конденсатора плюс напряжение на
сопротивлении R
равно ЭДС самоиндукции.
Но
,
. Отсюда:
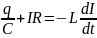
По
определению, сила тока I=
. Тогда предыдущее уравнение преобразуется
к виду:
или,
= 0 , или
= 0, или
q
=
0,
где
— собственная частота контура, β
=
— коэффициент затухания. Чем больше R
и меньше L,
тем больше коэффициент затухания.
Это
уравнение есть однородное дифференциальное
уравнение второго порядка для затухающих
колебаний.
Решениями
этого уравнения
являются
функции:
.
(1)
Здесь
— частота колебаний заряда на
конденсаторе, напряжения на конденсаторе,
силы тока в цепи,
— коэффициент затухания, который
определяет скорость убывания амплитуды
колебаний. Циклическая частота колебаний
определяется по формуле:
, qm
–
начальное значение амплитуды, φ –
начальная фаза колебаний. Чем меньше
β, тем меньше затухание колебаний.
.
Пусть
заряд на конденсаторе изменяется по
закону косинуса:
.
График этой функции представлен на
рис. 2. Верхняя пунктирная линия
представляет собой закон изменения
амплитуды колебаний q(t)
=
. Очевидно, что амплитуда со временем
убывает по экспоненте.

Рис.
2.
Найдем
выражение для силы тока в контуре:
. (2)
Пусть
в начальный момент времени заряд равен
qo
,
а сила тока равна нулю. Тогда из соотношений
(1) и (2) получаем:
и
.
Соответственно,
начальная
фаза оределяется
из соотношения:
tgφ
= —
.
Согласно
тригонометрической формуле,
Тогда:
.
Отсюда,
начальная
амплитуда:
.
Таким
образом, начальная фаза и начальная
амплитуда колебаний в контуре зависят
от его параметров: емкости, индуктивности
и активного сопротивления.
Вернемся
к выражению (2) для силы тока и несколько
преобразуем его:
.
(3)
Представим
функцию сила тока следующим образом:
. (4)
С
учетом тригонометрических преобразований,
получаем:
,
или:
(5)
Найдем
изменение фазы α, сравнивая зависимости
(3) и (5):
,
и
.
Отметим
для себя, что
,
а
.
Следовательно, угол α лежит в пределах:
, то есть при наличии в контуре активного
сопротивления R
колебания тока опережают по фазе
колебания напряжения на конденсаторе
и колебания заряда более, чем на
. При отсутствии активного сопротивления
опережение составляет
.
Вернемся
к случаю собственных незатухающих
колебаний, рассмотренному на прошлой
лекции (R=0).
Амплитуда напряжения на обкладках
конденсатора
, а амплитуда силы тока
, тогда можно записать:
,
а величина
получила название волнового
сопротивления контура.
Период
Т затухающих колебаний в колебательном
контуре равен:
.
Когда
202,
или сопротивление R
очень мало, период колебаний практически
равен периоду собственных незатухающих
колебаний:
.
С
увеличением коэффициента затухания
,
когда растет сопротивления R,
период колебаний увеличивается, и
при
обращается в бесконечность. При 2
>02
(
), колебания не совершаются, а происходит
монотонная разрядка конденсатора. Такой
разряд называется апериодическим.
Найдем
время релаксации
как время, за которое амплитуда
колебаний уменьшается в e
раз:
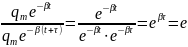
Отсюда,
= 1,
и
. Иначе: время релаксации – величина,
обратная коэффициенту затухания.
Для
характеристики скорости затухания
электромагнитных колебаний служат
несколько параметров: декремент затухания
D,
логарифмический декремент
и добротность Q.
Декремент
затухания показывает, во сколько раз
уменьшается амплитуда колебаний за
время, равное периоду колебаний Т:
D
=
,
a(t)
– амплитуда соответствующей величины
– заряда на обкладках конденсатора,
напряжения на конденсаторе, силы тока
в цепи.
Натуральный
логарифм от декремента затухания есть
логарифмический декремент :
.
(6)
Так
как
, то
, где Ne
— число колебаний за время релаксации
,
или за время, за которое амплитуда
уменьшается в е раз.
Найλдем
добротность Q
колебательного контура. Этот параметр
пропорционален отношению энергии
системы в некоторый момент времени t
к изменению энергии за период Т после
t.
Q
= 2
.
При
малых коэффициентах затухания
,
и , соответственно,
,
можно получить:
Q
=
.
(7)
То
есть добротность пропорциональна числу
колебаний, которые успевают совершиться
за время релаксации.
Взяв
вместо логарифмического декремента
его значение βТ, получим
.
При
малых коэффициентах затухания
можно положить ω = ω0
=
.
Тогда:
Q
=
. (8)
Вынужденные
колебания. Резонанс.
Для
получения незатухающих электромагнитных
колебаний необходимо извне подводить
энергию, компенсирующую потери при
рассеивании джоулевой теплоты. В этом
случае будут уже не свободные, а
вынужденные
электромагнитные колебания.
Для осуществления таких колебаний
необходимо включить в колебательный
контур источник тока, обладающий
периодически изменяющейся ЭДС ε = εm
cos(Ωt+ψ
). Здесь Ω –греческая буква омега
заглавная, частота внешней ЭДС.

Рис.
3.
Тогда,
по аналогии с предыдущими случаями,
дифференциальное уравнение электромагнитных
колебаний с учетом внешней ЭДС запишется
так:
(9)
Решением
неоднородного дифференциального
уравнения второго порядка является
сумма общего решения однородного
уравнения и частного решения неоднородного:
+
qm
cos(Ωt
+ψ
), ψ
– греческая буква пси, начальная фаза
вынужденных колебаний заряда.
Поскольку
первое слагаемое очень быстро стремится
к нулю, то решением этого уравнения
будет:
q
= qm
cos(Ωt
— ψ) , (10)
причем
Ω — частота вынужденных колебаний,
совпадает с частотой колебаний внешней
ЭДС, а ψ – начальная фаза вынужденных
колебаний заряда.
Амплитуда
установившихся вынужденных колебаний
заряда qm
является сложной функцией частоты
внешней ЭДС Ω и коэффициента затухания
:
(11)
Зависимости
амплитуды колебаний заряда qm
от Ω и
представлены на рис.4 (123).
При Ω=0 все кривые сходятся в одной
точке оси ординат
– это заряд на конденсаторе, возникающий
при подключении его к источнику
постоянного напряжения
. При различных значениях
амплитудные кривые имеют максимумы,
которые соответствуют частотам:
Ω1
, Ω2
и Ω3
.
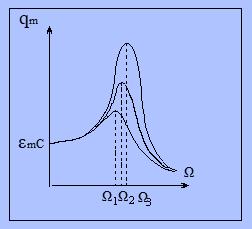
Рис.
4.
Начальная
фаза колебаний ψ определяется по формуле:
tg
ψ =
. (12)
Зависимость
амплитуды вынужденных колебаний заряда
от частоты
внешней ЭДС называется резонансной
характеристикой или резонансной кривой.
На графике рис.5 показаны резонансные
кривые для случаев: 1 – колебательная
система без сопротивления R,
при резонансе амплитуда вынужденных
колебаний неограниченно возрастает,
2, 3, 4 – реальные резонансные кривые для
колебательных систем с различными
сопротивления R
и, соответственно, разными коэффициентами
затухания (4
3
0
2).
Чем меньше сопротивление R,
тем больше и острее амплитуда вынужденных
колебаний при резонансе. При различных
значениях
резонансные характеристики имеют
максимумы, которые соответствуют
частотам: Ω1
, Ω2
, Ω3
, Ω4.

Рис.
5.
Частоты
Ω1,
Ω2,
… , которым соответствуют максимумы
амплитуды, называются резонансными
частотами Ωрез.
Чтобы определить их значения, необходимо
найти максимум для функции амплитуды
или, что то же самое, минимум знаменателя
функции А(Ω) —
.
,
2(
.
Значение
не равно 0, поэтому можно поделить
уравнение на
.
Получаем:
.
Или,
значение частоты, при которой наблюдается
резонанс:
, или,
. (13)
Найдем
зависимость установившегося тока от
времени:
(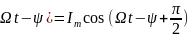
Амплитуда
тока с учетом формулы амплитуды заряда
имеет вид:
Резонанс
по току будет наблюдаться при частотах,
когда
то есть при Ωрез=
ω0
.
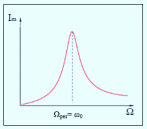
Рис.
6.
Резонансное
значение силы тока будет равно:
.
Разделив
заряд q
на емкость С, получим напряжение на
конденсаторе:
,
где
Отсюда
следует, что для резонанса напряжения
будет та же резонансная частота, что и
для заряда. Зависимости амплитуды
напряжения на обкладках конденсатора
от времени имеют характер, аналогичный
графикам на рис.5 для характеристик
заряда. При малом затухании, когда
, резонансную частоту для напряжения
можно принять равной ω0
:
U
= ω0
=
.
Тогда
, и отношение амплитуды напряжения на
конденсаторе при резонансе к амплитуде
внешней ЭДС будет равно:
,
где
Q
– добротность контура.
Последовательный
колебательный контур широко применяется
на практике в различных электро- и
радиотехнических схемах и устройствах
главным образом в качестве резонансной
системы, то есть системы, усиливающей
в Q
раз гармонические колебания, поступающие
на вход. Резонанс в контуре с последовательно
соединенными индуктивностью и емкостью
называют резонансом напряжений.
Переменный
ток.
Закон
Ома и правила Кирхгофа для постоянного
тока будут справедливыми и для мнгновенных
значений переменного тока и напряжения,
если только их изменения не происходят
слишком быстро. В пределах периода
колебаний тока до 10-6
с токи можно считать квазистационарными.
Рассмотрим частные случаи.
Переменный
ток в цепи активного сопротивления.

Рис.
7.
Пусть
к сопротивлению R
(рис. 7 ), не обладающему емкостью и
индуктивностью, (такие сопротивления
называются активными), приложено
напряжение, изменяющееся по закону
косинуса: U=Umcoswt.
Тогда по закону Ома:
. Причем, для амплитудных значенийсоотношение
выглядит так:
.
Видно,
что напряжение и ток изменяются синфазно,
что можно показать с помощью диаграммы
на рис. 8.

Рис.
8.
Переменный
ток в цепи с индуктивностью.
Подадим
переменное напряжение на концы
индуктивности L,
с бесконечно малым сопротивлением R
и емкостью С.
Схема
цепи представлена на рис. 9.
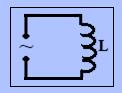
Рис.9.
При
прохождении переменного тока через
индуктивность, возникнет ЭДС самоиндукции.
Тогда по закону Ома для неоднородного
участка цепи можно записать: Umcoswt
— L
=0, или Umcoswt
= L
.
Поскольку
все внешнее напряжение приложено к
катушке, то UL
= L
-это падение напряжения на индуктивности.
С помощью интегрирования получим
выражение зависимости силы тока в цепи
от времени:
(14)
где
.
Роль
сопротивления в данном случае играет
величина XL
= wL.
Эту величину называют реактивным
индуктивным сопротивлением, которое
растет с увеличением частоты w.
Соответственно,
падение напряжения на индуктивности:
UL
= wLImcoswt.
(15)
Если
сравнить выражение для тока (14) и выражение
(15) стоновится видно, что падение
напряжения на индуктивности опережает
по фазе ток на
.
Диаграмма для тока и напряжения
представлена на рис.10.
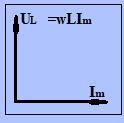
Рис.
10.
Переменный
ток в цепи с электроемкостью.
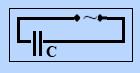
Подадим
переменное напряжение на обкладки
конденсатора С, причем сопротивление
и индуктивность подводящих проводов
будем считать бесконечно малыми. Схема
цепи представлена на рис. 11.
Рис.
11.
Напряжение
на конденсаторе будет равно внешнему
напряжению:
. (16)
По
определению, сила тока:
.
(17)
,
или
.
Величина ХС
=
называется реактивным емкостным
сопротивлением.
Напряжение
на конденсаторе
отстает по фазе от текущего через
емкость тока (17) на
(рис.12 ).
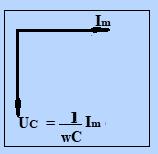
Рис.
12.
Цепь
переменного тока, содержащая емкость,
индуктивность и сопротивление.
Рассмотрим
цепь, составленную из сопротивления R
, емкости С и индуктивности L.
Подадим на концы этой цепи напряжение
Umcoswt
. В цепи возникнет переменный ток той
же частоты w,
амплитуда и фаза которого, как мы видели
в случае колебательного контура,
определяются параметрами цепи R,
C,
L.
Этот ток вызовет на активном сопротивлении
падение напряжения UR
, фаза которого совпадает с фазой тока
(рис.13).
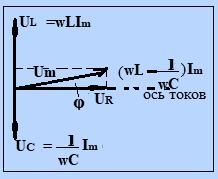
Рис.
13.
Падение
напряжения на индуктивности и емкости
отложены по вертикали, с учетом сказанного
ранее. Падения напряжений UR,
UL,
UC
в сумме должны быть равны приложенному
напряжению U.
Поэтому, сложив векторы UR,
UL
и UC
мы получим вектор, показывающий U,
а его длина равна Um.
Этот вектор образует с осью токов угол
φ, тангенс которого равен:
tg
φ =
.
Этот
угол φ
показывает разность фаз между напряжением
U
и силой тока I.
Из рис. 13 видно, что:
.
Откуда
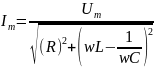
Итак,
если напряжение на зажимах цепи
Umcoswt
, то в цепи течет ток I
= Imcos(wt
-φ)
.
Величина
Z=
называется полным сопротивлением
цепи.
Величина
X=
называется реактивным сопротивлением.
Таким образом,
Z
=
.
Ток
в цепи отстает от напряжения (φ>0)
или опережает его (φ
< 0)
в зависимости от соотношения между
.
Если
,
изменения тока и напряжения происходят
синфазно. Сила тока в этом случае
максимальна. При этом падение напряжения
на активном сопротивлении равно внешнему
напряжению. Частота, при которой это
происходит, называется резонансной
частотой. При этой частоте напряжения
на емкости и на индуктивности равны по
амплитуде и противоположны по фазе
.
Мощность,
выделяемая в цепи переменного тока.
Мнгновенное
значение мощности, выделяемой в цепи,
равно произведению мнгновенных значений
напряжения и силы тока. С помощью
тригонометрических преобразований
можно получить выражение:
P(t)
=
.
Среднее
по времени значение мощности Р=
, так как среднее по времени от
равно нулю. Из рис. 13 видно, что
.
Отсюда
P
=
, такую же мощность развивает постоянный
ток I
=
. Эта величина получила название
действующего
или
эффективного
значения силы тока.
Аналогично: U
=
— действующее
значение напряжения.
С использованием действующих значений
средняя мощность выглядит так: P
= U
Icosφ
.
Приборы,
работающие на переменном токе, встречаются
во всех областях нашей жизни: при передаче
энергии от источника потребителю, в
генераторах переменного тока,
трансформаторах. В технике часто
стремятся сделать cosφ
как можно больше для выделения необходимой
мощности.
The notation is mostly taken from the book «Markov chains and mixing times» by Levin, Peres, and Wilmer.
Consider an irreducible, aperiodic, time-reversible, discrete-time Markov chain on a finite state space $S$ whose Markov kernel is $K$ and unique stationary distribution is $pi.$ Then, reversibility means $pi(x)K(x,y) = pi(y)K(y,x)$ for all $x,yin S.$ The Markov kernel $K$ has real eigenvalues given by:
$$-1leq beta_{|S|-1}leq ldots leq beta_1 leq beta_0 = 1.$$
Define the spectral gap as $gamma(K):=1-max{beta_1,|beta_{|S|-1}|}.$
The relaxation time of the Markov chain is defined as: $t_{mathrm{rel}}:=frac{1}{gamma}.$
Let $d(t) = sup_mu ||mu K^t — pi||_{mathrm{TV}}$ where $mathrm{TV}$ is the total variation distance. Then, the mixing time is defined as
$$t_{mathrm{mix}}(epsilon):=min{t: d(t)leq epsilon}.$$
Levin-Peres-Wilmer (Theorem 12.3, 12.4)
$$(t_{mathrm{rel}}-1)logfrac{1}{2epsilon}leq t_{mathrm{mix}}(epsilon)leq t_{mathrm{rel}}logfrac{1}{epsilonmin_xpi(x)}~.$$
Observe that if $K(x,y) = pi(y)$ for all $x,y,$ we have the lower bound almost tight since $t_{mathrm{rel}}=t_{mathrm{mix}}(epsilon)=1.$ Note that this is true no matter how small $min_xpi(x)$ is.
Also, observe that if the Markov chain is simply a random walk on a 3-regular expander graph, then $t_{mathrm{rel}}$ is a constant, but $t_{mathrm{mix}}$ is $Theta(log|S|)$ since $Theta(log|S|)$ is the diameter of the graph. In this case, $min_xpi(x) = frac{1}{|S|}$ and so, the upper bound gives the right behavior of $t_{mathrm{mix}}(epsilon).$
My question is the following:
For a fixed size of state space $|S|,$ and a fixed value of spectral gap $gamma,$ hence also a fixed value of $t_{mathrm{rel}},$ can we have the upper bound on $t_{mathrm{mix}}(epsilon)$ close to being tight for arbitrarily small values of $min_xpi(x)$?
Intuitively, I expect the answer to be No. If a chain has a fixed positive spectral gap, I expect the chain to mix quickly. But if $min_xpi(x)$ is very tiny, the upper bound suggests a potentially large mixing time.


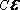
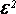
 .
. Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.
Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.