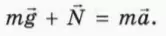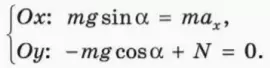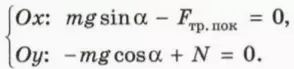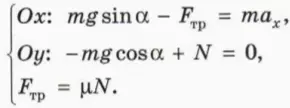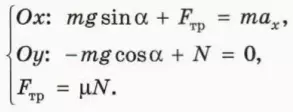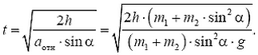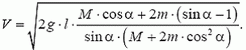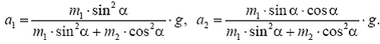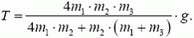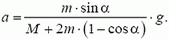1. Тело на гладкой наклонной плоскости
Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.
На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m

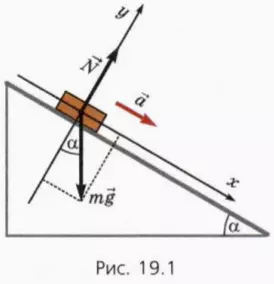
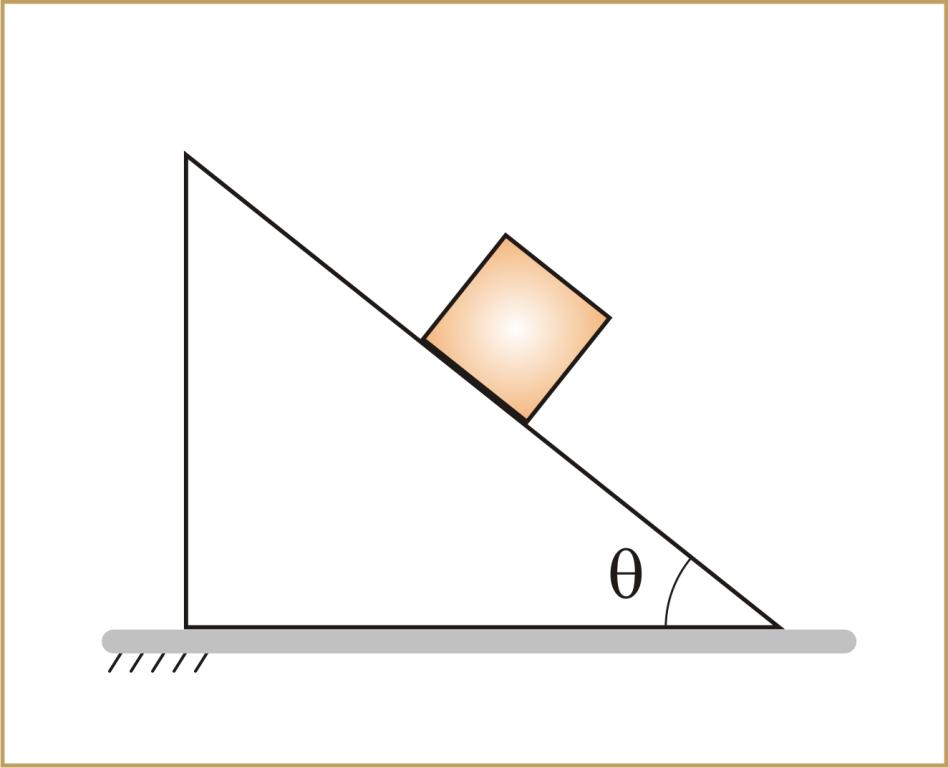
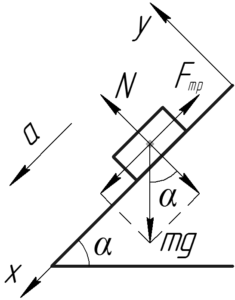
Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.
Уравнение второго закона Ньютона в векторной форме имеет вид
? 1. Объясните, почему справедливы следующие уравнения:
? 2. Чему равна проекция ускорения тела на ось x?
? 3. Чему равен модуль силы нормальной реакции?
? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?
? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?
При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.
? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v0.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?
? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?
2. Условие покоя тела на наклонной плоскости
Будем теперь учитывать силу трения между телом и наклонной плоскостью.
Если тело покоится на наклонной плоскости, на него действуют сила тяжести m


Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:
Fтр.пок x = –Fтр.пок
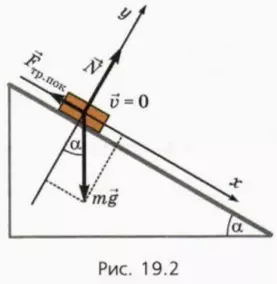
? 8. Объясните, почему справедливы следующие уравнения:
? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?
? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством
μ ≥ tgα.
Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству Fтр.пок ≤ μN.
Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).
? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?
? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?
Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!
? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:
а) вниз? б) вверх?
3. Движение тела по наклонной плоскости с учетом трения
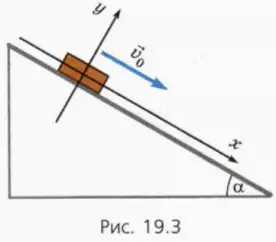
Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.
? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:
? 16. Чему равна проекция ускорения тела на ось x?
? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?
? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?
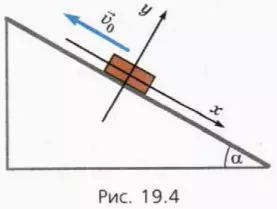
Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).
? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:
? 20. Чему равна проекция ускорения тела на ось x?
? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?
? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v0. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?
б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?
? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?
Зацените!! Езда Электро-Велосипеда по воде
Дополнительные вопросы и задания
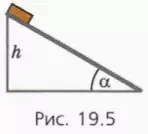
24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?
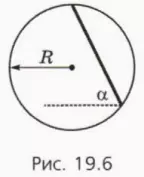
25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.
26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?
27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см. Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?
28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.
Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.
Основная формула динамики
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
F¯ = m*a¯
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
M = I*α
Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Здесь v0 — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.
Линейные и угловые характеристики друг с другом связаны формулами:
a = α*r;
v = ω*r
Здесь r — радиус вращения.
Движение по наклонной плоскости: силы
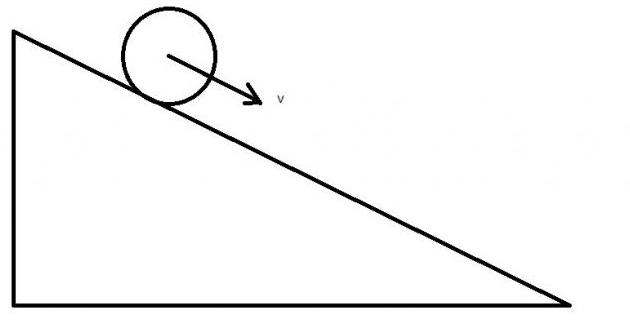
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
- тяжести;
- реакции опоры;
- трения качения и/или скольжения;
- натяжение нити;
- сила внешней тяги.
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.
Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Ff = µ*N
Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a
Здесь φ — это угол наклона плоскости к горизонту.
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
F = m*g*sin(φ) — Fr = m*a
Где Fr — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, Fr создает следующий момент:
M = Fr*r = I*α
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
m*g*(sin(φ) — µ*cos(φ)) = m*a =>
a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с2
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
S = a*t2/2
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
Задача со скатывающимся по плоскости цилиндром
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
m*g*sin(φ) — Fr = m*a;
Fr*r = I*α = I*a/r
Момент инерции I цилиндра вычисляется по формуле:
I = 1/2*m*r2
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) — 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
S = a*t2/2 =>
t = √(2*S/a)
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.
Черноуцан А.И. Кинематические связи в задачах динамики // Квант. — 1988. — № 2. — С. 57-62.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В задачах по механике часто встречается ситуация, когда движение тел не является свободным. Ограничения могут создавать твердые поверхности, нерастяжимые нити, жесткие стержни и т. п.
В простейших случаях мы учитываем подобные ограничения автоматически, часто даже не оговаривая их существования. Например, ускорение тела на плоскости мы направляем вдоль плоскости (учитывая наличие твердой поверхности), скорости буксира и баржи считаем одинаковыми (принимая во внимание присутствие нерастяжимого троса) и т. д. Однако иногда возникает необходимость выразить эти ограничения в виде специального уравнения, которое мы будем называть «кинематической связью». Начнем с такой задачи.
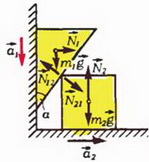
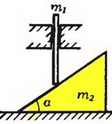
Задача 1. Найдите ускорения призмы массой m1 и куба массой m2, изображенных на рисунке 1, а. Трением пренебречь.
а
б
Рис. 1.
Запишем второй закон Ньютона для каждого тела (в проекции на направление, совпадающее с соответствующим ускорением):
m1·g – N·sin α = m1·a1, (1)
N·cos α = m2·a2. (2)
Мы учли, что по третьему закону Ньютона 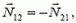
1) Рассмотрим два близких положения системы, разделенные промежутком времени Δt (рис. 1, б). В треугольнике ABC сторона АВ равна перемещению призмы Δx1, а сторона ВС — перемещению куба Δx2. Имеем
Δx2 = Δx1·tg α.
Разделив обе части равенства на Δt, получаем
υ2 = υ1·tg α.
Так как это соотношение справедливо для произвольного момента времени, из него следует искомое соотношение
a2 = a1·tg α. (3)
Такой подход к получению кинематической связи будем называть прямым методом.
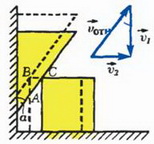
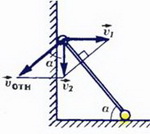
2) Другой способ получения необходимой связи основан на переходе в такую систему отсчета, где условие контакта становится тривиальным. В системе отсчета, связанной с призмой (см. рис. 1, б), скорость куба 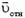
из соответствующего векторного треугольника получаем
υ2 = υ1·tg α и a2 = a1·tg α.
Решаем совместно уравнения (1)-(3) и находим
В этой задаче второй метод выглядит несколько искусственно. Однако в некоторых случаях именно правильный выбор системы отсчета позволяет существенно упростить проблему кинематических связей. Вот пример.
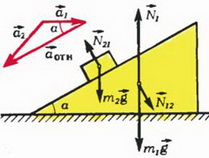
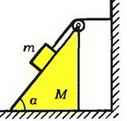
Задача 2. Клин высотой h с углом наклона α стоит на гладкой горизонтальной плоскости (рис. 2). Масса клина m1. С вершины клина начинает соскальзывать без трения брусок массой m2. Найдите ускорение клина и время соскальзывания бруска.
Рис. 2.
Начнем со второго закона Ньютона. Запишем его для клина в проекции на горизонтальное направление, а для бруска пока что в векторной форме:
N·sin α = m1·a1, (4)
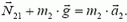
Как и раньше, 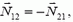
Кинематическая связь между ускорениями должна отразить тот факт, что в процессе движения брусок все время остается на поверхности клина. Записать это в виде прямого уравнения оказывается непросто. Вместо этого перейдем в систему отсчета, связанную с клином. В этой системе скорость бруска 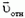
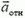
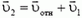
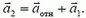
Отсюда видно, что от неизвестных a1 и a2 удобнее перейти к неизвестным a1 и aотн, решив тем самым проблему кинематической связи. Подставляя равенство (6) в уравнение (5) и проектируя это уравнение на направления вдоль поверхности клина и перпендикулярно к ней, получаем
m2·g·sin α = m2·(aотн – a1·cos α), (5׳)
N – m2·g·cos α = –m2·a1·sin α. (5״)
Из уравнений (4), (5′) и (5″) находим
Для ответа на второй вопрос задачи нам не надо искать a1, так как время соскальзывания выражается как раз через aотн:
Отсюда находим
Как уже говорилось, ограничение на движение может определяться не только прямым контактом рассматриваемых тел, но и наличием в системе соединительных элементов — стержней, нитей и т. п. В большинстве случаев, даже если в условии это не оговорено, соединительные элементы считаются идеальными, т. е. нити — невесомыми и нерастяжимыми, стержни — невесомыми и абсолютно жесткими, для блоков кроме невесомости предполагается также отсутствие трения на оси. (На самом деле слово «невесомый» означает, что масса данного элемента пренебрежимо мала по сравнению с массами других тел системы, слово «нерастяжимый» — что удлинение элемента мало по сравнению с перемещениями тел системы и т. д.) Перед тем, как разбирать конкретные примеры, выясним, что следует из идеальности соединительных элементов. Рассмотрим три частных случая.
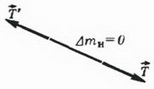
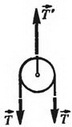
1. Невесомость нити. Напишем второй закон Ньютона для участка нити массой Δmн (рис. 3, а):
T – T´ = Δmн·a.
Так как Δmн = 0, то T – T´, т. е. сила натяжения не меняется вдоль нити.
2. Невесомость подвижного блока и отсутствие трения на его оси. Для раскручивания невесомого блока, в котором нет трения, не нужен вращательный момент. Из этого следует, что натяжение одной и той же нити по обе стороны блока одинаково (рис. 3, б), кроме того
T´ – 2T = 0, т. е. T´ = 2T.
3. Невесомость стержня. Это условие означает, что сумма сил и сумма моментов сил, действующих на стержень, равны нулю. Например, если к стержню приложены две силы, то они равны по модулю, противоположны по направлению и действуют вдоль стержня (рис. 3, в). (В отличие от нити, стержень может быть не только в растянутом, но и в сжатом состоянии.)
а
б
в
Рис. 3.
Нерастяжимость и жесткость нитей и стержней приводит к появлению кинематических связей, которые мы разберем отдельно в следующих задачах.
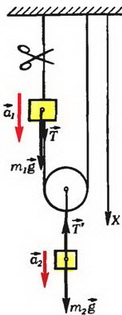
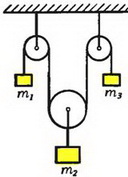
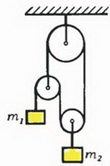
Задача 3. Найдите ускорения грузов массой m1 и m2 после перерезания верхней нити (рис. 4). Нити и блок считать идеальными.
Рис. 4.
Выберем положительное направление оси вертикально вниз и запишем второй закон Ньютона для обоих тел:
T + m1·g = m1·a1, (7)
m2·g – 2T = m2·a2 (8)
(мы учли свойства блока и нити, описанные выше).
Для нахождения кинематической связи между a1 и а2 применим, как мы его назвали, прямой метод. Запишем длину нити в виде
l = x2 + π·R + (x2 – x1),
где х1 — координата груза массой m1, x2 — координата центра блока, R — его радиус, и учтем, что длина нити при движении грузов не изменяется. Тогда для перемещений грузов получим соотношение
2Δx2 – Δx1 = 0,
откуда
2υ2 – υ1 = 0,
2a2 – a1 = 0. (9)
Решая уравнения (7)-(9) совместно, находим
(Обратите внимание на то, что a1 > g. Подумайте, почему получился такой ответ.)
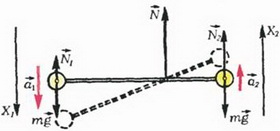
Задача 4. Невесомый стержень с одинаковыми грузами массой m на концах шарнирно закреплен на оси, которая делит его длину в отношении 2:1 (рис. 5). Стержень удерживают в горизонтальном положении и в некоторый момент освобождают. Найдите ускорения грузов сразу после этого, а также давление стержня на ось в этот момент.
Рис. 5.
Запишем второй закон Ньютона для грузов, выбрав положительные направления осей в сторону соответствующих ускорений:
m·g – N1 = m·a1, (10)
N2 – m·g = m·a2, (11)
где N1 и N2 — силы, действующие на грузы со стороны стержня. Так как сумма моментов сил, действующих на невесомый стержень, равна нулю, то
где l — длина стержня. Отсюда
N2 = 2N1. (12)
Осталось записать кинематическую связь между a1 и а2. Для этого изобразим на рисунке 5 положение стержня через малый промежуток времени Δt после начала движения. Из подобия получаем
x1 = 2x2,
откуда
υ1 = 2υ2,
a1 = 2a2. (13)
Решая совместно уравнения (10)-(13), находим
Так как сумма сил, действующих на невесомый стержень, равна нулю, то сила реакции оси (равная по модулю силе давления на ось) равна
***
Во многих задачах, рассчитанных на применение закона сохранения энергии, требуется найти скорости тел к определенному моменту времени. В этом случае надо установить кинематические связи не между ускорениями, а между скоростями тел. При решении таких задач полезно использовать тот факт, что полная работа, совершаемая любым идеальным соединительным элементом, равна нулю. Физическая причина этого состоит в том, что в таком элементе не может запасаться никакая энергия — ни кинетическая (его масса равна нулю), ни потенциальная (элемент не деформируется).
Последнее утверждение требует пояснения. Может показаться, что даже при малой деформации очень жесткого стержня (или другого элемента) потенциальная анергия его деформации 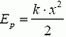
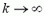
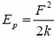
Эта и следующая задачи по своему уровню несколько выходят за пределы задач, предлагаемых обычно на вступительных экзаменах в вузы. Однако знакомство с ними для абитуриентов окажется небесполезным.
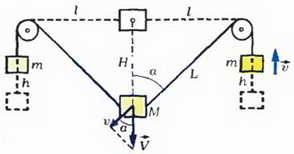
Задача 5. Груз массой М сначала удерживают на уровне блоков, а затем освобождают (рис. 6). Считая нити и блоки идеальными, размеры блоков малыми по сравнению с расстоянием 2l между ними, а массу m грузиков, висящих на концах нитей, известной, найдите скорость груза в тот момент, когда нити составляют угол α с вертикалью. Полученный ответ исследуйте.
Рис. 6.
К рассматриваемому моменту груз массой М опустился на H = l·ctg α, а грузики массой m поднялись на 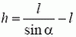
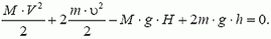
Для того чтобы найти связь между υ и V, можно, например, применить прямой метод. Из рисунка 6
l2 + H2 = L2.
Дифференцируя по времени (и учитывая, что l´ = 0), находим
2H·H´ = 2L·L´.
Так как L´ = υ, H´ = V, a H/L = cos α, то получаем искомую связь
υ = V·cos α. (15)
Однако проще получить это соотношение из следующих соображений. Раз расстояние L от груза массой М до блока в рассматриваемый момент увеличивается со скоростью υ (с такой скоростью вытягивается нить), то проекция скорости 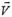
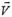
Из уравнений (14) и (15) находим
Выясним, будет ли центральный груз все время опускаться (мы считаем нити очень длинными) или при каком-то α он остановится и начнет подниматься. Уравнение V = 0 (условие остановки) преобразуется к виду
т. е. остановка и обратное движение грузов происходят только при М < 2m. Если М > 2m, то центральный груз будет все время перевешивать и его скорость будет неограниченно возрастать (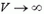
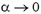
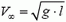
Хотелось бы обратить внимание на то, что при использовании закона сохранения энергии сила натяжения нити вообще не вошла в расчеты.
Последний пример иллюстрирует методы получения кинематических связей при движении твердых стержней (или других твердых связей). Напомним, что при движении твердого тела расстояние между любыми двумя его точками не изменяется.
Задача 6. Невесомый стержень длиной l с грузами массой m на концах соскальзывает по сторонам прямого двугранного угла (рис. 7, а). Найдите скорости грузов в тот момент, когда стержень составляет с горизонтом угол α. Трения нет. В начальный момент стержень находился в вертикальном положении.
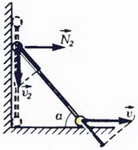
а
б
Рис. 7.
Из закона сохранения энергии получаем
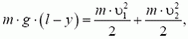
где y = l·sin α — координата второго груза в рассматриваемый момент. Для получения кинематической связи можно применить прямой метод, как это было сделано в предыдущей задаче (проделайте это сами). Быстрее же и нагляднее кинематическая связь получается из таких соображений. Раз расстояние между грузами остается неизменным, то в каждый момент скорость, с которой первый груз «удаляется» от второго, равна скорости, с которой второй груз «приближается» к первому. Иначе говоря, проекции скоростей грузов на стержень в любой момент времени одинаковы (см. рис. 7, a):
υ1·cos α = υ2·sin α. (17)
Подставляя (17) в (16), находим
В кинематике твердого тела часто используется «разложение» сложного движения на поступательное и вращательное. Чтобы продемонстрировать этот метод, применим его для получения кинематической связи (17). В системе отсчета, связанной с первым грузом, стержень совершает чисто вращательное движение. Значит, в этой системе скорость второго груза 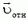
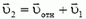
Может показаться, что найденные выражения для скоростей дают полное решение задачи. Однако в этой задаче содержится поучительный подвох, разбором которого мы и закончим статью.
Решение было бы полным, если бы второй груз не мог оторваться от вертикальной стены. (Для этого можно было бы, например, посадить грузы на гладкие штанги, а стержень присоединить к ним шарнирно). Однако в нашем варианте задачи (см. рис. 7, а) при некотором угле произойдет отрыв второго груза от вертикальной стены, после чего найденный ответ будет неприменим. Дело в том, что горизонтальный импульс системы определяется только движением первого груза, скорость которого, в соответствии с выражением для υ1, до некоторого угла возрастает, а потом начинает убывать. Это означает, что в какой-то момент должна изменить направление внешняя горизонтальная сила, действующая на систему. Но есть только одна горизонтальная сила — сила реакции вертикальной стенки, которая не может изменить свое направление. Таким образом, в тот момент, когда реакция стенки обращается в нуль, происходит отрыв второго груза от стенки. Дифференцируя выражение для υ1 по времени, находим, что υ1 максимальна при sin α = 2/3. При угле 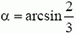
Упражнения
1. Найдите ускорения стержня и клина, изображенных на рисунке 8. Трения нет.
Рис. 8.
2. Найдите натяжение нити в системе, изображенной на рисунке 9.
Рис. 9.
3. (для любителей каверз и ловушек). Чему равны ускорения грузов в системе, изображенной на рисунке 10?
Рис. 10.
4. Найдите ускорение клина на рисунке 11. Трения нет. Указание. Примените метод, использованный при решении задачи 2 в статье.
Рис. 11.
Ответы
1.
2.
3. a1 = a2 = g.
4.
Hi4ko — 11 января, 2011 — 20:32
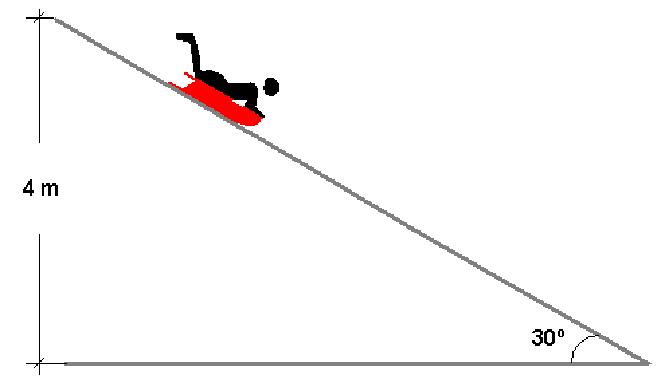
Наклонная плоскость составляет с горизонтом угол α = 30°. На плоскость положили тело и толкнули вверх. В течение времени t1 = 0,7 с тело прошло расстояние l = 1,4 м, после чего начало соскальзывать вниз. Сколько времени длится соскальзывание до начального положения тела? Каков коэффициент трения тела о наклонную плоскость?
Источник: Мякишев, механика. Профильный уровень. 10 класс, упражнение 8.
Теги:
- механика
- сила трения
- задачи с подсказками
- наклонная плоскость
- законы Ньютона
- версия для печати
Условие задачи:
По наклонной плоскости с углом наклона 30° к горизонту скользит вниз тело. Определить скорость тела в конце второй секунды скольжения, если коэффициент трения 0,15.
Задача №2.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(alpha=30^circ), (mu=0,15), (t=2) с, (upsilon-?)
Решение задачи:
[upsilon = at;;;;(1)]
Получается, что нам нужно определить ускорение тела (a). Чтобы это сделать, покажем на схеме все силы, действующие на тело, и запишем второй закон Ньютона в проекции на ось (x):
[ma = mg cdot sin alpha – {F_{тр}};;;;(2)]
Тело покоится вдоль оси (y), применим первый закон Ньютона в проекции на ось (y):
[N = mg cdot cos alpha ;;;;(3)]
Запишем формулу для определения силы трения скольжения:
[{F_{тр}} = mu N]
Сила реакции опоры (N) определяется формулой (3), поэтому:
[{F_{тр}} = mu mg cdot cos alpha ;;;;(4)]
Подставим (4) в (2), тогда:
[ma = mg cdot sin alpha – mu mg cdot cos alpha ]
[a = gleft( {sin alpha – mu cos alpha } right)]
Полученное выражения для ускорения подставим в формулу (1), в итоге получим решение задачи в общем виде:
[upsilon = gtleft( {sin alpha – mu cos alpha } right)]
Посчитаем численный ответ:
[upsilon = 10 cdot 2 cdot left( {sin 30^circ – 0,15 cdot cos 30^circ } right) = 7,4; м/с = 26,65; км/ч]
Ответ: 26,65 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
2.3.5 Санки можно удержать на ледяной горке с уклоном 0,2 (отношение высоты к длине)
2.3.6 Тело массой 1 кг, имеющее у основания наклонной плоскости скорость 6 м/с