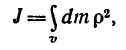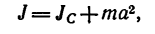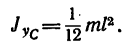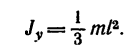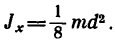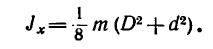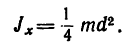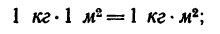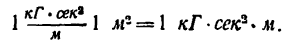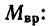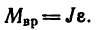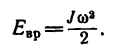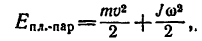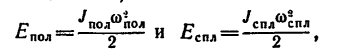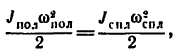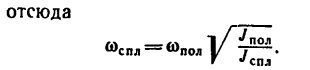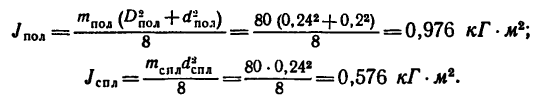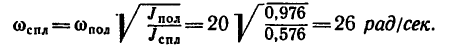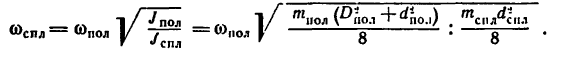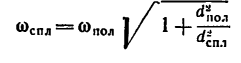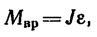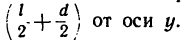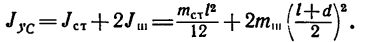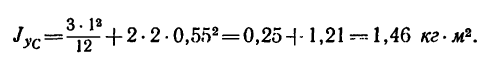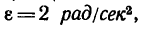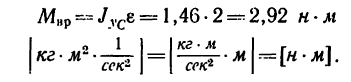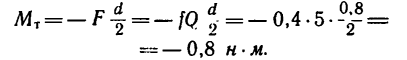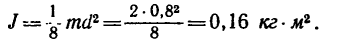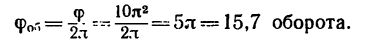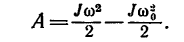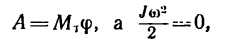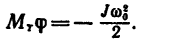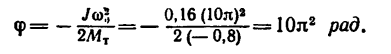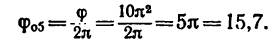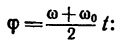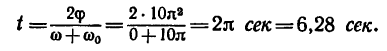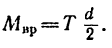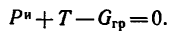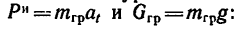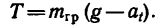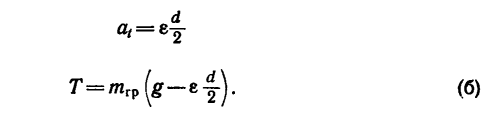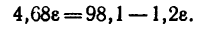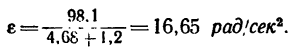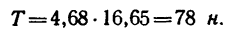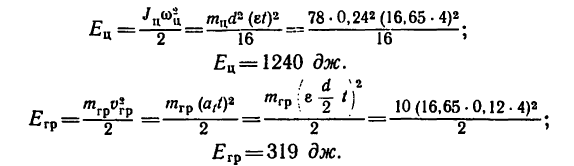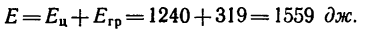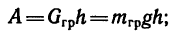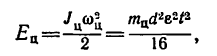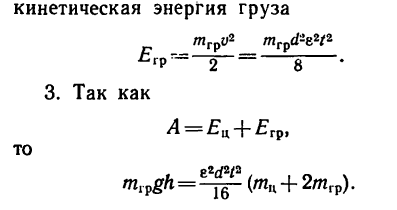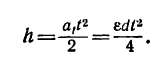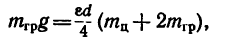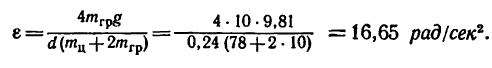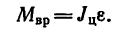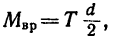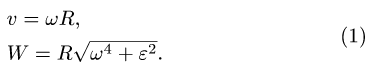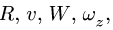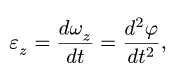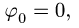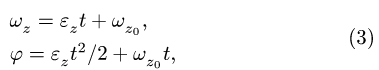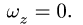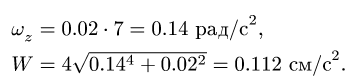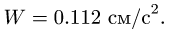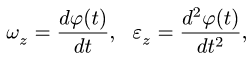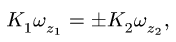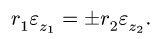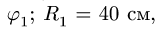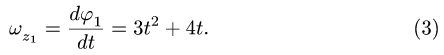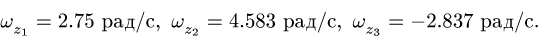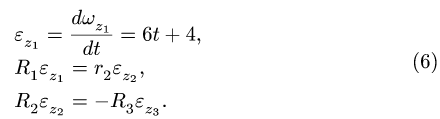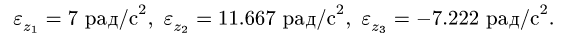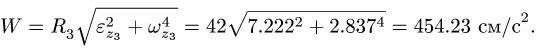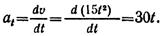Как найти время торможения при вращении

[an error occurred while processing this directive]

[an error occurred while processing this directive]

Известно, что грузовой автомобиль массой пять тысяч килограмм движется по горизонтальному пути со скоростью семьдесят два километра в час (20 метров в секунду).
Необходимо: определить силу и время торможения автомобиля, если тормозной путь составил пять метров.

Дано: m=5000 кг; v=20 м/сек; s=5 м
Найти: F-?; t-?

Решение

Исходя из того, что работа силы торможения численно равна изменению кинетической энергии движущегося автомобиля , получаем формулу для определения силы торможения

Подставив в формулу численные значения, рассчитаем силу торможения грузового автомобиля

н

Из формулы , при условии, что v_t=0: , где , получаем формулу времени торможения

Время торможения автомобиля

сек

Ответ: сила торможения автомобиля составила двести тысяч ньютон, время торможения равно половине секунды.

Задачи на вращательное движение тела:

Мерой инертности материальной точки, а также тела при поступательном движении является их масса.

Если же тело вращается, то мерой инертности служит его момент инерции —величина, зависящая от величины массы тела и от того, каким образом масса распределена относительно оси вращения тела.

Как известно, моментом инерции тела относительно некоторой оси называется величина, составленная из суммы произведений масс всех материальных точек тела на квадраты расстояний от этих точек до оси вращения.

В математической форме величину момента инерции тела можно представить такой формулой:

Этой формулой можно пользоваться для определения моментов инерции тел, имеющих геометрическую форму тел вращения.

Если тело составлено из нескольких частей, имеющих определенную геометрическую форму, удобно использовать еще формулу

где Jc—момент инерции тела относительно центральной оси (т. е. относительно оси, проходящей через центр тяжести тела); J — момент инерции тела относительно оси, параллельной центральной оси; m—масса тела и а —расстояние между осями.

Если тело имеет очень сложную форму, то момент инерции определяется либо из опыта, либо по формулам, приведенным в различных технических справочниках.

Приведем несколько формул для определения моментов инерции тел (во всех формулах т—масса тела, а линейные размеры обозначены на рисунках).

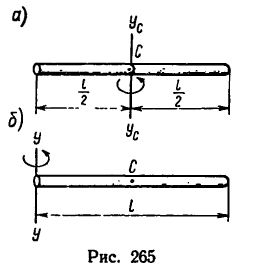
1.    Момент инерции тонкого прямого    

стержня относительно его центральной оси, перпендикулярной к стержню (рис. 265,а)

2.    Момент инерции тонкого прямого стержня относительно оси, перпендикулярной к стержню и расположенной у одного из его концов (рис. 265, б):

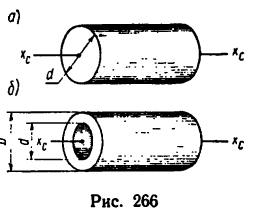
3.    Момент инерции сплошного однородного цилиндра относительно его геометрической оси (рис. 266, а)

4.    Mомент инерции полого однородного цилиндра относительно его геометрической оси (рис. 266, б)

Сопоставляя между собой при помощи рисунков формулы (I) и (2), а также (3) и (4). необходимо учитывать то, что при одной и тон же массе стержней и одинаковой длине второй стержень обладает в четыре раза большим моментом инерции (см. рис. 265, б), а также при одинаковых внешних размерах цилиндров и одинаковой массе (если цилиндры изготовлены из различных материалов, например из алюминия и стали) полый цилиндр обладает большим моментом инерции.

Если в формуле (4) пренебречь толщиной стенки цилиндра, т. е считать, что D—d. (вся масса распределена по ободу цилиндра), то

Единицей измерения момента инерции тела являются в СИ:

в системе МКГСС:

При вращательном движении (см. § 45-11) движущим фактором является вращающий момент (пара сил).

Если алгебраическая сумма моментов всех пар сил, приложенных к телу, имеющему ось вращения, не равна нулю, то тело приобретает угловое ускорение, числовое значение которого прямо пропорционально вращающему моменту

В этом уравнении, выражающем основной закон динамики для вращательного движения тела, множителем пропорциональности является момент инерции тела. Тело с большим моментом инерции труднее привести во вращение.

Кинетическая энергия вращающегося тела

Если тело находится в плоскопараллельном движении, например катящееся колесо, то его кинетическая энергия складывается из двух слагаемых:

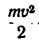
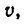
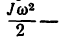
где —кинетическая энергия, получающаяся от поступательной части этого сложного движения (см. § 37-8) при скорости равной скорости центра тяжести тела, а     кинетическая энергия от вращательной части, причем J —момент инерции относительно оси, проходящей через центр тяжести тела.

Задача №1

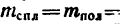
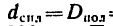
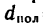
Два цилиндра, изготовленных из различных материалов (см. рис. 266), имеют одинаковую массу  = 80 кг; их наружные диаметры = 240 мм, а внутренний диаметр полого цилиндра = 200 мм. Полый цилиндр вращается вокруг собственной оси с угловой скоростью С какой скоростью должен вращаться сплошной цилиндр, чтобы оба цилиндра имели одинаковый запас кинетической энергии?

Решение.

1. Если кинетические энергии обоих цилиндров обозначить, соответственно,

то по условию задачи

2.    Если определять числовые значения моментов инерции обоих цилиндров, то

Определим скорость сплошного цилиндра

3.    Если же числовые значения моментов инерции не определять, то
 
В полученную формулу

подставим числовые значения диаметров:

Для второго варианта решения, как видно, массу цилиндров можно и не задавать.

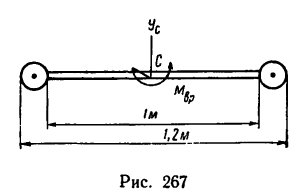
Задача №2

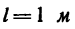
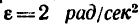
Стержень длиной и массой 3 кг имеет на концах шарообразные массы по 2 кг каждая (диаметры шариков d—10 см). Какой вращающий момент нужно приложить к стержню, чтобы привести его во вращение с угловым ускорением вокруг оси, перпендикулярной к стержню и

проходящей через центр тяжести системы (рис. 267)?

Решение.

1. Чтобы определить необходимый вращающий момент, нужно воспользоваться уравнением основного закона динамики для вращательного движения тела

но предварительно надо определить момент инерции системы стержня и шариков.

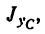
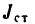
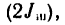
2. Находим момент инерции этой системы который складывается из момента инерции стержня и двух моментов инерции шариков которые считаем материальными точками, т. е. при определении моментов инерции шариков принимаем, что их массы сосредоточены в центрах шариков на расстоянии

Следовательно,

Подставим числовые значения:

3.    И теперь определим вращающий момент, необходимый для сообщения стержню ускорения

 

Задача №3

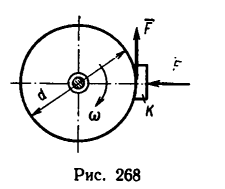
Тормозной шкив, масса которого m— 2 кг, диаметр d—0,8 м, имеет форму сплошного диска и вращается но инерции с угловой скоростью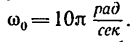Для остановки вала

к шкиву прижимают тормозную колодку k с силой Q—5 н. Через сколько секунд вал остановится и сколько оборотов он сделает до остановки, если коэффициент трения колодки о шкив f — 0,4? Трением в подшипниках вала, на котором насажен шкив, пренебречь; массу вала не учитывать.

Решение 1 — при помощи основного закона для вращающегося тела.

1.    Изобразим шкив на рис. 268. Прижатая к шкиву колодка создает силу трения F=fQ, направленную в сторону, противоположную вращению колеса. Таким образом, на шкив с момента прижатия колодки начинает действовать тормозной момент, направленный в сторону, противоположную его

вращению,

2.    Шкив имеет форму сплошного диска, его момент инерции определяется но формуле

3.    Из основного уравнения динамики для вращательного движения 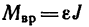находим угловое ускорение е:

4.    Из формулы для углового ускорения равнопеременного вращения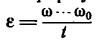 находим время торможения:

5.    По уравнению равнопеременного вращения определяем угол поворота шкива (вала) за это время:

6. Находим число оборотов вала, сделанное им с момента начала торможения до остановки:

Эту задачу можно решить и другим способом (используя закон кинетической энергии для вращающегося тела).

Решение 2.

1.    Закон кинетической энергии вращающегося тела выражается уравнением

2.    В данном случае тормозной момент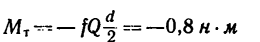 производит при остановке шкива (вала) работу

так как конечная угловая скорость 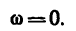  энергии шкива имеет вид

Отсюда (значение J —найдено в первом решении)

Число оборотов вала

4. Время торможения можно найти из формулы

 

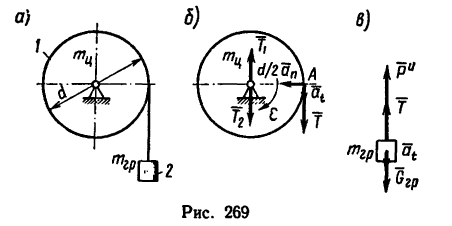
Задача №4

Цилиндр 1, масса которого 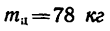и диаметр d=24 сж, может свободно вращаться около горизонтальной оси. На цилиндр намотана гибкая нить, имеющая на конце груз 2

массой 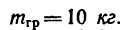Падая, груз разматывает нить и вращает цилиндр (рис. 269, а).

Определить угловое ускорение цилиндра, натяжение нити, кинетическую энергию груза А и цилиндра через t = 4 сек после начала движения.

Массой нити и трением в оси цилиндра пренебречь.

Решение — при помощи метода кинетостатики и уравнения основного закона динамики для вращающегося тела.

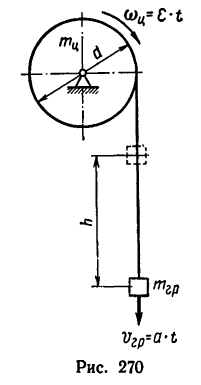
1.    В задаче рассматриваются два связанных между собой тела: вращающийся цилиндр и поступательно двигающийся груз. Мысленно разрежем нить и изобразим оба тела с действующими на них силами отдельно друг от друга.

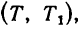
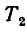
2.    На рис. 269, б показан цилиндр, на который действует вращающий момент нары сил созданной натяжением нити (сила приложена к подшипнику цилиндра, см. § 45-11):

3. Вращение цилиндра определяется уравнением:

(а)
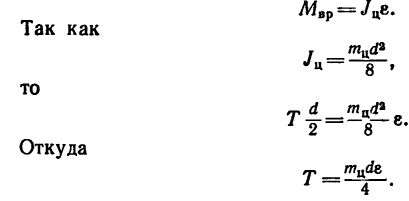
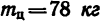
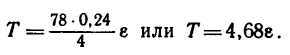
В полученное выражение для Т входит вторая неизвестная величина е. Чтобы облегчить дальнейшие вычисления, подставим сюда те величины, которые известны (в единицах СИ: и d = 0,24 м):
(а’)
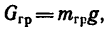
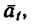
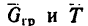
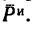
4.    Изобразим теперь (рис. 269, в) груз, на который действуют его вес реакция нити Т, равная ее натяжению. Так как цилиндр падает с ускорением то силы не уравновешивают друг друга. Добавим к ним силу инерции Тогда уравнение равновесия сил примет вид

Заменим в последнем уравнении силу инерции и вес груза их значениями

5.    Считая нить нерастяжимой, получаем, что ускорение а, груза равно ускорению любой точки нити, а следовательно, и точки А на ободе цилиндра (см. рис. 269, б). Но точка А принадлежит телу, вращающемуся с угловым ускорением е, поэтому

и теперь

Получено второе уравнение с теми же неизвестными Т и е.

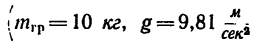
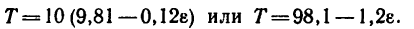
Подставив в (б) числовые значения и d=0,24 м), получаем

    (б’)

6.    Решим систему уравнений (а’) и (б’). Правые части обоих уравнений равны 7, значит

Отсюда

Подставим найденное значение е в любое из уравнений, например в (а’):

7.    Определим кинетическую энергию цилиндра и груза через t = 4 сек после начала движения системы:

8.    Таким образом, общий запас кинетической энергии обоих тел

Решение 2 —при помощи закона кинетической энергии.

1. Второе решение начинается с того, чем заканчивается первое.

Через t — 4 сек оба тела приобретают кинетическую энергию благодаря работе, произведенной грузом 2 при падении с высоты h (рис.70)

2. Работа груза

кинетическая энергия цилиндра

Здесь h —путь, пройденный грузом за t = 4 сек с ускорением 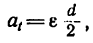поэтому

4.    Подставим в левую часть равенства (а) значение h и сократим обе части равенства на общие множители:

откуда

5. Натяжение Т нити найдем при помощи уравнения основного
закона динамики        
Здесь        
        
поэтому        
       

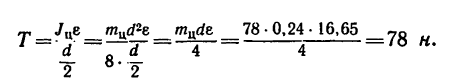
6.    Так как значение углового ускорения е известно, легко найти величины кинетических энергий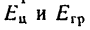(см. п. 2 решения).

Вращательное движение тела

При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы научитесь решать простые задачи кинематики тела. В таких задачах вводятся векторные величины — угловая скорость 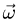и угловое ускорение Важно понять, что для вращательного движения тела эти векторы постоянно направлены по оси вращения. При сферическом движении (§ 10.1) векторы угловой скорости и углового ускорения могут лежать на разных прямых, и направления их в общем случае зависят от времени.

ПОСТАНОВКА ЗАДАЧИ. Твердое тело вращается вокруг неподвижной оси. Заданы некоторые кинематические характеристики движения тела и (или) кинематические характеристики движения точки этого тела. Найти остальные кинематические характеристики движения тела или точки.

План решения:

Пусть тело вращается вокруг оси z. Кинематические характеристики движения тела:

Кинематические характеристики точки на теле:

1. Записываем систему уравнений для всех величин, входящих в условие задачи. В зависимости от условия возможны три основных варианта решения.
Гл.7.Вращательное движение тела

—    Неизвестный закон вращения. Записываем систему двух уравнений для скорости 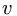точки, лежащей на расстоянии R от оси вращения, и ее ускорения W:

Для решения задачи необходимо, чтобы три из пяти величин 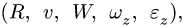входящих в (1), были заданы в условии.

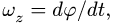
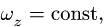
—    Вращение с постоянной угловой скоростью. Интегрируя уравнение ,приполучаем

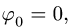
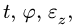
Как правило, отсчет ведется от поэтому в системе трех уравнений (1-2) содержатся семь величин четыре из которых должны быть заданы в условии задачи.

—    Вращение с постоянным угловым ускорением. Дважды интегрируя уравнение

получаем, при

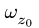
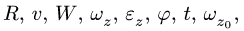
где — начальная угловая скорость. Совместно с (1) получаем систему четырех уравнений для восьми величин четыре из которых должны быть заданы в условии задачи.

2. Решаем систему. Находим искомые величины.

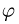
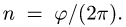
Замечание. Ряд величин задан в тексте задач неявно. Например, угол поворота может быть задан числом оборотов Слова «покой» и «остановка» соответствуют математической записи

Задача №5

Диск вращается вокруг неподвижной оси с постоянным угловым ускорением 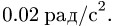Найти ускорение точки, лежащей на расстоянии 4 см от оси вращения, через 7 с после начала движения из состояния покоя.

Решение

1. В задаче задано постоянное угловое ускорение. Записываем систему уравнений для величин, входящих в условие задачи:

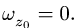
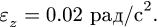
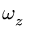
По условию задачи диск в начальный момент находился в покое, следовательно, Кроме того, при t = 7 с, даны значения R = 4 см, Решая систему двух уравнений (4) с двумя неизвестными и W, находим

Ответ.

Передача вращения

Постановка Задачи. Механизм состоит из вращающихся на неподвижных осях блоков и поступательно движущихся элементов. Все элементы находятся во фрикционном, зубчатом или ременном зацеплениях. Задана какая-либо кинематическая характеристика одного из тел. Найти кинематические характеристики других тел.

План решения:

1.    Определяем кинематические характеристики тела, с заданным законом движения. Если это тело движется прямолинейно поступательно, то скорость и ускорение любой его точки имеет вид

где 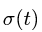— закон движения тела. При заданном вращательном движении находим угловую скорость и угловое ускорение:

где 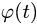— закон вращения тела (зависимость угла поворота в радианах от времени).

2.    Определяем угловую скорость тела, связанного нерастяжимой нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с телом, угловая скорость которого известна:

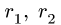
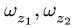
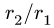
где — радиусы ободов колес (блоков) 1, 2, на которые надет ремень в случае ременной передачи, или радиусы колес, находящихся в зацеплении; — проекции угловых скоростей колес на ось, параллельную осям вращения. Знак минус берем при внешнем зацеплении, или крестообразной ременной передаче, когда вращение колес происходит в разные стороны. При внутреннем зацеплении (рис. 83) или простой ременной передаче (рис. 84) берем знак плюс. Отношение называется передаточным числом от тела 1 к телу 2. Для зубчатых соединений аналогом (1) является соотношение угловых скоростей

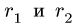
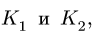
в которое вместо радиусов входят числа зубцов пропорциональные длинам окружностей шестеренок.

Если поступательное движение тела 1 передается вращательному движению тела 2 (или наоборот), то связь линейной и угловой скоростей имеет вид

где 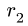— радиус обода, находящегося в контакте с поступательно движущимся телом.

3.    Повторяя п.2 для всех пар кинематически связанных тел, составляем и решаем систему уравнений для неизвестных линейных и угловых скоростей.

4.    Дифференцируя уравнения полученной системы, получаем аналогичную систему для угловых и линейных ускорений. Например, из уравнения (1) следует, что 

Аналогично, из (2) следует связь линейного ускорения поступательно движущегося тела и углового ускорения связанного с ним вращающегося тела:

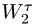
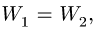
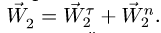
где — тангенциальная составляющая ускорения точки вращающегося тела в месте контакта. Было бы ошибкой считать так как полное ускорение точки на вращающемся теле включает в себя и нормальную составляющую Решаем систему уравнений для ускорений.

Задача №6

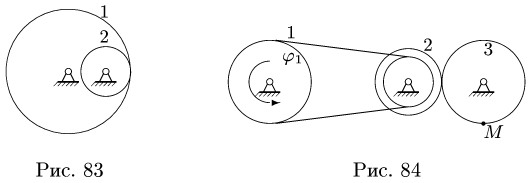
Механизм состоит из двух колес 1, 3 и блока 2, вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено ремнем с внутренним ободом блока 2. Внешний обод блока находится во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.

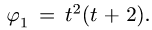
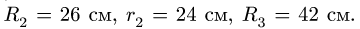
Задан закон движения ведущего колеса: Стрелкой указано положительное направление изменения угла При t = 0.5 с найти ускорение точки М, лежащей на ободе колеса 3.

Решение

1. Находим угловую скорость ведущего колеса 1:

7.2.Передача вращения

2.    Определяем угловую скорость блока 2, связанного нерастяжимым ремнем с колесом 1:

где 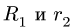— радиусы ободов, огибаемые ремнем.

3.    Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в разные стороны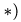, следовательно

Уравнения (3-5) образуют систему, решая которую, при t = 0.5 с, получаем

4.    Дифференцируя уравнения системы (3-5), получаем аналогичную систему для угловых ускорений:

Решаем систему уравнений для ускорений (6) и получаем

Вычисляем ускорение точки М:

Ответ.

0 Пользователей и 1 Гость просматривают эту тему.

---

---

Время, скорость, расстояние

О чем эта статья:

Расстояние

Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.

Расстояние — это длина от одного пункта до другого.

• Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.

Расстояние обозначается латинской буквой s.

Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).

Формула пути

Чтобы найти расстояние, нужно умножить скорость на время движения:

s = v × t

Скорость

Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.

Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.

Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.

Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.

Формула скорости

Чтобы найти скорость, нужно разделить путь на время:

v = s : t

Показатели скорости чаще всего выражаются в м/сек или км/час.

Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.

Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.

Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.

Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.

Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.

Время

Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.

Время — это продолжительность каких-то действий, событий.

• Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.

Время движения обозначается латинской буквой t.

Чаще всего вам будут встречаться такие единицы времени, как секунды, минуты и часы.

Формула времени

Чтобы найти время, нужно разделить расстояние на скорость:

t = s : v

Эта формула пригодится, если нужно узнать, за какое время тело преодолеет то или иное расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес-браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров в минуту на 15 минут, мы определим расстояние от дома до магазина:

s = v × t = 50 × 15 = 750 (м)

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние между двором и площадкой — 100 метров. Первый школьник добежал за 25 секунд, второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников — это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит, будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

Значит, скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

Скорость первого школьника больше. Значит, он добежал до спортивной площадки быстрее.

Ответ: первый школьник добежал быстрее.

Если известны скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос, нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое дойдем до стадиона:

t = s : v = 500 : 100 = 5 (мин)

Ответ: от школы до стадиона мы дойдем за 5 минут.

Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x ( t ) = x 0 + v 0 t + a t 2 2 . .

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

s = v 0 t + a t 2 2 . .

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Примеры решения задач

Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод срав­нения заданного уравнения с уравнениями различных видов движе­ний в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

• начальный путь, пройденный до начала отсчета – 10 м;
• начальная скорость 20 м/с;
• постоянное касательное ускорение a_t/2 = 5 м/с ; a_t= — 10 м/с .
• ускорение отрицательное, следовательно, движение замедлен­ное (равнозамедленное), ускорение направлено в сторону, противо­положную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.

Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, гра­фик пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.

Решение

1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).

Нормальное ускорение (а_п = v 2 /r) при переходе через точку В уве­личивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.

2. На участке ВС:

— касательное ускорение равно нулю: a_t = 0;

— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение стано­вится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.

3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, прой­денный за время движения (рис. 10.6).

Решение

1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; a₂ = 0.

Третий участок — торможение до остановки (равнозамедленное движение).

2. Путь, пройденный за время движения, будет равен:

Пример 4. Тело, имевшее начальную скорость 36 км/ч, про­шло 50 м до остановки. Считая движение равнозамедленным, опре­делить время торможения.

Решение

1. Записываем уравнение скорости для равнозамедленного дви­жения:

Определяем начальную скорость в м/с: v_о = 36*1000/3600 = 10 м/с.

Выразим ускорение (замедление) из уравнения скорости: a = — v₀/t

2. Записываем уравнение пути: S = v_ot/2 + at 2 /2. После подстановки получим: S = v_ot/2

3. Определяем время до полной остановки (время торможения):

Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.

Решение

1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = a_t = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = a_t = —10 м/c 2 = const) с начальной скоростью v₀ = 20 м/с.

2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав мас­штабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Напри­мер, если расстояние s = 5 м изображать на графике длиной отрезка l_s = 10 мм, то 5м = μ_s*10мм, где коэффициент пропорциональности μ_s и есть масштаб по оси Os : μ_s = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изобра­жать на графике длиной l_v =10 мм, то 10 м/c = μ_v * 10 мм и масштаб по оси Ov μ_v = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком l_a = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μ_a = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток време­ни Δt = 1 с отрезком μ_t = 10 мм, получим на всех графиках масштаб по осям Ot μ_t = 0,1 с/мм (0,1 с в 1 мм).

4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сто­рону).

За 4 с точка прошла путь s_o_₄ = 40 м. На­чав движение со скоростью v₀ = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.

Если условно принять ускорение свободно­го падения g = 10 мс 2 и пренебречь сопротивле­нием воздуха, то можно сказать, что графики описывают движение точки, брошенной верти­кально вверх со скоростью а₀ = 20 м/с.

Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.

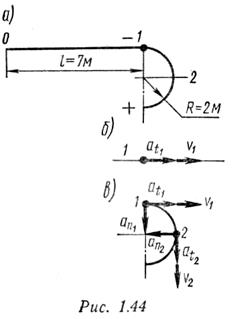
Решение

Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, опреде­лим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точ­ки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Ско­рость и ускорение точки в конце этого участка траекто­рии показаны на рис.1.44, б.

Определим скорость и уско­рение точки в начале криво­линейного участка траектории. Очевидно, что v₁ = 11,5 м/с, а_t1 = 14,2 м/с 2 .

Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участ­ка показаны на рис. 1.44, в (векторы a_t1 и a_a1 изобра­жены без соблюдения масштаба).

Положение 2 движущейся точки определяется прой­денным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей цент­ральному углу 90°:

Время, необходимое для перемещения точки из поло­жения 0 в положение2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и а_Пг изображены без соблюде­ния масштаба).

Пример 7. Точка движется по заданной траекто­рии (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в мет­рах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t₁, когда скорость точки v₁ = 135 м/с.

Решение

Уравнение изменения скорости

Время t₁ определим из уравнения изменения скорости, подставив частные значения скорости и времени:

Определим положение точки на траектории в момент 3 с:

Дуга окружности длиной 135 м соответствует цент­ральному углу

Уравнение изменения касательного ускорения

Касательное ускорение точки в момент t_t

Нормальное ускорение точки в момент t_t

Ускорение точки в момент t_x

Скорость и ускорение точки в момент времени t₁ по­казаны на рис. 1.45, б.

Как видно из рис. 1.45, б

Пример 8. В шахту глубиной H = 3000 м с по­верхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверх­ности земли. Скорость звука 333 м/с.

Решение

Уравнение движения свободно падающего тела

Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравне­ния движения:

Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука

Время достижения звуком поверхности земли

Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли

Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и уско­рение точки в момент времени t = 2 с.

Решение

Для определения траектории точки нужно из уравнений движения исключить параметр t — время.

Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.

Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движе­ния точки, ответьте, чему равны начальная скорость и ускорение.

5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.

6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).

7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).