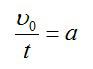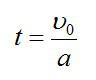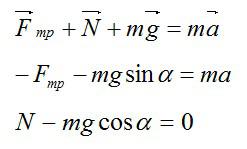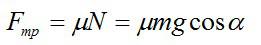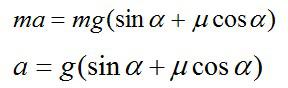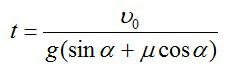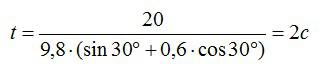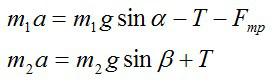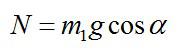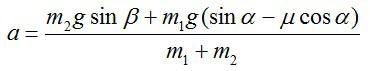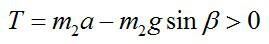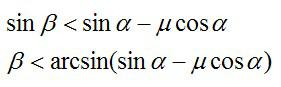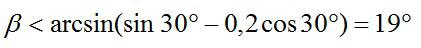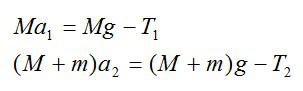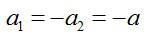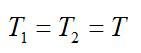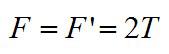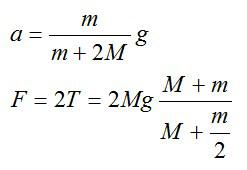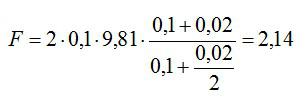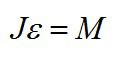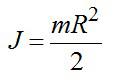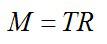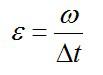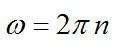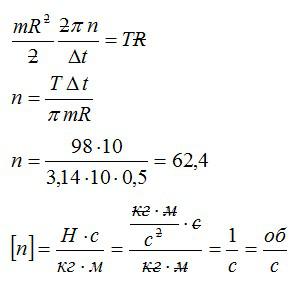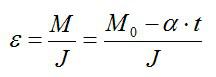Динамика – раздел механики, которому уделяется больше всего учебных часов. Уделите 5 минут на то, чтобы прочесть нашу статью и чуть больше разобраться в решении задач по динамике.
Наш телеграм – место, где мы скрупулезно отбираем, фильтруем и выкладываем все, что может быть полезно современному студенту. Под лежачий камень вода не течет, подписывайтесь!
Для начала, вопрос. Какой алгоритм решения задач по динамике? Собственно, алгоритм такой же, как и для любой задачи по физике. Мы уже писали об этом в памятке по решению задач. Не забываем держать под рукой полезные формулы, повторяем вопросы из теории, и можно приступать к практическим заданиям.
Вопросы по теме «Динамика»
Вопрос 1. Что изучает динамика?
Ответ. Динамика – раздел механики, который изучает взаимодействия между телами.
Вопрос 2. Каково основное уравнение динамики?
Ответ. Основное уравнение динамики устанавливает связь между приложенной к телу силой, его массой и ускорением тела.
Вопрос 3. Что такое вес тела и зависит ли он от местоположения тела на поверхности Земли?
Ответ. Вес – это сила, с которой тело действует на опору. Вес зависит от ускорения свободного падения, а значит и от географического местоположения на поверхности планеты. А вот масса тела всегда неизменна (за исключением движения со скоростью, близкой к скорости света).
Вопрос 4. В каких системах отсчета справедлив второй закон Ньютона?
Ответ. Второй закон Ньютона справедлив в инерциальных системах отсчета.
Вопрос 5. Сила тяжести на земле является отдельным проявлением одного из фундаментальных физических взаимодействий. Что это за взаимодействие.
Ответ. Конечно, это гравитационное взаимодействие. А сила тяжести – проявление силы всемирного тяготения.
Задачи по динамике поступательного движения с решениями
Задача №1. Определение времени движения
Условие
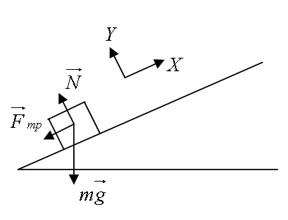
Тело находится у основания наклонной плоскости с углом при основании α = 30°. Коэффициент трения о поверхность равен µ = 0,6 и масса тела m = 2 кг. Сколько времени тело будет двигаться по наклонной плоскости, если его толкнуть вверх вдоль плоскости со скоростью υ0 = 20 м/с? (g = 9,8 м/с2).
Решение
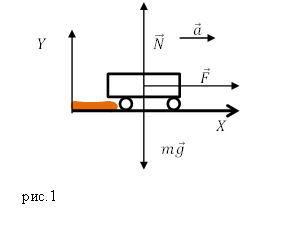
Для начала, выполним рисунок:
Тело будет двигаться равнозамедленно с ускорением, равным –a в течение времени t, при этом
Откуда
Определим ускорение a. Запишем второй закон Ньютона в векторной форме и в проекциях на оси Х и Y соответственно:
Сила трения определяется выражением
Тогда,
Следовательно, время, в течение которого тело будет двигаться по наклонной плоскости:
Подставим числовые значения:
Ответ: 2 секунды.
Задача №2. Применение второго закона Ньютона
Условие
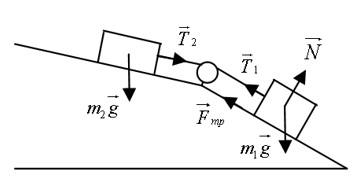
В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30, а верхний брусок – вдоль наклонной плоскости, составляющий с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и наклонной плоскостью равен µ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси, найдите, при каких значениях угла β нить будет растянута.
Решение
Так как тангенс угла α больше, чем коэффициент трения между бруском и поверхностью, нижний брусок будет скользить по наклонной плоскости даже при ненатянутой нити. Следовательно, в том случае, когда оба бруска движутся и нить натянута, модули ускорений брусков будут одинаковыми. Обозначим массу нижнего бруска как m1, массу верхнего бруска как m2, а силу натяжения соединяющей их нити как T. Тогда для каждого из брусков можно записать второй закон Ньютона в проекции на направление его движения:
где Fтр – действующая на нижний брусок сила трения скольжения, N – действующая на него сила нормальной реакции опоры.
Так как нижний брусок не движется в направлении, перпендикулярном плоскости, то из второго закона Ньютона следует:
Решая совместно полученные уравнения, найдем:
Для того, чтобы нить была натянута, должно выполняться неравенство:
С учетом полученного выражения для модуля ускорения a, это неравенство можно переписать в следующем виде:
Подставим числовые значения и найдем искомый угол:
Ответ: 19°.
Задача №3. Нахождение силы
Условие
Два одинаковых груза массой M = 100 г каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой m = 20 г, после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь.
Решение
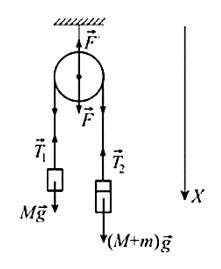
На основании второго закона Ньютона уравнение движение для обоих грузов с учетом перегрузки на одном из них в проекции на вертикальную ось, направленную вниз, выглядит следующим образом:
где a1 и a2 – проекции ускорений грузов M и (M+m) на вертикальную ось;
T1 и T2 – проекции сил натяжения нити на вертикальную ось. Так как нить не растяжима (по условию задачи), то
Из-за невесомости блока и нити и отсутствия трения, справедливо равенство:
В силу третьего закона Ньютона:
где F с индексом штрих – сила, действующая на блок со стороны его оси. Из первых двух уравнений получим:
Подставим числовые значения:
Ответ: 2,14 Ньютона.
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задачи по динамике вращательного движения с решениями
Задача №4. Нахождение числа оборотов маховика
Условие
Маховик радиусом R=0,5 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно Т=98 Н. Какое число оборотов в секунду будет делать маховик через Δt=10 с после начала движения. Маховик считать однородным диском.
Решение
Основное уравнение динамики вращательного движения:
где J — момент инерции маховика. Принимая маховик за однородный диск, можно записать:
Момент силы натяжения ремня:
Угловое ускорение маховика:
Угловая скорость маховика:
Решая уравнения, записанные выше, получим ответ:
Ответ: 62,4 оборота в секунду
Задача №5. Нахождение углового ускорения
Условие
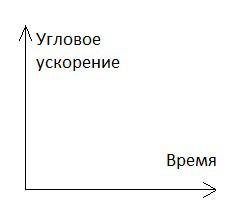
Момент силы, приложенный к вращающемуся телу изменяется по закону M=M0-αt. Момент остаётся постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке. Найти выражение для углового ускорения.
Решение
Согласно основному закону динамики вращательного движения:
Это уравнение прямой с отрицательным углом наклона, что соответствует рисунку.
Нужна помощь в решении задач по динамике, теоретической механике, деталям машин, химии, etc? Обращайтесь за ней в профессиональный студенческий сервис.
Содержание:
- Динамика материальной точки
- Прямая задача динамики точки
- Основные законы динамики
- Уравнения движения материальной точки в декартовых и естественных системах отсчета
- Две основные задачи динамики материальной точки
- Порядок решения прямой задачи динамики невольной материальной точки
- Примеры решения задач на тему: Динамика материальной точки
- Решение задач на тему: Движение материальной точки по криволинейной траектории
Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Динамика материальной точки
Динамикой называется раздел теоретической механики, в котором изучается механическое движение материальных объектов в зависимости от физических факторов, то есть от причин, вызывающих это движение.
Напомним, что в классической механике движение материальных объектов рассматривается с помощью абстрактных моделей: материальной точки, механической системы и абсолютно твердого тела.
Материальная точка — это материальное тело, размерами и разницей в движении его частей которого можно пренебречь.
Механической системой (системой материальных точек) называется совокупность материальных точек, которые между собой взаимодействуют, то есть, положение и движение которых взаимосвязаны.
Абсолютно твердым телом называется совокупность материальных точек, расстояния между которыми во время движения не меняются.
Движение механической системы определяется движением всех его точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.
В динамике точки рассматриваются две основные задачи:
— движение точки задается, а необходимо найти силы, которые это движение реализуют (первая, или прямая задача);
— силы задаются, а необходимо определить закон движения, который является результатом действия этих сил.
Для решения этих задач используются базовые сведения из статики и кинематики, а также законы динамики, то есть, общие законы движения тел и механических систем под действием приложенных к ним сил. Эти законы впервые в наиболее полном виде сформулированы Исааком Ньютоном в конце XVII века.
Прямая задача динамики точки
Первая (прямая) задача динамики содержит условие: По заданному движению, совершаемому точкой данной массы, требуется найти неизвестную действующую силу.
Основные законы динамики
В динамике изучается движение материальных систем в связи с действующими на них силами. Самым простым объектом механики является материальная точка.
Материальная точка — тело, размерами которого при решении данной задачи можно пренебречь.
Если на положение материальной точки и на ее движение не наложены никакие ограничения, точка называется свободной, в противном случае имеем дело с движением несвободной точки.
Движение механической системы определяется движением всех ее материальных точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.
В основе динамики лежат три закона И. Ньютона, которые впервые в наиболее полном и законченном виде были сформулированы в книге «Математические начала натуральной философии» (1686 г.).
1. Первый закон (закон инерции):
изолированная от внешних действий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит этого состояния.
2. Второй закон (основной закон динамики):
cила, которая действует на материальную точку, равна произведению массы точки на ее ускорение, а направление силы совпадает с направлением ускорения:
Если на точку действует несколько сил, то их можно заменить равнодействующей:
Если точка движется по какой-то поверхности, то на нее, кроме активных сил действует и реакция связи 
Таким образом в общем случае в уравнении (1.1):
3. Третий закон (закон равенства действия и противодействия):
Силы взаимодействия двух материальных точек равны между собой по модулю и направлены вдоль одной прямой, которая соединяет эти точки, в противоположные стороны.
Уравнения движения материальной точки в декартовых и естественных системах отсчета
Вместо уравнения движения (1.1) в векторной форме можно получить уравнение в скалярной форме, если спроектировать (1.1) на оси декартовой или естественной систем координат.
Уравнение движения в декартовых координатах:
Здесь 



Две основные задачи динамики материальной точки
Первая задача (прямая): зная массу точки 
определить равнодействующую приложенных к точке сил.
Сначала нужно определить проекции ускорения точки на оси координат:
Используя уравнение движения точки в декартовых координатах (1.3), определяем значения проекций равнодействующей приложенных к точке сил, а также ее модуль:
Направление вектора силы относительно осей координат определяется с помощью направляющих косинусов:
Вторая задача (обратная): зная силы, которые действуют на материальную точку, ее массу, а также первоначальные условия (положение точки и ее скорость в некоторые моменты времени, не обязательно в начальный), получить уравнение движения точки.
Порядок решения прямой задачи динамики невольной материальной точки
1. Изобразить на рисунке материальную точку в промежуточном положении.
2. Показать активные силы и реакции связей, которые на нее действуют.
3. Выбрать систему отсчета.
4. Записать векторное уравнение движения точки в форме второго закона динамики (1.1).
5. Спроектировать векторное уравнение движения точки на выделенные оси координат.
6. Из полученных уравнений определить необходимые величины.
Примеры решения задач на тему: Динамика материальной точки
Задача № 1
В шахту начинает опускаться равноускорено лифт, масса которого 
Определить натяжение 
Решение. Изобразим кабину лифта в произвольном положении (рис.1.1). На лифт действует сила тяжести 

Движение происходит по вертикали, поэтому направим ось 
Запишем уравнение движения кабины лифта в форме второго закона Ньютона:
где 
С учетом сил, действующих на кабину лифта, уравнение будет иметь вид:
Спроектируем это уравнение на ось 
С учетом того, что 
Мы получили зависимость натяжения каната от ускорения, с которым движется кабина лифта.
Проанализируем эту зависимость. Может быть три случая:
В первом случае
То есть, если кабина лифта движется без ускорения в любом направлении, натяжение троса будет равняться силе тяжести кабины лифта.
Во втором случае натяжение троса меньше силы тяжести кабины лифта, потому что 

В третьем случае натяжение троса всегда больше силы тяжести кабины лифта, потому что 
Например, когда 
В нашей задаче ускорение определится с выражения для пути при равнопеременном движении с учетом того, что начальная скорость 
Тогда:
Ответ: натяжение троса
Задача № 2
К телу весом 
Определить, с каким ускорением 
Решение: Изобразим тело с привязанной к нему нитью (рис.1.2). Покажем силы, которые действуют на тело: сила тяжести 


Запишем уравнение движения тела в векторной форме:
Спроектируем это уравнение на ось 
Откуда:
Если учесть числовые данные, то
Ответ:
Задача № 3
Пуля весом 



Определить силу сопротивления среды 
Решение. Изобразим шар в произвольном положении на траектории и покажем силы, которые на него действуют (рис.1.3):


Движение шара происходит вдоль вертикали, поэтому направим ось 

Запишем уравнение движения шара в векторной форме:
и спроектируем его на ось 
откуда
Таким образом, чтобы определить силу сопротивления 

Поскольку закон изменения координаты 
Находим первую и вторую производные от закона движения пули:
Таким образом,
Из выражения 

то есть
Ответ:
Задача № 4
Движение тела массой 
где 


Определить силу 
Решение. Проекции на оси координат силы 
где 

В данном случае
Итак
Модуль силы 
Сила 


Ответ:
Задача № 5
Прямолинейное движение ножа 



Определить силу 

Объяснение: Для привода ножа резального аппарата жатки используются плоские и пространственные механизмы. Среди плоских механизмов нашли применение кривошипно-шатунные, которые состоят из кривошипа 1, шатуна 2 и ножа жатки 3. Механизм преобразует вращательное движение кривошипа 1 в обратно поступательное движение ножа 3.
В уборочных машинах ось кривошипного пальца 

Решение. Изобразим нож резного аппарата в среднем положении на перемещении 
На нож 




Запишем уравнение движения ножа в векторной форме:
Проектируем это уравнение на направление движения ножа (ось 

Из последнего уравнения следует, что для определения силы 

Поскольку задан закон движения ножа 


Итак,
Учтем, что 
Ответ:
Задача № 6
Нагруженная вагонетка массой 


Определить натяжение каната при равномерном опускании и при торможении вагонетки, если время торможения 

Решение. Изобразим вагонетку в произвольном положении. Покажем силы, которые действуют на нее: силу тяжести 



Выбираем декартовую систему координат: ось 

Проектируем векторное уравнение движения на оси координат:
Поскольку 

Тогда общая сила сопротивления движению составляет:
Для определения натяжения 
При равномерном опусканье 

При равнозамедленном торможении
где 

Таким образом
Тогда
Ответ:
Из полученных результатов следует, что при торможении нагрузка на канат увеличивается по сравнению с нагрузкой при равномерном движении.
Задача № 7
Вагон весом 

Определить силу торможения вагона 

Решение. Изображаем вагон в виде материальной точки в произвольном положении на наклонной плоскости и показываем силы, которые на него действуют (рис.1.7): 


Выбираем декартовую систему координат, причем ось 

Запишем уравнение движения вагона в векторной форме:
и спроектируем его на оси выбранной системы координат:
По уравнению (2) определим силу торможения вагона:
По условиям задачи вагон движется с ускорением 


Если подставим в уравнение (3) 
Определим значение угла 
то
где 
Откуда получим
Из этого уравнения вытекает, что при изменении угла 


Поскольку известно, что коэффициент трения равен тангенсу угла трения 
Таким образом, при углу наклона рельсов к горизонту, что равен углу трения 
Ответ:
Задачи, которые рекомендуются для самостоятельной работы: 26.2, 26.8, 26.10, 26.20, 26.24 [2].
Решение задач на тему: Движение материальной точки по криволинейной траектории
При решении задач, связанных с движением точки по криволинейной траектории, если траектория известна, удобно рассматривать движение точки в естественной системе координат 
где 

В уравнениях (1.6) и (1.8) 



Порядок решения прямой задачи динамики точки в случае использования уравнений (1.6) и (1.8) совпадает с рекомендациями пунктов 1 и 6 занятия № 1.
Если задано уравнение движения материальной точки по траектории в виде 



Далее, с уравнений (1.6), (1.7) находим значения касательной и нормальной проекции силы 
Модуль приложенной к материальной точке силы, при естественном способе обозначения движения, будет равен
Задача № 1
Материальная точка массой 

Определить модуль 
Решение. В задаче движение материальной точки задано естественным способом, поэтому для определения равнодействующей сил воспользуемся зависимостями (1.6) и (1.7):
Определим касательное и нормальное ускорение материальной точки:
Поскольку 

Находим нормальную составляющую равнодействующей сил:
Модуль равнодействующей определим из выражения (1.11):
Таким образом, заданное движение материальной точки происходит под действием силы, постоянной по модулю и направленной вдоль радиуса к центру окружности.
Ответ:
Задача № 2
Материальная точка массой 

Определить проекцию 
Решение. Для определения проекции 
Сначала найдем значение скорости материальной точки:
При
Определяем величину касательного ускорения
при
Подставив в уравнение (1) значения 

Ответ:
Задача № 3
Материальная точка массой 

Определить модуль 
Решение. Поскольку движение материальной точки задано естественным способом, то модуль равнодействующей сил, приложенных к точке, определяется по зависимостям (1.10) и (1.11):
Величины касательного и нормального ускорения материальной точки определяются по уравнениям (1.9):
Учитывая, что скорость точки
то касательное ускорение точки равно:
Поскольку в момент времени 
то нормальное ускорение точки составит:
Определяем 

Тогда модуль равнодействующей сил, действующих на материальную точку, равен:
Ответ:
Задача № 4
На криволинейных участках железнодорожного пути наружный рельс поднимают выше над внутренним (рис.1.9). При движении поезда на этом участке его скорость 
Определить величину 


Решение. На вагон действуют: сила тяжести 


Запишем уравнение движения вагона в векторной форме:
где 
Поскольку движение происходит по криволинейной траектории, то выбираем естественную систему координат: ось 


Проектируем уравнение движения (1) на ось 

Из рис. 1.8 видно, что
Итак,
Подставив числовые значения известных величин, получаем:
Ответ:
Задача № 5
Груз 




Определить величину скорости груза 

Решение. Изобразим груз 



Для решения задачи выбираем естественную систему координат: ось 


Запишем уравнение движения груза в векторной форме:
Проектируем это векторное уравнение на оси координат:
Модуль силы натяжения нити 

Из второго из уравнений (1) найдем 
Тогда
Откуда
Ответ:
Задача № 6
Материальная точка весом 




Определить модуль силы 
Решение. Изобразим точку 



С точкой 


Запишем уравнение движения точки в виде второго закона Ньютона:
Спроектируем это векторное уравнение на оси выбранной системы координат:
Поскольку закон движения известен, то:
По условиям 
Тогда:
Учитывая, что масса точки равна 
Определяем модуль искомой силы:
Ответ:
Задача № 7
Радиус закругления моста в точке 

Определить, с какой силой автомобиль давит на мост в точке 

Решение. Рассмотрим автомобиль как материальную точку, поскольку его размерами по сравнению с размерами моста можно пренебречь. Изобразим автомобиль в точке 


Поскольку автомобиль движется по криволинейной траектории, то для решения задачи воспользуемся естественной системой координат 
Запишем уравнение движения автомобиля в векторной форме:
и спроектируем его на оси выбранной системы координат:



Из уравнения (2) определяем реакцию моста 
Сила давления 
Поскольку вес автомобиля 
то, если мост выпуклый, сила давления автомобиля на него уменьшается по сравнению с тем случаем, когда автомобиль движется по горизонтальному мосту.
Зададим дополнительный вопрос: с какой скоростью 

Поскольку 

Отсюда
Ответ:
Задача № 8
Камень весом 

Определить наименьшее значение угловой скорости вращения, при которой нить разорвется, если ее сопротивление разрыву составляет
Решение. Представим камень 



На камень (точку 


С точкой 


Спроектируем это уравнение на оси выбранной системы координат:
Заметим, что 

Отсюда
Из уравнения (3) вытекает, что при 






Ответ:
Задача № 9
Трек для испытания автомобилей на кривых отрезках пути имеет виражи, профиль которых (рис.1.14) в поперечном пересечении является прямой, которая наклонена к горизонту так, что внешний край трека выше внутреннего.
Определить, с какой наименьшей и самой большой скоростью можно ехать по виражу, имеющему радиус кривизны 


Решение. На автомобиль, который движется по виражу, действуют: сила тяжести 


Рассмотрим движение центра тяжести автомобиля (точка 






Запишем уравнение движения автомобиля в векторной форме:
и спроектируем это уравнение на оси координат 

Из уравнения (1) найдем величину нормальной реакции 
Подставим найденное значение 
При максимальной скорости автомобиля 

Векторное уравнение движения автомобиля в этом случае будет иметь вид:
Проектируем уравнение (4) на оси 
Уравнение (5) перепишем в виде:
откуда
Подставим значение 

Отсюда:
Если скорость автомобиля минимальная 

Из уравнений (8) и (9) получаем:
Ответ:
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Инертность, масса, ускорение
m1, m2 — массы взаимодействующих тел
a1, a2 — ускорение
Сила, масса, ускорение
F — сила
m — масса
a — ускорение
Сила тяжести
N — сила тяжести
m — масса
g — ускорение свободного падения
Сила трения
F_тр — сила трения
μ — коэффициент трения
N — сила тяжести
Сила трения
F_тр — сила трения
μ — коэффициент трения
m — масса
g — ускорение свободного падения
Закон всемирного тяготения
F — сила
G — гравитационная постоянная
m1, m2 — массы взаимодействующих тел
r — расстояние
Центростремительное ускорение спутника
a — ускорение
v — скорость
R — радиус земли
h — высота
Скорость спутника
v — скорость
G — гравитационная постоянная
M — масса Земли
R — радиус земли
h — высота
Первая космическая скорость (движение по круговой орбите)
v — скорость
g — ускорение свободного падения
R — радиус земли
Вторая космическая скорость (преодоление гравитации)
v — скорость
g — ускорение свободного падения
R — радиус земли
Третий закон Кеплера
T1, T2 — периоды обращения двух планет вокруг Солнца
a1, a2 — длины больших полуосей их орбит
Ускорение свободного падения на поверхности земли
g — ускорение свободного падения
G — гравитационная постоянная
M — масса Земли
R — радиус земли
Вес тела
P — вес
m — масса
g — ускорение свободного падения
Вес тела: невесомость
Вес тела, когда ускорение тела совпадает по направлению с ускорением свободного падения
P — вес
m — масса
g — ускорение свободного падения
a — ускорение
Вес тела: перегрузка
Вес тела, когда ускорение тела противоположно направлению ускорения свободного падения
P — вес
m — масса
g — ускорение свободного падения
a — ускорение
Время торможения
t — время
m — масса
v — скорость
F_тр — сила трения
Время торможения
t — время
v — скорость
μ — коэффициент трения
g — ускорение свободного падения
Путь торможения
s — путь
m — масса
v — скорость
F_тр — сила трения
Путь торможения
s — путь
v — скорость
μ — коэффициент трения
g — ускорение свободного падения
Сила трения качения
F_тр — сила трения качения
μ — коэффициент трения качения
N — сила тяжести
R — радиус
Сила упругости
F_упруг — сила упругости
k — жёсткость
x — удлинение (сокращение) предмета
Кинетическая энергия вращающегося тела
W_k — кинетическая энергия
J — момент инерции
ω — угловая скорость
Динамика в физике, теория и онлайн калькуляторы
Динамика
Определение
Динамикой называют раздел механики, рассматривающий причины механического движения.
Иначе говоря, динамика — это часть механики, которая изучает движение тела, связывая характер перемещения тела с действующими на него силами.
Сила рассматривается как мера взаимодействия тела с окружающими его объектами природы (другими телами, полями).
Законы классической динамики были сформулированы И. Ньютоном и имеют его имя. Основные законы динамики являются обобщением экспериментальных данных. Эти законы следует рассматривать в совокупности, как взаимосвязанные. Экспериментальной проверке стоит подвергать не каждый закон отдельно, а всю систему законов динамики целиком.
Основная задача динамики
Многие задачи науки и техники формулируют следующим образом: имеется тело, известны силы, действующие на тело, следует сформулировать закон движения тела, то есть записать координаты рассматриваемого тела как функции времени.
И так, кратко основную задачу динамики определим так: найти закон движения материальной точки (тела), при известных силах, действующих на нее.
Для решения такой задачи при помощи основного закона динамики (второго закона Ньютона) определяют ускорение движения точки. Затем при помощи кинематических уравнений находят функции скорости и координат зависящих от времени. Такие функции позволяют предсказывать поведение частицы в любой момент времени.
Решение этой задачи в общем виде может быть проблематично. Частное решение любой задачи в классической динамике можно получить при помощи численных методов приближенно, но заданной степенью точности. Точное решение задачи часто удается получить только в самом простом случае, когда проводится расчет движения тела под воздействием постоянной силы. Численные методы применимы для решения любых задач, но они требуют проведения большого числа арифметических операций.
Выделяют и такую задачу динамики, как определение равнодействующей сил, приложенных к телу (материальной точке) при известном характере его движения.
Для определения закона движения материальной точки необходимы:
- Сила, которая действует на материальную точку. Ее можно задать как функцию времени или координат.
- Начальные условия: координаты и скорость точки в некоторый момент времени. Вместо начальной скорости иногда используют начальный импульс.
Основные законы классической динамики
Законы Ньютона составили основу динамики, и по сей день играют в ней исключительную роль.
- Первый закон Ньютона: Если тело не взаимодействует с другими телами или действие других тел скомпенсировано, то скорость тела не изменяется ни по модулю, ни по направлению. Тело перемещается равномерно и прямолинейно.
- Второй закон Ньютона: если тело движется с ускорением, по отношению к инерциальной системе отсчета, то на него действует сила. Сила, вызывает ускорение, величина которого пропорциональна модулю этой силы. Направление ускорения совпадает с направлением, действующей силы.
[overline{F}=moverline{a}left(1right).]
Выражение (1)- это второй закон Ньютона в классической динамике.
Этот закон можно записать в иной форме:
[overline{F}=frac{dleft(moverline{v}right)}{dt}=frac{dleft(overline{p}right)}{dt}left(2right),]
где $overline{p}=moverline{v}$ — импульс тела. Тогда второй закон Ньютона формулируют так: сила равна производной от импульса по времени — это наиболее общая формулировка основного закона динамики.
- Третий закон Ньютона: Силы взаимодействия тел равны по величине, направлены вдоль одной прямой и имеют противоположные направления.
То есть, если тело 1 действует на тело 2 с силой ${overline{F}}_{12}$, то в этот же момент тело 2 действует на тело 1 с силой ${overline{F}}_{21}$, при этом:
[{overline{F}}_{12}=-{overline{F}}_{21}left(3right).]
Релятивистское уравнение движения
Как известно, динамика Ньютона носит ограниченный характер. Ее законы применяют, рассматривая движение макроскопических тел со скоростями много меньшими скорости света. При больших скоростях используют законы и уравнения релятивистской динамики, которая основывается на теории относительности.
Релятивистское уравнение движения материальной точки, являющееся обобщением уравнения движения Ньютона, записывают в виде:
[overline{F}=frac{d}{dt}left(frac{m_0overline{v}}{sqrt{1-frac{v^2}{c^2}}}right)left(4right),]
где $m_0$ — масса покоя частицы; $v$ — скорость движения частицы; $c$ — скорость света в вакууме. Уравнение (4) часто записывают в виде:
[overline{F}=frac{dleft(moverline{v}right)}{dt}=frac{dleft(overline{p}right)}{dt},]
где импульс называют релятивистским импульсом; $m$ — релятивистская масса, равная:
[m=frac{m_0}{sqrt{1-frac{v^2}{c^2}}}left(5right).]
Следует иметь в виду, что сила и ускорение точки в релятивистском случае совпадают. Сила совпадает по направлению с изменением импульса.
Примеры задач с решением
Пример 1
Задание. Железнодорожный вагон нагружен песком. Начальная масса вагона с грузом составляет $m_n$ кг. Вагон движется прямолинейно из состояния покоя под действием силы тяги равной $overline{F}$. Эта сила направлена горизонтально и она постоянна (рис.1). В дне вагона имеется отверстие, через него высыпается песок с постоянной скоростью $sigma frac{кг}{с}$. Запишите функцию скорости в зависимости от времени ($v(t)$). Силой трения пренебречь.
Решение. Запишем второй закон Ньютона для сил, действующих на вагон:
[moverline{g}+overline{N}+overline{F}=moverline{a}left(1.1right).]
Запишем проекцию уравнения (1.1) на ось X:
[F=ma left(1.2right),]
где $m=m_n-sigma t$. Выразим ускорение из (1.2):
[a=frac{F}{m_n-sigma t}left(1.3right).]
Учитывая кинематическое уравнение вида:
[a=frac{dv}{dt}left(1.4right)]
скорость найдем как:
[vleft(tright)=int{aleft(tright)dt=int{frac{F}{m_n-sigma t}dt=frac{F}{sigma }}}{ln left(frac{m_n}{m_n-sigma t}right) }+Cleft(1.5right).]
Из начального условия ($vleft(0right)=0$) найдем постоянную интегрирования $C$:
[vleft(0right)=frac{F}{sigma }{ln left(frac{m_n}{m_n-sigma cdot 0}right) }+C=0to C=0.]
Получаем:
[vleft(tright)=frac{F}{sigma }{ln left(frac{m_n}{m_n-sigma t}right) }.]
Ответ. $vleft(tright)=frac{F}{sigma }{ln left(frac{m_n}{m_n-sigma t}right) }$
Пример 2
Задание. Закон движения тела в плоскости задан уравнениями:
[left{ begin{array}{c}
x=A{sin omega t; } \
y=B{cos omega t. } end{array}
right.]
где $A$, $B$, $omega $ — постоянные величины. Каков модуль силы, действующий на тело?
Решение. Основой для решения задачи служит второй закон Ньютона:
[overline{F}=moverline{a}left(2.1right).]
Используем для решения также кинематические уравнения для ускорения:
[a_x=frac{d^2x}{dt^2} и a_y=frac{d^2y}{dt^2}left(2.2right).]
Подставляя уравнения движения точки из условий задачи в (2.2), получим проекции ускорения:
[a_x=frac{d}{dt}left(frac{d}{dt}left(A{sin omega t }right)right)=frac{d}{dt}left(Aomega {cos omega t }right)=-A{omega }^2{sin omega t };]
[a_y=frac{d}{dt}left(frac{d}{dt}left(B{cos omega t }right)right)=frac{d}{dt}left(-B{sin omega t }right)=-B{omega }^2{cos omega t. }]
Модуль ускорения найдем как:
[a=sqrt{a^2_x+a^2_y}=sqrt{{(A{omega }^2{sin omega t })}^2+{(B{omega }^2{cos omega t })}^2}={omega }^2sqrt{x^2+y^2}left(2.3right).]
Из (2.1) и (2.3) получим модуль силы:
[F=m{omega }^2sqrt{x^2+y^2}.]
Ответ. $F=m{omega }^2sqrt{x^2+y^2}$
Читать дальше: закон сохранения импульса.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!